Selection of Positive Position Feedback Controllers for Damping and Precision Positioning Applications

Abstract

Positive Position Feedback (PPF) is a widely used control technique for damping the lightly damped resonant modes of various dynamic systems. Though PPF controller is easy to implement any rigorous mathematical optimization is not possible due to the controller structure. Therefore, almost all PPF designs reported in literature use a trial-and-error approach to push the closed-loop system poles adequately into the left-half plane to achieve adequate damping. In this paper, a full parametric study of the PPF controller based on the closed-loop DC gain vs achievable damping relationship is carried out. It is shown that the PPF controller best suited to only damp the resonance is not the best if both damping and tracking control is required (as is the case in most precision positioning systems). This leads to a more systematic and goal-oriented selection of appropriate PPF controller for specific applications, hitherto unreported in literature. Experiments performed on a piezoelectric-stack actuated nanopositioning platform are presented to support this conclusion.

1 Introduction

The PPF control design was first introduced in [1] for the vibration control of the space structures. In [2] it shows that PPF is capable of controlling several vibration modes. In [3] the Modal PPF (MPPF) controller is used to control the independent modal space of an undamped flexible structure. [4] demonstrated optimal control methods to design PPF controllers. Adaptive PPF (APPF) is suggested for the vibration control of frequency-varying structures (multi-modal control) in [5]. Further authors of [6] presented that PPF controller has global stability and which is verified with the help of negative imaginary theory. It has since been successfully implemented in nanopositioning stages to damp the dominant resonant mode of nanopositioner in conjunction with integral tracking controller with suitable gain [7,8,9]. It is known that the tracking controller changes the location of damped poles [8] and hence the characterized PPF controller for damping tracking application is essential.

PPF controller is popular and show adequate robustness under parameter uncertainties, its design is based on pole-placement via trial-and-error. As such, a systematic design strategy of the controller design against certain application-specific indices has remained elusive. Consequently, the selection of the closed-loop pole-location that delivers best damping performance has proved difficult. It is also noticed in several cases that increased damping comes at the cost of increased closed-loop DC sensitivity. In positioning applications such as nanopositioning, increased DC sensitivity is undesirable, but inherently unavoidable if positive-feedback damping controllers are incorporated [7].

In this work, the PPF controller is parametrically analyzed for closed-loop damping versus closed-loop DC gain. A method for selecting PPF controllers for best positioning performance is presented. It is shown that for a given open loop system, infinitely many PPF controllers can be designed. Yet, there is only one controller that delivers maximum closed-loop damping ($\zeta _{max}$). For any other closed-loop damping value ($\zeta _{cl}$), two controllers with different DC gains exist. Simulation and experimental analysis shows that choosing the PPF controller with a DC gain higher of the two possible controllers for the same closed-loop damping ($\zeta _{cl}$), results in best overall positioning performance.

Fig. 1.

Typical closed-loop combined damping and tracking control implementation. r(t) is the reference input, y(t) is the output.

1.1 Organization

The paper is organized as follows. In Sect. 2, background theory for second-order resonant systems is presented. In Sect. 3, the full parametric analysis of the PPF damping controller is presented along with the parametric relationships between the achievable closed-loop damping vs DC gain. In Sects. 4 and 5, an experimental setup, method of identification of the experimental platform is explained, further closed-loop combined damping and tracking experimental results for each of the controller implementations are presented and discussed. Section 6 concludes the paper.

2 Background Theory

Structural dynamics of flexible structures are very intricate to model with accuracy and high precision because of boundary conditions. Hence, there will always be uncertainty and unmodeled dynamics present in the models of flexible structures [6]. Such flexible structures are best described using a number of methods viz: partial differential equations, ordinary differential equations, Finite Element Method (FEM) or with hybrid models and hence they are infinite dimensional systems [10].

The best suited mathematical model for analyzing the vibration suppression problem in practical applications is the Finite Element Method (FEM) model which is of the form:

$$\begin{aligned} M\ddot{d} + C\dot{d} + K d = Bu, \end{aligned}$$

(1)

where d is the vector of generalized displacements, M is the symmetric positive definite mass matrix, C is the symmetric positive semi-definite damping matrix, K is the symmetric positive (semi-)definite matrix, u is the vector of control variables, B is the input matrix, which transforms control variables of the generalized actuator forces.

For the purpose of control design, however, one typically tends to include only a small finite number of modes in the modeling of such systems, which results in spillover unmodeled dynamics. Most techniques focus on damping the first resonant mode of the system as it tends to dominate the overall system dynamics at low frequencies and subsequently, controller designs are based on a plant model consisting of a second-order transfer-function modeling the first dominant resonant mode.

The single axis of a nanopositioning platform can be modeled as a mass-spring-damper system, having equation of motion:

$$\begin{aligned} M_p \ddot{d}+ c_f \dot{d}+ k d = F_a, \end{aligned}$$

(2)

where $M_p$ is the mass of the platform, $c_f$ is the damping coefficient of the flexures, k is the sum of the spring stiffness of the flexures, $k_f$, and the actuator, $k_a$, and $F_a$ is the force applied by the actuator.

Taking the Laplace transform of (2), and after rearrangement, the transfer function measured from the applied force, $F_a$, to the displacement, d, is

$$\begin{aligned} G_{dF_a}(s) = \frac{d(s)}{F_a(s)}= & {} \frac{{\gamma }^{2}}{s^2+2\zeta _{p}\omega _{p} s+{\omega }_{p}^{2}}, \end{aligned}$$

(3)

where $\zeta _{p}$ is the damping ratio for the first mode and $\omega _{p}$ is the resonant frequency.

The force generated by the actuator can be related to the unconstrained piezoelectric expansion, $\delta$, by

$$\begin{aligned} F_a(s) = K_a(s) \delta , \end{aligned}$$

(4)

and $\delta$ can be related to the reference input voltage, r(s), by

$$\begin{aligned} \delta = g_{\delta _r}r(s)= & {} d_{33}n g_a r(s), \end{aligned}$$

(5)

where $g_{\delta _r}$ is a constant gain which is the product of the piezoelectric strain constant, $d_{33}$, the number of actuator layers, n, and the amplifier gain, $g_a$. Likewise, the displacement, d, can be related to the measured voltage, y(s), by

$$\begin{aligned} d= & {} g_sy(s). \end{aligned}$$

(6)

where $g_s$ is the sensor gain. The transfer function from the reference input, r, to the measured voltage, y, is then

$$\begin{aligned} G(s) = \frac{y(s)}{r(s)} = \frac{\frac{k_a g_{\delta _r}}{g_s}}{M_ps^2+c_fs+k}= & {} \frac{\frac{k_a g_{\delta _r}}{g_s M_p}}{s^2+\frac{c_f}{M_p}s+\frac{k}{M_p}}. \end{aligned}$$

(7)

substituting standard variables, becomes

$$\begin{aligned} G(s)= & {} \frac{{\gamma }^{2}}{s^2+2\zeta _{p}\omega _{p}s + {\omega }_{p}^{2}}. \end{aligned}$$

(8)

3 Positive Position Feedback Control Design

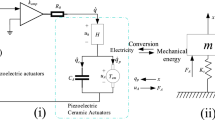
An important property of PPF controllers is that to suppress one dominant resonant mode it requires only one second-order term. PPF controllers are implemented in positive feedback as shown in Fig. 1 and their generic structure is given by:

$$\begin{aligned} C_{PPF}(s)= & {} \frac{\kappa }{s^2+2\zeta \omega s+\omega ^{2}} \end{aligned}$$

(9)

where $\zeta$ and $\omega$ are the damping ratio and natural frequency of the controller and $\kappa$ is a positive scalar gain. The underlying principle of the PPF control design is to push the closed-loop system poles further in to LHP (Left Hand Plane), thereby imparting additional damping.

3.1 Strategy and Design

Using the plant model given by (8) and the controller transfer-function given by (9), the overall transfer-function of the closed-loop damped system can be computed as follows:

$$\begin{aligned} G^{cl}_{damp}(s)= & {} \frac{G(s)}{1-G(s)C_{PPF}(s)} \end{aligned}$$

(10)

The characteristic polynomial of the closed-loop damped system is given by:

$$\begin{aligned} P(s)= & {} s^{4}+[2\zeta _{p}\omega _{p}+2\zeta \omega ]s^{3}\\ \nonumber+ & {} [\omega _{p}^{2}\!+\!2\zeta _{p}\omega _{p}(2\zeta \omega ) + \omega ^{2}]s^{2}\\ \nonumber+ & {} [2\zeta _{p}\omega _{p}\omega ^{2}+\omega _{p}^{2}2\zeta \omega ]s\\ \nonumber+ & {} \omega _{p}^{2}\omega ^{2}-\gamma ^{2}\kappa = 0 \nonumber \end{aligned}$$

(11)

Further (11) can be written as:

$$\begin{aligned} P(s) = s^{4}+K^{\prime }_{1}s^{3}+K^{\prime }_{2}s^{2}+K^{\prime }_{3}s+K^{\prime }_{4}=0 \end{aligned}$$

(12)

where the resulting coefficients $K^{\prime }_{i}$ are:

$$\begin{aligned} K^{\prime }_{1}= & {} {2\zeta _{p}\omega _{p}+2\zeta \omega }\\ \nonumber K^{\prime }_{2}= & {} {\omega }_{p}^{2}+2\zeta _{p}\omega _{p} {2\zeta \omega }+{\omega ^{2}}\\ \nonumber K^{\prime }_{3}= & {} {2\zeta _{p}\omega _{p} \omega ^{2}+2\zeta \omega \omega _{p}^{2}}\\ \nonumber K^{\prime }_{4}= & {} {\omega ^{2}{\omega }_{p}^{2}-\gamma ^{2}\kappa } \end{aligned}$$

(13)

In the following subsection, the ideal pole-placement technique is briefly revisited. Then, using the closed-loop damping and the closed-loop DC gain as the desired performance metrics, controller parameters $K^{\prime }_{i}$ are computed in an iterative fashion to identify best suited PPF controller designs for (i) Damping only and (ii) Precision Positioning (combined damping and tracking) applications.

3.2 Ideal Pole-Placement

Let the ideal pole-placement for the $4^{th}$-order closed-loop damped system whose characteristic equation is given by be given by (11) be given by:

$$\begin{aligned} P_{1}, P_{2} = \sigma _{c}\pm j\omega _{c} \quad \quad \quad P_{3}, P_{4} = \sigma _{c}\pm j\omega _{c} \end{aligned}$$

(14)

Then, the desired characteristic polynomial, $P_{d}(s)$, that has as its roots, the poles as given in (14) is:

$$\begin{aligned} \nonumber P_{d}(s)= & {} s^{4} - 4\sigma _{c}s^{3}+(6\sigma _{c}^{2}+2\omega _{c}^{2})s^{2}-4\sigma _{c}(\sigma _{c}^{2}+\omega _{c}^{2})s\\ {}+ & {} (\sigma _{c}^{2}+\omega _{c}^{2})^{2} = 0 \end{aligned}$$

(15)

The abbreviated form of this desired characteristic polynomial is:

$$\begin{aligned} P_{d}(s) = s^{4}+K^{\prime }_{d_{1}}s^{3}+K^{\prime }_{d_{2}}s^{2}+K^{\prime }_{d_{3}}s+K^{\prime }_{d_{4}}=0 \end{aligned}$$

(16)

where

$$\begin{aligned} K^{\prime }_{d_{1}}= & {} -4\sigma _{c}\\ \nonumber K^{\prime }_{d_{2}}= & {} (6\sigma _{c}^{2}+2\omega _{c}^{2})\\ \nonumber K^{\prime }_{d_{3}}= & {} -4\sigma _{c}(\sigma _{c}^{2}+\omega _{c}^{2}) \\ \nonumber K^{\prime }_{d_{4}}= & {} (\sigma _{c}^{2}+\omega _{c}^{2})^{2} \end{aligned}$$

(17)

In order to locate the closed-loop poles of the actual system (8) in the exact location as desired (14) the following equality must be satisfied:

$$\begin{aligned} P(s) \equiv P_{d}(s) \end{aligned}$$

(18)

Combining (13) and (17) to satisfy (18) results in the following equalities:

$$\begin{aligned} K^{\prime }_{1}= & {} -4\sigma _{c}\\ \nonumber= & {} {2\zeta _{p}\omega _{p}+2\zeta \omega }\\ \nonumber K^{\prime }_{2}= & {} (6\sigma _{c}^{2}+2\omega _{c}^{2})\\ \nonumber= & {} {\omega }_{p}^{2}+2\zeta _{p}\omega _{p} {2\zeta \omega }+{\omega ^{2}}\\ \nonumber K^{\prime }_{3}= & {} -4\sigma _{c}(\sigma _{c}^{2}+\omega _{c}^{2}) \\ \nonumber= & {} {2\zeta _{p}\omega _{p} \omega ^{2}+2\zeta \omega \omega _{p}^{2}}\\ \nonumber K^{\prime }_{4}= & {} (\sigma _{c}^{2}+\omega _{c}^{2})^{2} \\ \nonumber= & {} {\omega ^{2}{\omega }_{p}^{2}-\gamma ^{2}\kappa } \end{aligned}$$

(19)

By setting the controller parameters $\kappa =\varGamma _{1}$, $2\zeta \omega = \varGamma _{2}$ and $\omega ^{2} = \varGamma _{3}$, (19) can be restructured to result in (20). This set of equations will be utilized in identifying the best choice of parameters for the PPF controller design. In (19) there are more equations than unknowns and hence no exact solution exists in this.

$$\begin{aligned} \nonumber \varGamma _{2}= & {} (-2\zeta _{p}\omega _{p}+K^{\prime }_{1})\\ \nonumber 2\zeta _{p}\omega _{p}\varGamma _{2}+\varGamma _{3}= & {} (K^{\prime }_{2}-\omega _{p}^{2})\\ \nonumber \omega _{p}^{2}\varGamma _{2}+2\zeta _{p}\omega _{p}\varGamma _{3}= & {} K^{\prime }_{3}\\ -\gamma ^{2}\varGamma _{1}+\omega _{p}^{2}\varGamma _{3}= & {} K^{\prime }_{4} \end{aligned}$$

(20)

$$\begin{aligned} \left[ \begin{array}{cccc} 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 2\zeta _{p}\omega _{p} &{} 1 &{} 0\\ 0 &{} \omega _{p}^{2} &{} 2\zeta _{p}\omega _{p} &{} 0 \\ -\gamma ^{2} &{} 0 &{} \omega _{p}^{2} &{} 0 \\ \end{array} \right] \left[ \begin{array}{c} \varGamma _{1} \\ \varGamma _{2} \\ \varGamma _{3} \\ \varGamma _{4} \\ \end{array} \right] = \left[ \begin{array}{c} (K^{\prime }_{1}-2\zeta _{p}\omega _{p})\\ (K^{\prime }_{2}-\omega _{p}^{2})\\ K^{\prime }_{3} \\ K^{\prime }_{4} \\ \end{array} \right] \end{aligned}$$

(21)

3.3 Family of PPF Controllers for a Second-Order Resonant System

As the system of Eq. (21) is over-determined, ideal pole-placement cannot be achieved using the PPF control scheme. This is a well-known limitation of the technique. Therefore, controller parameters are identified via a least-squares approach by using the generalized inverse of the coefficient matrix. The details of this procedure are as follows: Let (21) be written as:

$$\begin{aligned} A \varGamma = K^{\prime }, \end{aligned}$$

(22)

where $A = \left[ \begin{array}{cccc} 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 2\zeta _{p}\omega _{p} &{} 1 &{} 0\\ 0 &{} \omega _{p}^{2} &{} 2\zeta _{p}\omega _{p} &{} 0\\ -\gamma ^{2} &{} 0 &{} \omega _{p}^{2} &{} 0\\ \end{array} \right]$, $\varGamma = \left[ \begin{array}{c} \varGamma _{1} \\ \varGamma _{2} \\ \varGamma _{3} \\ \varGamma _{4} \\ \end{array} \right]$ and $K^{\prime } = \left[ \begin{array}{c} (K^{\prime }_{1}-2\zeta _{p}\omega _{p})\\ (K^{\prime }_{2}-\omega _{p}^{2})\\ K^{\prime }_{3} \\ K^{\prime }_{4} \\ \end{array} \right]$.

Then,

$$\begin{aligned} \varGamma = A^{T}(AA^{T})^{-1}K^{\prime } \end{aligned}$$

(23)

Using the parameters computed in (23) will result in a new set of coefficients given by (24).

$$\begin{aligned} \left[ \begin{array}{c} K^{\prime \prime }_{1}\\ K^{\prime \prime }_{2}\\ K^{\prime \prime }_{3} \\ K^{\prime \prime }_{4} \\ \end{array} \right] = A\varGamma + \left[ \begin{array}{c} 2\zeta _{p}\omega _{p}\\ \omega _{p}^{2}\\ 0 \\ 0 \\ \end{array} \right] \end{aligned}$$

(24)

Therefore, the $P_{d}(s)$ as given in (12) will change to:

$$\begin{aligned} P^{\prime }_{d}(s) = s^{4} + K^{\prime \prime }_{1}s^{3}+K^{\prime \prime }_{2}s^{2}+K^{\prime \prime }_{3}s+K^{\prime \prime }_{4}=0 \end{aligned}$$

(25)

There are two combination of roots possible: (i) The desired polynomial has two pairs of complex conjugate roots (ii) The desired polynomial has one pair of complex conjugate roots and one pair of negative real roots. If the poles of the closed-loop system are $P_{1}, P_{2} = \sigma ^{\prime }_{c} \pm j\omega ^{\prime }_{c}$ and $P_{3}, P_{4} = \sigma ^{\prime }_{c} \pm j\omega ^{\prime }_{c}$. The closed-loop damping can be approximated by:

$$\begin{aligned} \zeta _{cl} \cong \cos \left( \tan ^{-1}\left( \frac{\omega ^{\prime }_{c}}{\sigma ^{\prime }_{c}}\right) \right) \end{aligned}$$

(26)

A parametric search is carried out over a wide range of $\sigma ^{\prime }_{c}$ and the closed-loop damping approximation given by (26) is monitored. Due to the over-determined nature of the system of equations, no control can be exerted over the closed-loop DC gain of the system. The trajectory followed by the PPF controllers in the closed-loop damping vs closed-loop DC gain space is plotted in Fig. 2.

Remarks: Once the second-order resonant system parameters are fixed, the plot of the closed-loop DC gain vs closed-loop damping ($\zeta _{cl}$) achieved using PPF control demonstrates the following:

• (i) Closed-loop DC gain is greater than the open-loop DC gain for any increase in damping.

• (ii) There exists only one unique controller that achieves maximum closed-loop damping $\zeta _{max}$.

• (iii) For any other value of achievable closed-loop damping ($\zeta _{cl}$), two distinct controllers exist. Each of the two controllers results in a different value for closed-loop DC gain.

Fig. 2.

Plot of the DC gain of the damped closed-loop vs the damping achieved using the PPF controller. Each point on the upward convex curve (green) and downward convex curve (red) represents a unique PPF controller. (Color figure online)

4 Experimental Setup and System Identification

In the following subsections, a brief description of the experimental setup is provided, followed by the details of the system identification carried out to model the dynamics of one axis of the piezoelectric-stack actuated nanopositioner within the bandwidth of interest.

4.1 Experimental Setup

Figure 3 shows the experimental setup used in this work. It consists of a two-axis piezoelectric-stack actuated serial kinematic nanopositioner designed at the EasyLab, University of Nevada, Reno, USA. It has an input range of ±100 V resulting in a displacement range of ±20 $\upmu$m. Two low-noise, linear voltage amplifiers (PDL200) from Piezodrive, each with an output range of 0–200 V, a variable bias capability of 0–200 V and a fixed voltage gain of 20 are used to supply voltage inputs to the piezoelectric-stack actuators. The displacement is measured by a Microsense 4810 capacitive displacement sensor and a 2805 measurement probe with a measurement range of ±50 $\upmu$m for a corresponding voltage output of ±10 V. A PCI-6621 data acquisition card from National Instruments installed on a PC running the real-time module from LabVIEW is used to interface between the experimental platform and the control design.

Fig. 3.

A two-axis serial kinematic nanopositioner designed at the EasyLab, University of Nevada, Reno, USA.

4.2 Identification of the Experimental Platform

To identify the linear model of the plant, small signal frequency response functions (FRFs) were utilized. The FRFs are determined by applying a sinusoidal chirp signal (from 10 to 2000 Hz) with an amplitude of 0.2 V as input to the voltage amplifier of the x-axis and measuring the output signal in the same axis. Subsequently, the FRFs are computed by taking the Fourier transform of the recorded data. It should be noted that, using small amplitudes, the nonlinear effects of the Piezo Electric Actuators (PEAs) such as hysteresis can be considered negligible. In Fig. 4 the magnitude and phase responses (FRF) of G(s) are plotted for a sampling time of 50 $\upmu$s. The x-axis of the platform is used to conduct the experiments presented in this work. However, the y-axis was set to 0 V as input to mimic a realistic platform operation. The platform axis shows a lightly-damped resonant mode at 716.2 Hz and open-loop damping coefficient of this resonant mode is $\zeta _{ol} = 0.011$. A second-order transfer-function that accurately captures the dominant resonant dynamics of this axis was procured using a least squares fit. The resulting transfer function is given by (27).

$$\begin{aligned} G(s) = \frac{1.024\times 10^7}{s^2 + 99s + 2.035\times 10^7}. \end{aligned}$$

(27)

The experimental system has a significant delay. Hence, the theoretical model of the platform had to be modified in order to include the effects of the delay. The resulting system model is given by the following transfer function:

$$\begin{aligned} G(s) = \frac{1.024\times 10^7 \times e^{-\tau s}}{s^2 + 99s + 2.035\times 10^7}. \end{aligned}$$

(28)

where the value of $\tau$ is determined by the following equation:

$$\begin{aligned} \tau = \frac{1}{2} T_s + 90\times 10^{-6}. \end{aligned}$$

(29)

where $T_s$ is the sampling time. Both the sampling time $T_s$ and the delay $\tau$ are expressed in seconds.

5 Experimental Results

5.1 Damping Only

PPF controller is designed using the procedure detailed in Sect. 3. The trajectory in Fig. 2 represents DC gain vs achievable damping using PPF controller. Each point on the convex curve represents a unique controller. It further shows that

• (i) There is only one unique controller that achieves maximum damping $\zeta _{max}$ = 0.218 and DC gain = −1.456 dB.

• (ii) For every other achievable closed-loop damping ratio, two distinct controllers with different DC gains are possible.

Minimal change in DC gain is usually desired in most damping applications. Thus for damping only application, It is advisable to choose the controller parameters resulting in low closed-loop DC gain (downward convex curve). Ideally, the PPF controller delivering the maximum closed-loop damping ($\zeta _{max}$) would be chosen. However, if DC sensitivity or other implementations exist, for damping only applications the controllers represented by points on the downward convex (red curve) would be preferred over the upward convex (green curve) region for the same closed-loop damping ratio.

5.2 Precision Positioning (combined Damping and Tracking)

In precision positioning applications, it is popular practice to impart maximum damping to the resonant mode via a suitable damping controller first (in the inner loop) and then implement a suitably gained tracking controller (in the outer loop) to deliver precise positioning [7]. Tracking is usually effected by utilizing an integrator ($C_{track}(s)= \frac{K_t}{s}$) in feedback with the damped system [11].

To check if PPF controllers in downward convex region or upward convex region of the closed-loop DC gain vs closed loop damping curve result in better positioning performance, two $\zeta _{cl}$ values were arbitrarily selected viz: $\zeta _{cl}$ = 0.15 and $\zeta _{cl}$ = 0.2. For achieving closed-loop damping of $\zeta _{cl}$ = 0.15, two distinct controllers at points denoted by $\zeta _{A1}$ and $\zeta _{B1}$ with different closed-loop DC gains can be designed. Similarly, for $\zeta _{cl}$ = 0.2, there exist two distinct controllers denoted by $\zeta _{A2}$ and $\zeta _{B2}$ with different closed-loop DC gains respectively. For a full comparative analysis, the PPF controller that delivers the maximum closed-loop damping ($\zeta _{cl}$) was also selected and the positioning performance of all five controllers was evaluated both via simulations and experiments. The overall block diagram for the combined damping and tracking scheme is shown in Fig. 1.

Both simulated and experimental results are in good agreement and show that for precision positioning performance (combined damping and tracking), controllers from the upward convex region deliver a superior positioning performance when compared with controllers from the downward convex region. The PPF controller transfer functions for the five selected cases, the respective closed-loop damping achieved and the corresponding closed-loop DC gains are given in Table 1.

Table 1. Damping performance of selected controllers

The suitable tracking gain for each damped system is determined via the root-locus method. The respective tracking gains, maximum and RMS positioning errors for the five controllers are tabulated in Table 2. The closed-loop frequency responses are shown in Fig. 4.

The overall combined closed-loop damping and tracking transfer function is given by

$$\begin{aligned} G^{cl}(s)= & {} \frac{C_{track}(s) G^{cl}_{damp}(s)}{1+C_{track}(s) G^{cl}_{damp}(s)} \end{aligned}$$

(30)

where $C_{track}=\frac{K_t}{s}$, $K_t$ is tracking gain and $G^{cl}_{damp}(s)$ is given by (10).

Table 2. Closed-loop positioning performance (combined damping and tracking

Fig. 4.

Frequency responses for the combined damping and tracking closed-loop systems.

Fig. 5.

Steady-state combined damping and tracking closed-loop time domain traces and respective position errors for a 4 $\upmu$m triangle wave at 50 Hz. Each trace is offset by 0.5 $\upmu$m for clarity.

A common input signal in nanopositioning is a triangle wave (used with a ramp or pseudo-ramp signal to generate a typical raster scanning pattern). For experimental validation, the nanopositioner axis was made to track a triangle wave at 50 Hz with an amplitude of 4 $\upmu$m. The recorded time domain output trajectories as well as position errors are plotted in Fig. 5.

6 Conclusion

In this paper, a systematic approach for selecting suitable PPF damping controllers for damping only as well as precise positioning applications is proposed and experimentally validated. Using the closed-loop DC gain vs closed-loop damping curve as a guideline, the following conclusions can be drawn.

• (i) Only one unique PPF controller delivers maximum closed-loop damping $\zeta _{max}$ = 0.218.

• (ii) For all other $\zeta _{cl}$ < $\zeta _{max}$, two possible PPF controllers can be designed. Both these controllers results in different DC gains.

• (iii) For damping only applications, the best choice is the PPF controller results in lower DC gain (of the 2 possible controllers) for the same $\zeta _{cl}$.

• (iv) For precision positioning application (combined damping and tracking) the best choice is the PPF controller which results in higher DC gain (of the 2 possible controllers) for the same $\zeta _{cl}$.