Keywords

1 Introduction

Recently, the increasing interests have been attracted to the complexity of networks due to the successful research results in some practical fields such as biological, physical sciences, social and engineering [1]. With the presentation of small-world and scale-free characters of complex networks [2, 3], amount of efforts have been devoted to investigating the dynamical behaviours of complex networks in several different domains, mainly involving synchronization, state estimation, fault diagnosis and topology identification.

With the emergence of the large scale networks, it is common that merely partial information of nodes is accessible in the network outputs [4, 5]. It is imperative to estimate the unknown states of nodes via an effective state estimator. Lots of research achievements have been obtained for state estimation of complex networks [6,7,8,9]. For instance, state estimation of complex neural network with time delays was discussed in [6]. Moreover, state estimation of complex networks concerning the transmission channel with noise was studied in [8]. Also, state estimation for complex networks with random occurring delays was investigated in [9].

In reality, transmission congestion probably lead to packet dropout in network linking, which has an influence on the performance of complex networks. There exists some research concerning Bernoulli packet dropout for complex networks [10,11,12].

The robust filtering for complex networks with Bernoulli packet dropout was studied in [10]. Similarly, the synchronization of complex networks with Bernoulli packet losses was investigated in [11]. In addition, state estimation for complex networks with stochastic packet dropout that described as a Bernoulli random variable was studied in [12].

In practical networked systems, especially in wireless communication networks, the random packet dropout is often regarded as a time-relevant Markov process. That is to say, the Markovian packet losses model would sufficiently utilize the temporal relevance of channel conditions in the process of transmission. As a result, some research achievements have been existed on Markovian packet dropout for the networked systems [13,14,15,16]. Minimum data rate stability in the mean square with Markovian packet losses was studied in [15]. Also, stabilization of uncertain systems with random packet losses which described as a Markov chain was investigated in [16]. However, the research considering Markovian packet losses for state estimation of complex dynamical networks is relatively scarce.

In the paper, we focus on the state estimation for discrete-time complex networks with Markovian packet losses, where the transition probability is known. The network is output coupled that could economize on the channel resource. An effective state estimator is established to ensure such the stability of the state error. By employing the Lyapunov stability approach plus stochastic analysis theory, we derive the criteria sufficiently in the form of LMIs.

The rest of this paper is arranged as follows. In Sect. 2, an output coupled complex network with Markovian packet losses and the corresponding state estimator are presented. In Sect. 3, a sufficient criteria is exploited in terms of LMIs and the desired estimator gain matrix is obtained. In Sect. 4, illustrative simulations are provided to testify the applicability of the results derived. In the end, conclusions are drawn in Sect. 5.

2 Problem Formulation

We consider the following discrete-time complex network consisting of \( N \) coupled nonlinear nodes:

$$ \left\{ \begin{array}{l} x_{i} (k + 1) = A_{i} x_{i} (k) + f(x_{i} (k)) + \sum\limits_{j = 1}^{N} {w_{ij} }\Gamma y_{j} (k)\\ {y_{i} (k) = C_{i} x_{i} (k)} \quad\;\; (i = 1,2,\ldots,N)\end{array} \right. $$
(1)

where \( x_{i} (k) = (x_{i1} (k),x_{i2} (k), \ldots ,x_{in} (k))^{T} \in R^{n} \) denote the state vector of the \( i^{th} \) node, \( y_{i} (k) \in R^{m} \) is the output vector of the \( i^{th} \) node, \( A_{i} \in R^{n \times n} \) denotes a constant matrix, \( f( \cdot ):R^{n} \times R^{n} \) represents a nonlinear function with \( f(0) \equiv 0 \), \( W = (w_{ij} )_{N \times N} \) is the coupling configuration matrix which describes the topological structure of the network. If there is a connection from node \( i \) to node \( j(j \ne i) \), then \( w_{ij} = 1 \); otherwise \( w_{ij} = 0 \). As usual, matrix \( W \) satisfies \( w_{ii} = - \sum\limits_{j = 1,j \ne i}^{N} {w_{ij} } \), \( \Gamma \in R^{n \times n} \) is the inner coupling matrix, \( C_{i} \in R^{m \times n} \) stands for the output matrix.

In fact, it is quite tough to access the states of some complex networks completely. In order to obtain the state variables of network (1), the output \( y_{i} (k) \) is transmitted to the observer network. Actually, losing data such as packet dropout may occur in the process of transmission. So it is of great value to take the advantage of accessible state information to approximate the unknown information of nodes in network (1), regardless of packet losses.

In this paper, the network measurements from the transmission channel are of the following form:

$$ \bar{y}_{i} (k) = r_{i} (k)y_{i} (k)\quad (i = 1,2, \ldots ,N) $$
(2)

where \( \bar{y}_{i} (k) \in R^{m} \) is the actual measured output. The random variable \( r_{i} (k) \in {{\{ }}0,1{\}} \) indicates the state of the packet at time \( k \). If \( r_{i} (k) = 0 \) then the packet is lost; else it would succeed. The process of packet in the transmission channel is regarded as a Markov chain with two states: reception and loss. Furthermore, the transition probability matrix of the Markov chain is defined by

$$ \Lambda _{i} = Prob(r_{i} (k + 1) = c\,|\,r_{i} (k) = b)_{b,c \in \zeta } = \left[ {\begin{array}{*{20}c} {1 - q} & q \\ p & {1 - p} \end{array} } \right] $$
(3)

where \( \zeta = {{\{ }}0,1{\}} \) is the state space of the Markov chain, \( p \) is the failure probability when the previous packet succeed, and \( q \) is the recovery probability from the loss state. To make the process \( \{ r_{i} (k)\} \) ergodic, we believe that \( p,q \in (0,1) \). Without loss of generality, the transmitted signal in the initial state is assumed received successfully, that is, \( r_{i} (0) = 1 \).

For the purpose of estimating the states of network (1), we construct a state estimator as follows:

$$ \left\{ {\begin{array}{*{20}l} {\hat{x}_{i} (k + 1) = A_{i} \hat{x}_{i} (k) + f(\hat{x}_{i} (k)) + \sum\limits_{j = 1}^{N} {w_{ij} }\Gamma \hat{y}_{j} (k) + K_{i} (\bar{y}_{i} (k) - \hat{y}_{i} (k))} \\ {\begin{array}{*{20}l} {\hat{y}_{i} (k) = C_{i} \hat{x}{}_{i}(k)} &\quad {(i = 1,2, \ldots ,N)} \end{array} } \end{array} } \right. $$
(4)

where \( \hat{x}_{i} (k) = (\hat{x}_{i1} (k),\hat{x}_{i2} (k), \ldots ,\hat{x}_{in} (k))^{T} \in R^{n} \) represents the estimation states of the nodes in network (1). \( \hat{y}_{i} (k) \in R^{m} \) denotes the output of the nodes in network (4), \( K_{i} \in R^{n \times m} \) stands for the observer gain to be determined.

By applying the Kronecker product, networks (1), (2) and (4) can be expressed as the following concise form:

$$ \left\{ {\begin{array}{*{20}l} {x(k + 1) = Ax(k) + f(x(k)) + (W \otimes\Gamma )y(k)} \hfill \\ {y(k) = Cx(k)} \hfill \\ \end{array} } \right. $$
(5)
$$ \bar{y}(k) = r(k)Cx(k) $$
(6)
$$ \left\{ {\begin{array}{*{20}l} {\hat{x}(k + 1) = A\hat{x}(k) + f(\hat{x}(k)) + (W \otimes \varGamma )\hat{y}(k) + K[\bar{y}(k) - \hat{y}(k)]} \hfill \\ {\hat{y}(k) = C\hat{x}(k)} \hfill \\ \end{array} } \right. $$
(7)

where

  • \( x(k) = (x_{1}^{T} (k),x_{2}^{T} (k), \ldots ,x_{N}^{T} (k))^{T} \), \( \hat{x}(k) = (\hat{x}_{1}^{T} (k),\hat{x}_{2}^{T} (k), \ldots ,\hat{x}_{N}^{T} (k))^{T} \), \( y(k) = (y_{1}^{T} (k),y_{2}^{T} (k), \ldots ,y_{N}^{T} (k))^{T} \), \( \hat{y}_{i} (k) = (\hat{y}_{1}^{T} (k),\hat{y}_{2}^{T} (k), \ldots ,\hat{y}_{N}^{T} (k))^{T} \), \( \bar{y}_{i} (k) = (\bar{y}_{1}^{T} (k),\bar{y}_{2}^{T} (k), \ldots ,\bar{y}_{N}^{T} (k))^{T} \), \( f(x(k)) = (f^{T} (x_{1} (k)),f^{T} (x_{2} (k)), \ldots ,f^{T} (x_{N} (k)))^{T} \), \( f(\hat{x}(k)) = (f^{T} (\hat{x}_{1} (k)),f^{T} (\hat{x}_{2} (k)), \ldots ,f^{T} (\hat{x}_{N} (k)))^{T} \), \( A = diag\{ A_{1} ,A_{2} , \ldots ,A_{N} \} \), \( C = diag\{ C_{1} ,C_{2} , \ldots ,C_{N} \} \), \( K = diag\{ K_{1} ,K_{2} , \ldots ,K_{N} \} \), \( r(k) = (diag\{ r_{1} (k),r_{2} (k), \ldots ,r_{N} (k)\} ) \otimes I_{n} \), \( I_{n} \) is the identical matrix of \( n \) dimensions.

Letting the state error be

$$ \tilde{x}(k + 1) = x(k + 1) - \hat{x}(k + 1) $$
(8)

It follows from (5)–(7) that

$$ \begin{aligned} \tilde{x}(k + 1) & = A[x(k) - \hat{x}(k)] + [f(x(k)) - f(\hat{x}(k))] + (W \otimes\Gamma )C[x(k) - \hat{x}(k)] \\ & \quad - K[r(k)Cx(k) - C\hat{x}(k)] \\ & = A\tilde{x}(k) + \tilde{f}(x(k)) + (W \otimes\Gamma )C\tilde{x}(k) - K[r(k)Cx(k) - C\hat{x}(k)] \\ & = A\tilde{x}(k) + \tilde{f}(x(k)) + (W \otimes\Gamma )C\tilde{x}(k) - KC\tilde{x}(k) + K(I_{Nn} - r(k))Cx(k) \\ & = \tilde{f}(x(k)) + [(A - KC) + (W \otimes\Gamma )C]\tilde{x}(k) + K(I_{Nn} - r(k))Cx(k) \\ \end{aligned} $$

where \( \tilde{x}(k) = x(k) - \hat{x}(k) \), \( \tilde{f}(x(k)) = f(x(k)) - f(\hat{x}(k)) \). For the sake of concise expression, we could assume that \( H = I_{Nn} - r(k) \) and \( 0 < H < I_{Nn} \), then

$$ \tilde{x}(k + 1) = [(A - KC) + (W \otimes\Gamma )C]\tilde{x}(k) + \tilde{f}(x(k)) + KHCx(k) $$
(9)

Since that \( x(k) \) and \( \tilde{x}(k) \) both exist in (9) at the same time, we take the augmented state vector to be

$$ e(k) = \left[ {\begin{array}{*{20}c} {x(k)} \\ {\tilde{x}(k)} \end{array} } \right] $$
(10)

It follows from (5) and (9) that

  • \( \begin{aligned} & e(k + 1) = \left[ {\begin{array}{*{20}c} {x(k + 1)} \\ {\tilde{x}(k + 1)} \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} {Ax(k) + f(x(k)) + (W \otimes\Gamma )Cx(k)} \\ {[(A - KC) + (W \otimes\Gamma )C]\tilde{x}(k) + \tilde{f}(x(k)) + KHCx(k)}\end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} {f(x(k))} \\ {\tilde{f}(x(k))} \end{array} } \right] + \left[ {\begin{array}{*{20}c} {A + (W \otimes\Gamma )C} & 0 \\ {KHC} & {(A - KC) + (W \otimes\Gamma )C} \end{array} } \right]\left[ {\begin{array}{*{20}c} {x(k)} \\ {\tilde{x}(k)} \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} {f(x(k))} \\ {\tilde{f}(x(k))} \end{array} } \right] + \left[ {\begin{array}{*{20}c} {A + (W \otimes\Gamma )C} & 0 \\ 0 & {(A - KC) + (W \otimes\Gamma )C} \end{array} } \right]\left[ {\begin{array}{*{20}c} {x(k)} \\ {\tilde{x}(k)} \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 & 0 \\ {KHC} & 0 \end{array} } \right]\left[ {\begin{array}{*{20}c} {x(k)} \\ {\tilde{x}(k)} \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} {f(x(k))} \\ {\tilde{f}(x(k))} \end{array} } \right] + \left[ {\begin{array}{*{20}c} {A + (W \otimes\Gamma )C} & 0 \\ 0 & {(A - KC) + (W \otimes\Gamma )C} \end{array} } \right]\left[ {\begin{array}{*{20}c} {x(k)} \\ {\tilde{x}(k)} \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & K \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 & 0 \\ {HC} & 0 \end{array} } \right]\left[ {\begin{array}{*{20}c} {x(k)} \\ {\tilde{x}(k)} \end{array} } \right] \\ \end{aligned} \)

suppose

  • \( B = \left[ {\begin{array}{*{20}c} {A + (W \otimes \varGamma )C} & 0 \\ 0 & {(A - KC) + (W \otimes \varGamma )C} \end{array} } \right] \), \( D_{1} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & K \end{array} } \right] \), \( D_{2} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ {HC} & 0 \end{array} } \right] \), \( h(x(k),\hat{x}(k)) = \left[ {\begin{array}{*{20}c} {f(x(k))} \\ {\tilde{f}(x(k))} \end{array} } \right] \),

then

$$ e(k + 1) = Be(k) + D_{1} D_{2} e(k) + h(x(k),\hat{x}(k)) $$
(11)

Before deriving the main results, an available assumption and a useful lemma are given as follows throughout this paper.

Assumption 1:

Suppose that \( f(0) = 0 \) and there exists a positive constant \( a \) such that

$$ ||f(u) - f(v)|| \le a||u - v||,\forall u,v \in R^{n}. $$

Lemma 1 (Schur Complement):

For a given real symmetric matrix \( \Pi = \left[ {\begin{array}{*{20}c} {\Pi _{11} } & {\Pi _{21} } \\ {\Pi _{12} } & {\Pi _{22} } \end{array} } \right] \), where \( \Pi _{11} =\Pi _{11}^{T} \), \( \Pi _{12} =\Pi _{21}^{T} \), \( \Pi _{22} =\Pi _{22}^{T} \), the condition \( \Pi < 0 \) is equivalent to

$$ \left\{ {\begin{array}{*{20}l} {\Pi _{22} < 0} \hfill \\ {\Pi _{11} -\Pi _{12}\Pi _{22}^{ - 1}\Pi _{12}^{T} < 0} \hfill \\ \end{array} } \right.. $$

3 Main Results

In the section, the LMIs approach is applied to deal with the issue on state estimation of network (1), which was put forward previously.

Theorem 1:

Under Assumption 1, network (4) becomes an effective state estimator of network (1) if there exist such matrixes \( P = P_{r(k)} > 0 \), \( \bar{P} = P_{r(k + 1)} = (\Lambda \otimes I_{n} )P_{r(k)} > 0 \), that \( P = P^{T} = \left[ {\begin{array}{*{20}c} {P_{1} } & 0 \\ 0 & {P_{2} } \end{array} } \right] \), \( \bar{P} = \bar{P}^{T} = \left[ {\begin{array}{*{20}c} {\bar{P}_{1} } & 0 \\ 0 & {\bar{P}_{2} } \end{array} } \right] \) and \( \Lambda = diag(\Lambda _{1} ,\Lambda _{2} , \ldots ,\Lambda _{N} ) \), matrix \( K \), scalar \( \alpha > 0 \) such that the LMI \( \varphi < 0 \) in (12) hold.

$$ \varphi = \left[ {\begin{array}{*{20}c} {\pi_{1} } & {\pi_{2} } & {A^{T} \bar{P}_{1} + C^{T} (W \otimes \varGamma )^{T} \bar{P}_{1} } & {C^{T} H^{T} K^{T} \bar{P}_{2} } & {C^{T} H^{T} K^{T} \bar{P}_{2} } & 0 \\ * & {\pi_{3} - C^{T} K^{T} \bar{P}_{2} KC} & 0 & {\pi_{4} } & { - C^{T} K^{T} \bar{P}_{2} } & {C^{T} K^{T} \bar{P}_{2} } \\ * & * & {\bar{P}_{1} - \alpha I} & 0 & 0 & 0 \\ * & * & * & {\bar{P}_{2} - \alpha I} & 0 & 0 \\ * & * & * & * & { - \bar{P}_{2} } & 0 \\ * & * & * & * & * & { - \bar{P}_{2} } \end{array} } \right] $$
(12)

where

  • \( \begin{aligned} \pi_{1} & = A^{T} \bar{P}_{1} A + A^{T} \bar{P}_{1} (W \otimes\Gamma )C + C^{T} (W \otimes\Gamma )^{T} \bar{P}_{1} A + C^{T} (W \otimes\Gamma )^{T} \bar{P}_{1} (W \otimes\Gamma )C - P_{1} + \alpha a^{2} I \\ \pi_{2} & = C^{T} H^{T} K^{T} \bar{P}_{2} A + C^{T} H^{T} K^{T} \bar{P}_{2} (W \otimes\Gamma )C \\ \pi_{3} & = A^{T} \bar{P}_{2} A - C^{T} K^{T} \bar{P}_{2} A - A^{T} \bar{P}_{2} KC + A^{T} \bar{P}_{2} (W \otimes\Gamma )C - C^{T} K^{T} \bar{P}_{2} (W \otimes\Gamma )C \\ & \quad + C^{T} (W \otimes\Gamma )^{T} \bar{P}_{2} A - C^{T} (W \otimes\Gamma )^{T} \bar{P}_{2} KC + C^{T} (W \otimes\Gamma )^{T} \bar{P}_{2} (W \otimes\Gamma )C - P_{2} + \alpha a^{2} I \\ \pi_{4} & = A^{T} \bar{P}_{2} - C^{T} K^{T} \bar{P}_{2} + C^{T} (W \otimes\Gamma )^{T} \bar{P}_{2} . \\ \end{aligned} \)

Moreover, the state estimator gain can be determined by

$$ K = \bar{P}_{2}^{ - 1} Y $$
(13)

Proof:

Construct a Lyapunov functional candidate as follows:

$$ V(k,\,r(k)) = e^{T} (k)P_{r(k)} e(k) $$
(14)

For calculating the difference of \( V(k,\,r(k)) \) along the trajectories of (11) and getting the mathematical expectation, one can obtain that

$$ \begin{aligned} E\{ \Delta V(k,\,r(k))\} & = E\{ V(k + 1,r(k + 1)) - V(k,r(k))\} \\ & = E\{ e^{T} (k + 1)P_{r(k + 1)} e(k + 1) - e^{T} (k)P_{r(k)} e(k)\} \\ & = E\{ [Be(k) + D_{1} D_{2} e(k) + h(x(k),\hat{x}(k))]^{T} \bar{P} \\ & \quad\; [Be(k) + D_{1} D_{2} e(k) + h(x(k),\hat{x}(k))] - e^{T} (k)Pe(k)\} \\ & = E\{ e^{T} (k)B^{T} \bar{P}Be(k) + e^{T} (k)B^{T} \bar{P}D_{1} D_{2} e(k) \\ & \quad\; + e^{T} (k)B^{T} \bar{P}h(x(k),\hat{x}(k)) + e^{T} (k)D_{2}^{T} D_{1}^{T} \bar{P}Be(k) \\ &\quad \; + e^{T} (k)D_{2}^{T} D_{1}^{T} \bar{P}D_{1} D_{2} e(k) + e^{T} (k)D_{2}^{T} D_{1}^{T} \bar{P}h(x(k),\hat{x}(k)) \\ &\quad \; + h^{T} (x(k),\hat{x}(k))\bar{P}Be(k) + h^{T} (x(k),\hat{x}(k))\bar{P}D_{1} D_{2} e(k) \\ & \quad\; + h^{T} (x(k),\hat{x}(k))\bar{P}h(x(k),\hat{x}(k)) - e^{T} (k)Pe(k)\} \\ & = E\{ \chi^{T} \varphi_{1} \chi \} \\ \end{aligned} $$
(15)

where

  • \( \chi = \left[ {\begin{array}{*{20}c} {e(k)} \\ {h(x(k),\hat{x}(k))} \end{array} } \right] \), \( P = P_{r(k)} > 0 \), \( \bar{P} = P_{r(k + 1)} = (\Lambda \otimes I_{n} )P_{r(k)} > 0, \)

  • \( \varphi_{1} = \left[ {\begin{array}{*{20}c} {B^{T} \bar{P}B + B^{T} \bar{P}D_{1} D_{2} + D_{2}^{T} D_{1}^{T} \bar{P}B + D_{2}^{T} D_{1}^{T} \bar{P}D_{1} D_{2} - P} & {B^{T} \bar{P} + D_{2}^{T} D_{1}^{T} \bar{P}} \\ {\bar{P}B + \bar{P}D_{1} D_{2} } & {\bar{P}} \end{array} } \right]. \)

From Assumption 1, it is easy to show that

$$ \alpha h^{T} (x(k),\hat{x}(k))h(x(k),\hat{x}(k)) \le \alpha a^{2} e^{T} (k)e(k). $$
(16)

From (15) and (16), we obtain that

$$ \begin{aligned} E\{ \Delta V(k,\,r(k))\} & \le E\{ \chi^{T} \varphi_{1} \chi + [\alpha a^{2} e^{T} (k)e(k) - \alpha h^{T} (x(k),\hat{x}(k))h(x(k),\hat{x}(k))]\} \\ & = E\{ \chi^{T} \varphi_{2} \chi \} \\ \end{aligned} $$
$$ \begin{aligned} \varphi_{2} & = \left[ {\begin{array}{*{20}c} {B^{T} \bar{P}B + B^{T} \bar{P}D_{1} D_{2} + D_{2}^{T} D_{1}^{T} \bar{P}B + D_{2}^{T} D_{1}^{T} \bar{P}D_{1} D_{2} - P + \alpha a^{2} I} & {B^{T} \bar{P} + D_{2}^{T} D_{1}^{T} \bar{P}} \\ {\bar{P}B + \bar{P}D_{1} D_{2} } & {\bar{P} - \alpha I} \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} {\pi_{1} + C^{T} H^{T} K^{T} \bar{P}_{2} KHC} & {\pi_{2} - C^{T} H^{T} K^{T} \bar{P}_{2} KC} & {A^{T} \bar{P}_{1} + C^{T} (W \otimes \varGamma )^{T} \bar{P}_{1} } & {C^{T} H^{T} K^{T} \bar{P}_{2} } \\ * & {\pi_{3} + C^{T} K^{T} \bar{P}_{2} KC} & 0 & {\pi_{4} } \\ * & * & {\bar{P}_{1} - \alpha I} & 0 \\ * & * & * & {\bar{P}_{2} - \alpha I} \end{array} } \right] \\ \end{aligned} $$

By Lemma 1, we can obtain that \( \varphi_{2} < 0 \) is equivalent to the inequality \( \varphi < 0 \). It can be derived that the estimation error network is asymptotically stable in the mean square by applying the Lyapunov functional approach. It means that network (4) is an effective state estimator of network (1).

4 Simulations

In the section, an example is given to justify the criteria proposed in the previous section. Considering an output coupled discrete-time complex network with 3 nodes. Following are the parameters for the network:

$$ \begin{array}{*{20}l} {\begin{array}{*{20}l} {\begin{array}{*{20}c} {f(x_{i} (k)) = ( - 1.4x_{i1} (k) + 2.4\tanh (x_{i1} (k)), - 1.4x_{i2} (k) + 2.4\tanh x_{i2} (k)),} \\ { \, - 1.4x_{i3} (k) + 2.4\tanh x_{i3} (k)))^{T} } \\ \end{array} } \hfill & {(i = 1,2,3)} \hfill \\ \end{array} } \hfill \\ {A_{i} = \left[ {\begin{array}{*{20}c} {0.47} & 0 & 0 \\ 0 & {0.4} & 0 \\ 0 & 0 & {0.25} \\ \end{array} } \right],\,A = diag(A_{1} ,A_{2} ,A_{3} ),\,C_{i} = \left[ {\begin{array}{*{20}c} {0.8} & 0 & 0 \\ 0 & {0.8} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right],\,C = diag(C_{1} ,C_{2} ,C_{3} ),} \hfill \\ {W = \left[ {\begin{array}{*{20}c} { - 2} & 1 & 1 \\ 1 & { - 1} & 0 \\ 1 & 1 & { - 2} \\ \end{array} } \right],\,\Gamma = \left[ {\begin{array}{*{20}c} {0.3} & { - 0.1} & {0.2} \\ 0 & { - 0.3} & {0.2} \\ { - 0.1} & { - 0.1} & { - 0.2} \\ \end{array} } \right],\,\Lambda _{i} = \left[ {\begin{array}{*{20}c} {0.1} & {0.9} \\ {0.2} & {0.8} \\ \end{array} } \right] \, ,\,\Lambda = diag(\varLambda_{1} ,\varLambda_{2} ,\varLambda_{3} ),} \hfill \\ {r(k) = [b_{i1} ,b_{i2} ,b_{i3} ]^{T} \quad \, (b_{i1} ,b_{i2} ,b_{i3} \in \{ 0,1\} \, (i = 1,2,3))\,H = I_{9} - diag(r(k),r(k),r(k)),} \hfill \\ \end{array} $$

then select \( a = 0.4 \) in (16). Applying the MATLAB LMI Toolbox, we obtain the equations including the gain matrix in Theorem 1 as follows:

$$ \begin{array}{*{20}l} {\bar{P}_{1} = diag(M,M,M)\;\;\;M = \left[ {\begin{array}{*{20}c} {1.0021} & { - 0.0151} & {0.0079} \\ { - 0.0151} & {0.9576} & { - 0.0002} \\ {0.0079} & { - 0.0002} & {1.0246} \end{array} } \right],} \\ {\bar{P}_{2} = diag(N,N,N)\;\;\;N = \left[ {\begin{array}{*{20}c} {1.0117} & { - 0.0088} & {0.0061} \\ { - 0.0088} & {0.9834} & {0.0012} \\ {0.0038} & {0.0012} & {1.0255} \end{array} } \right],} \\ {K = diag(K_{0} ,K_{0} ,K_{0} )\;\;\;K_{0} = \left[ {\begin{array}{*{20}c} {0.1166} & {0.0458} & {0.0080} \\ {0.0384} & {0.1340} & {0.0150} \\ { - 0.0095} & {0.0007} & {0.0681} \end{array} } \right],} \end{array} $$

meanwhile, \( \alpha = 1.9009 \) is obtained in (16).

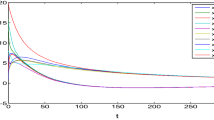
We choose the third state of each node to show the state trajectories of nodes, the simulations are presented in Fig. 1. Meanwhile, the simulations for all states of error system are shown in Fig. 2. From these simulations, we can conclude that the estimator (4) could effectively estimate the state of nodes in network (1), which exists Markovian packet losses. The proof is then verified.

Fig. 1.
figure 1

The states and estimation states of \( x_{i3} (i = 1,2,3) \)

Full size image
Fig. 2.
figure 2

The node states of error system

Full size image

5 Conclusions

In the paper, we have dealt with the problem of state estimation for discrete-time directed complex networks with coupled outputs. It often occurs the packet losses in practical transmission channel. We describe it as a Markovian packet dropout and the transition probability is known. By employing the Lyapunov functional theory and stochastic analysis method, a state observer has been constructed to witness the estimation error to be asymptotically stable in the mean square. The criteria has been established to guarantee the existence of the desired estimator gain matrix. The simulations have been shown to illustrate the applicability of the criteria obtained.