Keywords

Introduction

The USDA soil conservation service (SCS) (now called as the natural resources conservation service, NRCS) curve number (CN) method, often designated as the SCS-CN method, was first published in 1956 in Sect. 4 of the National Engineering Handbook (SCS 1956). The SCS-CN method was originally developed for predicting runoff from small agricultural watersheds for individual rainfall events but has since been revised several times and extended to rural, forest, and urban watersheds and is now applied to a range of environments, including soil erosion and water quality modeling (Walker et al. 2006; Mishra et al. 2006b; Singh 2013). Although many hydrologic models are available for the estimation of direct runoff from storm rainfall, most models are limited because of their intensive input data and calibration requirements, and, therefore, the SCS-CN method seems to fulfill our demands with few data requirements and clearly stated assumptions. The method has also been coupled with several standard hydrologic software packages such as storm water management model (SWMM) (Metcalf and Eddy 1971); constrained linear simulation (CLS) (Natale and Todini 1976a, b); hydrologic engineering center-1 (HEC-1) (HEC 1981); agricultural nonpoint source model (AGNPS) (Young et al. 1989); chemicals, runoff, and erosion from agricultural management systems (CREAMS) (Smith and Williams 1980); areal nonpoint source watershed environment response simulation (ANSWERS) (Beasley and Huggins 1980); and soil and water assessment tool (SWAT) (Neitsch et al. 2002).

Since its inception, the method has witnessed myriad applications in various fields of hydrology, even for those it was not originally intended to be applied. A curve number (CN) that is descriptive of major runoff-producing characteristics of watershed such as soil type, land use/treatment classes, hydrologic soil group, hydrologic condition, most importantly the antecedent moisture condition (AMC) is required in the method. The wider applicability of the SCS-CN methodology can be attributed to its multifaceted characteristic inherited such as its simplicity, ease of use, major runoff-producing characteristics (as enumerated above), widespread acceptance, and the significant infrastructure and institutional momentum for this procedure within NRCS (Garen and Moore 2005). Recently, Singh (2013) revisited SCS-CN methodology using entropy theory (Kapur and Kesavan 1992; Singh 2013). More recently, the SMA procedure has been a key component of transmutation of the existing SCS-CN method to various improved variants (Michel et al. 2005; Sahu et al. 2007, 2010; Ajmal et al. 2015; Singh et al. 2015).

Therefore, keeping in view of the aforementioned discussion, this paper revisits the popular SCS-CN methodology in the context of recent modifications along with various applications based on these modifications and different fields of applications and much beyond that it also explores the newer fields of application in hydrologic sciences.

Background of SCS-CN Methodology

The SCS-CN method was developed in 1954, and it is documented in Sect. 4 of the National Engineering Handbook (NEH-4) published by the Soil Conservation Service (now called as Natural Resource Conservation Service), US Department of Agriculture in 1956. The document has since been revised in 1964, 1965, 1971, 1972, 1985, and 1993. It computes the volume of surface runoff for a given rainfall event from small agricultural, forest, and urban watersheds (SCS 1986). The SCS-CN method is the result of exhaustive field investigations carried out during the late 1930s and 1940s and the works of several investigators, including Mockus (1949), Sherman (1949), Andrews (1954), and Ogrosky (1956). The passage of Watershed Protection and Flood Prevention Act (Public Law 83-566) in August 1954 led to the recognition of the method at the Federal level, and the method has since witnessed myriad applications all over the world.

The SCS-CN method is a conceptual model of hydrologic abstraction of storm rainfall, supported by empirical data. Its objective is to estimate direct runoff volume from storm rainfall depth, based on a curve number CN (Ponce and Hawkins 1996). Its popularity is rooted in convenience, simplicity, authoritative origin, and responsiveness to four readily grasped catchment properties, viz., soil type, land use/treatment, surface condition, and antecedent moisture condition. To date, there has been no alternative that possesses so many advantages, which is why it has been and continues to be commonly used, whether or not it is, in a strict scientific sense, appropriate. Though appealing to many practising hydrologists by its overwhelming simplicity, the method contains some unknowns and inconsistencies (Chen 1982). Due to its origin and evolution as agency methodology, it is effectively isolated from the rigors of peer review. The information given in NEH-4 was not intended to be exhaustive. No complete account of the method’s foundation is available to date, despite some noteworthy attempts made by Ponce and Hawkins (1996), Mishra and Singh (2003a), and Garen and Moore (2005), Chung et al. (2010). The method has been structurally diagnosed and critically reviewed by several researchers worldwide for its enhanced performance without disfiguring its inherent simplicity. The diagnostic works of Rallison and Miller (1982), Chen (1982), Ponce and Hawkins (1996), Mishra and Singh (1999, 2002a, b, 2003a, b, 2004a, b), Michel et al. (2005), and Chung et al. (2010) are noteworthy. Based on the works of Ponce and Hawkins (1996) and Mishra and Singh (2003a), it was concluded that the SCS-CN method is a conceptual model of hydrologic abstraction of storm rainfall supported by empirical data dedicated to estimate direct runoff volume based on a single numeric parameter CN.

The SCS-CN method is based on the water balance equation along with two fundamental hypotheses. The first hypothesis equates the ratio of actual amount of direct surface runoff (Q) to the total rainfall (P) (or maximum potential surface runoff) to the ratio of actual infiltration (F) to the amount of the potential maximum retention (S). The second hypothesis relates the initial abstraction (I a) to S, also described as potential post-initial abstraction retention (McCuen 2002).

  1. (a)

    Water balance equation

$$P = I_{\text{a}} + F + Q$$
(1)
  1. (b)

    Proportional equality (first hypothesis)

$$\frac{Q}{{P - I_{\text{a}} }} = \frac{F}{S}$$
(2)
  1. (c)

    I a–S relationship (second hypothesis)

$$I_{\text{a}} = \lambda S$$
(3)

where P = total rainfall; I a = initial abstraction; F = cumulative infiltration excluding I a; Q = direct runoff; and S = potential maximum retention or infiltration. The values of P, Q, and S are in depth or volumetric dimensions, while the initial abstraction coefficient (λ) is dimensionless. In a typical case, a certain amount of rainfall is initially abstracted as interception, evaporation, infiltration, and surface storage before runoff begins. A sum of these four elements at initiation of surface runoff is usually termed “initial abstraction.”

The first hypothesis (Eq. 2) is primarily a proportionality concept, and the second hypothesis (Eq. 3) is a linear relationship between initial abstraction I a and potential maximum retention S. Coupling Eqs. (1) and (2), the expression for Q can be written as:

$$\begin{array}{*{20}c} {Q = \frac{{\left( {P - I_{\text{a}} } \right)^{2} }}{{P - I_{\text{a}} + S}}; } & {{\text{for }}P \ge I_{\text{a}}; } \\ { = 0;} & {\text{otherwise}} \\ \end{array}$$
(4)

Equation (4) is the general form of the popular SCS-CN method and is valid for P ≥ I a; Q = 0 otherwise.

For λ = 0.2, the coupling of Eqs. (3) and (4) results in:

$$Q = \frac{{\left( {P - 0.2S} \right)^{2} }}{P + 0.8S}$$
(5)

Equation (5) is well recognized as a popular form of the existing SCS-CN method. Thus, the existing SCS-CN method with λ = 0.2 is a one-parameter model for computing surface runoff from daily storm rainfall, having versatile importance, utility, and vast untapped potential. The parameter S of the SCS-CN method depends on soil type, land use, hydrologic condition, and antecedent moisture condition (AMC). Similarly, the initial abstraction coefficient λ is frequently recognized as a regional parameter depending on geologic and climatic factors. Many other studies carried out in the USA and other countries (SCD 1972; Springer et al. 1980; Cazier and Hawkins 1984; Ramasastri and Seth 1985; Bosznay 1989) report λ to vary in the range of (0, 0.3). Hawkins et al. (2001) suggested that the value of \(\lambda\) = 0.05 gave better fit to data and is more appropriate for use in runoff calculations. Since the existing SCS-CN method assumes λ to be equal to 0.2 for practical applications, it has frequently been questioned for its validity and applicability (Hawkins et al. 2001), invoking many researchers to carry out a critical examination of the I a–S relationship for pragmatic applications (Mishra and Singh 2004b).

Mockus (1949) described the physical significance of parameter S of Eq. (6) as “it is a constant and is the maximum difference of (P − Q) that can occur for the given storm and watershed characteristics”. The parameter S is limited by either the rate of infiltration at the soil surface or the amount of water storage available in the soil profile, whichever gives its smaller value. Since S can vary in the range of 0 ≤ S ≤ ∞, it is mapped onto a dimensionless curve number CN, varying in a more appealing range 0 ≤ CN ≤ 100, as:

$$S = \frac{25400}{\text{CN}} - 254$$
(6)

where S is in mm. The difference between S and CN is that the former is a dimensional quantity (L), whereas the latter is nondimensional. The highest possible numerical value of CN (i.e., 100) symbolizes a condition of zero potential maximum retention (S = 0), which in a real physical situation represents an impermeable watershed. On the contrary, the lowest possible numerical value of CN indicates a situation of highest potential maximum retention (S = ∞), reflecting a physical situation of an infinitely abstracting watershed, which remains an unlikely situation in real-world conditions.

Advantages and Disadvantages of SCS-CN Methodology

The major advantages and disadvantages of SCS-CN methodology are summarized as below.

Major advantages:

  • It is a simple, predictable, stable, and lumped conceptual model.

  • It relies on only one parameter, CN, and is well suited for ungauged situations.

  • It is the single available technique for wider applications in the majority of computer-based advanced hydrologic simulation models (Singh 1995).

  • It responds to four readily grasped catchment properties: soil type, land use/treatment, surface condition, and antecedent moisture condition.

  • It requires only a few basic descriptive inputs that are convertible to numeric values for estimation of direct surface runoff.

  • The technique has tremendous capabilities for its adoption toward environmental and water quality modeling.

  • It is well compatible with recent GIS and remote sensing tools in hydrologic applications.

Major disadvantages:

  • Choice of fixing the initial abstraction coefficient λ = 0.2 leads to preempted regionalization based on geologic and climatic conditions.

  • The method has no explicit provisions for spatial scale effects on CN, which remains highly sensible and truly governs the runoff.

  • The discrete relationship between CN and AMC classes permits a sudden jump in CN, resulting in an equivalent quantum jump in computed runoff.

  • It does not have any expression of time and ignores the impact of rainfall intensity and its temporal distribution.

  • It lacks the expression for antecedent moisture, which plays a crucial and significant role in governing runoff generation process.

CN Estimation Techniques

The errors in CN may have much more consequences on runoff estimation than errors of similar magnitude in storm rainfall P (Hawkins 1975). This indicates the importance of accurate CN estimation in SCS-CN methodology. However, despite widespread use of SCS-CN methodology, an accurate estimation of CN has been a topic of discussion among hydrologists worldwide (Hawkins 1978; Chen 1982; Bonta 1997; Mishra and Singh 2006). In hydrologic literature, there are three different procedures available to compute CN for a given rainfall-runoff records, i.e., (i) using NEH-4 Table, (ii) ordered P and Q data (asymptotic CN estimation), and (iii) derived frequency distribution (Hjelmfelt 1980; Bonta 1997). A detailed diagnosis and description of these methods can be found in Mishra and Singh (2003a). Still, there has been no agreement advocating a single-CN procedure based on rainfall-runoff data (Soulis and Valiantzas 2013).

For any change in AMC (say from AMCI to AMCIII) on a given catchment, a sudden jump in CN value (i.e., from CNI to CNIII) invariably occurs, and this variability is discontinuous in nature, which ultimately results in a sudden jump in computed runoff. Thus, indirectly, it gives a reflection of the discrete nature of CN–AMC relationship. Depending on five-day antecedent rainfall, CNII is convertible to CNI and CNIII using the relationships given by Sobhani (1975), Hawkins et al. (1985), Neitsch et al. (2002), and Mishra et al. (2008) and also directly from the NEH-4 tables (SCS 1972; McCuen 1982, 1989; Ponce 1989; Singh 1992; Mishra and Singh 2003a). Mishra et al. (2008) compared CN conversion formulae (Table 1) developed by Sobhani (1975), Hawkins et al. (1985), Chow et al. (1988), and Neitsch et al. (2002) and found the Neitsch formulae to exhibit poorest correspondence with NEH-4 values taken as target values. The Sobhani formula best corresponded in CNI-conversion, and the Hawkins formula in CNIII. However, in field application, Mishra et al. (2008) model performed best of all. However, more recently, to negate the classic problem of quantum jump in runoff computations (due to AMC change), the concept of soil moisture accounting (SMA) procedure has nowadays been at the forefront of the research community (Michel et al. 2005; Sahu et al. 2010; Ajmal et al. 2015; and Singh et al. 2015).

Table 1 CN conversion formulae
Full size table

Slope Considerations in CN Estimation

In the standard NRCS model, the CN values for runoff estimation have been obtained experimentally from the measured rainfall-runoff data over a wide range of geographic, soil, and land management conditions. However, the watershed slope adjustment has not been taken into account and it is an important factor determining water movement within a landscape (Huang et al. 2006). The slope-adjusted CN can improve the runoff estimation capabilities of the NRCS model. The CNs obtained from the NRCS handbook (NRCS 2004) are usually assumed to correspond to a 5% slope (Sharpley and Williams 1990; Huang et al. 2006; Mishra et al. 2014).

Few attempts have been made in the past to incorporate watershed slope in CN estimation. Sharpley and Williams (1990) assumed that CNII obtained from NEH-4 (SCS 1972) corresponds to a slope of 5%. The slope-adjusted CNII (named as CN2α) was expressed as:

$${\text{CN}}_{{{\text{II}}\alpha }} = \frac{ 1}{ 3}\left( {{\text{CN}}_{\text{III}} - {\text{CN}}_{\text{II}} } \right)\left( { 1- 2 {\text{e}}^{ - 1 3. 8 6\alpha } } \right) + {\text{CN}}_{\text{II}}$$
(7)

Huang et al. (2006) tested Eq. (7) and found that it had limited applications, and, therefore, he developed an improved version for climatic and steep slope conditions observed in Loess Plateau of China as:

$${\text{CN}}_{{{\text{II}}\alpha }} = {\text{CN}}_{\text{II}} \left[ {\frac{ 3 2 2. 7 9+ 1 5. 6 3\alpha }{{\left( {\alpha + 3 2 3. 5 2} \right)}}} \right]$$
(8)

More recently, Ajmal et al. (2016) developed an improved version of CNIIα using a large amount of measured rainfall-runoff data from 39 mountainous watersheds in South Korea. The developed relationship can be expressed as:

$${\text{CN}}_{{{\text{II}}\alpha }} = {\text{CN}}_{\text{II}} \left[ {\frac{1.927\alpha + 2.1327}{{\left( {\alpha + 2.1791} \right)}}} \right]$$
(9)

However, the credibility of the above equation needs to be validated for other regions having similar climatic and slope conditions. The constant α is the watershed slope in m/m.

C−\(I_{\text{a}}^{*}\)−λ Spectrum (I a–S Relationship)

According to Plummer and Woodward (2002), the I a was not a part of the SCS-CN model in its initial formulation; however, as the developmental stages continued, it was included as a fixed ratio of I a to S. Because of the larger variability, the I a = 0.2S relationship has been the focus of discussion and modification since its very inception (Mishra and Singh 2003a). As an example, Aron et al. (1977) suggested λ ≤ 0.1 and Golding (1979) provided λ values for urban watersheds depending on CN as λ = 0.075 for CN ≤ 70, λ = 0.1 for 70 < CN ≤ 80, and λ = 0.15 for 80 < CN ≤ 90. Hawkins et al. (2001) found that a value of \(\lambda\)  = 0.05 gives a better fit to data and would be more appropriate for use in runoff calculations.

Mishra and Singh (1999) suggested that the initial abstraction component accounts for the short-term losses such as interception, surface storage, and infiltration before runoff begins, and, therefore, λ can take any nonnegative value. Mishra and Singh (2004a) developed a criterion for validity of the SCS-CN method with \(\lambda\) variation using the following relationships:

$$\lambda = \frac{{CI_{\text{a}}^{*} }}{{\left( {1 - I_{\text{a}}^{*} } \right)\left( {1 - I_{\text{a}}^{*} - C} \right)}}$$
(10a)

and

$$S \le \frac{{\left( {P - Q} \right)}}{\lambda }$$
(10b)

where \(I_{\text{a}}^{*}\) = I a/P; varies as 0 ≤ \(I_{\text{a}}^{*}\) ≤ 1, and for \(I_{\text{a}}^{*}\) > 1, C = Q/P = 0.

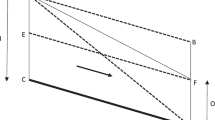
Graphically, Eqs. (10a) and (10b) are shown in Fig. 1. It can be inferred from the figure that \(\uplambda\) can take any nonnegative value (0, ∞); for a given value of \(I_{\text{a}}^{*}\), \(\lambda\) increases with C and reaches ∞ as (C + \(I_{\text{a}}^{*}\)) approaches 1; for a given value of C, \(\lambda\) increases with \(I_{\text{a}}^{*}\); as \(I_{\text{a}}^{*}\) → 0, \(\lambda\) → 0. It is due to this reason, the existing SCS-CN method performs poorly on very low runoff-producing (or low C values) lands, such as sandy soils and forest lands. Figure 1 also shows that the existing SCS-CN method has widest applicability on those watersheds exhibiting C values in the approximate range of (0.4–0.6) and the initial abstraction amount of the order of 10% of the total rainfall. On the basis of Fig. 1, they defined the applicability bounds for the SCS-CN method as: \(\lambda\) ≤ 0.3; \(I_{\text{a}}^{*}\) ≤ 0.35; and C ≥ 0.23.

Fig. 1
figure 1

Variation of initial abstraction coefficient \(\lambda\) with runoff factor C and nondimensional initial abstraction \(I_{\text{a}}^{*}\)

Full size image

The I a–S relationships developed by Jain et al. (2006) and Mishra et al. (2006a) are the improvements over the existing I a = 0.2S relationship. Considering to the fact that P is an implicit function of climatic/meteorological characteristics, Jain et al. (2006) developed a more general nonlinear I a-S relation, expressed as:

$$I_{\text{a}} = \lambda S\left( {\frac{P}{{\left( {P + S} \right)}}} \right)^{\alpha }$$
(11)

where α is a constant. Equation (13) reduces to I a = 0.2S for λ = 0.2 and α = 0 and hence could be taken as a generalized form of I a–S relationship. Based on the hypothesis that I a largely depends on initial soil moisture M, as Mishra et al. (2006a) developed a modified nonlinear I a–S relationship:

$$I_{\text{a}} = \frac{{\lambda S^{2} }}{{\left( {S + M} \right)}}$$
(12)

The generalized nature of the above equation can be seen as, for M = 0 or a completely dry condition, Eq. (12) reduces to Eq. (3), which is the basic I a–S relationship. Therefore, it can be concluded that these relationships (or their modification) can be further explored in different hydro-climatological regions for their enhanced applicability and versatility.

Soil Moisture Accounting (SMA) Procedure

A sound soil moisture accounting procedure (SMA) in combination with the CN procedure is needed to predict runoff from rainfall realistically, because CN is not a constant, but varies from event to event. Under wet soil conditions, much of the rainfall is converted to runoff. Therefore, the CN value has to be high for realistic prediction of runoff and vice versa. A sound SMA has to incorporate all soil moisture conditions (Mishra et al. 2004a; Mishra and Singh 2004a; Michel et al. 2005; Kannan et al. 2008).

The SMA concept was for the first time introduced by Williams and LaSeur (1976) to develop a continuous water yield model using the existing SCS-CN methodology. Here, the SMA procedure was based on the concept that the “Curve Number” (CN) should vary continuously with soil moisture, and thus there should be many values of CN instead of only three, i.e., CNI, CNII, CNIII. Later on, a good attempt was further made by Hawkins (1978) to account soil moisture on continuous basis. However, their models ignore the inherent structural deficiency of the existing SCS-CN methodology to account for SMA procedure.

The structural deficiency in terms of SMA of the existing SCS-CN method was highlighted by Mishra et al. (2004a) and an improved SMA-inspired SCS-CN model was developed and evaluated using large data set of US watersheds. Later on based on this concept, Mishra and Singh (2004a) developed versatile SCS-CN model (VSCS-CN) using soil moisture budgeting on continuous basis. Here, the SMA procedure was based on the notion that “higher the antecedent soil moisture amount before start of rainfall in the soil, higher will be the runoff and lesser will be the void space available for storage of rainfall.” This was also well addressed by Michel et al. (2005) through SMA procedure. A brief discussion about SMA procedure explicit in SCS-CN method is being discussed here as follows (Mishra et al. 2004a).

Using the C = Sr concept, where C is the runoff coefficient (= Q/(P − I a)) and Sr = degree of saturation (F/S), Mishra and Singh (2002a) modified Eq. (2) for antecedent moisture M as:

$$\frac{Q}{{(P - I_{\text{a}} )}} = \frac{{F + V_{0} }}{{S + V_{0} }}$$
(13)

which upon substitution into Eq. (2) leads to

$$Q = \frac{{\left( {P - I_{\text{a}} } \right)\left( {P - I_{\text{a}} + V_{0} } \right)}}{{\left( {P - I_{\text{a}} + V_{0} + S} \right)}}$$
(14)

Here V0 is computed as:

$$V_{0} = \frac{{\left( {P_{5} - 0.2S_{1} } \right)S_{1} }}{{P_{5} + 0.8S_{1} }}$$
(15)

where P 5 is the antecedent 5-d precipitation amount, and SI (= S + V 0) is the potential maximum retention corresponding to AMC I. Equation (15) assumes the watershed to be dry 5 days before the onset of the rainstorm. Based on this concept, a no. of improved SCS-CN-based models (e.g., Sahu et al. 2007, 2010; Geetha et al. 2008; Durbude et al. 2011; Jain et al. 2012; Ajmal et al. 2015; Singh et al. 2015) have been developed with changed degree of complexities in mathematical structure and parameterization to address the issue of quantum jump of runoff estimation.

SCS-CN Method Using Entropy Theory

In an attempt to provide an analytical treatment to the SCS-CN method, Mishra and Singh (2002a) derived it from early rainfall-runoff models such as Mockus (1949) and Zoch (1934, 1936) with Horton infiltration model and first- (linear) and second- (nonlinear) order hypotheses. Recently, Singh (2013) derived the SCS-CN method using the entropy theory and developed probability distributions of its variables CN, S, P, F, I a, and Q, assuming they are random in nature. It was found that the SCS-CN method requires no information for the probability distribution of runoff associated with it, other than obeying the total probability law. The entropy associated with SCS-CN method can be expressed using following expressions as follows:

$$H\left( Q \right) = \int\limits_{0}^{{P - I_{\text{a}} }} {\frac{1}{{P - I_{\text{a}} }}} \ln \left[ {\frac{1}{{P - I_{\text{a}} }}} \right]{\text{d}}Q = \ln \left( {P - I_{\text{a}} } \right)$$
(16)

or

$$H\left( Q \right) = \ln \, S - \ln {F} + \ln {Q}$$
(17)

Equation (16) can also be expressed in terms of CN as:

$$H\left( Q \right) = \ln \left[ {P - \lambda \left( {\frac{25,400}{\text{CN}} - 254} \right)} \right]$$
(18)

Likewise, Eq. (17) can be cast as

$$H\left( Q \right) = \ln \left[ {\left( {\frac{25,400}{\text{CN}} - 254} \right)} \right] - \ln F + \ln Q$$
(19)

where H(Q) is the Shannon entropy (Shannon 1948) of Q, expressed as:

$$H\left( Q \right) = - \int\limits_{0}^{{P - I_{\text{a}} }} {f(Q)} \ln \left[ {f(Q)} \right]{\text{d}}Q$$
(20)

in which f(Q) is the probability density function of Q, expressed as: [F/QS]. Equations (16)–(19) provide alternative ways of expressing the uncertainty or entropy associated with the SCS-CN method. The study shows that the gamma distribution represents the “best” distribution of CN, Q, P, S, Q/(P − I a), and F/S. The uncertainty in Q depends mainly on (P − I a) and the infiltration acts as a filter to this uncertainty, and, therefore, the quantities, P and I a (which depends upon S or CN), must be determined as accurately as possible.

Some Advanced Applications of SCS-CN Methodology

Although the SCS-CN method was originated as an empirical, event-based procedure for flood hydrology, however, it has witnessed myriad and variety of applications throughout the spectrum of hydrology, due to the reason of its simplicity, stability, and accountability for most runoff-producing watershed characteristics: soil type, land use treatment, surface condition, and antecedent moisture condition. Singh and Frevert (2002) edited a book titled “Mathematical Models of Small Watershed Hydrology and Applications,” in which at least 6 of the 22 chapters have the models based on SCS-CN approach. This reflects the robustness and versatility of SCS-CN methodology.

Though primarily intended for event-based rainfall-runoff modeling of the ungauged watersheds, the SCS-CN method has been applied successfully in the realm of hydrology, watershed management, and environmental engineering, such as long-term hydrologic simulation (LTHS) (Williams and LaSeur 1976; Hawkins 1978; Choi et al. 2002; Mishra et al. 2004a; Mishra and Singh 2004a; Michel et al. 2005; Sahu et al. 2007; Geetha et al. 2008; Kannan et al. 2008; Durbude et al. 2011; Sahu et al. 2010; Williams et al. 2012), hydrograph simulation (Aron et al. 1977; Mishra and Singh 2002a, 2004b); evapotranspiration (Mishra et al. 2014), soil moisture accounting (Mishra et al. 2004a; Michel et al. 2005; Sahu et al. 2010; Ajmal et al. 2015; Singh et al. 2015), sediment yield modeling (Mishra et al. 2006b; Tyagi et al. 2008; Singh et al. 2008; Bhunya et al. 2010), metal partitioning (Mishra et al. 2004b, c), urban hydrology (Pandit and Gopalakrishnan 1996; Singh et al. 2013), and river bank filtration and water quality (Ojha 2012).

The conceptualization and prevailing status of SCS-CN methodology has become so popular and versatile that many researchers have integrated it into their new hydrologic models, besides its direct applications (Singh et al. 2010). According to Walter and Stephen (2005), the criticisms of SCS-CN method should not be interpreted as “negative reflections” on its developer(s), rather these are enticements to engage the same creative effort that those early “developers” invoked to find appropriate approaches to current problems based on current science’, which fortifies ongoing developmental efforts toward SCS-CN methodology. A brief description on some of these applications is being discussed here as follows.

Long-Term Hydrologic Simulation (LTHS) Models

Long-term hydrologic simulation is used for augmentation of hydrologic data, water resources planning, and watershed management. Long-term daily flow data are specifically needed for analysis of water availability, computation of fortnightly or monthly flows for reservoir operation, and drought analysis (Mishra and Singh 2004a). This section discusses some of the important and widely used LTHS models based on SCS-CN method.

Williams–LaSeur (1976) Model

Williams and LaSeur (1976) were probably the first to introduce the concept of soil moisture accounting (SMA) procedure to develop a model based on the existing SCS-CN methodology. The model is based on the notion that CN varied continuously with soil moisture, and thus considering many values of CN instead of only three (CNI, CNII, CNIII). The model computes a soil moisture index (SMI) depletion parameter that forces an agreement between the measured and predicted average annual runoff. The model eliminates sudden jump in the CN values while changing from one AMC.

Hawkins ET-CN Model

Hawkins (1978) developed a continuous hydrologic simulation model by linking evapotranspiration (ET) and CN. The model uses the volumetric concept for accounting the site moisture on a continuous basis. The model accounts the soil moisture on continuous basis and thus eliminates the problem of sudden jump in CN. The model yields Q equal to 0.05S for no rainfall condition, which is impossible and, therefore, violates the law of mass conservation. Furthermore, it considers the SCS-CN method to be based on (I a + S) scheme, whereas Ia is separate from S in the existing SCS-CN method (Mishra and Singh 2004a, b).

Versatile SCS-CN (VSCS-CN) Model

Mishra and Singh (2004a) critically reviewed of the long-term hydrologic simulation models such as Hydrologic Simulation Package Fortran (HSPF), US Department of Hydrograph Laboratory (USDAHL) (Holtan and Lopez 1971), William–LaSeur (1976) model, Hawkins (1978) model, Systeme Hydrologique European (SHE) (Abbott et al. 1986a, b), and Hydrologic Engineering Centre-Hydrologic Modeling System (HEC-HMS) (HEC 2000) in terms of their architecture and structure, degree of complexity of inputs, time interval used in simulation, and their applicability particularly in the context of developing countries. They developed a four parameter versatile SCS-CN (VSCS-CN) model to remove the inconsistencies and complexities associated with the existing long-term hydrologic simulation models. The developed model obviates the sudden jumps in CN values, exclusively considers the soil moisture budgeting on continuous basis, evapotranspiration, and watershed routing procedures. These characteristics make the model versatile. The model paved the way for structural diagnosis of the existing SCS-CN method, and since then, a plethora of SMA-based models have been developed in hydrologic literature.

The model exclusively accounts for dynamic and static components of infiltration and expresses the evapotranspiration ET in terms of pan coefficient (PANC) and absolute maximum potential retention S abs = (S + S a), where S a is the threshold soil moisture = (V 0 + I a). The pan coefficient was found to be the ratio of the S, to the absolute potential maximum retention, S abs. Table 2 shows the different variants of the VSCS-CN model. These models could be further explored for their applicability and improved understanding of the processes involved in their formulations.

Table 2 VSCS-CN model and its variants (Mishra and Singh 2003a, b)
Full size table

Michel SCS-CN Model

An enhanced version of SCS-CN model was developed by Michel et al. (2005) based on the analysis of the continuous soil moisture accounting (SMA) procedure implied by the SCS-CN equation. In model development, it was hypothesized that the SCS-CN model is valid not only at the end of the storm but at any instant along a storm. The SMA procedure is based on the notion that higher the moisture store level, higher the fraction of rainfall will be converted into runoff. The Michel SCS-CN model eliminates initial abstraction (I a) and introduces a new parameter (threshold soil moisture) S a = (I a + V 0) to compute the direct surface runoff.

Sahu et al. SCS-CN Model

Sahu et al. (2007) developed a continuous hydrologic simulation model using SCS-CN method based on advanced SMA procedure. They hypothesized that the initial soil moisture (V 0) depends not only on antecedent five-day precipitation (P 5), but also on S. The dependency on S is based on the fact that the watershed with larger retention capacity S must retain higher moisture compared to the watershed with lesser S for a given P 5. The developed model obviates sudden jump in runoff computations and is an improvement over MSCS-CN model (Michel et al. 2005) based on SMA procedure.

SCS-CN-Based MLTHS ASMA Model

Jain et al. (2012) proposed modified long-term hydrologic simulation advance soil moisture accounting (MLTHS ASMA) model by suitably amalgamating the advanced soil moisture accounting (ASMA) procedure, the modified subsurface drainage flow concept, and curve number (CN)-based model for simulating daily flows. The proposed model uses the ASMA procedure both for surface and subsurface flows.

Modified Michel SCS-CN Model

Based on sound hydrologic perception of soil moisture accounting procedure (SMA) and changed parameterization with improved relationships for estimation of parameters, Singh et al. (2015) developed modified Michel SCS-CN (MMSCS-CN) model for runoff computations. Simple expressions of V 0 and S a were provided to obviate the manual adjustments in V 0 to accommodate all the three AMCs and fixation of S a with S.

Parsimonious SCS-CN Model

Based on in-depth structural diagnosis of the SCS-CN model and implicit inconsistencies in model parameterization, Ajmal et al. (2015) developed a parsimonious SCS-CN model based on soil moisture proxies (SMP) (a synonym for SMA) and developed improved relationships for V 0 and S a. The model is very simple in use and has only one parameter as the existing SCS-CN method.

CN-Based PET and IWR Models

The proportionality concept (C = Sr concept) of the SCS-CN method was used by Mishra et al. (2014) in the simple water balance equation to derive a power relationship between CN and mean PET using the usually available long-term daily rainfall-runoff data. The general form of the CN (S) versus PET (ET) model can be expressed as:

$${\text{ET}} = \alpha S^{\beta }$$
(21)

where α and β are the coefficient and exponent, respectively. Because there exists an inverse relationship between S and CN (Eq. 4), Eq. (16) suggests ET to be high for the watersheds of low CN and vice versa. This ET-CN rationale was based on the following relationship as expressed here:

$$E = I_{\text{a}} + \frac{{\left( {P - I_{\text{a}} } \right)\left( {E^{*} - I_{\text{a}} } \right)}}{{\left( {P - I_{\text{a}} + S} \right)}}$$
(22a)
$$E \, = {\text{ ET }} + {\text{ ES }} + {\text{ EI}}$$
(22b)

where ET is the daily transpiration (moisture transferred from the soil to the atmosphere through the root-stem-leaf system of vegetation); ES is the daily soil evaporation (moisture transferred from the soil to the atmosphere by hydraulic diffusion through the pores of the soil); EI is the daily interception loss (water evaporated from the wet surface of the vegetation and wet surface of the soil) during rainstorm; and E* is the daily potential evapotranspiration. The concept was applied to eight catchments falling under different climatic and geographic settings of India, and a high correlation coefficient (= 0.96) was observed between S (CN) and PET values as shown in Fig. 2a, b.

Fig. 2
figure 2

Relation between Penman–Monteith PET and potential maximum retention for dry condition (SI) for Hemavati and Ghodahado catchments, India

Full size image

Erosion, Sedimentation, and Water Quality Models

This section briefly discusses some of the recently developed models based on SCS-CN method for erosion, sedimentation, and metal partitioning in hydrologic and environmental engineering. As discussed previously, most of the computer-based sedimentation simulation models such as AGNPS (Young et al. 1989), CREAMS (Knisel 1980), SWRRB (Arnold et al. 1990), SWAT (Neitsch et al. 2002), EPIC (Sharpley and Williams 1990), and GWLF (Haith and Shoemaker 1987) use the SCS-CN method as a component model for runoff estimation. However, as a model itself, the SCS-CN method has not witnessed many applications in the field of soil erosion, sedimentation, and water quality, despite some noteworthy works of Mishra et al. (2006b), Tyagi et al. (2008), Singh et al. (2008), and Bhunya et al. (2010).

Garen and Moore (2005) explored the applicability of SCS-CN methodology in water quality modeling and named it as “Curve Number Hydrology,” which signifies the versatility of the model itself. Therefore, the SCS-CN method has enormous potential and it is one of the “hydrological modeling techniques” available to the scientific community with its broad applicability.

SCS-CN-Based Metal Partitioning Models

The basic proportionality concept (C = Sr; where C = runoff coefficient = Q/(P − I a) and Sr = degree of saturation = (F/S); where F = cumulative infiltration) of the SCS-CN method was used by Mishra et al. (2004b) for partitioning of 12 metal elements, i.e., Zn, Cd, Pb, Ni, Mn, Fe, Cr, Mg, Al, Cu, and Na between dissolved and particulate-bound form. In metal partitioning analogy, two parameters, namely (i) the potential maximum desorption (\(\Psi\)) and (ii) the partitioning curve number (PCN) were postulated as analogous to the parameters S and CN of the SCS-CN model, respectively. These parameters were introduced, along with Ψ-PCN and Ψ-ADP, where ADP is the antecedent dry period similar to the AMC. The governing equations of the PCN model can be expressed as:

$$\begin{array}{*{20}l} {C_{p} = \frac{{\left( {C_{\text{T}} - i_{\text{f}} } \right)^{2} }}{{C_{\text{T}} - i_{\text{f}} + \psi }};} \hfill & {{\text{for}}\,C_{\text{T}} \ge i_{\text{f}} } \hfill \\ \end{array}$$
(23)
$${\text{if-}}\varPsi \;{\text{hypothesis}}:i_{\text{f}} = \lambda_{t} \psi$$
(24)
$$\varPsi {\text{-CN mapping}}\;{\text{PCN}} = \frac{1000}{1000 + \psi }$$
(25)

where C P = particulate-bound metal; C T = total metal; C d = dissolved metal; Ψ = potential maximum desorption; and i f = initial flush. Further, a new partitioning curve number (PCN) approach was also developed for partitioning heavy metals into dissolved and particulate-bound forms from urban snow melt, rainfall/runoff, and river flow environments using the analogy between SCS-CN method-based infiltration and metal sorption processes.

USLE Coupled SCS-CN-Based Sediment Yield Model

The popular and widely used models of SCS-CN method and universal soil loss equation (USLE) were coupled by Mishra et al. (2006b) for modeling rainstorm generated sediment yield from a watershed. The coupling is based on three hypotheses: (i) the runoff coefficient (C) is equal to the degree of saturation (Sr); (ii) the potential maximum retention (S) can be expressed in terms of the USLE parameters, and (iii) the sediment delivery ratio (DR) is equal to the runoff coefficient (C). Table 3 shows the summary of the developed models for different conditions. The developed models have ample potential for application to the ungauged watersheds.

Table 3 Formulation of rainfall-sediment yield and rainfall-runoff models (Mishra and Singh 2003a, b)
Full size table

SCS-CN-Based Conceptual Sediment Graph Model

The popular and extensively used Nash model (Nash 1957) -based instantaneous unit sediment graph (IUSG), SCS-CN method, and Power law (Novotny and Olem 1994) were coupled by Singh et al. (2008) to develop conceptual sediment graph models to get time distributed sediment yield on storm basis. The developed models consider different factors responsible for soil erosion and sediment yield. The sediment graph models (SGMs) for four different cases, depending on the number of model parameters, and these are designated as SGM1 through SGM4, respectively, as shown in Table 4. For SGM1, both the initial soil moisture V 0 and initial abstraction I a are assumed to be zero, i.e., V 0 = 0 and I a = 0. For SGM2, V 0 = 0, but I a ≠ 0. For SGM3, V 0 ≠ 0 and I a = 0. Finally, for SGM4, V 0 ≠ 0 and I a ≠ 0.

Table 4 Formulation of conceptual sediment graph models
Full size table

The models could be very useful in computation of time distributed sediment yield as well as total sediment yield and can be successfully applied for ungauged conditions as well. The models can be very useful for computing dynamic pollutant loads in water quality modeling if the sediment transports the pollutants that are toxic at high concentrations, requiring determination of peak, rather than average sediment flow rate.

SCS-CN-Based River Bank Filtration Model

The SCS-CN method was applied by Ojha (2012) in water quality modeling of the river bank filtration (RBF) process through coupling of the curve number (CN), filtration/kinetic coefficient (K), and the input applied to the system. It was found that the CN is related with the performance (output to input ratio, R) of a water quality system. Therefore, CN is dependent on all the parameters that influence the filtration/kinetic coefficient such as filtration velocity, medium properties and the distance between source water and abstraction point, and the source water quality. The model could be further explored for similar applications for its enhanced applicability and understanding.

Future Applications

Looking into diversified applications of SCS-CN methodology, including for the disciplines it was neither structured nor instituted, however, it has ample scope and should be explored for its’ greater role and applicability in the following fields of hydrology such as:

Environmental flow studies

Climate change studies

Irrigation scheduling

Surface and subsurface drainage studies

Droughts and Flood studies

Water resources vulnerability and reliability

Water quality modeling

Conclusions

With the versatile applications of the SCS-CN methodology throughout the spectrum of hydrologic problems, including for those it was neither structured nor instituted by its’ developers, this paper critically examines the hydrologic and structural modifications through which this methodology has undergone such as: (i) C = Sr concept and SMA procedure; (ii) CN estimation and their conversion techniques; (iii) linear/nonlinear initial abstraction (I a) and S relationships; (iv) storm duration and dynamic vs static infiltration; (v) slope and CN relationships; (vi) overall renewal of SCS-CN methodology through different concepts and theories. Some of the most recent and advanced applications of SCS-CN method were also discussed in this paper. Lastly, looking into its vast applicability, the future fields of applications were also explored to maintain its hierarchy in hydrologic models.