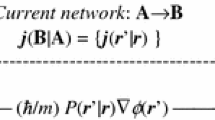Electron Communications and Chemical Bonds

Abstract

Recent developments in Orbital Communication Theory (OCT) of the chemical bond are summarized. Conditional probabilities defining molecular information networks are generated using the bond-projected Superposition Principle (SP) of quantum mechanics. The communications between atomic orbitals (AO) are proportional to squares of elements in the Charge-and-Bond-Order (CBO) matrix, thus being related to Wiberg’s quadratic indices of the chemical bond-order. Molecular propagation of information exhibits the communication-noise due to electron delocalization via the system chemical bonds, the entropic bond-covalency, measured by the channel conditional entropy. Information bond-ionicity is reflected by the channel mutual information (information flow) descriptor. The amplitude and probability information systems are distinguished, with the former being capable of the communication interference. This phase-aspect is lost in the probabilistic treatment of classical Information Theory (IT). The OCT perspective identifies the “indirect” chemical bonds in the “cascade” propagation realized via AO intermediates. These through-bridge “bonds” extend range of chemical interactions and supplement the “direct” (through-space) bonds realized by the constructive AO interference or direct communications between them. The flexible-input extension of OCT provides a continuous description of the fragment dissociation, giving a fair agreement between chemical expectations, OCT bond-multiplicities, and Wiberg bond-orders. The occupational orbital decoupling in OCT is properly represented, when separate communication systems for each occupied MO are used and their occupation-weighted entropy/information contributions are classified as bonding (positive) or antibonding (negative), in accordance with the signs of CBO matrix elements reflecting AO phases. These developments are illustrated in two-orbital model and representative π-electron systems. Resultant amplitude communications in multiconfiguration theory are explored, AO communications in Valence-Bond (VB) structures of H₂ are examined, and intrinsic nonorthogonality problem of VB description is discussed. The covalent structure generates noiseless channel involving solely the offdiagonal (inter-orbital) propagations, while the ionic state corresponds to deterministic channel of the diagonal (intra-atomic) communications.

The following tensor notation is adopted throughout this chapter: A denotes a scalar, A is the row (or column) vector, A represents a square or rectangular matrix, and the dashed symbol ${\hat{\mathbf{A}}}$ stands for the quantum-mechanical operator of the physical property A. The logarithm of the Shannon-type information measure is taken to an arbitrary but fixed base. In keeping with the custom in works on IT, the logarithm taken to base 2, log = log2, corresponds to the information content measured in bits (binary digits), while selecting log = ln expresses the amount of information in nats (natural units): 1 nat = 1.44 bits.

14.1 Introduction

The Information Theory (IT) [1,2,3,4,5,6] plays a unifying role in physics by facilitating derivation of its basic laws from a common principle of the Extreme Physical Information (EPI) [7,8,9,10,11,12,13]. Successful applications of IT to electronic structure phenomena have also demonstrated the theory potential in extracting chemical interpretations from calculated electron distributions, in terms of bonded atoms and chemical bonds [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. The theory allows one to describe hypothetical stages in a reconstruction of the electron distribution in chemical processes. The density-based concepts and techniques of classical IT of Fisher and Shannon [1, 2] have been successfully used to probe molecular electronic structure, the system chemical bonds, and reactivity. Displacements in the Shannon entropy and entropy deficiency relative to the promolecular reference constitute effective probes into the information origins of the chemical bonds [11,12,13, 25,26,27,28,29,30,31,32,33,34,35]. They provide efficient tools for an objective definition of bonded atoms [11, 18, 36], detecting the direct chemical bonds [26, 32,33,34,35], and monitoring the promotion/hybridization changes the Atoms-in-Molecules (AIM) undergo in their molecular environments. The nonadditive Fisher information in Atomic-Orbital (AO) resolution [8, 11,12,13, 37] generates the Contragradience (CG) probe [11,12,13, 26, 32,33,34,35] for locating bonding regions in molecules, while its analog in the Molecular Orbital (MO) perspective [37] defines the key concept of the Electron Localization Function (ELF) [38,39,40,41,42]. These gradient information quantities stress the importance of electronic kinetic energy in an exploration of the chemical bond pattern [33, 43,44,45].

Diverse information probes of molecular electron distributions increase our understanding of the chemical bond from the entropic perspective of IT. The communication-noise (covalency) and information-flow (ionic) components of entropic bond multiplicities have been shown to adequately reflect the accepted chemical intuition [11,12,13,14]. These IT descriptors can be generated for both molecule as a whole and its fragments. The OCT treatment of Diatomics-in-Molecules (DIM) [13, 14] reproduces the Wiberg [46] bond-orders in diatomic molecules and closely approximates these quadratic indices in polyatomic molecules. The extra computational effort of such IT analysis of the molecular bonding patterns is negligible, compared to the cost of standard SCF LCAO MO calculations of the molecular electronic structure, since practically all computations in orbital approximation already determine the CBO and kinetic energy data required in the CG probe of the bond localization or the OCT exploration of bond multiplicities and their composition.

There is a wide range of problems in the theory of electronic structure and chemical reactivity which can be successfully tackled using concepts and techniques of IT. For example, the IT-optimum pieces of electron density in molecular fragments have been derived from alternative global or local variational principles of IT [11,12,13, 18,19,20,21,22, 31, 36]. This approach has been shown to lead to the “stockholder” fragments of Hirshfeld [47]. It provides an entropic justification of this popular density-partitioning scheme, generates criteria of molecular similarity, tackles the Polarization/Promotion (P) and Charge-Transfer (CT) phenomena in the reorganization of the system constituent atoms, etc. Additional diagnostic problems in the theory of molecular electronic structure deal with the shell structure and electron localization in atoms and molecules. The theory allows one to locate electrons and chemical bonds [11,12,13, 26, 32,33,34,35], offers a thermodynamic-like perspective on density fluctuations and flows of electrons between constituent fragments in molecules [18, 23, 48], and formulates a new class of entropic descriptors of the chemical bond multiplicity and its covalent/ionic composition [11,12,13,14, 19, 49,50,51,52,53,54,55,56,57,58,59,60].

In molecules, the information content of their electronic states is constantly scattered between bonded atoms and AO they contribute to the bond system. The spread of information is affected via the network of chemical bonds. In a sense, AIM talk to one another. This exchange of information takes the form of either the direct communication, a “dialog” between the interacting AO, or the indirect information propagation, a “gossip” spread via AO intermediates. These two mechanisms give rise to the direct- and indirect-bond components, respectively, related to the mutual and cascade communications between AO, respectively. Therefore, the chemical interactions between the specified pair of “terminal” AO have both the direct (through-space) and indirect (through-bridge) components. The “order” of the former quickly vanishes with increasing separation between atoms. The overall bond-order between more distant atomic partners can still assume appreciable values when some of the remaining atoms form an effective chemical bridge which links these terminal AIM.

The chemical bond multiplicities, reflecting the IT bond “orders” in bits, have been adequately probed using techniques and entropic quantities developed in IT of communication devices (information systems) [2, 5, 6, 11,12,13,14, 19]. This additional perspective, called the Orbital Communication Theory (OCT) [61,62,63,64,65,66,67,68,69,70], increases our insight and understanding of the information origins of chemical bonds. In OCT, one introduces the entropic bond multiplicities and determines their IT-covalent and IT-ionic components. The resultant IT-covalency and IT-ionicity components have been related to the nonadditive and additive information descriptors of AO probability-channels [78]. The cascade extension allows one to identify the indirect mechanism of chemical interactions effected through “bridges” (orbital intermediates) [71,72,73,74,75,76], which complements the familiar direct mechanism realized through “space,” via a constructive interference between orbitals. The (bond-projected) Superposition Principle (SP) of quantum mechanics [77] has been used to generate the orbital conditional probabilities determining electron communications in molecules [11,12,13,14, 68]. The inter-orbital conditional probabilities it generates are proportional to the quadratic bond indices formulated in MO theory, and hence strong communications correspond to strong Wiberg [46] bond-orders. The IT approach has also revealed new stages in the bond-breaking-bond-forming mechanisms of elementary chemical reactions [79,80,81].

In OCT, the direct bond reflects the mutual communications between bonded atoms, while the bridge bond is realized indirectly, through the cascade communications involving remaining orbitals/atoms. The latter form effective bridges for the implicit chemical coupling between more distant atoms. The most efficient bridges are the real (chemical) bridges of bonded atoms connecting the specified “terminal” atoms. The bonded status of AIM can be thus felt also at larger separations provided there exists a real chemical bridge of the direct bonds connecting them. This indirect coupling of basis functions in molecular states has been first conjectured to explain the central bond in small propellanes, lacking the charge/information accumulation between the bridgehead carbons. This bonding phenomenon has also prompted the alternative, Valence-Bond (VB) [82] inspired explanation, through the charge-shift mechanism [83], which attributes such an indirect “bond” to instantaneous charge fluctuations between distant atoms.

It has already been demonstrated how important the “entropic” tools of IT are for gaining a better understanding of the “chemistry” behind the calculated molecular states, e.g., [11,12,13,14]. A chemical understanding of the electronic structure of molecular systems calls for transforming the computational results into statements in terms of such chemical concepts as bonded atoms, building blocks of molecules, their collections forming functional groups, and chemical bonds representing AIM “connectivities.” A collection of the constituent free atoms shifted to their actual positions in a molecule determines the so-called “promolecule” [47], which constitutes the standard reference for extracting changes in the electron distribution due to the bond formation, reflected by the density difference (deformation) function [11]. In Schrödinger’s quantum mechanics, the molecular electronic state is determined by the system wavefunction, the (complex) amplitude of the particle probability distribution, which carries its resultant information content. Both the electron density or its shape-factor—the probability distribution determined by the wavefunction modulus—and the system current-distribution related to the gradient of the wavefunction phase ultimately contribute to the resultant information content of molecular states. The probability reveals the state classical-information contribution, while distributions of the spatial phase or its gradient (electronic current) determine the state nonclassical complement in the resultant information measure [14, 84,85,86,87,88,89,90,91,92,93]. Similar generalizations of the entropy-deficiency or information-distance concepts and molecular information channels have also been established. In such a combined IT description, the principle of the extreme overall information content is used to determine the molecular phase-equilibria in molecules [14, 84,85,86,87,88,89,90,91,92,93]. This maximum entropy rule has been shown to give rise to the phase-transformation of molecular electronic states into their equilibrium counterparts. Thermodynamic analogies have been discussed, and a local phenomenological description of molecular processes has been introduced [14, 88], in spirit of the ordinary irreversible thermodynamics [94]. The continuity equation for the state resultant entropy has been explored [95, 96], and a local temporal aspect of the promolecule→molecule reconstruction in the system electronic structure has been addressed [97].

This IT perspective, complementary to the MO description of quantum chemistry, brings important new insights and enhances our understanding of the complex phenomena of the chemical bond and reactivity. It generates new probes for detecting chemical bonds in molecules, uncovers the entropic and communication origins of chemical interactions, and explains the direct and indirect sources of their resultant multiplicities. In the present overview, we emphasize some additional possibilities of OCT in exploring patterns of chemical bonds, understanding the orbital-decoupling and communication interference phenomena, and probing the competition between entropic bond-covalency and bond-ionicity components.

14.2 Amplitude and Probability Channels

For simplicity, we focus on molecular information channels in the electronic state described by a single Slater determinant, e.g., the ground-state configuration Ψ ^UHF₀ (N) = det[ψ ⁰] ≡ |ψ ⁰₁ , ψ ⁰₂ , …, ψ ⁰ _N |, where spin-MO (SMO) ψ ⁰(q) = {φ ⁰ _s (r) ξ ⁰ _s (σ)} combine the spatial (MO) components φ ⁰(r) = {φ ⁰ _s (r)} and spin functions ξ ⁰(σ) = {ξ ⁰ _s (σ)} of an electron. In typical Unrestricted Hartree–Fock (UHF) SCF LCAO MO calculations or the spin-resolved Kohn–Sham (KS) Density Functional Theory (DFT) an exploration of chemical bonds calls for the (orthonormal) AO basis set χ = (χ ₁, χ ₂, …, χ _m ), which expresses the spatial (orthonormal) MO components φ = {φ _s } = χ C. The ground-state Ψ₀(N) is then shaped by N-lowest, singly-occupied SMO ψ ⁰ or their spatial (MO) components φ ⁰ = {φ ⁰ _s }, the configuration bonding subspace of the occupied MO, φ ⁰ = χ C ⁰, which defines the associated MO-projector

$$ {\hat{\text{P}}}_{\varvec{\varphi }}^{0} = \sum\nolimits_{s} {\left| {\varvec{\varphi}_{s} } \right\rangle n_{s}^{0} \left\langle {\varvec{\varphi }_{s} } \right|} = \left| {\varvec{\varphi }^{0} } \right\rangle {\mathbf{n}}^{0} \left\langle {\varvec{\varphi}}^{0} \right| = \left|\varvec{\chi}\right\rangle {\mathbf{C}}^{0} \,{\mathbf{C}}^{0\dag } \left\langle\varvec{\chi}\right| \equiv \left|\varvec{\chi}\right\rangle {\varvec{\upgamma}}^{0} \left\langle\varvec{\chi}\right|; $$

(14.1)

here the diagonal matrix n ⁰ = {n ⁰ _s δ _s,s′} combines the MO occupation numbers in the ground-state configuration: n ⁰ _s  = {1, s ≤ N; 0, s > N}. This projection operator gives rise to the corresponding (idempotent) Charge-and-Bond-Order (CBO) matrix in AO representation,

$$ {\varvec{\upgamma}}^{0} = \{ \gamma_{i,j}^{0} \} = \left\langle\varvec{\chi}\right|{\hat{\text{P}}}_{\varvec{\varphi }}^{0} \left|\varvec{\chi}\right\rangle = \left\langle {\varvec{\chi}|\varvec{\varphi }} \right\rangle {\mathbf{n}}^{0} \left\langle {\varvec{\varphi }|\varvec{\chi}} \right\rangle = \left\langle {\varvec{\chi}|\varvec{\varphi }^{0} } \right\rangle \left\langle {\varvec{\varphi }^{0} |\varvec{\chi}} \right\rangle = {\mathbf{C}}^{0} {\mathbf{C}}^{0\dag } ,\,({\varvec{\upgamma}}^{0} )^{2} = {\varvec{\upgamma}}^{0} . $$

(14.2)

In accordance with the quantum-mechanical SP [77], the joint probability of the given pair of the input (χ _i ) and output (χ _j ) AO events in the molecular state Ψ₀ defined by its bond system φ ⁰ is given by the square of the corresponding amplitude proportional to the CBO matrix element coupling the two basis functions [11,12,13,14]:

$$ \begin{aligned} P(\chi_{i} ,\,\chi_{j} |\Psi _{0} ) & \equiv P^{0} (i,\,j) = |A(\chi_{i} ,\,\chi_{j} |\Psi _{0} )|^{2 } = \gamma_{i,j}^{0} \,\gamma_{j,i}^{0} /N \\ & = \left\langle {\chi_{i} } \right|{\hat{\text{P}}}_{\varvec{\varphi }}^{0} \left| {\chi_{j} } \right\rangle \left\langle {\chi_{j} } \right|{\hat{\text{P}}}_{\varvec{\varphi }}^{0} \left| {\chi_{j} } \right\rangle \equiv \left| {\chi_{i} } \right\rangle \equiv \left\langle {\chi_{i} } \right|{\hat{\text{P}}}_{\varvec{\varphi }}^{0} {\hat{\text{P}}}_{j}^{{}} {\hat{\text{P}}}_{\varvec{\varphi }}^{0} \left| {\chi_{i} } \right\rangle \equiv \left\langle {\chi_{i} } \right|{{\hat{\tilde{\text{P}}}}}_{j}^{0} \left| {\chi_{i} } \right\rangle \\ & = P^{0} (j,\,i) = \left\langle {\chi_{j} } \right|{\hat{\text{P}}}_{\varvec{\varphi }}^{0} \left| {\chi_{i} } \right\rangle \left\langle {\chi_{i} } \right|\,{\hat{\text{P}}}_{\varvec{\varphi }}^{0} \,\left| {\chi_{j} } \right\rangle \equiv \left\langle {\chi_{j} } \right|{\hat{\text{P}}}_{\varvec{\varphi }}^{0} {\hat{\text{P}}}_{i}^{{}} {\hat{\text{P}}}_{\varvec{\varphi }}^{0} \left| {\chi_{j} } \right\rangle \equiv \left\langle {\chi_{j} } \right|{{\hat{\tilde{\text{P}}}}}_{i}^{0} \left| {\chi_{j} } \right\rangle , \\ \end{aligned} $$

$$ \sum\nolimits_{j} {P^{0} (i,\,j)} = N^{ - 1} \sum\nolimits_{j} {\gamma_{i,j}^{0} \gamma_{j,i}^{0} = \gamma_{i,i}^{0} /N = P(i|\Psi _{0} ) \equiv p_{i}^{0} ;} $$

(14.3)

here ${{\hat{\tilde{\text{P}}}}}_{k}^{0} = {\hat{\text{P}}}_{\varvec{\varphi }}^{0} {\hat{\text{P}}}_{k}^{{}} {\hat{\text{P}}}_{\varvec{\varphi }}^{0}$ denotes the resultant AO projection within the bond-subspace φ ⁰. The associated conditional AO probabilities P ⁰(χ′|χ), of the output events χ′ = {χ _j } given the input events χ = {χ _i }, P ⁰(χ′|χ) = {P ⁰(j|i) ≡ $P_{i \to j}^{0}$  = P ⁰(i, j)/p ⁰ _i }, the squared moduli of the corresponding amplitudes { $P_{i \to j}^{0}$≡| $A_{i \to j}^{0}$|²}, then read:

$$ P^{0} (j|i) \equiv P_{i \to j}^{0} \equiv |A_{i \to j}^{0} |^{2 } = (\gamma_{i,i}^{0} )^{ - 1} \gamma_{i,j}^{0} \gamma_{j,i}^{0} \equiv N_{i}^{0} \gamma_{i,j}^{0} \gamma_{j,i}^{0} ,\,\sum\nolimits_{j} {P^{0} (j|i)} = 1; $$

(14.4)

here N ⁰ _i  = ($\gamma_{i,i}^{0}$)⁻¹ stands for the normalization constant of the scattering probabilities originating from the specified input χ _i , P ⁰(χ′|i) = {P ⁰(j|i), j = 1, 2, …, m}, the ith row of P ⁰(χ′|χ). They reflect the electron delocalization in the occupied MO subspace and identify the scattering amplitudes A ⁰(χ′|χ) = {A ⁰(j|i) ≡ $A_{i \to j}^{0}$ } related to the corresponding elements of the CBO matrix γ ⁰:

$$ A_{i \to j}^{0} = (\gamma_{i,i}^{0} )^{ - 1/2} \gamma_{i,j}^{0} \equiv \left[ {N_{i}^{0} } \right]^{1/2} \gamma_{i,j}^{0} $$

(14.5)

In the RHF description of the closed-shell state, each of the N/2 lowest (doubly-occupied) MO, φ ^o = (φ ₁, φ ₂, …, φ _N/2), accommodates two spin-paired electrons: Ψ ^RHF₀ (N) = |φ ₁ α, φ ₁ β, …, φ _N/2 α, φ _N/2 β|, so that ${\hat{\text{P}}}_{\varvec{\varphi }}^{0} = 2\left| {\varvec{\varphi }^{o} } \right\rangle \left\langle {\varvec{\varphi }^{o} } \right|$ ≡ $2 {\hat{\text{P}}}_{\varvec{\varphi }}^{o}$. The CBO idempotency then implies

$$ ({\hat{\text{P}}}_{\varvec{\varphi }}^{0} )^{2} = [2\left| {\varvec{\varphi }^{o} } \right\rangle \left\langle {\varvec{\varphi }^{o} } \right|]^{2} = 4\left| {\varvec{\varphi }^{o} } \right\rangle \left\langle {\varvec{\varphi }^{o} } \right| = 2 {\hat{\text{P}}}_{\varvec{\varphi }}^{o} = {\hat{\text{P}}}_{\varvec{\varphi }}^{0} $$

(14.6)

and hence:

$$ {{\varvec{\upgamma}}^{0} } = \left\langle\varvec{\chi}\right|{\hat{\text{P}}}_{\varvec{\varphi }}^{0} \left|\varvec{\chi}\right\rangle = 2\left\langle\varvec{\chi}\right|{\hat{\text{P}}}_{\varvec{\varphi }}^{o} \left|\varvec{\chi}\right\rangle \equiv 2{{\varvec{\upgamma}}^{0} } ,\,({{\varvec{\upgamma}}^{0} } )^{2} ={{\varvec{\upgamma}}^{0} } = \{\gamma_{i,j}^{o} \} ,\,\left( {{\varvec{\upgamma}}^{0} } \right)^{2} = 4({{\varvec{\upgamma}}^{0} } )^{2} = 4{{\varvec{\upgamma}}^{0} } = 2{{\varvec{\upgamma}}^{0} } . $$

(14.7)

For such states, the representative conditional probability of the molecular AO channel reads:

$$ \begin{aligned} P^{0} (j|i) & \equiv P_{i \to j}^{0} = |A_{i \to j}^{0} |^{2} = (2\gamma_{i,i}^{0} )^{ - 1} \gamma_{i,j}^{0} \gamma_{j,i}^{0} \equiv N_{i}^{0} \gamma_{i,j}^{0} \gamma_{j,i}^{0} = (\gamma_{i,i}^{o} )^{ - 1} \gamma_{i,j}^{o} \gamma_{j,i}^{o} \equiv N_{i}^{o} \gamma_{i,j}^{o} \gamma_{j,i}^{o} , \\ A^{0} (j|i) & \equiv A_{i \to j}^{0} = \left( {N_{i}^{0} } \right)^{ - 1/2} \gamma_{i,j}^{0} = \left( {N_{i}^{o} } \right)^{ - 1/2} \gamma_{i,j}^{o} . \\ \end{aligned} $$

(14.8)

The classical, probability-channel, is determined by these conditional AO probabilities P(χ′|χ) = {P(j|i) = P _i→j },

$$ \varvec{\chi}- {\mathbf{P}}(\varvec{\chi}^{{\prime }} |\varvec{\chi}) \to\varvec{\chi}^{{\prime }} . $$

(14.9)

It loses the memory of the AO phases in the scattering amplitudes A(χ′|χ) = {A _i→j }, i.e., phases of { $\gamma_{i,j}^{0}$}. These “coherencies” are preserved only in the associated amplitude channel for the direct electron communications in a molecule,

$$ \left|\varvec{\chi} \right\rangle - {\mathbf{A}}(\varvec{\chi}^{{\prime }} |\varvec{\chi} ) \to \left|\varvec{\chi}^{{\prime }} \right\rangle , $$

(14.10)

which is thus capable of reflecting the quantum-mechanical interference between such elementary communications.

This observation also applies to a sequential (“product”) arrangements of several direct channels, called the information “cascades,” for indirect (“bridge”) communications between atomic orbitals in molecules. For example, the single-AO intermediates χ′′ in the sequential three-orbital scatterings χ→χ′′→χ′ define the probability- and amplitude-cascades:

$$ \varvec{\chi}- [{\mathbf{P}}(\varvec{\chi}^{{\prime \prime }} |\varvec{\chi}) \to\varvec{\chi}^{{\prime \prime }} - {\mathbf{P}}(\varvec{\chi}^{{\prime }} |\varvec{\chi}^{{\prime \prime }} )] \to\varvec{\chi}^{{\prime }} \equiv\varvec{\chi}- {\mathbf{P}}[(\varvec{\chi}^{{\prime }} |\varvec{\chi});\varvec{\chi}^{{\prime \prime }} ] \to\varvec{\chi}^{{\prime }} , $$

$$ \left| \varvec{\chi} \right\rangle - [{\mathbf{A}}(\varvec{\chi}^{{\prime \prime }} |\varvec{\chi} ) \to \left| {\varvec{\chi}^{{\prime \prime }} } \right\rangle - {\mathbf{A}}(\varvec{\chi}^{{\prime }} |\varvec{\chi}^{{\prime \prime }} )] \to \left| {\varvec{\chi}^{{\prime }} } \right\rangle \equiv \left| \varvec{\chi} \right\rangle - {\mathbf{A}}[(\varvec{\chi}^{{\prime }} |\varvec{\chi} );\,\varvec{\chi}^{{\prime \prime }} ] \to \left| {\varvec{\chi}^{{\prime }} } \right\rangle . $$

(14.11)

The indirect conditional probabilities between AO events and their amplitudes are then given by products of the elementary two-orbital communications in each direct subchannel:

$$ P[(j|i);\,k] \equiv P_{i \to j;k} = P_{i \to k} P_{k \to j} ,\quad A[(j|i);\,k] \equiv A_{i \to j;k} = A_{i \to k} A_{k \to j} . $$

(14.12)

Therefore, such bridge probabilities and underlying amplitudes can be straightforwardly derived from the direct scatterings. They satisfy the relevant bridge-normalizations, expressed by the sum-rules over AO events in the intermediate and final outputs:

$$ \sum\nolimits_{k} {(\sum\nolimits_{j} {P_{i \to j;k} } )} = \sum\nolimits_{k} {P_{i \to k} } = 1. $$

(14.13)

This single-cascade development can be straightforwardly generalized to any bridge-order t. The amplitude $A_{i \to j}^{(t)}$ for the complete t-cascade, consisting of t consecutive direct channels involving all AO, preserves the direct scattering probabilities [14, 73],

$$ {\mathbf{P}}[(\varvec{\chi}^{{\prime }} |\varvec{\chi});t -\varvec{\chi}] = \{ \left| {A_{i \to j}^{(t)} } \right|^{2} = \left| {A_{i \to j}^{{}} } \right|^{2} = P_{i \to j} \} = {\mathbf{P}}(\varvec{\chi}^{{\prime }} |\varvec{\chi}), $$

(14.14)

thus satisfying the important consistency requirement of the stationary character of the molecular channel. The relevant sum-rules for such bridge conditional probabilities read:

$$ \begin{aligned} \sum\nolimits_{k} {} \sum\nolimits_{l} {} \ldots \sum\nolimits_{m} {} \sum\nolimits_{n} {} \left[ {\sum\nolimits_{j} {P_{i \to j;k,l, \ldots ,m,n} } } \right] & = \sum\nolimits_{k} {} \sum\nolimits_{l} {} \ldots \sum\nolimits_{m} {} \left[ {\sum\nolimits_{n} {P_{i \to n;k,l, \ldots ,m} } } \right] \\ & = \sum\nolimits_{k} {} \sum\nolimits_{l} {} \ldots \left[ {\sum\nolimits_{m} {P_{i \to m;k,l, \ldots } } } \right] = \ldots & \\ & = \sum\nolimits_{k} {} \left[ {\sum\nolimits_{l} {P_{i \to l;k} } } \right] = \sum\nolimits_{k} {P_{i \to k} } = 1. \\ \end{aligned} $$

(14.15)

For the specified pair of “terminal” AO, say χ _i ∈ χ and χ _j ∈ χ′, one can similarly examine the indirect scatterings via the molecular bond system in the incomplete cascades consisting of the remaining (“bridge”) functions χ ^b = {χ _k≠(i,j)}, with the two terminal AO being then excluded from the set of admissible intermediate scatterers. The associated bridge-communications give rise to the indirect (through-bridge) components of the entropic bond multiplicities [71,72,73,74,75,76], which complement the familiar direct (through-space) chemical “bond-orders” and provide a novel IT perspective on chemical interactions between more distant AIM, alternative to the fluctuational Charge-Shift mechanism [83] in VB theory.

14.3 Entropic Multiplicities of Direct and Bridge-Bonds

We continue with a brief summary of the entropy/information descriptors of a transmission of the electron-assignment “signals” in such molecular communication systems. The classical orbital networks propagate the conditional probabilities of electron assignments to basis functions of SCF LCAO MO calculations. The probability networks lose memory of the phase-aspect of this information propagation, preserved in the amplitude systems, which becomes crucial in the multi-stage (cascade, bridge) propagations. The underlying conditional probabilities or the associated amplitudes, for the quantum scattering from the emitting (input) AO states to alternative monitoring (output) AO states, follow from the bond-projected SP.

In a classical communication device, the signal emitted from n “inputs” a = (a ₁, a ₂, …, a _n ) of the channel source A is characterized by the input-probability distribution P(a) ≡ p = (p ₁, p ₂, …, p _n ), which describes the way the channel is exploited. It is received (monitored) at m alternative “outputs” b = (b ₁, b ₂, …, b _m ) in the system receiver B. The system communication noise is then generated by the conditional probabilities of observing specific “outputs” given “inputs”,

$$ {\mathbf{P}}({\mathbf{B}}|{\mathbf{A}}) \equiv {\mathbf{P}}({\varvec{b}}|{\varvec{a}}) = \{ P(b_{j} |a_{i} ) = P\left( {a_{i} ,\,b_{j} } \right)/P\left( {a_{i} } \right) \equiv P(j|i)\} , $$

(14.16)

where P(a, b) = {P(a _i , b _j ) ≡ P(i, j)} groups probabilities of the joint occurrence of the specified pair of the input-and-output events. The distribution of the output signal among the detection events b then reads:

$$ \varvec{P(b)} \equiv \varvec{q} = (q_{1} ,\,q_{2} ,\, \ldots ,\,q_{m} ) = \varvec{p}\,{\mathbf{P}}(\varvec{b}|\varvec{a}). $$

(14.17)

In general, the input and output probabilities are mutually dependent. One thus decomposes the joint probabilities P(a, b) ≡ P of the joint events (a, b) as products of the “marginal” probabilities of events in one set, say P(a), and the corresponding conditional probabilities P(b|a) = {P(j|i)} of outcomes in the other set b, given that events a have already occurred: P = {P(i, j) = p _i P(j|i)}. The Shannon [2] entropy of the joint distribution P(a, b) can be then expressed as the sum of the average entropy S(p) = −∑ _i p _i logp _i in the marginal probability distribution and the average conditional entropy S(q|p) in q given p,

$$ S\left( {\mathbf{P}} \right) = S\left( \varvec{p} \right) + S\varvec{(q|p)} = S\left( \varvec{q} \right) + S\varvec{(p|q)}, $$

(14.18)

$$ S\varvec{(q|p)} = - \sum\nolimits_{i} {} \sum\nolimits_{j} {} P\left( {i,\,j} \right)\,\log \left[ {P\left( {i,\,j} \right)/p_{i} } \right] = - \sum\nolimits_{i} {p_{i} } \sum\nolimits_{j} {P(j|i)} \,\log \,P(j|i) \equiv S, $$

measuring the network average communication “noise” and describing the indeterministic (delocalization) facet of molecular communications. The channel complementary descriptor, the mutual information I(p: q) in the network output and input probability distributions,

$$ \begin{aligned} I\left( {\varvec{p:q}} \right) & = \sum\nolimits_{i} {} \sum\nolimits_{j} {P\left( {i,\,j} \right)} \,{ \log }\left[ {P\left( {i,\,j} \right)/\left( {p_{i} q_{j} } \right)} \right] \\ & = S\left( \varvec{p} \right) + S\left( \varvec{q} \right) - S\left( {\mathbf{P}} \right) = S\left( \varvec{q} \right) - S\varvec{(q|p)} = S\left( \varvec{p} \right) - S\varvec{(p|q)} \equiv I, \\ \end{aligned} $$

(14.19)

then reflects its deterministic (localization) aspect. The input probabilities p reflect the way the channel is used or probed. The conditional entropy S(q|p) measures the average noise in the A→B transmission, i.e., the residual indeterminacy about the output signal, when the input signal is known beforehand. The conditional entropy S(p|q) reflects a fraction of S(p) = S(p|q) + I(p : q) which has been transformed into “noise” as a result of the input signal being scattered in the information channel. Accordingly, S(q|p) reflects the noise part of S(q) = S(q|p) + I(p : q). An observation of the output signal provides the amount of information given by mutual information I(p : q), which reflects the channel information flow.

In OCT, the AO molecular channel propagates signals (probabilities or amplitudes) of the electron assignments to basis functions χ = (χ ₁, χ ₂, …, χ _m ). The underlying conditional probabilities of the output AO events, given the input AO events, P(χ′|χ) = {P(χ _j |χ _i ) ≡ P(j|i) ≡ P _i→j ≡ A(j|i)² ≡ (A _i→j )²}, or the associated scattering amplitudes A(χ′|χ) = {A(j|i) = A _i→j } of the emitting (input) states $\left| \varvec{a} \right\rangle = \left| \varvec{\chi} \right\rangle = \left\{ {\left| {\varvec{\chi}_{i} } \right\rangle } \right\}$ among the receiving (output) states $\left| \varvec{b} \right\rangle = \left| {\varvec{\chi}^{{\prime }} } \right\rangle = \left\{ {\left| {\varvec{\chi}_{j} } \right\rangle } \right\}$, have been discussed in the preceding section. The entropy/information indices of the overall IT-covalent and IT-ionic components (in bits) of the system chemical bonds represent the complementary descriptors of the average communication noise and the amount of information flow in the AO-resolved molecular channel.

One observes that the molecular input signal P(a) ≡ p ⁰ generates the same distribution in the output of this network,

$$ \varvec{q}^{0} = \varvec{p}^{0} \,{\mathbf{P}}^{0} \varvec{(b|a)} = \{ \sum\nolimits_{i} {p_{i}^{0} } \,P^{0} (j|i) \equiv \sum\nolimits_{i} {P^{0} \left( {i,j} \right)} = p_{j}^{0} \} = \varvec{p}^{0} , $$

(14.20)

thus identifying p ⁰ and q ⁰ as stationary vectors of AO probabilities in the molecular ground state. This purely molecular channel is devoid of any reference (history) of the chemical bond formation and generates the average noise index of the IT bond-covalency measured by the average conditional entropy of the system AO outputs given AO inputs: S(q ⁰|p ⁰) ≡ S. The AO channel with the promolecular input signal P(a ₀) = p ₀ = {p _i,0}, of AO in the system free constituent atoms, refers to the initial stage in the bond-formation process. It corresponds to the ground-state occupations of AO contributed to chemical bonds by the system constituent atoms, before their mixing into MO. These reference input probabilities give rise to the average information-flow index of the system IT bond-ionicity, given by the mutual information in the channel promolecular inputs and molecular outputs:

$$ \begin{aligned} I\left( {\varvec{p}_{0} :\,{\mathbf{q}}^{0} } \right) & = \sum\nolimits_{i} {} \sum\nolimits_{j} {P^{0} \left( {i,\,j} \right)} \,\log \left[ {p_{i}^{0} \,P^{0} \left( {i,\,j} \right)/\left( {p_{i}^{0} \,q_{j}^{0} \,p_{i,0} } \right)} \right] \\ & = \sum\nolimits_{i} {} \sum\nolimits_{j} {P^{0} \left( {i,\,j} \right)} [ - \log q_{j}^{0} + \log \left( {p_{i}^{0} /p_{i,0} } \right) + \log P^{0} (j|i)] = S\left( {\varvec{q}^{0} } \right) + \Delta S(\varvec{p}^{0} |\varvec{p}_{0} ) - S \equiv I_{0} , \\ \end{aligned} $$

(14.21)

where the entropy deficiency (missing-information) of Kullback and Leibler [3],

$$ \Delta S\varvec{(p}^{\varvec{0}} \varvec{|p}_{\varvec{0}} \varvec{)} = \sum\nolimits_{i} {p_{i}^{0} \log \left( {p_{i}^{0} /p_{i,0} } \right)} , $$

(14.22)

measures the entropic similarity (information distance) between the compared probability vectors. The common amount of information I(p ₀ : q ⁰) in the promolecular and molecular probability distributions reflects the fraction of the initial information content S(p ⁰) which has not been dissipated as noise in the molecular communication system. In particular, for the molecular input p ⁰ and hence: ΔS(p ⁰|p ⁰) = 0, I(p ⁰: q ⁰) = S(q ⁰) − S ≡ I.

The sum of these bond-multiplicity components, e.g.,

$$ M_{0} \left( {\varvec{p}_{0} \varvec{;}\,\varvec{q}^{0} } \right) = S + I_{0} = S\left( {\varvec{q}^{0} } \right) + \Delta S(\varvec{p}^{0} |\varvec{p}_{0} ) \equiv M_{0} , $$

(14.23)

measures the overall IT bond-multiplicity index relative to the promolecular reference, of all bonds in the molecular system. For the molecular input, this quantity preserves the Shannon entropy of the molecular probabilities:

$$ M_{0} \left( {\varvec{p}^{0} ;\,\varvec{q}^{0} } \right) = S(\varvec{q}^{0} |\varvec{p}^{0} ) + I\left( {\varvec{p}^{0} \,:\,\varvec{q}^{0} } \right) = S\left( {\varvec{q}^{0} } \right) \equiv M. $$

(14.24)

These IT bond-multiplicity descriptors can be expressed in terms of the additive and nonadditive components of the Shannon entropy contained in the CBO matrix γ ⁰:

$$ \begin{aligned} S^{total} \left( {\varvec{\upgamma}^{0} } \right) & \equiv N\,\{ S\left[ {{\mathbf{P}}^{0} \left( {\varvec{a,}\,\varvec{b}} \right)} \right] - \log N\} = - \sum\nolimits_{i} {} \sum\nolimits_{j} {} \gamma_{i,j}^{0} \gamma_{j,i}^{0} \log (\gamma_{i,j}^{0} \gamma_{j,i}^{0} ) \equiv S^{add.} \left( {\varvec{\upgamma}^{0} } \right) + S^{nadd.} \left( {\varvec{\upgamma}^{0} } \right), \\ S^{add.} \left( {\varvec{\upgamma}^{0} } \right) & = N\,[S\left( {\varvec{p}^{0} } \right) - \log N] = - \sum\nolimits_{i} {} \gamma_{i,i}^{0} \log \gamma_{i,i}^{0} , \\ S^{nadd.} \left( {\varvec{\upgamma}^{0} } \right) & = S^{total} \left( {\varvec{\upgamma}^{0} } \right) - S^{add.} \left( {\varvec{\upgamma}^{0} } \right) = N\,\{ S\left[ {{\mathbf{P}}^{0} \left( {\varvec{a,}\,\varvec{b}} \right)} \right] - M\left( {\varvec{p}^{0} ;\,\varvec{q}^{0} } \right)\} . \\ \end{aligned} $$

(14.25)

The covalent descriptor S(q ⁰|p ⁰) = S is then decomposed into the difference between the total and additive contributions,

$$ \begin{aligned} S & = - \sum\nolimits_{i} {} \sum\nolimits_{j} {P^{0} \left( {i,\,j} \right)\,} \log \left[ {P^{0} \left( {i,\,j} \right)/p_{i}^{0} } \right] = S[{\mathbf{P}}^{0} \left( {\varvec{a},\,\varvec{b}} \right)] - S\left( {\varvec{p}^{0} } \right) \\ & = N^{ - 1} [ - \sum\nolimits_{i} {} \sum\nolimits_{j} {\gamma_{i,j}^{0} \gamma_{j,i}^{0} \log (} \gamma_{i,j}^{0} \gamma_{j,i}^{0} ) + \sum\nolimits_{i} {\gamma_{i,i}^{0} \log \gamma_{i,i}^{0} ]} \\ & \equiv N^{ - 1} \,\{ S^{total} \left( {{\varvec{\upgamma}}^{0} } \right) - S^{add.} \left( {{\varvec{\upgamma}}^{0} } \right)\} \equiv N^{ - 1} S^{nadd.} \left( {{\varvec{\upgamma}}^{0} } \right), \\ \end{aligned} $$

(14.26)

which defines the associated nonadditive component S ^nadd.(γ ⁰), while the molecular information-flow quantity I(p ⁰: q ⁰) of Eq. (14.19) is determined by the difference between the additive and nonadditive components:

$$ \begin{aligned} I\left( {\varvec{p}^{0} :\varvec{q}^{0} } \right) & = \sum\nolimits_{i} {} \sum\nolimits_{j} {P^{0} \left( {i,\,j} \right)} \log \left[ {P^{0} \left( {i,\,j} \right)/\left( {p_{i}^{0} \,q_{j}^{0} } \right)} \right] = S\left( {\varvec{p}^{0} } \right) + S\left( {\varvec{q}^{0} } \right) - S[{\mathbf{P}}^{0} \left( {\varvec{a},\varvec{b}} \right)] \\ & = N^{ - 1} [2S^{add.} \left( {{\varvec{\upgamma}}^{0} } \right) - S^{total} \left( {{\varvec{\upgamma}}^{0} } \right)] + \log N = N^{ - 1} [S^{add.} \left( {{\varvec{\upgamma}}^{0} } \right) - S^{nadd.} \left( {{\varvec{\upgamma}}^{0} } \right)] + \log N. \\ \end{aligned} $$

(14.27)

These two components generate the molecular bond-multiplicity index of Eq. (14.24) related to the additive contribution alone:

$$ M\left( {\varvec{p}^{0} ;\,\varvec{q}^{0} } \right) = S(\varvec{q}^{0} |\varvec{p}^{0} ) + I\left( {\varvec{p}^{0} :\varvec{q}^{0} } \right) = S\left( {\varvec{q}^{0} } \right) = N^{ - 1} S^{add.} ({\varvec{\upgamma}}^{0} ) + \log N. $$

(14.28)

To summarize, in this single-determinant approximation, the additive part of the Shannon entropy due to molecular communications between AO generates the overall IT bond-multiplicity index, the nonadditive contribution reflects the channel covalent (indeterministic) descriptor, while their difference measures the bond ionic (deterministic) component.

Consider the 2-AO model of the chemical bond A–B, consisting of the orthonormal basis functions, e.g., the Löwdin Orthogonalized AO (OAO) contributed by atoms A and B: χ = χ′ = (χ _A, χ _B). They give rise to two independent (spatial) MO combinations φ = (φ _b , φ _a ),

$$ \begin{aligned} & {\text{bonding}}: \quad \varphi_{b} = \chi_{\text{A}} C_{{{\text{A}},b}} + \chi_{\text{B}} C_{{{\text{B}},b}} \equiv \chi_{\text{A}} \left( P \right)^{1/2} + \chi_{\text{B}} \left( Q \right)^{1/2} \equiv \varvec{\chi} \,\varvec{C}_{b} \quad {\text{and}} \\ & {\text{antibonding}}:\quad \varphi_{a} = \chi_{\text{A}} C_{{{\text{A}},a}} + \chi_{\text{B}} C_{{{\text{B}},a}} \equiv - \chi_{\text{A}} \left( Q \right)^{1/2} + \chi_{\text{B}} \left( P \right)^{1/2} \equiv \varvec{\chi} \,\varvec{C}_{a} , \\ \end{aligned} $$

(14.29)

or in the compact matrix notation

$$ \boldsymbol{\varphi} =\varvec{\chi}\left[ {\varvec{C}_{b} |\varvec{C}_{a} } \right] \equiv\varvec{\chi}\,{\mathbf{C}},\quad {\mathbf{C}} = \left[ {\begin{array}{*{20}c} {\sqrt P } & { - \sqrt Q } \\ {\sqrt Q } & {\sqrt P } \\ \end{array} } \right], $$

(14.30)

which have been also expressed in terms of complementary (conditional) AO probabilities:

$$ \begin{aligned} P & = P(\chi_{\text{A}} |\varphi_{b} ) = (C_{{{\text{A}},b}} )^{2} = P(\chi_{\text{B}} |\varphi_{a} ) = [C_{{{\text{B}},a}} ]^{2} \quad {\text{and}} \\ Q & = 1 - P = P(\chi_{\text{B}} |\varphi_{b} ) = (C_{{{\text{B}},b}} )^{2} = P(\chi_{\text{A}} |\varphi_{a} ) = [C_{{{\text{A}},a}} ]^{2} . \\ \end{aligned} $$

(14.31)

We further assume that each atom of the “promolecule” contributes a single electron to the molecular bond system consisting of N = 2 electrons.

In the model ground-state configuration, when both (spin-paired) electrons occupy the bonding MO φ _b , the relevant CBO matrix γ ⁰ reads:

$$ {\varvec{\upgamma}}^{0} = 2\varvec{C}_{b} \varvec{C}_{b}^{\dag } = 2\left[ {\begin{array}{*{20}c} P & {\sqrt {PQ} } \\ {\sqrt {QP} } & Q \\ \end{array} } \right] \equiv 2{\varvec{\upgamma}}^{o} . $$

(14.32)

It generates the following conditional probabilities P ⁰(b|a) and their amplitudes A ⁰(b|a) defining communications between the input a = χ and output b = χ′ AO events in the molecular probability-channel of Fig. 14.1:

Fig. 14.1

Probability-channel in 2-AO model of the chemical bond and its entropic descriptors (in bits) of bond multiplicity and composition

$$ {\mathbf{P}}^{0} (\varvec{\chi}^{{\prime }} |\varvec{\chi} ) = \{ P^{0} (j|i)\} = \left[ {\begin{array}{*{20}c} P & Q \\ P & Q \\ \end{array} } \right],\quad {\mathbf{A}}^{0} (\varvec{\chi}^{{\prime }} |\varvec{\chi} ) = \{ A^{0} (j|i)\} = \left[ {\begin{array}{*{20}c} {\sqrt P } & {\sqrt Q } \\ {\sqrt P } & {\sqrt Q } \\ \end{array} } \right]. $$

(14.33)

In this nonsymmetric binary channel, one adopts the molecular input signal, p ⁰ = (P, Q), to extract the bond IT-covalency reflected by the conditional entropy S(q ⁰|p ⁰) = S(P) measuring the channel average communication noise. Adopting the promolecular input signal p ₀ = (½, ½), reflecting that each of the two basis functions has contributed a single electron to form the chemical bond, allows one to determine the associated index of IT-ionicity I(p ₀ : q ⁰) = I ₀(P), which measures the information capacity of this model channel.

As shown in Figs. 14.1 and 14.2, these bond components preserve the overall information multiplicity of this model chemical bond: M ₀(p ₀ ; q ⁰) = M ₀(P) = S(P) + I ₀(P) = 1 bit, for all admissible values of the bond-polarization parameter P: 0 ≤ P ≤ 1. As shown in Fig. 14.2, the bond IT-covalency S(P) is determined by Binary Entropy Function of the complementary conditional probabilities of AO in MO, H(P) = −P log₂ P − Q log₂ Q, reaching the maximum value H(½) = 1 bit for the symmetric bond P = Q = ½, e.g., the two prototype covalent bonds of chemistry: the σ bond in H₂ or the π-bond in ethylene. It vanishes for the lone-pair configurations, when P = (0 or 1), H(0) = H(1) = 0, marking the alternative ion-pair configurations A⁺B⁻ and A⁻B⁺, respectively, relative to the initial AO occupations N ⁰ = (1, 1) in the assumed covalent promolecular reference. The complementary descriptor I ₀(P) = 1 − H(P) of the bond IT-ionicity, which determines the channel mutual information relative to the promolecular input, is thus correctly diagnosed to reach the highest value for the two electron-transfer pairs: I ₀(0) = I ₀(1) = H(½) = 1 bit; it is also predicted to identically vanish for the purely covalent, symmetric bond, I ₀(½) = 0. As explicitly shown in Fig. 14.2, these two components of the chemical bond multiplicity compete with one another, yielding the conserved overall IT bond index M ₀(P) = S(P) + I ₀(P) = 1 bit, which in OCT marks the full single bond, in the whole range of admissible bond polarizations P ∈ [0, 1]. This simple model thus properly accounts for the competition between the bond covalent and ionic components, preserving the single bond-multiplicity measure of the model chemical bond.

Fig. 14.2

Conservation of the overall entropic bond multiplicity M ₀(P) = 1 bit in the 2-AO model, combining the conditional entropy (average noise, bond IT-covalency) S(P) = H(P) and the mutual information (information capacity, bond IT-ionicity) I ₀(P) = 1 − H(P). In MO theory, the quadratic bond-order of Wiberg is represented by the (broken-line) parabola W _A,B(P) = 4P(1−P) ≡ 4PQ

Consider now the quadratic bond-multiplicity indices formulated in the MO theory [79, 98,99,100,101,102,103,104,105]. For example, for the 2-AO model, the quadratic bond-order of Wiberg [46] is given by the parabola W _A,B(P) = [γ _A,B (P)]² = 4PQ = 4P(1 − P), which in Fig. 14.2 closely resembles the entropic plot S(P) = H(P). Indeed, a reference to Eq. (14.4) indicates that strong diatomic Wiberg index implies a strong communication between the interacting orbitals, and hence also a high IT-covalency of the direct chemical bond they generate. Similar relation transpires from the indirect-bonds realized via orbital intermediates, delineating a chain of chemical bonds defining the bridge α in question [see Eq. (14.12)]. The bridge resultant conditional probability is then proportional to a product of Wiberg indices {W _k,l } of each diatomic (k∈X, l∈Y), X≠Y segment of the direct {X—Y} bonds connecting the two terminal orbitals (i, j) in the orbital bridge i—{(k—l)}—j under consideration:

$$ W_{i,j} (\alpha )\varpropto \prod\limits_{(k,l) \in \alpha } {W_{k,l} } . $$

Therefore, strong intermediate bonds {k–l}∈α again imply strong resultant communication between terminal orbitals, and hence high resultant entropic covalency realized via the bridge constituent direct-bond segments. The sum of contributions due to all relevant chemical bridges {α},

$$ W_{i,j} \left( {bridges} \right) = \sum\limits_{\alpha } {\,W_{i,j}^{{}} (\alpha )} , $$

(14.34)

determines the Wiberg-type bond-order of the overall indirect interactions between the specified terminal AO, which supplements the direct component W _i,j  = γ ² _i,j in the full quadratic measure of bond-multiplicity between the specified terminal orbitals χ _i and χ _j in presence of all remaining basis functions in the given molecular environment:

$$ W\left( {i,\,j} \right) \, = W_{i,j} + W_{i,j} \left( {bridges} \right). $$

(14.35)

This indirect mechanism reflects the implicit dependencies between (nonorthogonal) bond-projections of AO, $\left| {\varvec{\chi}^{b} } \right\rangle \equiv {\hat{\text{P}}}_{\varvec{\varphi }}^{0} \left|\varvec{\chi}\right\rangle$. In this generalized outlook on the bond-order concept of chemistry, one thus identifies the bond multiplicity as a measure of the “dependence” (nonadditivity) between orbitals on different atomic centers in the whole bond system of a molecule. On one hand, this dependence between basis functions can be realized directly, through “space,” by a constructive interference of orbitals (probability amplitudes) on two atoms, which generally increases the electron density between them. On the other hand, it can also have an indirect origin, through the dependence on orbitals originating from the remaining AIM. In the nonorthogonal bond-projected AO basis χ ^b, these “geometrical” dependencies are embodied in the idempotent density matrix of Eq. (14.7):

$$ {\mathbf{D}}^{0} = \{ D_{i,j}^{0} = \left\langle {i^{b} |j^{b} } \right\rangle \} = {\mathbf{C}}^{o} {\mathbf{C}}^{o\dag } ,\quad ({\mathbf{D}}^{0} )^{n} = {\mathbf{D}}^{0} . $$

(14.36)

Each pair of AO (or AIM) thus exhibits partial through-space and through-bridge components. The bond-order of the former quickly vanishes with an increasing inter-atomic separation and when the interacting AO are heavily engaged in forming chemical bonds with other atoms, while the latter can still assume appreciable values, when the remaining atoms form an effective bridge of the neighboring, chemically interacting atoms, which links the specified AO. The bridging atoms must be mutually bonded to generate a substantial through-bridge overlap between the bond-projections of interacting AO, so that significant bridges are in fact limited to real chemical bridges of atoms in the structural formula of a molecule.

As an illustration, let us summarize the indirect π-bonds between carbon atoms in benzene ring using MO from the familiar Hückel approximation. For the consecutive numbering of carbons in the π-system, the relevant CBO matrix elements read:

$$ \gamma_{i,i} = 1,\quad \gamma_{i,i + 1} = 2/3,\quad \gamma_{i,i + 2} = 0,\quad \gamma_{i,i + 3} = - 1/3. $$

They generate the following (direct) π-bond multiplicities:

$$ W_{i,i + 1} = 0.44\,\left( {ortho} \right),\quad W_{i,i + 2} = 0\,\left( {meta} \right),\quad W_{i,i + 3} = 0.11\,\left( {para} \right). $$

These through-space bond-orders are complemented by the associated estimates of the resultant multiplicities of the indirect π-interactions due to all most important chemical bridges:

$$ W_{i,i + 1} \left( {bridges} \right) = 0.06\,\left( {ortho} \right),\quad W_{i,i + 2} \left( {bridges} \right) = 0.30\,\left( {meta} \right),\quad W_{i,i + 3} \left( {bridges} \right) = 0.18\,\left( {para} \right). $$

Together these two mechanisms give rise to the following resultant π-bond-orders:

$$ W\left( {para} \right) \cong W\left( {meta} \right) = 0.3 < W\left( {ortho} \right) = 0.5. $$

The artificial distinction in Wiberg’s scheme of the π-interactions with the vanishing direct CBO matrix element as nonbonding is thus effectively removed when the through-bridge contributions are also taken into account. One observes the difference in composition of the resultant indices for the cross–ring interactions: the para interactions exhibit comparable through-space and through-bridge components, the meta multiplicities are realized exclusively through bridges, while the strongest ortho bonds have practically direct, through-space origin.

Of interest also is a comparison of the indirect π-bond-orders in benzene realized through the ring bridges of increasing length:

$$ \begin{aligned} & W_{i,i + 2} \left( {i + 1} \right) = \left( {W_{i,i + 1} } \right)^{2} = 0.20,\quad W_{i,i + 3} \left( {i + 1,i + 2} \right) = \left( {W_{i,i + 1} } \right)^{3} = 0.09, \\ & W_{i,i + 4} \left( {i + 1,i + 2,i + 3} \right) = \left( {W_{i,i + 1} } \right)^{4} = 0.04,\quad W_{i,i + 5} \left( {i + 1,i + 2,i + 3,i + 4} \right) = \left( {W_{i,i + 1} } \right)^{5} = 0.02. \\ \end{aligned} $$

Thus, the longer the bridge, the smaller the indirect bond-order it contributes. The model and HF calculations on linear polyenes and representative polymers [75, 76] indicate that the range of bridge interactions is effectively extended up to the third-neighbors in the chain, where the direct interactions practically disappear.

The conditional probabilities defining the molecular information channel for direct communications between AO generate the associated covalency (noise) and ionicity (information flow) descriptors of the through-space chemical bonds. They can be also used to derive the corresponding cascade communications and the associated entropy/information descriptors of the bridge-bonds. This allows one to generate the IT descriptors of the most important indirect interactions, via chemical bridges between the specified (terminal) orbitals χ _i and χ _j from descriptors of the associated AO information cascades. The resulting overall indices of such indirect IT bond multiplicities compare favorably with the bridge-generalized Wiberg-type bond-orders.

14.4 Orbital Decoupling

There are two challenging MO-decoupling phenomena in the bond-multiplicity theory, which have to be adequately represented in all bona fide approaches: the so-called populational-decoupling for the “frozen” shapes of MO, leading to a steady decrease of the overall bond-multiplicity descriptors accompanying an increased electron occupation of the antibonding MO, and the shape-decoupling accompanying the bond-breaking processes, when AO are effectively prohibited from getting involved in the chemical bond formation (orbital communications), e.g., due to the symmetry requirements or bond-elongation. The above fixed-input OCT using the information probability-channels fails to predict a steady decrease in the resultant bond-order with increasing occupation of the antibonding MO (see Fig. 14.3) and to properly represent the normalization requirements of the input signals in the shape-decoupling limit. A satisfactory solution [14, 64] calls for an ensemble of the separate amplitude (phase-dependent) communication systems, due to either the specified input events or MO, with a flexible-input signal shaped by the orbital conditional probabilities.

Fig. 14.3

Populational decoupling with increasing occupation of antibonding MO in 2-AO model. Panels a and b summarize the bonding (b) and antibonding (a) MO probability channels, while Panel c reports the (occupation-weighted) entropic indices, which properly represent the populational decoupling phenomenon

Consider first the populational-decoupling problem in the simplest 2-AO model of the chemical bond in a diatomic molecule M = A—B. For N = 3, the ground-state corresponds to configuration [M(3)] = [φ ² _b φ ¹ _a ] for which the fixed-input OCT predicts: S = 0.47, I ₀ = 0.48 and M ₀ = 0.95 (bits). Despite a single occupation of the antibonding MO φ _a the predicted overall bond multiplicity M ₀ thus remains almost the same as in the bonding configuration [M(2)] _b  = [φ ² _b ]. Furthermore, this classical (probabilistic) approach cannot distinguish between configurations [M(1)] _b  = [φ ¹ _b ] and [M(1)] _a  = [φ ¹ _a ], or between [M(1)] _b and [M(2)] _b , predicting the same bond indices reported in the first part of Fig. 14.3. For [M(4)] _n  = [φ ² _b φ ² _a ], one similarly predicts S = 0, I ₀ = M ₀ = 1 bit, which also contradicts the chemical intuition associated with this nonbonding state.

This failure of classical molecular channels is because the probability connections loose “memory” about relative phases of AO in MO. It is retained in elements of both the overall CBO matrix and their MO contributions, which reflect the associated amplitudes of AO communications, with their signs properly recognizing a chemical character of the mutual interaction between AO:

$$ \begin{aligned} & bonding\left( {\text{positive}} \right):\gamma_{a,b}^{{}} (\varphi_{s} ) > 0;\quad nonbonding\left( {\text{zero}} \right):\gamma_{a,b}^{{}} (\varphi_{s} ) = 0 \\ & antibonding\left( {\text{negative}} \right):\gamma_{a,b}^{{}} (\varphi_{s} ) < 0. \\ \end{aligned} $$

(14.37)

To remedy this problem within the probability-channel, one thus has to examine separate MO channels {P _s (b|a)}, weight their diatomic IT bond-multiplicities in accordance with a degree of the MO occupation, and recognize in the corresponding resultant measures the character (sign) of the chemical interaction between the specified AO. Let us illustrate this procedure for the 2-AO model of the chemical bond A—B originating from the quantum–mechanical interaction between two AO: χ = (χ _A∈A, χ _B∈B), which define the whole AO basis of the model. The bond contributions for these two AO are determined by the conditional entropy S _a,b (φ _s ), mutual information I _a,b (φ _s ), and the overall bond-multiplicity M _a,b (φ _s ) descriptors of the fragment-renormalized information channel P _s (b|a) for φ _s ,

$$ \begin{aligned} & S_{a,b} (\varphi_{s} ) = S[{\mathbf{P}}_{s} (\varvec{b}|\varvec{a})], \quad I_{a,b} (\varphi_{s} ) = S\left( {p_{s}^{0} } \right) - S_{{a,b{\kern 1pt} }} (\varphi_{s} ), \\ & M_{a,b} (\varphi_{s} ) = S_{a,b} (\varphi_{s} ) + I_{{a,{\kern 1pt} b}} (\varphi_{s} ) = S\left( {\varvec{p}_{s}^{0} } \right), \\ \end{aligned} $$

(14.38)

where S(p ⁰ _s ) stands for the Shannon entropy of the reference input probability p ⁰ _s . Alternatively, the purely molecular estimate of the mutual information descriptor I _s [p _s: p _s ] can be used to index the bond IT-iconicity.

In a larger m > 2 set of AO, the definition of such two-orbital MO indices for the specified pair (i, j) of AO, {S _i,j (φ _s ), I _i,j (φ _s ), M _i,j (φ _s )} requires an appropriate probability renormalization. The reference (promolecular) signal is then related to AO occupations N ⁰ = {N ⁰ _k } in the separated (free) atoms,

$$ p_{s}^{0} \left( {ij} \right) = \{ p_{k}^{0} \left( {ij} \right) = N_{k}^{0} /N_{ij}^{0} , k\,\in \left( {i,j} \right)\} ,\quad N_{ij}^{0} = N_{i}^{0} + N_{j}^{0} , $$

while its molecular analog involves the AO populations in φ _s :

$$ p_{s} \left( {ij} \right) = \{ p_{k,s} \left( {ij} \right) = N_{k} (\varphi_{s} )/N_{ij} (\varphi_{s} ), k \in \left( {i,j} \right)\} ,\quad N_{k} (\varphi_{s} ) = \gamma_{k,k} (\varphi_{s} );\quad N_{ij} (\varphi_{s} ) = N_{i} (\varphi_{s} ) + N_{j} (\varphi_{s} ). $$

One similarly extracts the appropriate two-orbital channel from the MO conditional-probability matrix P _s (b|a):

$$ {\mathbf{P}}_{s} [(\varvec{b}|\varvec{a});ij] = \{ P_{s} [(l|k);ij] = P_{s} (l|k)/P_{s} \left( {ij|k} \right),k,\,l \in \left( {i,j} \right)\} ,\quad P_{s} \left( {ij|k} \right) = P_{s} \left( {i|k} \right) + P_{s} \left( {j|k} \right). $$

The bond descriptors for this pair of AO then read:

$$ \begin{aligned} S_{i,j} (\varphi_{s} ) & = - \sum\nolimits_{k,l \in ij} {p_{k,s} } \left( {ij} \right)\,P_{s} [(l|k);\,ij]\log P_{s} [(l|k);ij], \\ I_{i,j} (\varphi_{s} ) & = \sum\nolimits_{k,l \in ij} {p_{k}^{0} } \left( {ij} \right)\,P_{s} [(l|k);\,ij]\log \{ P_{s} [(l|k);\,ij]/p_{k}^{0} \left( {ij} \right)\} , \quad M_{i,j} (\varphi_{s} ) = S_{i,j} (\varphi_{s} ) + I_{i,j} (\varphi_{s} ). \\ \end{aligned} $$

In combining such MO contributions into the corresponding resultant bond indices for the specified pair (i, j) of AO, these increments should be multiplied by the MO occupation factor f ^MO = {f _s  = n _s /2}, which recognizes that the full bonding/antibonding potential of the given MO is realized only when it is fully occupied, and by MO probability P ^MO = {P _s  = n _s /N}. The resultant A—B descriptors are then obtained by summation of such occupation-weighted bonding or antibonding contributions from all occupied MO, which determine the bond system of a molecule:

$$ \begin{aligned} S\left( {i, \, j} \right) & = \sum\limits_{s} {sign\,[\gamma_{i,j} (\varphi_{s} )]\,} P_{s} f_{s} S_{i,j} (\varphi_{s} ),\quad I\left( {i, \, j} \right) = \sum\limits_{s} {sign\,[\gamma_{i,j} (\varphi_{s} )]\,} P_{s} f_{s} I_{i,j} (\varphi_{s} ), \\ M\left( {i, \, j} \right) & = \sum\limits_{s} {sign\,[\gamma_{i,j} (\varphi_{s} )]\,} P_{s} f_{s} M_{i,j} (\varphi_{s} ). \\ \end{aligned} $$

(14.39)

As explicitly shown in the second part (Panel c) of Fig. 14.3, such weighed resultant indices adequately represent the population-decoupling trends in 2-AO model for N = 1 ÷ 4 electrons.

Resolving the shape-decoupling problem in classical probability channels calls for the flexible-input approach. The essence of this proposition lies in a determination of the entropy/information contributions due to each AO input {χ _i } in the molecular channel P(b|a) = {P(j|i), (i, j) ∈ (1, 2, …, m)}. These IT indices describe partial communications originating from χ _i , i.e., the molecular subchannel determined by the ith row of P(b|a), using separate probability distributions tailored for each AO input. The hitherto single molecular propagation of the molecular input signal p in the fixed-input approach is now replaced by series of m molecular propagations of the separate signals p(i) = {p(k; i)} for each input i = 1, 2, …, m. This partial propagation generates the associated IT-covalency descriptor,

$$ S\left( i \right) = - \sum\nolimits_{k} {p\left( {k;\,i} \right)} \sum\nolimits_{j} {P(j|k)} \,\log P(j|k) \equiv \sum\nolimits_{k} {p\left( {k;\,i} \right)} \,S\left( {k;i} \right) = S\left[ {\varvec{p}\left( i \right)} \right], $$

(14.40)

molecular IT-ionic contribution,

$$ I\left( i \right) = \sum\nolimits_{k} {p\left( {k;i} \right)} \sum\nolimits_{j} {P(j|k)} \,\log [P(j|k)/p\left( {k;i} \right)] \equiv \sum\nolimits_{k} {p\left( {k;i} \right)} \,I\left( {k;i} \right) = I\left[ {\varvec{p}\left( i \right)} \right], $$

(14.41)

and the corresponding overall bond-multiplicity index for ith input:

$$ M\left( i \right) = I\left( i \right) + S\left( i \right) = M\left[ {\varvec{p}\left( i \right)} \right]. $$

(14.42)

The bond descriptor of a molecule as a whole is then generated as the ensemble average of all such contributions determined in separate propagations using these separate input signals, weighted with the molecular AO probabilities p = {p _i  = γ _i,i /N}:

$$ S_{av.} = \sum\nolimits_{i} {p_{i} S\left( i \right),} \quad I_{av.} = \sum\nolimits_{i} {p_{i} I\left( i \right),} \quad M_{av.} = \sum\nolimits_{i} {p_{i} M\left( i \right)} = S_{av.} + I_{av.} $$

(14.43)

There are some obvious sum-rules to be satisfied by these input-dependent probabilities. Consider first the fully coupled molecular channel, in which all orbitals are allowed to interact chemically, thus exhibiting nonvanishing direct communications with the system remainder. In this case, all molecular inputs have to be effectively probed to the full extent of the unit condensed probability of the molecule as a whole:

$$ \sum\nolimits_{k} {p\left( {k;i} \right)} ] \equiv |\varvec{p}\left( i \right)| = 1,\quad i = 1,2, \ldots ,m. $$

(14.44)

This normalization requirement identifies a general category of these input-dependent probabilities as molecular conditional probabilities of two-orbital events: p(k; i) ≡ P(k|i). Indeed, to make the AO decoupling continuous in this generalized description, the input probabilities {p(i)} have to reflect the actual participation of ith AO in chemical bonds (communications) with the remaining basis functions. One thus selects the input-tailored probabilities as the corresponding rows of the molecular conditional-probability matrix:

$$ \varvec{p}\left( i \right) = \varvec{P}(\varvec{b}|i) = \{ P(k|i)\} ,\quad i = 1,2, \ldots ,m. $$

(14.45)

These partial input probabilities generate the following effective information system for ith input, called the row-subchannel [11],

$$ \{ P(k|i) \to k - P(j|k) \to j \to P(j|i)\} , $$

(14.46)

where we have recognized the complete-cascade conservation of the direct scattering probabilities [see Eq. (14.14)]:

$$ \sum\nolimits_{k} {P(k|i)} P(j|k) = P(j|i). $$

(14.47)

In calculating the “ensemble” average bond components, the product

$$ p_{i} \sum\nolimits_{k} {P(k|i)} \,P(j|k) = p_{i} P(j|i) \equiv P\left( {i,j} \right) $$

(14.48)

thus represents the joint probability of orbitals χ _i and χ _j in the molecule.

Consider the conditional entropy contribution for ith input:

$$ S\left( i \right) = - \sum\nolimits_{k} {P(k|i)} \,[\sum\nolimits_{j} {P(j|k)} \,\log_{2} P(j|k)]. $$

(14.49)

In the ensemble-average quantity, this entropy covalency has to be weighted by the actual probability p _i of this input in the molecule as a whole [Eq. (14.43)]. It can be directly verified that such averaging procedure indeed reproduces the molecular IT-covalency index:

$$ \begin{aligned} S_{av.} & = \sum\nolimits_{i} {p_{i} S\left( i \right)} \equiv \sum\nolimits_{i} S_{i} = - \sum\nolimits_{i} {} \sum\nolimits_{k} {} \sum\nolimits_{j} {[p_{i} P(k|i)]\,P(j|k)\,\log_{2} P(j|k)} \\ & = - \sum\nolimits_{k} {} \sum\nolimits_{j} {} [\sum\nolimits_{i} {P\left( {k,i} \right)} ]P(j|k)\,\log_{2} P(j|k) = - \sum\nolimits_{k} {} \sum\nolimits_{j} {p_{k} P(j|k)} \,\log_{2} P(j|k) \\ & = - \sum\nolimits_{k} {} \sum\nolimits_{j} {P\left( {j,k} \right)} \,\log_{2} P(j|k) = S. \\ \end{aligned} $$

(14.50)

A similar averaging of the mutual information (IT-ionic) contributions,

$$ \begin{aligned} I\left( i \right) & = \sum\nolimits_{k} {P\left( {k|i} \right)} \,[\sum\nolimits_{j} {P(j|k)} \,\log_{2} [P(j|k)/p_{j} ] = - S\left( i \right) - \sum\nolimits_{j} {} [\sum\nolimits_{k} {P\left( {k|i} \right)} \,P(j|k)]\,\log_{2} p_{j} \\ & = - S\left( i \right) - \sum\nolimits_{j} {} P\left( {j|i} \right)\,\log_{2} p_{j} , \\ \end{aligned} $$

(14.51)

then gives:

$$ \begin{aligned} I_{av.} & = \sum\nolimits_{i} {p_{i} I\left( i \right)} \equiv \sum\nolimits_{i} {I_{i} } = - S - \sum\nolimits_{i} {} \sum\nolimits_{j} {p_{i} P\left( {j|i} \right)} \,\log_{2} p_{j} \\ & = - S - \sum\nolimits_{j} {} [\sum\nolimits_{i} {P\left( {i,j} \right)} ]\,\log_{2} p_{j} = - S + S\left( \varvec{p} \right) = I. \\ \end{aligned} $$

(14.52)

Therefore, the overall molecular bond index, the mean value of the input AO contributions

$$ M\left( i \right) = S\left( i \right) + I\left( i \right) = - \sum\nolimits_{j} {P\left( {j|i} \right)} \,\log_{2} p_{j} , $$

then reproduces the Shannon entropy in molecular AO probabilities:

$$ M_{av.} = \sum\nolimits_{i} {p_{i} M\left( i \right)} \equiv \sum\nolimits_{i} {M_{i} } = - \sum\nolimits_{j} {} [\sum\nolimits_{i} {P\left( {i,j} \right)} ]\,\log_{2} p_{j} = - \sum\nolimits_{j} {p_{j} } \,{ \log }_{2} p_{j} = S\left( \varvec{p} \right). $$

(14.53)

One also observes that the input-resolved quantities {S _i , I _i , M _i } describe the following resultant channel for ith input [see Eq. (14.46)],

$$ \begin{aligned} & p_{i} \to \{ P(k|i) \to k - P(j|k) \to j \to P(j|i)\} \\ & \quad \equiv \{ P\left( {i,k} \right) \to k - P(j|k) \to j \to P\left( {i,j} \right)\} , \\ \end{aligned} $$

(14.54)

with the joint probabilities of AO shaping the effective input signal of this ith row-subchannel.

14.5 Illustrative Applications

As an illustration, let us first consider the flexible-input generalization [Eq. (14.46)] of the 2-AO channel, shown in Fig. 14.4. We first observe that the input- and output-dependent distributions in this model are identical with the molecular distribution [see Eq. (14.33)]:

Fig. 14.4

Flexible-input generalization of the 2-AO channel. The corresponding AO partial and average entropy/information descriptors (in bits) of the chemical bond are also reported

$$ \varvec{p}(\chi_{\text{A}} ) = \varvec{p}(\chi_{\text{B}} ) = \left( {P,Q} \right) = \varvec{p}. $$

Also reported in the diagram are the partial and average IT descriptors, including the IT-ionicity contributions relative to the reference probabilities p ⁰ = (½, ½) of the atomic-promolecule, when two AO contribute a single electron each to form the chemical bond. The flexible-input generalization of this model channel is seen to exactly reproduce the overall IT bond-multiplicity and its components reported in Fig. 14.1.

It follows from the input (conditional) probabilities of Fig. 14.1 that in the limit of the decoupled lone-pair (nonbonding) MO, φ _b  = χ _A, for P = 1 and Q = 0, or φ _b  = χ _B, when Q = 1 and P = 0, the input probability of the doubly-occupied AO becomes 1, while that of the other, empty AO identically vanishes. The unit input probability of the doubly-occupied AO in the channel input is then deterministically transmitted to the same AO in the channel output, with the other (unoccupied) AO not participating in the channel deterministic communication, so that both orbitals do not contribute to the vanishing resultant IT-covalent index. The average ionicities, relative to atomic-promolecule [χ ¹_A χ ¹_B ], I _av. = 1 bit, and relative to coordination-promolecule [χ ²_A ], I _av. = 0, then correctly predict the single bond multiplicity identifying the molecular lone-pair configuration [φ ² _b ] ≡ [χ ²_A ] as multiplicity of the ion-pair [A⁻B⁺], displaced by an electron transfer relative to atomic-promolecule, and the vanishing multiplicity of the undisplaced configuration relative to the coordination promolecule.

In the limit R _AB→∞, the molecule A—B dissociates into atoms [A] = [χ ¹_A ] and [B] = [χ ¹_B ]. Such decoupled AO correspond to the equivalent configurations [φ ¹ _b φ ¹ _a ] and [χ ¹_A χ ¹_B ], both producing identical Slater determinants: |φ _b , φ _a | = |χ _A, χ _B|. Indeed, using the orthogonal transformations between χ = (χ _A, χ _B) and φ = (φ _b , φ _a ),

$$ \varvec{\varphi } =\varvec{\chi}\,{\mathbf{C}}\quad {\text{and}}\quad\varvec{\chi}= \varvec{\varphi }\left[ {\begin{array}{*{20}r} \hfill {\sqrt P } & \hfill {\sqrt Q } \\ \hfill { - \sqrt Q } & \hfill {\sqrt P } \\ \end{array} } \right] \equiv \varvec{\varphi }\,{\mathbf{C}}^{\text{T}} ,\quad {\mathbf{C}}^{\text{T}} {\mathbf{C}} = {\mathbf{CC}}^{\text{T}} = {\mathbf{I}}, $$

(14.55)

one can directly verify that γ[φ ¹ _b φ ¹ _a ] = CC ^T = I = P(b|a), so that the decoupled AO inputs become: p(a) = p(a ⁰) = (1, 0) and p(b) = p(b ⁰) = (0, 1), each separately unity-normalized.

To summarize, while still retaining the essence of the fixed-input approach, the generalized proposition introduces in OCT the desired input-flexibility, which generates a continuity in the IT description of the fragment decoupling processes. In a common framework, the ensemble approach covers both the fully coupled AO in the molecule as well as the limiting cases of its subsystems being effectively decoupled in the molecular channel. In the former case, the resultant input signal corresponds to the unit norm of the probability distribution. In the case of n-mutually separated fragments, this flexible normalization is automatically increased to n by the choice of the molecular conditional probabilities as signals for each row-subchannel. The flexible-input generalization dramatically improves the agreement between predicted bond descriptors and the accepted chemical intuition [70]. It also has the conceptual and interpretative advantages, by providing a unifying description capable of tacking both the coupled and decoupled molecular fragments in a single theoretical framework. It generates a continuous description of the fragment dissociation (shape-decoupling) limit, when the separated subsystems exhibit vanishing mutual communications.

Consider next the N = 3 π-electrons in allyl, with the consecutive numbering of 2p _π  = 2p _z ≡ z orbitals in the carbon chain. In Hückel’s approximation, this π-system involves two MO,

$$ \varphi_{1} = \frac{1}{\sqrt 2 }\left[ {\frac{1}{\sqrt 2 }(z_{1} + z_{3} ) + z_{2} } \right]\quad \left( {{\text{doubly}}\,{\text{occupied}}} \right),\quad \varphi_{2} = \frac{1}{\sqrt 2 }(z_{1} - z_{3} )\left( {{\text{singly}}\,{\text{occupied}}} \right). $$

(14.56)

They generate the following MO and molecular CBO matrices:

$$ {\varvec{\upgamma}}_{1} = \frac{1}{2}\left[ {\begin{array}{*{20}c} 1 & {\sqrt 2 } & 1 \\ {\sqrt 2 } & 2 & {\sqrt 2 } \\ 1 & {\sqrt 2 } & 1 \\ \end{array} } \right],\quad {\varvec{\upgamma}}_{2} = \frac{1}{2}\left[ {\begin{array}{*{20}c} 1 & 0 & { - 1} \\ 0 & 0 & 0 \\ { - 1} & 0 & 1 \\ \end{array} } \right],\quad {\varvec{\upgamma}} = {\varvec{\upgamma}}_{1} + {\varvec{\upgamma}}_{2} = \frac{1}{2}\left[ {\begin{array}{*{20}c} 2 & {\sqrt 2 } & 0 \\ {\sqrt 2 } & 2 & {\sqrt 2 } \\ 0 & {\sqrt 2 } & 2 \\ \end{array} } \right] . $$

(14.57)

The corresponding molecular and MO probability-channels are shown in Figs. 14.5 and 14.6, respectively [64]. The latter use the AO-input probabilities p _s  = {p(i|s) =  $\gamma_{i,i}^{{}} (s)/n_{s}$}. The overall channel predicts roughly 3/2 π-bonds in this molecular system, including a marginal IT-ionicity contribution, in full accord with chemical intuition.

Fig. 14.5

Overall probability channel for π-electrons in allyl and its IT bond indices in bits

Fig. 14.6

Molecular probability channels for two occupied π-MO in allyl. The corresponding bond contributions (in bits) for these MO communication systems are also reported

There are no obvious combination formulas for grouping the partial MO bond indices of Fig. 14.6 into their overall analogs of Fig. 14.5. Indeed, the MO channels are determined by their own CBO structure, and a variety of their nonvanishing communication connections between AO generally differs from that of the system as a whole. Moreover, the input probabilities of Fig. 14.6 do not reflect the two MO channels being a part of the whole molecular channel. The latter requirement is satisfied only when, in spirit of the MO averaging of Fig. 14.3, the two networks are parallely coupled into the combined information system, in which the input probabilities are given by the corresponding products { $\bar{\varvec{p}}_{s}$  = P _s p _s }, with MO probabilities P ^MO = {P _s  = n _s /N} = (2/3, 1/3). In allyl, such a combination rule gives the following IT descriptors (in bits) of the two MO channels:

$$ \begin{aligned} & \bar{S}_{1} = P_{1} S(\varphi_{1} ) = 1,\quad \bar{I}_{1} = - P_{1} \log_{2} P_{1} = 0.39\quad {\text{and}} \\ & \bar{S}_{2} = P_{2} S(\varphi_{2} ) = 1/3, \quad \bar{I}_{2} = - P_{2} \log_{2} P_{2} = 0.53. \\ \end{aligned} $$

Such molecular inputs generate nonvanishing MO ionicities, which sum up to

$$ \bar{I} = \bar{I}_{1} + \bar{I}_{2} = - \sum\nolimits_{s} {P_{s} \log_{2} P_{s} } = S\left( {\varvec{P}^{\text{MO}} } \right) = 0.92. $$

The overall bond-multiplicity index of Fig. 14.5, M = 1.58 = S(p ⁰), predicting about 3/2 π-bond multiplicity in allyl, is reconstructed by adding to this ionicity measure the sum of the bonding (positive) IT-covalency $\bar{S}_{1}$ in first MO and the antibonding (negative) contribution $( - \bar{S}_{2} )$ due to the second MO:

$$ \bar{S}_{1} + ( - \bar{S}_{2} ) + \bar{I} = M. $$

The MO-weighting procedure of Fig. 14.3, with f ₁ = 1 and f ₂ = ½, predicts a roughly single π-bond in allyl:

$$ \bar{M} = f_{1} (\bar{S}_{1} + \bar{I}_{1} ) - f_{2} (\bar{S}_{2} + \bar{I}_{2} ) \equiv f_{1} \bar{M}_{1} - f_{2} \bar{M}_{2} = 0.96. $$

It reflects the fact that only first (bonding) MO φ ₁ is fully occupied, while the second (nonbonding) MO φ ₂ groups practically separated AO on peripheral carbon atoms.

The delocalized π-bonds in butadiene are determined by two doubly-occupied canonical MO in Hückel approximation,

$$ \begin{aligned} \varphi_{1} & = a(z_{1} + z_{4} ) + b(z_{2} + z_{3} ),\quad \varphi_{2} = b(z_{1} - z_{4} ) + a(z_{2} - z_{3} ),\quad 2\left( {a^{2} + b^{2} } \right) = 1; \\ a & = \frac{1}{2}\sqrt {1 - 1/\sqrt 5 } = 0.372,\quad b = \frac{1}{2}\sqrt {1 + 1/\sqrt 5 } = 0.602 \\ \end{aligned}, $$

(14.58)

with P ^MO = (½, ½) and f ^MO = (1, 1). The corresponding CBO matrices for these occupied MO and the whole π-electron system, respectively,

$$ {\varvec{\upgamma}}_{1} = 2\left[ {\begin{array}{*{20}c} {a^{2} } & {ab} & {ab} & {a^{2} } \\ {ab} & {b^{2} } & {b^{2} } & {ab} \\ {ab} & {b^{2} } & {b^{2} } & {ab} \\ {a^{2} } & {ab} & {ab} & {a^{2} } \\ \end{array} } \right],\quad {\varvec{\upgamma}}_{2} = 2\left[ {\begin{array}{*{20}c} {b^{2} } & {ab} & { - ab} & { - b^{2} } \\ {ab} & {a^{2} } & { - a^{2} } & { - ab} \\ { - ab} & { - a^{2} } & {a^{2} } & {ab} \\ { - b^{2} } & { - ab} & {ab} & {b^{2} } \\ \end{array} } \right], $$

(14.59)

$$ {\varvec{\upgamma}} = {\varvec{\upgamma}}_{1} + {\varvec{\upgamma}}_{2} = \frac{1}{\sqrt 5 }\left[ {\begin{array}{*{20}c} {\sqrt 5 } & 2 & 0 & { - 1} \\ 2 & {\sqrt 5 } & 1 & 0 \\ 0 & 1 & {\sqrt 5 } & 2 \\ { - 1} & 0 & 2 & {\sqrt 5 } \\ \end{array} } \right], $$

(14.60)

generate AO probability-channels shown in Figs. 14.7 and 14.8. The overall data of Fig. 14.8 correctly predict the overall double multiplicity of all π-bonds in butadiene. In this OCT treatment, they exhibit rather substantial IT-ionicity, which indicates a high degree of determinism (localization) in the orbital probability scattering. The bonding and antibonding components in S ₂ cancel each other, when one attributes different signs to these AO contributions.

Fig. 14.7

Hückel probability scattering in the occupied π-MO of butadiene for representative input orbital z _i  = 2p _{z,  i} , and the associated IT bond indices (in bits)

Fig. 14.8

Overall probability channel for π-electrons in butadiene (Hückel theory) and its bond-multiplicity/composition descriptors in bits

The group ionicity $\bar{I}$  =  $\bar{I}_{1}$  +  $\bar{I}_{2}$  = S(P ^MO) = 1, and hence, the overall MO-average bond multiplicity reads:

$$ \bar{S}_{1} + (\frac{1}{2}\bar{S}_{2} - \frac{1}{2}\bar{S}_{2} ) + \bar{I} = 1.925, $$

(14.61)

where $\bar{S}_{s}$  = P _s S(φ _s ), thus again predicting roughly two bonds in this π-system.

Three occupied MO in Hückel theory, which determine π-bonds in benzene ring, P ^MO = (1/3) 1, where 1 stands for the unit row matrix, read:

$$ \begin{aligned} \varphi_{1} & = \frac{1}{\sqrt 6 }(z_{1} + z_{2} + z_{3} + z_{4} + z_{5} + z_{6} ), \\ \varphi_{2} & = \frac{1}{2}(z_{1} + z_{2} - z_{4} - z_{5} ), \\ \varphi_{3} & = \frac{1}{{\sqrt {12} }}(z_{1} - z_{2} - 2z_{3} - z_{4} + z_{5} + 2z_{6} ). \\ \end{aligned} $$

(14.62)

They give rise to the overall CBO matrix elements reflecting the electron population on orbital χ _i  = z _i , γ _i,i  = 1, and mutual coupling between AO in relative ortho-, meta-, and para-positions: γ _i,i+1 = 2/3, γ _i,i+2 = 0, γ _i,i+3 = −1/3. The resultant scattering of AO probabilities of π-electrons in benzene is summarized in Fig. 14.9. The predicted overall IT-multiplicity of π-bonds is somewhat lower than M ₀ = 3 predicted for the three localized π-bonds in the alternated hexagon structure of cyclohexatriene. This is because in benzene, the π-bond alternation is prevented by stronger σ-bonds, which assume their maximum strength in the regular hexagon structure [106].

Fig. 14.9

Probability scattering in benzene (Hückel theory) for representative input orbital z _i  = 2p _z, i , and the molecular entropy/information descriptors of the π-electron probability channel

Let us explore the CBO matrices of the benzene occupied MO:

$$ {\varvec{\upgamma}}_{s} = \left\langle {\varvec{\chi}|\varphi_{s} } \right\rangle n_{s} \left\langle {\varphi_{s} |\varvec{\chi}} \right\rangle = 2\left\langle\varvec{\chi}\right|{\hat{{\rm P}}}_{\rm s} \left|\varvec{\chi}\right\rangle ,\quad\varvec{\chi}= (z_{1} ,z_{2} , \ldots ,z_{6} ),\quad s = \, 1,2,3. $$

In ${\varvec{\upgamma}}_{1}$ =  $({1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3})\,{\mathbf{1}}$, where all elements in the square matrix 1 are equal to 1, all matrix elements are positive (bonding), while a half of them in ${\varvec{\upgamma}}_{2}$ and ${\varvec{\upgamma}}_{3}$ is negative, thus representing the antibonding interactions between AO. The nonvanishing elements in ${\varvec{\upgamma}}_{2}$ are limited to the subset χ′ = (z ₁, z ₂, z ₄, z ₅):

$$ {\varvec{\upgamma}}_{2}^{{}} = 2\left\langle {\varvec{\chi}} \right|{\hat{\text{P}}}_{2} \left| {\varvec{\chi}} \right\rangle = \frac{1}{2}\left[ {\begin{array}{*{20}c} {\;{\kern 1pt} 1} & {\;{\kern 1pt} {\kern 1pt} 1} & { - 1} & { - 1} \\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1} & {\;{\kern 1pt} {\kern 1pt} 1} & { - 1} & { - 1} \\ { - 1} & { - 1} & {\;\;{\kern 1pt} 1} & {\;\;1} \\ { - 1} & { - 1} & {\;\;{\kern 1pt} 1} & {\;\;1} \\ \end{array} } \right], $$

(14.63)

while ${\varvec{\upgamma}}_{3}$ explores the whole AO basis:

$$ {\varvec{\upgamma}}_{3} = 2\left\langle\varvec{\chi}\right|{\hat{\text{P}}}_{3} \left|\varvec{\chi}\right\rangle = \frac{1}{6}\left[ {\begin{array}{*{20}r} \hfill 1 & \hfill { - 1} & \hfill { - 2} & \hfill { - 1} & \hfill 1 & \hfill 2 \\ \hfill { - 1} & \hfill 1 & \hfill 2 & \hfill 1 & \hfill { - 1} & \hfill { - 2} \\ \hfill { - 2} & \hfill 2 & \hfill 4 & \hfill 2 & \hfill { - 2} & \hfill { - 4} \\ \hfill { - 1} & \hfill 1 & \hfill 2 & \hfill 1 & \hfill { - 1} & \hfill { - 2} \\ \hfill 1 & \hfill { - 1} & \hfill { - 2} & \hfill { - 1} & \hfill 1 & \hfill 2 \\ \hfill 2 & \hfill { - 2} & \hfill { - 4} & \hfill { - 2} & \hfill 2 & \hfill 4 \\ \end{array} } \right] . $$

(14.64)

These partial CBO matrices give rise to the following AO communications and input probabilities in the associated probability channels of the occupied MO:

$$ \begin{aligned} {\mathbf{P}}_{1} (\varvec{b}|\varvec{a}) & = \frac{1}{6}\,\,{\mathbf{1}},\quad \varvec{p}_{\varvec{1}} = \left( {1/6} \right)\,\varvec{1}; \\ {\mathbf{P}}_{2} (\varvec{b}|\varvec{a}) & = \frac{1}{4}\left[ {\begin{array}{*{20}r} \hfill 1 & \hfill 1 & \hfill 0 & \hfill 1 & \hfill 1 & \hfill 0 \\ \hfill 1 & \hfill 1 & \hfill 0 & \hfill 1 & \hfill 1 & \hfill 0 \\ \hfill 0 & \hfill 0 & \hfill 0 & \hfill 0 & \hfill 0 & \hfill 0 \\ \hfill 1 & \hfill 1 & \hfill 0 & \hfill 1 & \hfill 1 & \hfill 0 \\ \hfill 1 & \hfill 1 & \hfill 0 & \hfill 1 & \hfill 1 & \hfill 0 \\ \hfill 0 & \hfill 0 & \hfill 0 & \hfill 0 & \hfill 0 & \hfill 0 \\ \end{array} } \right],\quad \varvec{p}_{2} = 1/4\left( {1, \, 1, \, 0, \, 1, \, 1, \, 0} \right); \\ {\mathbf{P}}_{3} (\varvec{b}|\varvec{a}) & = \frac{1}{12}\left[ {\begin{array}{*{20}r} \hfill 1 & \hfill 1 & \hfill 4 & \hfill 1 & \hfill 1 & \hfill 4 \\ \hfill 1 & \hfill 1 & \hfill 4 & \hfill 1 & \hfill 1 & \hfill 4 \\ \hfill 1 & \hfill 1 & \hfill 4 & \hfill 1 & \hfill 1 & \hfill 4 \\ \hfill 1 & \hfill 1 & \hfill 4 & \hfill 1 & \hfill 1 & \hfill 4 \\ \hfill 1 & \hfill 1 & \hfill 4 & \hfill 1 & \hfill 1 & \hfill 4 \\ \hfill 1 & \hfill 1 & \hfill 4 & \hfill 1 & \hfill 1 & \hfill 4 \\ \end{array} } \right],\quad \varvec{p}_{3} = \left( {1/12} \right)\left( {1, \, 1, \, 4, \, 1, \, 1, \, 4} \right). \\ \end{aligned} $$

(14.65)

Their entropy/information descriptors read:

$$ \begin{aligned} & S(\varphi_{1} ) = M(\varphi_{1} ) = 2.58, I(\varphi_{1} ) = 0; \\ & S(\varphi_{2} ) = M(\varphi_{2} ) = 2,I(\varphi_{2} ) = 0; \\ & S(\varphi_{3} ) = M(\varphi_{3} ) = 2.25,I(\varphi_{3} ) = 0. \\ \end{aligned} $$

The resultant MO-average iconicity descriptor $\bar{I}$  =  $\bar{I}_{1}$  +  $\bar{I}_{2}$  +  $\bar{I}_{3}$  = S(P ^MO) = 1.58 and $\bar{S}_{1}$  = S(φ ₁)/3 also give rise to roughly 2.5 bits of the IT bond-multiplicity, with the bonding (positive) and negative (antibonding) contributions in $\bar{S}_{2} \,{\text{and}}\,\bar{S}_{3}$ approximately canceling each other.

14.6 Amplitude Communications in Valence-Bond Structures

In this section, we compare the probability and amplitude-averaging schemes over configurations [107], using the 2-AO model of the chemical bond A—B as an illustrative example. The original VB [82] description of the homonuclear bond in H₂, at equilibrium internuclear separation R = 1.40 a.u., uses the overlapping 1s orbitals contributed by both hydrogens, χ = (χ _B, χ _A), S _A,B =  $\left\langle {\chi_{\text{A}} |\chi_{\text{B}} } \right\rangle$  = 0.75, and introduces two prototype chemical structures,

$$ \Psi _{cov.} \left( 2 \right) = N\{ [{\text{A}} - {\text{B}}\left] { \, + \, } \right[{\text{B}} - {\text{A}}]\} ,\quad\Psi _{ion.} \left( 2 \right) = N\{ [{\text{A}}^{ - } {\text{B}}^{ + } \left] { \, + \, } \right[{\text{A}}^{ + } {\text{B}}^{ - } ]\} ,\quad N = 0.566, $$

(14.66)

expressed in terms of the four elementary AO products,

$$ \begin{aligned} & covalent:\quad \{ [{\text{A}} - {\text{B}}\left] { = \chi_{\text{A}} \left( 1 \right)\,\chi_{\text{B}} \left( 2 \right),\quad } \right[{\text{B}} - {\text{A}}] = \chi_{\text{B}} \left( 1 \right)\,\chi_{\text{A}} \left( 2 \right)\} ,\quad {\text{and}} \\ & ionic: \quad \{ [{\text{A}}^{ - } {\text{B}}^{ + } \left] { = \chi_{\text{A}} \left( 1 \right)\,\chi_{\text{A}} \left( 2 \right),\quad } \right[{\text{A}}^{ + } {\text{B}}^{ - } ] = \chi_{\text{B}} \left( 1 \right)\,\chi_{\text{B}} \left( 2 \right)\} , \\ \end{aligned} $$

(14.67)

which span the model two-electron Hilbert space.

One recalls that this classical description in terms of overlapping AO suffers from a severe nonorthogonality problem. For the equilibrium internuclear separation, $\left\langle {\Psi ^{ion} |\Psi ^{\text{cov}} } \right\rangle$  = 0.96, and this hampers a clear chemical interpretation of independent bond components in quantum chemistry and hinders an interpretation of the bond information origins and of its covalent/ionic composition in the electronic ground state:

$$ \Psi ^{{\text{VB}}} \left( 2 \right) = 0.801\,\Psi _{cov.} \left( 2 \right) + 0.206\,\Psi _{ion.} \left( 2 \right). $$

(14.68)

One also observes that the VB structures Ψ _cov. (2) and Ψ _ion. (2) also represent the reference atomic and ionic dissociation limits, respectively, with the former attributing electrons to different atoms and the latter locating both electrons on a single atom. The ionic structure indeed represents an equal participation of the two admissible ion-pairs, relative to the assumed (atomic) promolecular reference, while the covalent structure corresponds to the equal participation of the two covalent (electron-sharing) products.

One way to extract the independent ionic component is to Schmidt-orthogonalize Ψ _ion. (2) with respect to Ψ _cov. (2): Φ _ion. (2) = 3.362 Ψ _ion. (2)–3.428 Ψ _cov. (2). This gives

$$ \Psi ^{{\text{VB}}} \left( 2 \right) = 0.998\,\Psi _{cov.} \left( 2 \right) + 0.058\,\Phi _{ion.} \left( 2 \right), $$

(14.69)

and hence predicts the bond (0.058)² = 0.003 independent ionic character, from quantum-mechanical SP, i.e., a practically pure covalent chemical bond [108]. This is in sharp contrast to 32% iconicity predicted in Shull’s Natural Orbital model [108,109,110].

The alternative approach uses the symmetric (Löwdin) orthogonalization of AO basis into the associated orthonormal AO (OAO) set,

$$ \tilde{\varvec{\chi }} =\varvec{\chi}\,\,\left[ {\begin{array}{*{20}c} {1.378} & { - 0.622} \\ { - 0.622} & {1.378} \\ \end{array} } \right] = (\tilde{\chi }_{\text{A}} ,\,\,\tilde{\chi }_{\text{B}} ), $$

(14.70)

which generates the associated orthonormal VB structures:

$$ \Phi ^{cov.} \left( 2 \right) = 2^{ - 1/2} [\tilde{\chi }_{\text{A}} (1)\,\tilde{\chi }_{\text{B}} (2) + \tilde{\chi }_{\text{B}} (1)\,\tilde{\chi }_{\text{A}} (2)],\quad\Phi ^{ion.} \left( 2 \right) = 2^{ - 1/2} [\tilde{\chi }_{\text{A}} (1)\,\tilde{\chi }_{\text{A}} (2) + \tilde{\chi }_{\text{B}} (1)\,\tilde{\chi }_{\text{B}} (2)]. $$

(14.71)

At the equilibrium bond-length, these two sets of VB configurations are related by transformations:

$$ \begin{aligned} & [\Phi ^{cov.} ,\Phi ^{ion.} \left] { \, = \, } \right[\Psi _{cov.} ,\Psi _{ion.} ] \left[ {\begin{array}{*{20}c} {2.587} & { - 2.142} \\ { - 2.142} & {2.587} \\ \end{array} } \right]\quad {\text{and}} \\ &\Psi _{cov.} ,\Psi _{ion.} \left] { \, = \, } \right[\Phi ^{cov.} ,\Phi ^{ion.} ]\left[ {\begin{array}{*{20}c} {0.799} & {0.599} \\ {0.599} & {0.799} \\ \end{array} } \right] \\ \end{aligned}, $$

(14.72)

which allow one to transform Eq. (14.68) into expression in terms of orthogonal VB structures:

$$ \Psi ^{{\text{VB}}} \left( 2 \right) = 0.764\,\Phi ^{cov.} \left( 2 \right) + 0.645\,\Phi ^{ion.} \left( 2 \right). $$

(14.73)

For H₂, when model probabilities equalize, P = Q = ½, these orthonormal structures can be expressed in terms of the spatial functions of two (orthonormal) MO configurations Ψ = {Ψ _α } of the familiar CID expansion, “bonding,” Ψ _b (2) = det[φ ⁺ _b φ ⁻ _b ], and “antibonding,” Ψ _a (2) = det[φ ⁺ _a φ ⁻ _a ],

$$ \Phi ^{cov/ion} = \sum\nolimits_{\alpha = b,a} {c_{\alpha}^{cov/ion} }\Psi _{\alpha } , $$

(14.74)

determined by the two MO combinations φ _b  = 2^−1/2 $(\tilde{\chi }_{\text{A}} + \tilde{\chi }_{\text{B}} )$ and φ _a  = 2^−1/2 $(\tilde{\chi }_{\text{B}} - \tilde{\chi }_{\text{A}} )$:

$$ \begin{aligned} &\Phi ^{cov.} \left( 2 \right) \equiv 2^{ - 1/2} [\Psi _{b} \left( 2 \right) -\Psi _{a} \left( 2 \right)]\quad {\text{and}}\quad\Phi ^{ion.} \left( 2 \right) \equiv 2^{ - 1/2} [\Psi _{b} \left( 2 \right) +\Psi _{a} \left( 2 \right)], \\ &\Psi _{b} \left( 2 \right) \equiv 2^{ - 1/2} [\Phi ^{cov.} \left( 2 \right) +\Phi ^{ion.} \left( 2 \right)]\quad {\text{and}}\quad\Psi _{a} \left( 2 \right) \equiv 2^{ - 1/2} [\Phi ^{ion.} \left( 2 \right) -\Phi ^{cov.} \left( 2 \right)]. \\ \end{aligned} $$

(14.75)

The two independent “chemical” states of VB theory correspond to equal configuration probabilities {p ^cov/ion _α  = |c ^cov/ion _α |²},

$$ \varvec{p}^{ion.} = \varvec{p}^{cov.} = \left( {1/2,1/2} \right), $$

but differ in phases of the configuration coefficients {c ^cov/ion _α }. The associated expression for the VB ground state then reads:

$$ \Psi ^{{\text{VB}}} \left( 2 \right) = 0.996\,\Psi _{b} \left( 2 \right) - 0.084\,\Psi _{a} \left( 2 \right). $$

(14.76)

Let us now examine the OCT predictions from two admissible averaging schemes over configurations [107]. The classical probability-averaging over configurations,

$$ \left\langle {{\mathbf{P}}^{ion./cov.} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})} \right\rangle_{ens.} = \sum\nolimits_{\alpha = a,b} {p_{\alpha }^{ion./cov.} } {\mathbf{P}}^{(\alpha )} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }}), $$

(14.77)

generates identical ensemble-average communications in both VB structures,

$$ \left\langle {{\mathbf{P}}^{cov.} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})} \right\rangle_{ens.} = \left\langle {{\mathbf{P}}^{ion.} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})} \right\rangle_{ens.} = 1/2\,[{\mathbf{P}}^{(b)} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }}) + {\mathbf{P}}^{(a)} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})] = \frac{1}{2}{\mathbf{1}}, $$

(14.78)

where (see Fig. 14.3a, b):

$$ {\mathbf{P}}^{(b)} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }}) = \left[ {\begin{array}{*{20}c} P & Q \\ P & Q \\ \end{array} } \right]\quad {\text{and}}\quad {\mathbf{P}}^{(a)} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }}) = \left[ {\begin{array}{*{20}c} Q & P \\ Q & P \\ \end{array} } \right]. $$

(14.79)

The ensemble-average channel, 〈P($\tilde{\varvec{\chi }}'$ $\left| {\tilde{\varvec{\chi }}} )\right\rangle_{ens.}$ = ½ 1, common to both VB structures, represents in OCT the purely covalent communication system, 〈S($\tilde{\varvec{\chi }}'$ $\left| {\tilde{\varvec{\chi }}} ) \right\rangle_{ens.}$ = 1 bit and 〈I ⁰($\tilde{\varvec{\chi }}$:$\left. {\tilde{\varvec{\chi }}^{{\prime }} } )\right\rangle_{ens.}$ = 0, of the complete dissipation of the initial (input) information into the communication “noise.” It thus reflects the maximum IT-covalency and minimum IT-ionicity in the 2-AO model of the chemical bond (see Fig. 14.2).

Therefore, the classical (probability) averaging scheme does not reveal the basic chemical difference between the two VB structures, which is embodied in phases of coefficients multiplying the MO configurations in the two VB combinations of Eq. (14.74). It also wrongly predicts the identical ensemble-average bond-orders between AO in these two chemical states,

$$ \begin{aligned} & \left\langle {{\varvec{\upgamma}}^{ion./cov.} } \right\rangle_{ens.} = \sum\nolimits_{a = b,a} {} p_{\alpha }^{ion./cov.} {\varvec{\upgamma}}^{(\alpha )} = 1/2({\varvec{\upgamma}}^{\left( b \right)} + {\varvec{\upgamma}}^{\left( a \right)} ) = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right] \equiv {\mathbf{I}} = {\varvec{\upgamma}}^{{\left( {nb} \right)}} , \\ & {\varvec{\upgamma}}^{\left( b \right)} = 2\left[ {\begin{array}{*{20}c} P & {\sqrt {PQ} } \\ {\sqrt {QP} } & Q \\ \end{array} } \right]\quad {\text{and}}\quad {\varvec{\upgamma}}^{(a)} = 2\left[ {\begin{array}{*{20}c} Q & {\sqrt {QP} } \\ {\sqrt {PQ} } & P \\ \end{array} } \right], \\ \end{aligned} $$

(14.80)

which mark the nonbonded (nb) status of AO, for the vanishing chemical bond!

Let us next examine the amplitude-averaging scheme giving rise to the resultant covalent amplitudes:

$$ \begin{aligned} \left\langle {{\mathbf{A}}^{cov.} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})} \right\rangle_{res.} = \sum\nolimits_{\alpha = a,b} {c_{\alpha }^{cov.} {\mathbf{A}}^{(a)} } (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }}) & = \frac{1}{\sqrt 2 }\left( {\left[ {\begin{array}{*{20}c} {\sqrt P } & {\sqrt Q } \\ {\sqrt P } & {\sqrt Q } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {\sqrt Q } & { - \sqrt P } \\ { - \sqrt Q } & {\sqrt P } \\ \end{array} } \right]} \right) \\ & = \frac{1}{\sqrt 2 }\left[ {\begin{array}{*{20}c} {\sqrt P - \sqrt Q } & {\sqrt P + \sqrt Q } \\ {\sqrt P + \sqrt Q } & {\sqrt Q - \sqrt P } \\ \end{array} } \right]. \\ \end{aligned} $$

(14.81)

Their squares generate the associated resultant communications between AO in this covalent state (see Fig. 14.10):

Fig. 14.10

Diagonal (Panel a) and offdiagonal (Panel b) resultant communications, corresponding to prototype (orthonormal) ionic and covalent VB structures, respectively

$$ \left\langle {{\mathbf{P}}^{cov.} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})} \right\rangle_{res} = \frac{1}{2}\left[ {\begin{array}{*{20}c} {1 - 2\sqrt {PQ} } & {1 + 2\sqrt {PQ} } \\ {1 + 2\sqrt {PQ} } & {1 - 2\sqrt {PQ} } \\ \end{array} } \right]. $$

(14.82)

In the homonuclear case, when P = Q = ½, this resultant channel represents the deterministic offdiagonal (inter-orbital) communications of Fig. 14.10b, between different AO [53], which conforms to the electron-sharing intuition behind the covalent bond component.

For the ionic configuration, one similarly finds the following resultant amplitudes,

$$ \begin{aligned} \left\langle {A^{ion.} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})} \right\rangle_{res.} & = \sum\nolimits_{\alpha = a,b} {} c_{\alpha }^{ion.} \,A^{(\alpha )} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }}) \\ & = \frac{1}{\sqrt 2 }\left( {\left[ {\begin{array}{*{20}c} {\sqrt P } & {\sqrt Q } \\ {\sqrt P } & {\sqrt Q } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\sqrt Q } & { - \sqrt P } \\ { - \sqrt Q } & {\sqrt P } \\ \end{array} } \right]} \right) = \frac{1}{\sqrt 2 }\left[ {\begin{array}{*{20}c} {\sqrt P + \sqrt Q } & {\sqrt Q - \sqrt P } \\ {\sqrt P - \sqrt Q } & {\sqrt Q + \sqrt P } \\ \end{array} } \right], \\ \end{aligned} $$

(14.83)

the squares of which generate the resultant scattering probabilities:

$$ \left\langle {{\mathbf{P}}^{ion.} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})} \right\rangle_{res.} = \frac{1}{2}\left[ {\begin{array}{*{20}c} {1 + 2\sqrt {PQ} } & {1 - 2\sqrt {PQ} } \\ {1 - 2\sqrt {PQ} } & {1 + 2\sqrt {PQ} } \\ \end{array} } \right]. $$

(14.84)

In the homonuclear H₂ case, when P = Q = ½, this resultant channel represents the noiseless diagonal (intra-orbital) communications [53] of Fig. 14.10a.

To summarize, the amplitude-interference scheme in the CID expansion distinguishes between the chemical characters of both VB structures and gives the correct prediction of the resultant communications between AO: orbital-mixing in the covalent state and orbital-localizing in the ionic structure. These two prototype chemical states separate in the resultant channel the additive (ionic, diagonal) communications in H₂,

$$ \left| {\chi_{\text{A}} } \right\rangle \to \left| {\chi_{\text{A}} } \right\rangle \quad {\text{and}}\quad \left| {\chi_{\text{B}} } \right\rangle \to \left| {\chi_{\text{B}} } \right\rangle , $$

from the nonadditive (covalent, offdiagonal) probability propagations:

$$ \left| {\chi_{\text{A}} } \right\rangle \to \left| {\chi_{\text{B}} } \right\rangle \quad {\text{and}}\quad \left| {\chi_{\text{B}} } \right\rangle \to \left| {\chi_{\text{A}} } \right\rangle . $$

The two VB structures of the chemical bond in H₂ are seen to represent the independent (noiseless) 2-electron components of the effective OAO-promotion channel, with the IT-covalency (noise) then being generated solely by the CI coefficients in the molecular ground state [Eq. (14.76)].

This dichotomous distinction of the electron AO communications in two chemical states of the orthogonal VB (OVB) structures allows one to generate the resultant AO-promotion amplitudes of the system ground state [see Eq. (14.73)],

$$ \left\langle {{\mathbf{A}}^{\text{VB}} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }}} \right\rangle_{res.} = 0.764\left\langle {{\mathbf{A}}^{cov.} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})} \right\rangle_{res.} + 0.645\left\langle {{\mathbf{A}}^{ion.} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})} \right\rangle_{res.} , $$

(14.85)

which generates the resultant probability-channel shown in Fig. 14.11. It is seen to generate 2% iconicity of the overall (1 bit) IT bond-multiplicity, thus again reflecting the bond practically purely covalent character. This result is qualitatively similar to that obtained from the Schmidt orthogonalization [Eq. (14.69)].

Fig. 14.11

Resultant OAO-promotion channel in VB ground-state and its entropic bond descriptors (in bits)

One can also directly verify that the configuration expansion of Eq. (14.76) generates the same OAO-promotion channel in VB ground state:

$$ \begin{aligned} & \left\langle {{\mathbf{A}}^{\text{VB}} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})} \right\rangle_{res.} = 0.996\left\langle {{\mathbf{A}}_{b} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})} \right\rangle_{res.} - 0.084\left\langle {{\mathbf{A}}_{a} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})} \right\rangle_{res.} , \\ & \left\langle {{\mathbf{A}}_{b} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})} \right\rangle_{res.} = \frac{1}{\sqrt 2 }\left[ {\begin{array}{*{20}c} 1 & 1 \\ 1 & 1 \\ \end{array} } \right],\quad \left\langle {{\mathbf{A}}_{a} (\tilde{\varvec{\chi }}^{{\prime }} |\tilde{\varvec{\chi }})} \right\rangle_{res.} = \frac{1}{\sqrt 2 }\left[ {\begin{array}{*{20}c} {\;\,\,1} & { - 1} \\ { - 1} & {\;{\kern 1pt} {\kern 1pt} {\kern 1pt} 1} \\ \end{array} } \right]. \\ \end{aligned} $$

(14.86)

14.7 Conclusion

Predictions from OCT are explicitly basis-set-dependent [64, 70], since alternative choices of these elementary atomic functions ultimately identify different discrete resolution levels (“events”) of molecular communication systems. The minimum basis of AO occupied in the separated atoms or the related subset of an extended basis set transformed to exhibit the maximum resemblance to the minimum basis has been found to generate the IT interpretation in close agreement with chemical intuition [70].

The OCT extends our understanding of the complex chemical bond phenomenon from the complementary IT viewpoint. This perspective on the entropic origins of chemical bonds is thus very much in spirit of the Eugene Wigner’s observation, often quoted by Walter Kohn, that the understanding in science requires insights from several different points of view. Indeed, the IT probes of molecular systems and chemical reactions generate such an additional perspective on both the genesis of chemical bonds and the elementary reaction mechanisms. It complements the familiar MO interpretations of quantum chemistry and ultimately gives rise to a deeper understanding of these complex phenomena.