Effect of the First Two Wheelset Bending Modes on Wheel–Rail Contact Behavior

Abstract

The objective of this paper is to develop a new wheel–rail contact model, which is suitable for considering the effect of wheelset bending deformation on wheel–rail contact behavior at high speeds . Dummies of the two rigid half wheelsets are introduced to describe the spacial positions of the wheels of the deformed wheelset. In modeling the flexible wheelset , the first two wheelset bending modes are considered. Based on the modal synthesis method, these mode values of the wheelset axle are used to solve the motion equations of the flexible wheelset axle modeled as an Euler–Bernoulli beam . The wheel is assumed to be rigid and always perpendicular to the deformed axle at the wheel center. In the vehicle model , two bogies and one car body are modeled as lumped masses. Spring–damper elements are adopted to model the primary and secondary suspension systems . The ballasted track is modeled as a triple-layer discrete elastic supported model. Two high-speed vehicle–track models, one considering rigid wheelset models and the other considering flexible wheelset models, are used to analyze the differences of the numerical results of the two models in both frequency and time domains. In the simulation, a random high-speed railway track irregularity is used as wheel–rail excitations. Wheel–rail forces are calculated and analyzed in the time and frequency domains . The results clarify that this new contact model can characterize very well the influence of the first two bending modes of the wheelset on contact behavior .

1 Introduction

High-speed railways are currently popular globally. However, there are some problems including passenger riding comfort, noise pollution, and even operational safety (Jin et al. 2013). Rail corrugation , rail welding irregularity , wheel burning, and wheel out-of-roundness (OOR) generate high-frequency components of the dynamic wheel–rail contact forces that contribute significantly to the total wheel–rail contact forces (Nielsen et al. 2003), and reduce the life of the components of track and vehicle, such as wheels, rails, and fasteners. Rail grinding and wheel reprofiling are the most common measures that have been proved to be effective in controlling rail irregularities and wheel OOR. However, these measures lead to notably high maintenance costs. A lot of measurements at the sites and coupling vehicle–track dynamics modeling have been carried out to investigate the mechanism and development of these phenomena. In the vehicle–track dynamics modeling, a rigid multi-body system is often adopted to simulate railway vehicles, based on several commercial codes available for the low-frequency domain, such as GENSYS, NUCARS, SIMPACK, and VAMPIRE. These computer programs are generally used to analyze railway vehicle dynamics responses at frequencies below 20 Hz, where the influence of rigid motions of the vehicle on wheel–rail contact forces is dominant (Nielsen et al. 2005). To analyze the vehicle dynamic responses at mid- and high frequencies, the vehicle structural flexibility should be taken into account in the modeling. It is obvious that wheelset structural flexibility has an influence on wheel–rail contact behaviors at mid- and high frequencies. Different flexible wheelset models have been set up due to various motivations in the past (Chaar 2007).

The methods applied to modeling flexible wheelset can be summarized as three major categories (Chaar 2007). The first is a lumped model developed in a simple and convenient way, in which a wheelset is divided into several parts interconnected with springs and dampers. This model can describe the bending and torsional motions of the wheelset with only a few degrees of freedom, which could not be applied to studying wear phenomena on wheel treads or rails (Popp et al. 1999). The second is a continuous model developed by Szolc (1998a, b), in which the wheelset axle was modeled as a beam, and two wheels and brake disks were modeled as rigid rings attached to the axle through a massless, elastically isotropic membrane. The model can characterize the wheelset dynamic behavior in the frequency range of 30–300 Hz. In the model proposed by Popp et al. (2003), the wheelset axle was considered as a 1D continuum, having the properties of a bar, a torsional rod, and a Rayleigh beam. The wheel was considered as a 2D continuum, having the properties of a disk and a Kirchhoff plate. The third was developed based on finite element method (FEM) , which simulates wheelset flexibility more realistically than the first two categories of model. The wheelset modes and corresponding natural frequencies were obtained through the modal analysis of the finite element (FE) model by using the commercial software, and they were input into the simulation by means of the commercial codes (SIMPACK, NEWEUL) (Meinders and Meinker 2003) or some non-commercial multi-body dynamic system codes. The non-commercial code developed by Fayos et al. (2007) and Baeza et al. (2008, 2011) introduced the Eulerian coordinate system to replace the Lagrangian coordinate system in the flexible wheelset modeling. In this way, it is convenient to obtain the motion of fixed physical nodes and consider the inertial effect due to wheelset rotation. Relying on current computing power, it is feasible to use FEM to consider the effect of flexible wheelset in modeling a railway vehicle coupling with a track.

Regarding the wheel–rail contact treatment in considering flexible wheelset influence, wheel–rail rolling contact condition is simplified based on different prior assumptions, especially in the detection of wheel–rail contact points . This is the prerequisite for the calculation of wheel–rail creepages and contact forces . Baeza et al. (2011) neglected the effect of the high-frequency deformation and the deviation of a rotating flexible wheelset rolling over a flexible track model on the wheel–rail contact point in the investigation into the effect of the rotating flexible wheelset on rail corrugation . Through the detailed calculation, Kaiser and Popp (2006) found that the contact point was in the location where the wheel and the rail had positive penetration maxima, and the penetration direction was orthogonal to the common tangent plane of the wheel and the rail before their deformations . A linear wheel–rail contact model was proposed and used to carry out the detection of wheel–rail contact point and the contact zone’s normal direction (Andersson and Abrahamsson 2002). In the detection, the functions were created using a first-order Taylor expansion around a reference state described by a group of parameters which represent a configuration, in which the train was in static equilibrium and the wheel and the track were free from geometric imperfections. The advantage of this approach is that the contact position and orientation in each time step can be calculated by interpolation replacing iterations, which results in a low computational cost. But the approach is only suitable for the case that the effect of all the parameters is very small on the contact point position and the contact patch orientation around the references is in static equilibrium. The wheel–rail contact point position and the contact patch orientation greatly depend on parameters, such as the curvatures of wheel and rail . In (Torstensson et al. 2012; Torstensson and Nielsen 2011), the contact point detection was done before the simulation and used in the subsequent time integration analysis in the form of lookup table. The commercial software GENSYS allows for such calculations using the preprocessor KPF (from Swedish contact point function). In the KPF, the location and orientation of the contact patch were assumed to be dependent only on the relative displacement in the lateral direction between the wheelset and the rails, and hence, the influence of the wheelset yaw angle was not taken into account. In some other papers, detailed discussions on the wheel–rail contact model were omitted. In this study, the wheel–rail contact model considering the effect of wheelset flexibility (Zhong et al. 2013, 2014) is further improved and the new contact model is suitable for the analysis on the effect of the local higher-frequency deformation of the wheels on the wheel–rail contact behavior .

2 Vehicle–Track Coupling Dynamic System

A flexible wheelset model (to be illustrated in Sect. 2.1) and a suitable wheel–rail contact model (to be discussed in Sect. 2.2) are integrated into the vehicle–track coupling dynamic system model. All parts of the vehicle system, except for its four wheelsets, are considered as rigid bodies. The primary and secondary suspension systems of the vehicle are modeled with spring–damper elements. A triple-layer model of discrete elastic support is adopted to simulate the ballasted track . The rails are modeled as Timoshenko beams. The sleepers are modeled as rigid bodies, and the ballast model consists of discrete equivalent masses. The equivalent spring–damper elements are used as the connections between the rails and the sleepers, the sleepers and the equivalent ballast bodies, and the ballast bodies and the roadbed. Figure 1 shows the vehicle–track coupling dynamic system model. The equations of motion of each component of the vehicle excluding wheelsets and the track are illustrated in detail in (Xiao et al. 2007, 2008, 2010). The parameters and their values describing the dynamic models are given in Appendix A.

Fig. 1

Vehicle–track coupling model (elevation)

2.1 Flexible Wheelset Model

The wheelset structural flexibility is considered by modeling the wheelset axle as an Euler–Bernoulli beam in two planes, one perpendicular to the track centerline and the other parallel to the track level. The crossing effect of the bending deformations in the two planes is ignored. In the first two bending modes obtained using the modal analysis of the FE model of a wheelset, two wheels have little deformation (Fig. 2), and their frequencies are in the available frequency range (0–500 Hz) of an Euler–Bernoulli beam model. Therefore, two wheels can be treated as rigid bodies in this study.

Fig. 2

First two bending modes obtained using FE model

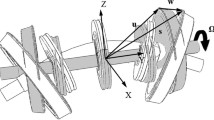
There are two force systems acting on the wheelset, one is the wheel–rail contact forces and the other is the forces of the primary suspension system (Fig. 3).

Fig. 3

Force analysis diagram of the flexible wheelset

In Fig. 3, O _fL and O _fR are the left and right points on the axle, respectively, where the primary suspension force systems are applied. O _CL and O _CR are the left and right contact points of wheel–rail, respectively. O indicates the origin of the coordinate system O-XYZ that is a coordinate system with a translational motion along the tangent track centerline at operational speed. If the speed is constant, this coordinate system is an inertial coordinate system and therefore regarded as an absolute coordinate system (geodetic coordinate system).

To analyze the axle’s deformation, the force systems from wheel–rail interaction acting on the left and right wheel treads are translated to the nominal circle centers O _L and O _R, respectively, and extra moments are produced in the procedure of translating contact forces . Thus, the force systems acting on the axle in the two planes are obtained in Fig. 4.

Fig. 4

Force analysis diagram in the plane O-YZ (a) and in the O-XY plane (b)

The notations of the variables and symbols are defined in Table 1. The subscript p denotes the primary suspension, the subscripts x, y, and z denote X-, Y-, and Z-direction, respectively, and A denotes the axle.

Table 1 Notations of the variables

The differential equation for the flexural vibration of an Euler–Bernoulli beam (the axle) in the plane O-YZ is written as

$$ {\text{EI}}_{x} \frac{{\partial^{4} u_{z} (y,t)}}{{\partial y^{4} }} + \rho A\frac{{\partial^{2} u_{z} (y,t)}}{{\partial t^{2} }} = Q_{z} (y,t) - \frac{{\partial M_{x} (y,t)}}{\partial y}, $$

(1)

where

$$ Q_{z} (y,t) = F_{{\text{AL}z}} \delta (y - y_{\text{wL}} ) + F_{{\text{pL}z}} \delta (y - y_{\text{pL}} ) + F_{{\text{AR}z}} \delta (y - y_{\text{wR}} ) + F_{{\text{pR}z}} \delta (y - y_{\text{pR}} ), $$

(2)

$$ \begin{aligned} M_{x} (y,t) & = M_{{\text{AL}}x} \delta (y - y_{\text{wL}} ) \\ & \quad + ( - F_{{\text{pL}}y} u_{{\text{pL}}z} + F_{{\text{pL}}z} u_{{\text{pL}y}} )\delta (y - y_{\text{pL}} ) \\ & \quad + M_{{\text{AR}}x} \delta (y - y_{\text{wR}} ) \\ & \quad + ( - F_{{\text{pR}}y} u_{{\text{pR}}z} + F_{{\text{pR}}z} u_{{\text{pR}}y} )\delta (y - y_{\text{pR}} ). \\ \end{aligned} $$

(3)

The force analysis diagram of the two wheels including the D’Alembert forces is shown in Fig. 5, based on which differential equations of motion of the two wheels are written as

Fig. 5

Force analysis diagram of the two wheels

$$ m_{\text{w}} \frac{{{\partial }^{2} }}{{{\partial }t^{2} }}u_{z} (y_{\text{w(L,R)}} ,t) = m_{\text{w}} g - F_{{{\text{A(L,R)}}z}} - F_{{{\text{wr(L,R)}}z}} , $$

(4)

$$ \begin{aligned} J_{\text{w}} \frac{{{\partial }^{2} }}{{{\partial }t^{2} }}u^{\prime}_{z} (y_{\text{w(L,R)}} ,t) & = - F_{{{\text{wr(L,R)}}y}} u_{{{\text{c(L,R)}}z}} \\ & \quad - F_{{{\text{wr(L,R)}}z}} u_{{{\text{c(L,R)}}y}} - M_{{{\text{A(L,R)}}x}} . \\ \end{aligned} $$

(5)

Note that the lateral accelerations of the wheels are assumed to be the same as the wheelset axle so there is no relative motion between wheels and axle.

Substituting the expressions of F _A(L,R)z and M _A(L,R)x obtained through Eqs. (4) and (5) into Eqs. (2) and (3), respectively, we can obtain:

$$ \begin{aligned} Q_{z} (y,t) & = F_{{\text{pL}z}} \delta (y - y_{\text{pL}} ) \\ & \quad + \left( {m_{\text{w}} g - F_{{{\text{wrL}}z}} - m_{\text{w}} \frac{{{\partial }^{2} }}{{{\partial }t^{2} }}u_{z} (y_{\text{wL}} ,t)} \right)\delta (y - y_{\text{wL}} ) \\ & \quad + \left( {m_{\text{w}} g - F_{{{\text{wrR}}z}} - m_{\text{w}} \frac{{{\partial }^{2} }}{{{\partial }t^{2} }}u_{z} (y_{\text{wR}} ,t)} \right)\delta (y - y_{\text{wR}} ) \\ & \quad + F_{{\text{pR}z}} \delta (y - y_{\text{pR}} ), \\ \end{aligned} $$

(6)

$$ \begin{aligned} M_{x} (y,t) & = ( - F_{{{\text{pL}}y}} u_{{\text{pL}z}} + F_{{{\text{pL}}z}} u_{{\text{pL}y}} )\delta (y - y_{\text{pL}} ) \\ & \quad + \left( { - F_{{{\text{wrL}}y}} u_{{{\text{cL}}z}} - F_{{{\text{wrL}}z}} u_{{{\text{cL}}y}} - J_{\text{w}} \frac{{\partial^{2} }}{{\partial t^{2} }}u_{z}^{{\mathbf{\prime }}} (y_{\text{wL}} ,t)} \right)\delta (y - y_{\text{wL}} ) \\ & \quad + ( - F_{{{\text{pR}}y}} u_{{\text{pR}z}} + F_{{{\text{pR}}z}} u_{{\text{pR}y}} )\delta (y - y_{\text{pR}} ) \\ & \quad + \left( { - F_{{{\text{wrR}}y}} u_{{{\text{cR}}z}} - F_{{{\text{wrR}}z}} u_{{{\text{cR}}y}} - J_{\text{w}} \frac{{\partial^{2} }}{{\partial t^{2} }}u_{z}^{{\mathbf{\prime }}} (y_{\text{wR}} ,t)} \right)\delta (y - y_{\text{wR}} ), \\ \end{aligned} $$

(7)

$$ \begin{aligned} & EI_{x} \frac{{\partial^{4} u_{z} (y,t)}}{{\partial y^{4} }} + \rho A\frac{{\partial^{2} u_{z} (y,t)}}{{\partial t^{2} }} + m_{\text{w}} \frac{{\partial^{2} }}{{\partial t^{2} }}u_{z} (y,t)\delta (y - y_{\text{wL}} ) \\ & \quad + m_{\text{w}} \frac{{\partial^{2} }}{{\partial t^{2} }}u_{z} (y,t)\delta (y - y_{\text{wR}} ) - J_{\text{w}} \frac{{\partial^{2} }}{{\partial t^{2} }}u^{\prime}_{z} (y,t)\delta (y - y_{\text{wL}} ) \\ & \quad - J_{\text{w}} \frac{{\partial^{2} }}{{\partial t^{2} }}u^{\prime}_{z} (y,t)\delta (y - y_{\text{wR}} ) = W_{0} , \\ \end{aligned} $$

(8)

where

$$ \begin{aligned} W_{0} & = (m_{\text{w}} g - F_{{{\text{wrL}}z}} )\delta (y - y_{\text{wL}} ) + F_{{\text{pL}z}} \delta (y - y_{\text{pL}} ) \\ & \quad + (m_{\text{w}} g - F_{{{\text{wrR}}z}} )\delta (y - y_{\text{wR}} ) + F_{{\text{pR}z}} \delta (y - y_{\text{pR}} ) \\ & \quad - \frac{\partial }{\partial y}[( - F_{{{\text{wrL}}y}} u_{{{\text{cL}}z}} - F_{{{\text{wrL}}z}} u_{{{\text{cL}}y}} )\delta (y - y_{\text{wL}} ) \\ & \quad + ( - F_{{{\text{pL}}y}} u_{{\text{pL}z}} + F_{{{\text{pL}}z}} u_{{\text{pL}y}} )\delta (y - y_{\text{pL}} ) \\ & \quad + ( - F_{{{\text{wrR}}y}} u_{{{\text{cR}}z}} - F_{{{\text{wrR}}z}} u_{{{\text{cR}}y}} )\delta (y - y_{\text{wR}} ) \\ & \quad + ( - F_{{{\text{pR}}y}} u_{{\text{pR}z}} + F_{{{\text{pR}}z}} u_{{\text{pR}y}} )\delta (y - y_{\text{pR}} )]. \\ \end{aligned} $$

(9)

Consider a solution of Eq. (8) in the form:

$$ u_{z} (y,t) = U_{z} (y)\sin (\omega t + \sigma ). $$

(10)

Using the calculus of variation (Qiu et al. 2009), the modal function satisfies:

$$ \begin{aligned} m_{ij} & = \int\limits_{0}^{L} {\rho A(U_{zi} U_{zj} ){\text{d}}y} \\ & \quad + m_{\text{w}} \left( {U_{zi} (y_{\text{wL}} )U_{zj} (y_{\text{wL}} ) + U_{zi} (y_{\text{wR}} )U_{zj} (y_{\text{wR}} )} \right) \\ & \quad + J_{\text{w}} \left( {U_{zi}^{\prime } (y_{\text{wL}} )U_{zj}^{\prime } (y_{\text{wL}} ) + U_{zi}^{\prime } (y_{\text{wR}} )U_{zj}^{\prime } (y_{\text{wR}} )} \right) = \delta_{ij} , \\ \end{aligned} $$

(11)

$$ k_{ij} = \int\limits_{0}^{L} {EI_{x} \left( {U_{zi}^{\prime \prime } U_{zj}^{\prime \prime } } \right)} {\text{dy}} = \omega_{j}^{2} \delta_{ij} $$

(12)

$$ \begin{aligned} & EI_{x} \int\limits_{0}^{L} {U_{zj} U_{zi}^{{{\prime \prime \prime \prime }}} {\text{d}}y} \\ & \quad + J_{\text{w}} \left( {U_{zj}^{{\prime }} (y_{\text{wL}} )U_{zi}^{{\prime }} (y_{\text{wL}} ) + U_{zj}^{{\prime }} (y_{\text{wR}} )U_{zi}^{{\prime }} (y_{\text{wR}} )} \right) \\ & \quad + J_{\text{w}} \left( {U_{zj} (y_{\text{wL}} )U_{zi}^{{\prime }} (y_{\text{wL}} ) + U_{zj} (y_{\text{wR}} )U_{zi}^{{\prime }} (y_{\text{wR}} )} \right) = \omega_{i}^{2} \delta_{ij} , \\ \end{aligned} $$

(13)

where δ _ij is the Kronecker delta. For i = j, Eq. (11) can be written as

$$ \begin{aligned} m_{jj} & = \int\limits_{0}^{L} {\rho A(U_{zj}^{2} )\text{d}y} + m_\text{w} \left( {U_{zj}^{2} (y_{\text{wL}} ) + U_{zj}^{2} (y_{\text{wR}} )} \right) \\ & \quad + J_\text{w} \left( {U_{zj}^{\prime 2} (y_{\text{wL}} ) + U_{zj}^{\prime2} (y_{\text{wR}} )} \right) = 1. \\ \end{aligned} $$

(14)

To obtain the mode shape functions with the wheelset axle modeled as a uniform Euler–Bernoulli beam carrying two particles (wheels), the segment of the beam from the left end to the first particle is referred to as the first portion, in between the two particles as the second portion, and from the second particle to the right end as the third portion. The beam mode shape will be the superposition of the mode shapes of the three portions. The derivation of the mode shape functions is presented in Appendix B. The first three modes have the frequencies of f ₁ = 111 Hz, f ₂ = 245 Hz, and f ₃ = 547 Hz, respectively. These mode shape functions are normalized so as to satisfy Eq. (14), as shown in Fig. 6. The third mode is not in the frequency range of 0–500 Hz where the Euler–Bernoulli beam is available to analyze the system. Hence, the effect of the first two modes on dynamic responses is conducted in this study.

Fig. 6

First three bending mode shapes of the wheelset

According to the modal analysis, we let the solution of Eq. (8) have the form:

$$ u_{z} = \sum\limits_{i = 1}^{N} {U_{zi} q_{zi} } . $$

(15)

Substituting Eq. (15) into Eq. (8), the differential equation can be written as

$$ \begin{aligned} & {EI}_{x} \sum\limits_{i = 1}^{N} {U_{zi}^{{{\prime \prime \prime \prime }}} q_{zi} } + \rho A\sum\limits_{i = 1}^{N} {U_{zi} \ddot{q}_{zi} } \\ & \quad + m_{\text{w}} \sum\limits_{i = 1}^{N} {U_{zi} (y_{\text{wL}} )\ddot{q}_{zi} } + m_{\text{w}} \sum\limits_{i = 1}^{N} {U_{zi} (y_{{\text{wR}}} )\ddot{q}_{zi} } \\ & \quad - J_{\text{w}} \sum\limits_{i = 1}^{N} {U_{zi}^{{\prime }} (y_{\text{wL}} )\ddot{q}_{zi} } - J_{\text{w}} \sum\limits_{i = 1}^{N} {U_{zi}^{{\mathbf{\prime \prime }}} (y_{\text{wR}} )\ddot{q}_{zi} } = W_{0} . \\ \end{aligned} $$

(16)

Multiplying both sides of Eq. (16) by $U_{zj}$ and integrating over the domain 0 < y < L, we can obtain:

$$ \begin{aligned} & {{EI}}_{x} \sum\limits_{i = 1}^{N} {\left[ {q_{zi} \int\limits_{0}^{L} {U_{zj} U_{zi}^{{{\prime \prime \prime \prime }}} {\text{d}}y} } \right]} + \rho A\sum\limits_{i = 1}^{N} {\left[ {\ddot{q}_{zi} \int\limits_{0}^{L} {U_{zj} U_{zi} {\text{d}}y} } \right]} \\ & \quad \cdot m_{\text{w}} \sum\limits_{i = 1}^{N} {\left[ {\ddot{q}_{zi} \int\limits_{0}^{L} {U_{zj} U_{zi} \delta (y - y_{\text{wL}} ){\text{d}}y} } \right]} \\ & \quad + m_{\text{w}} \sum\limits_{i = 1}^{N} {\left[ {\ddot{q}_{zi} \int\limits_{0}^{L} {U_{zj} U_{zi} \delta (y - y_{\text{wR}} ){\text{d}}y} } \right]} \\ & \quad - J_{\text{w}} \sum\limits_{i = 1}^{N} {\left[ {\ddot{q}_{zi} \int\limits_{0}^{L} {U_{zj} U_{zi}^{{\prime }} \delta (y - y_{\text{wL}} ){\text{d}}y} } \right]} \\ & \quad - J_{\text{w}} \sum\limits_{i = 1}^{N} {\left[ {\ddot{q}_{zi} \int\limits_{0}^{L} {U_{zj} U_{zi}^{{\prime }} \delta (y - y_{\text{wR}} ){\text{d}}y} } \right]} = W_{1j} . \\ \end{aligned} $$

(17)

Using the orthogonality of the modal shape function as expressed in Eqs. (11) and (13), Eq. (17) can be written as

$$ \begin{aligned} & \sum\limits_{i = 1}^{N} {\left\{ {q_{zi} \left[ {\omega_{i}^{2} \delta_{ij} - J_{\text{w}} \left( {U^{\prime}_{zj} (y_{\text{wL}} )U^{\prime}_{zi} (y_{\text{wL}} )} \right.} \right.} \right.} \\ & \quad + \left. {U^{\prime}_{zj} (y_{\text{wR}} )U^{\prime}_{zi} (y_{\text{wR}} )} \right) - J_{\text{w}} \left( {U_{zj} (y_{\text{wL}} )U^{\prime}_{zi} (y_{\text{wL}} )} \right. \\ & \quad + \left. {\left. {U_{zj} (y_{\text{wR}} )U^{\prime}_{zi} (y_{\text{wR}} )} \right)} \right] \\ & \quad + \ddot{q}_{zi} \left[ {\delta_{ij} - J_{\text{w}} \left( {U^{\prime}_{zj} (y_{\text{wL}} )U^{\prime}_{zi} (y_{\text{wL}} )} \right.} \right. \\ & \quad + \left. {U^{\prime}_{zj} (y_{\text{wR}} )U^{\prime}_{zi} (y_{\text{wR}} )} \right) - J_{\text{w}} \left( {U_{zj} (y_{\text{wL}} )U^{\prime}_{zi} (y_{\text{wL}} )} \right. \\ & \quad + \left. {\left. {\left. {U_{zj} (y_{\text{wR}} )U^{\prime}_{zi} (y_{\text{wR}} )} \right)} \right]} \right\} = W_{1j} , \\ \end{aligned} $$

(18)

where

$$ \begin{aligned} & W_{1j} = \int\limits_{0}^{L} {U_{zj} W_{0} {\text{d}}y} \\ & = (m_{\text{w}} g - F_{{{\text{wrL}}z}} )U_{zj} (y_{\text{wL}} ) + F_{{\text{pL}z}} U_{zj} (y_{\text{pL}} ) \\ & \quad + (m_{\text{w}} g - F_{{{\text{wrR}}z}} )U_{zj} (y_{\text{wR}} ) + F_{{\text{pR}z}} U_{zj} (y_{\text{pR}} ) \\ & \quad + ( - F_{{{\text{wrL}}y}} u_{{{\text{cL}}z}} - F_{{{\text{wrL}}z}} u_{{{\text{cL}}y}} )U^{\prime}_{zj} (y_{\text{wL}} ) \\ & \quad + ( - F_{{{\text{pL}}y}} u_{{\text{pL}z}} + F_{{{\text{pL}}z}} u_{{\text{pL}y}} )U^{\prime}_{zj} (y_{\text{pL}} ) \\ & \quad + ( - F_{{{\text{wrR}}y}} u_{{{\text{cR}}z}} - F_{{{\text{wrR}}z}} u_{{{\text{cR}}y}} )U^{\prime}_{zj} (y_{\text{wR}} ) \\ & \quad + ( - F_{{{\text{pR}}y}} u_{{\text{pR}z}} + F_{{{\text{pR}}z}} u_{{\text{pR}y}} )U^{\prime}_{zj} (y_{\text{pR}} ). \\ \end{aligned} $$

(19)

Equation (18) can be expressed as:

$$ \begin{aligned} & \ddot{q}_{zj} + \omega_{j}^{2} q_{zj} - J_{\text{w}} \sum\limits_{i = 1}^{N} {\left\{ {q_{zi} \left[ {U^{\prime}_{zj} (y_{\text{wL}} )U^{\prime}_{zi} (y_{\text{wL}} )} \right.} \right.} \\ & \quad + U^{\prime}_{zj} (y_{\text{wR}} )U^{\prime}_{zi} (y_{\text{wR}} ) \\ & \quad + \left. {U_{zj} (y_{\text{wL}} )U^{\prime}_{zi} (y_{\text{wL}} ) + U_{zj} (y_{\text{wR}} )U^{\prime}_{zi} (y_{\text{wR}} )} \right] \\ & \quad + \ddot{q}_{zi} \left[ {U^{\prime}_{zj} (y_{\text{wL}} )U^{\prime}_{zi} (y_{\text{wL}} ) + U^{\prime}_{zj} (y_{\text{wR}} )U^{\prime}_{zi} (y_{\text{wR}} )} \right. \\ & \quad + \left. {\left. {U_{zj} (y_{\text{wL}} )U^{\prime}_{zi} (y_{\text{wL}} ) + U_{zj} (y_{\text{wR}} )U^{\prime}_{zi} (y_{\text{wR}} )} \right]} \right\} = W_{1j} . \\ \end{aligned} $$

(20)

Equation (20) can be written in the matrix form:

$$ {\varvec{M}}_{1} \left[ {\ddot{q}_{zj} } \right] + {\varvec{M}}_{2} \left[ {q_{zj} } \right] = \left[ {W_{1j} } \right], $$

(21)

where

$$ \begin{aligned} ({\varvec{M}}_{11} )_{(i,j)} & =({\varvec{M}}_{21} )_{(i,j)} \\ & = - J_{\text{w}} \left[ {U^{\prime}_{zj} (y_{\text{wL}} )U^{\prime}_{zi} (y_{\text{wL}} ) + U^{\prime}_{zj} (y_{\text{wR}} )U^{\prime}_{zi} (y_{\text{wR}} )} \right. \\ & \quad + U_{zj} (y_{\text{wL}} )U^{\prime}_{zi} (y_{\text{wL}} ) + \left. {U_{zj} (y_{\text{wR}} )U^{\prime}_{zi} (y_{\text{wR}} )} \right], \\ {\varvec{M}}_{12} & = {\varvec{I}},\quad {\varvec{M}}_{22} = \left[ {\omega_{j}^{2} } \right]{\varvec{I}}, \\ {\varvec{M}}_{1} & = {\varvec{M}}_{11} + {\varvec{M}}_{12} ,\quad {\varvec{M}}_{2} = {\varvec{M}}_{21} + {\varvec{M}}_{22} . \\ \end{aligned} $$

(22)

The explicit integral method illustrated in Zhai (2007) is used to obtain the vector $\left[ {\ddot{q}_{zj} } \right]$ of each acceleration coordinate.

For the vibration in the plane YOX, the differential equation expressed with respect to $\left[ {\ddot{q}_{xy} } \right]$ can be written as:

$$ \begin{aligned} & \ddot{q}_{xj} + \omega_{xj}^{2} q_{xj} - J_{\text{w}} \sum\limits_{i = 1}^{N} {\left\{ {q_{i} \left[ {U^{\prime}_{xj} (y_{\text{wL}} )U^{\prime}_{xi} (y_{\text{wL}} )} \right.} \right.} \\ & \quad + U^{\prime}_{xj} (y_{\text{wR}} )U^{\prime}_{xi} (y_{\text{wR}} ) \\ & \quad + \left. {U_{xj} (y_{\text{wL}} )U^{\prime}_{xi} (y_{\text{wL}} ) + U_{xj} (y_{\text{wR}} )U^{\prime}_{xi} (y_{\text{wR}} )} \right] \\ & \quad + \ddot{q}_{i} \left[ {U^{\prime}_{xj} (y_{\text{wL}} )U^{\prime}_{xi} (y_{\text{wL}} ) + U^{\prime}_{xj} (y_{\text{wR}} )U^{\prime}_{xi} (y_{\text{wR}} )} \right. \\ & \quad + \left. {\left. {U_{xj} (y_{\text{wL}} )U^{\prime}_{xi} (y_{\text{wL}} ) + U_{xj} (y_{\text{wR}} )U^{\prime}_{xi} (y_{\text{wR}} )} \right]} \right\} = W_{1j}^{xoy} . \\ \end{aligned} $$

(23)

The derivation of Eq. (23) is similar to that of Eq. (20) and omitted here. Equation (23) can be expressed in matrix form:

$$ {\varvec{M}}_{1}^{xoy} \left[ {\ddot{q}_{xj} } \right] + {\varvec{M}}_{2}^{xoy} \left[ {q_{xj} } \right] = \left[ {W_{1j}^{xoy} } \right], $$

(24)

where

$$ \begin{aligned} & ({\varvec{M}}_{11} )_{(i,j)}^{xoy} = ({\varvec{M}}_{21} )_{(i,j)}^{xoy} \\ & \quad = - J_{\text{w}} \left( {U^{\prime}_{xj} (y_{\text{wL}} )U^{\prime}_{xi} (y_{\text{wL}} )} \right. + U^{\prime}_{xj} (y_{\text{wR}} )U^{\prime}_{xi} (y_{\text{wR}} ) \\ & \quad \quad + U_{xj} (y_{\text{wL}} )U^{\prime}_{xi} (y_{\text{wL}} ) + \left. {U_{xj} (y_{\text{wR}} )U^{\prime}_{xi} (y_{\text{wR}} )} \right), \\ & {\varvec{M}}_{12}^{xoy} = {\varvec{I}},\quad {\varvec{M}}_{22}^{xoy} = \left[ {\omega_{j}^{2} } \right]{\varvec{I}}, \\ & {\varvec{M}}_{1}^{xoy} = {\varvec{M}}_{11}^{xoy} + {\varvec{M}}_{12}^{xoy} ,\quad {\varvec{M}}_{2}^{xoy} = {\varvec{M}}_{21}^{xoy} + {\varvec{M}}_{22}^{xoy} . \\ \end{aligned} $$

(25)

2.2 Wheel–Rail Contact Model

As mentioned in Sect. 2.1, the main concern in this work is the wheelset axle bending. The wheels are assumed to be rigid, and their nominal rolling circles are always perpendicular to the deformed wheelset axle at their interference fit surfaces. Figure 7 shows that the flexible wheelset moves from its initial reference state (O ₁(t ₁)) to its t ₂ status (O ₂(t ₂)), which is described in the plane of O-YZ. O ₁ is the center of the undeformed wheelset at t ₁, and O ₂ is the center of the deformed wheelset at any time t. O ₁ O ₂ is the displacement vector of the wheelset center due to its rigid motion, and ϕ _R1 is the roll angle due to the wheelset rigid motion. The auxiliary line, $A_{\text{L}}^{0} A_{\text{R}}^{0} ,$ is the central line of the undeformed wheelset axle , $A_{\text{L}}^{1} A_{\text{R}}^{ 1}$ is obtained by moving $A_{\text{L}}^{0} A_{\text{R}}^{0}$ from O ₁(t ₁) to O ₂(t ₂), and $A_{\text{L}}^{2} A_{\text{R}}^{2}$ is obtained through rotating $A_{\text{L}}^{1} A_{\text{R}}^{1}$ by ϕ _R1. $A_{\text{L}}^{2} A_{\text{R}}^{2}$ is actually the central line of the rigid wheelset axle at t ₂. Figure 7 shows that the wheels are assumed to be rigid and always perpendicular to the deformed axle line at their connections at any time t ₂.

Fig. 7

A flexible wheelset moving from its initial reference state (O ₁(t ₁)) to its any status (O ₂(t)) in the plane of O-YZ

To clearly describe the new wheel–rail contact model, the dummies of the two rigid half wheelsets, as shown in Fig. 8, are employed to describe wheel–rail rolling contact behavior affected by the wheelset bending. The two dummies are indicated by DWL and DWR, respectively, and the wheels of the DWL and the DWR are assumed to overlap the left and right wheels of the flexible wheelset, respectively; all the time, namely, the motion of the assumed rigid wheels of the flexible wheelset can be described by the DWL and the DWR (Fig. 8). ϕ _R2 is the roll angle of the right wheel due to the bending deformation of the flexible wheelset. It is exactly the included angle between the line $A_{\text{L}}^{2} A_{\text{R}}^{2}$ and the axle line of the right wheel or the wheel of the DWR.

Fig. 8

Relationship between the two rigid half wheelset dummies and the flexible wheelset

It is not difficult to calculate the wheel–rail contact geometry considering the effect of the flexible deformation of the wheelset or the local high-frequency deformations of the wheels if the spatial positions of the DWL and the DWR are determined. Determining the spatial positions of the DWL and the DWR involves calculating their motion parameters, such as the lateral displacements of the centers of the wheels of the DWL and the DWR, indicated by y _DWL and y _DWR, respectively, the vertical displacements, z _DWL and z _DWR, the roll angles, ϕ _DWL and ϕ _DWR, and the yaw angles, ψ _DWL and ψ _DWR. These parameters are key to calculating the contact geometry of the flexible wheelset in rolling contact with a pair of rails by using this new wheel–rail contact model. This will now be demonstrated in detail.

Figure 8 describes the motion of the DWL and the DWR influenced by the wheelset bending and its rigid motion in the O-YZ plane only. After the rigid wheelset moves with the center displacement of O ₁ O ₂ and the rolling angle of ϕ _R1 in the O-YZ plane of the global reference, O-XYZ, its center position O ₁(t ₁) reaches the position O ₂(t ₂) and $A_{\text{L}}^{0} A_{\text{R}}^{0}$ reaches (or becomes) $A_{\text{L}}^{2} A_{\text{R}}^{2}$. Note that the vector O ₁ O ₂ and the roll angle ϕ _R1 around axis X are described in the O-YZ plane. The dash-dot line $A_{\text{L}}^{1} A_{\text{R}}^{1}$ is through point O ₂(t ₂) and parallel to $A_{\text{L}}^{0} A_{\text{R}}^{0}$. From Fig. 6, it is obvious that the rolling angle of the DWR caused by the wheelset rigid motion is just ϕ _R1 and that caused by the wheelset bending deformation is ϕ _R2, so the total rolling angle of the DWR is ϕ _DWR = ϕ _R1 + ϕ _R2, as shown in Fig. 6.

In addition, the displacement of the DWR is the vector O ₁ O _3R, which could be written as:

$$ {\varvec{O}}_{ 1} {\varvec{O}}_{{ 3 {\text{R}}}} = {\varvec{O}}_{ 1} {\varvec{O}}_{ 2} + {\varvec{O}}_{ 2} {\varvec{O}}_{{ 3 {\text{R}}}} . $$

(26)

In Fig. 8, the vector O ₂ A ₁ is parallel to O _3R A ₂ with the same length l ₀. l ₀ is actually the distance between the center of the wheel nominal circle and the center of the undeformed wheelset. The vector O ₂ O _3R is parallel to A ₁ A ₂, with the same length. Thus, O ₁ O _3R can be written as:

$$ {{\varvec{O}}_{ 1}} {{\varvec{O}}_{ 3 {\text{R}}}} = {{\varvec{O}}_{ 1}} {{\varvec{O}}_{ 2}} + {{\varvec{A}}_{ 1}} {{\varvec{A}}_{ 2}} = {{\varvec{O}}_{ 1}} {{\varvec{O}}_{ 2}} + \left( {{\varvec{O}}_{ 2}} {{\varvec{A}}_{ 2}} - {{\varvec{O}}_{ 2}} {{\varvec{A}}_{ 1}} \right). $$

(27)

Moreover, the vector O ₂ A ₁ is described by {x ₁ y ₁ z ₁}[i j k]^T in O-XYZ and can be obtained by rotating the vector {0 l ₀ 0}[i j k]^T (coinciding with the line $A_{\text{L}}^{1} A_{\text{R}}^{ 1}$) about the X-axis by ϕ _DWR. O ₂ A ₁ is written as:

$$ \begin{aligned} {\varvec{O}}_{2} {\varvec{A}}_{ 1} & = \left\{ {\begin{array}{*{20}c} {x_{1} } & {y_{1} } & {z_{1} } \\ \end{array} } \right\}\left[ {\begin{array}{*{20}c} {\varvec{i}} & {\varvec{j}} & {\varvec{k}} \\ \end{array} } \right]^{\text{T}} \\ & = \left\{ {\begin{array}{*{20}c} 0 \\ {l_{0} } \\ 0 \\ \end{array} } \right\}^{\text{T}} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos (\phi_{\text{R1}} + \phi_{\text{R2}} )} & {\sin (\phi_{\text{R1}} + \phi_{\text{R2}} )} \\ 0 & { - \sin (\phi_{\text{R1}} + \phi_{\text{R2}} )} & {\cos (\phi_{\text{R1}} + \phi_{\text{R2}} )} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{i}} \\ {\varvec{j}} \\ {\varvec{k}} \\ \end{array} } \right]. \\ \end{aligned} $$

(28)

The curve (Fig. 6) is the deformed axle centerline of the wheelset, which does not consider the influence of the rotation caused by the wheelset rigid motion. The point B _R is the center of the right nominal circle. The axle centerline of the deformed wheelset can be obtained by rotating about the X-axis by ϕ _R1. According to the definition of the curve , the vector O ₂ B _R is defined as:

$$ {\varvec{O}}_{2} {\varvec{B}}_{\text{R}} = \left\{ {\begin{array}{*{20}c} {x_{2} } \\ {y_{2} } \\ {z_{2} } \\ \end{array} } \right\}^{\text{T}} \left[ {\begin{array}{*{20}c} {\varvec{i}} \\ {\varvec{j}} \\ {\varvec{k}} \\ \end{array} } \right] = \left\{ {\begin{array}{*{20}c} {\Delta x_{2} } \\ {\Delta y_{2} + l_{0} } \\ {\Delta z_{2} } \\ \end{array} } \right\}^{\text{T}} \left[ {\begin{array}{*{20}c} {\varvec{i}} \\ {\varvec{j}} \\ {\varvec{k}} \\ \end{array} } \right], $$

(29)

where {Δx ₂ Δy ₂ Δz ₂}[i j k]^T is the displacement vector of the center of the right nominal circle due to the axle bending. Then, the vector O ₂ A ₂ is defined as {x ₃ y ₃ z ₃}[i j k]^T and can be written as:

$$ {\varvec{O}}_{2} {\varvec{A}}_{ 2} = \left\{ {\begin{array}{*{20}c} {x_{3} } \\ {y_{3} } \\ {z_{3} } \\ \end{array} } \right\}^{\text{T}} \left[ {\begin{array}{*{20}c} {\varvec{i}} \\ {\varvec{j}} \\ {\varvec{k}} \\ \end{array} } \right] = \left\{ {\begin{array}{*{20}c} {x_{2} } \\ {y_{2} } \\ {z_{2} } \\ \end{array} } \right\}^{\text{T}} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \phi_{\text{R1}} } & {\sin \phi_{\text{R1}} } \\ 0 & { - \sin \phi_{\text{R1}} } & {\cos \phi_{\text{R1}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{i}} \\ {\varvec{j}} \\ {\varvec{k}} \\ \end{array} } \right], $$

(30)

which is obtained according to the relationship between and or obtained by rotating by ϕ _R1. The wheelset center displacement vector O ₁ O ₂ is defined as {x ₀ y ₀ z ₀}[i j k]^T.

Substituting Eqs. (28) and (30) and the expression of O ₁ O ₂ into Eq. (27), the vector O ₁ O _3R can be written as:

$$ \begin{aligned} {\varvec{O}}_{1} {\varvec{O}}_{{ 3 {\text{R}}}} & = \left( {\left\{ {\begin{array}{*{20}c} {x_{0} } \\ {y_{0} } \\ {z_{0} } \\ \end{array} } \right\}^{\text{T}} + \left\{ {\begin{array}{*{20}c} {\Delta x_{2} } \\ {\Delta y_{2} + l_{0} } \\ {\Delta z_{2} } \\ \end{array} } \right\}^{\text{T}} {\varvec{M}}_{1} - \left\{ {\begin{array}{*{20}c} 0 \\ {l_{0} } \\ 0 \\ \end{array} } \right\}^{\text{T}} {\varvec{M}}_{2} } \right)\left[ {\begin{array}{*{20}c} {\varvec{i}} \\ {\varvec{j}} \\ {\varvec{k}} \\ \end{array} } \right], \\ {\varvec{M}}_{1} & = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \phi_{\text{R1}} } & {\sin \phi_{\text{R1}} } \\ 0 & { - \sin \phi_{\text{R1}} } & {\cos \phi_{\text{R1}} } \\ \end{array} } \right], \\ {\varvec{M}}_{2} & = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos (\phi_{\text{R1}} + \phi_{\text{R2}} )} & {\sin (\phi_{\text{R1}} + \phi_{\text{R2}} )} \\ 0 & { - \sin (\phi_{\text{R1}} + \phi_{\text{R2}} )} & {\cos (\phi_{\text{R1}} + \phi_{\text{R2}} )} \\ \end{array} } \right]. \\ \end{aligned} $$

(31)

Similarly, when considering the wheelset bending deformation in the plane O-XY, the vector O ₁ O _3R should be given as

$$ \begin{aligned} & {\varvec{O}}_{1} {\varvec{O}}_{{ 3 {\text{R}}}} = \left( {\left\{ {\begin{array}{*{20}c} {x_{0} } \\ {y_{0} } \\ {z_{0} } \\ \end{array} } \right\}^{\text{T}} + \left\{ {\begin{array}{*{20}c} {\Delta x_{2} } \\ {\Delta y_{2} + l_{0} } \\ {\Delta z_{2} } \\ \end{array} } \right\}^{\text{T}} {\varvec{M}}_{1} {\varvec{M}}_{3} - \left\{ {\begin{array}{*{20}c} 0 \\ {l_{0} } \\ 0 \\ \end{array} } \right\}^{\text{T}} {\varvec{M}}_{2} {\varvec{M}}_{4} } \right)\left[ {\begin{array}{*{20}c} {\varvec{i}} \\ {\varvec{j}} \\ {\varvec{k}} \\ \end{array} } \right], \\ & {\varvec{M}}_{3} = \left[ {\begin{array}{*{20}c} {\cos \psi_{\text{R1}} } & {\sin \psi_{\text{R1}} } & 0 \\ { - \sin \psi_{\text{R1}} } & {\cos \psi_{\text{R1}} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right], \\ & {\varvec{M}}_{4} = \left[ {\begin{array}{*{20}c} {\cos (\psi_{\text{R1}} + \psi_{\text{R2}} )} & {\sin (\psi_{\text{R1}} + \psi_{\text{R2}} )} & 0 \\ { - \sin (\psi_{\text{R1}} + \psi_{\text{R2}} )} & {\cos (\psi_{\text{R1}} + \psi_{\text{R2}} )} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right], \\ \end{aligned} $$

(32)

where ψ _R1 and ψ _R2 are the yaw angles caused by the rigid motion and the bending deformation in the plane O-XY, respectively.

ψ _DWR = ψ _R1 + ψ _R2 is the total yaw angle of the DWR. Similarly, the position of the DWL can be obtained. When the positions of the two dummies are known at t ₂, the wheel–rail contact geometry can be calculated. Then, the positions of the wheel–rail contact points are easily found, and the wheel–rail contact forces can be calculated. The normal wheel–rail contact forces are calculated by the Hertzian nonlinear contact spring model, and the tangent contact forces and spin moments are calculated by means of the model by Shen et al. (1983). Compared with the conventional wheel–rail contact model (Wang 1984; Zhai 2007), this new wheel–rail contact model can characterize the independent high-frequency deformations of the two wheels of the flexible wheelset more conveniently.

3 Results and Discussion

When a vehicle is running on an ideal track , it is only excited by sleepers. Note that the “flexible” wheelset model used in this section denotes the model considering the first two bending modes. The dynamic system with flexible wheelset models is used in the simulation on an ideal track at the speed of 300 km/h. Figure 9a, b shows the vertical forces in the frequency domain in steady and unsteady stages, respectively. In the unsteady stage, the peaks appear not only at a set of harmonic frequencies nf _s (n = 1, 2, 3, …) produced by passing sleeper but also at f _b1, while the influence of the second bending mode is small since there is no peak at f _b2. In the steady stage, the contribution of the component at f _b1 is weakened and only the peaks at nf _s (n = 1, 2, 3, …) remain. These results are reasonable because when a system comes to a steady stage, its responses only contain the component at the excitation frequency.

Fig. 9

Vertical contact force in steady (a) and unsteady (b) stages

Based on a large range of site measurements, the components of roughness on rails mostly appear in the range of 1–20 m. The natural frequencies of the first two bending modes are below 250 Hz, meaning the available frequency of this model is limited. Therefore, the components of the random irregularity on the rails are mainly in the frequency range of 0–150 Hz at the speed of 300 km/h. Figure 10a presents the local section of 900–950 m in the time domain, and Fig. 10b shows the irregularity in the frequency domain. Note that the results below are from the steady stage.

Fig. 10

Random irregularity in the time domain (a) and frequency domain (b)

Figures 11 and 12 show the wheel–rail contact forces acting on the rigid and flexible wheelsets in the time and frequency domains , respectively. As shown in Fig. 11a, the average of the oscillation of the lateral contact force acting on the flexible model is little smaller than that on the rigid wheelset model, and the shapes of the oscillation are different. As shown in Fig. 11b, the vertical contact forces acting on the two models oscillate around a similar average, while their shapes are different. These differences are caused by the wheelset flexibility.

Fig. 11

Lateral contact forces (a) and vertical contact forces (b) in the time domain

Fig. 12

Lateral contact forces (a) and vertical contact forces (b) in the frequency domain

In the frequency domain, the distributions of the components contained in both the lateral and vertical contact forces are in the excitation frequency range of the random irregularity. A peak at frequency 2 f _s appears in Fig. 11a, b. The contribution of the component at frequency f _s is overwhelmed by the effect of the irregularity . In addition, the uniform distribution in 0–150 Hz of the irregularity results in the non-uniform distribution of contact forces . As shown in Fig. 12a, b, the components in 80–150 Hz are higher than those in 0–80 Hz. This shows that under this present irregularity, this dynamic system is more sensitive to the excitation in 80–150 Hz than to that in 0–80 Hz.

In the frequency domain , the component at f _b1 of the lateral contact force acting on the flexible model is a little larger than that on the rigid model , as marked using the arrow in Fig. 12a. This shows that the first bending mode is excited, and the availability of the model to characterize the wheelset bending is proved. However, there is no evident difference at f _b1 for vertical contact forces acting on the two models. This shows that the wheelset bending deformation has a stronger effect on the lateral contact force than on the vertical contact force.

The wheel–rail contact force is affected by the position of the lateral contact points. Figure 13a, b shows the oscillations of the contact points in lateral direction described in the body coordinate system attached to the rail cross section in the time and frequency domains, respectively. The average of the magnitudes of oscillation of the contact points on the flexible model in the time domain is larger than that on the rigid model . This is caused by the wheelset bending. Moreover, it can weaken the relative movement between rail and wheel caused by the irregularity . Therefore, it is one cause of the smaller average of the lateral contact force acting on the flexible model (Fig. 11a). As shown in Fig. 13b, the difference of the components between the two models at f _b1 is evident. This explains the difference in the time domain (Fig. 13a) and again shows the effectiveness of the proposed model.

Fig. 13

Oscillation of contact points in lateral direction in the time domain (a) and frequency domain (b)

4 Conclusions

In this study, a new wheel–rail contact model is integrated into the high-speed vehicle–track coupling dynamics system model, which takes into account the effect of wheelset structural flexibility. Based on the new vehicle–track model, the effect of the first two bending modes of the wheelset on wheel–rail contact behavior is analyzed under the random irregularity in a frequency range of 0–150 Hz. The numerical results of the rigid wheelset model and the flexible wheelset model are compared in detail. The following conclusions can be drawn from the results:

• 1. The present vehicle–track model considering flexible wheelsets can very well characterize the effect of the flexible wheelset on wheel–rail dynamic behavior.

• 2. Under the excitation, the shapes of the oscillations of the wheel–rail contact forces and contact points for the new and conventional vehicle–track models are different. The difference is caused by the excited first bending mode of the wheelset.

For future work, the first improvement to be considered is to model a wheelset using the FEM or the Timoshenko beam theory to broaden the model’s available frequency range. This could allow it to help investigate the mechanisms behind the generation and development of wheel–rail wear and noise.

Appendices

Appendix A

The vehicle notations and track parameters are given in Table 2.

Table 2 The vehicle notations and track parameters

Appendix B

The axle is modeled as a uniform Euler-Bernoulli beam carrying two particles (wheels). The segment of the beam from the left end to the first particle is referred to as the first portion, in between the two particles as the second portion and from the second particle to the right end as the third portion. The beam mode shape will be the superposition of the mode shapes of the three portions. The mode shape of each portion has four constants of integration, i.e., a total of 12 for the three portions. It is necessary to satisfy: the boundary conditions; continuity of deflection and continuity of slope at the two ‘locations’; and compatibility of bending moments and compatibility of forces acting on the two particles.

Here we take the calculation of the mode shape functions in the plane O-YZ as an example. Fig. 14 shows a uniform Euler-Bernoulli beam O ₁ O ₃ of flexural rigidity EI _x , and length (R ₁ + R ₂ + R ₃)L carrying the first particle of mass m _w at axial coordinate R ₁ L from O ₁ and the second particle of mass m _w at axial coordinate R ₃ L from O ₃.

Fig. 14

Coordinate systems attached to the three sections of the wheelset axle

To write the equations of transverse vibrations of the system, three coordinate systems are chosen with origin at O ₁, O ₂, and O ₃. The choice of these coordinate systems has some algebraic advantages. In the text, the subscripts k = 1, 2, and 3 refer to the first portion, the second portion, and the third portion of the beam, respectively. For free vibration of the beam at frequency, if the amplitude of vibration of the beam is U _zk (y _k ) at axial coordinate y _k (in the range 0 < y _k  < R _k L), then based on the Euler-Bernoulli bending theory, the bending moment M _xk (y _k ), the shearing force Q _zk (y _k ), and the mode shape differential equation for the three portions are

$$ \left\{ {\begin{array}{*{20}l} {M_{xk} (y_{k} ) = EI_{x} \frac{{{\text{d}}^{2} U_{zk} (y_{k} )}}{{{\text{d}}y_{k}^{2} }},} \\ {Q_{zk} (y_{k} ) = - EI_{x} \frac{{{\text{d}}^{3} U_{zk} (y_{k} )}}{{{\text{d}}y_{k}^{3} }},} \\ {EI_{x} \frac{{{\text{d}}^{4} U_{zk} (y_{k} )}}{{{\text{d}}y_{k}^{4} }} - \rho A\omega^{2} U_{zk} (y_{k} ) = 0.} \\ \end{array} } \right. $$

(33)

To express these equations in dimensionless form, one defines the dimensionless axial coordinate Y _k , amplitude Z _k (Y _k ), operator Dⁿ, dimensionless bending moment M _xk (Y _k ), shearing force Q _zk (Y _k ), and a dimensionless natural frequency Ω as follows:

$$ \left\{ {\begin{array}{*{20}l} Y_{k} = \frac{{y_{k} }}{L},Z_{k} (Y_{k} ) = \frac{{U_{zk} (y_{k} )}}{L}, \\ {D}^{n} = \frac{{{\text{d}}^{n} }}{{{\text{d}}Y_{k}^{n} }},M_{xk} (Y_{k} ) = \frac{{M_{xk} (y_{k} )L}}{{EI_{x} }}, \\ Q_{zk} (Y_{k} ) = \frac{{Q_{zk} (y_{k} )L^{2} }}{{EI_{x} }},\varOmega^{2} = \frac{{\rho A\omega^{2} L^{4} }}{{EI_{x} }} = \alpha^{4} . \\ \end{array} } \right. $$

(34)

Therefore, Eq. (33) can be expressed in the dimensionless form:

$$ \left\{ {\begin{array}{*{20}l} M_{xk} (Y_{k} ) = D^{2} Z_{k} (Y_{k} ), \\ Q_{zk} (y_{k} ) = - D^{3} Z_{k} (Y_{k} ), \\ D^{4} Z_{k} (Y_{k} ) - \varOmega^{2} Z_{k} (Y_{k} ) = 0. \\ \end{array} } \right. $$

(35)

Consider the solution of the previous equation as

$$ \begin{aligned} Z_{k} (Y_{k} ) & = C_{k1} \sin (\alpha Y_{k} ) + C_{k2} \cos (\alpha Y_{k} )\\ \quad & + C_{k3} \sinh (\alpha Y_{k} ) + C_{k4} \cosh (\alpha Y_{k} ). \\ \end{aligned} $$

(36)

There are 12 unknown constants C _ki (i = 1, 2, 3, 4) for the three segments.

For free vibration the D’Alembert force and moment acting on the left wheel is $m_{\text{w}} \omega^{2} U_{z1} (R_{1} L)$ and $J_{\text{w}} \omega^{2} U^{\prime}_{z1} (R_{1} L),$ respectively (Fig. 15). Continuity of deflection and continuity of slope at O _wL together with compatibility of bending moments and compatibility of forces acting on the left wheel results in

Fig. 15

Wheel diagrams including D’Alembert forces

$$ \left\{ {\begin{array}{*{20}l} U_{z1} (R_{1} L) = U_{z2} (0), \\ \frac{{{\text{d}}U_{z1} (R_{1} L)}}{{{\text{d}}y_{1} }} = \frac{{{\text{d}}U_{z2} (0)}}{{{\text{d}}y_{2} }}, \\ M_{x1} (R_{1} L) = M_{x2} (0) + J_{\text{w}} \omega^{2} U^{\prime}_{z1} (R_{1} L), \\ Q_{z1} (R_{1} L) = Q_{z2} (0) + m_{\text{w}} \omega^{2} U_{z1} (R_{1} L). \\ \end{array} } \right. $$

(37)

The D’Alembert force and moment acting on the left wheel is $m_{\text{w}} \omega^{2} U_{z2} (R_{2} L)$ and $J_{\text{w}} \omega^{2} U^{\prime}_{z2} (R_{2} L),$ respectively. Continuity of deflection and continuity of slope at O _wR together with compatibility of bending moments and compatibility of forces acting on the right wheel results in

$$ \left\{ {\begin{array}{*{20}l} U_{z2} (R_{2} L) = U_{z3} (R_{3} L), \\ \frac{{{\text{d}}U_{z2} (R_{2} L)}}{{{\text{d}}y_{2} }} = - \frac{{{\text{d}}U_{z3} (R_{3} L)}}{{{\text{d}}y_{3} }}, \\ M_{x2} (R_{2} L) = M_{x3} (R_{3} L) + J_{\text{w}} \omega^{2} U^{\prime}_{z2} (R_{2} L), \\ Q_{z2} (R_{2} L) = - Q_{z3} (R_{3} L) + m_{\text{w}} \omega^{2} U_{z2} (R_{2} L). \\ \end{array} } \right. $$

(38)

Note that Eq. (38) takes into account the contra directions of the axial coordinates y ₂ and y ₃. Eqs. (37) and (38) in dimensionless form are

$$ \left\{ {\begin{array}{*{20}l} Z_{1} (R_{1} ) = Z_{2} (0), \\ {D}Z_{1} (R_{1} ) = {D}Z_{2} (0), \\ {D}^{2} Z_{1} (R_{1} ) = {D}^{2} Z_{2} (0) + \frac{{J_{\text{w}} \varOmega^{2} }}{{m_{\text{a}} L^{2} }}{D}Z_{1} (R_{1} ), \\ {D}^{3} Z_{1} (R_{1} ) = {D}^{3} Z_{2} (0) - \frac{{m_{\text{w}} }}{{m_{\text{a}} }}\varOmega^{2} Z_{1} (R_{1} ), \\ \end{array} } \right. $$

(39)

$$ \left\{ {\begin{array}{*{20}l} Z_{2} (R_{2} ) = Z_{3} (R_{3} ), \\ {D}Z_{2} (R_{2} ) = - {D}Z_{3} (R_{3} ), \\ {D}^{2} Z_{2} (R_{2} ) = {D}^{2} Z_{3} (R_{3} ) + \frac{{J_{\text{w}} \varOmega^{2} }}{{m_{\text{a}} L^{2} }}{D}Z_{2} (R_{2} ), \\ {D}^{3} Z_{2} (R_{2} ) = - {D}^{3} Z_{3} (R_{3} ) - \frac{{m_{\text{w}} }}{{m_{\text{a}} }}\varOmega^{2} Z_{2} (R_{2} ). \\ \end{array} } \right. $$

(40)

For the free boundary condition at the left end of the first portion and the right end of the third portion, the coefficients of the dimensionless mode shape functions satisfy

$$ C_{11} = C_{13} ,\;C_{12} = C_{14} ,\;C_{31} = C_{33} ,\;C_{32} = C_{34} . $$

(41)

Then one can write the dimensionless mode shape functions of the first and third portions as

$$ \begin{aligned} Z_{k} (Y_{k} ) & = C_{k1} \left( {\sin (\alpha Y_{k} ) + \sinh (\alpha Y_{k} )} \right) \\ & \quad + C_{k2} \left( {\cos (\alpha Y_{k} ) + \cosh (\alpha Y_{k} )} \right) \\ & = B_{k1} P_{k} (Y_{k} ) + B_{k2} V_{k} (Y_{k} ), \\ k & = 1,\;3. \\ \end{aligned} $$

(42)

Substituting Eqs. (42) and (36) into Eqs. (39), we can obtain:

$$ \left\{ {\begin{array}{*{20}l} B_{11} P_{1} (R_{1} ) + B_{12} V_{1} (R_{1} ) = C_{22} + C_{24} , \\ B_{11} {D}P_{1} (R_{1} ) + B_{12} {D}V_{1} (R_{1} ) = \alpha (C_{21} + C_{23} ), \\ B_{11} ({D}^{2} P_{1} (R_{1} ) - \frac{{J_{\text{w}} \varOmega^{2} }}{{m_{\text{a}} L^{2} }}{D}P_{1} (R_{1} )) \\ \quad \quad + B_{12} ( {\text{D}}^{2} V_{1} (R_{1} ) - \frac{{J_{\text{w}} \varOmega^{2} }}{{m_{\text{a}} L^{2} }}{D}V_{1} (R_{1} )) = \alpha^{2} ( - C_{22} + C_{24} ), \\ B_{11} ({D}^{3} P_{1} (R_{1} ) + \frac{{m_{\text{w}} }}{{m_{\text{a}} }}\varOmega^{2} P_{1} (R_{1} )) \\ \;\; + B_{12} ({D}^{3} V_{1} (R_{1} ) + \frac{{m_{\text{w}} }}{{m_{\text{a}} }}\varOmega^{2} V_{1} (R_{1} )) = \alpha^{3} ( - C_{21} + C_{23} ). \\ \end{array} } \right. $$

(43)

Then one can write the dimensionless mode shape function of the second portions as

$$ Z_{2} (Y_{2} ) = B_{11} P_{2} (Y_{2} ) + B_{12} V_{2} (Y_{2} ), $$

(44)

where

$$ \left\{ {\begin{array}{*{20}l} P_{2} (Y_{2} ) = P_{21} \sin (\alpha Y_{2} ) + P_{22} \cos (\alpha Y_{2} ) \\ \quad \quad+ P_{23} \sinh (\alpha Y_{2} ) + P_{24} \cosh (\alpha Y_{2} ), \\ V_{2} (Y_{2} ) = V_{21} \sin (\alpha Y_{2} ) + V_{22} \cos (\alpha Y_{2} ) \\ \quad \quad + V_{23} \sinh (\alpha Y_{2} ) + V_{24} \cosh (\alpha Y_{2} ). \\ \end{array} } \right. $$

(45)

The coefficients of sin(αY ₂), cos(αY ₂), sinh(αY ₂), and cosh(αY ₂) in Eq. (36) (when k = 2) correspond to those in the expression obtained by substituting Eq. (45) into Eq. (44), so we can obtain

$$ C_{2i} = B_{11} P_{2i} + B_{12} V_{2i} ,\quad i = 1,\;2,\;3,\;4. $$

(46)

The coefficients of B ₁₁ and B ₁₂ in Eq. (46) correspond to those in the expression by simplifying Eq. (43), so we can obtain:

$$ \left\{ {\begin{array}{*{20}l} P_{21} = \frac{{{D}P_{1} (R_{1} )}}{2\alpha } - \frac{{{D}^{3} P_{1} (R_{1} ) + \frac{{m_{\text{w}} }}{{m_{\text{a}} }}\varOmega^{2} {D}P_{1} (R_{1} )}}{{2\alpha^{3} }}, \\ P_{23} = \frac{{{D}P_{1} (R_{1} )}}{2\alpha } + \frac{{{D}^{3} P_{1} (R_{1} ) + \frac{{m_{\text{w}} }}{{m_{\text{a}} }}\varOmega^{2} {D}P_{1} (R_{1} )}}{{2\alpha^{3} }}, \\ P_{22} = \frac{{P_{1} (R_{1} )}}{2} - \frac{{{D}^{2} P_{1} (R_{1} ) - \frac{{J_{\text{w}} \varOmega^{2} }}{{m_{\text{a}} L^{2} }}{D}P_{1} (R_{1} )}}{{2\alpha^{2} }}, \\ P_{24} = \frac{{P_{1} (R_{1} )}}{2} + \frac{{{D}^{2} P_{1} (R_{1} ) - \frac{{J_{\text{w}} \varOmega^{2} }}{{m_{\text{a}} L^{2} }}{D}P_{1} (R_{1} )}}{{2\alpha^{2} }}, \\ \end{array} } \right. $$

(47)

$$ \left\{ {\begin{array}{*{20}l} V_{21} = \frac{{{D}V_{1} (R_{1} )}}{2\alpha } - \frac{{{D}^{3} V_{1} (R_{1} ) + \frac{{m_{\text{w}} }}{{m_{\text{a}} }}\varOmega^{2} {D}V_{1} (R_{1} )}}{{2\alpha^{3} }}, \\ V_{23} = \frac{{{D}V_{1} (R_{1} )}}{2\alpha } + \frac{{{D}^{3} V_{1} (R_{1} ) + \frac{{m_{\text{w}} }}{{m_{\text{a}} }}\varOmega^{2} {D}V_{1} (R_{1} )}}{{2\alpha^{3} }}, \\ V_{22} = \frac{{V_{1} (R_{1} )}}{2} - \frac{{{D}^{2} V_{1} (R_{1} ) - \frac{{J_{\text{w}} \varOmega^{2} }}{{m_{\text{a}} L^{2} }}{D}V_{1} (R_{1} )}}{{2\alpha^{2} }}, \\ V_{24} = \frac{{V_{1} (R_{1} )}}{2} + \frac{{{D}^{2} V_{1} (R_{1} ) - \frac{{J_{\text{w}} \varOmega^{2} }}{{m_{\text{a}} L^{2} }}{D}V_{1} (R_{1} )}}{{2\alpha^{2} }}. \\ \end{array} } \right. $$

(48)

So far the mode shape functions of the second and third portions have four unknown constants in total. These four unknown constants can be calculated using Eq. (40). The first two equations of Eq. (40) can be written as

$$ \left\{ {\begin{array}{*{20}l} B_{11} P_{2} (R_{2} ) + B_{12} V_{2} (R_{2} ) \\ \quad \quad = B_{31} P_{3} (R_{3} ) + B_{32} V_{3} (R_{3} ), \\ B_{11} {D}P_{2} (R_{2} ) + B_{12} {D}V_{2} (R_{2} ) \\ \quad \quad = - B_{31} {D}P_{3} (R_{3} ) - B_{32} {D}V_{3} (R_{3} ). \\ \end{array} } \right. $$

(49)

One considers

$$ \left\{ {\begin{array}{*{20}l} B_{31} = B_{11} P_{31} + B_{12} P_{32} , \\ B_{32} = B_{11} V_{31} + B_{12} V_{32} , \\ \end{array} } \right. $$

(50)

where

$$ \begin{aligned} P_{31} & = \frac{{{D}V_{3} (R_{3} )P_{2} (R_{2} ) + V_{3} (R_{3} ){D}P_{2} (R_{2} )}}{{{D}V_{3} (R_{3} )P_{3} (R_{3} ) - V_{3} (R_{3} ){D}P_{3} (R_{3} )}}, \\ P_{32} & = \frac{{{D}V_{3} (R_{3} )V_{2} (R_{2} ) + V_{3} (R_{3} ){D}V_{2} (R_{2} )}}{{{D}V_{3} (R_{3} )P_{3} (R_{3} ) - V_{3} (R_{3} ){D}P_{3} (R_{3} )}}, \\ V_{31} & = - \frac{{{D}P_{3} (R_{3} )P_{2} (R_{2} ) + P_{3} (R_{3} ){D}P_{2} (R_{2} )}}{{{D}V_{3} (R_{3} )P_{3} (R_{3} ) - V_{3} (R_{3} ){D}P_{3} (R_{3} )}}, \\ V_{32} & = - \frac{{{D}P_{3} (R_{3} )V_{2} (R_{2} ) + P_{3} (R_{3} ){D}V_{2} (R_{2} )}}{{{D}V_{3} (R_{3} )P_{3} (R_{3} ) - V_{3} (R_{3} ){D}P_{3} (R_{3} )}}. \\ \end{aligned} $$

(51)

Using the last two equations of Eq. (40), we can obtain:

$$ \left\{ {\begin{array}{*{20}l} B_{11} E_{11} + B_{12} E_{12} = 0, \\ B_{11} E_{21} + B_{12} E_{22} = 0, \\ \end{array} } \right. \Leftrightarrow \left[ {\begin{array}{*{20}l} {E_{11} } & {E_{12} } \\ {E_{21} } & {E_{22} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {B_{11} } \\ {B_{12} } \\ \end{array} } \right\} = 0, $$

(52)

where

$$ \left\{ {\begin{array}{*{20}l} E_{11} = {D}^{2} P_{2} (R_{2} ) - \frac{{J_{\text{w}} \varOmega^{2} }}{{m_{\text{a}} L^{2} }}{D}P_{2} (R_{2} ) \\ \quad \quad - P_{31} {D}^{2} P_{3} (R_{3} ) - V_{31} {D}^{2} V_{3} (R_{3} ), \\ E_{12} = {D}^{2} V_{2} (R_{2} ) - \frac{{J_{\text{w}} \varOmega^{2} }}{{m_{\text{a}} L^{2} }}{D}V_{2} (R_{2} ) \\ \quad \quad - P_{32} {D}^{2} P_{3} (R_{3} ) - V_{32} {D}^{2} V_{3} (R_{3} ), \\ E_{21} = {D}^{3} P_{2} (R_{2} ) + \frac{{m_{\text{w}} }}{{m_{\text{a}} }}\varOmega^{2} P_{2} (R_{2} ) \\ \quad \quad + P_{31} {D}^{3} P_{3} (R_{3} ) + V_{31} {D}^{3} V_{3} (R_{3} ), \\ E_{22} = {D}^{3} V_{2} (R_{2} ) + \frac{{m_{\text{w}} }}{{m_{\text{a}} }}\varOmega^{2} V_{2} (R_{2} ) \\ \quad \quad + P_{32} {D}^{3} P_{3} (R_{3} ) + V_{32} {D}^{3} V_{3} (R_{3} ). \\ \end{array} } \right. $$

(53)

Using the matrix form of Eq. (52), one can obtain

$$ \left| {\left[ {\begin{array}{*{20}l} {E_{11} } & {E_{12} } \\ {E_{21} } & {E_{22} } \\ \end{array} } \right]} \right| = E_{11} E_{22} - E_{12} E_{21} = 0. $$

(54)

Eq. (54) is the frequency equation, which is a transcendental equation. By using an iterative procedure based on linear interpolation, the first three natural frequencies are f ₁ = 111 Hz, f ₂ = 245 Hz, and f ₃ = 547 Hz, respectively.

The calculation of the coefficients of the three mode shape functions are demonstrated in detail in the following.

The dimensionless mode shape functions can be written as

$$ Z_{k} (Y_{k} ) = B_{11} P_{k} (Y_{k} ) + B_{12} V_{k} (Y_{k} ),\quad k = 1,2,3. $$

(55)

One may set the deflection of the first particle to be A and without loss of generality one may choose A = 1, hence

$$ A = 1 = Z_{1} (R_{1} ) = B_{11} P_{1} (R_{1} ) + B_{12} V_{1} (R_{1} ). $$

(56)

From the above equation and Eq. (52), one can obtain the following equations:

$$ \left\{{ \begin{array}{*{20}l} B_{11} = \frac{{AE_{12} }}{{P_{1} (R_{1} )E_{12} - V_{1} (R_{1} )E_{11} }}, \hfill \\ B_{12} = \frac{{ - AE_{11} }}{{P_{1} (R_{1} )E_{12} - V_{1} (R_{1} )E_{11} }}. \hfill \\ \end{array}} \right. $$

(57)

Subsequently, substituting the last equations into Eq. (55) (assuming k = 1) one can obtain the dimensionless mode shape function of the first portion $Z_{1} (Y_{1} )\;(0 \le Y_{1} \le R_{1} ).$ Substituting Eq. (55) into Eq. (55) (assuming k = 3) one can obtain the dimensionless mode shape function of the third portion.

$Z_{3} (Y_{3} )\;(0 \le Y_{3} \le R_{3} ).$ By inserting Eqs. (47) and (48) into Eq. (36) (assuming k = 2) one can obtain the dimensionless mode shape function of the second portion $Z_{2} (Y_{2} )\;(0 \le Y_{2} \le R_{2} ).$

Hence, the coefficient of the three mode shape functions can be calculated in Table 3.

Table 3 Coefficients of the three modes