Concepts: Assessing Tiger Population Dynamics Using Capture–Recapture Sampling

Abstract

Capture-recapture can be viewed as an animal survey method in which the count statistic is the total number of animals caught, and the associated detection probability is the probability of capture.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

9.1 Introduction

Capture-recapture can be viewed as an animal survey method in which the count statistic is the total number of animals caught, and the associated detection probability is the probability of capture. This probability is estimated using the pattern of captures and recaptures of animals over the survey period. For example, a typical design might involve a small mammal trapping grid. Traps are set, and animals trapped on the first sampling occasion are individually marked (tagged) to permit identification in subsequent sampling periods. On the second sampling occasion (e.g., the next day), animals that represent recaptures (they were caught at sampling occasion 1) are recorded, and newly captured animals are recorded and given individual marks. The process is repeated for the duration of the study (perhaps five consecutive days). The data resulting from the study then consist of the total number of animals that were caught and the record of when (i.e., on what sampling occasions) each animal was caught. The temporal sequence of encounter for each individual is referred to as the individual encounter history. The total number of animals caught is the count statistic, and the detection or capture probability is estimated from the records of the individual capture histories (Otis et al. 1978).

Although capture-recapture methods were originally developed for such cases where animals are physically caught and marked with artificial tags, the underlying concepts are valid even when animals are identified using natural markings. In the case of tigers (and other patterned animals such as leopard, chital, etc.), we can rely on their distinctive markings in the form of stripes or spots. In addition, identification of individuals based on DNA obtained from hair or scat has become widely adopted in surveys of carnivore populations (Long et al. 2008). As long as individuals can be identified reliably and sampling methods provide records of detection and non-detection over time (sampling periods) or space (traps or areas searched), then the resulting data can be used in a capture-recapture framework to estimate animal abundance.

As these new technologies for obtaining individual identity have been adopted, they have facilitated the study of species that could not have been effectively studied two decades ago and, at the same time, have produced vast quantities of spatially explicit encounter information. Using classical capture-recapture methods (Otis et al. 1978), such spatial information is not directly used (as data in the likelihood) in making inferences about population size or density. To make use of this spatial information, new classes of capture-recapture models have been developed. These are called spatial capture-recapture (SCR) or spatially explicit capture-recapture (SECR) methods (Efford 2004; Royle et al. 2014). They are spatially explicit in the sense that they involve explicit spatial models for both the sampling process and how individuals interact with the sampling process. A benefit of SCR is that they provide a means of direct estimation of population density. However, SCR is far more than simply an extension of technique meant to resolve certain technical deficiencies of ordinary capture-recapture or for improved density estimation. Rather, SCR is a general framework for the study of spatial population ecology, which allows ecologists to characterize wildlife populations and address many aspects of spatial population ecology from individual encounter history data, including such things as resource selection, movement, landscape connectivity, and factors that influence density (Royle et al. 2017).

9.2 Photo-Trapping Tigers

Camera trapping of tigers for the purpose of estimating abundance is described in some detail by Karanth (1995) and Karanth and Nichols (1998, 2000). The field has grown rapidly in the subsequent years, seeing publication of numerous syntheses and review articles on camera trapping including Long et al. (2008) and O’Connell et al. (2010).

The practical aspects of camera trapping tigers are explained in Chap. 5. The basic methodology involves setting out camera traps within some area of interest. The configuration of the traps can vary with the situation. As camera trapping methodology was being developed in the 1980s and 1990s, one of the main concerns in implementing field studies was to ensure that an area was covered fairly uniformly with cameras (Nichols and Karanth 2002; Chap. 11) in the sense that it would be difficult for a tiger in the sampled area to travel about and not encounter at least one camera trap. That is, traps should be set in a manner to prevent having “holes” in the sampled area in which tigers could move without any chance of being “captured” (photographed). The rationale for this “no holes” objective was to ensure that all individuals in a well-defined geographic area were catchable by at least one camera. Presumably the existence of holes implies p = 0 individuals which are not accounted for in the classical nonspatial capture-recapture models that were used. By assuming that no such individuals exist, then the estimate of N obtained by capture-recapture methods could be asserted to apply to a prescribed area containing the trap array. With spatial capture-recapture (SCR) models, there are no such restrictions necessary on the spatial arrangement of camera traps. This is because the population size is defined by the specification of the state space (see below), and the model explicitly accommodates p = 0 individuals, which arise as a result of individuals that are not in close proximity to any traps (Royle et al. 2014, Chap. 10).

In general, camera traps are set for several consecutive days. Each day is often considered as a sample period for defining encounter histories of individuals, although it could be sensible in some cases to group days together. In an ideal situation, there are sufficient camera traps to cover the entire area of interest with the available traps. However, if the area to be sampled is large, then various possible schemes for rotating traps to cover the entire area are possible. In these cases, the entire area is covered once every 2 or 3 days, perhaps. In this sampling situation, the sampling period is defined by the number of days necessary to cover the entire area. With the use of SCR methods, when the region being sampled is very large relative to the number of available traps, the use of cluster designs has proven to be very practical and efficient (Efford and Fewster 2013; Sun et al. 2014). Additional discussion of details associated with sampling designs will be presented in Sect. 7 below (also see Royle et al. 2014, Chap. 10).

The data obtained from camera trapping are summarized as capture history data, which is a record of the occasions and traps of capture for each individual. Each animal captured at least once during the survey has a capture history. While ordinary capture-recapture capture histories are simply a row vector of 1s and 0s indicating on what periods an animal was caught, the spatial encounter history for each individual consists of a two-dimensional matrix with J (number of traps) rows and K (occasions) columns where element (j,k) = 1 if an individual was encountered in trap j during occasion k. The programs such as SECR (Efford 2016) and SPACECAP (Gopalaswamy et al. 2012) make use of a compact encounter data file (EDF) and a trap deployment file (TDF) which describes the occasions in which each trap was operated. We note that capture histories need not be based on binary detection/non-detection data. Models can be developed based on total encounter frequencies per individual (Efford et al. 2009; Royle et al. 2009), and also recent advances in continuous time models have been made (Borchers et al. 2014; Dorazio and Karanth 2017).

In the remaining sections of this chapter, we elaborate on the basic modeling concepts that allow inference about encounter histories from camera trapping arrays. We cover classical capture-recapture methods and also relatively recent spatial capture-recapture methods. While the essential concepts are the same for both classes of methods, spatial capture-recapture models make use of spatial information on encounter and, in doing so, resolve some important technical limitations of classical capture-recapture and also allow researchers to study elements of spatial population ecology using individual encounter history data (Royle et al. 2017).

9.3 Closed Capture-Recapture

Capture-recapture models can be viewed as probabilistic expressions describing the processes that give rise to encounter history data (Nichols 1992, Williams et al. 2002). Capture-recapture models are frequently classified according to requisite assumptions about population closure. Closed population models are used when no gains to, or losses from, the population occur between sampling occasions. Because of this assumption of no population change, closed models are generally applied to studies conducted over relatively short time periods. Closed population models permit estimation of abundance or density. In contrast, open population models are used when there are gains, losses, or both occurring between sampling periods. Longer time intervals typically separate sampling occasions. Such models permit estimation of abundance and also local survival rate and number of recruits. Both closed and open models have been used with tiger camera trap data. For applications of closed population models, see Karanth (1995) and Karanth and Nichols (1998). Camera trap data from long-term studies at Nagarahole reserve, India have also been analyzed extensively to understand tiger population dynamics using open models (Karanth et al. 2006; Gardner et al. 2017).

9.3.1 Classical Closed Population Capture-Recapture Models

We suppose that the population of N individuals is subjected to repeated sampling for a specified number of occasions, say K (e.g., nights of a camera trapping study), where, in the first sampling occasion, all captured individuals are marked and released, and then at each subsequent sampling occasion, the detection of marked individuals is recorded and new unmarked individuals are marked or identified. This repeated sampling produces individual encounter histories that describe whether or not individuals were detected in each of the K occasions. For example, in a K = 5 occasion capture-recapture study, an individual with an encounter y _i  = (01010) was encountered two times; first on occasion 2, and then again on occasion 4, and it was not encountered in occasions one, three, or five. Estimating abundance using encounter history data collected using the general sampling scheme described above can be thought of as the process of estimating how many individuals were missed by the sampling, i.e., how many individuals have encounter history y _i  = (00000). Under the closure assumption, an individual detected at least once during the study was alive and present for the entire study, and therefore, failure to detect that individual in any occasion was due to imperfect detection alone. This information therefore allows for the estimation of the frequency of all-zero encounter histories.

The basic idea of all closed population capture-recapture methods is that the pattern of detections (the encounter histories) of individuals observed at least once provides information about detection probability, p, which, in turn, can be used to estimate the number of individuals that were not encountered. The underlying concept can be understood by recognizing that, under the assumption that $n\sim \rm{Binomial}\left(\it{N},\it{\tilde{p}}\right)$, the observed number of individuals n is related to the total population size N by the expression:

$$ E(n)=N\tilde{p} $$

where E() denotes statistical expectation, and $\tilde{p}$ is the probability that an individual is captured at least once during the study. Thus, the canonical estimator of N (also sometimes called the heuristic estimator) is obtained by plugging in an estimator of $\tilde{p}$ into this expression and rearranging to yield $\hat{N}=n/ \hat{\tilde{p}}$.

The simplest closed population capture-recapture model is often called “model M ₀,” or the null model. Under model M ₀, the encounter probability “per sample” p _i for each individual i = 1 , 2 ,  …  , N, is assumed to be the same for all individuals in the population, i.e., p _i =p. That is, there are no individual or temporal covariates that affect p. Then, whether or not we encounter an individual i=1,2,...,N during sampling occasion k, y _ik , is a Bernoulli trial (a “coin flip”) with constant probability p. In a study of K survey occasions, the probability of being captured at least once, $\tilde{p}$, is directly related to the “per sample” probability of detection parameter p by the formula

$$ \tilde{p}=1-{\left(1-p\right)}^K $$

The expression relating p to $\tilde{p}$ is different depending on the specific capture-recapture model being considered. The parameter p can be estimated from the observed encounter histories, and, in turn, this is used to estimate $\tilde{p}$, and then finally we estimate N using the canonical estimator introduced previously. Alternatively, one may obtain the MLE of N directly by maximizing what is usually referred to as the “full likelihood,” which is an explicit function of both p and N (Sanathanan 1972).

The assumption of constant encounter probability p is usually not satisfied in practice. Otis et al. (1978) described a family of models that can be used to deal with most sources of variation in individual encounter probabilities:

• M _o – The null model. Capture probability is constant.

• M _t – Time effects model. Capture probability is the same for all individuals but varies among sampling occasions. (Note that we use k for the time index here.)

• M _b – The behavioral response model. Capture probabilities vary depending on whether or not individuals have been captured previously.

• M _h – The individual heterogeneity model. Capture probabilities vary among individuals.

Variations of these different models exist, and the effects in some cases can be included together in a model. For example, the usual application of model M _t involves occasion-specific parameters p _k , but we can also consider systematic variation in detection probability that results from explicit covariates such as related to environmental conditions or systematic variation in time. For example, in classical small mammal trapping using catch traps, traps may be checked in the morning and evening, and we might expect encounter probability to vary over time (e.g., by sampling occasion). In camera trapping studies which usually involve a daily sample period then we might have systematic variation in encounter probability that varies by “day” according to a quadratic polynomial in Julian day, J _k , such as:

$$ \operatorname{logit}\left({p}_k\right)={\alpha}_0+{\alpha}_1{J}_k+{\alpha}_2{J_k}^2 $$

where the parameters α ₀ , α ₁ , and α ₂ are estimated. The behavioral response model is usually parameterized as a permanent change in p for individuals subsequent to their initial capture (i.e., p _pre and p _post , for capture probability before and after first capture, respectively). This could be the result of “trap happiness” due to using bait or lures at traps, or it could be the result of “trap shyness” due to aversion.

Model M _h has been an important model in capture-recapture because a number of factors usually induce variation in p among individuals, and it has long been recognized that the existence of individual heterogeneity in capture probability will lead to underestimation of N when it is not accounted for (Otis et al. 1978). Thus much attention has been focused on developing more flexible classes of model M _h (Dorazio and Royle 2003). Norris and Pollock (1996) formulated the model in terms of a finite mixture or latent class model in which each individual in the population belongs to a finite (and small) number of classes represented by distinct values of p (see Pledger 2000), but membership in these classes is not known. This finite mixture model is probably the most widely used version of model M _h .

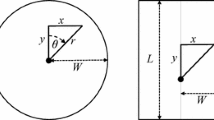
There are a number of basic technical or conceptual problems with the use of classical closed population capture-recapture models in camera trapping studies. For example, classical CR methods do not allow modeling of trap-level covariates, which may include type of trap (e.g., model of camera), effort (or days of operation of each camera), behavioral response which in many cases should depend on the specific trap, and local habitat conditions which might affect encounter probability through differential resource selection (Royle et al. 2013a). Another problem that has been widely recognized is that the spatial nature of camera trap arrays induces heterogeneity in encounter probability (Karanth and Nichols 1998) due to the juxtaposition of individual home ranges with the trap array (Fig. 9.1 below). Individuals with home ranges on the edge of an array will have lower probabilities than individuals with home ranges having a more interior location. This induced individual heterogeneity has traditionally been addressed by fitting individual heterogeneity models (i.e., “model M _h ”), although this approach has technical limitations (Link 2003). Alternatively, it may be preferable to explain heterogeneity using explicit covariates that are the cause, such as spatial proximity of individuals relative to traps. This was the idea behind Boulanger and McLellan (2001) who proposed using Huggins-Alho type models with a “distance to the edge” covariate, where distance to edge is computed as the distance from the average capture location to the boundary of a convex hull containing the trap locations. SCR models can be seen as an extension and formalization of this approach (Royle et al. 2014) by accommodating uncertainty in the definition of average capture location and making use of trap-level encounter data. However, one of the main deficiencies with classical closed population models is that they do not permit direct estimation of animal density because, in almost all practical field applications, it is not possible to precisely define the area sampled by a set of trapping devices. This is because individuals being captured move about space and can be captured without the biologists knowing whence those individuals originated or how much space they are using. Historically this has been accommodated in closed capture-recapture models by the use of buffer strips defined by the mean maximum distance moved (Wilson and Anderson 1985). Inference based on this method is discussed by Nichols and Karanth (2002; Chap. 11 of the first edition p. 129). Spatial capture-recapture models provide a formal technical framework for dealing with density estimation (Efford 2004; Borchers and Efford 2008; Royle and Young 2008; Royle et al. 2014) by prescribing an explicit “state space,” effectively a prior distribution on potential home-range locations, and estimating the number of points (individual activity centers) contained on that state space.

Fig. 9.1

Two home ranges of individuals (gray circles) juxtaposed with a spatial sampling grid of traps showing the variable exposure to trapping based on home range location

9.4 Closed Spatial Capture-Recapture

The sampling scheme for a spatial capture-recapture analysis is the same as described above, i.e., there is a population of N individuals, and we consider each individual having an individual covariate which is their activity center (s _i =[s _i,X , s _i,Y ]), a spatial coordinate. This is regarded as a latent variable (i.e., unobserved). Now the goal is to estimate the number of individuals (or activity centers) within a region of interest which is referred to as the state space, or S. The basic (“null”) SCR model assumes that individual activity centers are distributed uniformly throughout the state space:

$$ {\mathbf{s}}_i\sim \mathrm{Uniform}\ (S). $$

In SCR models, the realized density is the number of activity centers in the state space divided by the area of the state space: D = N / ||S||, where ||S|| is the area of S. Moreover, the realized density for any subset of the state space, say D(R) can be estimated. For example, using a fine partition of the state space allows explicit density maps to be produced. In some formulations of SCR, a prior distribution is imposed on N, e.g., N ∼ Poisson(λ||S||) (e.g., Borchers and Efford 2008), and instead of the realized density noted previously, the expected density λ is estimated.

As before, the population is subjected to sampling using camera traps. However, we explicitly acknowledge both how many traps there are, j=1,...,J traps, and the location of each of the traps, which we denote as x _j . The acknowledgment of the spatial structure of the traps means observations can be spatially indexed so encounter histories describe which individual (i), when (k), and importantly where (j) individuals were encountered, i.e., y _i,j,k . Typically, these observations are assumed to be Bernoulli outcomes:

$$ {y}_{i,j,k}\sim \mathrm{Bernoulli}\left({p}_{i,j,k}\right), $$

where p _i,j,k is the probability of encountering individual i in trap j and occasion k, which depends on the distance between the trap location (x _j ) and the individuals activity center (s _i ) as follows:

$$ {p}_{i,j,k}={p}_0\times {e}^{-\left(1/2{\upsigma}^2\right)d{\left({\boldsymbol x}_j,{\boldsymbol s}_i\right)}^2}. $$

It may also depend on sample occasion k in some manner and trap or time-varying covariates, as well as other individual covariates. This is referred to as the half-normal encounter model where the parameter logit(p ₀)=α ₀ is the baseline encounter probability, corresponding to the maximum probability of encountering an individual, which occurs when an individual’s activity center coincides with a trap location. The parameter σ describes the rate at which detection probability declines as a function of distance, and d(x _j ,s _i ) is the Euclidean distance between trap j and the activity center of individual i. In a spatial capture-recapture analysis, the parameters to be estimated are α ₀ and σ in addition to population size N. As in model M _h , the additional parameter σ accommodates individual heterogeneity in p, but, unlike model M _h , the parameter represents an explicit source of heterogeneity that is due to distance between individual activity or home-range centers and trap locations.

Thus, SCR models involve two very prominent modifications compared to ordinary capture-recapture models: (1) the encounter model describes trap-specific encounters and (2) the trap-level encounter probabilities are a function of a latent individual covariate, describing the activity center of individuals. These two modifications provide solutions to many of the technical and conceptual deficiencies of ordinary capture-recapture models. SCR provides an explicit model of heterogeneity in encounter probability induced by spatial sampling, and SCR models address the density estimation problem directly by specification of the model for activity centers and an explicit state space S. The inference problem then reduces to estimating the number of such activity centers in any well-defined subset of S.

SCR models are extremely flexible from the standpoint of modeling covariates on detection probability and also density. For example, occasion or trap-specific covariates (or even individual covariates such as individual’s sex) on baseline detection probability p ₀ can be modeled using logistic models of the form:

$$ \operatorname{logit}\left({p}_{0, ijk}\right)={\alpha}_0+{\alpha}_1\times {\mathrm{Sex}}_i+{\alpha}_2\times {\mathrm{Covariate}}_{jk} $$

Covariates can also be modeled on the parameter(s) of the encounter probability model. For example, on the σ parameter of the half-normal model:

$$ \operatorname{log}\left({\sigma}_{ik}\right)={\gamma}_0+{\gamma}_1\times {\mathrm{Sex}}_i+{\gamma}_t\times {\mathrm{Covariate}}_k. $$

The assumption that individual activity centers are uniformly distributed in space (i.e., constant density) is often regarded as being overly simplistic. However, other very general models describing the distribution of activity centers are possible. For example, when spatially referenced covariates, say z(s), can be identified which affect the density of individuals (Borchers and Efford 2008, Dorazio 2013), then we can formulate a point process model in which the intensity parameter of the point process is a function of such covariates:

$$ \operatorname{log}\!\left(\lambda\!\left(\mathbf{s}\right)\right)={\beta}_0+{\beta}_1z\left(\mathbf{s}\right) $$

where the parameter β ₁, to be estimated, allows density to depend on z(s).

9.5 Example: Analysis of the Nagarahole Data

We provide a brief example here using tiger camera trapping data collected in 2006 from the Nagarahole reserve, India. The data have been analyzed using spatial capture-recapture models by Royle et al. (2009) and Gopalaswamy et al. (2012) (the data are available as part of the R package SPACECAP). Both of those studies used Bayesian methods, but here we obtain a density estimate under two models using maximum likelihood in the R package oSCR (Sutherland et al. 2016). The study used 120 camera trap sites with 30 cameras rotated every 12 days (K = 12). The data set contains encounter histories of 44 individuals captured up to five times each. The state space was defined by a grid with 1000 m spacing and buffering the trap array by 3000 m (Fig. 9.2). We fit the null SCR model having constant p, σ, and D which produced the following summary results:

Fig. 9.2

120 camera trap locations (black dots) in Nagarahole reserve, India and the state-space grid (gray dots) used to fit the null SCR model

> print(out0) Model: D ~ 1 p0 ~ 1 sig ~ 1 Run time: 21.92167minutes AIC: 901.432 Summary table: Estimate SE z P(>|z|) p0.(Intercept) -5.515 0.269 -20.478 0 sig.(Intercept) 7.567 0.108 69.882 0 d0.(Intercept) -2.035 0.194 -10.494 0 *Density intercept is log(individuals per pixel) Nhat(state-space) = exp(d0.)*nrow(ssDF) (caution is warranted when model contains density covariates)

Because the default parameterization involves transformations of the basic parameters, we have to back-transform them to their natural scale for interpretation. Estimated density in the raw output is “per pixel” of the input state space (1000 m × 1000 m for the state space used here), on the log scale, and this has to be back-transformed and multiplied by 100 to get tigers per 100 km ²:

> 100*(exp(-2.035)) [1] 13.06805

(Note that results differ modestly from Royle et al. (2009) due to variations in the definition of the state space and parameterization used here.) The baseline detection probability is computed by taking the inverse logit transformation of the intercept parameter:

> plogis(-5.515) [1] 0.004009784

The estimated σ parameter, in meters, requires back-transforming the “sig.int” parameter which is estimated on the log scale:

Fig. 9.3

Estimated tiger density expressed in units of “individuals per state-space pixel” (individual activity centers per km²) of the Nagarahole reserve, India. Black dots are camera trap locations

> exp(7.567) [1] 1933.332

And finally we produce a realized density map using the predict.oSCR function and plotting the output shown in Fig. 9.3. This density map can be very useful in the context of conservation and management because it depicts where the population is distributed, and thus estimate of total population for subregions, such as management units, can be obtained directly.

9.6 Open Model Capture-Recapture (Conventional and Spatial)

9.6.1 Classical Open Models

As discussed above, capture-recapture models for closed populations are used when a marked population is sampled over a relatively short time span such that it is not expected to exhibit substantial changes from births, deaths, or movements in and out of the population. The quantities of primary interest are usually abundance (number of animals in the sampled area) or density (number of animal activity centers per unit area) of animals during this short sampling period. Encounter probabilities (ps) and (for SCR models) parameters describing the decrease in encounter probabilities associated with increasing distance between activity center and trap (σ) are also estimated.

Capture-recapture models for open populations shift the emphasis from statics to dynamics. Open populations are defined as those to which changes are expected to occur between sampling occasions. Those changes include births, deaths, and movement in and out of the sampled population. The very first capture-recapture models for open populations focused on losses to the population between sampling occasions (Cormack 1964; also see Jolly 1965; Seber 1965). We refer to these as Cormack-Jolly-Seber (CJS) models. The data for these models are encounter histories, the same as for classical closed population models, but the modeling differs in allowing for losses from the population between sampling occasions. The CJS model describes probabilities of these observable encounter histories in terms of detection probability and survival probability parameters.

We define the following CJS parameters used to model encounter history data:

• p _t = probability that an animal in the sampled population at time/occasion t is encountered during sampling efforts

• ϕ _t = probability that a member of the sampled population at occasion t is alive and in the population at occasion t + 1

Consider the detection history, 01010, arising during a K = 5 occasion study. Using the above parameters, the CJS probability associated with this history can be written as:

$$ \operatorname{Pr}\left(01010|\mathrm{release}\kern0.5em \mathrm{at}\kern0.5em \mathrm{occasion}\kern0.5em 2\right)={\phi}_2\left(1-{p}_3\right){\phi}_3{p}_4\left(1-{\phi}_4{p}_5\right) $$

The animal was initially encountered in occasion 2, so we condition on this encounter (i.e., we don’t model this initial encounter, but use it as a starting point, effectively focusing interest on the fate of the marked population). We know the animal survived until at least occasion 4, because we encountered the animal on that occasion, and the probability associated with surviving from occasion 2 to 4 is ϕ ₂ ϕ ₃. Despite being alive, the animal was not encountered at occasion 3 (1-p ₃) but was encountered at occasion 4 (p ₄). Uncertainty characterizes occasion 5, as the animal may have been lost (death or movement) from the population or may have survived but simply not been encountered. The probability associated with these two events can be written as the complement of the probability of surviving and being detected: (1-ϕ ₄ p ₅). Note that this CJS model incorporates both the observation process (the p _t ) and the dynamical ecological process (ϕ _t ) within the same model structure.

Every animal detected in a capture-recapture study has an associated encounter history, and each such history has an associated probability, as above. The product of these probabilities for all of the animals encountered during a study forms the likelihood and can be used to estimate the survival and detection/encounter parameters. The CJS model is very general, with many time-specific parameters to estimate in long-term studies. It is possible to constrain survival or encounter parameters to be constant over time, or they can be modeled as linear-logistic functions of time-specific covariates (e.g., weather variables) to yield more parsimonious models. Software is available to make computations relatively easy for the full CJS model, constrained models, and models with time-specific covariate relationships (e.g., MARK; White and Burnham 1999).

Although Cormack’s (1964) original model focused on survival, Jolly (1965) and Seber (1965) recognized that encounter data also contained information about population size and recruitment to the population. Under the Jolly-Seber (JS) model, abundance and recruitment are estimated as derived parameters. That is, survival and encounter probabilities are estimated directly as parameters of the model structure and then used to estimate these other quantities with an additional step. The two additional quantities in the JS modeling approach both concern ecological processes:

• N _t  = abundance, number of animals in the population at sampling occasion t

• B _t  = number of new individuals joining the population between occasions t and t + 1 and still in the population at time t + 1

Abundance is estimated by counting all of the individuals encountered at each occasion (denote n _t ) and then dividing this statistic by the estimate of encounter probability:

$$ \widehat{N}=\frac{n_t}{{\hat{p}}_t}. $$

(5.1)

Note that the above estimator represents another application of the canonical estimator of Chap. 3. Recruitment can then be estimated as the difference between the estimated abundance at occasion t + 1 and the expected survivors from occasion t:

$$ {B}_t={\hat{N}}_{t+1}-{\hat{N}}_t{\upphi}_t. $$

(5.2)

The basic JS approach for modeling open populations thus provides estimates of the time-specific state variable, ${\widehat{N}}_t$; the number of new recruits, ${\hat{B}}_t$; the rate of loss, $1-{\hat{\phi}}_t$; and the number of losses, ${\hat{N}}_t\left(1-{\hat{\phi}}_t\right)$. These estimates provide a remarkably good description of population dynamics, based only on a set of encounter histories, i.e., a set of vectors populated by 0s and 1s. Other open population modeling approaches have been developed more recently that include parameters associated with recruitment and change in abundance directly in the likelihoods (Crosbie and Manly 1985, Pradel 1996, Schwarz and Arnason 1996). The logic of these approaches is identical to that of Jolly (1965) and Seber (1965), however, and selection of a modeling approach should depend on the objectives of the analysis.

Several basic assumptions underlie these estimators (also see Williams et al. 2002). First, time-specific encounter and survival probabilities are assumed to be the same for all animals in the population. This assumption can be relaxed in numerous ways. For example, animals may be stratified by any variable relevant to either observation or ecological processes. Some variables remain constant throughout the study (e.g., sex), and the most general modeling approach essentially uses separate JS models for each stratum. Age and prior (to time t) encounter history are dynamic state variables for which specific models have been developed (e.g., Pollock 1975, Pollock 1981, Brownie and Robson 1983, Brownie et al. 1986, Williams et al. 2002). Stochastically dynamic variables that characterize animals (e.g., size, location, reproductive state) and may influence survival and/or detection can be dealt with using multistate models (Arnason 1972, 1973; Brownie et al. 1993; Lebreton et al. 2009). In addition to survival and encounter probabilities, these models also estimate probabilities of moving from one state to another between sampling occasions. These so-called multistate models are discussed more fully in Chap. 12.

Marks permitting individual identification are assumed to remain with animals (no loss of marks) and to be read accurately and not overlooked. Sampling occasions are assumed to be short relative to the periods between occasions, and mortality during sampling occasions is assumed to be negligible. Animals are assumed to behave independently with respect to probabilities of survival and/or encounter. Finally, all emigration from the sampled population is assumed to be permanent. This assumption can be relaxed using either the robust design (Kendall et al. 1997; see below) or open population models with certain constraints (Kendall and Nichols 2002).

The above assumptions are needed for CJS and JS modeling. One assumption required by JS and not CJS models is that previously encountered individuals have the same encounter probability as individuals not previously encountered. In CJS modeling, the p _t parameters only apply to previously encountered animals. However, under the JS model, these encounter probabilities are assumed to apply to animals not previously encountered (new animals) as well.

9.6.2 Robust Design

Pollock (1982) recognized that many sampling programs include groups of sampling occasions that are close together in time (e.g., a few days apart) but separated from the next group of occasions by a long time period (e.g., approximately 1 year). He noted that encounter data within a season (referred to as secondary period data) could be analyzed using models developed for closed populations, whereas encounters from one season to the next (primary period data) could be analyzed using models for open populations. Advantages of this approach included robust estimators and the ability to estimate quantities that might not be estimable using only open or only closed models (Pollock 1982, Kendall and Pollock 1992, Kendall et al. 1997, Williams et al. 2002).

Pollock’s (1982) initial proposal was to simply use open models (e.g., CJS) to estimate survival probabilities, to use classical closed models to estimate abundances, and then combine the two kinds of estimators to estimate recruitment using the basic structure of Eq. 5.2. More recent work has incorporated the closed and open model components into a single likelihood (Kendall et al. 1995), but historic work with tiger populations has thus far relied on Pollock’s (1982) initial ad hoc approach of combining estimates from closed and open population models. Note that a distinct advantage of this ad hoc approach is the ability to use SCR models for closed populations to estimate abundances (Duangchantrasiri et al. 2016). A clear advantage provided by SCR models is an explicit mechanism for dealing with an important source of heterogeneity in encounter probabilities, the spacing of animal activity centers relative to camera trap positions. Another advantage provided by SCR models is the ability to estimate time-specific density, ${\hat{D}}_t$, directly. Studies using capture-recapture models for open populations typically span multiple years (e.g., Karanth et al. 2006, Duangchantrasiri et al. 2016). A common occurrence in such studies is variation over time in the amount of area sampled. It is common to begin a camera trap study, for example, by covering a relatively small area. Additional funding often allows investigators to buy more cameras and increase areas surveyed. One consequence of such temporal changes in area surveyed is that traditional estimates of population change, ${\hat{\lambda}}_t=\raisebox{1ex}{${\hat{N}}_{t+1}$}\!/ \!\raisebox{-1ex}{${\hat{N}}_t$}$, reflect changes in both population dynamics and sampled area. However, we typically want to estimate λ _t in order to draw inferences about ecology, not sampling design changes. One way to deal with this issue is to base ecological inferences on ratios of density estimates, i.e., ${\hat{\lambda}}_t=\raisebox{1ex}{${\hat{D}}_{t+1}$}\!/ \!\raisebox{-1ex}{${\hat{D}}_t$}$. As long as the habitat characteristics of the added area sampled are similar to those of the original study area, then these density-based estimates of population change should pertain largely to ecological and not observational processes. A similar approach can be used for recruitment, replacing ${\hat{N}}_t$ in Eq. 5.2 with ${\hat{D}}_t$. The resulting ${\hat{B}}_t$ is now interpreted as new recruits per unit area, but their use restricts inference to ecological processes rather than to changes in study area.

The robust design has been used to draw inferences about tiger population dynamics in Nagarahole reserve, Karnataka state, India (Karanth et al. 2006), and in Huai Kha Khaeng Wildlife Sanctuary in the Western Forest Complex of Thailand (Duangchantrasiri et al. 2016). Both studies used CJS-type models to estimate annual survival rates. The Karanth et al. (2006) study used classical models for closed populations to estimate tiger abundance and density, as SECR models were not well developed at the time of their analyses. Duangchantrasiri et al. (2016) used SECR models to estimate densities and abundances over time.

The original references should be consulted for methodological details, but Table 9.1 shows some of the population dynamic parameters that can be estimated using the robust design (from Karanth et al. 2006). The increases in estimated abundances that accompanied increases in study area size emphasize the need to account for such changes when making ecological inferences. Because of the changing study area size, rate of population change, λ _t , was estimated using density estimates, and recruitment was estimated for the largest number of primary sampling occasions with unchanged area sampled. Annual survival rates were best estimated using a time constant model. Results of these analyses from India (Karanth et al. 2006) and Thailand (Duangchantrasiri et al. 2016) provided evidence of dynamic stability, with fluctuations in abundance and turnover of individuals, yet no sustained increases or decreases.

Table 9.1 Estimated abundance, annualized (not period to period) survival rate, area sampled by camera traps, population density, and rate of change in density for primary sampling periods, for the tiger population in Nagarahole, India, 1991–2000

9.6.3 Open SCR Models

Spatial capture-recapture models allow for a much richer class of open population models compared to classical Jolly-Seber and CJS models. Not only can explicit population dynamics (survival, recruitment) be modeled but also spatial dynamics such as dispersal and transience can be modeled by allowing for the point process model of activity centers to be temporally dynamic (Ergon and Gardner 2013; Schaub and Royle 2014; Royle et al. 2016; Gardner et al. in review). We describe basic ideas of open SCR models here. We note that so far all applications of open SCR models have been based on Bayesian analyses using MCMC because of the complexity of the latent variable structure in these models. That said, we imagine that such models are amenable to likelihood analysis using techniques of hidden Markov models.

One class of open SCR model which does not contain explicit dynamics is the multi-session models. These models assume that year-specific population sizes N _t are Poisson random variables that are independent from 1 year to the next: N _t ∼Poisson(λ _t ). This allows for variation among years to be modeled on the expected population size parameter λ _t such as log(λ _t ) = β ₀ + β ₁ × year _t for a simple trend model. Under this Poisson assumption for annual population size, it is possible to obtain MLEs of model parameters using marginal likelihoods (see Royle et al. 2014, ch. 6). These models are usually called multi-session models in the context of SCR (e.g., as implemented in the software package “SECR,” Efford 2016). Multi-session models provide a flexible framework for combining data from multiyear studies into a single analysis framework while at the same time providing year-specific density or population size estimates and also estimates of basic parameters that describe inter-annual variation in density or population size (recall that with SCR models, density is related directly to N _t and the area of the prescribed state space, as discussed above). Multi-session models do not preserve individual identity across years and so information about survival and recruitment is lost. Nevertheless the approach is straightforward to apply and versatile because the populations need not be strictly temporal but can be demographic groups, or different species, or different locations (such as different tiger reserves). However, as noted in the previous section, it is often important to be able to obtain explicit estimates of population dynamics (survival and recruitment, state-transition probabilities, growth rate, etc.). This is especially true in many camera trapping studies which are often focused on extremely rare carnivores for which little is known due to the difficulty in conducting population ecological studies of such species.

It is possible to incorporate explicit population dynamics into spatial capture-recapture models. So far, all applications of “open SCR” models have been based on a Bayesian formulation of the models using data augmentation (Royle and Dorazio 2008, ch. 10; Royle and Dorazio 2012; Kery and Schaub 2012, ch. 10; Royle et al. 2014, ch. 16). Bayesian analysis of these models has been done because SCR models contain many latent variables (i.e., the individual activity centers), and no one has worked out likelihood formulations yet, although in principle we imagine this can be done.

To specify a spatially explicit version of the Jolly-Seber model, let y _i,j,k,t be the encounter history for individual i, at trap j, occasion k, and during primary occasion t. We think of t here indexing biological seasons or years, or “primary periods” in the terminology of the robust design, such that dynamics occurs across the t index of the variables. We note that there may or may not be replication within primary periods (i.e., k=1 is allowable). The observation model is specified conditional on a latent state variable z _i,t which we define as the “alive state” of individual i in year t. That is, z _i,t =1 if individual i is alive in year t and z _i,t =0 if not. Thus, the observation model has the form:

$$ {y}_{i,j,k,t}\mid {z}_{i,t} \sim \mathrm{Bernoulli}\left(p\!\left(\boldsymbol{x}_j,\boldsymbol{s}_i\right){z}_{i,t}\right) $$

where p(x _j , s _i ) is an ordinary “closed” SCR encounter probability model such as the half-normal model defined above. Population dynamics are parameterized in a model for the individual state variable z _i,t (Royle and Dorazio 2008). The initial state is assumed to be a Bernoulli random variable: z _i , 1 ∼ Bernoulli(γ ₁), where the interpretation of γ ₁ is related to the initial population size. Under the data augmentation scheme (Royle and Dorazio 2012) where the maximum size of the super-population is set at M, then E(N ₁)=γ ₁ M. The latent state variable z _i,t is assumed to be Markovian so that values for t=2,...,T depend on the previous states. For t ≥ 2, z _i , t  ∼ Bernoulli(ϕ ^∗ z _{i , t − 1} + γ ^∗ r _i , t ); where r _i , t is an indicator of whether an individual is available to be recruited or not (set to 0 if that individual has ever been previously recruited and to 1 otherwise to ensure that individuals are recruited at most once). Thus if z _{i , t − 1}=1, then the individual can survive with probability ϕ, and if r _i , t  = 1, then an individual can be recruited with probability γ. In this parameterization of the Jolly-Seber model (Schwarz and Arnason 1996), the recruitment parameters are interpreted as “conditional entrance probabilities,” not per capita recruitment. Under this formulation, the number of recruits during interval t, R _t , is a derived parameter, being the sum of all values of z _i , t which transition is from z _i , t  = 0 to z _i , t  = 1. Further, per capita recruitment can be derived by dividing the number of recruits at time t, R _t by N _t − 1. We note that the model can also be formulated directly in terms of per capita recruitment (Chandler and Clark 2014; Gardner et al. in review).

An application of the spatial Jolly-Seber type model was first given by Gardner et al. (2010) for the simplest case where T=2 and the individual activity centers s _i were static from one year to the next. In general, however, it is possible to allow for explicit population dynamics (survival and recruitment) and also spatial dynamics in which individual activity centers are not static. Ergon and Gardner (2013) consider this in the context of modeling dispersal of voles using spatial capture-recapture data, while also modeling survival and recruitment. Schaub and Royle (2014) consider a Cormack-Jolly-Seber version of this type of system in which the spatially dynamic model allows for the explicit separation of dispersal and true survival from capture-recapture data. Recently Gardner et al. (in review) apply a fully open SCR model to Nagarahole camera trapping data in which the activity centers are modeled according to Gaussian random walk such that

$$ {\boldsymbol{s}}_{i,t}\sim \mathrm{Normal}\left({\boldsymbol{s}}_{i,t-1},{\sigma}_s^2\boldsymbol{I}\right), $$

where I is the 2×2 identity matrix. Here, ${\sigma}_s^2$ is the variance of the random walk (quantifying the degree of movement in activity centers between primary occasions), which is different than σ², the scale parameter in the encounter probability model defined above (quantifying within primary occasion movement about an individual’s activity center).

9.6.4 Spatially Dynamic Models, Without Population Dynamics

SCR models allow for both population dynamics (survival, recruitment) and also spatial dynamics (space-time dynamics of the point process model for activity centers). These two types of dynamics can be represented together in the same model (as in Gardner et al. in review), but, in addition, models can be developed that contain only one or the other dynamic components. For example, the basic open SCR model developed by Gardner et al. (2010) accommodates population dynamics but not spatial dynamics. In addition, a special kind of “open” population model which is only possible in the context of SCR is a model in which there are no population dynamics, but the individual activity centers are spatially dynamic (Royle et al. 2016). This type of model might be relevant when, during the study, some portion of the population disperses or when some portion of the population exhibits transient space usage. Royle et al. (2016) considered Markovian movement or dispersal models in demographically closed systems and showed that while parameters of the movement model could be estimated from repeated detections of individuals subject to demographic closure, ignoring movement dynamics did not produce biased estimates of density. Thus if estimating density is the main objective of a study then a misspecified encounter probability model that neglects movement is not necessarily detrimental to inferences.

We imagine intermediate types of models too in which some reduced population dynamics are paired with spatially dynamic activity centers. For example, we might allow for recruitment, but not survival, and spatially dynamic activity centers.

9.7 Survey Design Considerations

An overview of the sampling associated with camera trapping was provided above. Here we provide general considerations about important aspects of sampling when the objective is focused on estimating population size or density within a study area.

The basic consideration in all camera trapping studies is this: you need to sample “enough” (time and space) to accumulate a sufficient sample size of unique individuals and a sufficient sample size of recaptures, whether or not you intend to use ordinary CR or SCR models. If you are using SCR models then, in addition, you need to obtain sufficient “spatial recaptures” (i.e., captures of individuals in more than one trap). Unfortunately, what constitutes sufficient depends on just about everything: the actual unknown population size, the actual unknown detection probability and any other parameter of the model, and the extent and geometry of the space being sampled. Importantly, however, it depends on the length of time or number of occasions that camera traps are operational and also the number of traps and configuration of traps within the study area. As such, it is almost impossible, in general, to give prescriptive sample design guidance. As a practical matter, the best approach to make sensible choices of sampling design is to use Monte Carlo simulation. That is, propose a number of realistic sampling designs, and evaluate them by simulating populations and the sampling process using a priori guesses of the parameter values (or values taken from the literature). This should always be done, for any field study, before deployment of camera traps.

Using simulation we will usually seek to find a design to meet a certain precision target (e.g., CV of 10% for estimating N), or we will seek to evaluate a handful of logistically feasible designs and use the best one in terms of CV or perhaps also considering economic cost of implementing the design. All things being equal, we find for given true values of the parameters p and N (or other parameters of the model), you can always reduce the CV of an estimator by increasing the amount of effort (number of sample occasions, number of traps), because this produces larger sample sizes. On the other hand, this comes at increased economic cost. Thus the design problem always comes down to trading off a cost constraint with a statistical precision objective. As such, many study design problems are formulated in terms of optimizing precision for a fixed number of sample locations. This is roughly the same in practical terms as having a fixed project budget because “number of sites” is easy to translate into financial cost (cost of cameras, effort to establish sites, check cameras). In these situations, the design question boils down to “where do we allocate those traps?” Then various designs can be defined, and simulations run to produce a sequence of results (estimates). Then, looking at the results, you have to ask the question: is the realized statistical precision sufficient for management needs? If not, you increase the effort (number of traps, number of days operational) and repeat the exercise.

As in traditional capture-recapture models, most important design elements represent aspects of sampling in space and time: how many spatial samples (and where, and what spacing) and how long should sampling occur? We discuss some specific aspects of space and time here.

Study duration. A general objective in camera trapping is to keep sampling duration short relative to tiger population turnover so that demographically closed models can be used. However, the definition of short will be situation dependent and will likely be determined by the logistics of each sampling situation. It would be excellent, but likely impossible, to complete sampling within a 2-week period. Periods of 4–6 weeks or even longer will more likely be required. Longer time intervals increase the likelihood of models for open populations being needed. Closed models are preferred for reasons of precision and estimator robustness, but if closed models cannot be used, then open models are available (Seber 1982; Pollock et al. 1990) and can be used to accommodate non-closure. This general consideration relating to the duration of the study is relevant to both SCR and ordinary capture-recapture methods. From the standpoint of estimating density, it would be preferable to focus on simpler (demographically closed) models, but if it is necessary to increase the length of time in order to obtain sufficient sample sizes, the open models can be used to accommodate non-closure. An economical way to deal with non-closure that avoids having to model complex population dynamics is the use of multi-session models as described previously. These could involve one additional structural parameter per session and yet still accommodate temporal variation in density but “share” the parameters of the detection probability model among the sessions.

Trap spacing. General trap spacing is an important element of SCR models. Effective estimation requires that spatial recaptures are obtained, that is, recaptures of individuals in multiple traps. Intuitively, designing a study to have traps close together should maximize the number of spatial recaptures. On the other hand, the total sample size of unique individuals should be maximized if the traps are placed uniformly far apart in any prescribed region of interest. Thus, practical SCR design represents a compromise between obtaining sufficient spatial recaptures and a large sample size of individuals (Royle et al. 2014, ch. 10), and the two objectives contradict one another in the sense that close trap spacing is optimal for the former objective, while distant trap spacing is optimal for the latter. Simulation studies (Sollmann et al. 2013; Efford and Fewster 2013; Royle et al. 2014, ch. 10; Augustine unpubl. Results: https://groups.google.com/forum/#!topic/spatialcapturerecapture/SnswEKOwFb0) indicate that trap spacing of 1.5–2.5 times σ produces optimal designs for estimating population size or density under the half-normal encounter probability model with parameter σ. Thus if sufficient traps exist to achieve this spacing with uniform coverage of the area, then this should be done. Note that this approach (uniform coverage) is the same as the “Design 1” recommendation of Nichols and Karanth (2002) who recommended to “...spread [traps] throughout the area once and then checked each day for say 5-30 consecutive days”. This approach yields standard (spatial) capture history data amenable to analysis by the classes of models described in this chapter. On the other hand, if the study area is too large to cover uniformly given the number of available camera traps or effort to deploy them, then there are three additional design options available:

• (Design 2) Cover a central area of the study uniformly to achieve close to the optimal spacing.

• (Design 3) Use a type of cluster design where small clusters achieve optimal within-cluster spacing in order to generate spatial recaptures, but then clusters are more widely spaced to cover the area uniformly, expose a larger portion of the population to sampling, and obtain a higher sample size of encountered individuals.

• (Design 4) Cover a subregion uniformly and then rotate the traps so that a larger area is covered.

Design 2 is logistically appealing because it saves on the labor and cost of moving traps. On the other hand, by moving traps you can obtain a larger sample size of observed individuals and possibly more spatial recaptures. If there is a strong local behavioral response, then there is probably some statistical benefit to moving traps since the recaptures provide less information. When implementing this design, the area sampled should be representative of the area as a whole. If there is a strong gradient in density, then this approach is not necessarily robust to density models, and this should be studied by simulation for the specific landscape under consideration. The use of cluster designs (Design 3) has proved to be an effective and logistically practical way of carrying out studies for density estimation (Efford and Fewster 2013; Sun et al. 2014; Fuller et al. 2016). Spacing of within and between clusters can be analyzed by Monte Carlo simulation. As in the first edition of this manual, designs which involve sampling an area and then moving traps (rotating blocks of traps, Design 4) can be viable in some situations. The advice from Edition 1 is probably still good advice, as long as we keep the basic trap spacing considerations of SCR in mind. In that regard, we probably should define grid cells to be about 1.5–2 times σ and then rotate the traps to achieve uniform coverage of the grid cells over time but making sure that sufficient neighboring cells contain traps so as to produce the needed spatial recaptures.

9.8 Future Directions

The field of capture-recapture has undergone rapid and profound evolution over the last few years. This has been driven in large part by technological innovations such as camera trapping and DNA sampling which allow for capture-recapture studies of species such as tigers that could not be effectively studied using historical methods requiring physical capture and marking. Such methods produce huge quantities of spatially explicit encounter information that are informative about all aspects of spatial population ecology, not just estimation of density and population size. The development of spatial capture-recapture methods has been driven to some extent by the widespread adoption of these new technologies for sampling which produce rich spatial encounter data. Spatial capture-recapture methods have proved useful for modeling spatial variation in density, resource selection, movement, and population dynamics (Royle et al. 2017). We believe that SCR methods will continue to grow in importance, and there are many unresolved and important aspects related to the study of animal populations by capture-recapture that have received little or no attention in the literature so far but which we feel have enormous practical relevance for the study of tiger and other populations. We identify a few of these here.

Uncertain Identity

The advent of new technologies for noninvasive sampling, including camera trapping and DNA sampling, has increased the frequency of samples with uncertain identity. When a sample is obtained but cannot be identified to individual, observed encounter histories may not be the true encounter history of an individual. Accommodating uncertain identity is extremely important for unbiased population size estimation when, for example, it can produce “ghost” individuals which have the effect of inflating the population size estimation (Lukacs and Burnham 2005) or if behavioral response is present and not properly modeled in the presence of uncertainty (Augustine et al. 2014). Uncertain identity is especially relevant in camera trapping where, historically, obtaining photos of both sides of an individual has been necessary in order to identify an individual. However, a single-side photograph can be viewed as a sample having uncertain identity, and this uncertainty can be accommodated in capture-recapture models. Augustine et al. (2016) showed that spatial location of encounter is informative about sample identity and used this information in the development of SCR models to allow for single-side samples in camera trapping. Their method can be applied even to whole arrays of single cameras, in which case it may not ever be possible to obtain both sides of an individual.

Landscape Connectivity

SCR provides an empirical basis for estimating not only density but also connectivity of the landscape. For example, explicit models of connectivity, such as least-cost path, can be integrated directly in the SCR likelihood, and parameters that describe the resistance of the landscape to individual space usage can be estimated (Royle et al. 2013b; Sutherland et al. 2015; Fuller et al. 2016). Furthermore, SCR provides an empirical framework for making explicit landscape management decisions using population density and connectivity information. For example, Morin et al. (2017) evaluated the potential of camera trapping studies to estimate density-weighted connectivity (DWC) and proposed that landscape management (corridor, reserve design) should be based on maximizing DWC of a landscape or minimizing the loss of DWC. We imagine that these ideas might be useful in the development of connected landscapes for tigers and other large cats based on camera trapping studies.

Biologically Realistic Point Process Models

Most applications of SCR models to date are based on the simplistic homogeneous point process model in which individual activity centers are distributed uniformly and independent of one another. There is an obvious need for more biologically realistic point process models which accommodate important biological features of populations such as territorial behavior and territory overlap of individuals and among species. General classes of point process such as Markov point process models accommodate dependence among points (Illian et al. 2008) might be realistic for modeling such biological phenomenon. Reich and Gardner (2014) proposed an SCR model for territorial species based on a Strauss process model which accommodates point processes that are more regular than complete spatial randomness. To the best of our knowledge, no other examples of non-independent point process models in the context of capture-recapture modeling exist.

Continuous Time SCR Models

Both classical and spatial capture-recapture models accommodate the modeling of temporal variation in the form of time effects or behavioral response. In the vast majority of applications to date, these effects are modeled in discrete time, that is, assuming that sample occasions are registered in discrete time intervals k=1,2,...,K. Recent efforts toward developing continuous time models (Borchers et al. 2014; Dorazio and Karanth 2017) show promise in improving the modeling of biological processes such as a behavioral response (due to transient space use of an individual’s home range) and make more efficient use of detection data.