Numerical Solution of Unsteady Free Convective Flow Past a Vertical Plate with Heat and Mass Fluxes Considering Chemical Reaction and Heat Absorption

Abstract

Laminar boundary layer natural convection flow with heat and mass transfer of an optically thick heat-radiating and heat-absorbing fluid along with first-order chemical reaction has been investigated numerically. The partial differential equations (PDEs) governing the flow model are non-dimensionalized and solved using finite element technique. A grid independence analysis is carried out to ensure the convergence of solutions, and the code has been validated by comparing the results obtained via utilized method with those of earlier published results. To gain a better perspective of flow field, the solution of non-dimensional velocity, temperature, and concentration of the fluid is presented in a graphical form. Fluid temperature is observed to decrease through-out the thermal boundary layer on increasing the heat absorption. Chemical reaction has an adverse effect on species concentration.

1 Introduction

In nature, natural convection or free convection flows arise frequently either due to temperature differences or concentration differences, or also due to both. Natural convective flows along with the heat and mass transport arise in many natural and engineering processes such as convection in Earth’s mantle, formation of convection cells due to sunlight, evaporation at the surface of a water body, drying, flow in a desert cooler, and energy transfer in a wet cooling tower and have, therefore, attained a considerable attention by researchers in recent years. Owing to its inescapable application in various industries, viz. chemical, petroleum, biological, and agricultural industries, a great deal of importance has been given to study the simultaneous effects of heat and mass transfer due to natural convection by various researchers considering different aspects of flow geometry, thermal and solutal boundary conditions and various parameters affecting the flow. Some of the research articles by Mathers et al. (1957), Soundalgekar and Ganesan (1981), Narahari and Nayan (2011), Narahari and Dutta (2012), Hussanan et al. (2013), Jain (2013) are worth mentioning. A rigorous review of the literature concerning convective flow with heat and mass transfer problems is given in the books of Kays et al. (2012) and Bergman et al. (2011).

Gas turbines, nuclear power plants and numerous propulsion devices such as aircrafts, satellites, space vehicles, and missiles are some of the examples which require a very high temperature, and thus, the role of thermal radiation becomes indispensable (Sparrow and Cess 1978). A considerable amount of interest has been shown in the study of radiation interaction with free convection flow. Some of the relevant studies are due to Cess (1966), Hossain and Takhar (1996), Chamkha (1997), Muthucumaraswamy and Ganesan (2003), Seth et al. (2011), and Das et al. (2015).

Heat absorption phenomena become relevant in a non-isothermal flow domain, and consideration of heat absorption is significant while studying the heat transfer characteristics. Further, the study of chemical reaction phenomenon cannot be ignored while studying the transportation of heat mass with fluid flow due to its immense importance in industries of hydrometallurgical, chemical, polymer production, food processing, etc. Previous investigations dealing with heat absorption/generation and chemical reaction can be found in the works of Das et al. (1994), Takhar et al. (2000), Chamkha and Khaled (2001), Chamkha (2004), Seth et al (2015, 2016), Raju et al. (2016), Srinivasacharya and Reddy (2016).

The present study deals with time-dependent free convective fluid flow along with heat and mass transfer past a vertical flat plate of an infinite length under the influence of radiation, heat absorption (heat sink), and chemical reaction with uniform wall temperature/ uniform heat flux and variable mass flux, which have been investigated numerically. A careful survey of the literature suggests that no attempt has been made to study the above-mentioned fluid flow model.

2 Mathematical Formulation

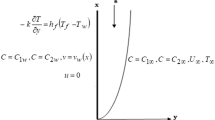
Consider the time-dependent natural convection flow of a viscous, incompressible, and optically thick heat-radiating and heat-absorbing fluid past an infinite vertical plate in the presence of first-order chemical reaction between the fluid and species concentration. The schematic model of the coordinate system of the problem is depicted in Fig. 1.

Fig. 1

Schematic diagram of the problem

Initially at time $t^{{\prime }} \le 0$, both the plate and the fluid are maintained at uniform temperature $T_{{\infty }}^{{\prime }}$ and uniform concentration $C_{{\infty }}^{{\prime }}$. For $t^{{\prime }} > 0$, the plate temperature is raised or lowered to $T_{\text{w}}^{{\prime }}$ for uniform wall temperature (UWT) case and heat transfer rate at the surface of plate is considered constant for uniform heat flux (UHF) case. Also, the mass transfer rate at the plate is proportional to the species concentration. The flow is generated solely due to thermal and solutal buoyancy forces. Since plate is assumed to be of an infinite length along $x^{{\prime }} \,{\text{and}}\,z^{{\prime }}$ axes, all the physical quantities are dependent of $t^{{\prime }} \,{\text{and}}\,y^{{\prime }}$ only. The radiative heat flux along $x^{{\prime }} {\text{-axis}}$ is considered to be insignificant in comparison to the radiative heat flux along $y^{{\prime }} {\text{-axis}}$ (Sparrow and Cess 1978).

By considering the aforementioned assumptions, the dimensional governing Prandtl’s boundary layer equations for unsteady natural convective flow of viscous, incompressible, chemically reacting, heat-absorbing, and radiative fluid under Boussinesq approximations are given by:

$$\frac{{\partial u^{{\prime }} }}{{\partial t^{{\prime }} }} = - \frac{1}{\rho }\frac{\partial p}{{\partial x^{{\prime }} }} + \upsilon \frac{{\partial^{2} u^{{\prime }} }}{{\partial y^{{{\prime }2}} }} + g\beta_{\text{T}} (T^{{\prime }} - T_{\infty }^{{\prime }} ) + g\beta_{\text{C}} (C^{{\prime }} - C_{{\infty }}^{{\prime }} ),$$

(1)

$$- \frac{1}{\rho }\frac{\partial p}{{\partial y^{{\prime }} }} = 0,$$

(2)

$$\frac{{\partial T^{{\prime }} }}{{\partial t^{{\prime }} }} = \frac{k}{{\rho C_{\text{p}} }}\frac{{\partial^{2} T^{{\prime }} }}{{\partial y^{{{\prime }2}} }} - \frac{1}{{\rho C_{\text{p}} }}\frac{{\partial q_{\text{r}} }}{{\partial y^{{\prime }} }} - \frac{{Q_{\text{H}} }}{{\rho C_{p} }}(T^{{\prime }} - T_{{\infty }}^{{\prime }} ),$$

(3)

$$\frac{{\partial C^{{\prime }} }}{{\partial t^{{\prime }} }} = D\frac{{\partial^{2} C^{{\prime }} }}{{\partial y^{{{\prime }2}} }} - k_{\text{r}} (C^{{\prime }} - C_{\infty }^{{\prime }} ).$$

(4)

where $u^{{\prime }}$ represents the fluid velocity along x′-axis, $T^{{\prime }}$ is the temperature of the fluid, $\beta_{\text{T}}$ is the coefficient of thermal expansion, g is the acceleration due to gravitational, $\beta_{\text{C}}$ is the volumetric expansion coefficient, $\upsilon$ is the kinematic viscosity, $\rho$ is the fluid density, k is the thermal conductivity, $C_{\text{p}}$ is the specific heat at constant pressure, D is the mass diffusivity, $q_{\text{r}}$ is the radiative heat flux, $Q_{\text{H}}$ is the heat absorption coefficient, and $K_{\text{r}}$ is the first-order chemical reaction coefficient.

The initial and boundary conditions (Das et al. 2015) of the problem as described above are as follows:

$$\left. {\begin{array}{*{20}l} {{\text{for}}\quad t^{\prime } \le 0\;\;\{ \forall \;y^{\prime } \ge 0\;\;u^{\prime } (y^{\prime } ,t^{\prime } ) = 0,\;\;T^{\prime } = T_{\infty }^{\prime },\;\; C^{\prime } = C_{\infty }^{\prime } } \\ {{\text{for}}\quad t^{\prime } > 0\left\{ {\begin{array}{*{20}l} {y^{\prime } = 0\;\;u^{\prime } (0,t^{\prime } ) = 0,\;\;\frac{{\partial T^{\prime } }}{{\partial y^{\prime } }} = - \frac{{q^{\prime } }}{k}(\text{UHF}),} \\ {T^{\prime } = T_{\text{w}}^{\prime } (\text{UWT}),\;\;\frac{{\partial C^{\prime } }}{{\partial y^{\prime } }} = - \frac{{q^{*} }}{{D^{*} }}C^{\prime } } \\ {y^{\prime } \to {\infty }\;\;u^{\prime } (\infty ,t^{\prime } ) \to 0,\;\;T^{\prime } (\infty ,t^{\prime } ) \to T_{\infty }^{\prime } ,} \\ {C^{\prime } (\infty ,t^{\prime } ) \to C_{\infty }^{\prime } } \\ \end{array} } \right.} \\ \end{array} } \right\}$$

(5)

where $q\,{\text{and}}\,q^{*}$ represents the heat and mass fluxes at the surface.

It is concluded from Eq. (1) that pressure p is independent of $y^{{\prime }}$, so the value of flow pressure is same throughout the boundary layer and in the free stream. Therefore, from Eq. (1) and initial and boundary conditions (5), we have $- \frac{1}{\rho }\frac{\partial p}{{\partial x^{{\prime }} }} = 0$, and thus Eq. (1) takes the form

$$\frac{{\partial u^{{\prime }} }}{{\partial t^{{\prime }} }} = \upsilon \frac{{\partial^{2} u^{{\prime }} }}{{\partial y^{{{\prime }2}} }} + g\left[ {\beta_{\text{T}} (T^{{\prime }} - T_{\infty }^{{\prime }} ) + \beta_{\text{C}} (C^{{\prime }} - C_{\infty }^{{\prime }} )} \right].$$

(6)

Applying Rosseland approximation (Raptis 1998), the net radiative heat flux term can be written as follows:

$$q_{\text{r}} = \frac{{ - 4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{{{\prime }4}} }}{{\partial y^{{\prime }} }}$$

(7)

where $\sigma^{*}$ and $k^{*}$ are Stefan–Boltzmann constant and Roseland mean absorption coefficient, respectively. One can linearize the nonlinear term $T^{{{\prime }4}}$ occurring in Eq. (10) with the help of Taylor series by assuming a small variation between the boundary layer fluid temperature and ambient fluid temperature, retaining terms up to first order only. Thus, $T^{{{\prime }4}}$ can be represented as follows:

$$T^{{{\prime }4}} \cong 4T_{\infty }^{{{\prime }3}} T^{{\prime }} - 3T_{\infty }^{{{\prime }4}}$$

(8)

Using Eqs. (7) and (8), Eq. (3) becomes:

$$\frac{{\partial T^{{\prime }} }}{{\partial t^{{\prime }} }} = \frac{k}{{\rho C_{\text{p}} }}\frac{{\partial^{2} T^{{\prime }} }}{{\partial y^{{{\prime }2}} }} + \frac{1}{{\rho C_{\text{p}} }}\frac{{16\sigma^{*} T_{\infty }^{{\prime }} }}{{k^{*} }}\frac{{\partial^{2} T^{{\prime }} }}{{\partial y^{{{\prime }2}} }} - \frac{{Q_{\text{H}} }}{{\rho C_{\text{p}} }}(T^{{\prime }} - T_{\infty }^{{\prime }} ).$$

(9)

The dimensional partial differential Eqs. (4), (6), and (9) are converted into dimensionless form with the help of following dimensionless variables:

$$\begin{aligned} y & = \frac{{q^{*} y^{{\prime }} }}{D}{\kern 1pt} ,\quad u = \frac{{u^{{\prime }} D^{*} }}{{\nu q^{*} }},\quad t = \frac{{q^{*2} t^{{\prime }} \nu }}{{D^{2} }},\quad \theta = \frac{{T^{{\prime }} - T_{\infty }^{{\prime }} }}{{T_{w}^{{\prime }} - T_{\infty }^{{\prime }} }}(\text{UWT}), \\ \theta & = \frac{{(T^{{\prime }} - T_{\infty }^{{\prime }} )q^{*} k}}{{q^{{\prime }} D^{*} }}(\text{UHF}),\quad C = \frac{{C^{{\prime }} - C_{\infty }^{{\prime }} }}{{C_{\infty }^{{\prime }} }} \\ \end{aligned}$$

(10)

The highly coupled, dimensionless governing partial differential equations are given by:

$$\frac{\partial u}{\partial t} = \frac{{\partial^{2} u}}{{\partial y^{2} }} + Gr\theta + GcC,$$

(11)

$$\frac{\partial \theta }{\partial t} = \frac{1}{Pr }\left( {1 + \frac{4R}{3}} \right)\frac{{\partial^{2} \theta }}{{\partial y^{2} }} - Q\theta ,$$

(12)

$$\frac{\partial C}{\partial t} = \frac{1}{Sc}\frac{{\partial^{2} C}}{{\partial y^{2} }} - KrC$$

(13)

where $R = \frac{{4\sigma^{*} T_{\infty }^{{{\prime }3}} }}{{kk^{*} }}$ is radiation parameter, $Gr = \frac{{g\beta_{T} (T_{\text{w}}^{{\prime }} - T_{\infty }^{{\prime }} )D^{3} }}{{\upsilon^{2} q^{*2} }}({\text{UWT}})$ is the thermal Grashof number for uniform wall temperature case, $Gr = \frac{{g\beta_{T} qD^{4} }}{{\upsilon^{2} kq^{*4} }}({\text{UHF}})$ is the thermal Grashof number for uniform heat flux case, $Gc = \frac{{g\beta_{\text{C}} D^{3} C_{\infty }^{{\prime }} }}{{\upsilon^{2} q^{*3} }}$ is the solutal Grashof number, $Pr = \frac{{\upsilon \rho C_{\text{p}} }}{k}$ is the Prandtl number, $Sc = \frac{\upsilon }{D}$ is the Schmidt number, $Kr = \frac{{k_{r} D^{2} }}{{\upsilon q^{*2} }}$ is the chemical reaction parameter, and $Q = \frac{{Q_{H} D^{2} }}{{\upsilon \rho C_{p} q^{*2} }}$ is the heat absorption parameter.

Corresponding transformed non-dimensional initial and boundary conditions are given as follows:

$$\left. {\begin{array}{*{20}l} {{\text{for}}\quad t \le 0\;\;\{ \forall \;y \ge 0\;\;u(y,t) = 0,\;\;\theta (y,t) = 0,\;\;C(y,t) = 0} \hfill \\ {{\text{for}}\quad t > 0\left\{ {\begin{array}{*{20}l} {{\text{at}}\;y = 0\;\;u(0,t) = 0,\;\;\frac{\partial \theta }{\partial y} = - 1\;({\text{UHF}}),} \\ {\theta (0,t) = 1\;(\text{UWT}),\;\;\frac{\partial C}{\partial y} = - (1 + C)} \\ {{\text{as}}\;y \to {\infty }\;\;u({\infty },t) \to 0,\;\;\theta ({\infty },t) \to 0,} \\ {C({\infty },t) \to 0} \\ \end{array} } \right.} \hfill \\ \end{array} } \right\}$$

(14)

3 Solution Methodology

The transformed system of linear, coupled, and dimensionless PDEs (11) to (13) along with the initial and boundary conditions (14) is solved numerically for fluid velocity, fluid temperature, and species concentration with the help of extensively validated and robust finite element technique. A typical finite element technique involves 5 fundamental steps which are domain discretization, derivation of the element equations, assembly of element equations, imposition of boundary conditions, and solution of the assembled equations. An excellent description of these steps is presented in the textbooks by Reddy (2006).

4 Grid Independence Study

The grid independence analysis is conducted by dividing the entire domain into successively sized grids $131 \times 131,151 \times 151$ and $171 \times 171$, which are presented in Table 1. The free stream boundary conditions are replaced by an appropriate large value where the fluid velocity, fluid temperature, and concentration profiles approach to zero asymptotically. We executed the developed code for different step sizes and found very good agreement between the results for all the profiles. After many trials for computational flexibility, we imposed $y_{\hbox{max} } = 8$ where $y_{\hbox{max} } \to {\infty }$. We adopted for all the computations $150$ intervals of equal step size 0.053. At every node, four unknowns are to be found so that, after the assembly of element equations, a set of 453 algebraic equations are formed; consequently, an iterative method is adopted and, by introducing boundary conditions, the system of algebraic equations are solved. The solution is expected to be converged when the difference between two successive iterates satisfies the desired accuracy 10⁻⁴. An excellent convergence for all the results is achieved.

Table 1 Grid independence analysis for fluid velocity, fluid temperature (UWT case), and species concentration at distinct points of boundary layer coordinate y

5 Validation of Numerical Results

To establish the correctness of these numerical results which are obtained through MATLAB code, we compared the present results for skin friction with the results obtained through analytical approach. It should be noted that solution approaches to the solution of Das et al. (2015) when $Kr = Q = 0$, which are shown in Table 2. These comparisons confirm that the present results are in agreement with the published reports. Therefore, these favorable comparisons gives us a great confidence and subsequently the developed code can be used in presenting the results graphically.

Table 2 Comparison of shear stress for various parameter values when $t = 0.5,\;R = 2,\;Q = 0\;{\text{and}}\;Kr = 0$

6 Results and Discussion

The primary aim of this paper is to study the transient chemically reacting and optically thick heat-radiating natural convective boundary layer flow of viscous, incompressible fluid past a vertically upward plate with heat absorption effect by employing finite element method with Galerkin weighted residual scheme. Additionally, the influences of $Gc,Gr,R,Q,Sc,$ and $Kr$ on the flow field variables, viz. fluid velocity, fluid temperature, and species concentration distributions, are discussed and represented graphically in Figs. 2, 3, 4, 5, 6, 7, 8, and 9. In this paper, we present the solutions for the above physical parameters by adopting the default values $Gr = 5,Gc = 3,t = 0.5$, $Pr = 0.71,R = 2,Q = 5,Sc = 2.62$, and $Kr = 1$ for finite element computation.

Fig. 2

Velocity profiles against y for different values of Gc

Fig. 3

Velocity profiles against y for different values of Gr

Fig. 4

Velocity profiles against y for different values of Q

Fig. 5

Velocity profiles against y for different values of Kr

Fig. 6

Temperature profiles against y for different values of R

Fig. 7

Temperature profiles against y for different values of Q

Fig. 8

Concentration profiles against y for different values of Sc

Fig. 9

Concentration profiles against y for different values of Kr

All the figures for fluid velocity u and fluid temperature T have been plotted for both cases of thermal boundary condition, i.e., for UHF and UWT conditions. It is seen that for all the flow parameters, the velocity rises from zero and obtains a peak value and then decreases exponentially as non-dimensional coordinate y approaches toward free stream.

Figure 2 is plotted for dimensionless velocity versus the non-dimensional boundary layer coordinate y for increasing values of $Gc$. The solutal Grashof number represents the ratio between solutal buoyancy force and viscous force; thus, the strength of buoyancy force gets stronger with the increasing value of $Gc$. The figure indicates that for both cases of thermal boundary conditions, the fluid velocity starts from zero and approaches to peak values in the proximity of plate and then decreases exponentially to zero as y approaches to the free stream. It is seen from Fig. 2 that the fluid velocity gets accelerated as $Gc$ increases.

Thermal Grashof number, $Gr$, represents the ratio of thermal bouncy force to viscous force; thus, $Gr$ is directly proportional to the thermal buoyancy force. An increase in $Gr$ leads to a higher buoyancy force which leads the fluid to move with higher velocity. This phenomenon can be seen in the Fig. 3 which is plotted for both cases of thermal boundary conditions, i.e., for UHF and UWT. It is interesting to see that the flow direction gets reversed for negative values of thermal Grashof number.

Effects of heat absorption Q and chemical reaction $Kr$ over dimensionless fluid velocity have been characterized in Figs. 4 and 5. These figures exhibit that the velocity has a declining nature for increasing value of both chemical reaction and heat absorption parameters. Since chemical reaction and heat absorption act as a destructing force for temperature and species concentration (Figs. 7 and 9), which results in a slow distribution of temperature and species concentration throughout the temperature and concentration boundary layers, respectively. It results in small temperature and species concentration differences and consequently a weak buoyancy force, which ultimately reduces the velocity.

Effect of radiation over dimensionless temperature distribution is shown in Fig. 6. The tendency of thermal radiation for optically thick heat-radiating fluid is to increases the temperature which is clearly evident from the figure.

Behavior of temperature corresponding to the heat absorption is shown in Fig. 7. Physically, the tendency of heat absorption effect is to diminish the fluid temperature, which is also evident from the figure.

Figure 8 exhibits that the surface concentration as well as concentration within its boundary layer reduces rapidly with increasing value of $Sc$. Since Schmidt number $Sc$ is inversely proportional to mass diffusivity, an increase in $Sc$ results in a weaker mass diffusion which reduces the concentration within the boundary layer.

Effect of chemical reaction $Kr$ over the species concentration $C$ has been demonstrated in Fig. 9, and it is clear from the figure that the species concentration falls with the increasing effect of chemical reaction.

It is important to note that the non-dimensional velocity is found to be higher in case of UWT condition than that for the UHF boundary condition for all pertinent flow parameters.

7 Conclusion

The present article investigates the flow characteristics of an unsteady laminar boundary layer free convective flow with heat and mass transfer of a viscous, incompressible, chemically reactive, heat-absorbing, and radiative fluid past a flat plate. The problem is investigated under two cases of thermal boundary conditions, i.e., for UWT and UHF conditions. The noteworthy findings of the investigation reveal that:

The fluid velocity is found higher in case of uniform wall temperature condition than that of uniform heat flux condition for all flow pertinent parameters. The flow is generated solely due to the buoyancy forces, and it found to be increasing with the increasing strength of buoyancy forces. The increasing strength of the heat absorption reduces the temperature as well as the fluid velocity. Optically thick heat-radiating fluids temperature is found to be increasing with the increasing strength of thermal radiation. Tendency of chemical reaction is to lessen the concentration distribution and also the fluid velocity. The concentration distribution within the boundary layer has decreasing tendency corresponding to the increasing strength of mass diffusion and chemical reaction.