Keywords

1 Introduction

The study of magnetohydrodynamic flow of an electrically conducting fluid with magnetic field has wide range of its applications in the technology, industries, geothermal power generation and metal-working processes. Such type of MHD flows have its attracted applications in design of magnetohydrodynamic power generators, plasma studies, nuclear reactor, the thermal recovery of oil, solar power collector and geological formulation etc. Globe (1959) has obtained the analytical solution of an electrically conducting and fluid flowing between two infinite long concentric annular cylinders under the presence of a radial magnetic field. Ramamoorthy (1961) has analysed both classical and magnetohydrodynamic velocity between concentric annulus of rotating cylinders in the presence of a radial magnetic field. In the above references, authors have neglected the induced magnetic field in the problem. Keeping it mind, Arora and Gupta (1971) have extended the same problem with considering the impact of induced magnetic field. The natural convection in the vertical annular cylinders with one boundary isothermal and opposite adiabatic boundary has analysed by El-Shaarawi and Sarhan (1981). Further, Joshi (1987) has considered the isothermal boundaries in which the temperature of inner boundary is higher than the outer boundary.

Singh et al. (1997) have studied the free convective flow in vertical concentric annuli with more general thermal boundary conditions and radial magnetic field. Seong and Choung (2001) have analysed the electrically conducting fluid flow past a circular cylinder under continuous and pulsed electromagnetic forces. Fadzilah et al. (2011) have emphasised the importance of induced magnetic field and heat transfer on the steady, viscous and electrically conducting magnetohydrodynamic boundary-layer flow over a stretching sheet. Singh and Singh (2012) have investigated the influence of induced magnetic field on free convective flow between non-conducting vertical concentric annulus cylinders. Further, Kumar and Singh (2013) have extended the same problem by considering the concentric cylinders heated/cooled asymmetrically.

In many practical situations, such as if you turn off the breaker when you go on vacation, then it can tell us how fast a water heater cools down and the hot water in pipes cools off. In this case, the heat transfer from the surface of object is similar to the local surface temperature, and we use the term Newtonian heating/cooling for this condition. This type of flow is known as conjugate convective flow. In a pioneered work, the influence of the Newtonian heating on free convective boundary-layer flow over a vertical flat plate, which immersed in a viscous fluid, was studied by Merkin (1994). An analytical solution of natural convective flow past an oscillating vertical plate with the effects of heat and mass transfer, and the Newtonian heating has been obtained by Hussanan et al. (2013). Very recently, Kumar and Singh (2015) have investigated the impact of induced magnetic field on hydromagnetic natural convective flow with the Newtonian heating/cooling in vertical concentric annuli by obtaining the exact solution of the problem. Also, Kumar and Singh (2016) have performed the exact study of effects of heat source/sink and induced magnetic field on free convective flow between vertical concentric cylinders.

Motivated with excellent science of the authors, we intend here to investigate the effect of the Newtonian heating/cooling on hydromagnetic natural convection between alternate conducting vertical concentric annulus cylinders with radial magnetic field. We have analysed the model by taking three cases on the boundary conditions of the induced magnetic field. In case (A), both cylinders are considering as non-conducting, in case (B) the outer cylinder is conducting and inner is non-conducting and finally in case (C) the inner is taking as conducting and outer is non-conducting. Here, we find the analytical solution for the temperature field and then fluid velocity and induced magnetic field by solving the non-dimensional governing linear simultaneous ordinary differential equations using the non-dimensional boundary condition. Also, we find the analytical solution for the governing differential equations at singular point Ha = 2.0. Finally, we focus on the effects of the Biot number (Newtonian heating/cooling parameter) and the Hartmann number on the velocity, induced magnetic, induced current density, Nusselt number, skin-friction and mass flux using graphics and tables.

2 Mathematical Formulation

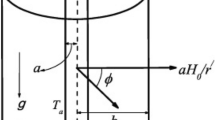
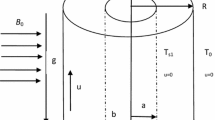
We have taken here the steady and laminar flow of a viscous, incompressible and electrically conducting fluid in the fully developed region bounded by vertical concentric annuli of infinite length with radial magnetic field as shown in Fig. 1. Also, we have considered the temperature of fluid and both cylinders different to each other. The temperatures of fluid and outer cylinder have taken as \({T}_{f}^{\prime }\) and \({T_b^{\prime }}\), respectively. Let \({z}^{\prime}\)- and \({r}^{\prime}\)-axes denote the axis of the co-axial cylinders taken in the vertical upward direction and the radial direction taken outward from the axis of the cylinder. Let a and b be the radius of inner and outer cylinders, respectively. The applied uniform magnetic field of strength \(\left\{ {{aB}_{0}^{\prime} {/r}^{\prime} } \right\}\) is taken as in the direction perpendicular to the direction of flow, and the Newtonian heating/cooling condition is applied at the inner cylinder of the annulus. Since \(z^{\prime}\)-axis is the direction of fluid flow so the radial and tangential components of velocity are taken as zero. Due to axial symmetry and infinite length of cylinders, the transport phenomena will depend only on the variable \(r^{\prime}.\) So, for the considered model the components of the velocity and applied uniform magnetic fields are taken as \(\{ {{0, 0, {v}^{\prime}({r}^{\prime})}}\}\) and \(\{ {aB}_{0}^{\prime } /{r}^{\prime}, 0, {h}^{\prime} \}\), respectively.

Fig. 1
figure 1

Physical configuration

Full size image

Thus, the mathematical model equations for the present physical configuration with the usual Boussinesq approximation are as follows (Singh and Singh 2012):

$$\frac{{{\text{d}}^{2} {v}^{\prime} }}{{{\text{d}r}^{{{\prime }\,{2}}} }} + \frac{1}{{{r}^{\prime} }}\frac{{{\text{d}v}^{\prime} }}{{{\text{d}r}^{\prime} }} + \frac{{{\mu }_{e} }}{\rho \nu }\frac{{{B}_{0}^{\prime } {a}}}{{{r}^{\prime} }}\frac{{{\text{d}h}^{\prime} }}{{{\text{d}r}^{\prime} }} + \frac{{{g}{\beta }}}{\nu }({T}^{\prime} - {{T}}_{f}^{\prime } ) = 0 ,$$
(1)
$$\frac{{{\text{d}}^{2} {h}^{\prime} }}{{{\text{d}r}^{{{\prime }\,{2}}} }} + \frac{1}{{{r}^{\prime} }}\frac{{{\text{d}h}^{\prime} }}{{{\text{d}r}^{\prime} }} + \frac{{{B}_{0}^{\prime } {a}}}{\eta }\frac{1}{r}\frac{{{\text{d}v}^{\prime} }}{{{\text{d}r}^{\prime}}} = 0,$$
(2)
$$\frac{{{\text{d}}^{2} {T}^{\prime} }}{{{\text{d}r}^{{{\prime }\,{2}}} }} + \frac{1}{{{r}^{\prime} }}\frac{{{\text{d}T}^{\prime}}}{{{\text{d}r}^{\prime}}} = {0}{.}$$
(3)

In view of the considered model, the boundary conditions corresponding to the velocity, induced magnetic field and temperature field are obtained as:

$${v}^{\prime} = {0,}\quad\frac{{{\text{d}h}^{\prime}}}{{{\text{d}r}^{\prime}}} = 0\;\; {\text{or}}\;\; {h}^{\prime} = {0},\quad\frac{{{\text{d}T}^{\prime}}}{{{\text{d}r}^{\prime}}} = {\alpha }{T}^{\prime},\;\; {\text{at}}\;\;{r}^{\prime} = {a},$$
(4)
$${v}^{\prime} = 0,\quad\frac{{{\text{d}h}^{\prime}}}{{{\text{d}r}^{\prime}}} = {0}\;\;\text{or}\;\;{h}^{\prime} = {0},\quad{T}^{\prime} = {T}_{b}^{\prime } ,\;\;{\text{at}}\;\;{r}^{\prime} = {b}.$$
(5)

In above equations, \({\rho },\) \({\mu }_{e},\) \({\nu },\) g, \({\eta },\) \({\sigma }\) and \({\beta }\) are density of the fluid, magnetic permeability, kinematic viscosity, acceleration due to gravity, magnetic diffusivity, conductivity of the fluid and coefficient of thermal expansion, respectively.

To make above system of equations in non-dimensional form, we use some dimensionless quantities given as:

$${u} = \frac{{{v}^{\prime}}}{U},\quad{r} = \frac{{{r}^{\prime}}}{a},\quad{\lambda } = \frac{b}{a},\quad{h} = \frac{{{h}^{\prime}}}{{{\sigma \mu }_{e} {H}_{0}^{\prime } {Ua}}},\quad{U} = {g}{\beta }\,{a}^{2} \frac{{({T}_{b}^{\prime } - {T}_{f}^{\prime } )}}{\nu },\quad{T} = \frac{{{T}^{\prime}}}{{({T}_{b}^{\prime } - {T}_{f}^{\prime }) }}.$$
(6)

Using Eq. (6), Eqs. (1)–(3) in the dimensionless form are obtained as follows:

$$\frac{{{\text{d}}^{2} {u}}}{{{\text{d}r}^{2} }} + \frac{1}{r}\frac{{{\text{d}u}}}{{{\text{d}r}}} + \frac{{{Ha}^{2} }}{r}\frac{{{\text{d}h}}}{{{\text{d}r}}} + ({T} - {R}) = {0,}$$
(7)
$$\frac{{{\text{d}}^{2} {h}}}{{{\text{d}r}^{2} }} + \frac{1}{r}\frac{{{\text{d}h}}}{{{\text{d}r}}} + \frac{1}{r}\frac{{{\text{d}u}}}{{{\text{d}r}}} = {0,}$$
(8)
$$\frac{{{\text{d}}^{2} {T}}}{{{\text{d}r}^{2} }} + \frac{1}{r}\frac{{{\text{d}T}}}{{{\text{d}r}}} = {0}{.}$$
(9)

The boundary conditions in non-dimensional form are obtained as:

$${u} = {0,} \quad\frac{{{\text{d}h}}}{{{\text{d}r}}} = {0} \;\; {\text{or}}\;\;{h} = {0},\quad\frac{{{\text{d}}T}}{{{\text{d}r}}} = {Bi}\,{T}\;\; {\text{at}}\;\;{r} = 1,$$
(10)
$${u} = {0,}\quad\frac{{{\text{d}h}}}{{{\text{d}r}}} = {0}\;\; {\text{or}}\;\;{h} = {0},\quad{T} = ({1} + {R})\;\;{\text{at}}\;\;{r} = {\lambda }{.}$$
(11)

Some other dimensionless physical parameters Bi, Ha and R occurring in the above equations are the Biot number, Hartmann number and buoyancy force distribution parameter, respectively, and they are defined as:

$${Bi} = {a}\,{\alpha },\quad{Ha} = {\mu }_{e} {H}_{0}^{\prime } {a}\sqrt {\frac{\sigma }{\mu }} ,\quad{R} = \frac{{{T}_{f}^{\prime } }}{{({T}_{b}^{\prime } - {T}_{f}^{\prime } )}} .$$
(12)

Here, the Biot number (Bi) and Hartmann number (Ha) have importance role on the flow of fluid between both the cylinders at \(R = 1.0\), i.e. \({2T}_{f}^{\prime } = {T}_{b}^{\prime }\).

3 Analytical Solution

3.1 Solution for Hartmann Number (Ha) ≠ 2.0

The exact solution of Eqs. (7)–(9) using boundary conditions (10)–(11) is obtained as follows:

$${u} = {A}_{k1} {r}^{Ha} + {A}_{k2} {r}^{{ - {Ha}}} + {A}_{k3} + \frac{{{r}^{2} ({1} + {R})}}{{({Bi}\,{ \log }\,{\lambda } + {1})}}({B}_{k1} { \log r} + {B}_{k2} ) + {B}_{k3} {r}^{2} {R},$$
(13)
$$\begin{aligned} {h} & = {A}_{k4} - \frac{1}{Ha}({A}_{k1} {r}^{Ha} - {A}_{k2} {r}^{{ - {Ha}}} ) + \frac{{{{r}}^{2} ({1} + {R})}}{{{4(Bi}\,{ \log }\,{\lambda } + {1)}}}\left\{ {{B}_{k1} ({1} - {2}\,{\log}\,{r}) - {2B}_{k2} } \right\} \\ & \quad - \frac{{{B}_{k3} {r}^{2} {R}}}{2}, \\ \end{aligned}$$
(14)
$${T} = ({1} + {R})\frac{{({Bi}\,{ \log }\,{r} + {1})}}{{({Bi}\,{ \log }\,{\lambda } + {1})}}.$$
(15)

Here, \({k} = {1}\) is for the case when both cylinders are non-conducting; \({k} = {2},\) when outer cylindrical wall is non-conducting and inner cylindrical wall is conducting and finally \({k} = {3},\) when inner cylindrical wall is non-conducting and outer cylindrical wall is conducting.

The skin-friction at outer surface of inner cylinder as well as inner surface of outer cylinder, Nusselt number at inner cylinder, induced current density and mass flux of fluid are obtained as:

$$\tau_{1} = \left( {\frac{{{\text{d}}u}}{{{\text{d}}r}}} \right)_{r = 1} = Ha(A_{k1} - A_{k2} ) + \frac{(1 + R)}{(Bi \, \log \lambda + 1)}(B_{k1} + 2B_{k2} ) + 2B_{k3} R,$$
(16)
$$\begin{aligned} \tau_{\lambda } & = \left( {\frac{{{\text{d}}u}}{{{\text{d}}r}}} \right)_{r = \lambda } = Ha(A_{k1} \lambda^{Ha - 1} - A_{k2} \lambda^{ - Ha - 1} ) \hfill \\ & \quad + \frac{(1 + R)}{(Bi \, \log \lambda + 1)}\{ 2\lambda \, (B_{k1} \log \lambda + B_{k2} ) + B_{k1} \lambda \} + 2B_{k3} \lambda R, \hfill \\ \end{aligned}$$
(17)
$$Nu_{\lambda } = - \left( {\frac{{{\text{d}}T}}{{{\text{d}}r}}} \right)_{r = \lambda } = \frac{Bi(1 + R)}{\lambda (Bi \, \log \lambda + 1)},$$
(18)
$$J_{\theta } = - \frac{{{\text{d}}h}}{{{\text{d}}r}} = A_{k1} r^{Ha - 1} + A_{k2} r^{ - Ha - 1} + \frac{r(1 + R)}{(Bi \, \log \lambda + 1)}(B_{k1} \log r + B_{k2} ) + B_{k3} rR,$$
(19)
$$Q = 2\pi \, \left[ \begin{aligned} & \frac{{A_{k1} }}{(Ha + 2)}(\lambda^{Ha + 2} - 1) + \frac{{A_{k2} }}{( - Ha + 2)}(\lambda^{ - Ha + 2} - 1) + \frac{{A_{k3} }}{2}(\lambda^{2} - 1) \hfill \\ & \quad + \frac{{\left( {1 + R} \right)}}{(Bi \, \log \lambda + 1)}\left\{ {\frac{{\lambda^{4} }}{16}(4B_{k1} \log \lambda + 4B_{k2} - B_{k1} ) + \frac{{B_{k1} }}{16}} \right\} + \frac{{B_{k3} }}{4}R(\lambda^{4} - 1). \hfill \\ \end{aligned} \right]$$
(20)

3.2 Solution for Hartmann number (Ha) = 2.0

Here, we have solved the governing differential equation for singular point \({Ha} = 2.0\) because the mathematical expressions \(B_{k1} = - \left\{ {\frac{Bi}{{(4 - Ha^{2} )}}} \right\},\) \(B_{k2} = \left\{ {\frac{4Bi}{{(4 - Ha^{2} )^{2} }} - \frac{1}{{(4 - Ha^{2} )}}} \right\}\) and \(B_{k3} = \frac{1}{{(4 - Ha^{2} )}}\) present in the above Eqs. (13) and (14) clearly show that they have the singularity at \({Ha} = 2.0.\) The velocity and induced magnetic field expressions are given by:

$$u = C_{k1} r^{2} + C_{k2} r^{ - 2} + C_{k3} + \frac{(1 + R)}{(Bi \, \log \lambda + 1)}\{ r^{2} \log r(D_{k1} \log r + D_{k2} )\} + \frac{{Rr^{2} \log r}}{4},$$
(21)
$$\begin{aligned} h & = C_{k4} - \frac{1}{2}(C_{k1} r^{2} - C_{k2} r^{ - 2} ) + \frac{R}{16}r^{2} (1 - 2\log r) \hfill \\ & \quad - \frac{(1 + R)}{(Bi \, \log \lambda + 1)}\{ (D_{k3} \log r + D_{k4} )r^{2} \log r + D_{k5} r^{2} \}. \hfill \\ \hfill \\ \end{aligned}$$
(22)

In this case, the skin-friction at surface of cylinders, induced current density and mass flux of fluid are obtained as follows:

$$\tau_{1} = 2(C_{k1} - C_{k2} ) + \frac{(1 + R)}{(Bi \, \log \lambda + 1)}D_{k2} + \frac{R}{4},$$
(23)
$$\begin{aligned} \tau_{\lambda } & = 2(C_{k1} \lambda - C_{k2} \lambda^{ - 3} ) + D_{k2} \lambda \} + \frac{R}{4}\lambda (2\log \lambda + 1) \hfill \\ & \quad + \frac{(1 + R)}{(Bi \, \log \lambda + 1)}\{ 2\lambda \, \log \lambda \, (D_{k1} \log \lambda + D_{k1} + D_{k2} ), \hfill \\ \end{aligned}$$
(24)
$$J_{\theta } = C_{k1} r + C_{k2} r^{ - 3} + \frac{(1 + R)}{(Bi \, \log \lambda + 1)}\{ r\log r(D_{k1} \log r + D_{k2} )\} + \frac{R}{4}r\log r,$$
(25)
$$\begin{aligned} Q &= 2\pi \left[ {\frac{{C_{k1} }}{4}(\lambda^{4} - 1) + C_{k2} \log \lambda + \frac{{C_{k3} }}{2}(\lambda^{2} - 1) + \frac{R}{64}\{ 4\lambda^{4} \log \lambda - (\lambda^{4} - 1)\} } \right. \, \hfill \\ & \quad + \frac{(1 + R)}{(Bi \, \log \lambda + 1)}\left\{ {\frac{{D_{k1} }}{32}\{ 8\lambda^{4} (\log \lambda )^{2} - 4\lambda^{4} \log \lambda + (\lambda^{4} - 1)\} } \right. \hfill \\ & \quad +\left. {\left. {\frac{{D_{k2} }}{16}\{ 4\lambda^{4} \log \lambda - (\lambda^{4} - 1)\} } \right\}} \right] \hfill \\ \end{aligned}$$
(26)

The constants \({A}_{k1}\), \({A}_{k2}\), \({A}_{k3}\), \({A}_{k4}\), \({B}_{k1}\), \({B}_{k2}\), \({B}_{k3}\), \({C}_{k1}\), \({C}_{k2}\), \({C}_{k3}\), \({{C}}_{\text{k4}}\) ,\({D}_{k1}\), \({D}_{k2}\), \({D}_{k3}\), \({D}_{k4}\) and \({D}_{k5}\) appearing in the above equations (for k = 1, 2 and 3) are defined in Appendix.

4 Results and Discussion

The main aim of the discussion is to bring out the impact of physical numbers such as Biot number and Hartmann number on the velocity field profiles, induced magnetic field profiles, induced current density field profiles, Nusselt number, sink friction and mass flux. The influence of these parameters (such as Biot number and Hartmann number) on the transport processes is illustrated by using the figures and tables. Here, we consider the case (A) when both cylindrical walls are non-conducting, case (B) when the outer cylindrical wall is conducting and inner is non-conducting and case (C) when the inner cylindrical wall is conducting and outer is non-conducting. As expected, it is found by numerical computations that the case (B) and case (C) have given almost same results. Therefore, we have discussed only two cases when both cylinders are non-conducting and when one is conducting and another is non-conducting. Figures 2, 3, 4 and 5 show the velocity profiles when both cylinders are non-conducting and when one cylinder is conducting and other is non-conducting, respectively. It is clear from these figures that the velocity profiles decrease with increasing values of the Hartmann number.

Fig. 2
figure 2

Velocity profile in case one (A) for Bi = 0.1 and 2.0 at R = 1.0 and λ = 2.0

Full size image
Fig. 3
figure 3

Velocity profile in case one (A) for Bi = −0.3 and −0.9 at R = 1.0 and λ = 2.0

Full size image
Fig. 4
figure 4

Velocity profile in case two (B) for Bi = 0.1 and 2.0 at R = 1.0 and λ = 2.0

Full size image
Fig. 5
figure 5

Velocity profile in case two (B) for Bi = −0.3 and −0.9 at R = 1.0 and λ = 2.0

Full size image

The influence of Biot number is to increase the velocity profiles for the Newtonian heating and decrease the velocity profiles for the Newtonian cooling. The region behind it is that as the Biot number increases the convective resistance of wall reduces in the Newtonian heating while it increases in the Newtonian cooling. A comparative study of Figs. 2 and 3 with Figs. 4 and 5 shows that the velocity of the fluid is less when one of the cylindrical surface is conducting in comparison to non-conducting cylindrical surfaces in case of Newtonian heating while it is just reverse in the case of Newtonian cooling. The shape of velocity profile is of parabolic type in upward direction.

Further, from Figs. 6, 7, 8 and 9, we have observed the influence of the Hartmann number, the Newtonian heating/cooling parameter on the induced magnetic field. When both the cylinders are non-conducting and when inner is conducting and outer is non-conducting, the induced magnetic field increases as the values of Biot number increases in case of the Newtonian heating while decreases in the Newtonian cooling. The influence of the Hartmann number implies that the induced magnetic field decrease in the both cases, i.e. when both cylinders are non-conducting and when inner is conducting and outer is non-conducting since the Lorentz force acts opposite to the direction of induced magnetic field. From a comparative study of Figs. 6 with 8 and 7 with 9, we have observed that the magnitude of induced magnetic field is less than the case when both cylindrical walls are non-conducting compared to the case when one of the cylinders is conducting.

Fig. 6
figure 6

Induced magnetic field profile in case one (A) for Bi = 0.1 and 2.0 at R = 1.0 and λ = 2.0

Full size image
Fig. 7
figure 7

Induced magnetic field profile in case one (A) for Bi = −0.3 & −0.9 at R = 1.0 and λ = 2.0

Full size image
Fig. 8
figure 8

Induced magnetic field profile in case two (B) for Bi = 0.1 & 2.0 at R = 1.0 and λ = 2.0

Full size image
Fig. 9
figure 9

Induced magnetic field profile in case two (B) for Bi = −0.3 & −0.9 at R = 1.0 and λ = 2.0

Full size image

The behaviour of the induced current density is shown in Figs. 10, 11, 12 and 13 for various values of the Hartmann number and the Biot number. We find that for both cases, the induced current density profiles increase with increasing values of the Biot number (Bi) in case of the Newtonian heating; while in case of the Newtonian cooling, it reduces with improving the Biot number. From the given figures, it can be observed that the induced current density decreases in both cases when the value of the Hartmann number increases. Figures 10 and 11 show that the maximum induced current density is induced in the middle region while minimum current density near the both cylindrical walls. The modulus of current density at the surface of the inner cylindrical wall is greater than the outer wall. Also, Figs. 12 and 13 show that the maximum current density is induced in the middle region, and then it has shifting tendency in direction of inner cylinder with increasing values of the heating/cooling parameter for the Newtonian heating while it has reverse effect in case of the Newtonian cooling. Comparing the induced current density profiles in Figs. 10 with 12 and 11 with 13, we observed that when one of the cylinders is conducting, the maximum value of induced current density is greater in comparison with if both cylindrical walls are non-conducting.

Fig. 10
figure 10

Induced current density profile in case one (A) for Bi = 0.1 and 2.0 at R = 1.0 and λ = 2.0

Full size image
Fig. 11
figure 11

Induced current density profile in case one (A) for Bi = −0.3 & −0.9 at R = 1.0 and λ = 2.0

Full size image
Fig. 12
figure 12

Induced current density profile in case two (B) for Bi = 0.1 & 2.0 at R = 1.0 and λ = 2.0

Full size image
Fig. 13
figure 13

Induced current density profile in case two (B) for Bi = −0.3 & −0.9 at R = 1.0 and λ = 2.0

Full size image

From Table 1, we can see the influence of the Hartmann number and the Biot number on the skin-friction, mass flux and Nusselt number at the surface of cylinders. It is observed that the skin-friction at outer surface of inlying cylindrical wall increases when both of the cylinders are non-conducting and vice versa when one of the cylindrical wall is conducting. It is also clear that with improving of the Hartmann number, the skin-friction at interface of exterior cylinder decreases in both cases when both cylindrical surfaces are non-conducting and one of them is conducting.

Table 1 Numerical values of dimensionless skin-frictions, mass flux and Nusselt number
Full size table

The numerical values of the skin-friction at inner cylindrical wall increase by increasing the value of the Biot number for the Newtonian heating and conversely for the Newtonian cooling. Moreover, the skin-friction at outer cylinder surface decreases by increasing the value of the Biot number for the Newtonian heating and reverse for the Newtonian cooling. We observe that the impact of increasing the Hartmann number is to reduce the mass flux in the cases when both cylinders are non-conducting and one of them is conducting. It is observed that the values of mass flux increase with improving the Biot number in the Newtonian heating and vice versa in the Newtonian cooling. Further, it is clear from the numerical calculation that the value of Nusselt number at inner and outer cylinders increases with increasing Biot number in case of Newtonian heating, and it is reverse in case of Newtonian cooling. Also, it is observed that the Nusselt number at cylindrical walls decreases with increasing ratio of outer radius to inner radius.

5 Conclusion

By obtaining analytical solution of the model, the effects of Newtonian heating/cooling and induced magnetic on hydromagnetic free convective flow between vertical concentric annular cylinders have been discussed. The influences of the various governing parameters such as the Hartmann number and the Biot number on the fluid velocity, induced magnetic field, induced current density, skin-friction, Nusselt number and mass flux have examined. The following conclusions have been drawn from the present analysis:

  1. 1.

    The fluid velocity, induced magnetic field and induced current density profiles have reducing tendency with increasing the Hartmann number.

  2. 2.

    Value of the velocity, induced magnetic field and induced current density increases for the Newtonian heating and vice versa for the Newtonian cooling.

  3. 3.

    The magnitude of the fluid velocity, induced magnetic field and induced current density profile is more if one of the cylindrical walls is conducting than if both walls are conducting.

  4. 4.

    The numerical values of Nusselt number at cylindrical walls increase in case of the Newtonian heating and vice versa in case of the Newtonian cooling with increasing values of the Biot number.

  5. 5.

    The skin-friction at inner cylinder decreases if one of the cylindrical walls is conducting and increases if both walls are non-conducting with increasing Hartmann number. Moreover, the skin-friction at outer cylinder increases in both cases with increasing Hartmann number.

  6. 6.

    The influence of Biot number is to increase/reduce the skin-friction in case of Newtonian heating/cooling at inlying cylinder and just reverse at outer cylinder.

  7. 7.

    The mass flux for the both cases has reducing nature with increasing Hartmann number. Further, values of mass flux increase with improve in value of Biot number in Newtonian heating and vice versa in Newtonian cooling.