Keywords

1 Introduction

Retrial queueing models are characterized by the feature of retrial phenomenon that an arriving customer who finds all servers (or resources) occupied, joins the virtual group of blocked customers, called orbit and retry again for service after a random amount of time. Models with retrials have been widely used to analyze several practical problems in telecommunication systems as the call centers, the cellular mobile networks [1,2,3] and the wireless sensor networks [4]. Significant surveys on this topic [5, 6] reveal the non-negligible impact of retrials, which arise due to the lack of available resources and which can negatively affect the system performances, because they generate more load. However, the consideration of retrial phenomenon introduces great analytical complications to obtain most important performance measures. In particular, for multiserver models, no explicit closed-form solution exist for the performance measures [6]. These analytical difficulties are due to the simultaneous presence of the repeated requests stream from the orbit and the normal stream of primary requests arrivals. Therefore, lots of attention have been paid to approximation methods, computational algorithms and tail asymptotics to estimate the performance measures [6].

On the other hand, the heterogeneity of customers from the point of view of customers characteristics such as the arrivals, the service and/or the retrial process distributions, is an another important problem in retrial queueing area, because models with different types of customers arise in various practical systems. For example, in cellular mobile networks, the base station channels are used by a class of fresh calls initiated in the same cell and a second class of handoff calls incoming from adjacent cells. Similarly, in modern call centers, multiple types of calls arrive at service station over different communication channels such as telephone, internet, e-mail, mobile device, etc.

However, retrial queues with multiple classes of customers (called also multiclass retrial queues) have been known to be far more difficult for mathematical analysis than models with a single class of customers (or homogeneous customers). So, explicit results for this subject are limited to some particular cases [7] and recently, sufficient stability conditions were defined for a multiserver multiclass retrial queue [8].

For the single server retrial queues with two classes of customers, a number of analytic results have been obtained [5, 6, 9]. As regards to multiserver case with two customers classes, as far as we know, there are no explicit formulae and only a few algorithmic methods are proposed using matrix geometric methods [10], matrix analytic methods [11] or computational approaches as the one we have proposed using the Colored Generalized Stochastic Petri nets formalism [12]. Recently, Kim et al. [13] studied the stability of a two-class two-server retrial queue.

The objective of this paper is to propose a new recursive algorithmic approach for the performance analysis of a multiserver retrial queue with two classes of customers: ordinary customers whose access to the service depends on the number of available servers and who join the retrial group with a certain degree of impatience when blocked; and priority customers who have access to all servers and leave definitively the system when no server is available. Hence, and in order to minimize the loss probability of priority customers, they should be given a higher priority over ordinary customers in access to the system resources. To this end, we give them the possibility to use all servers, unlike ordinary customers whose access to the service depends on a threshold on the number of available servers. Further, we assume that all servers follow the non-preemptive priority rule, which means that if one or more priority customers arrive during the service time of an ordinary customer, the current service of this non-priority customer continues and is not stopped.

Some papers considered retrial models with two customers classes and preemptive priority [9, 11, 14] or a non-preemptive priority in the single server case [15, 16]. However, there is no work that deals with multiserver retrial queueing systems with two customers classes and non-preemptive priority. That motivates us to investigate such queueing model in this work.

The layout of the paper is given as follows: After the introduction, a detailed mathematical description of the model under study is given in Sect. 2. Then, we present our analysis approach and the details of the recursive algorithm we propose to calculate the stationary states probabilities in Sect. 3. Next, we give the formulae of the main performance measures. In Sect. 5, we discuss through numerical examples, the effect of the dedicated servers number and retrial rate on the system performances, namely the blocking probability for ordinary customers and loss probability for priority customers. Finally, we give a conclusion.

2 Mathematical Description of the Model

We consider a retrial multi-server queueing system with two classes of customers; ordinary and priority ones. The service area consists of C, \((C\ge 1)\) homogeneous servers with the same exponential service rate \(\mu \). The ordinary (priority) customers arrive in the system following a Poisson process with a mean arrival rate \(\lambda _{1}\) (\(\lambda _{2}\) respectively). The global arrival rate is then given by \(\lambda =\lambda _{1}+\lambda _{2}\). In order to ensure that priority customers are served prior to ordinary (non-priority) ones, our strategy consists of reserving a certain number of servers d \((1\le d \le C)\), called dedicated servers only for priority class of customers. Thus, on the arrival of a priority customer, if at least one server of the C servers of the service station is idle, it will be served immediately, otherwise, it will be lost definitively, whereas an arriving ordinary customer must find at least \((d+1)\) available servers to get service, otherwise, it joins the orbit and retry for the service later. A blocked customer in the orbit decides to retry with probability \(\theta \) or give up and returns to the free state with probability \((1-\theta )\). Note that \(\theta \) is used to represent the degree of impatience of customers. The retrial time is exponentially distributed with rate \(\alpha \). All involved random variables are independent and identically distributed.

3 Recursive Analysis Algorithm

From the stochastic behavior of both two classes of customers and the servers allocation policy, the retrial system described above can be modeled by means of a two-dimensional Continuous-Time Markov Chain (CTMC) where each state is described by means of two random variables \((X(t),Y(t);t\ge 0)\). Let X(t) be the number of customers being in service (which equals the number of busy servers), and Y(t) the number of customers waiting in the orbit at time t. Hence, the steady state probabilities are defined by the probabilities \(\pi _{i,j}=Pr\left\{ X=i,Y=j\right\} ,i=0,1,...,C\;j=0,1,...,...\) of having i customers in service and j customers in the orbit.

The state space \(S=\left\{ 0,...,C\right\} \times {Z}_{+}\) of this CTMC is infinite because the population size and the orbit capacity are supposed to be infinite. In order to obtain a finite CMTC model, we propose the truncation of the state space to \(S^{\prime }=\left\{ 0,...,C\right\} \times \left\{ 0,...,q\right\} \) with q large enough. In other terms, the probability of being in states with a number of customers in orbit greater than q is neglected.

The balance equation describing the probability flux in and out of state (i, j) is defined by:

$$\begin{aligned} E(i,j): \sum _{(k,l)\in S^{\prime }\setminus (i,j)}\pi _{i,j}.R_{(i,j),(k,l)}=\sum _{(k,l)\in S^{\prime }\setminus (i,j)}\pi _{k,l}.R_{(k,l),(i,j)} \end{aligned}$$

where \(R_{(i,j),(k,l)}\) is the transition rate from state (i, j) to state (k, l).

We put \(K_{0}=\pi _{0,q}\), \(K_{1}=\pi _{0,(q-1)}\), ..., \(K_{d}=\pi _{(0,q-d)}\). We first should express all probabilities as a function of \(K_{i},\;i=0,...,d\).

$$\begin{aligned} \pi _{i,j}=K_{0}.u_{0}(i,j)+K_{1}.u_{1}(i,j)+...+K_{d}.u_{d}(i,j) \end{aligned}$$

Then, we express coefficients \(K_{i},\;i=0,...,d\) as a function of \(K_{0}\), and finally, we use the normalization equation, where the unique unknown is \(K_{0}\),

$$\begin{aligned} \sum _{i=0}^{C}\sum _{j=0}^{q}\pi _{i,j}=1 \end{aligned}$$
(1)

to find its value.

We now proceed to explain the details of the algorithm:

Step1. Expressing all probabilities in \(K_{i}\)

  1. 1.

    Columns q down to \(q-d\)

Starting with column q, it’s obvious that \(\pi _{(0,q)}=K_{0}\), such as \(u_{0}(0,q)=1\), \(u_{1}(0,q)=0\), . . ., \(u_{d}(0,q)=0\).

We calculate recursively, for \(i=1,...,C-(d+1)\), \(\pi _{i,q}\) using the balance equation \(E(i-1,q)\). We get:

$$\begin{aligned} \pi _{1,q}&=\frac{q.\alpha +\lambda }{\mu }.\pi _{0,q} \\ \pi _{i+1,q}&=\frac{q.\alpha +\lambda +i.\mu }{(i+1)\mu }\pi _{i,q}-\frac{\lambda }{(i+1)\mu }.\pi {}_{i-1,q} \end{aligned}$$

In the same way, we calculate for columns \((q-j),\,j=1,...,d\), the value of \(\pi _{1,q-j}\) using \(E(0,q-j)\) first, then \(\pi _{i+1,q-j}\) using \(E(i,q-j)\), \(i=0,...,C-d-1\). We get:

$$\begin{aligned} \pi _{1,q-j}&=\frac{(q-j).\alpha +\lambda }{\mu }.K_{j} \\ \pi _{i+1,q-j}&=\frac{(q-j).\alpha +\lambda +i.\mu }{(i+1)\mu }\pi _{i,q-j}-\frac{\lambda }{(i+1)\mu }\pi _{i-1,q-j}-\frac{(q-j+1)\alpha }{(i+1)\mu }\pi _{i-1,q-j+1} \end{aligned}$$

Then, inside the line \((C-d+1)\), columns from \(j=\left( q-d+1\right) \) to \(j=\left( q-1\right) \) can be calculated. Actually, for each probability \(\pi _{C-d+1,j}\), we use the balance equation \(E(C-d,j)\):

$$\begin{aligned}&\pi _{C-d+1,j}.[(C-d+1)\mu ]= [(C-d)\mu +\theta \lambda _{1}+\lambda _{2}+j(1-\theta )\alpha ].\pi _{C-d,j}-\lambda .\pi _{C-d-1,j} \\&\qquad -[(1-\theta )(j+1)\alpha ].\pi _{C-d,j+1} -\theta \lambda _{1}.\pi _{C-d,j-1}-[(j+1)\alpha ].\pi _{C-d-1,j+1} \end{aligned}$$

And for \(\pi _{C-d+1,q}\), we use \(E(C-d,q)\), we have:

$$\begin{aligned}&\pi _{C-d+1,q}.[(C-d+1)\mu ]= [(C-d)\mu +\lambda _{2}+(1-\theta )q\alpha ].\pi _{C-d,q}\\&\quad -\lambda .\pi _{C-d-1,q}-\theta \lambda _{1}.\pi _{C-d,q-1} \end{aligned}$$

For the rest of lines, i.e. from \(i=C-d+2\) to \(i=C\), only columns \(j=i+q-C,...,q\) can be deduced for the moment, they are calculated from balance equations \(E(i-1,j)\):

We have for \(j=i+q-C\) to \(j=q-1\):

$$\begin{aligned}&\pi _{i,j}.(i.\mu )= [(i-1).\mu +(1-\theta ).j.\alpha +\lambda _{2}+\theta .\lambda _{1}].\pi _{(i-1),j} \\&-\lambda _{2}.\pi _{(i-2),j}-(1-\theta ).(j+1).\alpha .\pi _{(i-1),(j+1)}-\theta .\lambda _{1}.\pi _{(i-1),(j-1)} \end{aligned}$$

And when \(j=q\):

$$\begin{aligned} \pi _{i,q}.(i.\mu )=[(i-1).\mu +(1-\theta ).q.\alpha +\lambda _{2}].\pi _{(i-1),q} -\lambda _{2}.\pi _{(i-2),q}-\theta .\lambda _{1}.\pi _{(i-1),(q-1)} \end{aligned}$$

From E(C, q), we obtain the value of \(\pi _{C,q-1}\) as follows:

$$\begin{aligned} \pi _{C,q-1}.\theta .\lambda _{1}=[C.\mu +(1-\theta ).q.\alpha ].\pi _{C,q}-\lambda _{2}.\pi _{(C-1),q} \end{aligned}$$

Now, in order to have the rest of columns, we proceed like this. For each \(j=q-2\) to \(q-d\), we obtain first \(\pi _{C,j}\) using \(E(C,j+1)\):

$$\begin{aligned}&\pi _{C,j}.\theta .\lambda _{1}=[(1-\theta ).(j+1).\alpha +C.\mu +\theta .\lambda _{1}].\pi _{C,(j+1)} \\&\quad -(1-\theta ).(j+2).\alpha .\pi _{C,(j+2)}-\lambda _{2}.\pi _{(C-1),(j+1)} \end{aligned}$$

Then, we obtain the other lines \(i=C-1\) to \(i=C+1+j-q\), thanks to \(E(i,j+1)\):

$$\begin{aligned}&\pi _{i,j}.\theta .\lambda _{1}= [(1-\theta ).(j+1).\alpha +i.\mu +\theta .\lambda _{1}+\lambda _{2}].\pi _{i,(j+1)} \\&-(1-\theta ).(j+2).\alpha .\pi _{i,(j+2)}-\lambda _{2}.\pi _{(i-1),(j+1)} -(i+1).\mu .\pi _{(i+1),(j+1)} \end{aligned}$$

Up to now, we have expressed all probabilities from column \(j=q\) to \(j=q-d\), in \(K_{0},...,K_{d}\).

  1. 1.

    Column \((q-d-1)\) down to 1

In a similar way as explained above, by invoking \(E(i-1,j)\), for each \(\pi _{i,j}\), we find:

$$\begin{aligned} \pi {}_{1,j}&=\frac{j.\alpha +\lambda }{\mu }.\pi _{0,j} \\ \pi _{i+1,j}&=\frac{j.\alpha +\lambda +i.\mu }{(i+1)\mu }\pi _{i,j} -\frac{\lambda }{(i+1)\mu }\pi _{i-1,j}-\frac{(j+1)\alpha }{(i+1)\mu }\pi _{i-1,j+1} \end{aligned}$$

In particular, when \(i=C-d-1\), we can find numbers \(v_{0}(C-d,j),v_{1}(C-d,j),...,v_{d+1}(C-d,j)\), such that:

$$\begin{aligned} \pi _{(C-d),j}= v_{0}(C-d,j).K_{0} +...+v_{d}(C-d,j).K_{d}+v_{(d+1)}(C-d,j).\pi _{0,j} \end{aligned}$$

On the other hand, by invoking \(E(C-d,j+1)\), we get:

$$\begin{aligned}&\pi _{(C-d),j}.\theta .\lambda _{1}=[(C-d).\mu +\theta .\lambda _{1}+\lambda _{2}+(1-\theta ).(j+1).\alpha ].\pi _{(C-d),(j+1)} -\lambda .\pi _{(C-d-1),(j+1)} \\&-(j+2).\alpha .\pi _{(C-d-1,j+2)}-(1-\theta ).(j+2).\alpha .\pi _{(C-d),(j+2)}-(C-d+1).\mu .\pi _{(C-d+1),(j+1)} \end{aligned}$$

which implies that we can find explicitly numbers \(u_{0}(C-d,j),u_{1}(C-d,j),...,\) \(u_{d}(C-d,j)\), such that:

$$\begin{aligned} \pi _{(C-d),j}=u_{0}(C-d,j).K_{0}+u_{1}(C-d,j).K_{1} +...+u_{d}(C-d,j).K_{d} \end{aligned}$$

From equation (2) and (2), we can deduce \(\pi _{0,j}\) value,

$$\begin{aligned} \pi _{0,j}=\frac{\sum _{k=0}^{d}[u_{k}(C-d,j)-v_{k}(C-d,j)].K_{k}}{v_{(d+1)}(C-d,j)} \end{aligned}$$

Thus, we calculate again \(\pi _{i,j}\), \(i=1,...,C-d\), in \(K_{0},K_{1},...,K_{d}\) only, we get for \(k=0,...,d\):

$$\begin{aligned} u_{k}(i,j)=v_{k}(i,j)+\frac{u_{k}(C-d,j)-v_{k}(C-d,j)}{v_{(d+1)}(C-d,j)}.v_{(d+1)}(i,j) \end{aligned}$$

After that, equations for \(\pi _{i,j}\), such that \(i=C-d+1,...,C\) can be easily derived from \(E(i,j+1)\).

Step2. Expressing coefficients \(K_{i},i=1,...,d\) in \(K_{0}\)

Let’s consider the balance equation E(C, 0):

$$\begin{aligned} \pi _{C,0}.(C.\mu +\theta .\lambda _{1})=\pi _{(C-1),0}.\lambda _{2}+\pi _{C,1}.(1-\theta ).\alpha \end{aligned}$$

Keeping in mind that both \(\pi _{C,0}\), \(\pi _{(C-1),0}\) and \(\pi _{C,1}\) can be written as a linear combination of \(K_{0},...,K_{d}\), equation (3) is equivalent to:

$$\begin{aligned} \sum _{k=0}^{d}u_{k}(C,0).K_{k}.(C.\mu +\theta .\lambda _{1})=\sum _{k=0}^{d}u_{k}(C-1,0).K_{k}.\lambda _{2} +\sum _{k=0}^{d}u_{k}(C,1).K_{k}.(1-\theta ).\alpha \end{aligned}$$

It’s a question of a simple algebra to extract \(K_{d}\) in \(K_{(d-1)},...,K_{0}\). In the same way, we consider E(i, 0), \(i=C-1,...,C-d+1\), to have \(K_{x}\) in \(K_{x-1},...,K_{0}\), \(x=d-1,...,1\)

Step3. Finding \(K_{0}\)

Finally, we solve the normalization equation (1), in order to extract the value of \(K_{0}\) which is the unique unknown.

4 Performance Measures

Once the stationary probabilities are determined thanks to the above algorithm, several performance measures can be calculated applying the following formulas. The most significant performance indices are as follows:

  • Mean number of busy servers:: \(N_{Busy}=\sum _{i=0}^{C}\sum _{j=0}^{q}i.\pi _{i,j}\)

  • Mean rate of ordinary customers served at the first attempt:

    $$\begin{aligned} \bar{\lambda }_{FS}=\lambda _{1}.\sum _{i=0}^{C-(d+1)} \sum _{j=0}^{q}.\pi _{i,j} \end{aligned}$$

  • Mean rate of blocked ordinary customers:

    $$\begin{aligned}\bar{\lambda }_{FU}=\lambda _{1}.\theta .\sum _{i=C-d}^{C}\sum _{j=0}^{q}.\pi _{i,j}\end{aligned}$$

  • Mean rate of blocked ordinary customers leaving the system without being served:

    $$\begin{aligned} \bar{\lambda }_{FB}=\lambda _{1}.(1-\theta ).\sum _{i=C-d}^{C}\sum _{j=0}^{q}\pi _{i,j} \end{aligned}$$

  • Effective mean ordinary customers arrival rate:

    $$\begin{aligned} \bar{\lambda }_{F}=\bar{\lambda }_{FS}+\bar{\lambda }_{FU}+\bar{\lambda }_{FB} \end{aligned}$$

  • Mean rate of retrials served at the first attempt:

    $$\begin{aligned} \bar{\alpha }_{RS}=\alpha .\sum _{i=0}^{C-(d+1)} \sum _{j=0}^{q}j.\pi _{i,j} \end{aligned}$$

  • Mean rate of blocked retrials: \(\bar{\alpha }_{RU}=\alpha .\theta .\sum _{i=C-d}^{C}\sum _{j=0}^{q}j.\pi _{i,j}\)

  • Mean rate of blocked retrials leaving the system without being served:

    $$\begin{aligned} \bar{\alpha }_{RB}=\alpha .(1-\theta ).\sum _{i=C-d}^{C}\sum _{j=0}^{q}j.\pi _{i,j} \end{aligned}$$

  • Effective mean retrial rate: \(\bar{\alpha }=\bar{\alpha }_{RS}+\bar{\alpha }_{RU}+\bar{\alpha }_{RB}\)

  • Mean rate of priority customers being served: \(\bar{\lambda }_{HS}=\lambda _{2}.\sum _{i=0}^{C-1}\sum _{j=0}^{q}\pi _{i,j}\)

  • Mean rate of lost priority customers: \(\bar{\lambda }_{HB}=\lambda _{2}. \sum _{j=0}^{q}\pi _{C,j}\)

  • Effective mean priority customers arrival rate: \(\bar{\lambda }_{H}=\bar{\lambda }_{HS}+\bar{\lambda }_{HB}\)

  • Blocking probability of ordinary customers: \(P_{BF}=\frac{\bar{\lambda }_{FU}+\bar{\lambda }_{FB}}{\bar{\lambda }_{F}}\)

  • Blocking probability of retrial customers: \(P_{BR}=\frac{\bar{\alpha }_{RU}+\bar{\alpha }_{RB}}{\bar{\alpha }}\)

  • Loss probability (of priority customers): \(P_{BH}=\frac{\bar{\lambda }_{HB}}{\bar{\lambda }_{H}}\)

Fig. 1
figure 1

Influence of the offered traffic and the number of dedicated servers on the blocking probability.

Full size image
Fig. 2
figure 2

Influence of the offered traffic and the number of dedicated servers on the loss probability.

Full size image

5 Numerical Results

In this section, we examine the impact that have some system parameters like the number of dedicated servers, degree of persistence and the arrival and service rates on the system performance, namely the blocking and loss probability. In that follows, unless otherwise stated, we assume that \(C=15\), \(1/\mu =120 s\), \(\alpha =\mu =20\), \(\lambda _{1}=\lambda _{2}=24\) and \(\theta =0.6\). The offered load is defined by \(\rho =\lambda /(C.\mu )\).

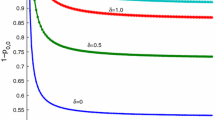
The effect of the traffic load \(\rho \) and the number of dedicated servers on the blocking probability and the loss probability is shown in Figs. 1 and 2 respectively. We can note that the increase in parameters \(\rho \) affects negatively both of the two probabilities. On the other hand, as expected, increasing the number of dedicated servers can significantly improve the loss probability of priority customers. It is just perfect (\(\simeq 0\)) when \(d=3\). We observe the opposite effect on the blocking probability, when more servers are reserved to priority customers, more ordinary customers are blocked at their arrival.

6 Conclusion

A recursive algorithmic approach for the performance analysis of a mobile network with repeated attempts, two classes of customers: ordinary (impatient) and priority customers and non-preemptive priority was investigated in this paper. In order to minimize the loss probability of priority customers, they should be given a higher priority over ordinary customers in access to the network servers. Our proposition was to reserve some servers to be used only by priority customers. The analysis of the model was performed using a bi-dimensional Time Continuous Markov chain, and an efficient recursive algorithm was proposed and implemented in order to calculate the steady state probability distribution. Moreover, the formulae of several performance measures were developed. We showed via numerical examples that dedicated servers technique improves the system performance, mainly the loss probability, but at the expense of ordinary customers.