Keywords

1 Introduction

During the last years, multiphase drives have gained interest for their advantages. Among their features are reduction of torque pulsations and reducing stator phase current [1,2,3]. The high phase order offers greater fault tolerance. Recently, PMSM has acquired interest [4, 5]. The advantages of this type of machine are numerous, among which we can mention: low inertia, robust and low maintenance cost [3, 4]. Various methodologies to achieve the control of multiphase motor drives are presented in the literature. The most famous one is the vector control [6] which has been used in most industrial drive applications due to its applicability and simplicity. Nevertheless, the five-phase PMSM is a highly nonlinear system so that the vector control, based on conventional PI and PID regulators, fails to achieve the high performance requirements of industrial applications. To compensate for the effects of nonlinearity, many nonlinear control strategies have been developed to control PMSM drives such as sliding mode control [7], the direct torque control [8] and the back stepping control [9,10,11,12]. Recently, back stepping control technique is widely developed and studied. A back stepping controller is known as a recursive and systematic design with the flexibility to avoid cancellations of useful nonlinearity [13]. It is a robust and powerful methodology that has been studied in the last two decades. Numerous researches have been focused on the back stepping controller to three-phase PMSM [9,11,11]. In [9], an adaptive backstepping technique is designed to achieve the sensorless control of PMSM supplied by a current source inverter. The control system is based on the adaptive backstepping observer and adaptive backstepping controller. In [10], an improved direct torque control method of three-phase PMSM based on backstepping control with a recursive least squares algorithm to identify machine parameters is presented. Another new adaptive nonlinear backstepping controller is proposed to compensate the unknown system parameters [11]. Furthermore, a novel trajectory generator is designed to constrain the motor reference current. Several research activities were dedicated to the concept of sensorless control technique of three-phase PMSM drives. One of the known classes of nonlinear observers is the sliding mode observer which posses many special characteristics, namely order reduction control, simple algorithm and disturbance rejection. Numerous papers were dedicated to the observation of PMSM based on SMO [14, 15].

In this paper, the sensorless backstepping controller of five-phase permanent magnet synchronous motor drive is proposed. This paper is organized in five sections including the introduction as follows. Section 2 introduces the model of five-phase PMSM. Then the backstepping controller is discussed in Sect. 3. Section 4 deals with simulation results and the conclusions are presented in Sect. 5.

2 Model of a Five-Phase PMSM

The five-phase PMSM model can be given in a decoupled rotating frame \( \left( {d_{1} q_{1} - d_{3} q_{3} } \right) \) [4]:

$$ \left\{ \begin{aligned} \frac{{dI_{d1} }}{dt} & = - b_{1} I_{d1} + \omega_{e} I_{q1} + \frac{1}{{L_{p} }}v_{d1} \\ \frac{{dI_{q1} }}{dt} & = - b_{1} I_{q1} - \omega_{e} I_{d1} - b_{2} \omega_{e} + \frac{1}{{L_{p} }}v_{q1} \\ \frac{{dI_{d3} }}{dt} & = - b_{3} I_{d3} + 3\omega_{e} I_{q3} + \frac{1}{{L_{s} }}v_{d3} \\ \frac{{dI_{q3} }}{dt} & = - b_{3} I_{qs} - 3\omega_{e} I_{d3} + \frac{1}{{L_{s} }}v_{q3} \\ \frac{d\varOmega }{dt} & = \frac{1}{J}\left( {\sqrt {\frac{5}{2}} \varPhi_{f} PI_{qp} - T_{l} } \right) - \frac{f}{J}\varOmega \\ \end{aligned} \right. $$
(1)

where

\( \left( {I_{d1} ,I_{q1} ,I_{d3} ,I_{q3} } \right) \): stator currents in \( \left( {d_{1} - q_{1} - d_{3} - q_{3} } \right) \) frame.

\( \left( {v_{d1} ,v_{q1} ,v_{d3} ,v_{q3} } \right) \): stator voltages in \( \left( {{d}_{1} - q_{1} - d_{3} - q_{3} } \right) \) frame.

\( \Omega \) and \( \omega_{\text{e}} \) are the mechanical and electrical speed respectively. J, f and \( \varPhi_{f} \) are the inertia moment, the friction coefficient and amplitude of magnet flux respectively. P pair poles and \( {{T}}_{l} \) load torque.

$$ b_{1} = \frac{{R_{s} }}{{L_{p} }};b_{2} = \frac{{\sqrt {\frac{5}{2}} \varPhi_{f} }}{{L_{p} }};b_{3} = \frac{{R_{s} }}{{L_{s} }} $$

\( R_{s} \) is stator resistance, \( L_{p} \) and \( L_{s} \) are the inductances of the main fictitious machine and secondary fictitious machine respectively

Equation (1) can be written as:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{dI_{d1} }}{dt} = g_{1} + \frac{1}{{L_{p} }}v_{d1} } \hfill \\ {\frac{{dI_{q1} }}{dt} = g_{2} + \frac{1}{{L_{p} }}v_{q1} } \hfill \\ {\frac{{dI_{d3} }}{dt} = g_{3} + \frac{1}{{L_{s} }}v_{d3} } \hfill \\ {\frac{{dI_{q3} }}{dt} = g_{4} + \frac{1}{{L_{s} }}v_{q3} } \hfill \\ {\frac{d\varOmega }{dt} = g_{5} } \hfill \\ \end{array} } \right., $$
(2)

where

$$ \left\{ \begin{aligned} g_{1} & = - b_{1} I_{d1} + \omega_{e} I_{q1} \\ g_{2} & = - b_{1} I_{q1} - \omega_{e} I_{d1} - b_{2} \omega_{e} \\ g_{3} & = - b_{3} I_{d3} + 3\omega_{e} I_{q3} \\ g_{4} & = - b_{3} I_{q3} - 3\omega_{e} I_{d3} \\ g_{5} & = b_{4} I_{qp} - \frac{1}{J}T_{l} - b_{5} \varOmega \\ \end{aligned} \right. $$
(3)

where

$$ b_{4} = \frac{{\sqrt {\frac{5}{2}} {\varPhi }_{f} P}}{J}; \, b_{5} = \frac{f}{J} $$

The control objective is to make the mechanical speed \( \varOmega \) track desired reference \( \varOmega_{c} \): such a tracking can be achieved through a backstepping controller algorithm. The stator voltages are \( \left( {v_{d1} ,v_{q1} ,v_{d3} ,v_{q3} } \right) \) considered as inputs.

3 Speed Backstepping Controller

The basic idea of the backstepping control strategy is to make the complex nonlinear closed-loop system equivalent in cascade subsystems of order one. The stability is provided by Lyapunov strategy. The synthesis of the backstepping controller proceeds in two steps.

3.1 Calculation of Current References

The system should follow the trajectory for output variable. The speed error is defined by:

$$ e_{1} = \varOmega_{c} - \varOmega $$
(4)

The derivative with respect to time of Eq. (4) gives:

$$ \dot{e}_{1} = \dot{\varOmega }_{c} - \dot{\varOmega } $$
(5)

Accounting for Eqs. (2), (5) can be written as:

$$ \dot{e}_{1} = \dot{\varOmega }_{c} - g_{5} $$
(6)

In order to check the tracking performances, let us define the first Lyapunov function \( v_{1} \) associated with speed error, such as:

$$ v_{1} = \frac{1}{2}e_{1}^{2} $$
(7)

Using Eq. (6), the derivative of Eq. (7) is given by:

$$ \dot{v}_{1} = e_{1} (\dot{\varOmega }_{c} - g_{5} ) $$
(8)

Equation (8) can be rewritten as follows:

$$ \dot{v}_{1} = e_{1} (\dot{\varOmega }_{c} - g_{5} ) = - k_{1} e_{1}^{2} $$
(9)

where \( k_{1} > 0 \), which gives:

$$ \dot{e}_{1} = \dot{\varOmega }_{c} - \dot{\varOmega } = - k_{1} e_{1} $$
(10)

The \( q_{1} \) axis current contributes towards torque whereas \( d_{1} ,\;d_{3} \;{\text{and}}\;3 \) current components do not. This allows maintaining \( d_{1} \) axis current, \( d_{3} \) axis current and \( q_{3} \) axis current equals to zero in order to obtain maximum average torque for given copper losses [2].

The references currents then are given by:

$$ \left\{ \begin{aligned} \left( {I_{q1} } \right)_{c} & = (\dot{\varOmega }_{c} + \frac{1}{J}T_{l} + b_{5} \varOmega + k_{1} e_{1} )/b_{4} \\ \left( {I_{d1} } \right)_{c} & = 0 \\ \left( {I_{q3} } \right)_{c} & = 0 \\ \left( {I_{d3} } \right)_{c} & = 0 \\ \end{aligned} \right. $$
(11)

3.2 Calculation of Currents References

The aim is to obtained the references current obtained by the previous step. The stator current errors are defined as:

$$ \left\{ {\begin{array}{*{20}l} {e_{2} = \left( {I_{q1} } \right)_{c} - I_{q1} } \hfill \\ {e_{3} = \left( {I_{d1} } \right)_{c} - I_{d1} } \hfill \\ {e_{4} = \left( {I_{d3} } \right)_{c} - I_{d3} } \hfill \\ {e_{5} = \left( {I_{q3} } \right)_{c} - I_{q3} } \hfill \\ \end{array} } \right. $$
(12)

Considering Eqs. (11), (12) is given by:

$$ \left\{ {\begin{array}{*{20}l} {e_{2} = (\dot{\varOmega}_{c} + \frac{1}{J}T_{l} + b_{5} \varOmega + \, k_{1} e_{1} )/b_{4} - \, I_{q1} } \hfill \\ {e_{3} = - \, I_{d1} \, } \hfill \\ {e_{4} = - \, I_{d3} \, } \hfill \\ {e_{5} = - \, I_{q3} \, } \hfill \\ \end{array} } \right. $$
(13)

Using Eqs. (13), (6) can be given as:

$$ \dot{e}_{1} = b_{4} e_{2} - k_{1} e_{1} $$
(14)

The derivative of Eq. (14) gives:

$$ \left\{ \begin{aligned} \dot{e}_{2} & = (\dot{I}_{q1} )_{c} - \dot{I}_{q1} \\ \dot{e}_{3} & = (\dot{I}_{d1} )_{c} - \dot{I}_{d1} \\ \dot{e}_{4} & = (\dot{I}_{d3} )_{c} - \dot{I}_{d3} \\ \dot{e}_{5} & = (\dot{I}_{q3} )_{c} - \dot{I}_{q3} \\ \end{aligned} \right. $$
(15)

By substituting Eq. (2) in Eq. (15), one obtains:

$$ \left\{ \begin{aligned} \dot{e}_{2} & = (\dot{I}_{q1} )_{c} - \dot{I}_{q1} = (\dot{I}_{q1} )_{c} - g_{2} - \frac{1}{{L_{p} }}v_{q1} \\ \dot{e}_{3} & = (\dot{I}_{d1} )_{c} - \dot{I}_{d1} = (\dot{I}_{d1} )_{c} - g_{1} - \frac{1}{{L_{p} }}v_{d1} \\ \dot{e}_{4} & = (\dot{I}_{3} )_{c} - \dot{I}_{d3} = (\dot{I}_{d3} )_{c} - g_{3} - \frac{1}{{L_{s} }}v_{d3} \\ \dot{e}_{5} & = (\dot{I}_{q3} )_{c} - \dot{I}_{q3} = (\dot{I}_{q3} )_{c} - g_{4} - \frac{1}{{L_{s} }}v_{q3} \\ \end{aligned} \right. $$
(16)

In order to prove the stability of the overall system, let us choose a new Lyapunov function defined as:

$$ v_{2} = \frac{{e_{1}^{2} + e_{{_{2} }}^{2} + e_{3}^{2} + e_{{_{4} }}^{2} + e_{{_{5} }}^{2} }}{2} $$
(17)

The derivative of Eq. (17) is given by:

$$ \begin{aligned} \dot{v}_{2} & = - k_{1} e_{1}^{2} - k_{2} e_{{_{2} }}^{2} - k_{3} e_{{_{3} }}^{2} - k_{4} e_{{_{4} }}^{2} - k_{5} e_{{_{5} }}^{2} \\ & \quad + e_{2} \left( {k_{2} e_{2} + a_{4} e_{1} + (\dot{I}_{q1} )_{c} - g_{2} - \frac{1}{{L_{p} }}v_{q1} } \right) + e_{3} \left( {k_{3} e_{3} + (\dot{I}_{d1} )_{c} - g_{1} - \frac{1}{{L_{p} }}v_{d1} } \right) \\ & \quad + e_{4} \left( {k_{4} e_{4} + (\dot{I}_{d3} )_{c} - g_{3} - \frac{1}{{L_{s} }}v_{d3} } \right) + e_{5} \left( {k_{5} e_{5} + (\dot{I}_{q3} )_{c} - g_{4} - \frac{1}{{L_{s} }}v_{q3} } \right) \\ \end{aligned} $$
(18)

The derivative of the whole Lyapunov function Eq. (18) is negative, if the quantities between parentheses in the same equation are equal to zero.

$$ \left\{ \begin{aligned} & k_{2} e_{2} + b_{4} e_{1} + (\dot{I}_{q1} )_{c} - g_{2} - \frac{1}{{L_{p} }}v_{q1} = 0 \\ & k_{3} e_{3} + (\dot{I}_{d1} )_{c} - g_{1} - \frac{1}{{L_{p} }}v_{d1} = 0 \\ & k_{4} e_{4} + (\dot{I}_{d3} )_{c} - g_{3} - \frac{1}{{L_{s} }}v_{d3} = 0 \\ & k_{5} e_{5} + (\dot{I}_{q3} )_{c} - g_{4} - \frac{1}{{L_{s} }}v_{q3} = 0 \\ \end{aligned} \right. $$
(19)

The stator voltages are given by:

$$ \left\{ \begin{aligned} v_{q1} & = L_{p} \left( {k_{2} e_{2} + b_{4} e_{1} + (\dot{I}_{q1} )_{c} - g_{2} } \right) \\ v_{d1} & = L_{p} \left( {k_{3} e_{3} + (\dot{I}_{d1} )_{c} - g_{1} } \right) \\ v_{d3} & = L_{s} \left( {k_{4} e_{4} + (\dot{I}_{d3} )_{c} - g_{3} } \right) \\ v_{q3} & = L_{s} \left( {k_{5} e_{5} + (\dot{I}_{q3} )_{c} - g_{4} } \right) \\ \end{aligned} \right. $$
(20)

where \( k_{2} \), \( k_{3} \), \( k_{4} \) and \( k_{5} \), are positive constants.

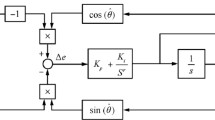
The synthesis of back stepping controller requires the rotor position and rotor speed information. So that the speed and rotor speed transducers should be installed in the shaft. However, these sensors are sensitive to environment conditions and increase the system cost. The algorithm-based sliding mode observer used in this work was developed with details in [2] but not described in this paper. The sliding mode observer was applied to five-phase PMSM to estimate the rotor speed and the rotor position. For more details refer to [2].

4 Simulation Results

A MATLAB/Simulink environment was used to simulate the feedback back stepping control based on SMO.

The corresponding results under the two different profiles: reversing transient and low speed are illustrated by Figs. 1 and 2 respectively. Figure 1 illustrates the drive performance to reversing the speed command. Figure 1a shows the reference, estimated and real speed. One notes that the observed speed converges to the reference one with good estimation. It seems clear from Fig. 1b that the developed observer displays good results in terms of speed estimation. Indeed, the estimation error of rotor speed is almost zero in steady state. Figure 1c displays the observed and the actual position. The five-phase PMSM performances at low speed are reported in Fig. 2. The reference speed is set at 10 rad/s. Figure 2a displays the real, observed and reference rotor speed. We can conclude a good estimation in terms of trajectory tracking. Nevertheless, there is a small estimation error in transient state as shown in Fig. 2b. Figure 2c displays the observed and real rotor position and its estimation error is shown in Fig. 2d. The corresponding results prove the performance of the SMO.

Fig. 1
figure 1

Performances of five-phase PMSM to speed change: a speed; b estimation error of rotor speed c rotor position

Full size image
Fig. 2
figure 2

Performances of five-phase PMSM to speed change: a speed; b estimation error of rotor speed c rotor position, d estimation error of rotor position

Full size image

5 Conclusion

This work presented the sensorless backstepping controller of a five-phase PMSM based on SMO. Developed controller satisfied the stability condition under Lyapunov criterion for both transient and dynamic behaviours. Numerical results verify the developed theoretical background in terms of rotor speed and rotor position estimation under different profiles.