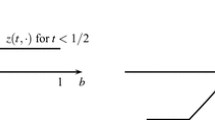On Sufficiently-Diffused Information in Bayesian Games: A Dialectical Formalization

Abstract

There have been substantive recent advances in the existence theory of pure-strategy Nash equilibria (PSNE) of finite-player Bayesian games with diffused and dispersed information. This work has revolved around the identification of a saturation property of the space of information in the formalization of such games. In this paper, we provide a novel perspective on the theory through the extended Lebesgue interval presented in Khan and Zhang (Adv Math 229:1080–1103, 2012) [26] in that (i) it resolves the existing counterexample of Khan–Rath–Sun (J Math Econ 31:341–359, 1999) [17], and yet (ii) allows the manufacture of new examples. Through the formulation of a d-property of an abstract probability space, we exhibit a process under which a game without a PSNE in a specific class of games can be upgraded to one with: a (counter)example on any n-fold extension of the Lebesgue interval resolved by its $(n+1)$-fold counterpart. The resulting dialectic that we identify gives insight into both the saturation property and its recent generalization proposed by He–Sun–Sun (Modeling infinitely many agents, working paper, National University of Singapore, 2013) [14] and referred to as nowhere equivalence. The primary motivation of this self-contained essay is to facilitate the diffusion and use of these ideas in mainstream non-cooperative game theory.                                     (190 words).

JEL Classification Numbers: C62, D50, D82, G13

2010 Mathematics Subject: 28C99, 28E05, 91A13, 91A44

This work draws on results in a paper titled “On Sufficiently Diffused Information and Finite-Player Games with Private Information,” and initially presented at the workshop on The Probabilistic Impulse behind Modern Economic Theory held by the Institute for Mathematical Sciences, National University of Singapore (NUS) during January 11–18, 2011. A substantial version formed the basis of a talk by Khan at The 6th Conference on Mathematical Analysis in Economic Theory held at Keio University, January 26–29, 2015. He thanks Professor Toru Maruyama for his invitation, and him and Professors Bob Anderson, Damien Eldridge, Josh Epstein, Chiaki Hara, Alexander Ioffe, Takashi Kamihigashi, Nobusumi Sagara, Takashi Suzuki and Vladimir Tikhomirov for delightful and stimulating conversation at the Conference. Both authors also thank Hülya Eraslan, John Quah and Metin Uyanik for their comments and encouragement of this project. Section 4 of the Keio version was presented at a study group on Statistical Decision Theory organized by Professors Idione Meneghel and Rabee Tourky when the author held the position of Visiting Research Fellow at the Australian National University, February 15-April 15, 2016. This final version is to be presented at a session organized by Professor Jean-Marc Bonnisseau at the 16th Conference of the Society for the Advancement of Economic Theory to be held at IMPA, July 6–9, 2016. This research program is also supported by NSFC (11201283).

• Article type: Research Article

• Received: July 29, 2015

• Revised: June 21, 2016

How Carathéodory came to think of this definition seems mysterious, since it is not in the least intuitive. It is rather difficult to get an understanding of the meaning of ... measurability except through familiarity with its implications... Carathéodory’s definition has many useful implications. The greatest justification of this apparently complicated concept is, however, its possibly surprising but absolutely complete success as a tool in proving the important and useful extension theorem.

                                           (Halmos (1950) and Hewitt-Stromberg (1965))¹

1 Introduction

In two ground-breaking papers published in 1950–1951, Nash defined for a finite game what, in anachronistic hindsight, is now termed a pure-strategy Nash equilibrium (henceforth PSNE) for a classical setting.² As is well-understood, Nash could not prove the existence of such an equilibrium for his game-theoretic set-up because of the obvious reason that it was not true in general. Two decades were to pass before Schmeidler [44] presented an existence proof for such an equilibrium in a class of games with a continuum of players, each of whose payoffs were restricted to depend on a suitably-defined aggregate of all the other players’ actions, rather than on each individual action as in Nash. In a complete information setting of one-shot simultaneous play, Schmeidler retained the assumption of a finite-action set for each player, and pointed out how his existence theorem, apart from being of interest for its own sake, implies the existence of a mixed-strategy Nash equilibrium , again as defined and shown by Nash in 1950–1951. Indeed, 1973–1974 were significant years for non-cooperative game theory as developed by Nash: Harsanyi in 1973 and Aumann in 1974 presented scenarios in which pure-strategies taken under incomplete information can be seen as rationalizing a given mixed-strategy Nash equilibrium of a classical finite game.³ Harsanyi focused on disturbed (perturbed) games , while Aumann considered games with private information and subjective beliefs . Both papers used as their subtext Harsanyi’s pioneering papers in 1967–1968 on games with incomplete information. We shall not have anything to say on Harsanyi’s work; his formulation and results drew on formalizations of genericity, and thereby applied to almost all games belonging to a well-specified class as opposed to a given game.⁴

The equivalence theorem of Aumann , on the other hand, deserves to be even better known than it is. Given a mixed-strategy Nash equilibrium of a classical finite player game of complete information, Aumann can be read as posing the question of what conditions on a space of information and of subjective beliefs would guarantee that the given equilibrium can be induced by each player playing a pure-strategy, where the notion of a pure-strategy strategy is now lifted up from being a point in an action set to being a function, a random variable, from the space of information to the action set. In other words, Aumann asked for conditions on information and beliefs that allow an equilibrium probability distribution of a classical finite game to be induced by random variables in equilibrium. As is by now well-known and well-understood, Aumann required that a player’s information be independent of, and his beliefs be atomless on, the pooled information of all the other players. Succinctly put, and in the vernacular that was subsequently to follow, it required the space of information be rich enough so as to allow independent atomless supplements. Aumann’s equivalence theorem is relevant to us here because of the significant role that it has played for the formulation of games with private information.⁵

The literature on games with non-atomic measure spaces then bifurcates into two distinct branches. Schmeidler’s paper originates the theory of large one-shot games of complete information in which the existence of pure and mixed strategy equilibria, as well as the relationship between them, as captured by the notion of a purification, is investigated. We may also mention here Mas-Colell’s complementation of Schmeidler’s existence result on non-anonymous (individualized) atomless games by anonymous (distributionalized) ones.⁶ In Mas-Colell’s setting too, pure and mixed strategy equilibria, as well as the relationship between them, as captured by the notion of a symmetrization, is investigated. Radner–Rosenthal [40], henceforth RR, is the originating paper for the other branch. It is rooted in Aumann’s equivalence theorem and is, in its undiluted essence, simply the observation that there are no independent atomless supplements for an arbitrary measure space of information. In three decisive examples, only the first of which is our concern here, they showed that a two-player matching-pennies game, when converted into a game of private information with each player’s information formalized by the Lebesgue interval, and the joint space of information by the lower triangle of the Lebesgue square, has no pure-strategy equilibria in the sense defined by Aumann. As such, there is then no possibility of an equivalence theorem whereby the mixed strategy equilibrium of the given matching-pennies game, one in which each player putting equal probability on each of the two actions, can be induced by a pure-strategy equilibrium of the game with private information. There is no pure-strategy equilibrium in the game underlying the RR example, and so it inducing the given mixed strategy equilibrium of the given matching-pennies game does not arise: it is aborted right at the very beginning.

The RR example proved decisive for Aumann’s equivalence theorem. However, if the assumption of independent and atomless information (dispersed and disparate in the vernacular of RR) was made right at the outset, rather than as an extraction requirement for the given space of information and beliefs, and the game with private information as an object of interest in its own right, the question can be reformulated from the search for an equivalence theorem to that for an existence theorem. Indeed, such an existence theorem is an obvious consequence of Aumann’s result, paired with Nash’s existence proved. If one allows the additional wrinkle that players’ payoffs also depend on their private information, one could show the existence of pure-strategy equilibria for a game of private information. These are the 1982 RR existence results. Their RR paper thus originates the theory of large one-shot games of incomplete information in which the existence of pure and mixed strategy equilibria, as well as the relationship between them, again formalized by the notion of purification, is investigated; also see here the contributions of Milgrom–Weber [34] and their followers; also [42, 46]. But it bears emphasis that the resulting theory, in so far as pure-strategy equilibria are concerned, is constrained to finite action sets, just as it is in the Schmeidler–Mas-Colell set up.

The question then arises as to what happens to both branches of this theory of non-atomic non-cooperative games when the restrictive assumption of finite-action sets no longer holds. It took another decade beyond the Radner–Rosenthal–Milgrom–Weber papers for a picture to emerge; see [40]. The outlines of this are by now well-understood, and the details available in the PNAS announcement and the Handbook chapter published as Khan–Sun [24], Khan–Sun [25] respectively. This need not concern us here other than the following summary statement:

• (i) Though they require some non-trivial technical work, the results all generalize to denumerably-infinite action sets with arbitrary atomless measure spaces.

• (ii) The results do not hold in general for uncountably-infinite action sets with arbitrary atomless measure spaces.

• (iii) The results hold for uncountably-infinite action sets if one restricts attention to atomless Loeb measure spaces, as in Loeb [30].

By 2005, it was well-understand that the entire theory could be generalized beyond atomless Loeb spaces to what were termed saturated or super-atomless measure spaces. The particular name was hardly the issue: the point was that one could work with abstract measures spaces of a type identified in Maharam [33], and conveniently characterized by Hoover–Keisler [11], and that these spaces were not only sufficient for the existence results, as atomless Loeb spaces were, but also necessary in some well-specified sense. The actual publications originating this new direction were Carmona–Podczeck [4] and Keisler–Sun [16].⁷ The point is that the $\sigma$-algebra of a saturated or a super-atomless measure spaces is one which, modulo null sets, is nowhere countably-generated. But what is it really? And what does it mean to say that it is necessary? This essay is devoted to the pursuit of an answer to this question. However, it is important for the reader to understand that in the sequel, we do this only in the context of the use of these measure spaces in finite Bayesian games with private information – the treatment of large games with complete information does not concern us here.

A saturated probability space is in some sense an idealized limit space, but to repeat, what is this sense? Again, even though one grants the validity of the necessity result, as one must, the question nags as the substantive meaning of this claim. What does it mean to say that a saturated space is necessary for the existence question? And why is this result of any substantive (economic or game-theoretic) importance? To be sure, the mathematical definition of a saturated space, and the various equivalences underlying it, are clear enough,⁸ but what is its meaning in terms of the language and vocabulary that mathematical economists and game theorists are used to? and also what is its characterization in terms of the mathematics with which they work, and are at ease, with? This essay then is addressed, at least in the first instance, to these questions. It takes as its point of departure a neglected 1999 (KRS) example on the non-existence of equilibria in Bayesian games based on an interval as a common action set, and the Lebesgue interval (LI) as the space of private information or types.⁹

In [28], the authors introduced the notion of a KRS-like game based on the KRS example, and that of a measure spaces with the d-property with respect to a measurable, measure-preserving function and thereby with respect to a sub-$\sigma$-algebra. These two concepts, though not technically intricate or in themselves mathematically deep, can nevertheless be used to give insight and feel for answers to the questions posed in the paragraph above. Specifically, we use these two concepts as crucial levers to show that:

• (i) an equilibrium does exist in the KRS example if the information spaces are upgraded from the unit Lebesgue interval (LI) to the extended LI presented in [26],

• (ii) there exists an upgraded KRS example of a game without an equilibrium when modeled on the extended LI,

• (iii) the upgrading process reveals an infinite recursion in that a (counter)example can always be constructed if the information spaces are modeled on any n-fold extended¹⁰ LI, n a natural number, but one which can be resolved by a $(n+1)$-fold extended LI, (Proposition 2 below),¹¹

• (iv) this “recursive upgrading ” or “dialectic ” then suggests the formulation of a KRS-like game , one based on an abstract, atomless probability space, for which a characterization and existence of PSNE can be established (Proposition 1 and Theorem 1 below),¹²

• (v) this infinite recursion establishes the importance of KRS-like games as a diagnostic tool to check whether a given information structure guarantees the existence of a PSNE for a general class of all private information games,

• (vi) a visual and analytical content can be imparted into private information structures that are relatively-diffused, as in He–Sun [13], or saturated, as in [27, 28].¹³

We now turn to an extended outline and overview of this essay.

After presenting the basic model and the antecedent results in Sect. 2, we recall in Sect. 3 the principle result in [28] based on the two notions of a notion of a KRS-like games , and the relative d-property with respect to a measure-preserving map. KRS-like games are two-player games with the interval $[-1,1]$ as the (common) action set, arbitrary atomless probability spaces, and with a structure of payoffs that lead their equilibrium distributions, potential or otherwise, to have the same sort of structure as those of the KRS example ; see Proposition 1 below.¹⁴ To be sure, one could consider such games modeled on compact metric action spaces,¹⁵ but as we shall see in the sequel, the underlying motivation for such games is to find the simplest setting that illustrates, and can be used as a criterion for getting a handle on, the difficulties that come up in regard to the existence of a PSNE for all private information games. With Proposition 1 relating to KRS-like games in place, we turn to what we explicitly identify as measure spaces satisfying the d-property with respect to a measurable, measure-preserving function , and thereby with respect to a sub-$\sigma$-algebra. Such a property of a probability space allows a measurable selection to be chosen from the so-called d-correspondence, and one that induces a uniform measure on the range of the correspondence.¹⁶ This property is motivated by a recent consideration in the mathematical literature of correspondences that do not admit measurable selections with pre-specified properties when based on the Lebesgue interval , but do so under an extended Lebesgue interval that goes back to Kakutani in the forties, and one whose $\sigma$-algebra is countably-generated.¹⁷ Sect. 3.4 places on the record sufficiency results for the existence of PSNE in KRS-like games , Theorem 1 and its three corollaries based on the d-property . The prominence that we give to measure spaces having the d-property is, to be sure, new to the literature: it undergirds the principal results of this entire work.

Section 4 is in keeping with the expositional thrust of this essay. It presents a leisurely introduction to the construction of the Lebesgue extension based on a 1944 lemma of Kakutani’s, and originally introduced in [26]. Since this essay is motivated to the non-expert reader, we also provide an exposition of the construction of the Lebesgue interval based on Carathéodory’s theorem . This material of is of course standard.

Section 5 is the dialectical backbone of the paper, and its dynamic turns on two sharp questions, the first of which is the following.

• (a) Does the extended probability space, an extension of the Lebesgue interval, resolve the KRS counterexample ?

Based on the intuitive discussion of the extension in Sects. 4, 5.1 answers this question in the affirmative. There exists a PSNE in the KRS example if the information spaces are modeled on the extension of the Lebesgue interval, rather than on the Lebesgue interval itself. And so this appears to be all that there is to it.¹⁸ Unfortunately, this success is more illusory than real. We show in Sect. 5.2 that the KRS example can be modified and resituated on the extended information spaces to yield another troublesome counterexample without a PSNE . This example is of a finite game with information spaces “richer” than those used in the KRS example, but with the payoffs suitably modified and refined to pertain to these spaces. It is this upgrading of the (counter)example that motivates both a KRS-like game and measure spaces satisfying the d-property . In any case, one can now reformulate/repeat the question under discussion, and ask:

• (b) Does a further extension of the extended probability space resolve this “new” counterexample?

Perhaps somewhat surprisingly, the answer is again affirmative in that the techniques of [26], and recapitulated in Sect. 3, are up to the task. However, a recursion now suggests itself and is indeed executable in the form of a general result. Even though a finite game $\Gamma _n$ based on an n-fold extension of the Lebesgue interval has no Nash equilibrium, we can construct an $(n+1)$-fold extension of the information spaces for which it has an equilibrium! And none of these constructed games $\Gamma _n$ can have Nash equilibria in any of the sub-extensions. The point is that all these constructed games are KRS-like games with their information spaces satisfying the d-property .¹⁹ Indeed, this recursive non-existence property culminates in a general theorem; see Proposition 2 in Sect. 5.3 below. The question then is what works? how can this unfortunate recursion be terminated? And it is at this point that our exposition leads to the punchline that we want to express. The dialectic can only be terminated when one relies on the idealized limit of a saturated space, or a space satisfying the relative diffuseness property. These observations relating to the results of [27], and their extension in [13], constitute the two-paragraphed Sect. 5.4.

The final substantive section of this essay concerns recent work of He–Sun–Sun [12, 14]. In a comprehensive treatment, the authors have posed the question as to “which measure spaces are most suitable for modeling many economic agents?” They propose a class of measure spaces that they refer to as satisfying a condition they term “nowhere equivalent.” Thus their work represents the next stage of the ongoing trajectory that we have tried to sketch in this introduction: one that begins with the Lebesgue interval and includes an atomless Loeb space. However, the authors principal focus is on large games and economies, and they do not consider the relevance of their novel concept to finite Bayesian games of private information, though they are undoubtedly aware of how their basic argumentation would extend to this setting. In Sect. 6, we consider how the Lebesgue extension can also be used to resolve a question raised in [14], the role that the dialectic that we have identified here also plays in this setting.

We conclude the paper in Sect. 7 with two further remarks, and with an Appendix that collects the purely technical arguments of this essay.

2 The Model

A private information game with independent types consists of a finite set of $\ell$ players, each of whom (say i) chooses actions from a compact metric space $A_{i}$ which is not necessarily finite, and has access to (private) information and events, represented by a measurable space $(T_{i},\mathcal {T}_{i}),$ and known only to him, and not necessarily to the other players. This information, or type, is independently drawn among players, moreover, the its distribution forms is a probability measure $\mu _i$ on $(T_{i},\mathcal {T}_{i})$ that is known to all players. We refer to $\{(T_{i},\mathcal {T}_{i}, \mu _i): i =1, \ldots , \ell \}$ as the private information structure of the game. The private information structure is called diffused if for every i, $\mu _i$ is an atomless probability measure. We shall follow convention and denote the product $\Pi _{j=1}^{\ell } A_{j}$ by A,  and $\Pi _{j\ne i} A_{j}$ by $A_{-i}$.

The payoff function of player i is $u_i:A \times T_{i} \rightarrow \mathbb {R},$ and it depends on the actions chosen by all the players and on his own private information $t_{i}\in T_{i}$. We consider the following assumption on the payoff function.²⁰

Assumption 1

For each player i,

• (i) $u_{i} (\cdot , t_{i})$ is a continuous function on A for every $t_i \in T_i$;

• (ii) for each $a \in A$, $u_{i}(a, \cdot )$ is $\mathcal {T}_{i}$-measurable on $T_{i}$;

• (iii) $u_i$ is integrably bounded, that is, there is an integrable function $\phi _i$ on $(T_i, \mathcal{T}_i, \mu _i)$ such that $|u_{i}(a, t_{i})| \le \phi _i (t_i)$ holds for each $a \in A$.

We denote a Bayesian game with independent private information by

$$\Gamma = \{(T_{i},\mathcal {T}_{i}, \mu _i), A_i, u_i \; : i =1, \ldots , \ell \}.$$

A pure strategy of a Bayesian game $\Gamma$ is a $\mathcal {T}_i$-measurable mapping from $T_i$ to $A_{i}$. A pure strategy profile $f = (f_{1}, \ldots , f_{\ell })$ of a Bayesian game $\Gamma$ is a pure-strategy Nash equilibrium (PSNE) for the game $\Gamma$ if for every player i, $f_i$ yields the maximal expected utility when the other players choose $f_{-i}$.

In the reminder of this section, we turn to the state-of-the-art results on the existence of PSNE in Bayesian games of independent private information that will serve as the backdrop for the results presented in this paper. In terms of background, the original existence RR results on games with finite moves, as in [18, 34, 40], were generalized first to games with countably-infinite moves, and then to those with uncountably infinite ones; see [25] for discussion and basic references. The latter generalization invoked an atomless Loeb probability space as the formalization of the space of private information. In [27], the authors show that a saturated private information structure is sufficient for the existence of PSNE in private information games.²¹ More interestingly, they also show that this saturation property is also necessary in the sense that if at least two players’ private information spaces are modeled by non-saturated spaces, there is a private information game without a PSNE! As such, it closes the circle.²²

In subsequent work, the sufficiency result has been generalized in an interesting way to which we turn. He–Sun [13] make a distinction between the aspects of information with respect to which a player chooses a particular strategy as opposed to those which lead his or her payoff functions to change. Following [14], they propose the concept of relative-diffuseness in Bayesian games . Given a private information structure $\{(T_i, \mathcal{T}_i, \mu _i): i = 1, \ldots , \ell \}$ with respect to which the players take strategies, let $\mathcal{F}_i$ be the smallest sub-$\sigma$-algebra of $\mathcal{T}_i$ with respect to which this player’s payoff function is measurable. This private information structure is called relatively diffused if $\mathcal{F}_i$ is setwise coarser than $\mathcal{T}_i$ in the sense that for every $S \in \mathcal{T}_i$ with positive $\mu$-measure, there exists an $\mathcal{T}_i$-measurable subset $S'\subseteq S$ such that $\mu \left( S' \Delta S'' \right) > 0$ for any $S''\in \mathcal{F}_i^S$ where $S' \Delta S'' = (S' \backslash S'') \cup (S'' \backslash S')$. For simplicity, we call $\{(T_i, \mathcal{T}_i, \mu _i), \mathcal{F}_i: i = 1, \ldots , \ell \}$ a relative private information structure. This leads to a natural variation of Assumption 1.

Assumption 1 $^{\prime }$ Conditions (ii) and (iii) in Assumption 1 are changed to

(ii)$^\prime$ :

for each $a \in A$, $u_{i}(a, \cdot )$ is $\mathcal{F}_i$-measurable on $T_{i}$;

(iii)$^\prime$ :

$u_i$ is integrably bounded, that is, there is an $\mathcal{F}_i$-integrable function $\phi _i$ on $(T_i, \mathcal{F}_i, \mu _i)$ such that $|u_{i}(a, t_{i})| \le \phi _i (t_i)$ holds for each $a \in A$.

We now denote a Bayesian game with relatively diffused independent private information by

$$\Gamma = \{((T_{i},\mathcal {T}_{i}, \mu _i),\mathcal {F}_{i}), A_i, u_i \, : i =1, \ldots , \ell \}.$$

As before, a pure strategy for player i is still a $\mathcal{T}_i$-measurable function from $T_i$ to her action space $A_i.$ In a phrase, payoffs functions hinge on $\mathcal{F}_i$ and strategies on $\mathcal{T}_i$.

It is then shown in [13, Theorem 1] that there exists a PSNE in a Bayesian game satisfying Assumption 1 $^{\prime }$ if the information on which the players condition their actions is relatively diffused with respect to the information related to the payoffs. This result is a generalization of the sufficiency result in [27, Theorem 1] based on saturated probability spaces . These require that for any nonnegligible subset $S\in \mathcal{T}$, the re-scaled probability space $\left( S,\mathcal{T}^S,\mu ^S \right)$ is not essentially countably-generated.²³ Since the $\sigma$-algebra generated by any given payoff function satisfying Assumption 1 is always setwise-coarser than the underlying $\sigma$-algebra of the saturated space, the relative diffuseness assumption is automatically fulfilled. It is worth underscoring, however, that there is no necessity result in [13].²⁴

3 KRS-Like Games Revisited

KRS-like games are studied in [28], these games are constructed based on an example of two-player private information games in [17], and now referred to as the KRS example. It is a two-player, private information game satisfying Assumption 1 with a common action set of uncountable cardinality. Each player $i = 1, 2,$ can take actions from $A_i = [-1,1]$. Let $(T_i, \mathcal {T}_i, \mu _i), i=1, 2$ be two atomless probability spaces, and let $h_i :T_i \rightarrow [0,1]$ be a $\mathcal {T}_i$-measurable mapping such that the induced distribution over [0, 1] is the Lebesgue measure $\eta$.²⁵ The payoff functions for both players are given as below:

$$\begin{aligned} u_1^{h_1}(a_1, a_2, t_1)&= u_1(a_1, a_2, h_1(t_1))= -|h_1(t_1)-|a_1|| + [h_1(t_1)-a_1] \cdot z(h_1(t_1), a_2), \end{aligned}$$

(1)

$$\begin{aligned} u_2^{h_2}(a_1, a_2, t_2)&= u_2(a_1, a_2, h_2(t_2))= - |h_2(t_2)-|a_2|| - [h_2(t_2)-a_2] \cdot z(h_2(t_2),a_1); \end{aligned}$$

(2)

where the function $z: [0,1] \times [-1,1] \rightarrow \mathbb {R}$ is defined as follows. For all $t \in [0, 1/2], b \in [-1, 1]$

$$z(t, b) = \left\{ \begin{array}{cl} b, &{} \text {if}\, 0 \le b \le t; \\ t, &{} \text {if}\, t< b \le 1;\\ -z(t, -b), &{}\text {if}\, b< 0; \end{array} \right. $$

and for any $t \in (1/2, 1], \; z(t, \cdot ) = z (1/2, \cdot )$; see Fig. 1 for the graph of $z(t, \cdot )$ for three different values of t.

In particular, $(T_i, \mathcal {T}_i, \mu _i)$ are the usual Lebesgue unit intervals and $h_i$ are the identity maps on [0, 1], this KRS-like game is the original KRS game in [17]. It is also clear that for each player i, and for each $t_i \in T_i$, $u_i (\cdot , \cdot , t_i)$ is a continuous function on $[-1, 1] \times [-1,1]$. For different $t_i \in T_i$, all $u_i (\cdot , \cdot , t_i)$ constitute an equicontinuous family. Thus, for any $a_1, a_2 \in [-1,1]$, $u_i (a_1, a_2, \cdot )$ is $\mathcal{T}_i$-measurable function. As a result, KRS-like games satisfy Assumption 1.

When the private information spaces are given, we denote this game by

$$\begin{aligned} \Gamma _{h_1, h_2} = \left\{ (T_i, \mathcal {T}_i, \mu _i), A_i=[-1,1], u_i^{h_i} : i =1,2 \right\} . \end{aligned}$$

In this games, for each i, a pure strategy of player i is a $\mathcal{T}_i$-measurable function from $T_i$ to $[-1,1]$. If $(g_1,g_2)$ be pure-strategy profile, and $\nu _i = \eta g_i^{-1}$ is the induced distribution on the action set $[-1,1]$.

We are now ready to introduce the equilibria in KRS-like games . First for any $t \in [0,1]$, any Borel probability measure $\nu$ on $[-1,1]$, let $w(t, \nu )$ be the integral of $z(t, \cdot )$ with respect to $\nu$, i.e.,

$$\begin{aligned} w(t,\nu ) = \int _{-1}^1 z(t, \cdot ) \mathrm {d}\nu . \end{aligned}$$

(3)

The best-response correspondence in the KRS-like game $\Gamma _{h_1, h_2}$ is as follows:

$$\begin{aligned} B_1(t_1; \nu _2) = \left\{ \begin{array}{cl} -h_1(t_1) \text{ or } h_1(t_1), &{} \text{ if } w(h_1(t_1),\nu _2) = 0; \\ h_1(t_1), &{} \text{ if } w(h_1(t_1),\nu _2) > 0; \\ -h_1(t_1), &{} \text{ if } w(h_1(t_1),\nu _2) < 0. \end{array} \right. \end{aligned}$$

$$\begin{aligned} B_2(t_2; \nu _1)= \left\{ \begin{array}{cl} -h_2(t_2) \text{ or } h_2(t_2), &{} \text{ if } w(h_2(t_2),\nu _1) = 0; \\ -h_2(t_2), &{} \text{ if } w(h_2(t_2),\nu _1) > 0; \\ h_2(t_2), &{} \text{ if } w(h_2(t_2),\nu _1) < 0. \end{array} \right. \end{aligned}$$

Fig. 1

Graph of $z(t, \cdot )$ for different t

Moreover, suppose that there exists a PSNE $(g_1^*, g_2^*)$ in the game $\Gamma _{h_1, h_2},$ where $g_i^*$ is a $\mathcal {T}_i$-measurable function from $(T_i, \mathcal {T}_i, \mu _i)$ to $[-1,1]$. Let $\nu _i^*$ be the induced distribution of $g_i^*$, i.e., $\nu _i^* = \mu _i \circ (g_i^*)^{-1}$. The equilibrium action distribution of each player’s strategy also satisfies the following statement.

Proposition 1

(Khan-Zhang [28]) Suppose that $\nu _1^*, \nu _2^*$ are the induced action distributions of a PSNE of the game $\Gamma _{h_1, h_2}$, then for $i = 1, 2$, $w(h_i(t_i), \nu ^*_i) = 0$ for $\mu _i$-almost all $t_i \in T_i$, and $\nu ^*_i ([0,s]) = \nu ^*_i ([-s,0]) = s/2$ for any $s \in [0,1/2]$.

Khan and Zhang also find that PSNE in KRS-like games is intimately related to the following d-property concept of probability spaces.

Definition 1

(i) Given an atomless probability space $(T, \mathcal{F}, \mu )$ and a $\mathcal{F}$-measurable measure-preserving map h from T to the Lebesgue interval $([0,1], \mathcal{L}, \eta )$,²⁶ $(T, \mathcal{F}, \mu )$ is said to have the relative d-property with respect to h if there is a $\mathcal{F}$-measurable map g from T to $[-1,1]$ such that $g(t) \in \{h(t), -h(t)\}$ and g induces the uniform distribution on $[-1,1]$. (ii) Given an atomless probability space $(T, \mathcal{G}, \mu )$ where $\mathcal{G}$ is a sub-$\sigma$-algebra of $\mathcal{F},\; (T, \mathcal{F}, \mu )$ is said to have the relative d-property with respect to $\mathcal{G}$ if for all $\mathcal{G}$-measurable measure-preserving map h from T to the Lebesgue interval $([0,1], \mathcal{L}, \eta )$, $(T, \mathcal{F}, \mu )$ has the relative d-property with respect to h.

It is clear that the usual Lebesgue unit interval $([0,1], \mathcal{L}, \eta )$ does not have relative d-property with respect to the identity map on the interval, which is obviously a measure-preserving map. The following is straightforward from Proposition 1.

Corollary 1

For $i = 1,2$, if an atomless probability space $(T_i, \mathcal{T}_i, \mu _i)$ has relative d-property with respect to a measure preserving map $h_i$ from $T_i$ to the Lebesgue interval, then there exists a pure-strategy Nash equilibrium in the KRS-like game $\Gamma _{h_1, h_2}$.

Here is a sufficient condition for the relative d-property.

Lemma 1

Given $(T, \mathcal{G}, \mu )$, $\mathcal{G}$ as in Definition 1. If there is a $\mathcal{F}$-measurable subset with $\mu$-measure (1/2), and it is independent with $\mathcal{G}$, then $(T, \mathcal{F}, \mu )$ has the relative d-property with respect to $\mathcal{G}$.

Moreover, the relative d-property of a probability space also furnishes a necessity condition for modeling the private information spaces such that KRS-likes games all have PSNE .

Theorem 1

(Khan-Zhang [28]) Given a diffused private information structure $\{(T_i, \mathcal{T}_i, \mu _i): i = 1 , 2\}$, if for some i, $(T_i, \mathcal{T}_i, \mu _i)$ does not have relative d-property with respect to a measure preserving map $h_i$ from $T_i$ to the Lebesgue unit interval, then there exists a KRS-like game possessing no pure-strategy equilibrium .

4 A Lebesgue Extension à la Kakutani

In this section , we attempt to lay out for the general reader the basic intuitions underlying the construction of the Lebesgue extension rather than simply using it as a black-box that furnishes a pure-strategy equilibrium in a class of games that do not possess such an equilibrium. To put the point another way, the principles underlying the extension go beyond the technical to the substantive considerations.

To be sure, the extension of the Lebesgue measure has by necessity to build on the construction of the Lebesgue measure itself, and we begin this section by recalling the basic (standard) principles underlying this construction.²⁷ Towards this end, we begin by recalling the notion of an outer measure $\theta$ on the power set $\mathcal{P}(X)$ of a space X. This is simply a non-negative function that gives zero value to the empty set, is monotonic and countably subadditive. This is to say

$$ \theta (\emptyset ) = 0,\; A \subseteq B \Longrightarrow \theta (A) \le \theta (B) \text{ and } \theta (\cup _{n\in \mathbb {N} } E_n) \le \sum _{n\in \mathbb {N} } \theta (E_n). $$

If the outer measure of X is unity, then it is a pre-probability, and what one needs to get a bona fide probability is to strengthen countable subadditivity to countably additivity. The point is that on restricting an outer measure to a specific class of subsets of X,  this can be done and it turns into a measure. It is important to understand this restricted class of sets, and we turn to it.

It is clear that any set A can be disjointly decomposed through another set B by viewing it as the intersection of it with E and the set of its points that do not belong to E. In symbols,

$$ A = (A \cap E) \cup (A \slash E) \text{ where } A, E \in \mathcal{P}(X).$$

We can refer to E as a decomposing set , and the sets $A \cap B$ and $A \slash E$ as its decompositions with respect to it. This much is entirely trivial.²⁸ Now focus on a set E that decomposes any subset of $\mathcal{P}(X)$ in a way that the outer measure of the set and the sum of the outer measures of the its decompositions with respect to E are identical. This is to ask for a focus on

$$ \sum = \{E \in \mathcal{P}(X): \theta (A) = \theta (A \cap E) + \theta (\cup (A \slash E)) \text{ for } \text{ all } A \in \mathcal{P}(X).$$

Now what is not trivial is that $\sum$ is a $\sigma$-algebra, which is to say in the language of probability theory, a bona fide event space: closed under complementation and countable unions. And more to the point, the outer measure $\theta$ restricted to this class is a measure which is to say countably additive for a disjoint sequence of events. Again, in the restricted language of probability theory, a pre-probability has been rendered by restriction to a probability, a result that goes by the name of Carathéodory .²⁹

So far, in the consideration of an abstract set X,  we have had nothing to say as regards a Lebesgue measure. Indeed, we have simply specified a methodology by which a given outer measure on a power set can be turned into a measure on a specific distinguished $\sigma$-algebra chosen from that power set. We now specialize X to $\mathbb {R} ,$ and rather than assume an outer measure, construct it. For any two real numbers a and b,  consider as a building block the half-open interval $\{x \in \mathbb {R} : a \le x < b\},$ and associate with it the number $b-a$ when $b \ge a,$ and zero otherwise. Refer to this association as a function $\ell$ on half-open intervals on $\mathbb {R} .$ This has the intuitive property³⁰ that the number associated with any half-open interval I, $\ell (I),$ is not greater than the sum of the numbers associated with any countable cover of half-open intervals $I_j, \; j \in \mathbb {N} ,$ which is to say, $\sum _{j \in \mathbb {N} }\ell (I_j).$ Two points need to be noticed: the statement pertains only to half-open intervals and to any countable cover of them, much less the most parsimonious one. As a consequence, $\lambda$ is not yet an outer measure on $\mathcal{P}( \mathbb {R} ).$

It is now a straightforward matter to use the function $\lambda$ defined on the basic building blocks to construct a function $\theta$ defined on $\mathcal{P}( \mathbb {R} )$ by limiting ourselves to the most parsimonious cover of an arbitrary subset A in $\mathbb {R} .$ The symbolism is transparent:

$$ \theta (A) = \inf _{\{I_j\}_{j\in \mathbb {N} }}\left\{ \sum _{j \in \mathbb {N} }\ell (I_j): A \subseteq \bigcup _{j \in \mathbb {N} } I_j\right\} ,$$

though it bears emphasis that the infimum is taken over all countable covers of A. The fact that $\theta$ gives the zero value to the empty set, and that it is monotonic is a triviality; in order to show that it is countably subadditive is a routine computation drawing what it means to have an infimum.³¹ But now we can appeal to Carathéodory’s procedure to obtain a distinguished $\sigma$-algebra in $\mathcal{P}(X),$ the (Lebesgue $\sigma$-algebra) and a measure (the Lebesgue measure) on it. This measure space furnishes the Lebesgue unit interval when it is restricted to the unit interval; and it is the extension of this space $(L=[0,1], \mathcal{L}, \eta )$ that is at issue.

Thus, consider the Lebesgue unit interval, $L=([0,1], \mathcal{L}, \eta )$ as the primitive object to which we seek an extension. Even a cursory perusal of the argumentation underlying the construction of the extended Lebesgue interval shows its dependence on a 1944 Lemma of Kakutani, [15]. To facilitate the intuition behind the procedures of this extension, think in terms of an allegory of a “treasure hunt” in which one is to find bills of denomination ranging from zero to one, $K=[0,1],$ buried in locations proxied by numbers between zero to one, $L=[0,1].$ The set of locations is already furnished with a Lebesgue measure-theoretic structure: this is to say that we have assumed an ability to measure the length of any interval between two locations $(\ell , \ell ^\prime ).$ Let us now also explicitly assume a Lebesgue measure-theoretic structure $([0,1], \mathcal{K}, \kappa )$ on the set of denominations K, and seek to estimate a measure of the size of the ‘treasure”– the total of the amount given by the bills of denomination between $(k, k')$ and buried in the strip of land between $(l, l').$ To repeat, we aim here for an exposition that gives the basic intuition behind the construction, and refer any reader interested in the details of the rigorous argumentation to [26].

Kakutani’s Lemma: There exists a partition of uncountable cardinality of $L= [0,1]$, denoted by $\{C_k :k \in K = [0,1] \}$, such that the Lebesgue outer-measure ³² of $C_k$ is one for all $k \in K = [0,1]$.

Now Kakutani’s lemma furnishes the rudiments from which a “treasure map” C in the space of all the locations and the denominations can be constructed. The lemma furnishes a partition of the unit interval indexed by each denomination. Heuristically, every location is assigned a unique amount of wealth, and the location of bills with a given denomination level k is rather dispersed among the set of all locations. Symbolically, we are furnished with $\{C_k \subseteq [0, 1] :k \in K \}$ such that $\displaystyle \cup _{k \in [0,1]} C_k = [0, 1]$ and $C_i \ne C_j,\; i \ne j.$ However, the point is that the length of these $C_k$ cannot be determined: none of them are in general Lebesgue measurable, but only Lebesgue outer-measurable, each with unit outer-measure. This is to say that the “smallest” Lebesgue measurable set containing a given $C_k$ has a unit Lebesgue measure. We can now take this partition and “unfold” it as the “treasure-map” C where

$$\displaystyle C = \cup _{k \in [0,1]} C_k \times \{k\} \subseteq L \times K.$$

The point is that this set C is also only outer-measurable with unit (square) Lebesgue measure $\eta \otimes \kappa .$ The “treasure map” is not accurate enough!

To overcome this deficiency, consider the $\sigma$-algebra generated by C and the sets in $\mathcal{L}\otimes \mathcal{K},$ and extend the square Lebesgue measure $\eta \otimes \kappa$ to this extended $\sigma$-algebra $\mathcal{T}$. Denote this extended measure by $\gamma ,$ and note that we have a measure-theoretic structure, $(C, \mathcal{T}, \gamma )$, on C such that the $\sigma$-algebra $\mathcal{T}$ is the restriction of the Lebesgue product $\sigma$-algebra $\mathcal{L}\otimes \mathcal{K}$ on C. This takes us to the second foothold of the extension procedure. It is simply that the size of any set of the form $((l, l') \times (k, k')) \cap C$ with respect to $\gamma$ inherits the size of the rectangle $(l, l') \times (k, k')$ in the square. This is to say that for all $0 \le l < l' \le 1$ and $0 \le k < k' \le 1$,

$$\begin{aligned} \gamma \left[ ((l, l') \times (k, k')) \cap C\right] = (l'-l)(k'-k). \end{aligned}$$

Finally, we project the unit square to the unit interval. This is to say that we consider the projection p from C to L,  and observe it to be a one-to-one measurable mapping. Hence it induces a probability structure on [0, 1] by projecting the probability structure on C.

Denote the new probability structure on [0, 1] by $( [0,1], \mathcal{I}, \lambda )$, and this is the extension of the Lebesgue unit interval that we seek. It is now worthwhile to summarize the procedure. Each type has a double identity: an explicit identity or trait (say, e.g., the location) indexed by elements of L and another implicit identity or trait (say, e.g., the wealth level) indexed by elements of K,  and the two traits co-exist in single-dimensional set I. The point of consequence is that these two traits are governed by two independent $\sigma$-algebras , and the extended Lebesgue measure is atomless on both. Next, we turn to this. For all $0 \le k < k' \le 1$, let $D_{kk'} = \cup _{k< k'' < k'} C_{k''}$, which is the set of all implicit traits lying between k and $k'$. Notice that $p^{-1} (D_{kk'} ) = \left( [0,1] \times [k,k')\right) \cap C$, and by virtue of the way that the extended $\sigma$-algebra $\mathcal{I}$ was obtained on I,  $D_{kk'} \in \mathcal{I}.$ Furthermore, by virtue of the way that the extended Lebesgue measure was obtained on $\mathcal{I},$ we have

$$\begin{aligned} \lambda (D_{kk'}) = \gamma \left[ p^{-1} (D_{kk'} )\right] = \gamma \left[ \left( [0,1] \times (k,k')\right) \cap C\right] = k' -k. \end{aligned}$$

That is, the probability of a type whose implicit trait lies between k and $k'$ is exactly $k' - k$. That is, the wealth level, viewed as a random variable on the extended Lebesgue interval, is a measurable measure-preserving map to the Lebesgue interval.

Next, we claim that the two random variables, the wealth level and the location, are independent. Fix $0 \le k < k' \le 1$ and $0 \le l < l' \le 1$, consider the probability of types where the wealth lies between k and $k'$ and the location lies between l and $l'$. Independence of the two random variables simply means that the probability of the types that lie in the intersection of the two sets is the product of the probability that the type lies in each of the sets. But this clear on account of the fact that $p^{-1} \left( D_{kk'} \cap (l,l') \right) = \left( (l, l') \times (k, k') \right) \cap C,$ and thus

$$\begin{aligned} \lambda \left( D_{kk'} \cap (l,l') \right) = \gamma \left[ p^{-1} \left( D_{kk'} \cap (l,l') \right) \right] = \gamma \left[ \left( (l, l') \times (k, k') \right) \cap C\right] = (l'-l)(k' -k). \end{aligned}$$

(4)

We thus completes the proof of the independence between the wealth level and the location.

In summary, the extension proceeds in the following steps: (i) the Kakutani partition of the Lebesgue unit interval, (ii) the lifting of this partition to a set C in the Lebesgue square, (iii) the extension of the square Lebesgue measure-theoretic structure to include C, (iv) restriction of this structure to C, and finally, (v) a projection of this restricted structure to the given Lebesgue interval.³³ The point is that one can now estimate the size of many more sets by $\lambda$ than we could before.

Once this extension is understood, only a little more is involved in understanding that a sequence of Lebesgue extensions $\left\{ ([0,1], \mathcal {I}_n, \lambda _n): n = 0, 1, \ldots \right\}$ can be constructed in which the first countably-generated Lebesgue extension $\left( [0,1], \mathcal{I}, \lambda \right)$ is denoted by $\left( [ 0,1], \mathcal {I}_0, \lambda _0 \right)$, and for any $n \in \mathbb {N}$, $([0,1], \mathcal {I}_{n}, \lambda _{n})$ is an extension of $([0,1], \mathcal {I}_{n-1}, \lambda _{n-1})$, where the former is obtained from the latter in precisely the way that $([0,1], \mathcal{I}, \lambda )$ is obtained from the Lebesgue interval.³⁴ We can now record the following properties of these extensions.

Lemma 2

(i) For each $n\in \mathbb {N} ,$ $\mathcal{I}_{n-1}$ is setwise coarser than $\mathcal{I}_n$. (ii) For every $n \in \mathbb {N}$, there exists an $\mathcal{I}_n$-measurable measure-preserving map $h_n$ such that for any $E \in \mathcal{I}_n$, there exists a Lebesgue measurable subset $S \subseteq [0,1]$ such that $\lambda _n [E \Delta h_n^{-1} (S)] =~0$ where $\Delta$ is the symmetric difference operator in $\mathcal{I}_n$. (iii) The n-fold Lebesgue extension does not have d-property with respect to $h_n$, for all $n \in \mathbb {N}$. In particular, when restricted to $h_n^{-1}([0,1/2])$, there is no selection of the corresponding d-correspondence of $h_n$ such that the induced distribution is uniform on $[-1/2, 1/2]$.

Remark 1

The m-th fold Lebesgue extension has d-property with respect to $\mathcal{I}_n$. We also note that Lemma 2(iii) allow us to assert that no matter how large a natural number n is, the n-fold Lebesgue extension extension is not a saturated space . The point in part (ii) is that $\left( [0,1], \mathcal{I}_n, \lambda _n \right)$ does not have the relative d-property with respect to the measure-preserving map $h_n$.

5 KRS-Like Games Based on Lebesgue Extensions

In this section, we turn to the KRS example itself, and ask whether one can obtain a PSNE in the game $\Gamma _0$ by jettisoning the usual Lebesgue unit interval, and turning not to a saturated or super-atomless probability space,³⁵ but to an atomless probability structure whose measure-theoretic is rich enough only to the point that is required to show the existence of a PSNE in the specific game $\Gamma _0$. This is to ask for a measure-theoretic structure that is oriented towards resolving and subduing the canonical counterexamples. We develop the answer to this question in Sect. 5.1 by using the countably-generated extension of the usual Lebesgue unit interval offered by the authors in [26]. However, in Sect. 5.2, we show that this “more sophisticated and enriched” atomless probability space generates its own example of finite-player games without a PSNE . As already stated informally in the introduction, this counter-example on the extended information space can in its turn be resolved by a further enrichment of the (extended) $\sigma$-algebra. In Sect. 5.3, we conclude with a general result formalizing this dialectic. However, prior to all this, we review for the reader the highlights of the construction of the extended Lebesgue interval.³⁶

5.1 The KRS Example Resolved

We now turn to the non-existence of a PSNE in the game $\Gamma ,$ and ask whether the use of extended Lebesgue interval as the space of private information resolves the problem. The affirmative answer to this question can now be routinely outlined. Consider the game,

$$\begin{aligned} \tilde{\Gamma }_0 = \{(T_i, \mathcal {T}_i, \mu _i) = ([0,1], \mathcal {I}, \lambda ), A_i = [-1,1], u_i: i = 1,2 \}, \end{aligned}$$

and note that $\tilde{\Gamma }_0$ is identical to $\Gamma _0$ except for the fact that each player’s private information space is replaced by the (countably-generated) Lebesgue extension . We have subdued the counterexample and resolved its negativity by this “tilde” operation involving a move from $\Gamma _0$ to $\tilde{\Gamma }_0.$ This move is important for the argument that is being developed here. We can now present

Claim 1

There exists a PSNE in the game $\tilde{\Gamma }_0$.

This result is an easy consequence of Proposition 1 and Lemma 2(i).

However, a natural question arises as to whether a general theorem can be developed for Bayesian games with compact metric actions sets based on information spaces modeled by the extended Lebesgue intervals. as we shall see in the next subsection, the answer is unfortunately resoundingly negative.

5.2 Yet Another Counterexample

In order to develop the counterexample, we return to Lemma 2(ii), and work with the measurable the measure-preserving map $h_0$ from $([0,1], \mathcal{I}, \lambda )$ to the usual Lebesgue interval guaranteed therein. Use this map $h_0$ to formulate the following KRS-like game, $\Gamma _{h_0, h_0}$.

$$\begin{aligned} \Gamma _{h_0, h_0} = \{(T_i, \mathcal {T}_i, \mu _i) = ([0,1], \mathcal {I}, \lambda ), A_i = [-1,1], u^{h_0}_i: i = 1,2. \} \end{aligned}$$

We can now appeal to Lemma 2(iii) to assert that

Claim 2

There does not exist a PSNE in the game $\Gamma _{h_0, h_0}$.

But now one is on a roll. One can ask whether the non-existence of a PSNE in the KRS-like game $\Gamma _{h_0, h_0}$ can be is resolved in precisely the same way that the non-existence issue for the KRS game $\Gamma _0$ was resolved. This is to check whether a further extension of the extended Lebesgue interval would subdue the new example. This can be done by a consideration of the following game,

$$\tilde{\Gamma }_{h_0, h_0} = \{(T_i, \mathcal {T}_i, \mu _i) = ([0,1], \mathcal {I}_1, \lambda _1), A_i = [-1,1], u^{h_0}_i: i = 1,2 \},$$

in which each player’s private information space is “upgraded” from $([0,1], \mathcal{I}, \lambda )$ to $([0,1], \mathcal{I}_1, \lambda _1)$. To use the earlier vernacular, the resolution hinges on a further “tilde” operation involving a move from $\Gamma _{h_0, h_0}$ to $\tilde{\Gamma }_{h_0, h_0}.$ We can now again record the following easy consequence of Proposition 1 and Lemma 2(i).

Claim 1 $^\prime$ There does exist a PSNE in $\tilde{\Gamma }_{h_0, h_0}$.

5.3 A General Negative Result

The interesting question is whether there is a general recursion theorem here. We develop such a result in this subsection. The point is that the argumentation in Sect. 5.2 can be continued inductively ad infinitum. First, a sequence of countably-generated probability spaces $\{([0,1], \mathcal {I}_n, \lambda _n): n = 0, 1, \ldots \}$ can be constructed, where the first countably-generated Lebesgue extension $([0,1], \mathcal{I}, \lambda )$ is denoted by $([0,1], \mathcal {I}_0, \lambda _0)$, and for any $n \in \mathbb {N}$, $([0,1], \mathcal {I}_{n}, \lambda _{n})$ is a countably-generated extension of $([0,1], \mathcal {I}_{n-1}, \lambda _{n-1})$. Second, if each player’s private information space is modeled by $([0,1], \mathcal {I}_{n-1}, \lambda _{n-1})$, there exists a KRS-like game $\Gamma _{h_{n-1}, h_{n-1}}$ without any PSNE . Such that there does not exist a PSNE . Third, as far as this KRS-like game is concerned, the “tilde” operation whereby each player’s private information space is modeled by the countably-generated space $([0,1], \mathcal {I}_n, \lambda _n)$, again guarantees a PSNE. This argumentation can be succinctly illustrated and summarized by Fig. 2, where $C\left( [-1,1]\times [-1,1]\right)$ means the space of all continuous functions on $[-1,1] \times [-1,1]$.

Fig. 2

Lebesgue extensions and KRS-like games

In terms of a formal statement, we can offer:

Proposition 2

For each $n \in \mathbb {N}$, there does not exist a PSNE in the KRS-like game $\Gamma _{h_{n}, h_{n}}$ but there does exist one in the game $\tilde{\Gamma }_{h_{n}, h_{n}}$, where the private information space for each player in $\tilde{\Gamma }_{h_{n}, h_{n}}$ is upgraded from the n-fold extension to the $(n+1)$-fold extension.

Proposition 2 embraces both a positive and a negative result, and in conclusion, it is worthy of note that Claims 1 and 2 above follow as its special cases.

5.4 A Discussion of the Results

The positive result in Proposition 2 can be viewed as an illustration of Theorem 1 of [13] since the relative diffuseness assumption in such KRS-like games are satisfied. However, as far as the KRS example and the KRS-like games $\Gamma _{h_n, h_n}$ are concerned, it follows from Lemma 1 that a rather simpler and more modest extension of the underlying private information space suffices: all one has to do is to include a subset with measure one-half and one that is independent of the underlying $\sigma$-algebra. It serves as the “right” model of the private information space.

The negative result in Proposition 2, the non-existence of PSNE in the KRS-like games $\Gamma _{h_n, h_n}$, can be viewed as a special case of the necessity result, Theorem 2, in [27]. There it states that if two players’ private information spaces are both modeled by non-saturated probability spaces, then there exists a counterexample of a private information game without any PSNE. In the KRS-like game $\Gamma _{h_n, h_n}$, the underlying private information spaces are both n-fold Lebesgue extensions , and thereby essentially countably generated spaces, and automatically not saturated spaces.³⁷ However, the non-existence argument here is different from the one in the proof of Theorem 2 in [27]: here it is a rather straightforward consequence of Proposition 1 and Lemma 2(iii). It is in this regard that the approach used in this paper is self-consistent, as far as the construction of the counterexamples $\Gamma _{h_n, h_n}$ are concerned.

6 A Condition of He–Sun–Sun

In work circulated in 2013, He et al. have proposed a far-reaching generalization of the saturation property in the form of condition they of nowhere equivalence of two $\sigma$-algebras of a probability space. They have relied on this condition to present a comprehensive theory of economies and games with a continuum of agents, and of the three basic mathematical operations that undergird it: integration, distribution and conditional expectation. This work is important enough this expository paper would not be complete in its scope without making some reference to this work. In this section we relate the Lebesgue extension and the ideas presented above to this important work.

He–Sun–Sun [14] motivate their condition, and their results based on it, by a series of examples of games and economies which show pathological features as far as the existence, closed graph and “determinateness” properties of the equilibria are concerned. Here we consider Example 3 of [14], henceforth the HSS example. In this example, there are two large games, both have Lebesgue interval as agent space, the common action space is $[-1,1]$. Moreover, in both games, each player’s payoff only depends on her own action, not anybody else’s. Namely, for all agent $i \in [0,1]$, $a \in [-1,1]$, and any action distribution $\nu$ on $[-1,1]$,

$$G_1(i, a, \nu ) = -(a+i )^2(a-i )^2, \text{ and } G_2(i, a, \nu ) = \left\{ \begin{array}{ll} G_1 (2i, a, \nu ), &{} \hbox { if } i \in [0, 1/2), \\ G_1 (2i-1, a, \nu ), &{} \hbox { if } i \in [1/2, 1]. \end{array} \right. $$

Note that in $G_1$, player i’s best strategy, no matter what the strategy of all others, is always either i or $-i$, while in $G_2$, the best strategy for Mr i is either 2i or $-2i$, for i less than one half, and either $2i-1$ or $1-2i$ for i great than one half. As a result, in $G_1$, a PSNE will be a Lebesgue measurable map from [0, 1] to $[-1,1]$ such that the value at i is either i or $-i$, or a Lebesgue-measurable selection of the correspondence $\Phi : [0,1] \twoheadrightarrow [-1,1]$ with $\Phi (i) = \{i, -i\}$. Similarly, a PSNE in $G_2$ is a Lebesgue-measurable selection of the correspondence $\Psi : [0,1] \twoheadrightarrow [-1,1]$ with

$$\Psi (i) =\left\{ \begin{array}{ll} \{2i, -2i\}, &{} \hbox { if } i \in [0, 1/2), \\ \{2i-1, 1-2i\}, &{} \hbox { if } i \in [1/2, 1]. \end{array} \right. $$

These two games $G_1$ and $G_2$ induce the same distribution on the space of payoff functions, namely space of all continuous functions on the product space of $[-1, 1]$ and all Borel probability measure on $[-1,1]$. However, the set of action distribution of all PSNE in $G_1$, denoted by $\mathcal{D}(G_1)$ is not the same as that in $G_2$, denoted by $\mathcal{D}(G_2)$; see Claim 3 in [14]. Namely, $\mathcal{D}(G_1)$ is the set of induced distribution by all Lebesgue-measurable selection of the correspondence $\Phi$, and $\mathcal{D}(G_2)$ the set of induced distribution by all Lebesgue-measurable selection of the correspondence $\Psi$. More precisely, the uniform distribution on $[-1, 1]$ is an element of $\mathcal{D}(G_2)$ but not of $\mathcal{D}(G_1)$; see Fig. 3 below.

Fig. 3

One selection of $\Phi$ and one of $\Psi$

However, if the agent spaces in these two games are both modeled by the Lebesgue extension as in Sect. 4, and if $\mathcal{D'}(G_1)$ is the set of induced distribution of all $\mathcal{L}^e$-measurable selections of $\Phi$ and $\mathcal{D'}(G_2)$ the set of induced distributions by all $\mathcal{L}^e$-measurable selections of $\Psi$, we obtain the following result.

Proposition 3

If in this example, both agent spaces are modeled by the Lebesgue extension , then $\mathcal{D'}(G_2) = \mathcal{D'}(G_1)$.

The proof is postponed to the appendix.

To summarize, the problem raised in Example 3 of [14] automatically disappears when modeling agent space by the Lebesgue extension . This result is not surprising because the extended sigma algebra in the Lebesgue extension satisfies the conditions in Theorem 3 of [14]. The following is a concept proposed in [14].

Definition 2

Given an atomless probability space, $(T, \mathcal{F}, \mu )$, and a sub-$\sigma$-algebra $\mathcal{G}$ of $\mathcal{F}$. $\mathcal{F}$ is said to be nowhere equivalent to $\mathcal{G}$ if for every $D \in \mathcal{F}$ with $\mu (D) > 0,$ there exists a $\mathcal{F}$-measurable subset $D_0$ of D such that $\mu (D_0\triangle D_1) > 0$ for any $D_1 \in \mathcal{G}^D.$

In the current context, we only need to claim that the extended Lebesgue $\sigma$-algebra in Sect. 5 is nowhere equivalent to the original Lebesgue $\sigma$-algebra. The proof of this claim is provided in the Appendix.

We conclude this subsection with two observations. First, we note that the HSS example, and the HSS theorems based on it, concern large games with a continuum of players; and that the reader can generalize the necessary and sufficient results presented in [27, 28] to a finite-player Bayesian games , focused on in the essay, where the analog of the HSS condition is expressed for the spaces of private information. Second, we leave it to the reader to think out for herself a dialectical argumentation underlying the HSS example of the kind that we have considered in his essay for the KRS example.

7 Concluding Remarks

In [27], the authors show that if each player’s private information space is modeled by a saturated probability space , then every private information game has a PSNE. As to whether such a saturated private information structure is a “minimal” one for the existence of PSNE in such games, a complete answer is provided in [28] that if every KRS-like game has a PSNE, the underlying information space for each player must be saturated. With these two results in hand, under a given private information structure, the hypothesis that all KRS-like games have PSNE implies that all private information games also have PSNE! In other words, KRS-like games are precisely the “trouble-makers” we need to consider and rule-out to establish a general theory on the existence of PSNE for a given private information structure. It is in this sense that we say that KRS-like games serve as a diagnostic tool for the existence of PSNE in private information games.

The dialectic arguments using Lebesgue extensions provide some further elaboration and elucidation on the above “minimal” requirement on the private information structure to guarantee the existence of PSNE. Note that in a saturated probability space , it has a “rich” sigma algebra such that when restricted to any non-negligible subset, the sub-sigma algebra under the restricted measure cannot be essentially countably generated, i.e., there is no hope to find a countable number of sets in the restricted sub-algebra to generate the restricted sub-algebra itself. However, in the n-fold extensions of the Lebesgue interval considered in this essay, the underlying sigma-algebra, no matter how large n is, is essentially countably generated; and, as a result, each n-fold Lebesgue extension cannot be saturated. This is why there is such a KRS-like game without a PSNE as claimed in Proposition 2, a result also implied by the necessity result in [28].

It is worth pointing out another distinction between the Lebesgue extensions considered in this paper and a saturated space. As is made clear in the construction of the Lebesgue extension in Sect. 5, the 1-fold Lebesgue extension, the original Lebesgue $\sigma$-algebra is enlarged in a way such that it can accommodate at most two independent random variables, each of which is a measurable measure-preserving from the Lebesgue extension to the Lebesgue interval. Similarly, in the n-fold Lebesgue extension, the underlying $\sigma$-algebra can at most accommodate n independent random variables, each of which is a measurable measure-preserving from the n-fold Lebesgue extension to the Lebesgue interval. In comparison, in a saturated probability space , the underlying $\sigma$-algebra can accommodate at least a countable number of such pairwise-independent random variables.

We conclude this discussion by an observation that looks at the dialectic of these results from another, and more critical, point of view. The necessity result ensures that for this extended probability space, there will always exist a large game without pure-strategy Nash equilibria , but this game may not have any substantive interest. It may be an artifice, a purely technical construction testifying to a mathematical necessity, but with no counterpart in terms of concrete “real-life” applications. Thus, one could legitimately hold the view that as far as the substantive applications are concerned, there is little need for a result that proceeds beyond the modest extension articulated in [26] all the way to a saturated space, or to the spaces satisfying the HSS condition. This is a point of view explicitly articulated in [26] in the context of large non-anonymous games, and further discussion and exploration of whether this is, or is not, only cold comfort for finite games with private information, must be left for future work that turns to concrete applications. For these, see [34, 43] and the references therein, especially to the work of Athey and McAdams. Recall also that the introduction of [34] opens with William Vickrey’s auction paper of 1961. The reader should keep this cautionary skepticism in mind now that she has worked through the dialectical argumentation.

8 Technicalities of the Proofs

prove Part (i). Note that for any natural number n, the n-fold Lebesgue extension is constructed from the $(n-1)$-fold in a similar way as $([0,1], \mathcal{I}, \lambda )$ from the Lebesgue unit interval. As a result, we only need to show that $([0,1], \mathcal{I}, \lambda )$ has the relative d-property for all measure preserving map from the Lebesgue interval to itself.

It follows from Lemma 2 of [26] that there exists a $\mathcal{I}$-measurable subset S such that $\lambda (S) = 1/2$, and both S and $S^c$ is independent with (0, t) for all $t \in [0,1]$, where $S^c$ is the complement of S. Note that the Lebesgue $\sigma$-algebra $\mathcal{L}$ is generated by these subsets $(0, t), t \in [0,1]$, as a result, both S and $S^c$ are independent with any Lebesgue measurable subset. Given any measure-preserving map h from the Lebesgue interval to itself, let $g : ([0,1], \mathcal{I}, \lambda ) \rightarrow [0,1]$ defined to be $g(t) = h (t)$ for all $t \in S$, and $g(t) = -h (t)$ for all $t \notin S$. It is clear that g is an $\mathcal{I}$-measurable map.

We finally check that g induces the uniform distribution on $[-1,1]$. For any $s \in [0,1]$, $\lambda \{t : g(t) \in [-s, 0]\} = \lambda (S^c \cap h^{-1} ([0,s])) = \frac{1}{2} \lambda (h^{-1} ([0,s])) = \frac{s}{2}$, where the second equation follows from that $S^c$ is independent with the Lebesgue subset $h^{-1} ([0,s])$ which is of measure s; similarly, $\lambda \{t : g(t) \in [0, s]\} = \frac{s}{2}$. We thus complete the proof of Part (i).

We next prove Part (ii). The existence of this measure preserving mapping $h_n$ from the n-fold Lebesgue extension to the Lebesgue unit interval is guaranteed by [26, Corollary 1, p. 1093], the key here is that the n-fold Lebesgue extension is an atomless (essentially) countably generated space. $\qquad \blacksquare$

Proof of Proposition 2. The existence of pure-strategy Nash equilibria in $\tilde{\Gamma }_{h_n, h_n}$, for all n, follows from Corollary 1 and Part (i) of Lemma 2.

We next prove the non-existence result for the KRS-like game $\Gamma _{h_n, h_n}$. By Proposition 1, it suffices to show that there does not exist an $\mathcal{I}_n$-measurable map from [0, 1] to the Lebesgue unit interval such that it takes value either $h_n (t)$ or $-h_n(t)$ for all t, and it induces the uniform distribution on when restricted on $[-1/2, 1/2]$. Suppose not, there is such a mapping g. Let $S = \{t : g(t) \ge 0\}$. It is clear that $S \in \mathcal{I}_n$ and $\lambda _n (S) = \frac{1}{2}$. By the construction of $h_n$ in Lemma 2, there exists an Lebesgue subset E, such that $\lambda _n (S \Delta h_n^{-1}(E)) = 0$. By Part (ii) of Proposition 1, for any $s \in [0,1/2]$, $\frac{s}{2} = \lambda _n \{t: g \in [0,s ]\} = \lambda _n (S \cap h_n^{-1} [0,s]) = \lambda _n (h_n^{-1}(E) \cap h_n^{-1} [0,s]) = \eta (E \cap [0,s])$, where the last equation follows from the measure preserving property. This contradicts the fact that there is no Lebesgue set which is independent with all sets [0, s],  $s \in [0, 1/2]$.$\qquad \blacksquare$

Proof of the claim in Sect. 6. Let D be an $\mathcal{I}$-measurable subset with $\lambda (D) >0$. Note that $[0,1] = D_{01}$, it is clear that there exists two numbers $k, k' \in [0,1]$, such that $0<\lambda ( D_{kk'} \cap D) < \lambda (D)$. We next fix such a pair of numbers $k, k'$ and construct a required subset $D_0 \in D$ as in Definition 2. Namely, for any subinterval $[l, l'] \subseteq [0,1]$, $[l,l'] \cap D$ and $D_0$ differ up to a non-negligible $\lambda$-null subset. If this $D_{kk'} \cap D$ and $[l,l'] \cap D$ do not differ up to a null set for all $l, l'$, let $D_0 = D_{kk'} \cap D$. Otherwise, for some $l, l'$, this subset $D_{kk'} \cap D$ and $[l,l'] \cap D$ differ up to a $\lambda$-null set. That is, $D_{kk'} \cap [l, l'] \subseteq D$ holds subject to a null set. Let $D_0 = D_{kk"} \cap D = D_{kk"} \cap [l, l']$ where $k'' = \frac{k + k'}{2}$. It is clear that $0<\lambda (D_0) < \lambda (D)$ and $D_0$ is a required subset in Definition 2, since $D_{kk"}$ is independent with all subsets [a, b] for all a, b. $\qquad \blacksquare$

Proof of Proposition 3. It is clear that $\mathcal{D'}(G_1) \subseteq \mathcal{D'}(G_2)$. What remains is to prove the converse direction. For any distribution $\mu$ generated by a $\mathcal{L}^e$-measurable selection of $\Psi .$ Now consider the restricted distribution on [0, 1], still denoted by $\mu$. It is clear that $\mu$ is absolutely continuous with respect to the Lebesgue measure on [0, 1], moreover, for any $t \in [0,1]$, $\mu ([0,t])$ is at most of value t. As such, all the conditions of Lemma 3 in [26] are satisfied, therefore, there exists $S_{\mu } \in \mathcal{L}^e$ such that for any $t \in [0,1]$, $\mu ([0,t]) = \lambda ^e (S_{\mu } \cap [0,t])$. Let f be a $\mathcal{L}^e$-measurable selection of $\Phi$ such that $f(i) = i$ if $i \in S_{\mu }$ and $f(i) = -i$ if $i \notin S_{\mu }$. It is clear that this f induces the same distribution $\mu$ on $[-1,1]$.$\qquad \blacksquare$