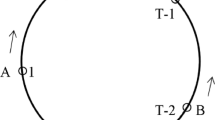Rendezvous in Heterogeneous Cognitive Radio Networks

Abstract

Rendezvous is a fundamental and important process in operating a distributed system, which can be applied in many distributed applications running on the system. In this chapter, we introduce the rendezvous process in a special type of cognitive radio network: Heterogeneous Cognitive Radio Network (HCRN) where different users have different capabilities to sense the licensed spectrum. Many elegant rendezvous algorithms have been proposed by constructing sequences based on the channels’ labels [1, 3, 7, 8, 10] or their identifiers (IDs) [2, 4, 5], and rendezvous can be guaranteed in a short time based on the special hopping sequences constructed. However, they all assume the users have the capability to sense and access all the licensed channels, which is unrealistic when the number of channels (N) is very large and some wireless devices may only operate on a small fraction of the channels. Therefore, HCRN is proposed, in which the users may have different spectrum-sensing capabilities. We introduce the system model and formulate the problem in Sect. 17.1. Rendezvous algorithms for the fully available spectrum are presented in Sect. 17.2, and rendezvous algorithms for the partially available spectrum are introduced in Sect. 17.3. Finally, we summarize the chapter in Sect. 17.4.

1 Preliminaries

We first introduce the system model of heterogeneous cognitive radio network (HCRN) and its difference with traditional cognitive radio network. Then, we define the rendezvous problem in the context of HCRN and show the challenges of designing efficient rendezvous algorithms for this kind of CRN.

1.1 System Model

The licensed spectrum is assumed to be divided into N non-overlapping channels:

$$\begin{aligned} U = \{1,2,\ldots ,N\} \end{aligned}$$

(17.1)

Each user (here we mean secondary users) is equipped with a cognitive radio to sense the licensed spectrum. We say a channel is available for the user if it is not occupied by any nearby primary users (PUs) who own these licensed channels. Actually, the users may have different spectrum sensing capabilities and suppose user i can sense a set of continuous channels:

$$\begin{aligned} C_i = \{c_x, c_{x+1}, \ldots , c_{x+k_i-1}\} \subseteq U \end{aligned}$$

(17.2)

which is assumed in [11, 12], where $c_x$ is the starting channel and $k_i = |C_i|$, $1\le x\le N-k_i+1$.

The channels in set $C_i$ are either occupied by nearby PUs or available for the (secondary) user i. We denote:

$$\begin{aligned} V_i \subseteq C_i \end{aligned}$$

(17.3)

as the set of all available channels after the spectrum sensing stage.

Time is also assumed to be divided into slots of equal length 2t, where t is sufficient for establishing a communication link if the users access the same channel at the same time slot. According to the IEEE 802.22 [9], t is often set to be 10 ms. The intuitive idea of setting each time slot to be 2t is to ensure that an overlap of t exists for link establishment even when the users do not start their process at aligned time slots (the idea is similar to the blind rendezvous for CRN in Chap. 5; we omit the details here).

Considering two users $u_a$ and $u_b$ with different spectrum sensing capability sets $C_a, C_b$, and the corresponding available channel sets $V_a, V_b$, they can rendezvous on some common available channel if $V_a \cap V_b \ne \emptyset$, which implies their capability sets must intersect.

Here we study two scenarios: fully available spectrum and partially available spectrum.

If all channels in the users’ sensing capability sets are available after the spectrum sensing stage, we call that the fully available scenario (i.e. $V_i = C_i$). But in most circumstances, some channels are likely occupied ($V_i \ne C_i$) and we call that the partially available scenario.

For example, in Fig. 17.1, two users $u_a$ and $u_b$ have different sets of sensing capabilities $C_a, C_b \subseteq U$. If some channels are occupied by some PUs, we label these channels as white in Fig. 17.2 and the figure shows an example that two users have different sets of available channels, $V_a \subseteq C_a$ and $V_b \subseteq C_b$ respectively.

In Fig. 17.1, all channels in the user’s sensing capability set are available and it is a fully available scenario, while Fig. 17.2 is a partially available scenario since some channels are occupied by the PUs [6].

In each time slot, user $u_i$ can access an available channel from set $V_i$ and attempt rendezvous with its potential neighbors. We say rendezvous happens when the users choose the same channel in the same time slot.

Time to rendezvous (TTR) denotes the number of time slots they take to rendezvous once all users have begun their attempt. Since the users are dispersed in different places and they may begin the rendezvous process in different time slots, we focus on designing efficient distributed algorithms for asynchronous users. We also use Maximum Time to Rendezvous (${ MTTR}$) to judge the performance of the rendezvous algorithms with respect to the worst situation.

Fig. 17.1

An example of different spectrum sensing capability sets of two users

Fig. 17.2

An example of different available channel sets of two users

1.2 Problem Definition

We formulate the rendezvous problem for the fully available spectrum scenario in HCRN as follows:

Problem 17.1

For any spectrum sensing capability set $C_i \subseteq U$, design an algorithm to access channels over different time slots:

$$\begin{aligned} t: f_{C_i}(t) \in C_i \end{aligned}$$

(17.4)

such that for any two users $u_a$ and $u_b$ with sets:

$$\begin{aligned} C_a,C_b \subseteq U, C_a \cap C_b \ne \emptyset \end{aligned}$$

(17.5)

Supposing user $u_a$ starts $\delta \ge 0$ time slots earlier than user $u_b$,

$$\begin{aligned} \exists T_{\delta }, \text { s.t. } f_{C_a}(T_\delta + \delta ) = f_{C_b}(T_\delta ) \end{aligned}$$

(17.6)

The TTR value is $T_\delta$ and the maximum time to rendezvous is defined as:

$$\begin{aligned} MTTR = \max _{\forall \delta } T_\delta \end{aligned}$$

(17.7)

The goal is to design rendezvous algorithms with bounded ${ MTTR}$.

Although the fully available spectrum scenario rarely happens in practice, it represents the best spectrum condition that may happen in designing rendezvous algorithms for HCRN. For more general situations, we formulate the rendezvous problem for the partially available spectrum scenario as follows:

Problem 17.2

For any spectrum sensing capability set $C_i \subseteq U$ and available channel set $V_i \subseteq C_i$, design an algorithm to access channels over different time slots:

$$\begin{aligned} t: f_{C_i, V_i}(t) \in V_i \end{aligned}$$

(17.8)

such that for any two users $u_a$ and $u_b$ with:

$$\begin{aligned} C_a,C_b \subseteq U, V_a\subseteq C_a, V_b\subseteq C_b, V_a \cap V_b \ne \emptyset \end{aligned}$$

(17.9)

Supposing user $u_a$ starts $\delta \ge 0$ time slots earlier than user $u_b$,

$$\begin{aligned} \exists T_{\delta }, \text { s.t. } f_{C_a,V_a}(T_\delta + \delta ) = f_{C_b,V_b}(T_\delta ) \end{aligned}$$

(17.10)

The TTR value is $T_\delta$ and the maximum time to rendezvous is defined as:

$$\begin{aligned} MTTR = \max _{\forall \delta } T_\delta \end{aligned}$$

(17.11)

The goal is to design rendezvous algorithms with bounded ${ MTTR}$.

Fig. 17.3

An example of rendezvous problem in HCRN

For example, $U = \{1,2,\ldots ,100\}$, and two capabilities sets are:

$$\begin{aligned} \left\{ \begin{array}{l} C_a = \{2,3,4,5,6\} \\ C_b = \{5,6,7\} \end{array}\right. \end{aligned}$$

Suppose that both users $u_a$ and $u_b$ adopt a simple algorithm by repeating the channels in their sensing capability set and user $u_a$ is 1 time slot earlier than user $u_b$. As depicted in Fig. 17.3, they rendezvous on channel 5 at time slot 9, and thus $TTR = 14-1=13$ time slots. In fact, if the users apply the extant algorithms based on all channels in U, the maximum rendezvous time could be $O(N^2) \approx 10,000$ time slots, which is unacceptable. This figure is a simple example of the fully available spectrum scenario. When some channels are occupied, for example:

$$\begin{aligned} \left\{ \begin{array}{l} V_a = \{2,5,6\} \\ V_b = \{6,7\} \end{array}\right. \end{aligned}$$

They cannot rendezvous on channel 5 and one more time slot is needed, as illustrated in Fig. 17.4. This is an example of the partially fully available spectrum scenario.

Fig. 17.4

An example of rendezvous problem in HCRN when two users have partial available channels

1.3 Challenges

In handling the blind rendezvous problem in HCRN, there are the following three challenges:

• (1) First, different users may have different capabilities to sense the licensed spectrum, we should design efficient algorithms under such heterogeneity.

• (2) Second, the users may start the rendezvous process at different time slots, and the rendezvous algorithms should work for both synchronous and asynchronous users with bounded rendezvous time.

• (3) Third, traditional rendezvous algorithms have maximum time to rendezvous (MTTR) as $MTTR = O(N^2)$, which is large when the user can only sense a small fraction of the channels. Thus, we should reduce the MTTR value and guarantee fast rendezvous even for the worst situations see the comparison in Table 17.1.

Table 17.1 MTTR comparison for fully and partially available scenarios in HCRN

2 Rendezvous for Fully Available Spectrum

In this section, we propose a new method called the Traversing Pointer (TP) algorithm for the users that have fully available channels. The intuitive idea is to accelerate the rendezvous process by accessing two channels at the same time, where one channel is fixed to be the first channel in the capability set, and the other is generated by hopping among the channels in the capability set. The method of generating such hopping sequence is similar to the method of time division in Chap. 7.

In the first place, we present a special construction for two available channels such that rendezvous can be guaranteed in $O(\log \log N)$ time slots if both users have only two available channels. Then, we introduce the TP algorithm on the basis of the special construction, which guarantees rendezvous for the two users with a fully available spectrum in a short time.

2.1 Rendezvous Scheme for Two Available Channels

Suppose each user has only two available channels, i.e. $|V_a| = |V_b| = 2$, and there exists at least one common channel, i.e. $V_a \cap V_b \ne \emptyset$. We present a special rendezvous scheme for the special scenario, which constructs a sequence of length $T_2 = 16(\lceil \log \log n\rceil + 1)$. The construction is based on three Disjoint Relaxed Difference Sets (DRDSs).

Supposing the available channel set of the user is:

$$\begin{aligned} V = \{v_1, v_2\} \subseteq U,\, where \, v_1 < v_2 \end{aligned}$$

(17.12)

the method is described in Algorithm 17.1.

Algorithm 17.1 finds the smallest number $c \in [1, l_1]$ such that the c-th bit of $v_2$ is 1 but the c-th bit of $v_1$ is 0, where $l_1 = \lceil \log N \rceil + 1$. Since $v_1<v_2$, c must exist. It is obvious that c can be represented by $l_2 = \lceil \log \log N\rceil + 1$ binary bits. We construct vector $\overrightarrow{D}$ by adding a special symbol $*$ to the binary representation as in Line 3, and we construct the rendezvous sequence in $l_2 + 1$ rounds. In each round, different sequences $S_*, S_0, S_1$ are added twice to S and the intuitive idea of designing these sequences comes from the good properties of DRDS (see Definition 8.3 in Chap. 8).

We define three sets as:

$$\begin{aligned} \left\{ \begin{array}{l} D_* = \{\{1,2,4,5\},\{3,6,7,8\}\} \\ D_0 = \{\{1,2,4,6\},\{3,5,7,8\}\} \\ D_1 = \{\{1,2,4,8\},\{3,5,6,7\}\} \end{array}\right. \end{aligned}$$

It is easy to check that they are three DRDS under $Z_8$. $S_*$, $S_0$ and $S_1$ are then constructed on the basis of $D_*, D_0, D_1$ respectively. We show the construction of sequences $S_0, S_1, S_*$ in Figs. 17.5, 17.6 and 17.7.

In each round, sequence $S_*, S_0$ or $S_1$ is added twice to the rendezvous sequence because the users can start the algorithm asynchronously. We first derive a useful lemma, as follows.

Lemma 17.1

Every 8 continuous time slots in each round corresponds to a DRDS.

Fig. 17.5

Construction of sequence $S_*$ on the basis of $D_*$

Proof

Consider the round containing two $S_0$ sequences where $S_0$ is constructed based on the DRDS $D_0$. Every 8 continuous time slots $[i,i+7]$ where $1\le i\le 9$ can be seen as rotating $S_0$ by $i-1$ time slots. From the definition of Relaxed Difference Set (RDS) in Chap. 8, the rotation of an RDS is also an RDS. Thus the rotation of $S_0$ also corresponds to a DRDS. For example, when $i=3$, the 8 continuous time slots are:

$$\begin{aligned} \{v_2,v_1,v_2,v_1,v_2,v_2,v_1,v_1\} \end{aligned}$$

(17.13)

and they correspond to the DRDS:

$$\begin{aligned} \{\{2,4,7,8\},\{1,3,5,6\}\} \end{aligned}$$

(17.14)

We can also derive the same result for the other two sequences $S_1, S_*$, and thus the lemma holds.

Fig. 17.6

Construction of sequence $S_0$ on the basis of $D_0$

Fig. 17.7

Construction of sequence $S_1$ on the basis of $D_1$

Consider two users $u_a$ and $u_b$ with available channel sets:

$$\begin{aligned} \left\{ \begin{array}{l} V_a = \{a_1, a_2\} \\ V_b = \{b_1, b_2\} \end{array}\right. \end{aligned}$$

Suppose the chosen numbers in Line 2 are $c_a, c_b$ respectively. We show the correctness of Algorithm 17.1 based on different relationships between $c_a, c_b$:

• (1) If $c_a = c_b$, rendezvous is guaranteed in 16 time slots as in Lemma 17.2.

• (2) If $c_a \ne c_b$, rendezvous is guaranteed in $16(\lceil \log \log N \rceil + 1)$ time slots as in Lemma 17.3.

Lemma 17.2

Algorithm 17.1 guarantees rendezvous in 16 time slots if $c_a = c_b$.

Proof

When $c_a = c_b$, we claim that:

$$\begin{aligned} a_1 \ne b_2 \, and \, a_2 \ne b_1 \end{aligned}$$

(17.15)

If $a_1 = b_2$, we can derive:

$$\begin{aligned} b_1< b_2 = a_1 < a_2 \end{aligned}$$

(17.16)

From Line 2, the $c_b$-th bit of $b_2$ is 1 and the $c_a$-th bit of $a_1$ is 0, but $c_a = c_b$, which leads to a contradiction. Thus $a_1 \ne b_2$. Similarly, $a_2 \ne b_1$.

Since the users have at least one common channel, that is:

$$\begin{aligned} a_1 = b_1 \, or \, a_2 = b_2 \end{aligned}$$

(17.17)

We show that both pairs $(a_1,b_1), (a_2,b_2)$ appear in the constructed sequences when two users have begun their process.

Denote the constructed sequences for the users as $S_a$ and $S_b$ respectively, and they are composed of $l_2 + 1$ rounds. We say the i-th round of user $u_a$ (denoted as r(a, i)) overlaps with the j-th round of user $u_b$ (r(b, j)) if their intersection length is at least 8 (time slots).

Without loss of generality, suppose user $u_a$ is $\delta$ time slots earlier than user $u_b$. We show the lemma from two situations:

• (1) If r(b, 1) overlaps with r(a, 1) and there are at least 8 overlapping time slots. By Lemma 17.1, the continuous 8 time slots correspond to two DRDSs for users $u_a$ and $u_b$. From the definition of the DRDS, we can check that $(a_1,b_1)$ and $(a_2,b_2)$ both exist in the 8 time slots, and thus they rendezvous in the first round of user $u_b$.

• (2) If r(b, 1) overlaps with r(a, i) where $1<i\le l_2 + 1$ and there are at least 8 overlapping time slots. If $(a_1,b_1)$ does not exist in the intersecting 8 slots, channel $b_1$ meets $a_2$ in four time slots and $b_2$ also has to meet $a_1$ in four time slots. However, the sequence added in r(b, 1) is different from the sequence in r(a, i). Actually, $S_*$ is added twice in r(b, 1) while $S_0$ or $S_1$ is added in r(a, i), and this situation cannot happen. Thus, $(a_1,b_1)$ exists in the first round of user $u_b$. Similarly, we can prove that $(a_2,b_2)$ exists. Thus they can rendezvous in 16 time slots.

Fig. 17.8

An example of r(b, 1) overlapping with r(a, 1) in Algorithm 17.1

Fig. 17.9

An example of r(b, 1) overlapping with r(a, i) where $1<i\le l_2 + 1$ in Algorithm 17.1

As depicted in Fig. 17.8, r(b, 1) overlaps with r(a, 1) and the first 8 overlapping time slots form two DRDSs are:

$$\begin{aligned} \left\{ \begin{array}{ll} \{\{2,3,7,8\},\{1,4,5,6\}\} &{} \text {for user} \, u_a \\ \{\{1,2,4,5\},\{3,6,7,8\}\} &{} \text {for user} \, u_b \end{array}\right. \end{aligned}$$

Then we can check that $(a_1,b_1)$ exists in the 2-nd time slot and $(a_2,b_2)$ happens in the 6-th time slot. Similarly, Fig. 17.9 shows the example that r(b, 1) overlaps with r(a, i) where $1<i\le l_2 + 1$, and both pairs $(a_1,b_1)$ and $(a_2,b_2)$ exist in the first overlapping 8 time slots. Therefore, the lemma holds.

Lemma 17.3

Algorithm 17.1 guarantees rendezvous in $T_2 = 16(\lceil \log \log N \rceil + 1)$ time slots if $c_a \ne c_b$.

Proof

When $c_a \ne c_b$, there are four possible combinations of rendezvous situations:

$$\begin{aligned} \left\{ \begin{array}{l} a_1 = b_1 \\ a_1 = b_2 \\ a_2 = b_1 \\ a_2 = b_2 \end{array}\right. \end{aligned}$$

Thus the two users’ overlapping sequences must contain the four pairs $(a_1,b_1)$, $(a_1,b_2)$, $(a_2,b_1)$, $(a_2,b_2)$. We show the lemma from two situations.

• (1) If r(b, 1) overlaps with r(a, 1), $(a_1,b_1), (a_2,b_2)$ exists in the overlapping part by Lemma 17.2. Since $c_a \ne c_b$, without loss of generality, suppose $c_a < c_b$ and there exists $1\le i\le l_2$ such that the i-th bit of $c_a$ is 0 but the i-th bit of $c_b$ is 1 (such i must exist). When $r(b,i+1)$ overlaps with $r(a,i+1)$, we claim that $(a_1,b_2)$ and $(a_2,b_1)$ exist in the overlapping part. If $(a_1, b_2)$ does not happen, $a_1$ has to meet $b_1$ four times and $a_2$ has to meet $b_2$ four times; however, $r(a,i+1)$ and $r(b,i+1)$ use different sequences ($S_0$ and $S_1$) and this situation cannot happen. Thus $(a_1,b_2)$ appears at least once during the intersecting part. Similarly, $(a_2,b_1)$ also exists. Therefore, rendezvous can be guaranteed in $16(i+1) \le T_2$ time slots.

• (2) If r(b, 1) intersects with r(a, i) where $1<i\le l_2 + 1$, the pairs $(a_1,b_1)$ and $(a_2,b_2)$ both exist by Lemma 17.2. Using the similar technique as the first situation, we can check that $(a_1,b_2)$ and $(a_2,b_1)$ exist in the first round of user $u_b$.

Combining the two situations, rendezvous can be guaranteed in $T_2$ time slots, and the lemma holds.

By Lemmas 17.2 and 17.3, we conclude the theorem:

Theorem 17.1

Algorithm 17.1 guarantees rendezvous in $T_2 = 16(\lceil \log \log n\rceil +1)$ time slots for the special situation that each user has two available channels.

2.2 Traversing Pointer Algorithm

For the fully available spectrum scenario, we propose the Traversing Pointer (TP) algorithm based on the rendezvous scheme for two channels. Consider two users $u_a$ and $u_b$ with spectrum sensing capability sets $C_a, C_b \subseteq U$, the TP algorithm is described as Algorithm 17.2.

To begin with, suppose user i has the spectrum sensing capability set as:

$$\begin{aligned} C_i = \{c_{x}, c_{x+1}, \ldots , c_{x+k_i-1}\} \subseteq U \end{aligned}$$

(17.18)

where $k_i = |C_i|$, $1\le x\le N - k_i + 1$ and $\forall c_j\in C_i$, channel $c_j$ is available.

The TP algorithm works on the basis of the rendezvous scheme for two available channels. There are two constructed ‘pointers’ where fp, i.e. fixed pointer, is fixed at the first channel $c_x$ and mp is a moving pointer that traverses the capability set back and forth. We divide the time into rounds where each round contains $L=2T_2$ time slots (we repeat the constructed sequence from Algorithm 17.1 twice to tackle the asynchronous situation). fp is fixed but mp changes in each round. As illustrated in Fig. 17.10, mp moves from the last channel $c_{x+k_i-1}$ to the first one $c_x$ in the first $k_i-1$ rounds, and then from the first one to the last one in the next $k_i-1$ rounds. The user continues the process until rendezvous.

Fig. 17.10

An illustration of Algorithm 17.2. fp is fixed at the first channel in all rounds, while mp traverses the channels back and forth and round by round

2.3 Correctness and Complexity

Consider any two users $u_a$ and $u_b$ with spectrum sensing capability sets:

$$\begin{aligned} \left\{ \begin{array}{l} C_a = \{c_{x},c_{x+1},\ldots ,c_{x+k_a-1}\} \\ C_b = \{c_{y},c_{y+1},\ldots ,c_{y+k_b-1}\} \end{array}\right. \end{aligned}$$

where $1\le x \le N - k_a+1, 1\le y \le N - k_b+1$. $C_a \cap C_b \ne \emptyset$ implies the following situation must happen:

$$\begin{aligned} c_{x} \in C_b \, or \, c_{y} \in C_a \end{aligned}$$

(17.19)

Therefore, the constructed two pointers can help guarantee rendezvous when one user’s moving pointer coincides with the other’s fixed pointer. We derive the time complexity to achieve rendezvous in Theorem 17.2.

Theorem 17.2

The TP algorithm (Algorithm 17.2) guarantees rendezvous for the fully available spectrum scenario in $O(\max \{|C_a|,|C_b|\}\log \log N)$ time slots.

Proof

Since the channels in the capability sets $C_a$ and $C_b$ are continuous and $C_a \cap C_b \ne \emptyset$, the first channel of $C_a$ is in $C_b$ (i.e. $c_{x} \in C_b$) or the first channel of $C_b$ is in $C_a$ (i.e. $c_{y} \in C_a$). Without loss of generality, suppose $c_{x} \in C_b$.

Denote the consecutive L time slots constructed in Line 11 as a round, and the chosen available channels in the r-th round of two users are $\{fp_{a,r}, mp_{a,r}\}$, $\{fp_{b,r}, mp_{b,r}\}$ respectively.

We say the i-th round of user $u_a$ (denoted as $r_{a,i}$) overlaps with the j-th round of user $u_b$ ($r_{b,j}$) if their intersection part contains at least L / 2 time slots. From Theorem 17.1, if $r_{a,i}$ overlaps with $r_{b,j}$ and $\{fp_{a,i}, mp_{a,i}\} \cap \{fp_{b,j}, mp_{b,j}\} \ne \emptyset$, two users can achieve rendezvous in $L = 32(\lceil \log \log N \rceil + 1)$ time slots. There are two different situations according to the start time of two users:

• (1) If user $u_a$ starts earlier (no later) than user $u_b$, suppose the i-th round of user $u_a$ overlaps with the first round of user $u_b$. We can find that, after $r = y+k_b-1-x$ rounds, $r_{a,i+r}$ overlaps with $r_{b,1+r}$ where user $u_b$’s moving pointer chooses channel:

  $$\begin{aligned} mp_{b,1+r} = c_{y+k_b - (1+r)} = c_x = fp_{a,i+r} \end{aligned}$$

  (17.20)

  thus, rendezvous is guaranteed in $(r+1) L \le |C_b| L$ time slots.

• (2) If user $u_b$ starts earlier than user $u_a$, suppose the i-th round of user $u_b$ overlaps with the first round of user $u_a$, there are two situations according to the moving direction of user $u_b$’s moving pointer (mp). It is easy to check that user $u_b$’s moving pointer chooses channel $c_x$ within $2k_b$ rounds no matter which direction it is heading. We omit the details and the reader may deduce the complexity of the situation. Therefore, rendezvous is guaranteed in $2|C_b|L$ time slots.

Similarly, when $c_{y} \in C_a$, rendezvous is also guaranteed in $2|C_a|L$ time slots. Therefore, the TP algorithm (Algorithm 17.2) guarantees rendezvous in $2\max \{|C_a|,|C_b|\}L = O(\max \{|C_a|,|C_b|\}\log \log N)$ time slots when the spectrum is fully available.

In order to show the efficiency of the TP algorithm, we show a constructive lower bound in Theorem 17.3.

Theorem 17.3

$max\{|C_a|,|C_b|\}$ time slots are needed to guarantee rendezvous for the fully available spectrum condition.

Proof

Suppose user $u_a$ can sense only 1 channel (i.e. $|C_a|=1$) which belongs to $C_b$. In order to discover the channel for rendezvous, user $u_b$ has to traverse all channels in $C_b$ at least once and thus (at least) $\max \{|C_a|,|C_b|\}$ time slots are needed, which concludes the theorem.

It is clear that the lower bound still holds if two users are synchronous, and the TP algorithm is nearly optimal with only an additional $O(\log \log N)$ factor. Compared with the state-of-the-art result $O(|C_a||C_b|)$ in [12], the TP algorithm removes an $O(\min \{|C_a|,|C_b|\})$ factor and it works more efficiently.

3 Rendezvous for Partially Available Spectrum

In this section, we propose the Moving Traversing Pointer (MTP) algorithm for the users that have partially available channels. The intuitive idea is also to accelerate the rendezvous process by accessing two channels at the same time, and the time to rendezvous is only impacted by an $O(\log \log N)$ factor. When it comes to the partially available scenario, the TP algorithm cannot work because the channel they rendezvous on may be unavailable. Therefore, we propose this modified algorithm where the ‘fixed pointer’ can also move after the ‘moving pointer’ has already traversed all channels in the capability set. Through such a modification, the MTP algorithm can guarantee rendezvous in $O((\max \{|V_a|,|V_b|\})^2 \log \log N)$ time slots.

3.1 Moving Traversing Pointer Algorithm

In practical situations, the sensed available channels may be only a fraction of the spectrum sensing capability set. For two users $u_a$ and $u_b$ with capability sets $C_a, C_b \subseteq U$ and available channel sets $V_a \subseteq C_a, V_b \subseteq C_b$, the TP algorithm may not guarantee rendezvous.

For example, suppose the first channel of user $u_a$ ($c_x$) belongs to user $u_b$’s capability set ($c_x \in C_b$), $c_x$ is available for user $u_a$ ($c_x \in V_a$), but it is not available for user $u_b$ ($c_x \notin V_b$). The fixed pointer of user $u_a$ stays at channel $c_x$ all the time but user $u_b$ cannot access $c_x$, and thus rendezvous may not happen. In order to overcome the disadvantage, we modify the TP algorithm and the intuitive idea is to move the ‘fixed pointer’ after the ‘moving pointer’ has already traversed the channels.

Similar to the assumption in the TP algorithm, suppose user i has the spectrum sensing capability set as:

$$\begin{aligned} C_i = \{c_x,c_{x+1},\ldots , c_{x+k_i-1}\}\subseteq U \end{aligned}$$

(17.21)

where $k_i = |C_i|$ and $1\le x\le n-k_i+1$, and the available channel set is denoted as $V_i \subseteq C_i$. Order the available channels by increasing order and denote:

$$\begin{aligned} V_i = \{c_{i,1},c_{i,2},\ldots , c_{i,m_i}\} \end{aligned}$$

(17.22)

where $m_i = |V_i|$ and the equation:

$$\begin{aligned} \forall 1\le j_1<j_2\le m_i, c_{i,j_1} < c_{i,j_2} \end{aligned}$$

(17.23)

holds. The MTP algorithm is presented in Algorithm 17.3.

Fig. 17.11

mp traverses the channels back and forth and round by round, while fp moves to the next available channel every $2(m_i-1)$ rounds

Fig. 17.12

mp traverses the channels back and forth and round by round, while fp moves to the next available channel every $2(m_i-1)$ rounds

The MTP algorithm (Algorithm 17.3) is different from the TP algorithm where the ‘fixed pointer’ does not always stay at the same channel. Assume time is divided into loops of length $P=2(m_i-1)L$ time slots and each loop contains $2(m_i-1)$ rounds of length $L{=}2T_2 {=} 32(\lceil \log \log N\rceil {+}1)$. The pointer fp stays at a fixed available channel in each loop and it moves to the next available one every P time slots as in Line 7. Similar to the TP algorithm, the ‘moving pointer’ stays at a fixed channel in each round and traverses the available channels back and forth round by round. As illustrated in Fig. 17.11, fp is fixed at channel $c_{i,1}$ for the first P time slots and mp traverses from the last available channel $c_{i,m_i}$ to the first one $c_{i,1}$, and then back to the last one every L time slots. In the next loop of P time slots, ${ fp}$ moves to channel $c_{i,2}$ as Fig. 17.12 and mp repeats the traversal. This process continues until rendezvous.

3.2 Correctness and Complexity

Consider users $u_a$ and $u_b$ with capability sets $C_a, C_b\subseteq U$ and available channel sets $V_a \subseteq C_a, V_b \subseteq C_b$ where $C_a \cap C_b \ne \emptyset$. Denote:

$$\begin{aligned} \left\{ \begin{array}{l} V_a = \{c_{a,1},c_{a,2},\ldots ,c_{a,m_a}\} \\ V_b = \{c_{b,1},c_{b,2},\ldots ,c_{b,m_b}\} \end{array}\right. \end{aligned}$$

where $m_a = |V_a|, m_b = |V_b|$. We show the correctness and the efficiency in the following theorem.

Theorem 17.4

The MTP algorithm (Algorithm 17.3) guarantees rendezvous for the partially available spectrum scenario in $O((\max \{|V_a|,|V_b|\})^2 \log \log N)$ time slots.

Proof

Since $V_a \cap V_b \ne \emptyset$, there exist $1\le x\le m_a, 1\le y\le m_b$ such that one common available channel exists:

$$\begin{aligned} c_{a,x}=c_{b,y} \end{aligned}$$

(17.24)

Denote the consecutive L time slots constructed in Line 14 as a round and every $2(m_i-1)$ rounds as a loop ($i=a$ or b). Denote the r-th round of l-th loop for users $u_a$ and $u_b$ as $r_{a}(l,r)$ and $r_{b}(l,r)$, and the chosen available channels in the round as $\{fp_{a}(l,r),mp_{a}(l,r)\}$ and $\{fp_{b}(l,r),mp_{b}(l,r)\}$ respectively.

Similar to the analysis of Theorem 17.2, we say round $r_a(l_a,r_a)$ overlaps with round $r_b(l_b,r_b)$ if their intersection part contains at least L / 2 time slots. From Theorem 17.1, if $r_a(l_a,r_a)$ overlaps with $r_b(l_b,r_b)$ and the chosen channels satisfy:

$$\begin{aligned} \{fp_{a}(l,r),mp_{a}(l,r)\} \cap \{fp_{b}(l,r),mp_{b}(l,r)\} \ne \emptyset \end{aligned}$$

(17.25)

rendezvous can be achieved in the intersection part.

Without loss of generality, assuming $m_a = |V_a| \le |V_b| = m_b$ and we show the theorem from two aspects.

• (1) If user $u_a$ starts the algorithm earlier than user $u_b$, suppose $r_a(l_a,r_a)$ overlaps with the first round of user $u_b$ ($r_b(1,1)$). After $(y-1)\cdot 2(m_b-1)$ rounds, user $u_b$’s fixed pointer (fp) stays at channel $c_{b,y}$ for the next $2(m_b-1)$ rounds. Since $2(m_b-1) \ge 2(m_a-1)$, user $u_a$’s moving pointer (mp) has enough time (rounds) to traverse all available channels including $c_{a,x} = c_{b,y}$, and therefore the chosen channels overlap in $2(m_a-1)$ rounds and rendezvous is guaranteed in $[2(m_b-1) \cdot (y-1) + 2(m_a-1)]\cdot L \le 2(m_b-1)m_bL$ time slots.

• (2) If user $u_b$ starts the algorithm earlier than user $u_a$, suppose $r_b(l_b,r_b)$ overlaps with the first round of user $u_a$ ($r_a(1,1)$). Obviously, user $u_b$ can get to the loop where the fixed pointer (fp) stays at channel $c_{b,y}$ in no more than $m_b-1$ loops (i.e. $(m_b-1)\cdot 2(m_b-1)$ rounds). By the same analysis, rendezvous can be guaranteed in the following $2(m_a-1)$ rounds, which implies the maximum rendezvous time can be bounded by:

  $$\begin{aligned}{}[(m_b-1)\cdot 2(m_b-1) + 2(m_a-1)] \cdot L \le 2(m_b-1)m_b L \end{aligned}$$

  (17.26)

  time slots.

Similarly, if $m_a \ge m_b$, we also can show that rendezvous is guaranteed in $2(m_a-1)m_aL$ time slots. Therefore, Algorithm 17.3 guarantees rendezvous in:

$$\begin{aligned} 2(\max \{m_a,m_b\})^2 \cdot 32(\lceil \log \log N\rceil + 1) = O((\max \{|V_a|,|V_b|\})^2 \log \log N) \end{aligned}$$

(17.27)

time slots. Thus, the theorem holds.

4 Chapter Summary

The rendezvous problem has been widely studied in Cognitive Radio Networks (CRNs) since the unlicensed spectrum is overcrowded due to the increasing number of wireless devices, while the licensed spectrum is often underutilized. In this chapter, we introduce rendezvous processes in dealing with a special type of CRN where the users (such as the mobile phones or other wireless devices) can only detect a fraction of all channels. The different capabilities of detecting the licensed channels of the users create a heterogeneous network and this kind of network is called Heterogeneous Cognitive Radio Network (HCRN).

In the chapter, we study the simplest version of modeling the users’ heterogeneous capabilities to detect the licensed channels, where each user can only sense a set of continuous channels. We mainly consider two scenarios, all channels in the users’ sensing range are available, or part of them are available.

For the first situation, we introduce the Traversing Pointer (TP) algorithm, where two pointers exist to traverse the channels that the user can detect. This idea originates from the method of traversing the elements in an array, but it cannot work if the users’ capability set is not continuous. For the second situation, we modify the TP algorithm and the proposed Moving Traversing Pointer (MTP) algorithm can traverse all channels in the users’ capability set, while it keeps moving slowly to all available channels.

Rendezvous in an arbitrary HCRN can be more difficult if the users’ capability set is discontinuous. The proposed “pointer” works well in the continuous capability set since we can regard it as an array, but we need to find out other efficient ways to handle more general heterogeneous capabilities.