Keywords

Introduction

Air pollution caused by the fast development of traffic motorization has become one of the main factors affecting the urban environmental quality. Bi-level programming model has been an effective and significant modeling tool in the field of traffic planning and traffic management, and it has a considerable degree of complexity due to containing the master–slave hierarchical decision-making process, which causes the upper-level and lower-level models to have their own decision variables, constraint conditions, and objective functions. Therefore, the optimization results of the upper-level model not only depend on the upper-level model decision variables, but are also affected by the optimal solutions of the lower-level model that are closely related to the upper decision variables. This decision-making model makes the entire system to get the best benefits during the process of cooperation and coordination, but can also make decisions freely with mutual constraints. Based on the design principle of stochastic user equilibrium, Michael J. Maher forecasted the path choice of congested road network and optimized the signal timing program of intersection by building bi-level optimizing model [1]. Sun [2] established a bi-level programming model on stochastic route choice and time-dependent demand in road network and developed heuristic solution approach consisting of genetic algorithm and cell transmission simulation-based incremental logit assignment procedure. Based on the route choice of users, Zhi-lin Lv developed a bi-level programming model to minimize the pollution emissions in urban expressway network and maximize traffic volumes entering the network [3]. Zhou [4] studied traffic signal cycle length and green ratio by taking environment factors into consideration, proposing a bi-level programming model based on user equilibrium route choosing model. Gao [5] optimized intersection signal control parameters, departure frequency, and routes of evacuation vehicle at assembly points through establishing bi-level programming model. In the terms of road coordinate control, Jian-min Xu built a urban arterial road coordinate control bi-level programming model by introducing group decision-making theory into conventional traffic signal control method, which could reduce delay and improve segment travel speed effectively [6]. Based on the regional coordinate signal control theory and user equilibrium, Yue Hu put forward a bi-level programming model for traffic assignment and signal control optimization [7]. Currently, the existing literature about bi-level programming model is just to optimize delay, stops, and environmental benefits in road networks, not to verify whether the total impedance of network to achieve optimal results under user optimal distribution.

Therefore, aiming at user route choosing problem under dynamic network signal control, this paper proposes bi-level multi-objective programming model consisting of traffic control and user route choice. The upper-level model is to minimize the system total impedance based on optimizing vehicle exhaust emissions, and the lower-level model for user route choice is established based on user equilibrium. Eventually, the bi-level multi-objective programming model is put forward on system equilibrium path selection model. In addition, this paper solves the model by designing heuristic particle swarm algorithm, which is compared with heuristic genetic algorithm, and is of great superiority and optimization ability.

Bi-level Programming Problem

Bi-level programming problem can be described as impartial combination games between traffic planners and road users. Therefore, the mathematical forms of bi-level programming problem are as follows:

$$ \left\{ {\begin{array}{*{20}l} {\mathop {\min}\limits_{{{\text{x}} \in {\text{X}}}} \, P(x,y)} \hfill \\ {{\text{s}}.{\text{t}}. \; G(x,y) \le 0} \hfill \\ {\mathop {\min}\limits_{{{\text{y}} \in {\text{Y}}}} \, p(x,y)} \hfill \\ {{\text{s}}.{\text{t}}.\; g(x,y) \le 0} \hfill \\ \end{array} } \right., $$
(1)

where \( P(x,y) \) and \( G(x,y) \) represent separately the objective function and constraints of the upper-level model, in which \( x \in X \subset R^{n} \) and \( y \in Y \subset R^{m} \) are the decision variables of upper-level and lower-level models, and m and n are integers. Likewise, \( p(x,y) \) and \( g(x,y) \), respectively, represent the objective function and constraints of the lower-level model, \( G(x,y) \le 0 \) and \( g(x,y) \le 0 \) are the equality and inequality constraints for variables, respectively. On the whole, this mathematical model takes the variable x of the upper-level issue as control parameters, optimizing the objective functions of the lower-level model.

Bi-level Multi-objective Programming Model

The Upper-Level Model

Since bi-level multi-objective programming model can more thoroughly convey the wishes of managers, the objective function of the upper-level model is to minimize the vehicle exhaust emissions in network and the total impedance of road users.

Firstly, the vehicle exhaust emissions in network are the summations of the exhaust emissions when the vehicle travels on the road and idling emissions at the intersection. As a result, the objective functions to make the least motor vehicle exhaust emissions in network are:

$$ \hbox{min} :\;E_{s} = \alpha_{1} E_{s}^{{\prime }} + \alpha_{2} E_{s}^{{\prime \prime }} , $$
(2)
$$ E_{s}^{{\prime }} = \sum\limits_{i \in I} {EF_{i,d}^{\text{PCU}} \cdot x_{i} \cdot d_{i} } , $$
(3)
$$ E_{s}^{{\prime \prime }} = \sum\limits_{i \in I} {EF_{i}^{\text{PCU}} \cdot x_{i} \cdot L_{i} } . $$
(4)

where \( E_{S} \) is the total automotive exhaust emissions in the network, \( E^{\prime}_{s} \) is the exhaust emissions when the vehicle travels on road, and \( E^{\prime \prime}_{s} \) is idle speed emissions at intersection. \( \alpha_{1} \) and \( \alpha_{2} \) is, respectively, the weight of the exhaust emissions at the intersection and road segments; \( EF_{i,d}^{\text{PCU}} \) and \( EF_{i}^{\text{PCU}} \), respectively, are the exhaust emissions factors under idle and driving conditions. \( d_{i} \) is the travel delay on road segment i, which is given by \( d_{i} = \frac{{C(1 - \lambda )^{2} }}{{2\left( {1 - \frac{{x_{i} }}{S}} \right)}} + \frac{{\left( {\frac{{x_{i} }}{\lambda S}} \right)^{2} }}{{2x_{i} \left( {1 - \frac{{x_{i} }}{\lambda S}} \right)}} \), in which C is the signal cycle, \( \lambda \) the splits, and S the saturating flow. \( x_{i} \) is the traffic on road segment i, and \( L_{i} \) is the length of road segment i.

Subsequently, road manager is always willing to minimize the total impedance that is the total travel time, making the system to achieve equilibrium; so the objective function equals to system optimal allocation model and is given by:

$$ \begin{array}{*{20}l} {\hbox{min} :\;Z^{{\prime }} (X) = \sum\limits_{i} {x_{i} t_{i} } (x_{i} )} \hfill \\ {{\text{s}}.{\text{t}}. \; \left\{ {\begin{array}{*{20}l} {\sum\limits_{k} {f_{k}^{rs} = q_{rs} } } \hfill \\ {f_{k}^{rs} \ge 0\quad \forall r,s,i} \hfill \\ \end{array} } \right.} \hfill \\ \end{array} , $$
(5)

where \( t_{i} (x_{i} ) \) is the impedance function of route, \( f_{k}^{rs} \) is the traffic of route k between the junctions r and s, \( q_{rs} \) is the OD volume between the junctions r and s. Due to the intersection delay, the impedance function of route is divided into two parts, namely the travel time on road and intersection delay, which is:

$$ t_{i} (x_{i} ) = t_{i}^{{\prime }} (x_{i} ) + D_{i} , $$
(6)

from which we use BPR function developed by US Bureau of Road to define the travel time on road, and its mathematical form is:

$$ t_{i}^{{\prime }} (x_{i} ) = t_{i} (0)\left[ {1 + \alpha \left( {x_{i} /S} \right)^{\beta } } \right], $$
(7)

where \( t_{i} (0) \) is the travel time required when there is none vehicle on the road; \( \alpha \) and \( \beta \) are the parameters to be calibrated of function and are supposed to be 0.15 and 4.

To sum up, the upper-level multi-objective model is as follows:

$$ \begin{array}{*{20}l} {\hbox{min} :\;F(X) = \alpha \left( {\alpha_{1} \sum\limits_{i \in I} {EF_{i,d}^{\text{PCU}} \cdot x_{i} \cdot d_{i} } + \alpha_{2} \sum\limits_{i \in I} {EF_{i}^{\text{PCU}} \cdot x_{i} \cdot L_{i} } } \right) + \beta \sum\limits_{i} {x_{i} t_{i} (x_{i} )} } \hfill \\ {{\text{s}}.{\text{t}}. \; \left\{ {\begin{array}{*{20}l} {\sum\limits_{k} {f_{k}^{rs} = q_{rs} } } \hfill \\ {f_{k}^{rs} \ge 0\quad \forall r,s,i} \hfill \\ C \ge 30,\lambda \ge 0.05 \hfill \\ C \le 120,\lambda \le 0.95 \hfill \\ \end{array} } \right.} \hfill \\ \end{array} , $$
(8)

where \( \alpha \) and \( \beta \) are weighting coefficients; during the traffic planning process, the value of which denotes, respectively, the impact of two goals, namely minimum emissions and the total independence, and is given by \( \alpha + \beta = 1 \).

The Lower-Level Model

During the model establishing process, the total impedance of road users in network is not only taken into thought, but the path choice is also taken into consideration to make user behavior to meet the requirements of system and user equilibrium simultaneously. Therefore, the lower-level model, namely traffic assignment model, is given by:

$$ \left\{ {\begin{array}{*{20}l} {\hbox{min} :\; Z(X) = \sum\limits_{i} {\int\limits_{0}^{{x_{i} }} {t_{i} (x_{i} ){\text{d}}x_{\text{i}} } } } \hfill \\ {{\text{s}}.{\text{t}}. \; \left\{ {\begin{array}{*{20}l} {\sum\limits_{k} {f_{k}^{rs} = q_{rs} } } \hfill \\ {f_{k}^{rs} \ge 0\quad\forall r,s,i} \hfill \\ \end{array} } \right.} \hfill \\ \end{array} } \right. . $$
(9)

The objective function of the lower-level model by taking Eqs. 6 and 7 into Eq. 9 and integrating is as follows:

$$ Z(X) = \sum\limits_{i} {\left[ {t_{i} (0)x_{i} + 0.03S \cdot t_{i} (0)\left( {\frac{{x_{i} }}{S}} \right)^{5} } \right.} \left. { + 0.5SC(1 - \lambda )^{2} \cdot \ln \left( {1 - \frac{{x_{i} }}{S}} \right) - \frac{{x_{i} }}{2\lambda S} - \frac{1}{2}\ln (x_{i} - \lambda S)} \right]. $$
(10)

Bi-level Multi-objective Programming Model

In summary, the bi-level multi-objective programming model is built to show:

$$ \begin{array}{*{20}l} {U :\;\hbox{min} :\;\alpha \left( {\alpha_{1} E_{s}^{\prime } + \alpha_{2} E^{\prime \prime } } \right) + \beta \sum\limits_{i} {x_{i} t_{i} (x_{i} )} } \hfill \\ {\quad \;{\text{s}}.{\text{t}}. \; \left\{ {\begin{array}{*{20}l} {\sum\limits_{k} {f_{k}^{rs} = q_{rs} } } \hfill \\ {f_{k}^{rs} \ge 0\quad\forall r,s,i} \hfill \\ {C \ge 30,\lambda \ge 0.3} \hfill \\ {C \le 120,\lambda \le 1} \hfill \\ \end{array} } \right.} \hfill \\ {D :\;{\text{min:}}\;Z(X) = \sum\limits_{i} {\int\limits_{0}^{{x_{i} }} {t_{i} (x_{i} ){\text{d}}x_{\text{i}} } } } \hfill \\ {\quad \;{\text{s}}.{\text{t}}. \; \left\{ {\begin{array}{*{20}l} {\sum\limits_{k} {f_{k}^{rs} = q_{rs} } } \hfill \\ {f_{k}^{rs} \ge 0\quad\forall r,s,i} \hfill \\ \end{array} } \right.} \hfill \\ \end{array} . $$
(11)

The objective function of the upper-level problem on the above is to minimize the automotive exhaust emissions in network and the total impedance; for each road user, the lower-level model of which is to minimize the travel cost.

Heuristic Particle Swarm Optimization Algorithm

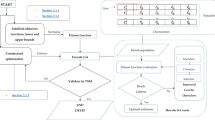
In 1995, Kennedy and Eberhart were inspired by birds foraging behavior to propose particle swarm optimization algorithm, namely PSO algorithm, which starts from a random solution and finds the optimal solution of problem by iterating and is of great ability to search the optimal solution in a global variable based on the current solution [8]. Zhao [9] solved bi-level programming problem based on layer iteration by advanced PSO algorithm, calculating the upper-level problem by means of PSO algorithm and the lower-level problem with conventional methods, then to obtain the global optimal solutions by layer iteration. Based on two metamorphic PSO algorithm, Xiang-yong Li dealt with the upper-level and lower-level problems by interactive iteration, then to solve common bi-level programming problem directly by simulating the decision making process of bi-level programming model [10]. Thus, we calculate, respectively, the upper-level and lower-level problems via using PSO algorithm and acquire the best solution by means of interactive iteration. The bi-level algorithm is outlined as follows:

  1. Step 1:

    Argument initialization. Initialize the size of particle swarm N, inertia weight w, learning factor \( c_{1} \), \( c_{2} \), maximum iteration M, the dimensions of bi-level problem D, and set k = 1.

  2. Step 2:

    According to the constraints of the upper-level problem, the initial solution \( x_{0} \) of upper-level decision variable x can be obtained and set \( fbest = {\text{INF}} \).

  3. Step 3:

    According to the initial solution \( x_{0} \), the corresponding optimal solution \( y_{0} \) of the lower-level problem can be calculated using PSO algorithm.

  4. Step 4:

    Return the optimal solution \( y_{0} \) to the upper-level problem and get the optimal solution and individual fitness with PSO algorithm, then to get the solution x and target function value f. Otherwise, for the constraints, the fitness function is formed by means of penalty function.

  5. Step 5:

    Compare the target function value f with \( fbest \), if \( f < fbest \), then set \( fbest = f \), \( xbest = x \), \( ybest = y{}_{0} \), or else go to Step 6.

  6. Step 6:

    If the termination condition is met, stop; otherwise, set \( x_{0} = xbest \), \( k = k + 1 \) and go to Step 3.

  7. Step 7:

    Output the optimal solution x, y, and target function value \( xbest \), \( ybest \) of the upper-level and lower-level modes.

Numerical Application

The proposed heuristic PSO algorithm is implemented in a simple network as shown in Fig. 1. There are two O–D pairs: from O1 to D1 and from O2 to D2. There are seven alternative paths for O–D pairs and each O–D traffic flow is 1000 veh/h. In this simple network, there are two signalized intersections A and B, and a straight forward control plan for each signalized intersections is maken in case of one-way traffic. \( T_{A} \) and \( T_{B} \) \( \left( {T_{i} \in \left[ {30,120} \right]} \right) \), respectively, represents the cycle length of the signalized intersections A and B. We suppose that \( l_{1} = l_{3} = 500\;{\text{m}} \), \( l_{2} = 300\;{\text{m}} \), \( l_{4} = l_{7} = 400\;{\text{m}} \), and \( l_{5} = l_{6} = 600\;{\text{m}} \). According to Fig. 1, we assume that the relationship of green ratio at signalized intersection A is: \( \lambda_{1} + \lambda_{4} = 1 \), \( \lambda_{i} \in \left[ {0.05,0.95} \right] \). Set the size of particle swarm \( N = 200 \), inertia weight \( w = 0.6 \), learning factor \( c_{1} = c_{2} = 1.5 \), maximum iteration \( M = 200 \), the dimensions of bi-level problem \( D = 7 \).

Fig. 1
figure 1

Structure diagram of road network

Full size image

Because the mathematical form of different pollutants is similar, based on different automotive exhaust emissions, the assignment is alike by balancing and distributing traffic [11]. Otherwise, due to the high proportion of CO in all exhaust emissions, this numerical example only analyzes the effects of CO pollutants on traffic assignment.

α = 0, β = 1

To rule out the single correlation between “the minimum total impedance of all road users” and “user optimal assignment,” set the parameters \( \alpha \) and \( \beta \) on the upper-level problem: When \( \alpha \) is zero and \( \beta \) is one, the upper-level problem can be simplified into single-objective programming problem. Meanwhile, set initialization: \( T_{A} = T_{B} = 80 \), \( \lambda_{1} = \lambda_{4} = \lambda_{2} = \lambda_{6} = 0.5 \).

Based on MATLAB software, write project on heuristic PSO algorithm, and the callable function is written by handling the target function and constraints of the upper-level and lower-level models with penalty function. Using the above heuristic PSO algorithm, after repeated checking, this paper takes assignment on segment 1, for example, to draw the flow curve of the upper-level and lower-level models, whose running results are shown as follows:

\( x_{1} = 234.255 \), \( x_{2} = 661.303 \), \( x_{3} = 371.287 \), \( x_{4} = 126.982 \), \( x_{5} = 327.382 \), \( x_{6} = 227.538 \), \( x_{7} = 177.345 \). \( T_{A} = 80.228 \), \( T_{B} = 80.831 \), \( \lambda_{1} = 0.666 \), \( \lambda_{4} = 0.334 \), \( \lambda_{2} = 0.805 \), \( \lambda_{6} = 0.195 \), \( Z^{\prime}(X) = 535,080 \) (Fig. 2).

Fig. 2
figure 2

Comparison of distribution flow in the road segment 1

Full size image

Assuming that the single correlation between “the minimum total impedance of all road users” and “user optimal assignment” exists, after each iteration, the assignment results for road segment 1 should be a trend in the same and complete coincidence curve. However, it can be obtained from Fig. 2, in the process of solving this bi-level programming model, which is the upper-level and lower-level model acquire their optimal solutions by interactive iteration, then to obtain the optimal solutions of this model.

α = 0.5, β = 0.5

In order to make the upper-level model to become a multi-objective optimization model, set parameters \( \alpha \) and \( \beta \), when \( \alpha \) is 0.5 and \( \beta \) is 0.5. Meanwhile, set initialization: \( T_{A} = T_{B} = 80 \), \( \lambda_{1} = \lambda_{4} = \lambda_{2} = \lambda_{6} = 0.5 \). Based on MATLAB software, using the above heuristic PSO algorithm, after repeated checking, the running results are shown as follows:

\( x_{1} = 234.255 \), \( x_{2} = 561.303 \), \( x_{3} = 371.287 \), \( x_{4} = 226.982 \), \( x_{5} = 257.382 \), \( x_{6} = 207.538 \), \( x_{7} = 247.345 \). \( T_{A} = 90.228 \), \( T_{B} = 85.831 \), \( \lambda_{1} = 0.566 \), \( \lambda_{4} = 0.434 \), \( \lambda_{2} = 0.705 \), \( \lambda_{6} = 0.295 \), \( F(X) = 455,080 \), \( E(X) = 405,080 \), and \( Z^{\prime}(X) = 485,080 \).

The Comparison of Optimization Results

This model is calculated, respectively, by heuristic PSO algorithm and heuristic genetic algorithm, which is also simulated by VISSIM to obtain the exhaust emissions and the total impedance, and the comparisons of them are shown in Table 1.

Table 1 Comparison of the model algorithm optimal results
Full size table

The above table shows that the signal cycle length with heuristic PSO algorithm is 90 and 85 s, and green ratio is 0.57, 0.43, 0.70, and 0.30, which reduces the total automotive exhaust emissions in the network by 41.21% and the total impedance by 16.15% by comparing with the VISSIM simulation results. Compared with heuristic genetic algorithm, both based on the optimization results of the single-objective model or multi-objective model, the optimization results using heuristic PSO algorithm have obvious superiority, which increase, respectively, the optimization rate of the exhaust emissions and the total impedance by 2.22 and 4.18%.

Summary

The problem of combined trip matrix estimation and system equilibrium assignment has been addressed in this paper. The proposed bi-level multi-objective programming model based on system equilibrium describes the automotive exhaust emissions problem in urban network and road manager’s estimation of travel time as well as user’s, in which the upper-level model minimizes the exhaust emissions and the total impedance from the perspective of manager; on the other hand, from road user perspective, the lower-level model establishes user equilibrium assignment model. At the same time, this paper designs heuristic PSO algorithm to solve this model, and the numerical example shows the great feasibility of the model and superiority of heuristic PSO algorithm compared with heuristic genetic algorithm.