Keywords

1 Introduction

Operation research has become increasingly important in the face of fast moving technology and increasing complexities in business and industry. Business andeconomic situation are concerned with planning activity. It can be maximum production, minimum cost, and maximum profit under limited resource constraints. Such problems are referred to as the problem of constraints optimization.

A linear programming is a technique for determining an optimum schedule of interdependent activities in view of accessible resources. A problem thus obtained, known as linear programming problem. Linear programming also called linear optimization is a technique to achieve the best outcome in a mathematical model. This new approach to systematic and scientific study of the operation of the system was called the operation research.

With the help of linear programming problem, the optimal solution and the best sense of efficiency can be emphasized.

In the mathematical model of LPP, the requirements are represented by linear relation. The representation of linear programming problem is as follows:

$$\begin{aligned} \begin{aligned}&\text {Maximize/Minimize} \quad \quad \quad \quad c^Tx \\&\text {subject to} \quad \quad \quad \quad \quad Ax \le b \\&\text {and} \quad \quad \quad \quad \quad \quad \quad x \ge 0 \\ \end{aligned} \end{aligned}$$
(1)

Standard Form of Linear Programming problem can be written as:

$$\begin{aligned} \begin{aligned}&\text {Maximize/Minimize} = c_1x_1+c_2x_2+\ldots +c_nx_n \\&\text {subject to} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\&a_{11}x_1+a_{12}x_2+\ldots +a_{1n}x_n(\le = \ge )b_1\\&a_{21}x_1+a_{22}x_2+\ldots +a_{2n}x_n(\le = \ge )b_2\\&a_{m1}x_1+a_{m2}x_2+\ldots +a_{mn}x_n(\le = \ge )b_m\\&\text {OR}\quad \quad \quad \quad \quad \quad \quad \\&\sum _{i=1,j=1}^{mn} a_{ij} x_j \le or \ge b_i\quad \quad \quad \\ \end{aligned} \end{aligned}$$
(2)

These linear equations are the constraints for the objective function. Here are the decision variables and represents the availability of m constraints Unfortunately, some times, the actual practical situations are often not deterministic. There exist certain types of dubieties in social, industrial and economic systems, such as randomness of occurrence of events can lead to improper optimization. Such types of dubieties (Feasible uncertainties) are associated with the difficulty of making sharp or precise decision. Feasible uncertainties deal with the situation where the information cannot be valued sharply or cannot be described clearly in linguistic term, such as preference related information. At a certain point of time, the availabilities of m constraints can be fluctuated in term of probabilistic increment, probabilistic decrement or in the both directions then general LPP cannot explicit the proper optimization. In these situations fuzzy lpp can provide the better optimization.

If the fluctuation is available in terms of increment or decrement then the use of triangular (right angle) fuzzy linear programming problem benefits inintroducing the credibility for the increase or decrease in the . This credibility fulfills the necessities to find out the lower and upper bounds for the initial LPP. If the fluctuation is available in the both directions then triangular (s, l, r) fuzzy linear programming problem can be proposed to achieve the required optimization. In this project we are proposing the triangular (s, l, r) fuzzy LPP to achieve realistic optimization. The triangular(s, l, r) Fuzzy LPP in which only the right hand side numbers \(B_i\) are fuzzy number can be expressed as:

$$\begin{aligned} \begin{aligned}&\text {Max} \sum _{j=1}^{n} c_{j} x_j\quad \quad \quad \quad \quad \\&\text {such that} \sum _{j=1}^{n} a_{ij}(s,l,r)x_j \le B_i(s,l,r)\\&\forall x_j \ge 0 \, \text {and} \, j \in N_n\quad \quad \quad \quad \end{aligned} \end{aligned}$$
(3)

where \(a_{ij}\) and \(B_i\) terms are fuzzy number. This model has an appropriate and reasonable interpretation of situational based optimization and it can fill the gap between the vagueness of constrains and standard optimization.

2 Fuzzy Set

Fuzzy sets [17] are those sets which allows partial membership i.e. between 0 and 1. A fuzzy set S can be defined on the universe of discourse U as follows:

$$\begin{aligned} \begin{aligned}&S=\{(x,\mu _S(x)) | x \epsilon U\} \end{aligned} \end{aligned}$$
(4)

where \(\mu _S\) is the membership function of fuzzy set S within range [0,1] and \(\mu _S(x)\) indicates the degree of membership of x in S lies in range [0,1].

2.1 Convex Fuzzy Set

If the membership value of any membership function are monotonically increase and decrease for some element in universe then those fuzzy set S in universe of discourse U is called a convex fuzzy set [9].

2.2 Normal Fuzzy Set

A fuzzy set [9] is said to be normal fuzzy set if there exists at least one element \(x \epsilon U\) such that \(\mu _S(x) = 1\) where no membership function has its value equal to 1 is called sub-normal fuzzy set.

2.3 Fuzzy Number

A fuzzy number [9] is a regular number in which the value corresponding to element between 0 and 1, called membership functions, instead of one single value.

2.4 Defuzzification

The process of converting the fuzzy number output to a crisp value is called defuzzification. In order to make decisions to maintenance the actions it is necessary to convert the fuzzy number output into a crisp value.

3 Literature Review

The fuzzy logic idea was first presented by Loft Zadeh, professor at the University of California at Berkley. This fuzzy logic when applied to linear decision making then fuzzy linear programming came in existence. Because of the continuous efforts of the researchers the fuzzy linear programming now days is broadly applicable to many fields. With the assistance of fuzzy programming we can calculate the variation in some objective function when there is variation in the constraints of the objective function. There are numerous real life applications of fuzzy linear programming similar in the analysis of future performance of organizations and factories.

The basic arithmetic operations for two generalized positive parabolic fuzzy numbers [7] by using the concept of the distribution functions. There is no need to compute the -cut of the fuzzy number which becomes more powerful than the standard method. A newly generalized improved score function [6] has been presented to incorporating the idea of weighted average in fuzzy set environment. The method for solving the multi-criteria decision making (MCDM) problem has also been presented for unknown attribute weights. Singh [16] proposed a method to reduce the large data-set using soft computing techniques, such as fuzzy sets and artificial neural network, which can decrease the dimensionality of data-set. Garg [5] proposed a method to quantify the uncertainties, generic, extensible for the application domain and sensitivity of system performance which investigates the various reliability parameters in terms of membership and non-membership functions by using -cut and the weakest t-norm based arithmetic operations on triangular intuitionistic fuzzy sets. Rani, Gulati, and Garg [14] demonstrated a method for solving multi-objective optimization problem under the optimistic and pessimistic view point. This problem considered as the parabolic multi-objective non-linear optimization programming problem (PMONLOPP) such as linear/non-linear membership functions corresponding to each objective has been taken.

Weldon A. Lodwick and Katherine A. Bachman [10] concentrated on solving large scale fuzzy and possibilistic optimization problems. They took an optimization problem in radiation therapy with many orders of complexity from 100 to 62,250 constraints for fuzzy and possibilistic linear and non-linear programming implementations possessing fuzzy inequalities, fuzzy right-hand side values and possibilistic right-hand side is used to show that fuzzy and possibilistic optimization are useful. In this project he concentrated on the uncertainty in the right side of limitations which arises in the context of the radiation therapy problem. The result shows that fuzzy and possibilistic optimization is a natural and effective way to model of various type of optimization under uncertainty problems.

P.K. De and D. Das [1] proposed a new ranking procedure for trapezoidal intuitionistic fuzzy number(TRIFN). To serve this purpose, the value and ambiguity index of TRIFNs have been defined. In order to define the rank of TRIFNs, they proposed a ranking function by taking the sum of value and ambiguity index.

Wan [13] proposed a technique on multi-attribute group decision making problems (MAGDM) in which attribute values are expressed with (TrIFNs), which are further solved by developing a new decision method based on the power average operators of (TrIFNs). Hereby the power average operator of real numbers is extended to four kinds of power operators of (TrIFNs) such as power average operator of (TrIFNs), the weighted power average operator of (TrIFNs), the power ordered weighted average operator of (TrIFNs), and the power hybrid average operator of (TrIFNs).

Ganesan and Veeramani [4] proposed fuzzy linear programming problem which involve symmetric trapezoidal fuzzy numbers. Some interesting and important results are obtained, to a solution of fuzzy linear programming problems without converting them to crisp linear programming problems.

Pandey [11] proposed four new aggregation operators based on the geometric and arithmetic means of L- and R- or right side and left side angles of apex for triangular and trapezoidal fuzzy numbers respectively. In this technique, a new aggregation operator for TFNs in which the L- and R- membership function of lines of the aggregate (TFN) in which slopes are the arithmetic means of the corresponding L- and R- slopes of the individual (TFNs).

Hassan Mishmast Nehi and Hamid Reza Maleki [12] worked on Intuitionistic fuzzy numbers and its applications in fuzzy optimization problem. He introduces the trapezoidal intuitionistic fuzzy numbers and proved some operation for them. He also introduces the intuitionistic fuzzy optimization problem by use of the membership and non-membership functions. Frank Rogers, J. Neggers and Younbae Jun [15] demonstrated method for optimizing linear problems with uncertain constraints. They have focused on linear fuzzy programing problem. When they were solving the problems they found that optimizing fuzzy constraints and objective that consist of triplet and appears like triangular fuzzy numbers but they differ in that way that they are a hybrid fuzzy number that has characteristics that are both fuzzy and crisp.

Ali Ebrahimnejad and Madjid Tavana [3] worked on method for solving linear programing problems with symmetric trapezoidal fuzzy numbers. They proposed a new method for solving fuzzy linear programming problem in which the coefficient of the objective function and the values and the of the right hand side are symbolized by symmetric trapezoidal fuzzy number while the elements of the coefficients matrix are represented as real numbers. Then they converted the fuzzy linear programming problem into an equivalent crisp Linear programming problem and solved the crisp problem with the general primal simplex method. They showed that the method they were using is simpler and computationally more efficient that two competing fuzzy linear programming technique commonly used in the literature.

Yenilmez and Gasimov [8] they concentrate on linear programming problem with only fuzzy technological coefficients. Only the case of fuzzy numbers with linear membership functions is being considered and the “modified sub gradient method” for solving these types of problems have proposed. They also compared this method with well known “fuzzy decisive set method”.

4 Methodology

4.1 Method of Calculation:

The general form of triangular Fuzzy LPP is (s, l, r) fuzzy LPP in which \(a_{ij}\) and \(B_i\) are fuzzy number is:

$$\begin{aligned} \begin{aligned}&\text {Max} \sum _{j=1}^{n} c_{j} x_j\quad \quad \quad \quad \quad \\&\text {such that} \sum _{j=1}^{n} a_{ij}(s,l,r)x_j \le B_i(s,l,r)\\&\forall x_j \ge 0 \, \text {and} \, j \in N_n\quad \quad \quad \quad \\ \end{aligned} \end{aligned}$$
(5)

where \(a_{ij}\) and \(B_i\) terms are fuzzy number.

Any triangular fuzzy number A can be represented by three real number (s, l, r) whose meaning is defined in the below Fig. 1.

Fig. 1.
figure 1

Triangular (s,1,r) fuzzy number

Full size image

Using this representation, we can write A= (s, l, r). Now according to D.K.J. Dipankar [2].

$$\begin{aligned} \begin{aligned}&\text {Max} \sum _{j=1}^{n} c_{j} x_j\quad \quad \quad \quad \quad \quad \quad \quad \\&\text {such that} \sum _{j=1}^{n} (s_{ij},l_{ij},r_{ij})x_{ij} \le (t_i,u_i,v_i)(i \in N_m)\quad \quad \\&\forall x_j \ge 0, (j \in N_m)\quad \quad \quad \quad \quad \quad \quad \\ \end{aligned} \end{aligned}$$
(6)

where \(a_{ij}=(s_{ij},l_{ij},r_{ij})\) and \(B_i=(t_i,u_i,v_i)\) are fuzzy number. The general structure of Eq. (3) is defined as follows:

$$\begin{aligned} \begin{aligned}&\text {Max} \sum _{j=1}^{n} c_{j} x_j \quad \quad \quad \quad \quad \quad \\&\text {such that} \sum _{j=1}^{n} s_{ij}x_{j} \le t_i \quad \quad \quad \quad \\&\sum _{j=1}^{n} (s_{ij}-l_{ij})x_j \le t_i-u_i\quad \quad \quad \quad \\&\sum _{j=1}^{n} (s_{ij}+r_{ij})x_j \le t_i+v_i(i \in N)\, \forall x_j \ge 0 \, \text {and} \, j \in N\\ \end{aligned} \end{aligned}$$
(7)

Here the problem is of second type i.e. the fuzzy linear programming problem with fuzzy right hand side numbers.

$$\begin{aligned} \begin{aligned}&\text {Max} \, z = \sum _{j=1}^n c_j x_j\quad \quad \quad \\&\text {subject to} \sum _{j=1}^n a_{ij}x_j \le \tilde{b_i}\quad \quad \\ {}&\text {where}\quad 1 \le i \le m,1\le j \le n, x_j \ge 0 \end{aligned} \end{aligned}$$
(8)

\(\tilde{b_i}\) represents the availability of constraints the accent symbol shows that this quantity is fuzzy means there is increase or decrease in this quantity after some time. But in this project work the optimization is with respect to increase in the availability of constraints. This means the problem will be converted into the LPP.

$$\begin{aligned} \begin{aligned}&\text {Max} \, z = \sum _{j=1}^n c_j x_j\quad \quad \quad \\&\text {subject to} \sum _{j=1}^n a_{ij}x_j \le b_i + p_i\quad \\ {}&\text {where}\quad 1 \le i \le m,\,1\le j \le n, x_j \ge 0 \end{aligned} \end{aligned}$$
(9)

In this LPP is the probabilistic increase in the availability of constraints. The main task is to optimize the problem when there is an increase in the availability of constraints.

In the above kind of problem, the membership grades can be introduced with respect to the increase in the availability of constraints. The membership grades for will be as follows:

$$\begin{aligned} \begin{aligned}&B_i = {\left\{ \begin{array}{ll} 1 &{} \text {when}\quad x \le b_i, \\ \frac{b_i+p_i-x}{p_i} &{} \text {when}\quad b_i \le x \le b_i+p_i, \\ 0 &{} \text {when}\quad x \ge b_i+p_i \end{array}\right. } \end{aligned} \end{aligned}$$
(10)

These are the membership grades for the right hand side coefficient i.e. the availability of constraints. Here x is the variable and x R. For the optimization of this type of problem we have to calculate the lower and upper bounds of the optimal values. The value for lower bound (\(Z_l\)) will be:

$$\begin{aligned} \begin{aligned}&\text {Max}\, z = \sum _{j=1}^n c_j x_j\quad \quad \quad \\&\text {subject to} \sum _{j=1}^n a_{ij}x_j \le b_i\quad \\ {}&\text {where}\quad 1 \le i \le m,\, 1\le j \le n, \, x_j \ge 0 \end{aligned} \end{aligned}$$
(11)

The LPP with the initial value of the right hand side coefficient will be the lower bound for the problem.

Now the value for the upper bound (\(Z_u\)) will be-

$$\begin{aligned} \begin{aligned}&\text {Max} \quad z = \sum _{j=1}^n c_j x_j\quad \quad \quad \\&\text {subject to} \sum _{j=1}^n a_{ij}x_j \le b_i + p_i\quad \\ {}&\text {where}\quad 1 \le i \le m, \, 1 \le j \le n, \, x_j \ge 0 \end{aligned} \end{aligned}$$
(12)

Here the right hand coefficient will be total probabilistic increase in the availability of constraints.

These LPPs for lower and upper bounds can be solved by using the Simplex method which is a technique for solving LPP. These lower and upper bounds will be used to get the optimized fuzzy LPP.

Optimized fuzzy LPP:

$$\begin{aligned} \begin{aligned}&\text {Max} \quad z = \lambda \quad \quad \quad \quad \quad \\&\text {subject to} \quad \lambda (Z_u-Z_l)-cx\le -Z_l\\&\lambda (p_i)+\sum _{j=1}^n a_{ij}x_j \le b_i + p_i \quad \\ {}&\text {where} \quad x \ge 0 \quad and \quad 0 \le \lambda \le 1 \quad \end{aligned} \end{aligned}$$
(13)

This fuzzy optimized LPP will give the membership grade for our initial LPP. Here represents the membership grade and \(Z_u\) and \(Z_l\) are the upper and lower bounds. is the objective function of the initial LPP. The term with summation sign represents the constraints of given LPP and is the probabilistic increase in the availability of the constraints.

5 Data and Problem Identification

The data given below in Table 1 is of the railway industry, Kapurthala of the year 2009–10. This data shows the manufacturing cost of different types constrains of coaches. Kapurthala railway was established in 1986, it is a coach manufacturing unit of Indian railway and manufactured more than 30000 passenger coaches of different types in Table 1 where LAB= labor, MAT= Material, AOH= Administrative overhead charge, FOH= Factory overhead charges, TOH= Township overhead charges, SOH= Shop overhead charges, PROF. CHAR= Performa charges.

Table 1. Production cost of different coaches
Full size table

In the year 2009–2010 the total cost of different coaches is taken as an objective function which is to be minimized with respect to the cost constraints. As per the given data the total availability of cost constraints is LAB, MAT, FOH, AOH, TOTAL O/HEAD, and PROF. CHAR: - 121.72, 2039.14, 193.02, 151.93, 32.41, 13.19, 356.27, 109.31 respectively. But they can be increased and decreased as per requirement. So, in this situation we are proposing a Triangular Fuzzy LPP (s, l, r) and Right Angle Triangular Fuzzy LPP to minimize the production cost. However, Table 2 shows the quantities of increments and decrements in the basic production cost.

Table 2. Total basic availability of cost parameter with probabilistic increments and decrements
Full size table

5.1 Modeling and Optimization:

The total cost is minimized using the real time data as follows

Minimize Z = \(66.14x_1+83.78x_2+58.37x_3+56.94x_4+59.61x_5+76.37x_6+255.51x_7+64.73x_8+139.14x_9+153.44x_{10}+92.87x_{11}+92.87x_{12}+217.31x_{13}+48.57x_{14}+48.77x_{15}+227.33x_{16}+342.66x_{17}+230.30x_{18}+258.99x_{19}+87.02x_{20}\)

\(4.11x_1+4.27x_2+3.82x_3+3.98x_4+3.78x_5+3.92x_6+9.33x_7+3.88x_8+7.11x_9+7.11x_{10}+5.91x_{11}+5.91x_{12}+6.70x_{13}+2.96x_{14}+2.99x_{15}+9.82x_{16}+9.94x_{17}+10.63x_{18}+10.73x_{19}+4.82x_{20}\le (121.72,6.086,6.086)\)

\(46.15x_1+62.28x_2+39.95x_3+38.03x_4+41.28x_5+56.65x_6+205.01x_7+45.77x_8+103.36x_9+116.88x_{10}+63.32x_{11}+63.32x_{12}+179.46x_{13}+34.16x_{14}+34.22x_{15}+178.21x_{16}+285.52x_{17}+177.81x_{18}+205.56x_{19}+62.2x_{20}\le (2039.14,101.957,101.957)\)

\( 6.2x_1+6.75x_2+5.76x_3+6.28x_4+5.70x_5+6.20x_6+14.13x_7+5.85x_8+11.24x_9+11.24x_{10}+10.22x_{11}+10.22x_{12}+10.13x_{13}+4.45x_{14}+4.73x_{15}+15.13x_{16}+17.82x_{17}+16.41x_{18}+16.17x_{19}+8.39x_{20}\le (193.02,9.651,9.651)\)

\( 5.49x_1+5.09x_2+5.10x_3+4.74x_4+5.05x_5+4.67x_6+12.51x_7+5.18x_8+8.48x_9+8.48x_{10}+7.27x_{11}+7.27x_{12}+8.97x_{13}+3.94x_{14}+3.57x_{15}+11.41x_{16}+12.05x_{17}+12.37x_{18}+14.32x_{19}+5.97x_{20}\le (32.41,7.5965,7.5965)\)

\( 1.10x_1+1.11x_2+1.02x_3+1.04x_4+1.01x_5+1.02x_6+2.49x_7+1.03x_8+1.86x_9+1.86x_{10}+1.69x_{11}+1.69x_{12}+1.79x_{13}+0.79x_{14}+0.78x_{15}+2.50x_{16}+2.68x_{17}+2.71x_{18}+2.85x_{19}+1.39x_{20}\le (32.41,1.6205,1.6205)\)

\( 0.18x_1+0.59x_2+0.15x_3+0.36x_4+0.16x_5+0.54x_6+0.78x_7+0.17x_8+0.96x_9+1.11x_{10}+0.37x_{11}+0.37x_{12}+0.68x_{13}+0.13x_{14}+0.33x_{15}+1.69x_{16}+1.73x_{17}+1.69x_{18}+0.78x_{19}+0.42x_{20}\le (13.19,0.6595,0.6595)\)

\( 12.97x_1+13.54x_2+12.03x_3+12.42x_4+11.92x_5+12.43x_6+29.91x_7+12.23x_8+22.54x_9+22.69x_{10}+19.55x_{11}+19.55x_{12}+21.57x_{13}+9.31x_{14}+9.41x_{15}+30.73x_{16}+34.28x_{17}+33.18x_{18}+34.12x_{19}+16.17x_{20}\le (356.27,17.8135,17.8135)\)

\( 2.91x_1+3.69x_2+2.57x_3+2.51x_4+2.63x_5+3.37x_6+11.26x_7+2.85x_8+6.13x_9+6.76x_{10}+4.09x_{11}+4.09x_{12}+9.58x_{13}+2.14x_{14}+2.15x_{15}+8.57x_{16}+12.92x_{17}+8.68x_{18}+8.58x_{19}+3.83x_{20}\le (109.31,5.4655,5.4655)\)

6 Results and Discussion

Sometimes classical optimization techniques fail to deliver the targeted result due to uncertainty of data. We can apply the fuzzy optimization techniques in these situations to mitigate the distortion of the result due to uncertainty of data. If the constraints are uncertain and have uncertain increment and decrement then Triangular Fuzzy linear programming problem (s, l, r) help to get the required outcome. Here we have proposed a TFLPP (s, l, r) and triangular fuzzy lpp model to optimize the cost of production of different coaches of RCF Kapurthala. The minimized cost with (s, l, r) fuzzy LPP is Z = 2792.887 . If the cost is minimized using increment, then the minimized cost with (s, r) fuzzy LPP is Z = 2808.6939934732. If the cost is minimized using decrement. The minimized cost with (s, l) is Z = 2541.1993274281. The minimized cost without the increments and decrement is Z = 2674.9466604506. Now these optimal solutions can be categorized into three different cases to achieve the desired membership grade with respect to optimal solution.

6.1 Case-I

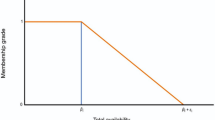
The optimized fuzzy lpp (Right angle triangle) for membership grade has been constructed using the optimal solution of (s, l, r)lpp as a lower bound and (s, r)lpp as an upper bound and then the membership grade has been derived. The following graph is representing the membership grade function of right angle triangular fuzzy LPP (Fig. 2).

Fig. 2.
figure 2

Membership function of optimized cost using optimal solution of (s, l r) and (s, r) LPP

Full size image

The optimized membership grade is derived that is 0.013

$$\begin{aligned} \begin{aligned}&B(X) = {\left\{ \begin{array}{ll} 1 &{} \text {when}\quad x \le 2792.887, \\ \frac{2808.693-x}{15.806} &{} \text {when}\quad 2792.887 \le x \le 2808.693, \\ 0 &{} \text {when}\quad x \ge 2808.693 \end{array}\right. } \end{aligned} \end{aligned}$$
(14)

The final optimal solution for Case-I is obtained by using the membership grade (0.013) and that is x=2808.483.

6.2 Case-II

The optimized fuzzy lpp (Right angle triangle) for membership grade has been constructed using the optimal solution of (s, l) as a lower bound and (s, l, r) as an upper bound and then the membership grade has been derived. The following graph is representing the membership grade function of right angle triangular fuzzy LPP (Fig. 3).

Fig. 3.
figure 3

Membership function of optimized cost using optimal solution of (s, l) and (s, l, r)

Full size image

The optimized membership grade is derived that is 0.541

$$\begin{aligned} \begin{aligned}&B(X) = {\left\{ \begin{array}{ll} 1 &{} \text {when}\quad x \le 2541.199, \\ \frac{2792.887-x}{251.687} &{} \text {when}\quad 2541.199 \le x \le 2792.887, \\ 0 &{} \text {when}\quad x \ge 2792.887 \end{array}\right. } \end{aligned} \end{aligned}$$
(15)

The final optimal solution for Case-II is obtained by using the membership grade (0.541) and that is x=2656.484.

6.3 Case-III

The optimized fuzzy lpp (Right angle triangle) for membership grade has been constructed using the optimal solution of (s)lpp as a lower bound and (s, l, r)lpp as an upper bound and then the membership grade has been derived. The following graph is representing the membership grade function of right angle triangular fuzzy LPP (Fig. 4).

Fig. 4.
figure 4

Membership function of optimized cost using optimal solution of (s, l) and (s, l, r)

Full size image

The optimized membership grade is derived that is 0.295

$$\begin{aligned} \begin{aligned}&B(X)= {\left\{ \begin{array}{ll} 1 &{} \text {when}\quad x \le 2674.946, \\ \frac{2792.887-x}{117.940} &{} \text {when}\quad 2674.946 \le x \le 2792.887, \\ 0 &{} \text {when}\quad x \ge 2792.887 \end{array}\right. } \end{aligned} \end{aligned}$$
(16)

The final optimal solution for Case-III is obtained by using the membership grade (0.295) and that is x=2758.007.

7 Conclusion and Future Scope

The modeling and optimization of production cost of RCF kapurthala has been done using the Triangular (s, l, r)triangular (Right angle) fuzzy linear programming problem. Owing to probabilistic increments in the availability of different constrains, the actual costs of production were vacillating or uncertain, the situational based Fuzzy models have been expressed to mitigate the destruction in the cost optimization and examined the credibility of optimized value. The production costs of different coaches from the year 2009–10 were considered as input. The total cost has been targeted in order to optimize. The lower and upper bound have been calculated using TFLPP-(s, l, r), TFLPP-(s, l), TFLPP-(s, r) and TFLPP-(s) for the objective function of the optimized fuzzy LPP. The minimized cost with (s, l, r) fuzzy LPP is Z = 2792.887. The cost is minimized using the TFLPP-(s, r) and that is Z = 2808. 6939934732.The cost is minimized using TFLPP-(s, l) and that is Z = 2541.1993274281 and the minimized cost without the increments and decrement is Z = 2674.9466604506. The following results have been made from described modelling. The optimized fuzzy lpp (Right angle triangle) for membership grade has been constructed using the optimal solution of TFLPP (s, l, r) as a lower bound and TFLPP (s, r) as an upper bound and then the membership grade has been derived. The final optimal solution for this case is obtained and that is x=2808.483 with membership grade 0.013 The optimized fuzzy lpp (Right angle triangle) for membership grade has been constructed using the optimal solution of TFLPP (s, l) as a lower bound and TFLPP (s, l, r) as an upper bound and then the membership grade has been derived. The final optimal solution for this case is obtained and that is x=2656.484 with membership grade 0.541 The optimized fuzzy lpp (Right angle triangle) for membership grade has been constructed using the optimal solution of TFLPP(s) as a lower bound and TFLPP (s, l, r) as an upper bound and then the membership grade has been derived. The final optimal solution for this case is obtained and that is x=2758.007 with membership grade 0.295.

The validity of the method has been evaluated by solving some problems to analysis and optimize the production cost with symmetric and right angle Triangular fuzzy number through fuzzy linear programming problem. Further, the proposed approach can be applied to engineering and mathematical science problems which can be taken for further research.