Statistical Methodologies for Dealing with Incomplete Longitudinal Outcomes Due to Dropout Missing at Random

Abstract

Longitudinal studies are based on repeatedly measuring the outcome of interest and covariates over a sequences of time points. These studies play a vital role in many disciplines of science, such as medicine, epidemiology, ecology and public health. However, data arising from such studies often show inevitable incompleteness due to dropouts or even intermittent missingness that can potentially cause serious bias problems in the analysis of longitudinal data. In this chapter we confine our considerations to the dropout missingness pattern. Given the problems that can arise when there are dropouts in longitudinal studies, the following question is forced upon researchers: What methods can be utilized to handle these potential pitfalls? The goal is to use approaches that better avoid the generation of biased results. This chapter considers some of the key modelling techniques and basic issues in statistical data analysis to address dropout problems in longitudinal studies. The main objective is to provide an overview of issues and different methodologies in the case of subjects dropping out in longitudinal data for both the case of continuous and discrete outcomes. The chapter focusses on methods that are valid under the missing at random (MAR) mechanism and the missingness patterns of interest will be monotone; these are referred to as dropout in the context of longitudinal data. The fundamental concepts of the patterns and mechanisms of dropout are discussed. The techniques that are investigated for handling dropout are: (1) Multiple imputation (MI); (2) Likelihood-based methods, in particular Generalized linear mixed models (GLMMs) ; (3) Multiple imputation based generalized estimating equations (MI-GEE) ; and (4) Weighted estimating equations (WGEE) . For each method, useful and important assumptions regarding its applications are presented. The existing literature in which we examine the effectiveness of these methods in the analysis of incomplete longitudinal data is discussed in detail. Two application examples are presented to study the potential strengths and weaknesses of the methods under an MAR dropout mechanism.

1 Introduction

Longitudinal studies play a vital role in many disciplines of science including medicine, epidemiology, ecology and public health. However, data arising from such studies often show inevitable incompleteness due to dropouts or lack of follow-up. More generally, a subject’s outcome can be missing at one follow-up time and be measured at the next follow-up time. This leads to a large class of dropout patterns. This chapter only pays attention to monotone dropout patterns that result from attrition, in the sense that if a subject drops out from the study prematurely, then on that subject no subsequent repeated measurements of the outcome are obtained. These commonly include studies done by the pharmaceutical industry as contained in protocols for many conditions where data are not collected after a study participant discontinues study treatment. This is highlighted in a recent report on the prevention and treatment of dropout by the National Research Council (Committee on National Statistics Division of Behavioral and Social Sciences and Education, http://www.nap.edu). A summary of the report was provided by Little et al. (2012). However, even in these studies, there typically is both unplanned and planned dropout. A predominately monotone pattern for missing outcome data is less common in clinical outcome studies and in publically-funded trials which are more of a pragmatic nature (e.g., trials in which the intention-to-treat estimand is the primary objective).

Given the problems that can arise when there are dropouts in longitudinal studies, the following question is forced upon researchers. What methods can be utilized to handle these potential pitfalls? The goal is to use approaches that better avoid the generation of biased results. The choice of statistical methods for handling dropouts has important implications on the estimation of the treatment effects, depending on whether one is considering a more of a pragmatic nature analysis or a more exploratory analysis. In case of a pragmatic analysis (intention-to-treat analysis), the goal of the clinical trial researchers is to produce a pragmatic analysis of the data. However, for incomplete longitudinal clinical trials, the dropouts complicate this process as most of the methods to be used when dealing with the dropout problem produce an exploratory analysis in nature rather than a pragmatic perspective. The literature presents various techniques that can be used to deal with dropout , and these range from simple classical ad hoc methods to model-based methods. These methods should be fully understood and appropriately characterized in relation to dropouts and should be theoretically proven before they are used practically. Further, each method is valid under some but usually not all dropout mechanisms, but one needs to realize that at the heart of the dropout problems it is impossible to identify the dropout mechanism (will be discussed later). Thus, it is important to address the mechanisms that govern dropouts. In this chapter, we present some of the various techniques to address the dropout problem in longitudinal clinical trials. The main objective is to investigate various techniques, and to discuss the most appropriate techniques for handling incomplete longitudinal data due to dropouts. The structure of the chapter is as follows. Section 2 presents the key notation and basic concepts used in the entire chapter but when new notation arises it will be explained at the point where it occurs. In Sects. 3 and 4, we give an overview of the various statistical methods in handling incomplete longitudinal studies due to dropout. Two application examples are provided for both cases, continuous and binary outcomes. The dropout generation schemes are also discussed. In addition, full analysis and results of the applications are also given. Finally, the chapter ends with a discussion and conclusion in Sect. 5.

2 Notation and Basic Concepts

Some notation is necessary to describe methods for analyzing incomplete longitudinal data with dropout . We will follow the terminology based on the standard framework of Rubin (1976), Little and Rubin (1987) in formulating definitions for data structure and missing data mechanisms. Let $Y_{i}$ = $(Y_{i1},...,Y_{in_{i}})'$ = $(Y^{o}_{i}, Y^{m}_{i})'$ be the outcome vector of $n_{i}$ measurements for subject i, i = 1,...,n, where $Y^{o}_{i}$ represents the observed data part and $Y^{m}_{i}$ denotes the missing data part. Let $R_{i}=(R_{i1},...,R_{in_{i}})'$ be the corresponding missing data indicator vector of the same dimension as $Y_{i}$, whose elements are defined as

$$\begin{aligned} R_{ij}=\left\{ \begin{array}{cc} 1&{}\text{ if } \;Y_{ij} \;\text{ is } \;\text{ observed },\\ 0&{}\text{ otherwise }. \end{array} \right. \end{aligned}$$

(1)

Complete data refers to the vector $Y_{i}$ of planned measurements. This is the outcome vector that would have been recorded if no data had been missing. The vector $R_{i}$ and the process generating it are referred to as the missingness process. In our case the $R_{i}$ are here restricted to represent participant dropout, and so it has a monotone pattern (Verbeke and Molenberghs 2000). Thus the full data for the ith subject can be represented as $(Y_{i}, R_{i})$ and the joint probability for the data and missingness can be expressed as: $f(y_{i}, r_{i}\mid X_{i}, W_{i}, \theta , \xi )=f(y_{i} \mid X_{i}, \theta )f(r_{i}\mid y_{i}, W_{i},\xi )$, where $X_{i}$ and $W_{i}$ are design matrices for the measurements and dropout mechanism, respectively, $\theta$ is the parameter vector associated with the measurement process and $\xi$ is the parameter vector for the missingness process. According to the dependence of the missing data process on the response process, Little and Rubin (1987), Rubin (1976) classified missing data mechanisms as: missing completely at random (MCAR), missing at random (MAR) and not missing at random (MNAR). The missingness process is defined as MCAR if the probability of non-response is independent of the response; that is, $f(r_{i}\mid y_{i}, W_{i}, \xi )=f(r_{i}\mid W_{i}, \xi )$ and the missingness process is defined as MAR when the probability of non-response depends on the observed values of the response; that is, $f(r_{i}\mid y_{i}, W_{i}, \xi )=f(r_{i}\mid y_{i}^{o}, W_{i}, \xi )$. Finally, the missingness process is defined as MNAR if neither the MCAR nor the MAR assumptions hold, meaning that dependence on unobserved values of the response cannot be ruled out. That is, the probability of nonresponse depends on the missing outcomes and possibly on the observed outcomes. Our main focus is on the MAR mechanism for the dropout process.

When missingness is restricted to dropout or attrition, we can replace the vector $R_{i}$ by a scalar variable $D_{i}$, the dropout indicator, commonly defined as

$$\begin{aligned} D_{i}=1+\sum _{j=1}^{n}R_{ij}. \end{aligned}$$

(2)

For an incomplete dropout sequence, $D_{i}$ denotes the occasion at which dropout occurs. In the formulation described above, it is assumed that all subjects are observed on the first occasion so that $D_{i}$ takes values between 2 and $n+1$. The maximum value $n+1$ corresponds to a complete measurement sequence. If the length of the complete sequence is different for different subjects then we only need to replace n with $n_{i}$. However a common n holds where for example by design all subjects were supposed to be observed for an equal number of occasions or visits. Accordingly, an MCAR dropout mechanism implies $f(D_{i}=d_{i} \mid y_{i}, W_{i}, \xi )=f(D_{i}=d_{i} \mid W_{i}, \xi )$, MAR dropout mechanism, $f(D_{i}=d_{i} \mid y_{i}, W_{i}, \xi )=f(D_{i}=d_{i} \mid y_{i}^{o}, W_{i}, \xi )$ and MNAR dropout mechanism, $f(D_{i}=d_{i} \mid y_{i}, W_{i}, \xi )=f(D_{i}=d_{i} \mid Y_{i}^{m}, Y_{i}^{o}, W_{i}, \xi )$. There are parameters associated with the measurement process but suppressed for simplicity. Note that the MCAR mechanism can be seen as a special case of MAR . Hence the likelihood ratio test can be used to test the null hypothesis that the MCAR assumption holds. However it is not obvious to say a model based on the MAR mechanism is a simplification of a model based on the MNAR assumption. This assertion is supported by the fact that for any MNAR model there is a MAR counterpart that fits the data just as good as the MNAR model (Molenberghs et al. 2008).

3 Dropout Analysis Strategies in Longitudinal Continuous Data

Much of the literature involving missing data (or dropout) in longitudinal studies pertains to the various techniques developed to handle the problem. This section is devoted to providing an overview of the various strategies for handling missing data in longitudinal studies.

3.1 Likelihood Analysis

An appealing method for handling dropout in longitudinal studies is based on using available data, and these only, when constructing the likelihood function. This likelihood-based MAR analysis is also termed likelihood-based ignorable analysis, or direct likelihood analysis Molenberghs and Verbeke (2005). Direct likelihood analysis uses the observed data without the need of neither deletion nor imputation. In other words, no additional data manipulation is necessary when a direct likelihood analysis is envisaged, provided the software tool used for analysis is able to handle measurement sequences of unequal length (Molenberghs and Kenward 2007). To do so, under valid MAR assumption, suitable adjustments can be made to parameters at times when data are prone to incompleteness due to the within-subject correlation. Thus, even when interest lies in a comparison between two treatment groups at the last measurement time, such a likelihood analysis can be conducted without problems since the fitted model can be used as the basis for inference. When a MAR mechanism is valid, a direct likelihood analysis can be obtained with no need for modelling the missingness process. It is increasingly preferred over ad hoc methods, particularly when tools like the generalized linear mixed mixed effect models (Molenberghs and Verbeke 2005) are used. The major advantage of this method is its simplicity, it can also be fitted in standard statistical software without involving additional programming, using such tools as SAS software, procedures MIXED, GLIMMIX and NLMIXED. The use of these procedures has been illustrated by Verbeke and Molenberghs (2000), Molenberghs and Verbeke (2005). A useful summary for these procedures is presented by Molenberghs and Kenward (2007). Despite the flexibility and ease of implementation of direct likelihood method, there are fundamental issues when selecting a model and assessing its fit to the observed data, which do not occur with complete data. The method is sensible under linear mixed models in combination with the assumption of ignorability. Such an approach, tailored to the needs of clinical trials, has been proposed by Mallinckrodt et al. (2001a, b). For the incomplete longitudinal data context , a mixed model only needs missing data to be MAR. According to Verbeke and Molenberghs (2000), these mixed-effect models permit the inclusion of subjects with missing values at some time points for both missing data patterns , namely dropout and intermittent missing values. Since direct likelihood ideas can be used with a variety of likelihoods, in the first application example in this study we consider the general linear mixed-effects model for continuous outcomes that satisfy the Gaussian distributional assumption (Laird and Ware 1982) as a key modelling framework which can be combined with the ignorability assumption. For $Y_{i}$ the vector of observations from individual i, the model can be written as follows

$$\begin{aligned} Y_{i}=X_{i}\beta +Z_{i}b_{i}+\varepsilon _{i}, \end{aligned}$$

(3)

where $b_{i}\sim N(0, D)$, $\varepsilon _{i}\sim N(0, \Sigma _{i})$ and $b_{1},...,b_{N}, \varepsilon _{1},...,\varepsilon _{N}$ are independent. The meaning of each term in (3) is as follows. $Y_{i}$ is the $n_{i}$ dimensional response vector for subject i, containing the outcomes at $n_{i}$ measurement occasions, $1\le i\le N$, N is the number of subjects, $X_{i}$ and $Z_{i}$ are $(n_{i}\times p)$ and $(n_{i}\times q)$ dimensional matrices of known covariates, $\beta$ is the p-dimensional vector containing the fixed effects, $b_{i}$ is the q-dimensional vector containing the random effects and $\varepsilon _{i}$ is a $n_{i}$ dimensional vector of residual components, combining measurement error and serial correlation. Finally, D is a general $(q\times q)$ covariance matrix whose (i, j)th element is $d_{ij}=d_{ji}$ and $\Sigma _{i}$ is a $(n_{i}\times n_{i})$ covariance matrix which generally depends on i only through its dimension $n_{i}$, i.e., the set of unknown parameters in $\Sigma _{i}$ will not depend upon i. This implies marginally $Y_{i}$ $\sim$ N($X_{i}$ $\beta$, $Z_{i}$ $D$ $Z_{i}'$ + $\Sigma _{i}$). Thus if we write $V_{i}=Z_{i}DZ_{i}'+\Sigma _{i}$ as the general covariance matrix of $Y_{i}$, then $f(y_{i},\beta , V_{i})=(2\Pi )^{\frac{-n}{2}}|V_{i}|^{\frac{-1}{2}} \exp \{ -(y_{i}-X_{i}\beta )'V_{i}^{-1}(y_{i}-X_{i}\beta )/2\}$ from which a marginal likelihood involving all subjects can be constructed to estimate $\beta$. In the likelihood context, Little and Rubin (1987) and Rubin (1976) showed that when MAR assumption and mild regularity conditions hold, parameters $\theta$ and $\xi$ are independent, and that likelihood based inference is valid when the missing data mechanism is ignored. In practice, the likelihood of interest is then based on the factor $f(y_{i}^{o} \mid \xi )$ (Verbeke and Molenberghs 2000). This is referred to as ignorability.

3.2 Multiple Imputation (MI)

Multiple imputation was introduced by Rubin (1978). It has been discussed in some detail in Rubin (1987), Rubin and Schenker (1986), Tanner and Wong (1987) and Little and Rubin (1987). The key idea behind multiple imputation is to replace each missing value with a set of M plausible values (Rubin 1996; Schafer 1997). The resulting complete data sets generated via multiple imputation are then analyzed by using standard procedures for complete data and combining the results from these analyses. The technique in its basic form requires the assumption that the missingness mechanism be MAR. Thus, multiple imputation process is accomplished through three distinct steps: (1) Imputation—create M data sets from M imputations of missing data drawn from a different distribution for each missing variable. (2) Analysis—analyze each of the M imputed data sets using standard statistical analysis. (3) Data pooling—combine the results of the M analyses to provide one final conclusion or inference. To discuss these steps in detail, we will follow the approach provided by Verbeke and Molenberghs (2000). Recall that we partitioned the planned complete data ($Y_{i}$) into $Y_{i}^{o}$ and $Y_{i}^{m}$ to indicate observed and unobserved data, respectively. Multiple imputation fills in the missing data $Y_{i}^{m}$ using the observed data $Y_{i}^{o}$ several times, and then the completed data are used to estimate $\xi$. If we know the distribution of $Y_{i}=(Y_{i}^{o}, Y_{i}^{m})$ depends on the parameter vector $\xi$, then we could impute $Y_{i}^{m}$ by drawing a value of $Y_{i}^{m}$ from the conditional distribution $f(y_{i}^{m}\mid y_{i}^{o},\xi )$. Because $\hat{\xi }$ is a random variable, we must also take its variability into account in drawing imputations. In Bayesian terms, $\hat{\xi }$ is a random variable of which the distribution depends on the data. So we first obtain the posterior distribution of $\xi$ from the data, a distribution which is a function of $\hat{\xi }$. Given this posterior distribution, imputation algorithm can be used to draw a random $\xi ^{*}$ from the distribution of $\xi$, and to put this $\xi ^{*}$ in to draw a random $Y_{i}^{m}$ from $f(y_{i}^{m}\mid y_{i}^{o}, \xi ^{*})$, using the following steps: (1) Draw $\xi ^{*}$ from the distribution of $\xi$, (2) Draw $Y_{i}^{m*}$ from $f(y_{i}^{m}\mid y_{i}^{o}, \xi ^{*})$, and (3) Use the complete data $(Y^{o}, Y^{m*})$ and the model to estimate $\beta$, and its estimated variance, using the complete data, $(Y^{o}, Y^{m*})$:

$$\begin{aligned} \hat{\beta _{m}}=\hat{\beta }(Y)=\hat{\beta }(Y^{o}, Y^{m*}), \end{aligned}$$

(4)

where the within-imputation variance is $U_{m}=\hat{Var}(\hat{\beta })$. The steps described above are repeated independently M times, resulting in $\hat{\beta _{m}}$ and $U_{m}$, for $m=1,...,M$. Steps 1 and 2 are referred to as the imputation task, and step 3 is the estimation task. Finally, the results are combined using the following steps for pooling the estimates obtained after $M$ imputations (Rubin 1987; Verbeke and Molenberghs 2000). With no missing data, suppose the inference about the parameter $\beta$ is made using the distributional assumption $(\beta -\hat{\beta })\sim N(0, U)$. The overall estimated parameter vector is the average of all individual estimates:

$$\begin{aligned} \hat{\beta }*=\frac{\sum _{m=1}^{M}\hat{\beta _{m}}}{M}, \end{aligned}$$

(5)

with normal-based inferences for $\beta$ based upon $(\hat{\beta }*-\beta )\sim N(0, V)$ (Verbeke and Molenberghs 2000). We obtain the variance (V) as a weighted sum of the within-imputation variance and the between-imputations variability:

$$\begin{aligned} V=W+\left( \frac{M+1}{M}\right) B, \end{aligned}$$

(6)

where

$$\begin{aligned} \displaystyle W=\frac{\sum _{m=1}^{M}U_{m}}{M} \end{aligned}$$

(7)

defined to be the average within-imputation variance, and

$$\begin{aligned} \displaystyle B=\frac{\sum _ {m=1}^{M}(\hat{\beta _{m}}-\hat{\beta }*)(\hat{\beta _{m}}-\hat{\beta }*)'}{M-1} \end{aligned}$$

(8)

defined to be the between-imputation variance (Rubin 1987).

3.3 Illustration

To examine the performance of direct likelihood and multiple imputation methods, four steps were planned. The steps were as follow: First, a model was fitted to the full data (no data are missing), thus producing what we refer to as true estimates. Second, we generated a dropout rate of 10, 15 and 20% in the outcome (selected at random) variable using defined rules to achieve the required mechanism under MAR assumption. Third, the resulting incomplete data was analyzed using the two different methods using multiple imputation and direct likelihood. Fourth, results from the complete and incomplete data analysis were compared. The actual-data results were presented and used as references. The study aims to investigate how direct likelihood and multiple imputation compare to each other and to the true analysis.

Data Set—Heart Rates Trial

This data set was used in Milliken and Johnson (2009) to demonstrate analyses of repeated measures designs and to show how to determine estimates of interesting effects and provide methods to study contrasts of interest. The main objective was to investigate the effects of three treatments involving two active treatments and a control (AX23, BWW9 and CTRL) on heart rates, where each treatment was randomized to female individuals and each patient observed over four time periods. Specifically, each patient’s heart rate was measured 5, 10, 15 and 20 min after administering the treatment. The only constraint is that the time intervals are not randomly distributed within an individual. In our case, we use the data to achieve a comparative analysis of two methods to deal with missing data. A model which is used to describe the data is similar to a split-plot in a completely randomized design. The model is

$$\begin{aligned} H_{ijk}=\mu +Time_{j}+\delta _{i}+Drug_{k}+(Time*Drug)_{jk}+\varepsilon _{ijk}, \end{aligned}$$

(9)

where $H_{ijk}$ is the heart rate of individual i at time j on drug k, $i=1,...,24$, $j=1, 2, 3,4$ and $k=1,2,3$. The model has two error terms: $\delta _{i}$ represents a subject random effect, and $\varepsilon _{ijk}$ represents a time error component. The ideal conditions for a split-plot in time analysis is that: (1) the $\delta _{i}$ are independently and identically $N(0,\sigma _{\delta }^ {2})$, (2) the $\varepsilon _{ijk}$ are independently and identically $N(0,\sigma _{\varepsilon }^ {2})$, and (3) the $\delta _{i}$ and $\varepsilon _{ijk}$ are all independent of one another. The main purpose of this example is to investigate the effects of the three drugs. Thus, the type III tests of fixed effects and the differences between effects were the quantities of interest in the study. The primary null hypothesis (the difference between the drug main effects) will be tested. The null hypothesis is no difference among drugs. The significance of differences in least-square means is based on Type III tests. These examine the significance of each partial effect; that is, the significance of an effect with all the other effects in the model. In analysis results we present the significance of drug main effects, time main effects and the interaction of time and drug effects.

3.4 Simulation of Missing Values

Since there are no missing values in the example data set described above, it provides us with an opportunity to design a comparative study to compare the two methods to deal with missing data using the results from the complete data analysis as the reference. We carry out an application study to generate the data set with dropouts. In this application, we distinguish between two stages: (1) The dropout generation stage. (2) The analysis stage.

3.4.1 Generating Missing Data

In the first stage, we use the full data set to artificially generate missing values by mimicking the dropout at random mechanism. From the complete data, we draw 1000 random samples of size $N=96$. The incomplete data was generated with 10, 15 and 20% dropout rate. We assume that the dropout depends only on the observed data. Furthermore, a monotone dropout pattern was imposed in the heart rate (outcome of interest); that is, if $H_{ij}$ is missing, then $H_{is}$ is missing for $s\ge j$. The explanatory variables drug, time and interaction between drug and time are assumed to be fully observed. In addition, in order to create the dropout model, we assume that dropout can occur only after the first two time points. Namely, dropout is based on values of H, assuming the H is fully observed in the first two time (time = 1, 2), while for the later times (time = 3, 4) some dropouts may occur. We assume an MAR mechanism for the dropout process and the dropout mechanism depends on individual previously observed values of one of the endpoints. For the MAR mechanism, H was made missing if its measurements exceeded 75 (the baseline mean for heart rate) the previous measurement occasion, beginning with the second post baseline observation. Thus in the generation, the missingness at time = 3, 4 was dependent on the most recently observed values. This was done to achieve the required mechanism under the MAR assumption.

3.4.2 Computations and Handling Missing Data

After generating the missing data mechanism and thus generating the data set with dropout, the next step was to deal with dropout. Handling dropout was carried out using direct likelihood analysis and multiple imputation methods with functions available in the SAS software package. Ultimately, likelihood, multiple imputation and analysis results from the fully observed data set can be compared in terms of their impact on various linear mixed model aspects (fixed effects and least squares means). The proposed methods dealt with the dropout according to the following:

• Imputing dropouts using multiple imputation techniques. This was achieved using procedures MI, MIXED and MIANALYZE with an LSMEANS option. The imputation model is based on model (9) which assumes normality of the variables. For the dropout under MAR , the imputation model should be specified (Rubin 1987). Thus, in the imputation model, we included all the available data (including the outcome, H) to predict the dropouts since they were potentially related to the imputed variable as well as to the missingness of the imputed variable. This means we used variables in the analysis model, variables associated with missingness of the imputed variable and variables correlated with the imputed variable. This was done to increase the plausibility of the MAR assumption, as well as to improve the accuracy and efficiency of the imputation. Once the multiple imputation model is chosen, the number of imputations must be decided. PROC MI was applied to generate M=5 complete data sets. We fixed the number of multiple imputations at M=5, since relatively small numbers are often deemed sufficient, especially for parameter estimation from normally distributed data (see, Schafer and Olsen 1998; Schafer 1999). PROC MIXED was used to set up effect parameterizations for the class variables and we used the ODS statement output to create output data sets that match PROC MIANALYZE for combining the effect mean estimates from the 5 imputed data sets. While PROC MIANALYZE cannot directly combine the least square means and their differences to obtain the effect means of drug and contrasts between drug groups from PROC MIXED, the LSMEANS table was sorted differently so that we enabled the use of the BY statement in PROC MIANALYZE to read it in.

• For comparison, the data was analyzed as they are, consistent with ignorability for direct likelihood analysis implemented with PROC MIXED with LSMEANS option. The REPEATED statement was used, in order to make sure the analysis procedure takes into account sequences of varying length and order of the repeated measurements. Parameters were estimated using Restricted Maximum Likelihood with the Newton-Raphson algorithm (Molenberghs and Verbeke 2005).

3.5 Results

A few points about the parameter estimates obtained by the proposed methods may be noted in the resulting tables. In Table 1, due to the similarities in the findings under the three dropout rates, the results for type III tests of fixed effects under 20 and 30% dropout rates are not presented but are available from the authors. Through the two evaluation criteria in Table 2, the largest bias, also the worst, are highlighted. For the efficiency criterion, the widest confidence interval, also the worst, 95% interval are highlighted.

Table 1 Statistical test for drug, time and drug $\times$ time effects of complete data, direct likelihood and multiple imputation, under 15% dropout rate

Table 2 Bias and efficiency of MI and direct-likelihood, under different dropout rates: MIXED least squares means—(interaction terms are not shown)

The results that show the significance of the effects using direct likelihood and multiple imputation to handle dropout are presented in Table 1. Compared with the results based on the complete data set, we see that type III tests of fixed effects show that both direct likelihood and multiple imputation methods yielded statistically similar results. The analysis shows that the drug effect has significant p-values as its p-values, around 0.004, indicating a rejection of the null hypothesis of equal drug means. The p-value of the drug effect under multiple imputation (0.0043) was slightly higher in comparison to that of the direct likelihood analysis (0.0040), but both methods indicate strong evidence of significance compared to the p-value of 0.0088 for the original complete data set. Evidently, there are no extreme differences between the direct likelihood and multiple imputation methods. However, the p-value for the drug effect was significantly reduced by about 50% compared to the actual data p-value. This indicates a real problem with dropout, both multiple imputation and direct likelihood may lead to rejection of the null hypothesis with a higher probability than would be the case if the data were complete. The test of significance for time effect in type III tests of fixed effects produced significant p-values of <0.0001 in both methods. The test for the interaction between drug and time effects gave a p-value of <0.0001 in both methods, indicating a strong evidence of time dependence on the drug effects. Generally, the proposed methods presented acceptable performance with respect to estimates of p-values in all cases when compared to that based on actual data. In two cases, namely p-values of time effect and interaction drug $\times$ time, the methods yielded the same results as those for complete data.

The results of MI and direct likelihood analysis in terms of bias and efficiency, under three dropout rates are presented in Table 2, which shows the results for the least square means. Note that, again due to similarities in the findings, we do not show full output, as the results of interactions terms are excluded. Examining these results we find the following. For 10% dropout rate, in terms of the biasedness of the estimates, the performance of both methods unsurprisingly yielded equally good performance. However, the benefits of MI over a direct likelihood are clearly evident. In some cases (estimates of time 1, time 2), the methods offered the same estimates as compared to the estimates from complete data. Such results are expected considering the fact that the first and second time points contained observed data for all patients considered in the analysis. An examination of the efficiency suggested that the estimates from MI were typically lower than those from direct likelihood. Nevertheless, the corresponding MI estimates estimates did not differ significantly from those of direct likelihood. Differences in efficiency estimates were never more than 0.03.

Considering the 20% dropout rate, the results revealed that direct likelihood slightly produces higher biases (the only exceptions to this rule occurred for estimate of AX23 and time 4). Regarding efficiency, both the MI and direct likelihood methods yielded estimates similar to each other, and in general, MI tends to have the smallest estimates. A comparison of 30% dropout rate again suggested that the estimates associated with MI were less biased than for direct likelihood, except for time 4. Efficiency results based on both methods were generally similar to their results with 10 and 20% dropout rates. Furthermore, between the two methods, the MI estimates were slightly different from those obtained by direct likelihood, although the degree of these differences was not very large. Overall, the performance of both methods appeared to be independent of the dropout rate.

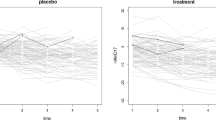
One would ideally need to compare various means with each other. If there is no drug by time interaction, then we will often need to make comparisons between the drug main effect means and the time main effect means. Since the interaction effect mean is significant (as shown in Table 1), we need to compare the drugs with one another at each time point and/or times to one another for each drug. Comparisons of the time means within a drug are given in Fig. 1. Since the levels of time are quantitative and equally spaced, orthogonal polynomials can be used to check for linear and quadratic trends over time for each drug. The linear and quadratic trends in time for all drugs reveal that drug BWW9 shows a negative linear trend, and drug AX23 shows a strong quadratic trend in all methods. Evidently, the differences occurred with drug CTRL in graphs (b) and (c) for direct likelihood and MI, respectively. Both methods yielded slightly different linear trends as compared to that from actual data. The graph in Fig. 1 displays these relationships.

Fig. 1

a The heart rate data—Means over time for each drug for the heart rate data. b Direct likelihood—Means over time for each drug for the heart rate data. c Multiple imputation—Means over time for each drug for the heart rate data

4 Dropout Analysis Strategies in Longitudinal Binary Data

There is a wide range of statistical methods for handling incomplete longitudinal binary data . The methods of analysis to deal with dropout comprise three broad strategies: semi-parametric regression, multiple imputation (MI) and maximum likelihood (ML). In what follows, we utilize three common statistical methods in practice, namely WGEE , MI-GEE and GLMM . First, we compare the performance of the two versions or modifications of the GEE approach, and then show how they compare to the likelihood-based GLMM approach.

4.1 Weighted Generalized Estimating Equation (WGEE)

Next, we follow the description provided by Verbeke and Molenberghs (2005) in formulating the WGEE approach, thereby illustrating how WGEE can be incorporated into the conventional GEE implementations. Generally, if inferences are restricted to the population averages, exclusively the marginal expectations $E(Y_{ij})=\mu _{ij}$ can be modelled with respect to covariates of interest. This can be done using the model $h(\mu _{ij})=x'_{ij}\beta$, where h(.) denotes a known link function, for example, the logit link for binary outcomes, the log link for counts, and so on. Further, the marginal variance depends on the marginal mean, with $Var(Y_{ij})=v(\mu _{ij})\Omega$, where v(.) and $\Omega$ denote a known variance function and a scale (overdispersion) parameter, respectively. The correlation between $Y_{ij}$ and $Y_{ik}$, where $j\ne k$ for $i,j=1, 2,...,n_{i}$, can be given through a correlation matrix $C_{i}=C_{i}(\rho )$, where $\rho$ denotes the vector of nuisance parameters. Then, the covariance matrix $V_i=V_i(\beta ,\rho )$ of $Y_{i}$ can be decomposed into the form $\Omega A_{i}^{1/2}C_{i}A_{i}^{1/2}$, where $A_{i}$ is a matrix with the marginal variances on the main diagonal and zeros elsewhere. Without missing data, the GEE estimator for $\beta$ is based on solving the equation

$$\begin{aligned} S(\beta )=\sum _{i=1}^{N} \frac{\partial \mu _{i}}{\partial {\beta }^{'}}(A_{i}^{1/2}C_{i}A_{i}^{1/2})^{-1}(y_{i}-\mu _{i})=0, \end{aligned}$$

(10)

in which the marginal covariance matrix $V_{i}$ contains a vector $\rho$ of unknown parameters. Now, assume that the marginal mean $\mu _{i}$ has been correctly modeled, then it can be shown that using Eq. (10), the estimator $\hat{\beta }$ is normally distributed with mean equal to $\beta$ and covariance matrix equal to

$$\begin{aligned} Var(\hat{\beta })=I_{0}^{-1} I_{1} I_{0}^{-1}, \end{aligned}$$

(11)

where

$$\begin{aligned} I_{0}=\left( \sum _{i=1}^{N}\frac{\partial \mu _{i}'}{\partial {\beta }}V_{i}^{-1}\frac{\partial \mu _{i}}{\partial {\beta }'}\right) , \end{aligned}$$

(12)

and

$$\begin{aligned} I_{1}=\left( \sum _{i=1}^{N}\frac{\partial \mu _{i}'}{\partial {\beta }}V_{i}^{-1}Var(y_{i}) V_{i}^{-1} \frac{\partial \mu _{i}}{\partial {\beta }'}\right) . \end{aligned}$$

(13)

For practical purposes, in (13), $Var(y_{i})$ can be replaced by $(y_{i}-\mu _{i})(y_{i}-\mu _{i})'$ which is unbiased on the sole condition that the mean is correctly specified (Birhanu et al. 2011). Note that GEE arises from non-likelihood inferences, therefore “ignorability” discussed above, cannot be invoked to establish the validity of the method when dropout is under MAR hold (Liang and Zeger 1986). Only, when dropout is MCAR; that is, $f(r_{i}\mid y_{i}, X_{i},\gamma )=f(r_{i}\mid X_{i},\gamma )$ will estimating equation (10) yield consistent estimators (Liang and Zeger 1986). Under MAR, Robins et al. (1995) proposed the WGEE approach to allow the use of GEE under MAR . The weights used in WGEE , also termed inverse probability weights, reflect the probability for an observation of subject to be observed (Robins et al. 1995). Therefore, the incorporation of these weights reduces possible bias in the regression parameter estimates. Based on Molenberghs and Verbeke (2005), we discuss the construction of these weights. According to them, such weights can be calculated as

$$\begin{aligned} \omega _{ij}\equiv P[D_{i}=j]=\prod ^{j-1}_{k=2}(1-P[R_{ik}=0\mid R_{i2}=...=R_{i,k-1=1}])\times \nonumber \\ P[R_{ij}=0\mid R_{i2}=...=R_{i,j-1}=1]^{I\{j\le n_{i}\}}, \end{aligned}$$

(14)

where $j=2, 3, ...,n_{i}+1$, $I \{\}$ is an indicator variable, and $D_{i}$ is the dropout variable. The weights are obtained from the inverse probability provided the actual set of measurements are observed. In terms of the dropout variable $D_{i}$, the weights are written as

$$\begin{aligned} \omega _{ij}=\left\{ \begin{array}{ll}\\ P(D_{i}=j\mid D_{i}\ge j)&{} \text {for}\, j=2 \\ P(D_{i}=j\mid D_{i}\ge j) \displaystyle \prod ^{j-1}_{k=2}[1-P(D_{i} =k\mid D_{i}\ge k)]&{}\text {for}\, j=3,...,n_{i}\\ \displaystyle \prod _{k=2}^{n_{i}}[1-P(D_{i} =k\mid D_{i}\ge k)]&{}\text {for}\, j=n_{i}+1. \end{array} \right. \end{aligned}$$

(15)

Now, from Sect. 2 recall that we partitioned $Y_{i}$ into the unobserved components ($Y^{m}_{i}$) and the observed components ($Y^{o}_{i}$). Similarly, the mean $\mu _{i}$ can be partitioned into observed ($\mu ^{o}_{i}$) and missing components ($\mu ^{m}_{i}$). In the WGEE approach, the score equations to be solved are:

$$\begin{aligned} S(\beta )=\sum _{i=1}^{N}\sum _{d=2}^{n_{i}+1}\frac{I(D_{i}=d)}{\omega _{id}} \frac{\partial \mu _{i}}{\partial {\beta }^{'}}(d)(A_{i}^{1/2}C_{i}A_{i}^{1/2})^{-1}(d)(y_{i}(d)-\mu _{i}(d))=0, \end{aligned}$$

(16)

where $y_{i}(d)$ and $\mu _{i}(d)$ are the first $d-1$ elements of $y_{i}$ and $\mu _{i}$ respectively. In Eq. (16), $\frac{\partial \mu _{i}}{\partial {\beta }^{'}}(d)$ and $(A_{i}^{1/2}C_{i}A_{i}^{1/2})^{-1}(d)$ are defined analogously, in line with the definitions of Robins et al. (1995). Provided that the $\omega _{id}$ are correctly specified, WGEE provides consistent estimates of the model parameters under a MAR mechanism (Robins et al. 1995).

4.2 Multiple Imputation Based GEE (MI-GEE)

An alternative approach that is valid under MAR is multiple imputation prior to generalized estimating equations, or, as we will term it in the remainder of this article, MI-GEE. The primary idea of the combination of MI and GEE comes from Schafer (2003). He proposed an alternative mode of analysis based on the following steps. (1) Impute the missing outcomes multiple times using a fully parametric model, such as a random effects type model. (2) After drawing the imputations, analyze the so-completed data sets using a conventional marginal model, such as the GEE method. (3) Finally, perform MI inference on the so-analyzed sets of data. As pointed out by Beunckens et al. (2008), MI-GEE comes down to first using the predictive distribution of the unobserved outcomes, conditional on the observed ones and covariates. Thereafter, when MAR is valid, missing data need no further attention during the analysis. In terms of the dropout mechanism, in the MI-GEE method, the imputation model needs to be specified. This specification can be done by an imputation model that imputes the missing values with a given set of plausible values (Beunckens et al. 2008). Details of this method can be found in Schafer (2003), Molenberghs and Kenward (2007) and Yoo (2009). In closely related studies, Beunckens et al. (2008) studied the comparison between the two GEE versions (WGEE and MI-GEE) , and Birhanu et al. (2011) compared the efficiency and robustness of WGEE, MI-GEE and doubly robust GEE (DR-GEE). In this paper, however, we restrict attention to study how the two types of GEE (WGEE and MI-GEE) compared to the likelihood-based GLMM for analyzing longitudinal binary outcomes with dropout.

In the previous section, GEE, a special case of inverse probability weighting, was described as a useful device for the analysis of incomplete data, under an MAR mechanism. In this section, MI was described, and this suggests an alternative approach to handling MAR missingness when using GEE: use MAR-based MI together with a final GEE analysis for the substantive model. This emphasizes the valuable flexibility that this facility brings to MI, and can be considered as an example of using uncongenial imputation model. The term uncongenial was introduced by Meng (1994) for an imputation model that is not consistent with the substantive model, and it is for this reason that MI has much to offer in this setting. Further, Meng (1994) stated that it is one of the great strength of MI that these two models (substantive and imputation) do not have to be consistent in the sense that the two models need not be derived from an overall model for the complete data. GEE is one of the examples of situations in which such uncongenial imputation models might be of value (Molenberghs and Kenward 2007). As noted above GEE is valid under MCAR but not MAR. An alternative approach that is valid under MAR is MI prior to GEE, in which the imputation model is consistent with the MAR mechanism, but not necessarily congenial with the chosen substantive model. The population-averaged substantive model does not specify the entire joint distribution of the repeated outcomes, particularly the dependence structure is left unspecified, and so cannot be used as a basis for constructing the imputation model. Since we consider the MI-GEE method, the M imputed data sets combined with GEE on the imputed data is an alternative technique to likelihood inference and WGEE. It requires MAR for valid inferences.

4.3 Generalized Linear Mixed Model (GLMM)

An alternative approach to deal with dropout under MAR is to use likelihood-based inference (Verbeke and Molenberghs 2000). A commonly encountered random effects (or subject-specific) model for discrete longitudinal data is the generalized linear mixed model (GLMM) which is based on specifying a regression model for the responses conditional on an individual’s random effects and assuming that within-subject measurements are independent, conditional on the random effects. The marginal likelihood in the GLMM is used as the basis for inferences for the fixed effects parameters, complemented with empirical Bayes estimation for the random effects (Molenberghs and Kenward 2007). As pointed out by Alosh (2010), the random effects can be included as a subset of the model for heterogeneity from one individual to another. Integrating out the random effects induces marginal correlation between the responses through the same individual (Laird and Ware 1982). Next, we briefly introduce a general framework for mixed effects models provided by Jansen et al. (2006) and Molenberghs and Kenward (2007). It is assumed that the conditional distribution of each $Y_{i}$, given a vector of random effects $b_{i}$ can be written as follows

$$\begin{aligned} Y_{i}\mid b_{i}\sim F_{i}(\theta , b_{i}), \end{aligned}$$

(17)

where $Y_{i}$ follows a prespecified distribution $F_{i}$, possibly depending on covariates, and is parameterized via a vector $\theta$ of unknown parameters common to all individuals. The term $b_{i}$ denotes the ($q\times 1$) vector of subject-specific parameters, called random effects, which are assumed to follow a so-called mixing distribution Q. The distribution Q depends on a vector of unknown parameter, say $\psi$; that is, $b_{i}\sim Q(\psi )$. In terms of the distribution of $Y_{i}$, the $b_{i}$ reflect the between unit-heterogeneity in the population. Further, given the random effects $b_{i}$, it is assumed that the components $Y_{ij}$ in $Y_{i}$ are independent of one another. The distribution function ($F_{i}$) provided in model (17) becomes a product over the $n_{i}$ independent elements in $Y_{i}$. Inference based on the marginal model for $Y_{i}$ can be obtained across their distribution $Q(\psi )$, provided one is not following a fully Bayesian approach. Now, assume that the $f_{i}(y_{i}\mid b_{i})$ represents the density function and corresponds to the distribution $F_{i}$, while $q(b_{i})$ represents the density function and corresponds to the distribution Q. Thus, the marginal density function of $Y_{i}$ can be written as follows

$$\begin{aligned} f_{i}(y_{i})=\int f_{i}(y_{i}\mid b_{i})q(b_{i})db_{i}. \end{aligned}$$

(18)

The marginal density is dependent on the unknown parameters $\theta$ and $\psi$. By assuming the independence of the units, the estimates of $\hat{\theta }$ and $\hat{\psi }$ can be obtained using the maximum likelihood function that is built into model (18). The inferences can be obtained following the classical maximum likelihood theory. The distribution Q is assumed to be of a specific parametric form, for example a multivariate normal distribution. The integration in model (18), depending on both $F_{i}$ and $Q_{i}$, may or may not be analytically possible. However, there are some proposed solutions based on Taylor series expansions of either $f_{i}(y_{i}\mid b_{i})$ or on numerical approximations of the integral, for example, adaptive Gaussian quadrature. Verbeke and Molenberghs (2000) noted that for the classical linear mixed model, $E(Y_{i})$ equals $X_{i}\beta$, meaning that the fixed effects have a subject-specific as well as a population-averaged interpretation. However, for nonlinear mixed models, the interpretation of random effects has important ramifications for the interpretation of the fixed effects regression parameters. The fixed effects only reflect the conditional effect of covariates, and the marginal effect is difficult to obtain, as $E(Y_{i})$ is given by

$$\begin{aligned} E(Y_{i})=\int y_{i}\int f_{i}(y_{i}\mid b_{i})q(b_{i})db_{i}dy_{i}. \end{aligned}$$

(19)

In GLMM, a general formulation is as follows. It assumes that the elements $Y_{ij}$ of $Y_{i}$ are conditionally independent, given a $(q\times 1)$ vector of random effects $b_{i}$, with density function based on a classical exponential family formulation with conditional mean depending on both fixed and random effects. This leads to the conditional mean $E(Y_{ij}\mid b_{i})=a'(\eta _{ij})=\mu _{ij}(b_{i})$, and the conditional variance is assumed to depend on the conditional mean according to $Y_{ij}\mid b_{i}=\Theta a''(\eta _{ij})$. One needs a link function, say h (for binary data, a canonical link is the logit link), and typically uses a linear regression with parameters $\beta$ and $b_{i}$ for the mean, i.e., $h(\mu _{i}(b_{i}))=X_{i}\beta +Z_{i}b_{i}$. Here, we note that the linear mixed model is a special case with an identity link function. The random effects $b_{i}$ are again assumed to be sampled from a multivariate normal distribution, with mean 0 and $(q\times q)$ covariance matrix. The canonical link function is usually used to relate the conditional mean of $Y_{ij}$ to $\eta _{i}$; that is, $h=a'^{-1}$, such that $\eta _{i}=X_{i}\beta +Z_{i}b_{i}$. In principle, any suitable link function can be used (Fitzmaurice et al., 2004). In considering the link function of the logit form and assuming the random effects to be normally distributed, the familiar logistic-linear GLMM follows. For a more detailed overview, see, Jansen et al. (2006) and Molenberghs and Verbeke (2005).

4.4 Simulation Study

Note that the parameters in a marginal model, such as GEE, and a hierarchical model, such as GLMM, do not have the same interpretation. Indeed, the fixed effects in the latter are to be interpreted conditional upon the random effect. While there is no difference between the two in the linear mixed model, this is not the case for non-Gaussian outcomes, in particular for binary data. Fortunately, as stated in Molenberghs and Verbeke (2005) and references therein, the GLMM parameters can be approximately transformed to their marginal counterpart. In particular, when the random-effects structure is confined to a random intercept $b_{i}$, normally distributed with mean 0 and variance $\sigma ^{2}$, then the ratio between the marginal and random effects parameter is approximately equal to $\sqrt{1+c^{2} \sigma }$, where $c=16\sqrt{3}/(15 \pi )$. This ratio will be used in our simulation study to make the parameters comparable.

4.4.1 Design

The main objective of this study was to compare WGEE, MI-GEE and GLMM for handling dropout missing at random in longitudinal binary data. To do so, we used the following steps: (1) A complete longitudinal binary data set was generated, and the marginal logistic regression was fitted to the data to derive the parameter estimators. (2) Once the complete dataset was generated, 100 random samples of N = 250 and 500 subjects were drawn. (3) MAR dropout was created, for various dropout rates. (4) The above methods were applied to each simulated data set. The results from the simulated data were then compared with those obtained from the complete data. (5) The performances of WGEE, MI-GEE and GLMM were evaluated in terms of bias, efficiency and mean square error (MSE). The GLMM estimates were first adjusted for comparability before this evaluation of performance.

4.4.2 Data Generation

Simulated data were generated in order to emulate data typically found in longitudinal binary clinical trials data. The longitudinal binary data with dropout were simulated by first generating complete data sets. Then, 100 random samples of sizes N = 250 and 500 subjects were drawn. We assumed that subjects were assigned to two arms (Treatment = 1 and Placebo = 0). We also assumed that measurements were taken under four time points ($j=1, 2, 3, 4$). The outcome ($Y_{ij}$) which is the measurement of subject i, measured at time j, was defined as 1 if the measurement is positive, and 0 if otherwise. The two levels of the outcome can represent a specific binary health outcome, but generally we labeled one outcome “success, i.e., 1” and the other “failure, i.e., 0”. Then, we looked at logistic regression as modeling the success probability as a function of the explanatory variables. The main interest here is in the marginal model for each binary outcome $Y_{ij}$, which we assumed follows a logistic regression. Consequently, longitudinal binary data were generated according to the following logistic model with linear predictor

$$\begin{aligned} logitE(y_ij=1|T_j, trt_i, b_i)=\beta _{0}+b_{i}+\beta _{1}T_{j}+\beta _{2}trt_{i}+\beta _{3}(T_{j}*trt_{i}), \end{aligned}$$

(20)

where $\beta =(\beta _{0}, \beta _{1},\beta _{2},\beta _{3})$, and the random effects $b_{i}$’s are assumed to account for the variability between individuals and assumed to be i.i.d. with a normal distribution, i.e., $b_{i}\sim N(0,\sigma ^{2})$. In this model, fixed categorical effects include treatment (trt), times (T) and treatment-by-time interaction $(T*trt)$. For this model, throughout, we fixed $\beta _{0}=-0.25$, $\beta _{1}=0.5$, $\beta _{2}=1.0$ and $\beta _{4}=0.2$. We also set a random intercept $b_{i}\sim N(0, 0.07)$. For each simulated data set, dropouts were created in the response variable, $Y_{ij}$, chosen stochastically. We assumed that the dropout can occur only after the second time point. Consequently, there are three possible dropout patterns. That is, dropout at the third time point, dropout at the fourth time point, or no dropout. The dropouts were generated at time j and the subsequent times were assumed to be dependent on the values of outcome measured at time ${j-1}$. Under model (20), we simulated a case where the MAR specification was different for the two outcomes (positive and negative). In particular, for time point, j = 3, we retained the criterion that if the dependent variable ($Y_{ij}$) was positive (i.e., $Y_{ij} = 1$), then the subject dropped out at the next time point, i.e., $j+1$. Dropouts were selected to yield approximate rates of 10, 20 and 30%. A monotone missing pattern (i.e., data for an individual up to a certain time) was considered, thus simulating a trial where the only source of dropout was an individual’s withdrawal.

4.5 Analysis

In the analysis, different strategies were used to handle dropout: by weighting, by imputation and by analyzing the data with no need to impute or weight, consistent with MAR assumption, for WGEE , MI-GEE and GLMM , respectively.

4.5.1 WGEE

As discussed above, the WGEE method requires a model for the dropout mechanism. Consequently, we first fitted the following dropout model using a logistic regression,

$$\begin{aligned} logitP(D_{i}=j\mid D_{i}\ge j)=\gamma _{0}+\gamma _{1}y_{i,j-1}+\gamma _{2}trt_{i}, j=3,4. \end{aligned}$$

(21)

where the predictor variables were the outcomes at previous occasions ($y_{i,j-1}$), supplemented with genuine covariate information. Model (21) is based on logistic regression for the probability of dropout at occasion j for individual i, conditional on the individual still being in the study (i,e., the probability of being observed is modeled). Note that mechanism (21) allows for the one used to generate the data and described in above only as a limiting case. This is because our dropout generating mechanism has a deterministic flavor. Strictly speaking, the probabilities of observation in WGEE are required to be bounded away from zero, to avoid issues with the weight. The effect of our choice is that WGEE is subjected to a severe stress test. It will be seen in the results section that, against this background, WGEE performs rather well. To estimate the probabilities for dropout as well as to pass the weights (predicted probabilities) to be used for WGEE, we used the “DROPOUT” and “DROPWGT” macros described in Molenberghs and Verbeke (2005). These macros could be used without modification. The “DROPOUT” macro is used to construct the variables dropout and previous. The outcome dropout is binary and indicates if individual had dropped out of the study before its completion, whereas, the previous variable refers to the outcome at previous occasions. After fitting a logistic regression, the “DROPWGT” macro is used to pass the weights to the individual observations in WGEE . Such weights, calculated as the inverse of the cumulative product of conditional probabilities, can be estimated as $w_{ij}=1/(\lambda _{i1}\times ...\times \lambda _{ij})$, where $\lambda _{ij}$ represents the probability of observing a response at time j for the ith individual, conditional on the individual being observed at the time $j-1$. Once the dropout model (21) was fitted and the weight distribution was checked, we merely included the weights by means of the WEIGHT statement in SAS procedure GENMOD. As mentioned earlier, the marginal measurement model for WGEE should be specified. Therefore, the model that we considered takes the form of

$$\begin{aligned} logitE(y_{ij})=\beta _{0}+\beta _{1}T_{j}+\beta _{2}trt_{i}+\beta _{3}(T_{j}*trt_{i}). \end{aligned}$$

(22)

Here, we used the compound symmetry (CS) working correlation matrix. A random intercept $b_{i}$ was excluded when considering WGEE.

4.5.2 MI-GEE

The analysis was conducted by imputing missing values using the SAS procedure MI, which employs a conditional logistic imputation model for binary outcomes. For the specification of the imputation model, an MAR mechanism is considered; that is, the imputation model comprises two-level covariate (i.e., treatment versus placebo classification) as well as longitudinal binary outcomes values at times $j = 1; 2; 3; 4$. To be precise, for the imputation model, we used a logistic regression with measurements at the second time point as well as the two-level covariate to fill in the missing values that occur at the third time point. In a similar way, the imputation at the fourth time point is done using the measurements at the third time point including both imputed and observed, as predictors, as well as the measurements at the second time point which is always observed and the two-level covariate. Note that we describe here multiple imputation in a sequential fashion, making use of the time ordering of the measurements. Therefore, the next value is imputed based on the previous values, whether observed or already imputed. This is totally equivalent to an approach where all missing values are imputed at once based on the observed sub-vector. This implies that the dropout process was accommodated in the imputation model. It appears that there is potential for misspecification here. However, multiple imputation is valid under MAR . Whether missingness depends on one or more earlier outcomes, MAR holds, so the validity of the method is guaranteed (Molenberghs and Kenward 2007). In terms of the number of the imputed data sets, we used M = 5 imputations. GEE was then fitted to each completed data set using SAS procedure GENMOD. The GEE model that we considered is based on (22). The results of the analysis from these 5 completed (imputed) data sets were combined into a single inference using Eqs. (5), (6), (7) and (8). This was done by using SAS procedure MIANALYZE. Details of implementation of this method are given in Molenberghs and Kenward (2007) and Beunckens et al. (2008).

4.5.3 GLMM

Conditionally on a random intercept $b_{i}$, the logistic regression model is used to describe the mean response, i.e., the distribution of the outcome at each time point separately. Specifically, we considered fitting model (20). This model assumed that there is natural heterogeneity across individuals and accounted for the within-subject dependence in the mean response over time. Model (20) was fitted using the likelihood method by applying the NLMIXED procedure in SAS software. This procedure relies on numerical integration and includes a number of optimization algorithms (Molenberghs and Verbeke 2005). Given that the evaluation and maximization of the marginal likelihood for GLMM needs integration, over the distribution of the random effects, the model was fitted using maximum likelihood (ML) together with adaptive Gaussian quadrature (Pinheiro and Bates 2000) based on numerical integration which works quite well in procedure NLMIXED. This procedure allows the use of Newton-Raphson instead of a Quasi-Newton algorithm to maximize the marginal likelihood, and adaptive Gaussian quadrature was used to integrate out the random effects. The adaptive Gaussian quadrature approach makes Bayesian approaches quite appealing because it is based on numerical integral approximations centered around the empirical Bayes estimates of the random effects, and permits maximization of the marginal likelihood with any desired degree of accuracy (Anderson and Aitkin 1985). An alternative strategy to fitting the GLMM is the penalized quasi-likelihood (PQL) algorithm (Stiratelli et al. 1984). However, in this study this algorithm is not used as it often provides highly biased estimates (Breslow and Lin 1995). Also, we ought to keep in mind that the GLMM parameters need to be re-scaled in order to have an approximate marginal interpretation and to become comparable to their GEE counterparts.

4.5.4 Evaluation Criteria

In the evaluation, inferences are drawn on the data before dropouts are created and the results used as the main standard against those obtained from applying WGEE , GLMM and MI-GEE approaches. We evaluated the performance of the methods using bias, efficiency, and mean square error (MSE). These criteria are recommended in Collins et al. (2001) and Burton et al. (2006). (1) Evaluation of bias: we defined the bias as the difference between the average estimate and the true value; that is, $\pi =(\bar{\hat{\beta }}-\beta )$ where $\beta$ is the true value for the estimate of interest, $\bar{\hat{\beta }}=\Sigma _{i=1}^{S}\hat{\beta }_{i}/S$, S is the number of simulation performed, and $\hat{\beta }_{i}$ is the estimate of interest within each of the $i=1,...,S$ simulations. (2) Evaluation of efficiency: we defined the efficiency as the variability of the estimates around the true population coefficient. In this chapter, it was calculated by the average width of the 95% confidence interval. The 95% interval is approximately four times the magnitude of the standard error. Therefore, a narrower interval is always desirable because it leads to more efficient methods. (3) Evaluation of accuracy: the MSE provides a useful measure of the overall accuracy, as it incorporates both measures of bias and variability (Collins et al. 2001). It can be calculated as follows: MSE=$(\bar{\hat{\beta }}-\beta )^{2}$+$(SE(\hat{\beta }))^{2}$, where $SE(\hat{\beta })$ denotes the empirical standard error of the estimate of interest over all simulations (Burton et al. 2006). Generally, small values of MSE are desirable (Schafer and Graham 2002).

4.5.5 Simulations Results

The simulations results of WGEE , MI-GEE and GLMM in terms of bias, efficiency and MSEs, under N=250 and 500 sample sizes are presented in Table 3. A few points about the parameter estimates obtained by the proposed methods through the three evaluation criteria may be noted for each estimate in Table 3. First, the largest bias, also the worst, are highlighted. Second, for the efficiency criterion, the widest confidence interval, also the worst, 95% interval are highlighted. Third, for the evaluation of MSEs, the greatest values, also the worst, are highlighted. As we will see, the findings in general favoured MI-GEE over both WGEE and GLMM, regardless of the dropout rates.

Table 3 Bias, efficiency and mean square error of the WGEE, MI-GEE and GLMM Methods, under MAR mechanism over 100 samples: N = 250 and 500 subjects.

By looking at this table, we observed that for 10% dropout rate, bias was least in the estimates of MI-GEE than in both WGEE and GLMM . In particular, the worst performance of WGEE and GLMM on bias permeated through the estimates of $\beta _{2}$ and ($\beta _{0}, \beta _{1}, \beta _{3}$), respectively, indicating a discrepancy between the average and the true parameter (Schafer and Graham 2002). Between the two MI-GEE and WGEE methods, the WGEE estimates were slightly different from those obtained by MI-GEE , although the degree of these differences was not very large. The efficiency performance was acceptable for both methods and comparable to each other, but low for most parameters under WGEE . The efficiency estimates associated with GLMM were larger than with WGEE and MI-GEE . In terms of MSEs, both WGEE and MI-GEE outperformed GLMM as they tend to have smallest MSEs. Overall, they yielded MSEs much closer to each other, however under 500 sample size, MI-GEE gave smallest MSEs.

Considering the 20% dropout rate, the results revealed that in most cases, GLMM consistently produced the most biased estimates. The only exception occurred for estimates of $\beta _{2}$ under 250 sample size as well as $\beta _{2}$ and $\beta _{3}$, under 500 sample size. For estimating all parameters, efficiency estimates by WGEE and MI-GEE were similar to each other and smaller than GLMM’s estimates, except for $\beta _{3}$ under 500 sample size. In comparison with WGEE and MI-GEE, GLMM gave larger MSEs in magnitude than the two, except for estimate of $\beta _{0}$ and $\beta _{2}$ under 250 and 500 sample sizes, respectively. Comparing WGEE and MI-GEE, the MSEs associated with both methods were closer to each other and in one case—MSE of $\beta _{3}$ under 250 sample size—they gave the same values. As was the case for 10% under 500 sample size, MSEs by WGEE tended to be larger than those obtained by MI-GEE.

A comparison of 30% dropout rate again suggested that the results based on GLMM typically displayed greater estimation bias than did WGEE and MI-GEE , indicating a difference between the average estimate and the true values. Efficiency by MI-GEE appeared to be independent of the sample size in most cases, meaning the MI-GEE method yielded more efficient estimates across both sample sizes. Thus, MI-GEE was more efficient than WGEE, yet more efficient than GLMM . The latter yielded the largest values in most cases. With respect to MSEs, results that are computed by GLMM yielded largest values, showing no substantial improvement over GLMM under different sample sizes when compared with the results computed by WGEE and MI-GEE. Under 500 sample size, it can also be observed that in terms of the estimate of $\beta _{3}$, the MSE value for WGEE was equal to that based on GLMM, and they gave larger MSEs than did MI-GEE, whereas compared to WGEE, the MI-GEE still resulted in smaller MSEs. Generally, with increasing sample size, the performance of MI-GEE was better than that for WGEE and GLMM .

Table 4 Number and percentage of patients with severe toenail infection at each time point, for each treatment arm separately

Table 5 Toenail data: Number of available repeated measurements for each patient, by treatment arm separately

Table 6 Toenail data: (parameter estimates; standard errors) and p-values for WGEE, MI-GEE and GLMM

4.6 Application Example: Dermatophyte Onychomycosis Study

These data come from a randomized, double-blind, parallel group, multi-center study for the comparison of two treatments (we will term them in the remainder of this article, active and placebo) for toenail dermatophyte onychomycosis (TDO). Toenail dermatophyte onychomycosis is a common toenail infection, difficult to treat, affecting more than 2% of population. Further background details of this experiment are given in De Backer et al. (1996) and in its accompanying discussion. In this study, there were 2 $\times$ 189 patients randomized under 36 centers. Patients were followed 12 weeks (3 months) of treatment. Further, patients were followed 48 weeks (12 months) of total follow up. Measurements were planned at seven time points, i.e., at baseline, every month during treatment, and every 3 months afterward for each patient. The main interest of this experiment was to study the severity of infection relative to treatment of TDO for the two treatment groups. At the first occasion, the treating physician indicates one of the affected toenails as the target nail, the nail that will be followed over time. We restrict our analyses to only those patients for which the target nail was one of the two big toenails. This reduces our sample under consideration to 146 and 148 patients, in active group and placebo group, respectively. The percentage and number of patients that are in the study at each month is tabulated in Table 4 by treatment arm. Due to a variety of reasons, the outcome has been measured at all 7 scheduled time points for only 224 (76%) out of the 298 participants. Table 5 summarizes the number of available repeated measurements per patient, for both treatment groups separately. We see that the occurrence of missingness is similar in both treatment groups. We now apply the aforementioned methods to this data set. Let $Y_{ij}$ be the severity of infection, coded as yes (severe) or no (not severe), at occasion j for patient i. We focus on assessing the difference between both treatment arms for onychomycosis. An MAR missing mechanism is assumed. For the WGEE and MI-GEE methods, we consider fitting Model (22). For the GLMM method, the above mentioned ratio is used. A random intercept $b_{i}$ will be included in Model (22) when considering the random effects models. The results of the three methods are listed in Table 6. It can be seen from the analysis that the associated p-values for the main variable of interest, i.e., treatment are all nonsignificant, their p-values being all greater than 0.05. Such results should be expected considering the fact both marginal and random effect model may present similar results in terms of hypothesis testing (Jansen et al. 2006). However, when compared to WGEE and MI-GEE , the GLMM method provided different results. Namely, its estimates were much bigger in magnitude. This in line with previous study conducted by Molenberghs and Verbeke (2005). In addition, the parameter estimates as well as the standard errors are more varied for GLMM than in the WGEE and MI-GEE methods.

5 Discussion and Conclusion

In the first part of this chapter, we have compared two methods applied to incomplete longitudinal data with continuous outcomes. The findings of our analysis in general suggest that both direct likelihood and multiple imputation performed best under all three dropout rates, and they are more broadly similar in results. This is to be expected as both approaches are likelihood based and Bayesian analysis, respectively, and therefore valid under the assumption of MAR (Molenberghs and Kenward 2007). The result of direct likelihood are in line with the findings that likelihood-based analyses are appropriate for the ignorability situation (Verbeke and Molenberghs 2000; Molenberghs and Verbeke 2005; Mallinckrodt et al. 2001a, b). Because of simplicity, and ease of implementation using many statistical tools such as the SAS software procedures MIXED, NLMIXED and GLIMMIX, direct likelihood might be adequate to deal with dropout data when the MAR mechanism holds, provided appropriate distributional assumptions for a likelihood formulation of the data also hold. Moreover, a method such as multiple imputation can be conducted without problems using statistical software such as the SAS procedures MI and MIANALYZE, and if done correctly, is a versatile, powerful and reliable technique to deal with dropouts that are MAR in longitudinal data with continuous outcomes. It would appear that the recommendation of Mallinckrodt et al. (2003a), Mallinckrodt et al. (2003b) to use direct likelihood and multiple imputation for dealing with incomplete longitudinal data with continuous outcomes is supported by the current analysis. At this point, we have to make it clear that the scope of this study is limited to direct likelihood and multiple imputation strategies. We note that there are several other strategies available to deal with incomplete longitudinal data with continuous outcome under ignorability assumption, however these methods are not covered in this study.

From the second part of the chapter that is based on dealing with binary outcomes, the results in general favoured MI-GEE over both WGEE and GLMM . This MI-GEE advantage is well documented in Birhanu et al. (2011). However, the current analysis differs from that based on Birhanu et al. (2011) as their analysis compared MI-GEE, WGEE and Doubly robust GEE in terms of the relative performance of the singly robust and Doubly robust versions of GEE in a variety of correctly and incorrectly specified models. Furthermore, the bias for MI-GEE based estimates in this study was fairly small, demonstrating that the imputed values did not produce markedly more biased results. This was to be expected as many authors, for example, Beunckens et al. (2008) noted that the MI-GEE method may provide less biased estimates than a WGEE analysis when the imputation model is correctly specified. From an extensive small and high sample sizes (i.e., N=250 and 500) simulation study, it emerged that MI-GEE is rather efficient and more accurate than other methods investigated in the current paper, regardless of dropout rate which also shows that the method does well as the dropout rate increases. Overall, the MI-GEE performance appeared to be independent of the sample sizes. However, in terms of efficiency, in some cases, it was less efficient than WGEE, yet more efficient and accurate than GLMM. This was specially true for WGEE when the rate of dropout was small and the sample size was small as well. In summary, the results further recommended MI-GEE over WGEE. However, both MI-GEE and WGEE methods may be selected as the primary analysis methods for handling dropout under MAR in longitudinal binary outcomes, but convergence of the analysis models may be affected by the discreteness or sparseness of the data.

Molenberghs and Verbeke (2005) stated that the parameter estimates from the GLMM are not directly comparable to the marginal parameter estimates, even when the random effects models are estimated through a marginal inference. They also transformed the GLMM parameters to their approximate GEE counterparts, using a ratio that makes the parameter estimates comparable. Therefore, an appropriate adjustments need to be applied to GLMM estimates in order to have an approximate marginal interpretation and to become com- parable to their GEE counterparts. Using this ratio in the simulation study, the findings showed that, although all WGEE, MI-GEE and GLMM are valid under MAR, there were slight differences between the parameter estimates and never differed by a large amount, in most cases. As a result, it appeared that for both sample sizes, the GLMM based results were characterized by the larger estimates for nearly all cases, although the degree of the difference in magnitude was not very large. In addition, it did not appear that the magnitude of this difference differed between the three dropout rates.

Although there was a discrepancy between the GLMM results on the one hand, and both the WGEE and MI-GEE results on the other, there are several important points to consider in the GLMM analysis of incomplete longitudinal binary data . The fact is that the GLMM may be applicable in many situations and offers an alternative to the models that make inferences about the overall study population when one is interested in making inferences about individual variability to be included in the model (Verbeke and Molenberghs 2000; Molenberghs and Verbeke 2005). Furthermore, it is important to realize that GLMM relies on the assumption that the data are MAR, provided a few mild regularity conditions hold, and it is as easy to implement and represent as it would be in contexts where the data are complete. Consequently, when this condition holds, valid inference can be obtained with no need for extra complication or effort, and the GLMM assuming an MAR process, is more suitable (Molenberghs and Kenward 2007). In addition, the GLMM is very general and can be applied for various types of discrete outcomes when the objective is to make inferences about individuals rather than population averages, and is more appropriate for explicative studies.

As a final remark, recall that MI-GEE has been the preferred method for analysis as it outperformed both the WGEE and GLMM estimations in the simulation study results. Despite this, the current study has focussed on handling dropout in the outcome variable, the MI-GEE can be well conducted in terms of the missingness in the covariates in the context of real-life, and can yield even more precise and convincing results since the choice for the WGEE method is not that straightforward. This can be justified by the fact that in the imputation model, the covariates that are conditioned on the analysis model are not included. The other available covariates can be included in the imputation model without being of interest in the analysis model, therefore yielding better imputations as well as wider applicability. Additionally, multiple imputation methods such as MI-GEE avoid some severe drawbacks encountered using direct modeling methods such as the excessive impact of the individual weights in the WGEE estimation or the poor fit of the random subject effect in the GLMM analysis. For further discussion, see Beunckens et al. (2008).

Lastly, we submit that the scope of the second part of thus chapter is limited to three approaches. This work is not intended to provide a comprehensive account of analysis methods for incomplete longitudinal binary data . We acknowledge that there are several methods available for incomplete longitudinal binary data under the dropouts that are MAR. However, these methods are beyond the scope of the study. This article exclusively deals with the WGEE, MI-GEE and GLMM paradigms that represent different strategies to deal with dropout under MAR .