Abstract
The first steady-state analytical model for determining time mean longitudinal velocities in a coastal plain estuary was developed by Pritchard and Kent (1956) using the lateral and longitudinal components of the equation of motion, the tidal velocity amplitude, and the relationship between the vertical and lateral eddy stress.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
The first steady-state analytical model for determining time mean longitudinal velocities in a coastal plain estuary was developed by Pritchard and Kent (1956) using the lateral and longitudinal components of the equation of motion, the tidal velocity amplitude, and the relationship between the vertical and lateral eddy stress. In this article the relationship between the vertical and transverse eddy diffusion coefficients were demonstrated using the vertical velocity profile near the bottom. The method was applied and validated with data from stations sampled in the James river estuary (Virginia, USA) during several tidal cycles in the summer (June and July, 1950) in a water column with mean depth of 8 m. The theoretical velocity profiles agreed well with the observational data, showing typical velocity profiles of partially mixed estuary, with seaward and landward motions in the upper and lower layers, respectively, and no motion at mid depths. Pritchard and Kent’s paper was also a pioneering article showing the importance of comparing theoretical results with observational data.
Complementing the results of this pioneering study. This chapter presents analytical investigations of relatively narrows estuaries, assumed to be bi-dimensional systems in the Oxz plane, with vertical salinity stratification, and thus classified as partially mixed estuaries (types 2 or B). Stable salinity stratification reduces the intensity and scale turbulence in open channel flow, thereby reducing the rate of vertical mixing. Theoretically, partially mixed estuaries are adequately represented by lateral averages of the equations of mass and salt conservation and motion, as presented in Chaps. 7 and 8 which have as unknowns the density, salinity the velocity components (u, w) and the slope of free surface as a function of the independent variables (x, z, t). Laboratory investigations were conducted by Sumer and Fischer (1977) to investigate whether the rate of transverse mixing is similarly reduced in this type of estuary. However, to determine relatively simple analytical solutions, steady-state conditions must be assumed and, for validation, the theoretical solutions must be compared with time mean velocity and salinity values calculated from observational data for one or more tidal cycles.
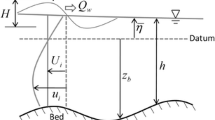
The influences of topography, transverse salinity (density) gradient and free surface elevation, may cause lateral non-homogeneity and circulation in estuaries, and a simple longitudinal and transverse section will be used (Fig. 11.1). The estuary width, B = B(x), will be considered only as a function of the longitudinal distance, and its depth dependence will not be taken into account.
Longitudinal (a, b) and transverse (c) sections of a bi-dimensional model with the adopted referential system (Oxz). H0 is the depth in relation to a level surface, and Ho + η is the local depth, and B = B(x) is the estuary width. The Oz axis is positively oriented in the direction of the gravity acceleration
Neglecting topographic effects makes the mathematics considerably more tractable; however, the features of the depth dependent circulation are still basic, even though there will be modifications due to transverse effects which are not accounted for by the laterally averaged equations (Hamilton and Rattray 1978). With these simplifications, the dynamic influence of the Earth’s rotation may be disregarded, and the Coriolis acceleration (f0) does not need to be included in the longitudinal component (Ox) of the equation of motion.
Pioneering investigations by Pritchard (1952a, 1954, 1956) demonstrate that for coastal plain estuaries, the dynamic balance of the mean motion is predominantly based on the barotropic and baroclinic pressure gradients, the dissipative friction forces and the tidal non-steady state circulation. The salt balance is mainly maintained by the advective and diffusive longitudinal and vertical fluxes. With these simplifications, for practical purposes, the steady-state equation of motion has its linearity granted, disregarding the advective acceleration. As indicated by Kjerfve et al. (1991), the inertial terms may be disregarded in shallow estuarine channels, in which the bottom friction becomes more important.
11.1 Physical-Mathematical Formulation
The simplified equations of mass conservation (Eq. 7.73a) and motion (Eq. 8.57a), which are necessary for analytical and numerical treatment of problems related to steady-state bi-dimensional estuaries, have been presented in Chaps. 7 and 8, and are reproduced below,
and
where B is the estuary width. The gradient pressure force decomposed in the barotropic and baroclinic pressure gradients are expressed as Eq. (2.10a, b and Chap. 2), but with the Oz axis oriented in the direction of gravity acceleration \( \left( {{\vec{\text{g}}}} \right), \)
For hydrodynamic closure, the inclusion of the steady-state salt conservation (Eq. 7.77 and Chap. 7) is necessary
as well as the linear equation of state of sea water (Eq. 4.11 and Chap. 4),
The analytical solution of the equation system (11.1) to (11.5) is dependent on the boundary and integral boundary conditions used for the determination of the unknowns u, w, η, S and ρ, under some simplifications. This system has been solved by Hansen and Rattray (1965), Fisher et al. (1972), Hamilton and Rattray (1978) among others. In these articles, the main results of which will be presented in this chapter, the basic foundations for the theoretical determinations of the following were established: the steady-state vertical velocity and salinity profiles generated by the river discharge, the longitudinal gradient pressure forces due to the longitudinal density (salinity) gradients caused by the wind stress and mixing processes (advection and diffusion).
The value of the kinematic eddy viscosity coefficient (Nz), and kinematic diffusion coefficients (Kx and Kz) of the conservation equations are usually unknown, however, if the solution for the above set of equations can be shown to agree with or be validated by observational data by proper fitting of these coefficients, one must assume that either all the neglected terms are zero, or more correctly, that the neglected terms have been absorbed into these coefficients.
In the analytical simulation of the u-velocity component and salinity profiles, the estuary mixing zone (MZ) will be approximated by a simple geometry (Fig. 11.1). For this solution, it will also be necessary to formulate the following simplifying assumptions:
-
The longitudinal salinity (density) gradient is independent of the depth ∂/∂z(∂S/∂x) = 0 or ∂/∂z(∂ρ/∂x) = 0.
-
The longitudinal term of the turbulent salinity diffusion is disregarded [first term on the right hand side of Eq. (11.4)].
-
The eddy kinematic coefficients of viscosity (Nz) and diffusion (Kz) are independent of the depth.
The first assumption may be justified, taking into account the results of Pritchard (1954, 1956) whose observational data demonstrated that in partially mixed estuaries the longitudinal salinity (density) gradient does not vary appreciably with depth, and the dynamical influence of this term is small in the central region of the MZ. Therefore, without great alterations in the physical aspects of the results, the longitudinal salinity (density) gradient, ∂S/∂x (∂ρ/∂x), will be substituted by the longitudinal gradients of a depth average salinity (density) \( \partial {\bar{\text{S}}}/\partial {\text{x}}\,\left( {\partial \bar{\uprho}/\partial {\text{x}}} \right), \) which will be calculated by the steady-state mean salinity (density) value in the water column, which will be denoted by \( \left( {{\bar{\text{S}}}} \right) \) or \( \left( {\bar{\uprho}} \right), \) and calculated by,
and a similar expression for the density, \( \bar{\uprho}. \)
The second simplifying assumption may also be justified, taking into account the observational results of Pritchard (1956) in the partially mixed James river estuary (Virginia, USA). In this estuary, the non-advective longitudinal term of the salt conservation equation (Eq. 11.4) (first term on the right hand side) has a relatively low contribution (about 1%) in comparison to the last term of this equation (vertical salt diffusion), and may be disregarded. Finally, the third assumption cannot be easily justified, and these coefficients (kinematic eddy viscosity and diffusion) will be considered as constants and representative of their mean value in the water column in order to simplify the mathematics and make the integration of equations easier.
With these assumptions, combining Eq. (11.3) with the linear equation of state of seawater (11.5) and substituting the result into the equation of motion (11.2), it follows that:
or in terms of the longitudinal salinity gradient,
where according to the Boussinesq approximation, ρ0/ρ ≈ 1, and \( \bar{\uprho}\left( {{\bar{\text{S}}}} \right) \) are vertical mean values of density (salinity) in the water column.
As the continuity Eq. (11.1) assures the non-divergence of the volume transport per unit width of the cross-section, it is possible to introduce the stream function \( \uppsi =\uppsi({\text{x}},{\text{z}}), \) with the definitions:
These equalities identically satisfy the continuity equation, and it should be pointed out that the stream function, ψ = ψ(x, z), with dimension [L3T−1], obeys the mathematical rules which state that its mixed derivatives should be equal. The introduction of this function is very convenient because the velocity components, u and w, may be calculated by a simple derivation.
Performing the derivative of Eq. (11.7b) in relation to z and taking into account that the barotropic pressure gradient and the longitudinal salinity gradient are independent of the depth, we have
and introducing the stream function, ψ = ψ(x, z), into this equation, it is reduced to
The salt conservation Eq. (11.4) may also be combined with the stream function definition, and is then reduced to
In this equation, only the salinity in the first term of the left hand side was substituted by a mean salinity value \( \left( {{\bar{\text{S}}}} \right), \) which will be considered a known quantity, allowing an analytical solution to be found. Only with this artifice the salinity will remain unknown, and will be determined with the salt balance between the steady-state longitudinal and vertical advection, and the vertical diffusivity terms (the first and second terms on the left hand side, and the term on the right hand side of this equation, respectively).
Equations (11.10) and (11.11) are formulations equivalent to the initial Eqs. (11.2) and (11.4), respectively. As the mean-depth salinity, \( {\bar{\text{S}}}, \) and the longitudinal gradient, \( \partial {\bar{\text{S}}}/\partial {\text{x}}, \) are given, this system of equations has two equations of fourth and second orders, respectively, with two unknowns, ψ = ψ(x, z) and S = S(z), which now govern the dynamics and the mixing processes in the MZ.
The boundary conditions necessary for finding a unique solution for the equation system (11.10) and (11.11) are the same as previously used in Chap. 10 (Eqs. 10.10 to 10.12), but now they will be expressed in terms of the stream function:
-
Upper boundary condition
At the free surface (z = η ≈ 0), the wind shear stress (τWx) acts seaward or landward (positive or negative) and also may be disregarded, which are expressed by:
where Az = ρNz, [Az] = [ML−1T−1], is the eddy viscosity coefficient.
-
Lower boundary condition
At the bottom, three conditions may be formulated:
-
(a)
Maximum friction (or no slip):
$$ (\frac{{\partial\uppsi}}{{\partial {\text{z}}}})_{{{\text{z}} = {\text{H}}_{0} }} = 0, $$(11.13) -
(b)
Moderate friction (or slippery):
$$ \frac{{\uprho{\text{N}}_{\text{z}} }}{\text{B}}(\frac{{\partial^{2}\uppsi}}{{\partial {\text{z}}^{2} }}) |_{{{\text{z}} = {\text{H}}_{0} }} = -\uptau_{\text{Bx}} . $$(11.14) -
(c)
Minimum friction (τBx = 0):
$$ \frac{{\partial^{2}\uppsi}}{{\partial^{2} {\text{z}}}} |_{{{\text{z}} = {\text{H}}_{0} }} = 0. $$(11.15)
The upper and lower boundary conditions to be applied for the salt conservation Eq. (11.1) must specify zero salt flux at the surface and at the bottom, which are expressed as:
and
To close the hydrodynamic system (Eqs. 11.10 and 11.11), it is necessary to impose integral boundary conditions. The first is formulated by Eq. (11.6), which defines the mean salinity in the water column, and the second condition is a consequence of the continuity Eq. (11.1). As the solution is under steady-state conditions the mass (fresh water) conservation can be accomplished by
which, combined with the stream function definition (11.8), is reduced to
As the stream function has the dimension of volume transport [L3T−1], which must be zero at the surface and bottom, the integral boundary condition may be expressed by: \( \uppsi({\text{x}},{\text{z}})\left| {_{{{\text{z}} =\upeta}} } \right. =\uppsi({\text{x}},{\text{z}})\left| {_{{{\text{z}} = 0}} } \right. = 0. \)
As with most fluid dynamics problems the analytical solution of the system of Eqs. (11.10 and 11.11) will be developed in a dimensionless form in order to permit generalized discussions of the results (Fisher et al. 1972). For this purpose, the following variables are defined:
In these definitions, S0 is the salinity at the coastal region, L is the mixing zone (MZ) length, and τW0 and τB0 are characteristics values of the wind shear and bottom stress, respectively. It should be observed that, as the axis Oz is oriented in the direction of the gravity acceleration, Z = 0 and Z = 1 are the dimensionless ordinates of the surface and bottom, respectively. With the introduction of the dimensionless variables, the equations of motion and salt conservation are expressed as:
and
where Ψ, $, \( \overline{\$ } \), X and Z are all dimensionless variables. These equations may be further simplified as,
and
with the coefficients, C1(X) and C2(X), expressed by:
and
The differential equations of this system (Eqs. 11.22 and 11.23) are dimensionless and at fourth and second degree, respectively, and its unknowns are: Ψ = Ψ(X, Z) and $ = $(X, Z). The quantities C1(X) and C2(X) are dimensionless, and their dependency on X is not well known and will not be taken into account.
Before being applied to the new equation system (11.22) and 11.23), the boundary conditions (11.12) to (11.18) must be altered to the following expressions:
and the integral boundary conditions are,
Taking into account the relations (11.8) and the equalities ∂z = H0∂Z, ∂x = L∂X and ∂ψ = Qf∂ Ψ, it follows that,
and
11.2 Hydrodynamic Solution: Maximum Bottom Friction
Consider the solution of Eq. (11.22). As the first member of this differential equation is a function of X and the mean longitudinal salinity gradient should be known, this equation may be solved for the stream function, Ψ = Ψ(X, Z). By integrating with Z four times, the general solution is:
The dimensionless quantities, a1(X), a2(X), a3(X) and a4(X), are all function of X and are calculated from the application of the boundary conditions (11.26) and (11.27) and the integral boundary condition (11.31). Applying the last condition Ψ(X, 0) = 1, it follows immediately that:
where Az = ρNz and
In the following step, with the boundary conditions (11.27) and Ψ(X, 1) = 0 from the integral boundary conditions (11.31), the result is an algebraic equation system with two unknowns, a1(X) and a3(X),
Subtracting these equations in order to eliminate a3(X) and solving the result for a1(X), we have
Finally, substituting Eqs. (11.39) into (11.37) or (11.38), it follows that the value for a3(X) is,
Substituting the expressions a1(X), a2(X), a3(X) and a4(X) into the general solution (11.34) yields
Combining this result with the expression of C1(X) (Eq. 11.24), it follows that,
Rewriting this solution as a function of the dimensional distance (x) and the salinity (S) yields,
or, recalculating the numeric coefficients and expressing the result as a function of the mean value of the longitudinal density gradient and the river velocity uf = Qf/A = Qf/BH0,
From this analytical expression the dimensionless stream function, the u- and w-velocity components may be calculated by derivation, according to the relations (11.32 and 11.33), and the results are:
and
When the wind stress is zero (τWx = 0), these solutions are similar to the solutions deduced in the article of Fisher et al. (1972), and the u-velocity component (Eq. 11.45) is also similar to the Officer (1976) solution, but it has been improved with the introduction of bottom nonlinear tidal frictional influences.
Solutions (11.45) and (11.46) determine the motion in any longitudinal position of the mixing zone (MZ) of a partially mixed estuary. This result indicates that the steady-state velocity field is dependent on the longitudinal density (salinity) gradient, the river discharge, and the wind stress. And the first (11.45) and the solution (10.22 and Chap. 10) are formally identical, even though solution (10.22) was developed for a well-mixed estuary using a different deduction. This is justifiable because the initial basic hydrodynamic equations were similar, and in relatively homogeneous deep estuaries, the integrated influence of the baroclinic pressure gradient may increase, generating the typical gravitational circulation of partially-mixed estuaries, characterized by bidirectional circulation.
Calculating the velocity at the surface (Z = 0) from Eqs. (11.45) and (11.46), gives the following expressions:
and u(x, 1) = w(x, 0) = w(x, 1) = 0, confirming the superior and inferior boundary conditions. A convenient expression, equivalent to the analytical profile (11.45), may be obtained combining with the surface expression, u(x, 0). For this purpose, we must solve the expression (11.47) for the first term of the right hand side, which is associated with the baroclinic pressure gradient,
Combining this expression with solution (11.45), it can be further simplified and yields:
The power series of the dimensionless variable (Z), on the right hand side of this equation, determinates the depth variation of the surface velocity, the velocity generated by the river discharge and, in the last term, the velocity component generated by the wind shear. Under the assumption that the river discharge and the wind shear stress may be disregarded, this solution simplifies and yields the theoretical profiles obtained by Officer (1976, 1977),
As the u-velocity component has been calculated (Eq. 11.45), we are able to calculate the free surface slope (∂η/∂x). In order to achieve this, the equation of motion (11.7b) must be applied to the free surface (z = η) and solved for, ∂η/∂x, and in terms of the non-dimensional depth (Z = z/H0) the result is,
The final step is to introduce the second derivative of u = u(x, Z) at the surface, (∂2u/∂Z2)|Z=0, into this equation and further simplified to the following expression:
This equation is equal Eq. (10.19 and Chap. 10), which has been obtained for a well-mixed estuary; however, for a partially-mixed estuary, the baroclinic pressure gradient predominates. For example, let us assume the following numeric values: H0 = 10.0 m, g = 10 m s−2, ρ = ρ0 = 103 kg m−3, ∂ρ/∂x ≈ Δρ/Δx = 3.0 × 10−3 kg m−4, uf = 0.1 m s−1, Nz = 10−2 m2 s−1 and τWx = 0.2 kg m−1 s−2. Then, it follows that ∂η/∂x > 0 and the first term of Eq. (11.52a) is 10 times greater than the other terms (10−5 compared to 10−6). Only stronger landward winds may invert the free surface slope (∂η/∂x < 0). To calculate the analytical expression of the free surface, η = η(x), the Eq. (11.52a) must be integrated, with the result being a linear variation from η(x)|x=0 = 0 to η = η(x),
11.3 Hydrodynamic Solution: Moderate Bottom Friction
Following the same development as in Topic 10.3 (Chap. 10), let us now adopt the bottom boundary condition (11.28) expressed by the semi-empirical relation TB = τBx/τB0, and expressed by the semi-empirical boundary condition \( {\uptau}_{\text{Bx}} = {\uptau}_{\text{B0}} {\text{T}}_{\text{B}} = {\uprho} (4/{\uppi} ){\text{kU}}_{\text{T}} {\text{u|}}_{{{\text{z}} = {\text{H}}_{ 0} }} = {\uprho} (4/{\uppi} ){\text{kU}}_{\text{T}} {\text{u}}_{{{\text{Z}} = 1}} \), indicating a moderate bottom friction (slippery condition). As previously indicated, this condition is applied when the tidal velocity amplitude is UT ≫ u (Bowden 1953). Let us also assume, according to Prandle (1985), that the kinematic eddy viscosity coefficient may be empirically simulated by Nz = kUTH0, where the numeric coefficient k = 2.5 × 10−3 is dimensionless. Applying the upper boundary condition (11.26) and the integral boundary condition (11.31), expressed by Ψ(x, 0) = 1, to the general solution (11.34) yields:
and
Therefore, with the bottom boundary condition (11.28) applied and if a2(X) is known, we have the following expression for a1(X):
and, applying the second integral boundary condition (11.31), that is, Ψ(X, 1) = 0, yields the integration function a3(X),
Substituting the integration functions a1(X), a2(X), a3(X) and a4(X), into the general solution (11.34) and further simplifying to the simplest expression yields the following expression for the stream function:
Substituting the expression of C1(X) (11.24) into (11.57), expressing them in terms of the dimensional longitudinal distance (x) and the mean salinity \( (\overline{\text{S}} ), \) it follows that:
which is directly proportional to the depth and the longitudinal salinity gradient and inversely proportional to the dynamic (kinematic) eddy viscosity coefficient. In function of the longitudinal density gradient and taking into account that Nz = kUTH0, another expression for the current function is:
According to the equalities (11.32) and (11.33), which define the u- and w-velocity components as derivatives of the stream function, the analytical expression (11.59) is used to calculate these velocity components as:
and
These solutions indicate that under normal conditions the u-velocity component is forced directly by the baroclinic pressure gradient, the river discharge and the wind stress, but the w-velocity component is dependent only on the density gradient and its second derivative.
Let us now calculate the u-velocity component (Eq. 11.60) at the bottom (Z = 1), in order to calculate the bottom stress. In doing so, and after simplifications, τBx is determined by,
Calculating the magnitude of these terms, it is possible to see that the second term is of higher magnitude than the others terms, and positive values of the bottom friction (τBx > 0) are generally found in natural estuarine environment. Combining this result with Eq. (11.60) and simplifying the resulting expression to a more convenient solution for practical applications gives,
This solution for the u-velocity component for a partially mixed estuary has the same formalism as (Eq. 10.48 and Chap. 10) for a well-mixed estuary (type 1 or C). Calculating this component at the surface (Z = 0) yields the following expression:
and, with a similar development to that used in the deduction of Eq. (11.49), under maximum friction at the bottom (non-slippery bottom), the equation to calculating the u-velocity component (11.63) may be rewritten as,
This solution is similar to Eq. (10.48), which was calculated with maximum bottom friction. Comparing these equations, we may observe an increase in the importance of the baroclinic pressure gradient and the wind stress in driving the motion, and a decrease in the river discharge forcing. It is also possible to apply the equality (11.51) to this solution to calculate the steady-state free surface slope (∂η/∂x),
In comparing this result with Eq. (11.52a) we may observe an accentuated variation in the river discharge coefficient (second term in the right hand side); its numeric coefficient changes from 3.0 to −2.21. Taking into account the same orders of magnitude in these equations, the free surface slope is positive (∂η/∂x > 0) in both equations, being slightly higher under the first boundary condition.
The development of solutions using zero friction at the bottom as a boundary condition are easy to be demonstrated, and derived in other books, such as Officer (1976).
11.4 Theoretical Vertical Salinity Profile
We will now proceed with the solution of the second order partial differential Eq. (11.23), complemented with its coefficients C1(X) (11.24) and C2(X) (11.25), to calculate the salinity field; in the first moment the dimensionless $ = $(X, Z) will be calculated, and further, its transformation to the solution S = S(x, Z) will be obtained. This solution is dependent on the stream function, Ψ = Ψ(x, Z), which has already been calculated for distinct boundary conditions (11.43) or (11.44) and (11.58) or (11.59). Of course, these solutions will be dependent on the upper and lower boundary conditions (11.29) and (11.30), respectively, and the integral boundary condition (11.31).
Let us introduce, according to Fisher et al. (1972), an auxiliary (dummy) continuous function f = f(X, Z), defined as f(X, Z) = ∂$/∂Z, to the solutions of these differential equations. As its second derivative is ∂f(X, Z)/∂2$/∂Z2, substituting these quantities into the Eq. (11.23) yields the following first order non-homogeneous partial differential equation with variable coefficients:
where C2 = C2(X) has previously been defined in (11.25), and the quantities A(X, Z) and B(X, Z) are expressed by,
and
These quantities are in function of the stream function, Ψ = Ψ(X, Z) (Eq. 11.57), and the longitudinal salinity gradient \( (\frac{{\partial \overline{\$ } }}{{\partial {\text{X}}}} ) \) in the A(X, Z) expression is assumed to be known.
With the definition of f = f(X, Z) yielding the differential Eq. (11.67), the boundary conditions (11.29) must be applied separately and are given by,
and
Therefore, in order for the salt flux (or salt transport) through the free surface and bottom to be zero, the f = f(X, Z) function must satisfy the conditions f(X, 0) = f(X, 1) = 0, respectively.
The general solution of Eq. (11.67) may be found in Wylie (1960) and Fisher et al. (1972) and is given by:
The function b1(X) in the last term of the right hand side of this equation may be calculated using one of the boundary conditions, (11.70) or (11.71); however, it is convenient to adopt the latter condition because it equals zero, and then the solution is reduced to
As the quantities C2(X), A(X, Z) and B(X, Z) are given by (11.25), (11.68) and (11.69), respectively, and taking into account Eqs. (11.32) and (11.33), the integrand ratios, A/C2 and B/C2, are transformed in,
and
where Ψ, u and w are known functions of x and Z, and its analytical expressions are dependent on the boundary conditions. Then, although the function f = f(X, Z) has a complicated expression (11.73), it may be numerically calculated without as many difficulties in terms of the stream function and the velocity components. Using the velocity components yields the following expression:
With the analytical expression of the function f(x, Z) known, the steady-state vertical salinity profile may be calculated by:
where b2(x) is the integration function, which is calculated by the integral boundary condition, and S0 is the constant salinity value at the coastal region, as previously defined. This condition may be expressed by Eq. (11.30) or its equivalent mean salinity value at the water column,
yielding,
and the integration function, b2(x), is calculated by
Substituting (11.80) into the partial solution (11.77) yields an analytical expression for calculating the steady-state vertical salinity profile:
Although this solution is apparently complicated, when rewritten in terms of the stream function or the velocity components, it may be calculated by numerical integration. Combining Eq. (11.76) with the solution (11.81), the result is the following expression for calculating S = S(x, Z) as function of the velocity components (Fisher et al. 1972):
The second term on the right hand side of this equation is an indefinite integral, and its result is an expression with Z as an independent variable; the third term is a definite integral calculated in the closed interval [0 − 1], and its final result is a numeric value.
It should be noted that the theoretical steady-state velocity and salinity profiles deduced by Fisher et al. (1972) were evaluated with laboratory experimental data from the Vicksburg and the Delft Hydraulic Laboratory (Delft, Holland) salinity flume and observation data from the James River estuary (Virginia, USA). The combined dataset covered a wide range of flow conditions and degrees of salinity stratification, some of which may be partially invalidate the model assumptions, but these studies helped to define the limits of the analytical model application.
As the intensity of the u-velocity component is several orders of magnitude higher than the vertical component (w), several authors, for example, Officer (1976) and Hamilton and Wilson (1980), had neglected the vertical salt advection. With this assumption, the theoretical vertical salinity profile is established by the balance of the longitudinal advection and the vertical eddy diffusion, according to the simplified expression of Eq. (11.11):
and the simplest solution of which may be obtained from Eq. (11.82) with the simplification w(x, Z) = 0 is:
This solution may also be obtained directly by integrating the differential Eq. (11.83). In doing so, rewriting this equation in terms of the dimensionless depth (Z) and separating the variables yields (Officer (1976, 1978):
where the quantity, b3(x), is a dimensionless variable of integration. Taking into account the assumption that at the upper boundary condition there is no salt flux, \( \frac{{{\uprho} {\text{K}}_{\text{z}} }}{{{\text{H}}_{ 0} }}\frac{{\partial {\text{S}}}}{{\partial {\text{Z}}}} |_{{{\text{z}} = 0}} = 0, \) it follows that b3(x) = 0. Then, with a new integration,
To calculate this second dimensionless variable of integration, b4(x), the integral boundary condition (11.78) must be applied, and its value is given by
Then, substituting b4(x) into solution (11.86), the result is the vertical analytical salinity profile, S = S(x, Z), which is the same as expression (11.84).
The dependence of the u-velocity and salinity vertical profiles on the Nz (or its dynamic value, Az), and on the kinematic eddy diffusion coefficient (Kz), which makes the comparison between experimental and theoretical results more difficult. However, as we will be seen later in this chapter, the best numerical values for these coefficients may be estimated, when the validation methodology is applied to improve the comparison of experimental data and theoretical results.
11.5 Theoretical and Experimental Velocity and Salinity Profiles
To exemplify the analytical solution of steady-state vertical profiles of the u- and w-velocity components and the salinity, let us consider an estuary with a transverse section with width B = 103 m and a depth of 12 m, forced by a river discharge of Qf = 20 m3 s−1, where the wind stress is disregarded (τWx = 0).
11.5.1 Longitudinal and Vertical Velocity Profiles
The analytical expressions that will be used to calculate the u-velocity component, u = u(x, Z) are Eqs. (11.49) and (11.65), respectively, for maximum and moderate bottom friction, respectively. To calculate the vertical velocity profile, w = w(x, Z), the corresponding simplified Eqs. (11.46) and (11.61) will be used with the same bottom friction characteristics.
As the transverse area at a longitudinal position, x, is BH0 = 12 × 103 m2 the velocity generate by the river discharge is uf ≈ 0.017 m s−1. Let us adopt for the kinematic eddy viscosity coefficient Nz = kUTH0 = 1.2 × 10−2 m2 s−1, and k = 2.5 × 10−3, considering the tidal amplitude velocity UT = 0.4 m s−1. Under the assumption that the mixing zone (MZ) has a length of 104 m (10 km) and the salinity at the mouth is 30‰, the mean longitudinal salinity gradient has an order of magnitude of 3.0 × 10−6 m−1 and its second derivative, ∂2S/∂x2, is estimated in 2.5 × 10−8 m−2. These values may be converted in the corresponding values of the mass field using the linear equation of state of seawater (Eq. 11.5) with the saline contraction coefficient, β = 7.0 × 10−4 and ρo = 1.0 × 103 kg m−3, and the following estimates are obtained: ρ(30) = 1021.0 kg m−3, \( \partial \overline{{\uprho}} /\partial {\text{x}} = 2.1 \times 10^{ - 3} \) kg m−4, and \( \partial^{ 2} \overline{{\uprho}} /\partial {\text{x}}^{ 2} = 4.0 \times 10^{ - 8} \) kg m−5.
In the u-velocity profile, u = u(x, Z), shown in Fig. 11.2 upper (a), we may observe gravitational circulation that is typical of partially mixed estuaries (types 2 or B), which is symmetric to the velocity generated by the river discharge (≈0.017 m s−1). In the moderate bottom friction condition (Fig. 11.2 upper b), the motion has higher velocity in comparison to the first condition, u(x, 1) = 0, to compensate due to the moderate bottom friction.
Vertical velocity profiles, u = u(x, Z) and w = w(x, Z), calculated with Eqs. (11.49) and (11.65), and (11.46) and (11.61), respectively, with the following surface and bottom boundary conditions: zero wind stress (τWx = 0), maximum friction at the bottom, u(x, 1) = 0, (bold line), and a moderate bottom friction u(x, 1) ≠ 0 (dashed line)
Values of the vertical velocity component, w = w(x, Z), can be various orders of magnitude lower than the u-velocity component, and its intensity is higher for a moderate bottom friction condition (Fig. 11.2 lower a, b). The negative value indicates the occurrence of upward motions (note that the Oz axis is oriented in the direction of the gravity acceleration), closing the continuity of the longitudinal motion, and the maximum value occurs at the middle of the water column.
11.5.2 Vertical Salinity Profile
To calculate the vertical salinity profile, S = S(x, Z), it is necessary that the mean salinity value in the water column is known, and let us adopt the value \( \overline{\text{S}} = 2 0 \)‰. As the salinity is dependent on mixing processes (advection and diffusion), the advective process will be simulated by the u-velocity profile given by the solution (11.49) under the assumption that τwx = 0, and, for the diffusive process, the kinematic eddy diffusion coefficient will be taken as: Kz = 1.0 × 10−6 m2 s−1.
Combining the simplified solution of the vertical salinity profile (Eq. 11.84) with the analytical equation u = u(x, Z) indicated above, which satisfies the bottom boundary condition, u(x, 1) = 0, the steady-state vertical salinity profile is calculated by:
where the u-velocity component at the surface, u = u(x, 0), must be calculated by Eq. (11.64), and its solution is presented in Fig. 11.3a. Using the u-velocity component with the moderately bottom boundary condition (Eq. 11.65), we have the following expression for the vertical salinity profile:
where the current velocity at the surface (Z = 0) must be calculated by Eq. (11.64). The steady-state vertical salinity profiles under these boundary conditions are presented in Fig. 11.3.
In the Fig. 11.3a we may observe that under maximum friction bottom boundary condition, u(x, 1) = 0, the stratification parameter (\( \updelta{\text{S}}/\overline{S} \)) is equal to 0.23. However, with a moderate bottom friction (Fig. 11.3b), there is an increase in the stratification parameter which is equal to 0.78. This increase is due to a higher influence of the advection in the vertical salinity distribution as the u-velocity component is higher under this bottom boundary condition (Fig. 11.2b-upper). Due to these changes in the vertical stratification, the circulation parameter increases from us/uf = 4.4 to us/uf = 9.6, and the images of these parameters on the Stratification-Circulation Diagram (Fig. 3.11, Chap. 3) are located in the semi-plane of partially mixed estuaries and highly stratified (type 2b), because \( \updelta{\text{S}}/\overline{S} > 0.1. \)
11.5.3 Validation of Experimental Velocity and Salinity Vertical Profiles
Practical examples on the validation of nearly steady-state observational u-velocity components and salinity vertical profiles with the solutions using Eqs. 11.45 and 11.84 are shown in Figs. 11.4 (upper and lower), according to the investigations of Bernardes (2001) and Bernardes and Miranda (2001). The hydrographic and current velocity were sampled in a mooring station located in the southern region of Cananéia Estuarine System (Fig. 1.5 and Chap. 1), and good agreement between theoretical and experimental data may be observed.
11.6 Hansen and Rattray’s Similarity Solution
Hansen and Rattray (1965) theory is a classical theoretical development using the similarity method to obtain the solution of a coupled set of partial differential Eqs. (11.1) to (11.4) and associated boundary conditions, in order to describe the circulation and the salt-flux steady-state processes for coastal plain and laterally homogeneous estuaries, where turbulent mixing is primarily forced by tidal currents.
The longitudinal salinity distribution in many coastal plain estuaries takes the general form of the hyperbolic tangent function, with the maximum gradient in the estuarine region named central regime and tailing off asymptotically to terminal values towards the mouth and the estuary head. In the central regime, the vertical salinity stratification is nearly independent of the longitudinal position, while in the outer and inner regimes, it is proportional to the departure of the sectional mean salinities from their asymptotic values.
The salinity stratification characteristic in the central regime makes it possible for a theoretical treatment to describe the bi-dimensional velocity and salinity fields generated by external (river discharge and wind), and internal (gradient pressure and friction) forces. As noted by (Hansen and Rattray, op. cit.), analysis of the estuarine regime, therefore, constitutes a problem of both forced and free convection, with the latter influenced by density gradients on the velocity distribution. Thus, the basic non-tidal circulation associated with, and active in, maintaining the salinity distribution in estuaries consists of a seaward flow of river water and a system of currents induced by the density difference between freshwater and seawater.
In the central regime, the following assumptions are made: the estuary has a laterally homogeneous geometry (width and depth), and the river discharge is constant and there is a known salinity (S0) at the estuary mouth. The basic partial differential equations, which formulate the physical-mathematical problem in relation to the Oxz referential system (Fig. 11.1), in terms of the stream function, ψ = ψ(x, z), and the linear equation of state of seawater, the equation of motion and the salt conservation equations are:
and
The salt conservation equation presents the following differences in relation to the former formulation (Eq. 11.11): all terms of this equation have the salinity as an unknown, and the term that formulates the longitudinal salt diffusion (first on the right hand side) is included.
The boundary conditions that guarantee a unique solution to Eq. (11.90) are: the wind stress acting on the free surface and maximum bottom friction (non slip bottom), which are formulated by (11.12) and (11.13), respectively. The net volume transport is equal to the river discharge (11.18), due to the steady-state hypothesis. As in the salt conservation Eq. (11.91), the salt fluxes due to advection and turbulent diffusion are included, and the salt balance at the estuary mouth must be null. With the exception of the surface and bottom boundary conditions which annul the salt fluxes through these surfaces, it is necessary to impose the following integral boundary condition:
or
In the second integral, it was taken into account that by the current function definition (11.8), u = −(1/B)∂ψ/∂z. Then, according the steady-state condition, the resulting salt transport TS, [TS] = [MT−1], due to the advection and diffusion, must be null. The sought solutions will portrait the transition from river (S = 0) to the oceanic conditions, i.e., for ∂S/∂x > 0, and in the classical article of Hansen and Rattray (1965), three types of similarity solutions with this property were developed. The particular conditions required for these solutions indicate relationships among the external parameters which may be expected to result in particular velocity and salinity distributions. However, for mathematical simplicity, only the central regime of an idealized estuary, which has a rectangular cross-section and the exchange coefficients independent of the depth, will be presented. Further results on the outer and inner regimes may be found in the Hansen and Rattray’s article.
In the similarity method, solutions for the stream function and salinity fields are investigated, with the following separation of variables:
and
where ν is a dimensionless (mixing parameter), Z = z/H0 is the non-dimensional depth, ξ = ξ(x) = Qfx/BH0Kx0 = ufx/Kx0 is the non-dimensional longitudinal distance, Kx0 is the longitudinal kinematic eddy diffusion coefficient at the estuary mouth and S0 its mean salinity. As the estuary is laterally homogeneous, S0 is the mean value in the water column, located at the estuary mouth. Taking into account these definitions, the stream function and the salinity are now functions of the dimensional coordinates (z) and (x, z), respectively, because Ψ[Z(z)] = Ψ(z) and S[ξ(x), Z(z)] = S(x, z).
As the river discharge, Qf, is taken as constant, the stream function (11.93) is independent of the longitudinal distance (x). Then, the w-velocity component, according to its definition in terms of the stream function (Eq. 11.8), is not resolved by this analytical model, and its influence on the salt conservation Eq. (11.91) is null.
The linear longitudinal salinity variation in the central regime is assured by the linear dependence of ξ = ξ(x),
or
and the diffusive upstream salt flux (per density unit) at estuary mouth (x = 0) is the fraction of the mixing parameter (ν) of the advective the salt flux advected seaward by the river flow and is the product of the mean cross-section salinity, S0, and the river velocity. Solving this equation for the dimensionless mixing parameter (ν), we have:
This result indicates that the mixing parameter, ν, is determined by the following salt flux ratio: the landward salt transport by eddy diffusion to the advective seaward salt transport by the river discharge. To close the salt balance in the central regime, an advective term related to the up-estuary salt flux due to the gravitational circulation (Φadv) must be included, and the mixing parameter is defined as:
From this expression of the mixing parameter, it follows that 0 < ν≤1, and when ν = 1, there is no gravitational circulation (Φadv → 0) and the salt flux ratio (11.96b) is in balance; otherwise, if ν → 0 the salt transport by diffusion is less important (Φdif ≪ Φadv), and the salt flux is mainly due to advection (river discharge and gravitational circulation), and the tidal mixing is very low and may be disregarded (Hansen and Rattray 1966; Hamilton and Rattray 1978). As we have seen in the Stratification-circulation Diagram (Chap. 3), for ν = 1 and ν → 0 corresponds to estuaries classified as well-mixed and partially mixed, respectively.
The similarity condition in the central regime also needs to satisfy the following hypothesis: the kinematic eddy viscosity (Nz) and diffusion (Kz) coefficients are constant, as is the case of the Fisher et al. (1972) analytical model; however, the kinematic eddy diffusivity, Kx, increases seaward at a rate equivalent to the river discharge (Hansen and Rattray 1966),
Introducing the new formulations of the stream function (11.93) and salinity (11.94) into the Eqs. (11.90) and (11.91), respectively, and taking into account the last equality (11.97), yields the following dimensionless differential equations:
and
In these equations, Ra and M, are the dimensionless Rayleigh estuarine number Footnote 1 and the mixing tidal parameter,Footnote 2 respectively, which are defined by:
The Ra number is a measure of how efficiently the salinity (density) generates gravitational circulation, and M represents the ratio of the tidal mixing to the river discharge.
The system of differential Eqs. (11.98a) and (11.98b) must be solved in order to satisfy the following boundary conditions, which may be obtained from the corresponding expressions (11.12), (11.13), (11.15), (11.16a, b) and (11.18):
and
In the boundary condition (11.100b), the wind stress, Tw is the third dimensionless parameter and is given by: \( {\text{T}}_{\text{w}} = {\text{BH}}_{ 0}^{ 2} {\uptau}_{\text{Wx}} / {\text{K}}_{\text{z}} {\uprho} {\text{Q}}_{\text{f}} = {\text{H}}_{ 0} {\uptau}_{\text{Wx}} / {\text{A}}_{\text{z}} {\text{u}}_{\text{f}} \) .
To complete the boundary conditions of the salt conservation Eq. (11.98b), it is necessary to use the integral boundary condition (11.92b) in the dimensionless formulation, taking into account the similarity relations (11.93) and (11.94), and the expression of the longitudinal salinity gradient, ∂S/∂x = (νS0Qf)/(BH0Kx0),
To satisfy the salt conservation, the net salt transport at the estuary mouth (x = ξ = 0) must be null, and the equality Kx = Kx0, holds for this position. Then, the integral boundary condition (11.92b) in terms of the non-dimensional depth is simplified to:
The equation of motion (11.98a) may be solved with the same procedure as used in the non-dimensional Eq. (11.22). Then, by successive integrations, we find the solution which is equivalent to (11.43). By applying the boundary conditions (11.100a) and (11.100b), the integration functions a3(X) and a4(X) will be obtained, yielding the following expression for the stream function (Hansen and Rattray 1965):
With this analytical expression, which is equivalent to solution (11.43), we can easily calculate the u-velocity component in the central regime using the relationship u(Z) = −uf(dΨ/dZ),
where TW is the non-dimensional wind stress \( ( {\text{T}}_{\text{W}} = {\uptau}_{\text{Wx}} / {\uptau}_{\text{W0}} ). \) This result is similar to solution (11.45). Comparing these solutions, we may observe that the dimensionless coefficients νRa and \( ( {\text{gH}}_{ 0}^{ 3} / {\text{N}}_{\text{z}} {\text{u}}_{\text{f}} {\uprho}_{ 0} ) (\partial \overline{{\uprho}} /\partial {\text{x)}}, \) are equivalent, performing the same dynamical function (baroclinic pressure gradient) in the gravitational circulation.
Equation (11.104) expresses the steady-state circulation (u-velocity component) as the sum of three modes: (i) the gravitational-convection mode, associated with the Rayleigh (Ra) estuarine number; (ii) the river discharge mode; and, (iii) the wind-stress mode. If, for example, Ra and TW are null, the u-velocity profile assumes a parabolic form, which is characteristic of uniform motion and has a constant eddy viscosity. As νRa increases, the baroclinic pressure gradient associated with the density (salinity) field increases and the motion becomes bidirectional for Ra > 30, as illustrated in Fig. 11.5.
Relative horizontal velocity profiles (u/uf) with τWx = 0, parameterized by the Rayleigh number multiplied by the mixing parameter (νRa). Observed values (solid dots) are for the River James estuary (St. 17) (from Hansen and Rattray 1965)
The parabolic profile obtained from Eq. (11.104) when νRa = 0 and TW = 0, shown in Fig. 11.5, has almost the same analytic expression of that obtained from Eq. (8.86, Chap. 8).
As the stream function, Ψ = Ψ(Z), as a power series of the dimensionless depth, has already been determined (Eq. 11.103), the salt Eq. (11.98b) only has the salinity, S = S(Z), as an unknown. Integrating this equation and applying the boundary condition, (dS/dZ)|Z=0=0, yields the following expression for the vertical salinity gradient:
where b5 is an integration constant. The integration of the first term of the right hand side of this equation may be completed, and the variable of integration changes from Z to Ψ and the inferior integration limit becomes 1. Progressing further with this integration and applying the boundary condition (11.100a), which states that for Z = 1 → Ψ(1) = 0, gives:
Applying the boundary conditions (11.100a, b, c), it follows that Ψ(1) = 0, Ψ(0) = 1 and dS/dZ|Z=1=0, and we find b5 = ν/M. Substituting this constant into expression (11.106) and integrating the result, we find the following solution for the vertical salinity profile, S = S(Z):
where S(0) = Ss is the salinity at the surface, and b6 is a new dimensionless integration constant, which will be calculated with the boundary condition (11.102), resulting in:
Completing the integrations and solving to the constant, b6, yields,
Substituting this expression of the integration constant, b6, into the partial solution (11.108), we find the solution for the steady-state vertical salinity profile,
or, according to the expression (11.94), for S(x, Z) = S[ξ(x), Z], the final analytical expression to calculate the steady-state vertical salinity profile, obtained by Hansen and Rattray (1965), is:
where the integral in the last term on the right hand side of this solution is a constant value. Analysis of this solution indicates that the vertical salinity profile depends explicitly on the tidal mixing parameter (M). However, as the stream function Ψ = Ψ(Z), is dependent on the Rayleigh estuarine number (Ra), this profile depends simultaneously on these two dimensionless parameters.
The relative salinity profiles, in relation to the salinity at the estuary mouth (S0) multiplied by the dimensionless ratio M/ν, at ξ = 0 with no wind stress, and parameterized in the dimensionless product, νRa, are illustrated in Fig. 11.6. The relative stratification, like the gravitational convection, increases with νRa, but is also proportional to M/ν. Observational steady-state salinity profiles in the James river estuary (Virginia, USA) indicate good correspondence with the theoretical profiles for νRa = 750.
Vertical relative salinity profiles (M/ν)[(S − S0)/S0] at ξ = 0 and τWx = 0, parameterized by the Rayleigh number multiplied by the mixing parameter (νRa). Observed values (solid dots) for the James river estuary (St. 17), with νRa = 750 (from Hansen and Rattray 1965)
The wind forcing influences on the u-velocity component and salinity profiles were also investigated in the classical articles of Rattray and Hansen (1962) and Hansen and Rattray (1965). This theoretical study was expanded by Officer (1976, 1977), Prandle (1985), among others, imposing moderate bottom friction, and the tidal currents are predominantly responsible for the eddy diffusion, but without other influence in the steady-state circulation.
11.7 Estuary Classification: Stratification-Circulation Diagram
Applying the integral boundary condition (Eq. 11.102), the mixing parameter (ν) which measures the relative importance of diffusion and advection to the salt fluxes (Eq. 11.96b), may be correlated with the dimensionless parameters M, Ra and the wind stress TW. This correlation may be achieved by finding the positive square root of the following second degree algebraic equation (Hansen and Rattray 1965):
In the subsequent article, Hansen and Rattray (1966) used this equation as the starting point to analytically determine a quantitative method for use in estuary classification. This method was named the Stratification-circulation Diagram, and its practical application was presented in Chap. 3. For this purpose, Eq. (11.112) is simplified, disregarding the wind stress (Tw = 0). As an artifact, the first member of the equation is multiplied and divided by ν, and rearranging its terms yields the following incomplete second grade equation for the mixing parameter, ν:
For practical purposes, considering the parameter ν as unknown, this equation may be expressed as a function of the following dimensionless parameters: the ratio of the u-velocity at the surface (us) to the fresh water velocity (us/uf), and the ratio of the salinity at the bottom (Sb) minus the salinity at the surface (Ss), divided by the mean salinity value in the water column (\( \overline{\text{S}} \)), yielding \( ( {\text{S}}_{\text{b}} - {\text{S}}_{\text{s}} ) /\overline{\text{S}} \). As previously presented in Chap. 3, these parameters are the definitions of the circulation and stratification parameters, respectively. Then, calculating the solution of the u-velocity component (Eq. 11.104) at the surface (Z = 0), we have the following results:
and
In the following step, the vertical salinity profile presented in the Eq. (11.111) will be solved at the surface (Z = 0) and bottom (Z = 1), and the last two terms on the right hand side will be integrated in the closed interval [0 – 1], and the results are:
and
Substituting these results into the Eq. (11.111), yields the following values of the salinity at the surface (Z = 0) and bottom (Z = 1):
and
By subtraction of Eqs. (11.117) and (11.118), it follows that the stratification parameter may be calculated by,
or
Finally, substituting expressions (11.116a), (11.116b), (11.116c) and (11.120) into Eq. (11.113) the unknown (ν) of this equation may be calculated as a function of the stratification, \( \updelta{\text{S}}/\overline{\text{S}} \) , and circulation, us/uf, parameters. As previously seen, these parameters may be determined in the estuary region where the central regime predominates. Although this equation has already been presented and used in the estuaries classification (Chap. 3), it is presented bellow as a complementary equation for this topic,
This equation indicates the functional relation for the unknown, ν,
which has ν = 0 as a trivial solution. However, its solution in the real numeric field is only possible if the constant, 32, in the third term on the left hand side of the Eq. (11.121a) is disregarded. With this simplification, for ν = 1, when the turbulent eddy diffusion is predominant to the landward salt transport, the solution is us/uf = 1.5, and for ν → 0 the advective process is predominant to the seaward salt flux. Using this solution, Hansen and Rattray (1966) were able to classify estuaries with correlation of the parameters, (\( {\updelta} {\text{S}}/\overline{\text{S}} \)) and (us/uf), in the Stratification-circulation Diagram with ν (0 < ν ≤ 1) as parameter. The graphical solution of this equation, forming the base of an analytical method of estuary classification, has already been presented in figures of the Chap. 3, the defined parametric values enabling four estuary types to be identified, which were closely checked with observational data of natural estuaries.
11.8 Hansen and Rattray’s Velocity and Salinity Vertical Profiles: Results and Validation
For practical applications of the vertical u-velocity and salinity profile solutions of Hansen and Ratttray (1965) (Eqs. 11.104 and 11.111), describing the dynamical steady-state of the central regime of the mixing zone of estuaries due to the river discharge, the baroclinic pressure gradient and wind stress are obtained from derivations of the stream current function, Ψ = Ψ(Z) Eq. (11.103). However, it should be observed that the theoretical solution, u = u(Z), is only function of the vertical coordinate (z, or Z); however, the salinity solution, S = S(x, Z) or S = S(x, z), is also a function of the longitudinal coordinate, x, due to its dependence on the dimensionless longitudinal coordinate, ξ = ξ(x). In these applications, because the local depth is dependent on the longitudinal position, h = h(x), and the river discharge velocity (uf) must usually be substituted by the vertical mean velocity in water column (ua) at the transverse section in the longitudinal position x, the theoretical velocity becomes indirectly dependent on the longitudinal position. Thus, u = u(x, Z) or u = u(x, z).
In relation to the salinity, the theoretical mean value (\( \overline{\text{S}} \)) used in the calculation the stratification parameter, must be substituted by the corresponding value (Sa), i.e., the time-mean value at the transverse section. Furthermore, as the velocity is also dependent on the advective influence of the river velocity, it must be changed to the corresponding mean value at the section (ua). Then, due to these simplifications, in practical applications, the analytical expressions of the theoretical velocity and salinity profiles will be denoted by uc = uc(x, Z) and Sc = Sc(x, Z), respectively, and their analytical expressions are:
and
In these analytical formulae, the vertical Oz axis is oriented in the opposite direction of the acceleration of gravity, and the dimensionless depth varies from Z = 0 and Z = −1 at the surface and bottom, respectively. To obtain a detailed depth discretization, intervals of |ΔZ| = 0.1 are adequate.
These solutions indicate that others geometric and physical quantities which must be known are: longitudinal distance, x, the estuary depth, h, the longitudinal density gradient, ∂ρ/∂x ≈Δρ/Δx, salinities at the the estuary head, Shead, and mouth, Smouth, the wind stress, τWx, and the mixing parameter, ν, previously determined by the Stratification-circulation diagram. Taking into account the hypothesis of Hansen and Rattry’s theory the eddy coefficients Nz, Kz and Kx0, used in the definitions of the dimensionless quantities ξ = ξ(x) and M, and the wind stress (τWx) are considered free parameters, i.e., they must be conveniently adjusted to validate theoretical profiles in comparison to those from observational data. It is known that validation of analytical and numerical models for observational conditions requires a data set of sufficient length to cover variations in tidal cycles, river discharge and wind conditions.
There are several methods that can be used to establish the relative agreement between theoretical and experimental results. One of these is the validation method of the Relative Mean Absolute Error-RMAE (Walstra et al. 2001) and the Skill proposed by Wilmott (1981) which was further improved by Warner et al. (2005).
The method of the Relative Mean Absolute Error-RMAE is formulated by:
where \( \overrightarrow {\text{V}}_{\text{m}} \) and \( \overrightarrow {\text{V}}_{\text{c}} \) are the field measured and the computed velocity vectors, respectively, and the symbol 〈 〉 indicate time-mean values. This definition has been particularly applied for comparison of current velocities, but it may also be used to scalar properties. A limited and preliminary qualification of the RMAE ranges of this method indicate a variation between excellent (RMAE < 0.2) and bad (RMAE > 1.0) validation results.
The Skill method is defined by the following relationship of observed data (XObs), its time (or space) averaged value \( (\overline{\text{X}}_{\text{Obs}} ), \) and the corresponding theoretical results (XModel):
According to the definition, the Skill parameter varies between one (1) and zero (0), indicating a perfect adjustment between calculated and observed values, or a complete disagreement, respectively. The validation of theroretical results with this parameter was applied by Andutta et al. (2006), using observational data series over two tidal cycles to validate the u-velocity component and salinity profiles calculated with a tridimensional numerical model applied to the Curimatú river estuary (Rio Grande do Norte, Brazil).
To illustrate a practical exercise to validate the analytical simulation of the u-velocity component and salinity profiles (Eqs. 11.122 and 11.123), the following physical quantities, which were calculated from hourly observational data measured in the Piaçaguera estuarine channel during three semi-diurnal tidal cycles (northern region of the Santos-São Vicente Estuary, São Paulo, Brazil, Fig. 1.5), whose time-mean values represent nearly-steady values are listed bellow:
-
(i)
Mean values of velocity (ua ≈ uf). salinity (Sa), and depth (h).
-
(ii)
The mixing parameter, ν, obtained from the Stratification-circulation Diagram.
-
(iii)
Mean salinities at the mouth and head (Smouth, Shead).
-
(iv)
Longitudinal density gradient ∂ρ/∂x ≈ Δρ/Δx, adjusted to the best validated theoretical result.
Others physical quantities used were the mean depth, estuary length, distance of the data sampling position to the estuary mouth, wind stress and the free parameters Nz, Kz and KH0. The numerical values of these quantities are shown in Table 11.1.
Using the time-mean vertical profiles of salinity and the u-velocity obtained with the experimental data during three tidal cycles (tick profiles of Fig. 11.7), the calculate stratification and circulation parameters were SP = 0.07 and CP = 11.4, respectively, and the estuary was classified as partially mixed and low stratified (type 2a). The mixing parameter, ν = 0.85, associated with these parameters indicate that the diffusion and advection processes were responsible for 85 and 15 % to the mixing, respectively.
Theoretical (dashed line) and observational (tick line) profiles of salinity (upper), and u-velocity vertical (lower) validated with observational data with the Skill parameter. Measurements made during three semi-diurnal neap tidal cycles in the Piaçaguera Channel (Santos-São Vicente Estuary, São Paulo) (according to Miranda et al. 2012)
The theoretical vertical profiles of the salinity and the u-velocity component in comparison to the observational data are presented in the Fig. 11.7. In both profiles the mean Skill value is 0.96 and 1.0, respectively.
The nearly steady-state salinity stratification and the vertical velocity shear-stress, observed in these results were forced by the oscillatory motion generated by the tidal currents during the neap tidal cycle and a small contribution of the river discharge (≈0.01 m s−1); according to Miranda et al. (2012), these currents were almost the same intensity as those observed during the spring tidal period. The depth of no-motion at Z = −0.45 (≈−5 m) corresponds to a mean value observed during three semi-diurnal neap-tidal cycles.
11.9 Salinity Intrusion
A steady-state theory on the salinity intrusion length (XC) in salt wedge estuaries was presented in Chap. 9 (Eq. 9.72), based in classical theories and confirmed by experimental results. It was shown that this length is directly proportional to the reduced gravity times the square of the depth at the estuary mouth, and inversely proportional to the square of the velocity generated by the river discharge.
Due to the great importance on salt intrusion investigations into estuaries, experiments on these phenomena have been performed since the 1960 decade, in laboratory experiments at Waterways Experiment Station (WES), Vicksburg, Miss. (USA), and in the Delft Hydraulics Laboratory (DHL), Delft (Holland). The laboratory results of the maximum and minimum salt intrusions forced by fresh water discharge, tidal amplitude, mean water depth, roughness, and densities were further compared with in situ measurements and published in the articles of Ippen and Harleman (1961) and Rigter (1973).
In the Rigter’s article, experiments in a tidal salinity flume channel (101.5 m long) are described, taking into account the tidal amplitude induced by sinusoidal tides, mean-water depth, water input discharge and bottom roughness; the flume has a vertical scale (1:64) to approximate physical characteristics of Rotterdam Waterway (Holland). The intrusion length (Li) investigations in these experiments were supposed to be dependent on eleven physical quantities. Several experiments were investigated during which some properties were taken as constant, and others were submitted to controlled variations. A detailed analysis of these experiments, using the dimensional analysis approach may be found in the Rigter’s original article.
Further investigations indicated that the following functional equation to calculate the minimum saline intrusion length (Li) in a partially mixed estuary may be used (Prandle 1985, 2004):
where δ and k are dimensionless coefficients, H is the channel depth, û is the tidal velocity and \( \overline{\text{u}} \) its mean-depth value. The validity of this equation has been compared with observational data enabling its simplification and the following expression was suggested:
In this equation δ1 and δ2 are non-dimensional numeric values, \( {\uplambda} = ( {\text{gH)}}^{ 1 / 2} {\text{T}}_{\text{P}} \) (tidal wave velocity times the tidal period TP), and the second term in the right hand side (δ2λ) was introduced to allow for variations in the degree of mixing at the estuary mouth. A least square fitting procedure was used to determine the constants δ1 and δ2 values; in the Rotterdam Water Way the corresponding values were 0.187 and −0.006, respectively. Similar calculations in the WES tank produced values of δ1 = 0.134 and δ2 = 0.026. Comparisons of observed and computed values for intrusions lengths indicated excellent agreement between the in situ results and the laboratory experiments.
Investigation on the saline intrusion length in an estuary located in the Southern Brazilian coast (Santa Catarina, Brazil) was published by Döbereiner (1985, quoted in Schettini (2002)). In this article, the hydraulic and sediment behavior of the Itajaí-açu river estuary was investigated during low and high river discharges. A synthesis on the Döbereiner’s results is summarized as follow: for low river discharge (300 m3 s−1) the saline intrusion length (Li) was located at approximately 18 km landward from the estuary mouth, however, for river’s discharges higher than 1000 m3 s−1 the salt water was completely removed to the nearshore turbidity zone (NTZ).
Further studies by Schettini and Truccolo (1999) and Schettini (2002), based on seasonal observational data of saline intrusion lengths (Li), and the associated river discharges (Qf), were correlated by the following exponential relationship:
with the root mean square error estimated in 0.7.
11.10 Secondary Circulation
The hypothesis of a longitudinal circulation laterally uniform should not be generalized to most natural estuaries, because as a tridimensional system its water masses are also driven by the flow that is normal to the main along channel flow, usually known as secondary circulation. Thus, the composition of the longitudinal and secondary flow generates along the estuarine channel a complex tri-dimensional motion similar to a helical lateral flow.
In the decomposition of velocity measurements, it is usually possible to observe the presence of v-velocity components, although with low intensity. For example, in the velocity decomposition presented in Table 5.1 (Chap. 5), it is possible to observe the presence of the secondary flows (v-velocity components).
The occurrence of secondary circulation and the associated transverse mixing due to turbulent diffusion and advection in estuaries may be generated by the interaction of the following influences (Pritchard 1956; Dyer 1977; Sumer and Fischer 1977; Chant 2010):
-
Topographic deflection due to natural curvatures along the channel and irregularities at the bottom and margins;
-
Non-uniform lateral and vertical salinity (density) stratification generated by mixing processes;
-
Barotropic and baroclinic pressure gradients;
-
Coriolis and centrifuge accelerations.
Formation of fronts may also be observed in estuarine channels, having been generated by longitudinal and transverse motions. An analysis of these fronts has been made in terms of density forced motions in laboratory and in situ experiments by Nunes and Simpson (1985). The occurrence of this phenomenon may be visually observed because convergence lines frontal zones acts as a filter, gathering organic and inorganic detritus and debris.
The dynamical balance of the secondary circulation and the relative importance of its terms in the equation of motion, have been investigated by Pritchard (1956), Dyer (1973, 1977), Sumer and Fischer, 1977) and Ong et al. (1994) with in situ and laboratory experiments. Sumer and Fischer (op. cit.), Nunes and Simpson (op. cit.), Chant (2010) have provided evidence on the secondary circulation in laterally stratified partially stratified and well-mixed estuaries. Following the theoretical formulation of Nunes and Simpson (op. cit.) for an analytical solution of the secondary circulation, it is necessary to formulate some simplifying hypotheses:
-
Steady-state bi-dimensional motion in the Oyz plane.
-
Cross channel baroclinic pressure gradient force, ∂S/∂y = f(y) and ∂ρ/∂y = g(y).
-
Transverse density gradient is independent of the depth, ∂/∂z(∂ρ/∂y) = 0; and
-
Uniform longitudinal and transverse sections (centrifugal accelerations are disregarded).
As in the analytical solutions for calculating steady-state longitudinal circulation, let us consider an estuary which, by hypothesis, has a constant depth (H0), as indicated schematically in Fig. 11.8, and a known salinity (density) field. This figure indicates the reference (Oyz) with the Oz axis origin at the free surface and oriented in the acceleration gravity \( (\overrightarrow {\text{g}} ) \) direction, and schematically indicates the laterally non-homogeneous density field. Hence, according to the simplifying hypotheses, the cross-channel baroclinic pressure gradient force is formulated by:
As the transverse density gradient is independent of depth the baroclinic term on the right hand side of Eq. (11.128) increases linearly with depth.
As the longitudinal motion will not be taken into account in this simple model, the system of equations to be solved, associated with the linear equation of state of seawater, ρ = ρ0(1 + βS), are expressed by:
The dynamical balance expressed by Eq. (11.129a) does not take into account the dynamical balance between friction and the Coriolis acceleration, which has been investigated by Chant (2010). However, according to the latitudinal estuary position and intensity of the longitudinal and transverse motions, this effect may or may not be disregarded. Examples of estuaries in which these conditions may be found are presented in the articles of Dyer (1977) and Ong et al. (1994).
As the geometry of the cross-section, the salinity field and the turbulent kinematic eddy viscosity are known, this is a closed hydrodynamic system and the boundary and integral boundary conditions warrant a unique solution. In the continuity equation v- and w-velocity components may be expressed in terms of the current function, Ψ = Ψ(y, z), [Ψ] = [L2T−1], and the velocity components may be expressed by: \( {\text{v(y, z)}} = - \frac{{\partial {\uppsi}}}{{\partial {\text{z}}}} \) and \( {\text{w(y, z)}} = \frac{{\partial {\uppsi}}}{{\partial {\text{y}}}}. \) Manipulating and rewriting Eq. (11.129a) in terms of the barotropic and baroclinic pressure gradients, and using the linear equation of state of seawater, the general solution for the transverse velocity is:
where the notations \( {\text{S}}_{\text{y}} = \partial {\text{S/}}\partial {\text{y}}, \) \( {\upeta}_{\text{y}} = \partial {\upeta} /\partial {\text{y}}, \) and the \( \overline{\text{c}} \) and \( \overline{\text{a}} \) coefficients are expressed by \( \overline{\text{c}} = {\upbeta} {\text{g/N}}_{\text{z}} \) , and \( \overline{\text{a}} = - {\text{g/N}}_{\text{z}} \) , and the integration constants C1 and C2, with dimensions [C1] = [T−1] and [C2] = [LT−1], must be determined with the following surface and bottom boundary conditions: wind stress (τWy) and the maximum friction at the bottom:
and
Others solutions may be obtained simulating different bottom conditions as, for example, a moderate (slippery) bottom friction:
Applying the surface and boundary conditions (11.131a), (11.131b) the following values of the integration constants are obtained:
and
Combining these constants with the general solution (11.130) and simplifying the resulting expression, the solution for the v-velocity component is:
or in function of the non-dimensional depth Z,
This solution isn’t in the most convenient formulation for practical applications, because it contains the free surface slope (ηy) as an unknown, which may be calculated with the imposition of an integral boundary condition, that turns the transversal volume transport to zero:
or
As the integrand v = v(y, z) is already known (Eq. 11.134a) the integration may be concluded,
Solving this result for the unknown, ηy, and using the expressions \( \overline{\text{a}} = - {\text{g/N}}_{\text{z}} \) , and \( \overline{\text{c}} = {\upbeta} {\text{g/N}}_{\text{z}} \), we have:
or, neglecting the wind stress (τWy = 0),
This result is similar to the longitudinal component of the free surface slope of Eq. 10.19 (Chap. 10) with uf = 0 and τWx = 0, and the transverse slope of the free surface is directly proportional to the corresponding density gradient, but with the opposite signal (<0), because Ho > 0 and ∂ρ/∂y > 0. Thus, if ηy is known it may be substitute into Eq. (11.134a). Simplifying the result and writing the solution in terms of the non-dimensional depth and the transverse density gradient, it follows that the equation to calculate the v-velocity component according to (Nunes and Simpson 1985) is:
where ρoNz = Az. This result indicates that the direction and intensity v-velocity component is directly dependent on the local depth (H0) and the transverse density gradient (∂ρ/∂y), and is inversely proportional to the vertical dynamical eddy viscosity coefficient. Therefore, transverse intensity variations or orientation changes in the density gradient may generate convergence or divergence of the velocity field. When ∂ρ/∂y > 0, the steady-state free surface slope (Eq. 11.137b) is negative (∂η/∂y < 0), and velocity of the secondary circulation in the surface is positive and oriented in the direction of increasing density. If there is a change in the density gradient (∂ρ/∂y < 0) at a given depth along the transverse section, the secondary circulation has its direction inverted.
At the free surface (Z = 0), the solution (11.138) for the v-velocity component is reduced to:
Changes in the transverse density gradient, from ∂ρ/∂y > 0 to ∂ρ/∂y < 0 in the well-mixed Conway estuary (North Wales, Scotch) were successfully used by Nunes and Simpson (1985) to theoretically explain the visible accumulation of organic and inorganic matter and debris along axial convergence lines.
The vertical velocity profile of the v-velocity component, calculated with Eq. (11.138) is presented in Fig. 11.9a to exemplify the bilateral divergence of the velocity field, and was used to calculate the ascending vertical velocity component (w < 0). These profiles were calculated for different values of the transverse density gradient, ∂ρ/∂y = 2.5 × 10−2 kg m−4 and ∂ρ/∂y = 1.5 × 10−2 kg m−4, in water columns separated by a distance of 200 m. For the others quantities, the following values were used: H0 = 10.0 m, Nz = 1.0 × 10−2 m2 s−1, ρ0 = 1005.0 kg m−3, and Az ≈ 10 kg m−1s−1.
Once the transverse vertical velocity profile has been calculated, the profile of the vertical velocity component w = w(y, Z), generated by the convergence (divergence) of the v-velocity field, may be calculated using the continuity equation solved by finite increments,
with the following boundary conditions: w(y, 0) = w(y, 1) = 0. The vertical velocity profile, w = w(y, Z), calculated by finite increments is presented in Figure 11.9b, indicating a flow towards the bottom (w > 0). Comparing the magnitudes of the v- and w-velocity components, we may observe that |w| ≪ |v| and that the highest value of w (5.5 × 10−4 m s−1) is at Z ≈ 0.4.
Let us now apply the general solution (11.130) imposing the moderate bottom boundary condition (Eq. 11.132) and the no-wind stress (τWx = 0) will remain for the upper boundary condition. Let us assume, according to Prandle (1985), that the vertical kinematic eddy viscosity coefficient is given by the relation Nz = kUTHo, with the non-dimensional coefficient k equal to 2.5 × 10−3. With these boundary conditions, C1 = 0 and
Substituting these values of the integration constants into the general solution (11.130) and reducing it to the simplest analytical expression, we have the following solution, which is similar to (11.134a):
or in function of the non-dimensional depth Z,
As noted previously, this solution isn’t in the most convenient formulation for practical applications, because it contains the free surface slope (ηy) as an unknown, which may be calculated with the imposition of the integral boundary condition (11.135a), and the result is
which is similar to the solution (11.137b), but with a different numeric coefficient. Substituting this result into Eq. (11.142b), simplifying the result and introducing the non-dimensional depth (Z = z/H0), an alternative expression to calculate the transverse vertical velocity profile as a function of the density gradient is
or using the relation Nz = Az/ρ0 = kUTH0 (k = 2.5 × 10−3)
To close the circulation field the w-velocity component generated by the convergence or divergence of the v = v(y, Z) component may be calculated.
Experimental and theoretical investigations of the convergence and divergence of secondary circulation in well-mixed and laterally homogeneous estuaries may be found article of Nunes and Simpson (1985).
The simple steady-state analytic model just described, don’t take into account transverse bottom variations (∂H0/∂y ≠ 0 or ∂h/∂y ≠ 0), and has the lateral density gradients as the main forcing mechanism to drive the secondary circulation and the related axial convergences. Studies of the non-steady-state analytic model of lateral flow convergences, arising from the interaction of tidal flow with the estuary bathymetry are described by Li and Valle-Levinson (1999) and Valle-Levinson et al. (2000). The models are based on the solution of the depth-averaged, first order equations for momentum balance, forced by a single-frequency semidiurnal tide at the estuary mouth. In this model, the energy dissipation is simulated by a linear friction coefficient, κ, with dimension of velocity [κ] = [LT−1].
Considering a channel with straight parallel boundaries, with the Ox axis extended along the right estuary margin looking into the estuary, and the Oy axis along the open boundary, and with a laterally variable depth distribution, the depth-averaged first-order equation for momentum balance is:
The second term on the right hand side was introduced to simulate the energy dissipation by assuming a linear frictional dependence, which is directly and inversely proportional to the velocity u and depth, h, respectively. To the hydrodynamic system closure, the continuity Eq. (7.66a, Chap. 7) is
The Equations (11.145a), (11.145b) are formally derived from the Navier-Stokes equations by integrating these equations over a rectangular cross section, and are similar to the one-dimensional formulation used by Blumberg (1975) in studies of the wave propagation in a uniform channel.
For a single-frequency co-oscillating tide the solution for this equation system can be expressed in terms of the complex exponential number, expressed by (Li and Valle-Levinson 1999, and Valle-Levinson et al. 2000) as:
In these formulations U and V are the complex amplitudes of the longitudinal and the secondary circulation velocity (m s−1), and A is the amplitude (m) of the complex tidal elevation, σ is the tidal angular frequency (s−1), and i is the imaginary number unit (\( \sqrt { - i} \) ). Substituting (11.146) into (11.145a), (11.145b) yields:
and
Under the assumption that the co-oscillating tidal amplitude is known, and imposing the following boundary conditions: (i) at the estuary head (x = L) the velocity is U; and (ii) at the lateral side boundaries (y = 0, D), the velocity (V) vanishes. Thus, applying these conditions to Eq. (11.147a) yields the solution for the U-velocity component.
In this equation, the tidal elevation amplitude (A) may be treated as independent of the transverse direction (y), as demonstrated by Li (1996); Li and O’Donnell (1997) and Li et al. (1998). This assumption led to a dramatic simplification of the problem, and the solution of A may be expressed by (Li and Valle-Levinson 1999):
where η0 is the tidal amplitude. The longitudinal (U) and transverse (V) velocities components, and the angular frequency (ω) are calculated by,
and
As pointed out by Li and Valle-Levinson (1999), the transverse velocity (V) is insensitive to the transverse momentum balance, and may be obtained from the continuity Eq. (11.145b).
This non-steady-state analytic solution was applied by Li and Valle-Levinson (1999) and Valle-Levinson et al. (op. cit.) in two transects of the James river estuary (Virginia, USA), and were compared with observational ADCP measurements. The analytical model reproduced well the timing and location of the convergences in agreement with the experimental results. The mechanisms which generates convergences due to the laterally bottom variation, during flood and ebb conditions are schematically presented in Fig. 11.10.
Mechanisms generating bottom induced convergences for flood and ebb conditions are schematically represented. The upper and lower diagrams are looking into the estuary and towards its mouth, respectively. The ellipticity of the tidal motion is greatly exaggerated to illustrate the transverse flows. According to Valle-Levinson et al. (2000)
In addition to the cross-channel the baroclinic pressure gradient force and the interaction of tidal flow with the estuary bathymetry, a detailed analysis of the following mechanisms that can drive secondary flows have been presented by Chant (2010): (i) Ekman forcing characterized by the balance between friction and the Coriolis acceleration; (ii) flow curvature, which has long been recognized to drive a helical flow normal to the stream-wise flow; and (iii) diffusive boundary layers.
Notes
- 1.
This number is an analog of the Rayleigh number, which is used to forecast the convection of compressible fluids in between plates with different temperatures. This number is proportional to the cubic power of the distances between the plates and a dimensionless combination of physical properties such as: density, gravity acceleration, thermal expansion coefficient, viscosity, specific heat and thermal diffusion.
- 2.
References
Andutta, F. P.; Miranda, L. B., Castro, B. M. & Fontes, R. F. C. 2006. Numerical Simulation of the Hydrodynamic in the Curimataú Estuary, RN Brazil. Oceanography and Global Changes, SP-Brazil, pp. 545–558.
Bernardes, M.E.C. 2001. Circulação Estacionária e Estratificação de Sal em Canais Estuarinos parcialmente Misturados. Dissertação de Mestrado. São Paulo, Instituto Oceanográfico, Universidade de São Paulo. 202 p.
Bernardes, M.E.C. & Miranda, L.B. 2001. Circulação Estacionária e Estratificação de Sal em Canais Estuarinos: Simulação com Modelos Analíticos. Rev. bras. oceanogr., 49(1/2):115–132. (DOC 39).
Blumberg, A. F. 1975. A Numerical Investigation into the Dynamics of Estuarine Circulation. Tech. Rept. Chesapeake Bay Institute, The Jonhs Hopkins University. n. 91. 110 p. + Apêndices.
Bowden, K. F. 1953. Note on Wind Drift in a Channel in the Presence of Tidal Currents. Proc. R. Soc. Lond., A219, pp. 426–446.
Chant, R.J. 2010. Estuary secondary circulation. In: ed. Valle-Levinson A. Contemporary Issues in Estuarine Physics. Cambridge University Press, pp. 100–124.
Döbereiner, C.E. 1985. Comportamento hidráulico e sedimentológico do estuário do rio Itajaí, SC. Rio de Janeiro, Instituto Nacional de Pesquisas Hidroviárias (INPH), Relatório 700/03, 34 p. (quoted in Schettini (2002), p. 132).
Dyer, K. R. 1973. Estuaries: A Physical Introduction. London, Wiley. 140 p.
Dyer, K. R. 1977. Lateral Circulation Effects in Estuaries. Estuaries, Geophysics and the Environment. Washington, D. C., National Academy of Sciences, pp. 22–29.
Fisher, J. S.; Ditmars, J. D. & Ippen, A. T. 1972. Mathematical Simulation of Tidal‑Time Averages of Salinity and Velocity Profiles in Estuaries. Massachusetts Institute of Technology, Mass., Rept. MITSG 72–11, 157 p.
Hamilton, P. & Rattray Jr., M. 1978. Theoretical Aspects of Estuarine Circulation. In: Kjerfve B. (ed.). Estuarine Transport Processes. Columbia, Univesity of South Carolina, pp. 37–73. (Belle W. Baruch Library in Marine Science, 7).
Hamilton, A. D. & Wilson, R. E. 1980. Nontidal Circulation and Mixing Processes in the Lower Potomac Estuary. Estuaries, 3(1):11–19.
Hansen, D. V. & Rattray Jr., M. 1965. Gravitational Circulation in Sraits and Estuaries. J. Mar. Res., 23(1):102–122.
Hansen, D. V. & Rattray Jr., M. 1966. New Dimensions in Estuary Classification. Limnol. Oceanogr., 11(3):319–325.
Ippen, A. T. & Harleman, D. R. F. 1961. One-Dimensional Analysis of Salinity Intrusion in Estuaries. Committee on Tidal Hydraulics. Tech. Bull. Corps of Engineers U. S. Army, n. 5. 120 p.
Kjerfve, B.; Miranda, L. B. & Wolanski, E. 1991. Modelling Water Circulation in an Estuary and Intertidal Salt Marsh System. Neth. J. Sea Res., 28(3):141–147.
Li, C.; O’Donnell, J.; Valle-Levinson, A.; Li, H.; Wong, K-C & Lwiza, K.M.M., 1998. In: Tide induced mass-flux in shallow estuaries. in Ocean Waves Measurement and Analysis, (eds.) B.L. Edge and J.M. Hemsley,. Am. Soc. Civ. Eng., Reston, VA. of, v. 2, pp. 1510–1524.
Li, C. 1996. Tidally induced residual circulation with cross shelf bathymetry. Ph D. Dissertation, 242 pp. Univ. of Conn Storrs.
Li, C. & Valle-Levinson A. 1999. A two-dimensional analytical model for a narrow estuary of arbitrary lateral depth variation. The intra-tidal motion. J. Geophys. Res. 104, pp. 23,525–23,543.
Li, C. & O’Donnell, J. 1997. Tidally driven residual circulation in shallow estuaries with lateral depth variations. J. Geophys. Res. V. 102, pp. 27,915–27,1929.
Miranda, L. B.; Dalle Olle, E.; Bérgamo, A.L.; Silva, L.S. & Andutta, F.P. 2012. Circulation and salt intrusion in the Piaçaguera Channel, Santos (SP). Braz. J. Oceanography, 60(1):11–23.
Nunes, R. A. & Simpson, J. H. 1985. Axial Convergence in a Well-Mixed Estuary. Estuar. Coast. Shelf Sci., 20:637–649.
Ong, J. -E.; Gong, W. -K. & Uncles, R. J. 1994. Transverse Structure of Semi-diurnal Currents Over a Cross-section of the Merbok Estuary, Malaysia. Estuar. Coast. Shelf Sci., 38:283–290.
Officer, C. B. 1976. Physical Oceanography of Estuaries (and Associated Coastal Waters). New York, Wiley. 465 p.
Officer, C. B. 1977. Longitudinal Circulation and Mixing Relations in Estuaries. Estuaries, Geophysics, and the Environment. Washington, D. C., National Academy of Sciences, pp. 13–21.
Officer, C. B. 1978. Some Simplified Tidal Mixing and Circulation Flux Effects in Estuaries. In: Kjerfve, B. (ed.). Estuarine Transport Processes. Columbia, University of South Carolina Press, pp. 75–93. (The Belle W. Baruch Library in Marine Science, 7).
Prandle, D. 1985. On Salinity Regimes and the Vertical Structure of Residual Flows in Narrow Tidal Estuaries. Estuar. Coast. Shelf Sci., 20:615–635.
Prandle, D. 2004. Saline Intrusion in Partially Mixed Estuaries. Est. Coast. Shelf Sci. (59):385–397.
Pritchard, D. W. 1952a. Salinity Distribution and Circulation in the Chesapeake Bay Estuarine System. J. Mar. Res., 11(1):106–123.
Pritchard, D. W. 1954. A Study of Salt Balance in a Coastal Plain Estuary. J. Mar. Res., 13(1):133‑144.
Pritchard, D. W. 1956. The Dynamic Structure of a Coastal Plain Estuary. J. Mar. Res., 15(1):33–42.
Rattray Jr., M. & Hansen, D. V. 1962. A Similarity Solution for Circulation in an Estuary. J. Mar. Res., 20(2):121–133.
Rigter, B.P. 1973. Minimum Length of Salt Intrusion in Estuaries. Proceedings of the America Society of Civil Engineers. Journal of Hydraulics Division, 99 (HY9):1475–1496.
Schettini, C. A. F. & Truccolo. E. C. 1999. Dinâmica da Intrusão Salina no Estuário do Rio Itajaí-açu. In: Congresso Latino Americano de Ciências do Mar, 8, Trujillo, Peru, Resumenes ampliados, Tomo II, UNT/ALICMAR, p. 639–640.
Schettini, C. A. F. 2002. Caracterização Física do Estuário do Rio Itajaí-açu, SC. Revista Brasileira Recursos Hídricos, 7(1):123–142.
Sumer, S.M & Fischer, H.B. 1977. Transverse Mixing in Partially Stratified Flow. Proceedings of the American Society of Civil Engineers. Vol 103, No. HY6, pp. 587–600.
Valle-Levinson, A.; Li, C.; Wong, K-C & Lwiza, K.M.M. 2000. Convergence of lateral flow along a coastal plain estuary. J. Geophys. Res., v. 105, NO C7: pp. 17045–17061.
Walstra, D., Sutherland, J., Hall, L., Blogg, H., and van Ormondt, M. (2001) Verification and Comparison of Two Hydrodynamic Area Models for an Inlet System. Coastal Dynamics’ 01: pp. 433–442. doi:10.1061/40566(260)44.
Wilmott, C. J. 1981. On the Validation Models. Physical Geography, 2 (2), pp. 184–194.
Warner, J.C.; Geyer, W.R.; Lerczak, J.A. 2005. Numerical modeling of an estuary: A comprehensive skill assessment. J. Geophys. Res. V.110(CO5001), p. 1–13.
Wylie, C. R. 1960. Advanced Engineering Mathematics. New York, McGraw-Hill. 696 p.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2017 Springer Nature Singapore Pte Ltd.
About this chapter
Cite this chapter
Bruner de Miranda, L., Andutta, F.P., Kjerfve, B., de Castro Filho, B.M. (2017). Circulation and Mixing in Steady-State Models: Partially Mixed Estuary. In: Fundamentals of Estuarine Physical Oceanography. Ocean Engineering & Oceanography, vol 8. Springer, Singapore. https://doi.org/10.1007/978-981-10-3041-3_11
Download citation
DOI: https://doi.org/10.1007/978-981-10-3041-3_11
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-10-3040-6
Online ISBN: 978-981-10-3041-3
eBook Packages: EngineeringEngineering (R0)