Keywords

1 Introduction

A compliant mechanism transmits the applied forces from specified input ports to output ports by elastic deformation of its comprising material, fulfilling required kinematic functions analogous to a rigid-body mechanism [1]. There are two major design methods for compliant mechanisms: pseudo-rigid-body mechanism synthesis and continuum structure optimization.

A number of techniques have been developed to design the compliant mechanisms by continuum structure optimization. Simplified isotropic material with penalization (SIMP) [2, 3] is a fundamental method and will be discuss in this article. Many objective function of the optimization problem are proposed. Two formulations will be discussed. They are the mechanical advantage (MA) formulation and the output displacement formulation. The output displacement formulation includes an input spring to model the actuator’s stiffness [4]. The output displacement is the objective function. The mechanical advantage (MA) formulation applies constrain on the input displacement [5]. The mechanical advantage is the objective function.

The objective function which maximizes mechanical or geometrical advantage [6] is found to be a non-convex function [7]. And most of the topology optimization method updates the design viable according to the sensitive analysis. Thus, the result of the topology optimization of compliant mechanisms is usually the local optimum but not a global one. Sometimes, the result is far always from the global optimum. This is a serious problem. However, the researches about the local optimum in topology optimization of compliant mechanisms are rare.

Similar researches about the local optimum aim to deal with the structural topology optimization problem [8]. The structural topology optimization problems are modeled using material interpolation, e.g. simplified isotropic material with penalization, to produce almost solid-and-void designs. But the problems become non convex due to the use of these techniques when penalty factor is bigger than 1. The penalty continuation in structural topology optimization is used to avoid the local optimum in many researches [9, 10]. This method increases the penalty factor from 1 to a maximum number during topology optimization. The penalty continuation is reported to be helpful in topology optimization of compliant mechanisms [11, 12]. Instead of OC and MMA, GCMMA is proposed to update the design variable to avoid the local optimum [13]. However, the global optimal solution cannot always be obtained by continuation with respect to the penalization parameter and how far is the result away from the global optimum remains unknown. The theoretical upper bounds of the objective function in two formulations are deduced in this article. And the upper bound is equal to the global optimum when the stiffness of the spring is small.

In this article, the scheme composed of two steps is proposed to avoid most of the local optimum and find the solution next to the global optimum in topology optimization of compliant mechanisms. The scheme composed of two steps is based on the following discoveries. The theoretical upper bound of the objective function exists and is equal to the global optimum when the stiffness of the spring is very small. And in this case, topology optimization of compliant mechanisms is a process to find a rigid-body mechanism with a certain geometrical advantage. And the geometrical advantage is depended on the boundary condition.

The paper is organized as follows. Section 2 discusses the theoretical upper bounds of the objective function. Section 3 discusses the essence of topology optimization of compliant mechanisms in some cases. Section 4 introduces the scheme composed of two steps to avoid most of the local optimum. Section 5 is the discussion and conclusion.

2 The Theoretical Upper Bound of the Objective Function

The theoretical upper bound of the objective function in the output displacement formulation is deduced here. An input spring is introduced to model the actuator’s stiffness. The mathematical model is given as

$$ \begin{array}{*{20}c} {\mathop {\hbox{max} }\limits_{{{\mathbf{0}} \le \varvec{x} \le {\mathbf{1}}}} :} & {\Delta _{out} } \\ {s.t.\quad :} & {\varvec{F}_{in} - \varvec{KU} = {\mathbf{0}}} \\ {} & {V(\varvec{x}) \le V_{0} } \\ \end{array} $$
(1)

where \( \Delta _{out} \) is the displacement of the output node. \( \varvec{F}_{in} \) is the force vector applied on the input node. \( \varvec{U} \) is the displacement vector. \( V(\varvec{x}) \) is the volume factor. \( \varvec{K} \) is the stiffness matrix and is given by

$$ \varvec{K} = \varvec{K}_{S} + \varvec{K}_{in} + \varvec{K}_{out} $$
(2)

where \( \varvec{K}_{S} \) is the sum of stiffness matrix of all continuum elements. \( \varvec{K}_{in} \) is the stiffness matrix of input spring. \( \varvec{K}_{out} \) is the stiffness matrix of output spring.

The norm of the input force vector \( \left\| {\varvec{F}_{in} } \right\| \) can be divided into two parts and can be given as

$$ \left\| {\varvec{F}_{in} } \right\| = F_{ink} + F_{ins} $$
(3)

where \( F_{ink} \) is applied to the input spring and is given as

$$ F_{ink} = K_{in}\Delta _{in} $$
(4)

where \( K_{in} \) is the stiffness of input spring. \( \Delta _{in} \) is the displacement of the input node. \( F_{ins} \) is applied to the compliant mechanisms. Compliant mechanisms store the energy when they are deformed. Thus, the input energy is bigger than the output energy.

$$ F_{ins}\Delta _{in} \ge F_{out}\Delta _{out} $$
(5)

\( \eta \) is introduced as the energy transport efficiency and is given by

$$ \eta = \frac{{F_{out}\Delta _{out} }}{{F_{ins}\Delta _{in} }} $$
(6)

\( r \) is defined as the geometrical advantage and is given by

$$ r = \frac{{\Delta _{out} }}{{\Delta _{in} }} $$
(7)

Then, the objective function can be deduced by a combination of Eq. 1–7

$$ \Delta _{out} = \frac{{F_{in} }}{{\frac{{K_{in} }}{r} + \frac{{K_{out} r}}{\eta }}} $$
(8)

when

$$ r = \sqrt {\frac{{\eta K_{in} }}{{K_{out} }}} $$
(9)

The objective function is maximized. If the Young’s modulus of the material is large while the stiffness of input and output spring is small, the compliant mechanism is close to the rigid-body mechanism and the energy transport efficiency \( \eta \) is close to 1. The objective function reaches the theoretical upper bound and is given as

$$ \Delta _{out} = \frac{{F_{in} }}{{2\sqrt {K_{in} K_{out} } }} $$
(10)

The theoretical upper bound of the objective function in the output displacement formulation is deduced. In this case, the topology optimization of compliant mechanisms is a process to find a rigid-body mechanism with a certain geometrical advantage. And the geometrical advantage is depended on the stiffness of input spring and output spring as given in Eq. 9.

If there is no relationship between the energy transport efficiency and the geometrical advantage, then the objective function is maximized when the energy transport efficiency is equal to 1. This deduction is corresponded to the theory in other researches [14, 15].

In the MA formulation, constrain on the input displacement is applied. The mathematical model is given as

$$ \begin{array}{*{20}l} {\mathop {\hbox{max} }\limits_{{{\mathbf{0}} \le \varvec{x} \le {\mathbf{1}}}} :} \hfill & {MA(\varvec{x}) = \frac{{\left\| {\varvec{F}_{out} } \right\|}}{{\left\| {\varvec{F}_{in} } \right\|}} = \frac{{K_{out}\Delta _{out} }}{{\left\| {\varvec{F}_{in} } \right\|}}} \hfill \\ {s.t.\quad :} \hfill & {\varvec{F}_{in} - \varvec{KU} = {\mathbf{0}}} \hfill \\ {} \hfill & {V(\varvec{x}) \le V_{0} } \hfill \\ {} \hfill & {\Delta _{in} \le\Delta _{\hbox{max} } } \hfill \\ \end{array} $$
(11)

where \( \Delta _{\hbox{max} } \) is the upper bound of the input displacement. \( \varvec{K} \) is the stiffness matrix and is given by

$$ \varvec{K} = \varvec{K}_{S} + \varvec{K}_{out} $$
(12)

the output displacement can be deduced as

$$ \Delta _{out} = \hbox{min} \left\{ {\frac{{\eta F_{in} }}{{rK_{out} }},r\Delta _{\hbox{max} } } \right\} $$
(13)

and the objective function is given by

$$ MA = \hbox{min} \left\{ {\frac{\eta }{r},\frac{{K_{out} }}{{F_{in} }}r\Delta _{\hbox{max} } } \right\} $$
(14)

If \( \eta \approx 1 \), MA will reach the maximum value when the geometrical advantage

$$ r = \sqrt {\frac{{F_{in} }}{{\Delta _{\hbox{max} } K_{out} }}} $$
(15)

The maximum value, which is the theoretical upper bound of the objective function, is given by

$$ MA = \sqrt {\frac{{\Delta _{\hbox{max} } K_{out} }}{{F_{in} }}} $$
(16)

The theoretical upper bound of the objective function in the MA formulation is deduced above. In this case, the topology optimization of compliant mechanisms is a process to find a rigid-body mechanism with a certain geometrical advantage. And the geometrical advantage is depended on Eq. (15).

3 The Essence of Topology Optimization of Compliant Mechanisms

When the Young’s modulus of the material is large and the stiffness of input and output spring is small, topology optimization of compliant mechanisms is a process to find a rigid-body mechanism with a certain geometrical advantage. And the geometrical advantage is depended on the boundary condition.

A numerical example is illustrated. It is an inverter design problem. The boundary condition is showed as Fig. 1. Term E is the Young’s modulus of the material.\( \mu \) is the Poisson ratio. t is the thickness and V0 is the volume factor.

Fig. 1
figure 1

The boundary condition of the inverter design problem

Full size image

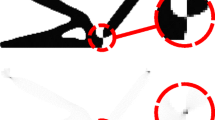
The design domain is discretized. The 105 line MATLAB code [4] is used to solve this problem. And the result of this problem is showed in Fig. 2.

Fig. 2
figure 2

The result of the inverter design problem

Full size image

The objective function of the result is 0.04996 mm. And the result is in accordance with Eq. (10) because

$$ \Delta _{out} = \frac{{F_{in} }}{{2\sqrt {K_{in} K_{out} } }} = 0.05\,{\text{mm}} $$
(17)

A check of the geometrical advantage r in this problem is done for further validation. The geometrical advantage r should be equal to 1 when the objective function is maximized in this problem according to Eq. (9). A rigid-body mechanism is extracted from Fig. 2 and is showed in Fig. 3.

Fig. 3
figure 3

Kinematic sketch of the rigid-body mechanism(upper half)

Full size image

The geometrical advantage r from the kinematic analysis is given by

$$ r = \frac{{\dot{\Delta }_{out} }}{{\dot{\Delta }_{in} }} = 0.9804 \approx 1 $$
(18)

The result is nearly the same as that in Eq. (9).

This numerical example indicates that in some cases the essence of topology optimization of compliant mechanisms is a process to find a rigid-body mechanism with a certain geometrical advantage. And the geometrical advantage is depended on the boundary condition. This phenomenon occurs when the Young’s modulus of the material is large and the stiffness of input and output spring is small.

4 The Scheme Composed of Two Steps to Avoid Most of the Local Optimum

Now that the upper bound of the objective function is deduced, evaluating the problem of the local optimum becomes an easier task. A method is proposed to find the solution next to the global optimum in topology optimization of compliant mechanisms.

This scheme is composed of two steps. The first step is to find a rigid-body mechanism with a certain geometrical advantage r. The geometrical advantage is given by Eqs. (9) or (15). In order to find the rigid-body mechanisms by topology optimization, the Young’s modulus is magnified and the stiffness of output spring is reduced. The second step is topology optimization of compliant mechanisms. The Young’s modulus and the stiffness of output spring the same as the original problem, but the initial guess is the result of the first step instead of the uniform density. The flow chart is showed in Fig. 4.

Fig. 4
figure 4

The flow chart of the scheme composed of two steps

Full size image

An example is used for illustration. The boundary condition of the inverter design problem is showed in Fig. 5. The objective function is the output displacement. And the result of the 105 line MATLB code is showed in Fig. 6. This result is used for comparison.

Fig. 5
figure 5

The boundary condition of the inverter design problem

Full size image
Fig. 6
figure 6

The result of the 105 line MATLB code, the output displacement is 0.408 mm

Full size image

When the proposed scheme is used, the first step is to find a rigid-body mechanism. The best geometrical advantage is equal to 20 in this problem according to Eq. (9). The Young’s modulus is magnified 1000 time and the stiffness of the output spring is set to be 625 N/m. Then, the program starts until the geometrical advantage reaches 20 as showed in Fig. 7a. The rough rigid-body mechanism design problem is finished. In order to get a reasonable result, the stiffness of the output spring is then set to be the same as the original problem. Then, a fine rigid-body mechanism whose geometrical advantage is next to 20 is got. The rigid-body mechanisms is showed in Fig. 7b. That is the first step. The second step is to find a compliant mechanism from the rigid-body mechanism. The Young’s modulus is set to be 2.09e11 Pa. The final result is showed in Fig. 7c.

Fig. 7
figure 7

a The geometrical advantage is 19.19. b The reasonable rigid-body mechanism. The objective function is equal to 1.00 mm and is next to the upper bound 1 mm in Eq. (10). (c) The result of the topology optimization of inverter, the output displacement is 0.832 mm. And the geometrical advantage is 12.8864

Full size image

Comparison between the traditional method starts from the uniform guess and the proposed method in this article is showed in Table 1 and discussed below.

Table 1 Comparison between the traditional method and the scheme composed of two steps
Full size table

The traditional 105 line MATLAB code finds the result that the output displacement is 0.408 mm. The proposed method finds the result that the output displacement is 0.832 mm. There are great differences between these two results and both of them are local optimum. The upper bound of the output displacement is 1 mm in this problem. However, it is not the result of global optimum because the soft material always stores energy and makes the energy transport efficiency \( \eta \) lower than 1.

5 Discussion and Conclusion

In output displacement formulation, the objective function is a function of two variable in Eq. (8). They are energy transport efficiency and the geometrical advantage. If the energy transport efficiency is close to 1, the output displacement is depended on the geometrical advantage. In this case, topology optimization of compliant mechanisms is a process to find a rigid-body mechanism with a certain geometrical advantage. And the objective function reaches the upper bound. Similar phenomenon occurs in MA formulation. The existence of the output spring and input spring is important. The problem will become ill-condition if one of their stiffness is zero. Because there won’t be a certain geometrical advantage which maximizes the output displacement as given in Eq. (9).

In future research, the analysis of the other objective function, e.g. efficiency formulation [16], Characteristic Stiffness (CS) Formulation [17] and Artificial I/O Spring Formulation [18], should be done. The quantity relation between the stiffness of spring and the Young’s modulus when a rigid body mechanism is design should be pointed out.

In conclusion, three discoveries are discussed in this article. First, the theoretical upper bounds of the objective function in two formulations are deduced. Second, it is pointed out that in some cases, topology optimization of compliant mechanisms is a process to find a rigid-body mechanism with a certain geometrical advantage. And the geometrical advantage is depended on the boundary condition. Third, based on the above discoveries, a method is proposed to find the solution next to the global optimum in topology optimization of compliant mechanisms. The numerical example indicates that this method is useful.