Keywords

1 Introduction

A machine tool linear axis consists of a worktable and a relative fixed frame, and is actually a prismatic joint or a slide way. A perfect linear axis, or an ideal prismatic joint, restrains five degrees of freedom (DOFs), and permits one linear displacement. If machining errors of the joint interfaces and component deformations are to be taken into consideration, the worktable actually moves in a three-dimensional manner and causes deviations from the ideal motion.

According to the standards ASME B5.54-2005 [2] and ISO 230-1-2012 [3, 4], the geometric accuracy of the linear axis consists of six error terms covering the linear displacement errors (including positioning accuracy) and the straightness errors (also called the roll, pitch and yaw). The measurement approaches of the linear error motion are defined in the standards above. The typical measuring instrument is the XD instrument with laser interferometer. Furthermore, many researchers proposed a number of methods for the linear error motion test. Lin [5] measured the volumetric errors by means of the laser tracker system which moved toward the space diagonal and only in need of one setup. Knapp [6], Okuyama [7], Ziegert [8] focused on the circular test for numerically controlled machine tools by CBP method and DBB method, analyzed the motion of each axis by error separation. With the multi-line method such as 9-line and 22-line method, Chen [9] and Tian [10] established the parameter identification model for geometric error assessment.

The common point above is that, the error evaluation is based on the measured function point. The result of the evaluation depends on the measurement coordinate system, and it is not the unique one. For example, the linear displacement errors can be affected by the angular displacement errors in tests, such as the Abbe error/offset and the Bryan principle [11]. Can the errors be clearly and strictly defined for a linear axis? Is there another convenient analysis method to decompose the angular and linear displacements and provide a theoretical base for evaluating accuracy of an individual linear axis of machine tools?

During testing the six error terms of an individual linear axis, the worktable occupies a series of permissible discrete positions. The points and lines on the worktable will trace the corresponding discrete trajectories whose geometric characteristics are used to evaluate the accuracy of the linear axis, which naturally is a DKG topic. In this paper, a kinematic geometry model, corresponding to a typical measuring scheme, is presented to describe and analyze the accuracy in testing a machine tool linear axis. The kinematic parameters of the worktable, three rotations and three translations, are determined using the proposed model and measured displacements. The discrete trajectories traced by the points and lines on the worktable are mapped into the directrixes and the spherical image curves, whose invariants are used to evaluate the accuracy of the linear axis.

2 The Kinematic Geometry Model

2.1 Description of Testing a Machine Tool Linear Axis

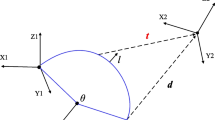
A typical scheme, similar to that mentioned in ASME B5.54-2005, is used to test machine tool linear axis by the XD measuring instrument, shown in Fig. 1. A fixed coordinate system {O f ; i f ; j f ; k f }, attached to the frame, is chosen in such a way that its coordinate axes coincide with the axes of the machine tool. A moving coordinate system {O m ; i m ; j m ; k m } attached to the moving worktable, or the assembling position of the laser instrument on the work table, is chosen in way that its origin O m coincides with the original-point of the laser, and its i m axis coincides with the direction of the laser, its k m and j m axes are perpendicular to i m . A discrete location is described in {O f ; i f ; j f ; k f } with superscript (i), such as \( \{\varvec{O}_{m}^{(i)} ;\varvec{i}_{m}^{(i)} ;\varvec{j}_{m}^{(i)} ;\varvec{k}_{m}^{(i)} \} \).

Fig. 1
figure 1

Schematic of testing a machine tool linear axis

Full size image

The six error terms of a linear axis, both linear and angular displacements, can be measured by the XD measuring instrument for a measuring position (i) of the worktable, as shown in Fig. 1. The linear displacements \( x_{om}^{(i)} \) of the worktable in the direction of the linear axis can be directly revealed by the laser interferometer; the two other linear displacements \( \left( {y_{om}^{(i)} , \, z_{om}^{(i)} } \right) \), or the lateral motion in the two directions orthogonal to the direction of the linear axis are measured and shown by means of the sensors in the fixed frame. The angular displacements (errors) corresponding to the yaw α (i), pitch β (i) and, roll γ (i) can be determined by the angular optical sensors mounted on the fixed frame. Generally, five of the six error terms come from the loci of the lines of the laser beam except that the angular displacement γ (i), measured by an electric level sensor.

In the ideal case, or the worktable moves straight in the desired direction, the trajectory of any line of the worktable, including the line of the laser beam, is a plane or a line in the fixed frame. In fact, the worktable has an error motion in six-DOF, five error terms come from the line-trajectory by comparing it with that in the ideal case. Hence, different positions of the laser beam line produce different line-trajectories. Some useful cases were pointed out by Abbe and Bryan [11].

2.2 Kinematical Geometry Model in Testing a Linear Axis

Figure 2 shows a typical machine tool linear axis with erroneous slide ways and erroneous worktable interfaces.

Fig. 2
figure 2

Sketch of a machine tool linear axis

Full size image

To study the kinematic geometry of the worktable, the relationship between the moving frame {O m ; i m ; j m ; k m } and the fixed frame{O f ; i f ; j f ; k f }, or the six kinematical parameters—three translations {x om , y om , z om } and three angles of rotation {α, β, γ} need to be established. The origin O m of the laser beam has the coordinates (0, 0, 0) in the coordinate system {O m ; i m ; j m ; k m } of the worktable \( \sum^{ * } \), and its coordinates are {x mf , y mf , z mf } in the fixed frame{O f ; i f ; j f ; k f }. The rotation transformation matrix from the coordinate system {O m ; i m ; j m ; k m } to the coordinate system {O f ; i f ; j f ; k f } can be written as

$$ [\varvec{R}_{mf} ] = \left[ {\begin{array}{*{20}c} {c\alpha c\beta } & {c\alpha s\beta s\gamma - s\alpha c\gamma } & {c\alpha s\beta c\gamma + s\alpha s\gamma } \\ {s\alpha c\beta } & {s\alpha s\beta s\gamma + c\alpha c\gamma } & {s\alpha s\beta c\gamma - c\alpha s\gamma } \\ { - s\beta } & {c\beta s\gamma } & {c\beta c\gamma } \\ \end{array} } \right] $$
(1)

A point P m on the worktable with coordinates (x pm , y pm , z pm ) moves with the worktable and traces a trajectory \( \varGamma_{P} \) in {O f ; i f ; j f ; k f }, whose vector equation is

$$ \varGamma_{P} :\varvec{R}_{Pf} = \varvec{R}_{Om} + [\varvec{R}_{mf} ]\varvec{R}_{Pm} $$
(2)

where \( \varvec{R}_{mf} { = [}x_{mf} ,y_{mf} ,z_{mf} ]^{T} \) is the vector of point O m ; and \( \varvec{R}_{Pm} = [x_{Pm} ,y_{Pm} ,z_{Pm} ]^{T} \) is the vector of point P m .

Similarly, a line L m on the worktable ∑ *with the direction angular (δ sm , θ sm ), passes through point P m can be represented in the matrix form as

$$ [l_{m1} ,l_{m2} ,l_{m3} ] = [{\text{s}}\delta_{sm} {\text{c}}\theta_{sm} ,{\text{s}}\delta_{sm} {\text{s}}\theta_{sm} ,{\text{c}}\delta_{sm} ] $$
(3)

Line L m of the worktable moves in {O f ; i f ; j f ; k f }, traces a line-trajectory ∑ lf , or a ruled surface, whose equation can be written as

$$ \sum\nolimits_{Lf} : \varvec{R}_{Lf} = \varvec{R}_{Pf} + \lambda [\varvec{R}_{mf} ]\varvec{l}_{m} $$
(4)

where \( \lambda \) is the parameter of the generatrix; \( \varvec{l}_{m} = [l_{m1} ,l_{m2} ,l_{m3} ] \) is the unit direction vector of line L m .

Specially, the line-trajectory ∑ lf traced by the line of the laser beam i m , shown in Fig. 3 for a series of discrete positions, can be denoted as

Fig. 3
figure 3

Line-trajectory of laser beam in the fixed frame

Full size image
$$ \sum\nolimits_{lf} : \varvec{R}_{lf} = \varvec{R}_{mf} + \lambda [\varvec{R}_{mf} ]i_{m} $$
(5)

In testing a machine tool linear axis, the loci traced by points and lines of the worktable in {O f ; i f ; j f ; k f } can be determined from the kinematic geometry equations in connection with the measurements. It is noted that the measurements of the actual motion of the worktable relative to the fixed frame with six DOFs including the nominal linear motion, need to be taken only once. The kinematic geometry characteristics of all point-trajectories and line-trajectories can be determined and described by the kinematic invariants of the erroneous motion of the worktable.

3 The Discrete Kinematic Invariants

3.1 Kinematical Geometry Model in Testing a Linear Axis

As mentioned above, both point-trajectories and line-trajectories can be described in Eqs. (1)–(5). However, the actual motion of the worktable are expressed by a series of discrete data, acquired using an instrumentation. Hence, in this paper, we propose to use the discrete kinematic invariants of spatial motion of a rigid body to study the actual erroneous motion of a machine tool linear axis.

A ruled surface in the fixed frame {O f ; i f ; j f ; k f }, traced by a line of the worktable, represented by Eq. (4) for continuous parameters, can be rewritten for the discrete parameters as

$$ \sum\nolimits_{Lf} : \varvec{R}_{Lf}^{(i)} = \varvec{R}_{Pf}^{(i)} + \lambda [{\mathbf{R}}_{mf}^{(i)} ]\varvec{l}_{m} $$
(6)

Corresponding to the discrete position in testing an individual linear axis \( x_{om}^{(i)} \), the geometric properties of a discrete ruled surface traced by a line of the worktable can be completely calculated by Eq. (6), whose vector equation can be written in a standard form as

$$ \sum\nolimits_{Lf} : \varvec{R}_{Lf} =\varvec{\rho}_{Lf}^{(i)} + \lambda \varvec{l}_{f}^{(i)} ;\quad i = 1, \ldots ,n $$
(7)

The kinematic invariants, independent of the coordinates system used, are naturally a set of most effective parameters for studying the geometric properties of discrete ruled surfaces. The directrix and spherical image curve are the typical invariants of a ruled surface. Consequently, the DKG approach is a powerful tool to compare geometric characteristics of two discrete ruled surfaces, which is believed as a novel approach in testing an individual linear axis.

3.2 The Minimal Directrix of Error Motion

The trajectory of any point \( P_{m}^{(i)} \) in the generator of the ruled surface, defined a directrix, could be written as following:

$$ \varGamma_{P}^{(i)} :\varvec{R}_{Pf}^{(i)} = \varvec{R}_{Om}^{(i)} + \left[ {\varvec{R}_{mf}^{(i)} } \right]\varvec{R}_{Pm} $$
(8)

Obviously, the directrix degenerates into a straight line without error motion. While in the actual situation, there is a minimal directrix in the fixed frame, corresponding to a point in the moving body, which has the minimal error respect to its fitting line. The mathematical model for the minimal directrix can be written as follows:

$$ \left\{ {\begin{array}{*{20}l} {\Delta = \hbox{min} \mathop {\hbox{max} }\limits_{1 \le i \le n} \{ f^{(i)} ({\varvec{x}})\} } \hfill \\ {f^{(i)} ({\varvec{x}}) = \sqrt {\left\| {{\varvec{R}}_{p}^{(i)} - {\varvec{R}}_{0} } \right\|^{2} - (({\varvec{R}}_{p}^{(i)} - {\varvec{R}}_{0} ) \cdot {\varvec{l}}_{0} )}^{2} } \hfill \\ {\varvec{R}_{0} = (x_{0} ,y_{0} ,0)} \hfill \\ {\varvec{x} = (x_{0} ,y_{0} ,\xi ,\eta )} \hfill \\ \end{array} } \right. $$
(9)
$$ \left\{ {\begin{array}{*{20}l} {\delta = \min\Delta (\varvec{p})} \hfill \\ {\varvec{p} = (x_{pm} ,y_{pm} ,z_{pm} )} \hfill \\ \end{array} } \right. $$
(10)

while (x Pm , y Pm , z Pm ) is the coordinate parameters of the point in the moving body, and (x 0, y 0, ζ, η) is the parameters for the fitting line l 0. The optimization model (9) is for the saddle line fitting [12] of all the points and their corresponding errors, while (10) is to search for the point corresponding to the minimal directrix called the minimal error point. Both the minimal directrix and the minimal error point are the invariants of the error motion of the worktable.

3.3 The Spherical Image Curve of Error Motion

The directions of the generatrix of the discrete ruled surface can be mapped into a curve on a unit spherical surface, or a spherical image curve of the direction vector l f , and can be calculated from the following equation

$$ \varvec{l}_{f}^{(i)} = [\varvec{R}_{mf}^{(i)} ]\varvec{l}_{m} ;\quad i = 1, \ldots ,n $$
(11)

In the case of ideal linear motion, the discrete spherical image curve is a single point on the unit spherical surface. Similar to the directrix, there is a vector with the minimal angular error, called as the minimal error vector. The optimization model for minimal error vector can be written as:

$$ \left\{ {\begin{array}{*{20}l} {\Delta = \mathop {\hbox{min} }\limits_{\varvec{a}} \{ g(\varvec{x})\} } \hfill \\ {g(\varvec{x}) = arc\sin (\varvec{l}_{0} \cdot \varvec{l}^{(i)} )} \hfill \\ {\varvec{x} = \left( {\delta_{1} ,\delta_{2} } \right)^{T} } \hfill \\ \end{array} } \right. $$
(12)
$$ \left\{ {\begin{array}{*{20}l} {\delta = \min\Delta (\varvec{p})} \hfill \\ {\varvec{p} = (\alpha_{m} ,\beta_{m} )} \hfill \\ \end{array} } \right. $$
(13)

while (α m , β m ) are the direction parameters of the vector in the moving body, and (δ 1, δ 2) are the parameters for the fitting orientation in the rigid system. All the orientations and their errors, including the minimal error orientation, can be solved.

From the viewpoint of the DKG of a rigid body, the global kinematic invariants, the directrix error space and the spherical image curve error surface can thoroughly describe the properties of the moving worktable in its erroneous motion, as discussed as follows.

4 Case Studies

4.1 Case 1: Line-Trajectory

In this test case shown in Fig. 4, the laser instrument is placed on the worktable of a machine center (DMG-DMC1035V) at approximated coordinates (150, 0, 0). The parameters of the instrument are as follows: the linear accuracy is 0.5 ppm, the straightness accuracy is 1 + 0.2 (μm/meter traveled), while the angular accuracy is 1.0 + 0.1 (arcsec/meter traveled). The six error terms measured are shown in Fig. 5.

Fig. 4
figure 4

Test apparatus for a linear axis (case 1)

Full size image
Fig. 5
figure 5

Erroneous linear and angular motions of the X-axis on the worktable (case 1)

Full size image

The line-trajectory of the laser beam can be calculated by means of the proposed kinematic geometric model and Eqs. (1)–(9). The line-trajectory ∑ lf of the laser beam line and its directrix are calculated and shown in the fixed frame in Fig. 6. The discrete spherical image curve of the line-trajectory of the laser is calculated by Eq. (9) and shown in Fig. 7.

Fig. 6
figure 6

The line-trajectory of laser beam and the directrix of line-trajectory of laser (case 1)

Full size image
Fig. 7
figure 7

Discrete spherical image curve of laser and the detail view (case 1)

Full size image

The laser line in Case 1 is just one of the lines of the worktable. Does it show the linear accuracy of the linear axis? If not, measurements for a different laser line can be obtained by putting the laser instrument on the worktable with another position, but is there is a most suitable position on the work table for the laser with least error? It would certainly be the global invariants of the linear axis error motion of the work table.

4.2 Results from Three Test Cases

The laser instrument is placed for other two test cases. All the three cases are described in Table 1 for the laser instrument on the worktable, shown in Fig. 8. One hundred discrete positions are measured in each case.

Table 1 Three cases for testing an individual linear axis
Full size table
Fig. 8
figure 8

Three measuring cases for locations of laser instrument

Full size image

By means of the XD measuring instrument, the measuring data was obtained corresponding to the three cases, the three linear errors are shown in Fig. 9a–c, and the angular errors are shown in Fig. 10a–c.

Fig. 9
figure 9

Linear errors of a linear axis for three cases

Full size image
Fig. 10
figure 10

Angular errors of a linear axis for three cases

Full size image

Three groups of data, shown in Figs. 9 and 10, for the erroneous motion of the worktable in testing a single linear axis, indicate that the measuring results are sensitive to the positions of the laser instrument, which agrees with the Bryan principle in the ASME standard. The question is how to choose a reasonable measuring position of the laser instrument on the worktable. Is there any intrinsic relationship among different groups of measurements? This is a fundamental question faced by today’s machine tool design and manufacture engineers.

4.3 Kinematic Invariants of the Error Motion

  1. (1)

    The directrix error space and the minimal straightness error point

In case one, the directrix error space and its 3-D contour lines are depicted by Eqs. (8)–(10) in Fig. 11a, b, which show the directrix errors of all points in the moving body. Particularly, the deep blue position with the coordinate (247.72, −220.25, −67.13) corresponds to the minimal straightness error point, and the trajectory is closest to a straight line with the spatial straightness error 1.79 μm. Figure 11c shows the contour lines on plane z = −87.13 mm.

Fig. 11
figure 11

The directrix error space and its contour lines in case one

Full size image

Similar to case one, the directrix error space and its contour lines in case two and case three can be obtained, shown in Figs. 12 and 13. The coordinates of minimal straightness error points are (256.17, −365.48, −69.62) and (253.22, −425.08, −188.47), corresponding to the minimal error 1.71 and 1.74 μm separately.

Fig. 12
figure 12

The directrix error space and its contour lines in case two

Full size image
Fig. 13
figure 13

The directrix error space and its contour lines in case three

Full size image

Actually, the trajectory of each point in the moving body lies on the linear error motion itself. When the working space and the moving coordinate system are confirmed, the directrix error space is uniquely determined. Therefore, the it can used as the global invariant and the minimal straightness error as a especial one to evaluate the position accuracy of an individual linear axis integrally and objectively.

  1. (2)

    The spherical envelope circle error surface, the minimal/maximal error vector

A line of the worktable will correspond to its discrete spherical image curve error and discrete directrix error. All of these errors are taken as the Z-coordinate and the direction parameters of the line of the worktable are designated as the X and Y coordinates, which form a spherical envelope circle (SEC) error surface in three dimensions in Fig. 14a and projecting plane with contour lines in Fig. 14b. There exists a minimal error vector R P1 on the SEC error surface, corresponding to line L m1 [0.1052, 0.9306, 0.3507] of the worktable, and its discrete spherical image curve error is 2.42e−06 rad. There also exists maximal error vector R P2 corresponding to L m2 [−0.0400, −0.3193, 0.9468], with the maximal error 2.31e−5 rad and forms an angle 88.23° with the minimal vector. The SEC error surface reveals the kinematic geometric properties of the erroneous motion and is independent of the measuring positions. The local coordinate system {O; L 1; L 2; L 3} of the SEC error surface can be set up to identify the position and orientations of the worktable, while L 3 = L 1 × L 2.

Fig. 14
figure 14

The local coordinate system of SEC error surface and with contour lines in case one

Full size image

Similarly, the SEC error surface in Case 2 can also be drawn in three dimensions in Fig. 15a, and the projecting plane with contour lines in Fig. 15b. Here line \( L_{m1} \) [−0.2490, 0.9218, 0.2970] of the worktable corresponds to a minimal error value of 2.47e−06 rad. Line \( L_{m2} \) [0.1941, −0.2254, 0.9563] corresponds to a maximal error 2.33e−5 rad forms an angle 88.43° with the minimal vector.

Fig. 15
figure 15

The SEC error surface and with contour lines in case two

Full size image

The local coordinate system of the SEC error surface in Case 3 can be established by the line of the worktable with the minimal SEC error value and the line with maximum error value shown in Fig. 16, which is same as that in Fig. 14 of Case 1.

Fig. 16
figure 16

The SEC error surface and with contour lines in case three

Full size image

In the same way, the SEC error surface in case three can be drawn in three dimensions in Fig. 16a, and the projecting plane with contour lines in Fig. 16b. Line L m1 [−0.1589, 0.7343, 0.6599] corresponds to a minimal error value of 2.44e−06 rad. Line L m2 [−0.8954, −0.3801, 0.2316] corresponds to a maximal error 2.27e−5 rad forms an angle 89.08° with the minimal vector.

The local coordinate system of the SEC error surface can be established by the line of the worktable in Fig. 16, which is similar to that in Fig. 14 of Case 1, and in Fig. 15 of Case 2. Eliminate the repeatability influence, both the line of the worktable with the minimal/maximal SEC error and the coordinate system of the SEC error surface are the same in all three cases since they are the invariant in testing a machine tool linear axis. This implies that one measuring position (location of laser beam on the worktable) is enough for testing to determine the line of worktable with the minimal SEC error, which is the benchmark of accuracy in testing a machine tool linear axis.

5 Conclusions

  1. (1)

    The kinematic geometric model of a typical testing device, XD measurement instrument, can completely describe the kinematic geometric properties of the actual motion of the worktable.

  2. (2)

    The discrete kinematic invariants, the spherical image curve and the directrix, of the ruled surfaces traced by lines of the worktable reveal the intrinsic geometric properties of the erroneous motion of the worktable.

  3. (3)

    The global kinematic invariants of the erroneous motion of the worktable including the directrix error space and the SEC error surface, are a new benchmark in evaluating the accuracy in testing a machine tool linear axis.