Keywords

1 Introduction

Processing and analysis of color images represented by a quaternion algebra provides better results than the traditional methods like processing of three (R, G, B) images separately because in the quaternion representation, a color image pixel is treated as a single unit. One of the first persons who employed the quaternion algebra for color images is Sangwine [1]. Since then may techniques like Fourier transform [2, 3], Winer filter [4], Zernike moments [5, 6], Disc-Harmonic moments [7–11], Legendre-Fourier moments [12], FourierMellin moments [13] and Bessel Fourier moments [14–16] are extended to color images using the Quaternion algebra. Recently, Karakasis et al. [17] published a unified methodology for computing accurate quaternion color moments. Another recent paper by Chen et al. [18] suggested a general formula for quaternion representation of complex type moments.

All these moments provided mixed results for image reconstruction, object recognition and water marking problems. Recently, Hu et al. [19] proposed an Exponent Fourier moments for gray level images. These moments are similar to Polar Complex Exponential Transforms and Radial Harmonic Fourier Moments. Exponent Fourier moments are computationally inexpensive as compared with other moments like Zernike Bessel Fourier moments [17]. Xia et al. [20] pointed out some errors in the above paper and proposed a better radial function. Unfortunately, this expression turns out to be incorrect. Hence, Hu et al. [21] recently suggested an improved version of it. Most of these moments suffer from numerical and geometric errors. In order to minimize these errors, Wang et al. [22] proposed a Circularly Semi-Orthogonal (CSO) moments for both binary and multilevel images only. Hence, in this paper, we extend the CSO moments proposed for gray level images to color images using the algebra of quaternion and propose a new quaternion circularly semi orthogonal (QCSO) moments for color images. Further, we also derive invariants properties of QCSO moments and verified them with simulation results. In this study we have chosen CSO moments because of the following advantages: (a) Higher order moments are numerically stable than the lower order moments. (b) Zeroth order approximation is more robust to numerical errors compared with other approximations and (c) no factorial terms in the radial function definition

This paper is organized into eight sections. In Sect. 2 we present the quaternion number system. In Sect. 3 circularly semi orthogonal moments are discussed in detail. In Sects. 4 and 5, expressions are derived for Quaternion circularly semi orthogonal forward and inverse moments. Invariant properties of QCSO moments are derived in Sect. 6. Finally, simulation results and conclusions are presented in Sects. 7 and 8 respectively.

2 Quaternion Number System

These numbers are extensions of complex numbers, that consists of one real part and three imaginary parts. A quaternion number with zero real part is called pure quaternion. Quaternion number system was introduced by the mathematician Hamilton [23] in 1843. Then Sang wine [1, 23] applied them for color image represntation. A quaternion number q is written as

$$q = a + b i + c j + d k.$$
(1)

Where a, b, c and d are real numbers, i, j and k are orthogonal unit axis vectors satisfies the following rules

$$i^{2} \, = \,j^{2} \, = \,k^{2} \, = \, - 1, \,ij\, = \, - ji\, = \,k$$
(2)
$$jk = - kj = i, ki = - ik = j$$

From these equations one can say that quaternion multiplication is not commutative. Both conjugate and modulus of a quaternion number q is

$$\begin{aligned} \bar{q} & = a - bi - cj - dk \\ \left| q \right| & = \sqrt {a^{2} + b^{2} + c^{2} + d^{2} } \\ \end{aligned}$$

For any two quaternion numbers say p and q we have \(\overline{p.q} = \bar{p}.\bar{q}\). Quaternion representation of a pixel in a color image is

$$f(x,\,y)\, = \,f_{R} (x,\,y)i\, + \,f_{G} (x,\,y)j\, + \,f_{B} (x,\,y)k$$
(3)

It is assumed that real part is zero. In the above expression \(f_{R} (x,\,y),\,f_{G} (x,\,y) and f_{B} (x,\,y)\) represents the red, green and blue components of a color pixel, similarly, polar representation of an image using the quaternion representation is

$$f(r,\,\theta )\, = \,f_{R} (r,\,\theta )i \, + \,f_{G} (r,\,\theta )j\, + \,f_{B} (r,\,\theta )k$$
(4)

In this expression \(f_{R } (r,\,\theta ), \,f_{G} (r,\,\theta ) \,and\,f_{B} (r,\,\theta )\) denote red, green and blue components of polar representation of image.

3 Circularly Semi-orthogonal Moments

Let \(f(r,\,\theta )\) be the polar representation of a gray level image of size N × M, then the general expression for circularly orthogonal moments (\(E_{nm} )\) of order n and repetition m of a polar image \(f(r,\,\theta )\) is

$$E_{nm} = \frac{1}{Z}\int\limits_{r = 0}^{1} {\int\limits_{\theta = 0}^{2\pi } {f(r,\theta )T_{n} ({\text{r}}) {\text{exp}}\left( { - jm\theta } \right)rdr} d\theta }$$
(5)

where \({\text{n}}\, = \, \pm 0, \, \pm 1,\, \pm 2\, \ldots \ldots \ldots .\) and \(m\, = \, \pm 0, \, \pm 1, \, \pm 2 \ldots \ldots\) are the moment order and repetition of a radial function \(T_{n} (r)\) and \(T_{n }^{*} (r)\) is the conjugate of radial function \(T_{n} (r)\). It is noted from the available literature that, most of the circularly orthogonal moments differ only in Radial functions and normalization constants. Hence, Table 1 shown below lists some of the radial functions proposed recently for defining moments.

Table 1 Radial functions and normalization constants of various moments
Full size table

Xia et al. [20] pointed out some errors in the radial function of Exponent Fourier moment-I. In order to correct them, a new expression was suggested for Exponent Fourier moments-I, which is given by

$$E_{nm} = \frac{1}{{2\pi a_{n} }}\int\limits_{r = \pi }^{\pi + 1} {\int\limits_{\theta = 0}^{2\pi } {f(r,\theta )T_{n} ({\text{r}})\exp \left( { - jm\theta } \right)rd\theta } dr}$$

where \(a_{n} = \exp ( - j4n\pi^{2} )\) is normalization constant. Modified radial function \(T_{r} (r)\) is given by

$$T_{n} (r) = \sqrt {\frac{1}{\pi + r}} e^{ - j2\pi n(r + \pi )}$$

Recently, Hu et al. [21] suggested an improved version of the above expression, because incorrect orthogonality condition was employed to find the normalization constant and when the limits for r are applied, no value will be within the 0 to 2 \(\pi\) range. Hence, an Improved Exponent Fourier moments (IEF) moment expression is suggested and it is given by.

$$E_{nm} = \frac{1}{2\pi }\int\limits_{r = k}^{k + 1} {\int\limits_{\theta = 0}^{2\pi } {f(r - k,\theta )T_{n} (r)\exp \left( { - jm\theta } \right)rd\theta } dr}$$

where k is a non negative integer and \(f\left( {r - k,\theta } \right)\) is the translated version of original image \(f(r,\theta )\). Another circularly semi orthogonal moments whose radial bases functions are same for forward and inverse transforms was proposed by Wang et al. [22]. Like the other radial bases functions this radial bases function also do not use factorial terms. Hence, it is computationally not expensive. Figure 1 display the graphs of real parts of \(T_{n} (r)\) for orders n = 0, 1, 2, 3, 4 and 5. These graphs are numerically stable and avoids the large value in the above expression when r = 0. Given a finite number of moments (N max and M max ) image reconstruction can be obtained using the expression given below

Fig. 1
figure 1

Real part of radial function T n (r) for n = 0, 1, 2, 3, 4, 5 values. x axis denotes ‘r’ values (1 to 2, in steps of 0.001) and y real part of radial function. Colors n = 0, blue, n = 1, green, n = 2, red, n = 3 black, n = 4, cyan, n = 5 magenta

Full size image
$$f(r - k,\,\theta ) = \sum\limits_{n = 1}^{{N_{max} }} {\sum\limits_{m = 1}^{{M_{max} }} {E_{nm} T_{n }^{*} (r)} \exp (jm\theta )}$$

According to the above equation, pixels of reconstructed image must be shifted by a distance k along the opposite direction. If we substitute \(T_{n} (r) = (15)^{{ - \frac{r}{4}}} \sin (n + 1)\pi r\) and Z = 2π in Eq. (5), we obtain an expression for Circularly semi orthogonal moments that is given below

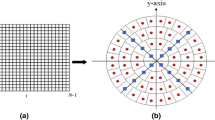
$$E_{nm} = \frac{1}{Z}\int\limits_{r = 0}^{1} {\int\limits_{\theta = 0}^{2\pi } {f(r,\theta )(15)^{{ - \frac{r}{4}}} \sin (n + 1)\pi r\exp \left( { - jm\theta } \right)rdr} d\theta }$$
(6)

In order to convert the above equation suitable for 2D images of size M × N, we need a polar representation of the image and replace the integrals by summation. In our work we employed the ‘Outer Unit Disk Mapping’ employed by Hu et al. [19] which fixes the image pixels inside the unit circle. Expression for coordinate mapping is

$$\begin{array}{*{20}c} {x_{i} = \frac{2i + 1 - N}{{\sqrt {M^{2} + N^{2} } }}} & {x_{j} = \frac{2j + 1 - M}{{\sqrt {M^{2} + N^{2} } }}} \\ \end{array}$$
(6a)

where i = 0, 1…M, j = 0, 1, …N. Final expression when zeroth order approximation of Eq. (6) is used

$$E_{nm} = \frac{1}{Z}\sum\limits_{i = 0}^{M - 1} {\sum\limits_{j = 0}^{N - 1} {f(x_{i} ,y_{j} )T_{n} (r_{ij} )e^{{ - jm\theta_{ij} }} } }$$
(7)

where \(\frac{1}{Z} = \frac{2}{{\pi \left( {M^{2} + N^{2} } \right)}}\), \(r_{ij} = \sqrt {x_{i}^{2} + y_{j}^{2} }\) and \(\theta_{ij} \, = \,\tan^{ - 1} \frac{{y_{j} }}{{x_{i} }}\)

More details can be seen in paper [19]. Next section presents Quaternion circularly semi orthogonal moments.

4 Quaternion Circularly Semi-orthogonal Moments

According to the definition of circularly semi-orthogonal moments (CSOM) (Eq. 6) for gray levels and quaternion algebra, the general formula for the right side CSOM of a color image \(f(r,\theta )\) of order n with repetition m is

$$E_{nm}^{R} = \frac{1}{2\pi }\int\limits_{r = 0}^{1} {\int\limits_{\theta = 0}^{2\pi } {f(r,\theta )T_{n} (r)\exp \left( { - \mu m\theta } \right)rd\theta } dr}$$

where \(\mu\) is a unit pure quaternion, generally it is a linear combination of i, j and k such that its magnitude is unity. In this work \(\mu\) is taken as \(\mu = \frac{i + j + k}{\sqrt 3 }\). Quaternion is not commutative. Hence, we obtain left side expression, which is given by

$$E_{nm}^{L} = \frac{1}{2\pi }\int\limits_{r = 0}^{1} {\int\limits_{\theta = 0}^{2\pi } {\exp \left( { - \mu m\theta } \right)f(r,\theta )T_{n} (r)rd\theta } dr}$$
(8)

In this work we consider only right side expression and drop out the symbol R. Relationship between these two expressions is \(E_{nm}^{L} = - \overline{{E_{n, - m}^{R} }}\), it can be derived using the conjugate property. Next, we derive an expression for implementation of \(E_{nm} ,\). substituting Eq. (4) into Eq. (8), we get

$$E_{nm} = \frac{1}{2\pi }\int\limits_{r = 0}^{1} {\int\limits_{\theta = 0}^{2\pi } {T_{n} (r)\left[ {f_{R} (r,\,\theta )i + f_{G} (r,\,\theta ) + f_{B} (r,\,\theta )k} \right]\exp \left( { - \mu m\theta } \right)rd\theta } dr}$$
(9)

Let

$$\begin{aligned} A_{nm} & = \frac{1}{2\pi }\left[ {\int\limits_{r = 0}^{1} {\int\limits_{r = 0}^{2\pi } {f_{R} (r,\,\theta )T_{n} (r)\exp \left( { - \mu m\theta } \right)rd\theta } dr} } \right] \\ B_{nm} & = \frac{1}{2\pi }\left[ {\int\limits_{r = 0}^{1} {\int\limits_{\theta = 0}^{2\pi } {f_{G} (r,\,\theta )T_{n} (r)\exp \left( { - \mu m\theta } \right)rd\theta } dr} } \right] \\ C_{nm} & = \frac{1}{2\pi }\left[ {\int\limits_{r = 0}^{1} {\int\limits_{\theta = 0}^{2\pi } {f_{B} (r,\,\theta )T_{n} (r)\exp \left( { - \mu jm\theta } \right)rd\theta } dr} } \right] \\ \end{aligned}$$

Equation (9) can be written as

$$E_{nm} = iA_{nm} + jB_{nm} + kC_{nm} .$$

\(A_{nm}\), \(B_{nm}\) and \(C_{nm}\) are complex values, hence, the above equation can be expressed as

$$E_{nm} = i\left( {A_{nm}^{R} + \mu A_{nm}^{I} } \right) + j\left( {B_{nm}^{R} + \mu B_{nm}^{I} } \right) + k(C_{nm}^{R} + \mu C_{nm}^{I} )$$

Substituting for \(\mu = \frac{i + j + k}{\sqrt 3 }\) and simplifying the above expression using Eq. 2 we get

$$\begin{aligned} E_{nm} & = \,i\left( {A_{nm}^{R} + \frac{(i + j + k)}{\sqrt 3 }A_{nm}^{I} } \right) + j\left( {B_{nm}^{R} + \frac{(i + j + k)}{\sqrt 3 }B_{nm}^{I} } \right) + k\left( {C_{nm}^{R} + \frac{(i + j + k)}{\sqrt 3 }C_{nm}^{I} } \right) \\ E_{nm} & = \, - \frac{1}{\sqrt 3 }\left[ {A_{nm}^{I} + B_{nm}^{I} + C_{nm}^{I} } \right] + i\left[ {A_{nm}^{R} + \frac{1}{\sqrt 3 }(B_{nm}^{I} - C_{nm}^{I} )} \right] + j\left[ {B_{nm}^{R} + \frac{1}{\sqrt 3 }(C_{nm}^{I} - A_{nm}^{I} )} \right] \\ & \quad + \,k\left[ {C_{nm}^{R} + \frac{1}{\sqrt 3 }(A_{nm}^{I} - B_{nm}^{I} )} \right]. \\ \end{aligned}$$

In order to express the above equation in a better way we let

\(S1 = - \frac{1}{\sqrt 3 }\left[ {A_{nm}^{I} + B_{nm}^{I} + C_{nm}^{I} } \right]\), \(S2 = \left[ {A_{nm}^{R} + \frac{1}{\sqrt 3 }\left( {B_{nm}^{I} - C_{nm}^{I} } \right)} \right]\), \(S3 = \left[ {B_{nm}^{R} + \frac{1}{\sqrt 3 }(C_{nm}^{I} - A_{nm}^{I} )} \right]\) and \(S4 = \left[ {C_{nm}^{R} + \frac{1}{\sqrt 3 }(A_{nm}^{I} - B_{nm}^{I} )} \right]\), now the above equation can be expressed as

\(E_{nm} = S1 + iS2 + jS3 + kS4\). In next we derive the expression for quaternion inverse circularly semi-orthogonal moments.

5 Quaternion Inverse Circularly Semi-orthogonal Moments

Given a finite number up to a given order L of Quaternion Circularly Semi orthogonal moments, we find the approximated image \(f(r,\theta )\) using the equation given below

$$f(r,\,\theta ) = \sum\limits_{n = 0}^{L} {\sum\limits_{m = - L}^{L} {E_{nm} T_{n} (r)e^{\mu m\theta } } }$$
(10)

Substituting \(E_{nm}\) from the above equation we get

$$f(r,\,\theta )\, = \,\sum\limits_{n = 0}^{L} {\sum\limits_{m = - L}^{L} {(S1\, + \,iS2\, + \,jS3 + kS4)T_{n} (r)e^{\mu m\theta } } }$$

Substituting, \(\mu = \left( {\frac{i + j + k}{\sqrt 3 }} \right)\) in the above expression and after simplification we get expression for inverse QCSO moments as

$$f(r,\,\theta )\, = \,\overline{{f_{s1} }} (r,\,\theta )\, + \,i\overline{{f_{s2} }} (r,\,\theta )\, + \,j\overline{{f_{s3} }} (r,\,\theta )\, + \,k\overline{{f_{s4} }} (r,\,\theta )$$

where each term is equal to

$$\begin{aligned} \overline{{f_{s1} }} (r,\theta ) & = real\left( {\overline{{s_{1} }} } \right) - \frac{1}{\sqrt 3 }\left[ {imag\left( {\overline{{s_{2} }} } \right) + imag\left( {\overline{{s_{3} }} } \right) + imag\left( {\overline{{s_{4} }} } \right)} \right] \\ \overline{{f_{s2} }} (r,\theta ) & = real\left( {\overline{{s_{2} }} } \right) + \frac{1}{\sqrt 3 }\left[ {imag\left( {\overline{{s_{1} }} } \right) + imag\left( {\overline{{s_{3} }} } \right) - imag\left( {\overline{{s_{4} }} } \right)} \right] \\ \overline{{f_{s3} }} (r,\theta ) & = real\left( {\overline{{s_{3} }} } \right) + \frac{1}{\sqrt 3 }\left[ {imag\left( {\overline{{s_{1} }} } \right) - imag\left( {\overline{{s_{2} }} } \right) + imag\left( {\overline{{s_{4} }} } \right)} \right] \\ \overline{{f_{s4} }} (r,\theta ) & = real\left( {\overline{{s_{4} }} } \right) + \frac{1}{\sqrt 3 }\left[ {imag\left( {\overline{{s_{1} }} } \right) + imag\left( {\overline{{s_{2} }} } \right) - imag\left( {\overline{{s_{3} }} } \right)} \right] \\ \end{aligned}$$

In this expression real (.) and imag (.) terms denote real and imaginary part of the value within the bracket. Each term represents the reconstruction matrix of s1, s2, s3 and s4 respectively and they are determined using

$$\begin{aligned} \overline{{s_{1} }} & = \sum\limits_{n = 0}^{L} {\sum\limits_{m = - L}^{L} {S_{1} T_{n} (r)e^{jm\theta } } } ,\overline{{s_{2} }} = \sum\limits_{n = 0}^{L} {\sum\limits_{m = - L}^{L} {S_{2} T_{n} (r)e^{jm\theta } } } \\ \overline{{s_{3} }} & = \sum\limits_{n = 0}^{L} {\sum\limits_{m = - L}^{L} {S_{3} T_{n} (r)e^{jm\theta } } } ,\overline{{s_{4} }} = \sum\limits_{n = 0}^{L} {\sum\limits_{m = - L}^{L} {S_{4} T_{n} (r)e^{jm\theta } } } \\ \end{aligned}$$

These expressions can be easily implemented using equation Eq. 7.

6 Invariant Properties of QCSO Moments

Let \((r,\theta )\) and \(f(r,\theta - \varphi )\) be the un rotated and rotated (by an angle φ) images expressed in polar form, then QCSO moments of a rotated image is

$$E_{nm} \, = \,\frac{1}{2\pi }\int\limits_{r = 0}^{1} {\int\limits_{\theta = 0}^{2\pi } {f\left( {r,\,\theta - \varphi } \right)T_{n} (r)\exp ( - \mu m\theta )rd\theta } dr}$$

Let \(\bar{\theta } = \theta - \varphi\) then d \({\text{d}}\theta = d\bar{\theta }\), substituting it in the above equation we obtain a rotated QCSO moments as

$$E_{nm}^{r} = E_{nm} \exp ( - \mu m\varphi )$$

Applying modulus operation on both sides of the above equation we get

$$\left\| {E_{nm}^{r} (f)} \right\| = \left\| {E_{nm} (f)} \right\|.1$$

Rotation of an image by an angle φ does not change the magnitude, but the phase changes from \({-}\mu m\theta\, to - (\mu m\theta + \mu m\varphi )\). Hence, we say that rotation does not change magnitude, therefore it is invariant to rotation. Translation invariant is achieved by using the common centroid \(\left( {x_{c} ,\,y_{c} } \right)\) obtained using R, G, B images. This procedure was suggested by Fluser [24] and employed by number of researchers like Chen et al. [18], Nisrine Das et al. [7]. Procedure consists of fixing the origin of the coordinates at the color image centroid obtained using

$$x_{c} = \frac{{(m_{1,0}^{R} + m_{1,0}^{G} + m_{1,0}^{B} )}}{{m_{00} }},y_{c} = \frac{{(m_{0,1}^{R} + m_{0,1}^{G} + m_{0,1}^{B} )}}{{m_{00} }}, m_{0,0} = m_{00}^{R} + m_{00}^{G} + m_{00}^{B} ,$$

where \(m_{00}^{R} ,\, m_{10}^{R} , \, m_{01}^{R}\) are the geometric moments of R image, whereas G and B superscripts denote green and blue images, using the above coordinates, QCSO moments invariants to translation is given by

$$E_{nm} \frac{1}{2\pi }\int\limits_{r = 0}^{1} {\int\limits_{\theta = 0}^{2\pi } {f\left( {\bar{r},\bar{\theta }} \right)T_{n} (\bar{r})\exp \left( { - \mu m\bar{\theta }} \right)\bar{r}d\bar{r}} d\bar{\theta }}$$
(11)

where \(\bar{r} = \sqrt {(x - x_{c} )^{2} + (y - y_{c} )^{2} }\) \(\bar{\theta } = \tan^{ - 1} \left( {\frac{{y - y_{c} }}{{x - x_{c} }}} \right)\).

Moments calculated using the above expression are invariant to translation. In most of the applications like image retrieval, images are scaled moderately, then the scale invariant property is fulfilled automatically, because, QCSO moments are defined on the unit circle using Eq. 6a [10].

Another useful property is flipping an image either vertical or horizontal. Let \(f(r,\theta )\) be the original image, \(f(r, - \theta )\) and \(f(r,\pi - \theta )\) be the vertical and horizontal flipped images. One of the color images flipped vertically and horizontally are shown in Fig. 2. We derive its QCSO moments. QCSO moments of the flip vertical image is

Fig. 2
figure 2

Flipped, rotated and translated images

Full size image
$$E_{nm}^{V} = \frac{1}{2\pi }\mathop \smallint \limits_{\theta = 0}^{2\pi } \mathop \smallint \limits_{r = 0}^{\infty } f(r,\, - \theta )T_{n} (r)e^{ - \mu m\theta } rdrd\theta$$

Substituting \(\emptyset = - \theta ,\) \(d\emptyset = - d\theta\), and Simplifying the above equation, we obtain the moments as

$$E_{nm}^{v} = - E_{nm}^{ \cdot }$$

where \(E_{nm}^{ \cdot }\) is the complex conjugate of the QCSO moments. QCSO moments of flip horizontal image is given by

$$E_{nm}^{h} = \frac{1}{2\pi }\int\limits_{\theta = 0}^{2\pi } {\int\limits_{r = 0}^{\infty } {f\left( {r,\pi - \theta } \right)T_{n} (r)e^{ - \mu m\theta } rdr} d\theta }$$

Substituting \(\varnothing = \pi - \theta\), \(d\varnothing = - d\theta\), we obtain the moments as

$$E_{nm}^{h} = - E_{nm}^{ \cdot } e^{{\frac{ - (i + j + k)}{\sqrt 3 }m\pi }}$$

Hence, one can compute the flipped image moments using the above equation. Some of the properties like invariance to contrast changes can be verified by normalizing moments by E 00.

7 Simulation Results

In order to verify the proposed Quaternion circularly semi orthogonal moments for both reconstruction capability and invariant for rotation, translation, and flipping we have selected four color images namely, Lion image, Vegetable image, Parrot image and painted Mona Lisa images and computed their QCSO moments and these color images are shown in Fig. 2, down loaded from Amsterdam Library of objects, reconstructed using only moments of order 40 (L = 40 in Eq. 10). Obtained results are shown in Fig. 3. High frequency information like edges is well preserved. These images (Lion image is shown in Fig. 2) are rotated by 2 degrees in clock wise using IMROTATE function available in MATLAB 2010 software and magnitude of only few QCSO moments are computed and results are reported in Table 2. From these results we can note that before and after rotation QCSO moments are almost equal. We have also verified translated property by translating Lion image and Vegetable images by 2 units in x direction (dx = 2) and 1 unit (dy = 1) in y direction. Their results (magnitude of E nm ) computed using Eq 11 are shown in Table 3. Difference, between the moments before and after translation is very small. Finally, moments (magnitude of E nm ) calculated for flipped vertical images are reported in Table 4.

Fig. 3
figure 3

Original and reconstructed Images using QCSO Moments

Full size image
Table 2 Rotation invariants of QCSO moments
Full size table
Table 3 Translation invariants of QCSO moments
Full size table
Table 4 Original and flipped image QCSO moments
Full size table

8 Conclusions

In this paper we proposed a new Quaternion circularly semi orthogonal moments for color images. Further, we have showed that these moments are invariant to rotation, scale, translation and we also derived moments for flipped color images. Presently, we are applying these moments both for color and monochrome super resolution problems.