An New Framework for MADM with Linguistic Information Under an IT2 FSs Environment

Abstract

The main purpose of this paper is to propose a framework to deal with multi-attribute decision making (MADM) problems under an interval type-2 fuzzy set (IT2 FS) environment where the decision information is provided with linguistic variables. First, we determine the weights of each attributes using IT2 FSs. Then MAGDM procedure based on the $\alpha$-based distance method and classical TOPSIS method under IT2 FSs environment is presented. In the framework, the linguistic decision information is represented by IT2 FSs. Finally, we apply the proposed MADM procedure to deal with a supplier selection problem to illustrate the practicality and effectiveness of the proposed method.

1 Introduction

A multiple attributes decision making (MADM) problem is a expert presents his testimony and finds the most suitable alternative among a finite set of projects based on a number of attributes. MADM has been widely applied to diverse fields [1]. In traditional decision-making problems, the preferences value expressed by the decision maker are precise numbers. Due to the fuzziness and uncertainty of decision-making problems and the inherent vagueness of human preferences, however, the best expression of decision-makers comes in natural language [2].

Traditionally, most linguistic terms are represented by type-1 fuzzy sets (T1 FSs). However, due to the inherent vagueness and uncertainty of human language, T1 FSs with crisp membership is not able to express it, adequately [3]. Unlike T1 FSs, type-2 fuzzy sets (T2 FSs) employ membership functions that are also fuzzy, called a secondary membership function [4]. The T2 FSs are superior to T1 FSs because they can model second-order uncertainties [5]. When the secondary membership is constantly equal to 1, the T2 FS is called an interval type-2 fuzzy set (IT2 FS) [3, 4]. The computational complexity of IT2 FSs is simpler than T2 FSs, while they have the almost same ability in expressing uncertainty. Therefore, IT2 FSs are the most widely used type of T2 FSs [3].

Each alternative is evaluated with respect to each attribute based on decision maker’s individual experience and judgement. In general, human decision-making process is subjective to a certain extent; which means decision maker acts and reacts based on their perceptions, not the objective reality [3]. Since individuals make decisions according to what they perceive to be reality, we should collect decision maker’s opinion regarding the evaluations of the alternatives using a linguistic rating system or other data collection approaches [3]. IT2 FSs are able to efficiently express linguistic evaluations or assessments by objectively transforming them into numerical variables [6]. Thus, we applied the non-negative IT2 FSs to denote the subjective importance weights of various decision attributes.

Even though IT2 FSs have better uncertainty expressiveness, processing abilities and simpler computation, few studies have considered using IT2 FSs to represent the weights of attributes. This framework differs from the traditional method as the weights of attributes are expressed by IT2 FSs and the new IT2 FSs distance measure method is applied into TOPSIS to select the best alternative. Additionally, it is important to note that this framework is flexible enough to solve other complex decision making problems, such as strategic decision making and medical decision making.

The rest of the paper is organized as follows. In Sect. 51.2, the required background knowledge for IT2 FSs is introduced. In Sect. 51.3, a new framework to handle the MADM problems is presented. In Sect. 51.4, a practical decision-making example is given to illustrate the proposed methods. Conclusion is given in Sect. 51.5.

2 Preliminaries

In this section, we briefly review the basic concepts for IT2 FSs. As T1 FSs require a crisp membership function, IT2 FSs are able to express uncertainty by providing a measure of dispersion to better capture inherent uncertainties in a better way. It is especially useful in problems that is difficult to determine the exact membership function of a fuzzy set [4].

Definition 51.1

Let X be a universe of discourse, then a type-2 fuzzy set is defined as follows [4]:

$$\begin{aligned} \widetilde{A}=\big \{(x,u),u_{\widetilde{A}}(x,u)\mid x\in X,u\in J_x\subseteq [0,1]\big \}, \end{aligned}$$

(51.1)

where $0\le u_{\widetilde{A}}(x,u)\le 1$ for each x and u. When the elements of the fuzzy numbers are continuous, the type-2 fuzzy set $\widetilde{A}$ is represented as follows:

$$\begin{aligned} \widetilde{A}=\int _{x\in X}\int _{u\subseteq {J_x}}u_{\widetilde{A}}(x,u)/(x,u)=\int _{x\in X}\left( \int _{u\subseteq {J_x}}u_{\widetilde{A}}(x,u)\bigg / u\right) \bigg / x, \end{aligned}$$

(51.2)

where $\int \int$ denotes the union for all x and u, $J_x\subseteq [0,1]$ is the primary membership of x in $\widetilde{A}$ and $\int _{u\subseteq {J_x}}u_{\widetilde{A}}(x,u)\diagup (x,u)$ indicates the secondary membership of $\widetilde{A}$. For discrete spaces, $\int$ is replaced by $\sum$.

Definition 51.2

Let $\widetilde{A}$ be a universe of discourse X, if all $u_{\widetilde{A}}(x,u)=1$, then $\widetilde{A}$ is an interval type-2 fuzzy set (IT2 FS) and expressed as follows [4]:

$$\begin{aligned} \widetilde{A}=\int _{x\in X}\int _{u\subseteq {J_x}}1/(x,u)=\int _{x\in X}\left( \int _{u\subseteq {J_x}}1\bigg / u\right) \bigg / x. \end{aligned}$$

(51.3)

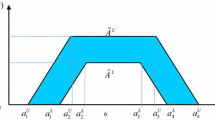
Based on [7], we also defined the IT2 FS $\widetilde{A}=\big (\overline{\mu }_{A}(x),\underline{\mu }_{A}(x)\big )$ as a trapezoidal interval type-2 fuzzy set in the universe of discourse $X=[0,1]$, as shown in Fig. 51.1, where $\widetilde{A}_i=\bigg (\big (a_{i1}^U,a_{i2}^U,a_{i3}^U, a_{i4}^U;H_{i1}^U,H_{i2}^U\big ),\big (a_{i1}^L,a_{i2}^L,a_{i3}^L, a_{i4}^L;H_{i1}^L,H_{i2}^L\big )\bigg )$, and $0\le a_{i1}^U\le a_{i2}^U\le a_{i3}^U\le a_{i4}^U\le 1$, $0\le H_{i1}^U\le H_{i2}^U\le 1$, $0\le a_{i1}^L\le a_{i2}^L\le a_{i3}^L\le a_{i4}^L\le 1$, $0\le H_{i1}^L\le H_{i2}^L\le 1$. Both of the $\overline{\mu }_{\widetilde{A}_i}(x)$ and $\underline{\mu }_{\widetilde{A}_i}(x)$ are type-1 fuzzy sets.

Definition 51.3

Suppose that there are two trapezoidal interval type-2 fuzzy sets $\widetilde{A}_1$ and $\widetilde{A}_2$ as follows [3]:

$$\begin{aligned} \widetilde{A}_{1}=\bigg (\big (a_{11}^U,a_{12}^U,a_{13}^U, a_{14}^U;H_{11}^U,H_{12}^U\big ),\big (a_{11}^L,a_{12}^L,a_{13}^L, a_{14}^L;H_{11}^L,H_{12}^L\big )\bigg ), \end{aligned}$$

(51.4)

$$\begin{aligned} \widetilde{A}_{2}=\bigg (\big (a_{21}^U,a_{22}^U,a_{23}^U, a_{24}^U;H_{21}^U,H_{22}^U\big ),\big (a_{21}^L,a_{22}^L,a_{23}^L, a_{24}^L;H_{21}^L,H_{22}^L\big )\bigg ). \end{aligned}$$

(51.5)

Then the arithmetic operations between them are defined as follows:

(1) Addition operation

$$\begin{aligned} \begin{aligned} \widetilde{A}_{1}\oplus \widetilde{A}_{2}=\,&\big (\overline{\mu }_{A_1}(x),\underline{\mu }_{A_1}(x)\big ) +\big (\overline{\mu }_{A_2}(x),\underline{\mu }_{A_2}(x)\big )\\ =\,&\bigg (\big (a_{11}^U+a_{21}^U,a_{12}^U+a_{22}^U,a_{13}^U+a_{23}^U, a_{14}^U+a_{24}^U;\min (H_{11}^U,H_{21}^U),\min (H_{12}^U,H_{22}^U)\big ), \\&\big (a_{11}^L+a_{21}^L,a_{12}^L+a_{22}^L,a_{13}^L+a_{23}^L, a_{14}^L+a_{24}^L;\min (H_{11}^L,H_{21}^L),\min (H_{12}^L,H_{22}^L)\big )\bigg ).\\ \end{aligned} \end{aligned}$$

(51.6)

(2) Subtraction operation

$$\begin{aligned} \widetilde{A}_{1}\Theta \widetilde{A}_{2}=\,&\big (\overline{\mu }_{A_1}(x),\underline{\mu }_{A_1}(x)\big ) -\big (\overline{\mu }_{A_2}(x),\underline{\mu }_{A_2}(x)\big ) \nonumber \\ =\,&\bigg (\big (a_{11}^U-a_{21}^U,a_{12}^U-a_{22}^U,a_{13}^U-a_{23}^U, a_{14}^U-a_{24}^U;\min (H_{11}^U,H_{21}^U),\min (H_{12}^U,H_{22}^U)\big ), \nonumber \\&\big (a_{11}^L-a_{21}^L,a_{12}^L-a_{22}^L,a_{13}^L-a_{23}^L, a_{14}^L-a_{24}^L;\min (H_{11}^L,H_{21}^L),\min (H_{12}^L,H_{22}^L)\big )\bigg ).\nonumber \\ \end{aligned}$$

(51.7)

(3) Multiplication operation

$$\begin{aligned} \widetilde{A}_{1}\otimes \widetilde{A}_{2}=\,&\big (\overline{\mu }_{A_1}(x),\underline{\mu }_{A_1}(x)\big ) \times \big (\overline{\mu }_{A_2}(x),\underline{\mu }_{A_2}(x)\big ) \nonumber \\ =\,&\bigg (\big (a_{11}^U\times a_{21}^U,a_{12}^U\times a_{22}^U,a_{13}^U\times a_{23}^U, a_{14}^U\times a_{24}^U; \min (H_{11}^U,H_{21}^U),\min (H_{12}^U,H_{22}^U)\big ), \nonumber \\&\big (a_{11}^L\times a_{21}^L,a_{12}^L\times a_{22}^L,a_{13}^L\times a_{23}^L, a_{14}^L\times a_{24}^L; \min (H_{11}^L,H_{21}^L),\min (H_{12}^L,H_{22}^L)\big )\bigg ).\nonumber \\ \end{aligned}$$

(51.8)

(4) Division operation

($a_{21}^U$, $a_{22}^U$, $a_{23}^U$, $a_{24}^U$, $a_{21}^L$, $a_{22}^L$, $a_{23}^L$ and $a_{24}^L$ are non-zero positive real numbers):

$$\begin{aligned} \widetilde{A}_{1}\emptyset \widetilde{A}_{2}&= \big (\overline{\mu }_{A_1}(x),\underline{\mu }_{A_1}(x)\big )/ \big (\overline{\mu }_{A_2}(x),\underline{\mu }_{A_2}(x)\big ) \nonumber \\&=\bigg [\bigg (\frac{a_{11}^U}{a_{21}^U},\frac{a_{12}^U}{a_{22}^U},\frac{a_{13}^U}{a_{23}^U},\frac{a_{14}^U}{a_{24}^U}; \min (H_{12}^U,H_{22}^U)\bigg ), \bigg (\frac{a_{11}^L}{a_{21}^L},\frac{a_{12}^L}{a_{22}^L},\frac{a_{13}^L}{a_{23}^L},\frac{a_{14}^L}{a_{24}^L}; \min (H_{12}^L,H_{22}^L)\bigg )\bigg ].\nonumber \\ \end{aligned}$$

(51.9)

(5) Multiplication by real number operation (k is a non-negative real number):

$$\begin{aligned} \begin{aligned} k\times \widetilde{A}_1=&\bigg (\big (k\times a_{11}^U,k\times a_{12}^U,k\times a_{13}^U, k\times a_{14}^U;H_{11}^U,H_{12}^U\big ), \\&\big (k\times a_{11}^L,k\times a_{12}^L,k\times a_{13}^L, k\times a_{14}^L;H_{11}^L,H_{12}^L\big )\bigg ).\\ \end{aligned} \end{aligned}$$

(51.10)

Fig. 51.1

The footprint of uncertainty (FOU) of interval type-2 fuzzy set $\widetilde{A}_i$

Definition 51.4

The UMF and LMF of $\widetilde{A}_i$, which are shown in Fig. 51.1, can be represented in algebraic form as follows [8]:

$$\begin{aligned} \overline{\mu }_{\widetilde{A}_i}(x)=\left\{ \begin{array}{ll} \frac{H_{i1}^U}{a_{i2}^U-a_{i1}^U}x-\frac{H_{i1}^Ua_{i1}^U}{a_{i2}^U-a_{i1}^U} &{} x\in [a_{i1}^U,a_{i2}^U];\\ \frac{H_{i2}^U-H_{i1}^U}{a_{i3}^U-a_{i2}^U}x+H_{i1}^U-\frac{(H_{i2}^U-H_{i1}^U)a_{i2}^U}{a_{i3}^U-a_{i2}^U} &{} x\in [a_{i2}^U,a_{i3}^U];\\ -\frac{H_{i2}^U}{a_{i4}^U-a_{i3}^U}x+\frac{H_{i2}^Ua_{i4}^U}{a_{i4}^U-a_{i3}^U} &{} x\in [a_{i3}^U,a_{i4}^U]. \end{array}\right. \end{aligned}$$

(51.11)

$$\begin{aligned} \underline{\mu }_{\widetilde{A}_i}(x)=\left\{ \begin{array}{ll} \frac{H_{i1}^L}{a_{i2}^L-a_{i1}^L}x-\frac{H_{i1}^La_{i1}^L}{a_{i2}^L-a_{i1}^L} &{} x\in [a_{i1}^L,a_{i2}^L];\\ \frac{H_{i2}^L-H_{i1}^L}{a_{i3}^L-a_{i2}^L}x+H_{i1}^L-\frac{(H_{i2}^L-H_{i1}^L)a_{i2}^L}{a_{i3}^L-a_{i2}^L} &{} x\in [a_{i2}^L,a_{i3}^L];\\ -\frac{H_{i2}^L}{a_{i4}^L-a_{i3}^L}x+\frac{H_{i2}^La_{i4}^L}{a_{i4}^L-a_{i3}^L} &{} x\in [a_{i3}^L,a_{i4}^L]. \end{array}\right. \end{aligned}$$

(51.12)

The $\alpha$-based distance, initially proposed by Figueroa-García et al. [9], is used to measure the distance between IT2 FSs.

Definition 51.5

Let $\widetilde{A}_1$ and $\widetilde{A}_2$ be non-negative IT2 FNs defined on X and $X\ne \{0\}$, the distance between them can be computed as follow:

$$\begin{aligned} d(\widetilde{A}_1,\widetilde{A}_2)\doteq \frac{1}{\varLambda }\sum \limits _{i=1}^nx_i\big [\big |\overline{\mu }_{A_1}(x_i)-\overline{\mu }_{A_2}(x_i)\big |+ \big |\underline{\mu }_{A_1}(x_i)-\underline{\mu }_{A_2}(x_i)\big |\big ], \end{aligned}$$

(51.13)

where $\varLambda =\sum _{i=1}^nx_i$.

If x is continuous and $x\in [0,1]$, then $\varLambda =\int _0^1xdx=\frac{1}{2}$, so d can be defined as:

$$\begin{aligned} d(\widetilde{A}_1,\widetilde{A}_2)\doteq 2\int _0^1x\big [\big |\overline{\mu }_{A_1}(x)-\overline{\mu }_{A_2}(x_)\big |+ \big |\underline{\mu }_{A_1}(x)-\underline{\mu }_{A_2}(x)\big |\big ]. \end{aligned}$$

(51.14)

3 Proposed Framework for MADM

As we all know, IT2 FSs can express the uncertainty of human language in a better way and have a simpler computation [10]. So we apply IT2 FSs to represent the linguistic terms in order to adequately illustrate the uncertainties in a complex situation. In this section, based on the $\alpha$-based distance, we construct a new framework to deal with MADM problems under IT2 FSs environment.

In the proposed framework, the attributes weights are determined by the subjective judgements of decision makers. The ranking process is practiced based on the classical TOPSIS method, which has been developed by Hwang and Yoon [11] and also is a technique for order the preference by its similarity to the ideal points. These methods are discussed in detail in the following.

3.1 Interval Type-2 Fuzzy Representation

We assume that the decision maker D expresses his preferences of m alternatives ${A_1},{A_2} \ldots ,{A_m}$ under n attributes ${C_1},{C_2} \ldots ,{C_n}$. Firstly, the decision maker assesses all alternatives, and gives out the preferences of them. Then, a decision matrix $Y={(S_{ij})}_{m\times n}$ is constructed under the linguistic terms set $S=(s_1,s_2,\ldots ,s_l)$, where the linguistic term $s_{ij}$ is the preference value for the $A_i$ with respect to $C_j$ given by D and $s_{ij}\in S$. After that, the linguistic information is translated into the IT2 FSs and each IT2 FS is normalized under the rule shown in Table 51.1. Finally, we obtain the normalized decision matrix $R_{ij}={(r_{ij})}_{m\times n}$, shown as follows:

$$\begin{aligned} R= \left( \begin{array}{cccc} r_{11} &{}r_{12} &{}\ldots &{}r_{1n} \\ r_{21}&{} r_{22} &{}\ldots &{}r_{2n} \\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ r_{m1}&{} r_{m2} &{} \ldots &{} r_{mn} \\ \end{array} \right) , \end{aligned}$$

(51.15)

where the parameter $r_{ij}$ indicate the performance values of $C_j$ with respect to $A_i$ given by D, where $1 \le i \le m$; $1 \le j \le n$.

The decision maker first provides his judgements to express the subjective importance weights for various attributes based on the linguistic terms in Table 51.1.

Table 51.1 The weights evaluation linguistic terms and their corresponding IT2 FSs

We translate the linguistic terms into IT2 FSs, and construct the vector as $(w_1,w_2,\ldots ,w_j,\ldots ,w_n)$, where $w_j=[w_j^L,w_j^U]=[(w_{1j}^L,w_{2j}^L,w_{3j}^L,w_{4j}^L;H_{1j}^L,H_{2j}^L)$, $(w_{1j}^U,w_{2j}^U,w_{3j}^U,w_{4j}^U;H_{1j}^U,H_{2j}^U)]$. The vector of attributes weights $\overline{W}=(\overline{w}_1,\overline{w}_2,\ldots ,\overline{w}_j,\cdots ,\overline{w}_n)$ is defined as following.

Definition 51.6

The attribute weight is a non-negative IT2 FS and obtained after normalizing process as follows:

$$\begin{aligned} \overline{w}_j=\frac{w_j}{w_1+w_2+\cdots +w_n}, \end{aligned}$$

(51.16)

where

$$\begin{aligned} \overline{w}_j=&[\overline{w}_j^L,\overline{w}_j^U]\nonumber \\ =&[(\overline{w}_{1j}^L,\overline{w}_{2j}^L,\overline{w}_{3j}^L,\overline{w}_{4j}^L;H_{1j}^L,H_{2j}^L), (\overline{w}_{1j}^U,\overline{w}_{2j}^U,\overline{w}_{3j}^U,\overline{w}_{4j}^U;H_{1j}^U,H_{2j}^U)]; \end{aligned}$$

(51.17)

The sum of attributes weights has the following property:

$$\begin{aligned} \sum _{j=1}^n\overline{w}_j=[(1,1,1,1;\min _{j=1}^n H_{1j}^L,\min _{j=1}^n H_{2j}^L),(1,1,1,1;\min _{j=1}^n H_{1j}^U,\min _{j=1}^n H_{2j}^U)]\qquad \end{aligned}$$

(51.18)

Proof

$\sum _{j=1}^n\overline{w}_j=\sum _{j=1}^n\frac{w_j}{w_1+w_2+\cdots +w_n}= [(\sum _{j=1}^n\frac{w_{1j}^L}{w_{11}^L+w_{12}^L+\cdots +w_{1n}^L}, \sum _{j=1}^n\frac{w_{2j}^L}{w_{21}^L+w_{22}^L+\cdots +w_{2n}^L},$

$\sum _{j=1}^n\frac{w_{3j}^L}{w_{31}^L+w_{32}^L+\cdots +w_{3n}^L}, \sum _{j=1}^n\frac{w_{4j}^L}{w_{41}^L+w_{42}^L+\cdots +w_{4n}^L}; \min _{j=1}^n H_{1j}^L\min _{j=1}^nH_{2j}^L),$

$(\sum _{j=1}^n\frac{w_{1j}^U}{w_{11}^U+w_{12}^U+\cdots +w_{1n}^U}, \sum _{j=1}^n\frac{w_{2j}^U}{w_{21}^U+w_{22}^U+\cdots +w_{2n}^U}, \sum _{j=1}^n\frac{w_{3j}^U}{w_{31}^U+w_{32}^U+\cdots +w_{3n}^U}, \sum _{j=1}^n\frac{w_{4j}^U}{w_{41}^U+w_{42}^U+\cdots +w_{4n}^U};$

$\min _{j=1}^n H_{1j}^U,\min _{j=1}^nH_{2j}^U)]=[(1,1,1,1;\min _{j=1}^n H_{1j}^L,\min _{j=1}^n H_{2j}^L),$

$(1,1,1,1;\min _{j=1}^n H_{1j}^U,\min _{j=1}^n H_{2j}^U)]$.

3.2 The Ranking Process

The attributes weights obtained above are then applied to the TOPSIS method based on the $\alpha$-based distance method to find the best alternative.

Based on the normalized decision matrix R, in which the alternative with a larger preference value is better, the positive ideal alternative $A^+$ is defined as follows:

$$\begin{aligned} A^+=(r_{1}^+,r_{2}^+, \ldots ,r_n^+), \end{aligned}$$

(51.19)

and

$$\begin{aligned} \begin{aligned} r_j^+= \max \limits _ir_{ij}=&\bigg (\big (\max \limits _ir_{ij1}^U,\max \limits _ir_{ij2}^U, \max \limits _ir_{ij3}^U, \max \limits _ir_{ij4}^U; \max \limits _iH_{ij1}^U,\max \limits _iH_{ij2}^U\big ),\\&\big (\max \limits _ir_{ij1}^L,\max \limits _ir_{ij2}^L, \max \limits _ir_{ij3}^L, \max \limits _ir_{ij4}^L; \max \limits _iH_{ij1}^L,\max \limits _iH_{ij2}^L\big )\bigg ) \\ =&\bigg (\big (r_{j1}^{U+},r_{j2}^{U+},r_{j3}^{U+}, r_{j4}^{U+};H_{j1}^{U+},H_{j2}^{U+}\big ), \\&\big (r_{j1}^{L+}, r_{j2}^{L+}, r_{j3}^{L+}, r_{j4}^{L+}; H_{j1}^{L+},H_{j2}^{L+}\big )\bigg ). \end{aligned} \end{aligned}$$

(51.20)

The maximum primary variable is regarded as the best review among all alternatives and the maximum membership represents the least uncertainty.

The negative ideal alternative $A^-$ is defined as follows:

$$\begin{aligned} A^-=(r_{1}^-,r_{2}^-, \ldots ,r_n^-), \end{aligned}$$

(51.21)

and

$$\begin{aligned} \begin{aligned} r_j^-= \min \limits _ir_{ij}=&\bigg (\big (\min \limits _ir_{ij1}^U,\min \limits _ir_{ij2}^U, \min \limits _ir_{ij3}^U, \min \limits _ir_{ij4}^U; \max \limits _iH_{ij1}^U,\max \limits _iH_{ij2}^U\big ),\\&\big (\min \limits _ir_{ij1}^L,\min \limits _ir_{ij2}^L, \min \limits _ir_{ij3}^L, \min \limits _ir_{ij4}^L; \max \limits _iH_{ij1}^L,\max \limits _iH_{ij2}^L\big )\bigg )\\ =&\bigg (\big (r_{j1}^{U-},r_{j2}^{U-},r_{j3}^{U-}, r_{j4}^{U-};H_{j1}^{U-},H_{j2}^{U-}\big ),\\&\big (r_{j1}^{L-}, r_{j2}^{L-}, r_{j3}^{L-}, r_{j4}^{L-}; H_{j1}^{L-},H_{j2}^{L-}\big )\bigg ), \end{aligned} \end{aligned}$$

(51.22)

in which the minimum primary variable represents the worst situation among m alternatives, and the maximum membership represents the least uncertainty.

We use the distance of each alternative from the ideal positive alternative to measure the goodness of each alternative and the distance is computed as follows:

$$\begin{aligned} \begin{aligned} RD^{i+}&=d(\sum \limits _{j=1}^n\overline{w}_jr_{ij},\sum \limits _{j=1}^n\overline{w}_jr_j^+)=d(WR_i,WR^+) \\&\doteq \frac{1}{\varLambda }\sum \limits _{i=1}^nx_i\big [\big |\overline{\mu }_{WR_i}(x_i)-\overline{\mu }_{WR^+}(x_i)\big |+ \big |\underline{\mu }_{WR_i}(x_i)-\underline{\mu }_{WR^+}(x_i)\big |\big ], \end{aligned} \end{aligned}$$

(51.23)

where $\varLambda =\sum _{i=1}^nx_i$.

We use the distance of each alternative from the ideal negative alternative to measure the negativity of each alternative and the distance is computed as follows:

$$\begin{aligned} \begin{aligned} RD^{i-}&=d(\sum \limits _{j=1}^n\overline{w}_jr_{ij},\sum \limits _{j=1}^n\overline{w}_jr_j^-)=d(WR_i,WR^-)\\&\doteq \frac{1}{\varLambda }\sum \limits _{i=1}^nx_i\big [\big |\overline{\mu }_{WR_i}(x_i)-\overline{\mu }_{WR^-}(x_i)\big |+ \big |\underline{\mu }_{WR_i}(x_i)-\underline{\mu }_{WR^-}(x_i)\big |\big ], \end{aligned} \end{aligned}$$

(51.24)

where $\varLambda =\sum _{i=1}^nx_i$.

In the end, we define the relative closeness to rank all alternatives. The relative closeness is defined as follows:

$$\begin{aligned} RV_i=\frac{RD^{i-}}{RD^{i+}+RD^{i-}}. \end{aligned}$$

(51.25)

The better alternative is supposed to have the larger $RV_i$.

4 Illustrative Example

Supplier selection is one of the most important issues in supply chain management area. In this section, we apply the proposed framework to a numerical supplier selection example.

A transformer manufacturer, whose main production is the domestic transformer, intends to elect a befitting coil supplier. Five suppliers labelled as $\{A_1$, $A_2$, $A_3$, $A_4$, $A_5\}$ enter this competition. The leader has to evaluate those three suppliers and gives his preference under four criteria, which are Company reputation $(C_1)$, Date of delivery $(C_2)$, Price $(C_3)$ and Quality $(C_4)$. The leader should provide his decision matrix based on linguistic terms $s_1, s_2, s_3, s_4, s_5, s_6, s_7$, as shown in Table 51.2. The decision matrix is shown in Tables 51.3 and 51.4

Table 51.2 The linguistic terms and their corresponding IT2 FNs [7]

Table 51.3 The decision matrix of leader

Table 51.4 The attributes weights decision matrix

Step 1.:

Normalize the decision matrices. Since the price $C_3$ is cost benefit, we normalize the decision matrix with the complementary sets and translate linguistic terms into corresponding IT2 FSs, based on Table 51.2.

Step 2.:

Calculate attributes weights. Based on Eqs. (51.16)–(51.18), we translate the linguistic terms into corresponding IT2 FSs and normalize them. Then the attributes weights are obtained as shown in Table 51.4.

Step 3.:

Obtain the positive and negative ideal alternatives. Based on Eqs. (51.19)–(51.22), we find the positive and negative ideal alternatives as shown in Table 51.5.

Step 4.:

Aggregate the decision matrix and the ideal points based on the attributes weights obtained in Step. 2. Then, calculate the $\alpha$-based distance of each aggregated alternative from the aggregated ideal alternatives, based on Eqs. (51.23)–(51.24), as shown in Table 51.6.

Step 5.:

Compute the ranking value of each alternative and obtain the ranking order of them. The ranking value of each alternative is shown in Table 51.7.

Table 51.5 The positive and negative ideal alternatives

Table 51.6 The Separation of each alternative from the ideal alternatives

Table 51.7 The relative closeness of each alternative

Finally, we obtain the ranking order of those five alternatives as $X_2\succ X_4\succ X_5\succ X_1\succ X_3$.

5 Conclusion

In this paper, we propose a framework to deal with multi-attribute decision making (MADM) problems under an interval type-2 fuzzy set (IT2 FS) environment where the decision information is provided with linguistic variables. Firstly, we define the non-negative IT2 FSs to represent subjective importance weights of attributes to avoid the information lost. Then, we apply the new IT2 FSs distance measure method, which is named $\alpha$-based distance, into TOPSIS method to select the best alternative.