Keywords

1 Introduction

A large number of sensor nodes constitute Wireless Sensor Networks (WSN), which are equipped with limited resources like memory, processing power and coverage area [1]. WSN applications in various area like military, intrusion detection, surveillance, disaster management, monitoring, healthcare, etc. [2]. Basically sensor nodes are used to create a wireless network in any type of territory. After deployment of nodes it collect data from its surroundings and delivers the collected data to the control node that is called sink node in multihop communication via its neighbor nodes. Sensor nodes have limited energy and it is very difficult to replace its battery because the working areas are very difficult. Therefore, when node exhausts its energy then it has no ability to transmit data in the network.

The WSN is one of the hot topics for academia and industry due to various applications. There are some challenges with sensor nodes such as energy consumption, deployment of nodes, security, etc. Sensor nodes are very soft target for worm attack due to weak defense mechanism. So securities are one of the important concerns for WSNs and need to be more attention. The other challenge is energy saving, for energy saving there are various parameters to be discussed like topology placement of nodes, etc. Working mode of sensor nodes also play an important role to save energy. Sensor nodes are working in two modes, sleep or active mode, in sleep mode, all functional units of the nodes are in an inactive state,ability to transmit directly and when the nodes are in active mode they are fully working and at that time the energy of nodes is dissipated. So cleverly use the nodes to save the energy that means, when no need to transmit or receive data the sensor node goes to sleep mode.

It is found that when worm appears in the sensor networks and nodes are in active mode they can spread it with data or may be independently from one node to another node, this happens due to lack of defense mechanism [3]. Figure 1 shows the sensor field in which sensor nodes are scattered and data transmit between nodes to nodes or from nodes to sink. When the data is transmitted from node to sink it will take more hop to reach at sink by different mechanisms [4]. When the source node sends data to sink via neighbor nodes, during the transmission of data there is some obstruction in WSN such as worms and virus attack.

Fig. 1
figure 1

Wireless sensor network field

Full size image

Computer viruses are self-replicating and they can propagate via network of computer without any manual interference [4, 5]. In the digital world one of the most dangerous threat is worm attack for communication network and computer. Now day’s new types of worms are surfacing specially for portable devices like laptops and phones. They have ability to transmit directly from device to device through wireless technology for example, as Bluetooth or Wi-Fi [4, 5] Wireless devices are targeted by malicious signals, for example Cabir worm and Mabir worm and spreading the behavior of these worms and are epidemic in nature [6]. Therefore, to prevent the malware attacks on sensor nodes security mechanism using epidemic models has been explored by various groups [4, 6–8]. Effect and control of malicious signals on the computer network have been studied by various authors by using the concepts of epidemical model [9–12]. Some researchers have described epidemic models to consider time delay and control mechanism for virus propagation [9–12].

To be able to understand the dynamical characteristics of worm propagation in WSNs to study different epidemic models,it is found that there is a similarity between computer network and WSNs in case of worm propagation. The epidemic models broadly are useful to study worm spread in WSNs by some authors [4, 13]. In [13], the authors proposed a SIRS model with feedback controller and analyzed Hopf bifurcation dynamics of malware prevalence in mobile wireless networks. The authors in [4] proposed an epidemic model with vaccination compartment which includes both temporal and spatial dynamics of worm spreading process, and some mathematical analysis and numerical simulations were done to verify this model. These models do not consider undetected nodes which is harmful for sensor network.

In the present study, we propose SITHR model to study the dynamics of spreading of a virus in WSNs and find the stability of the network. Assume that all the nodes are susceptible towards malicious attack and become infectious and transmit the worm with data or may be spread through wireless communication. It is found that some sensor nodes are not detected early the worm attack, so they are not using any antivirus to prevent malicious attacks. So, it is found that those undetected infectious nodes become highly infected with time. After some time infected nodes are detected, and these nodes are sent immediately into sleep mode. Because they do not spread worms to the neighbor nodes in sleep mode and run the antivirus to remove the worms from nodes. By this method the lifetime of a WSN  can be increased. An efficient antivirus is to be used either to recover these infected nodes or to remove them from the network without disturbing network stability, because these infected nodes become dangerous for WSN. Those sensor nodes, which are detected early, are sent to the treated compartment and malicious signals can be eradicated early from sensor network. It may be a possibility that due to slower treatment rate some nodes move to highly infected compartments. Hence, by increasing the treatment rate we may decrease the severity in the WSNs or we may say that overhead occurred due to the malicious signal can be removed. When the transmission overhead of the nodes is minimized, the energy dissipation of nodes can be minimized and it increases the lifetime of WSN. The diagnosed nodes which are not treated timely may move to highly infected state  they can remove or recover to elongate lifetime of a network. This model explores the treatment and control of early and late detected nodes to elongate WSNs life.

2 Model Formulation

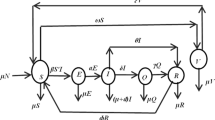
Different subclass of sensor nodes at any time t, are Susceptible S(t), Infectious I(t), Treatment T(t), Infected H(t), and Recovered R(t) of Total size N(t) i.e.,

$$N(t)\text{ = }S(t)\text{ + }I(t)\text{ + }T(t)\text{ + }H(t)\text{ + }R(t),$$
(2.1)

In Fig. 2 we describe the dynamical transfer of sub class. The SITHR model is given by:

Fig. 2
figure 2

Malicious signal transmission diagram in wireless system network

Full size image
$$\left. {\begin{array}{*{20}l} {\frac{{{\text{d}}S}}{{{\text{d}}t}} = \alpha N - \beta \frac{\text{SI}}{N} - \mu S,} \hfill \\ {\frac{{{\text{d}}I}}{{{\text{d}}t}} = \beta \frac{\text{SI}}{N} - (\gamma + \lambda + \mu )I,} \hfill \\ {\frac{{{\text{d}}T}}{{{\text{d}}t}} = \lambda I - (\sigma + \mu + \rho )T,} \hfill \\ {\frac{{{\text{d}}H}}{{{\text{d}}t}} = \gamma I + \sigma T - (\delta + \mu + \phi )H,} \hfill \\ {\frac{{{\text{d}}R}}{{{\text{d}}t}} = \rho T + \phi H - \mu R} \hfill \\ \end{array} } \right\}$$
(2.2)

where \(S(0)\text{ = }S_{0}\), \(I(0)\text{ = }I_{0}\), \(T(0) = T_{0}\), \(H(0)\text{ = }H_{0} \,\forall \,t{ \ge }0\). In order to express system of Eq. (2.2) as a portion of the entire population, and since the recovered class R(t) does not appear in the first four equations of system (2.2), we use the following substitution \(s\text{ = }\frac{S}{N},i\text{ = }\frac{I}{N},z\text{ = }\frac{T}{N},h\text{ = }\frac{H}{N}\). Hence resulting system of equation shall be:

$$\left. {\begin{array}{*{20}l} {\frac{{{\text{d}}s}}{{{\text{d}}t}} = \alpha - \beta{{si}} - \mu{s} ,} \hfill \\ {\frac{{{\text{d}}i}}{{{\text{d}}t}} = \beta{\text{si}} - (\gamma + \lambda + \mu )i,} \hfill \\ {\frac{{{\text{d}}z}}{{{\text{d}}t}} = \lambda{i} - (\sigma + \mu + \rho )z,} \hfill \\ {\frac{{{\text{d}}h}}{{{\text{d}}t}} = \gamma{i} + \sigma z - (\delta + \mu + \phi )h,} \hfill \\ \end{array} } \right\}$$
(2.3)

where α considered to be constant rate for new nodes which connected to the WSN, μ is the crashing rate of sensor nodes, β is coefficient of transmission, σ is the rate of transmission from T class to H class, λ is the rate of treatment, ϕ is the rate of recovery from H class to R class, ρ is the recovery rate from T class to R class, δ is the rate of hardware failure and γ the rate at which the infective individuals move from I class to H class. We will discuss the system in the domain \({\Gamma} = \left\{ {(s,i,z,h){ \in \Re }_{ + }^{4} } \right\}.\) Since the model monitors sensor nodes of different class, so all the state variables remain non negative for all t greater than or equal to zero.

3 Existence of Positive Equilibrium

For equilibrium points, we have \(\frac{{{\text{d}}s}}{{{\text{d}}t}} = 0;\frac{{{\text{d}}i}}{{{\text{d}}t}} = 0;\frac{{{\text{d}}z}}{{{\text{d}}t}} = 0;\frac{{{\text{d}}h}}{{{\text{d}}t}} = 0;\) and after a straight forward calculation, we get equilibrium points as: \(P_{0} \text{ = }(s,i,z,h)\text{ = }\left( {\frac{\alpha }{\mu },\text{0},\text{0},\text{0}} \right)\) for worm free state and \(P^{\text{ * }} \text{ = }\left( {s^{\text{ * }} ,i^{\text{ * }} ,z^{\text{ * }} ,h^{\text{ * }} } \right)\) for endemic state, where,

$$\begin{aligned} s^{\text{ * }} & \text{ = }\frac{{\gamma \text{ + }\lambda \text{ + }\mu }}{\beta },\;i^{\text{ * }} \text{ = }\frac{\mu }{\beta }\left( {R_{0} - \text{1}} \right),\;z^{\text{ * }} \text{ = }\frac{\lambda \mu }{{\beta (\sigma \text{ + }\mu \text{ + }\rho )}}(R_{0} - 1),\; \\ h^{*} & = \frac{\mu }{\beta }\left[ {\gamma + \frac{\sigma \lambda }{(\sigma + \mu + \rho )}} \right](R_{0} - 1); \\ \end{aligned}$$

where R 0 [14] is the basic reproduction number given by \(R_{0} = \frac{\alpha \beta }{\mu (\gamma + \lambda + \mu )}\). It is clear that P * exist and unique if and only if R 0 > 1.

4 The Stability Analysis

In this section we will discuss the stability analysis of the worm free equilibrium and endemic equilibrium

Theorem 1

The system ( 2.2 ) is locally asymptotically stable if basic reproduction number R 0 is less than unity at worm free equilibrium P 0 .

Proof

At worm free equilibrium point P 0, the Jacobian matrix is

$$J\left( {P_{0} } \right) = \left( {\begin{array}{*{20}c} { - \mu } & { - \frac{\beta \alpha }{\mu }} & 0 & 0 \\ 0 & {\frac{\beta \alpha }{\mu } - (\gamma + \lambda + \mu )} & 0 & 0 \\ 0 & \lambda & { - (\sigma + \mu + \rho )} & 0 \\ 0 & 0 & { - \sigma } & { - (\delta + \mu + \phi )} \\ \end{array} } \right)$$
(4.1)

Eigenvalues of (4.1) are: \(\omega_{1} \text{ = } - \mu ,\omega_{2} = \frac{\beta \alpha }{\mu } - (\gamma + \lambda + \mu )\), \(\omega_{3} = - (\sigma + \mu + \rho ),\omega_{4} = - (\delta + \mu + \phi )\). It is clear that ω 1 < 0, ω 3 < 0, ω 4 < 0 and ω 2 < 0 if \(\frac{\beta \alpha }{\mu } - (\gamma \text{ + }\lambda \text{ + }\mu )\) \(< 0{ \Rightarrow }\frac{\alpha \beta }{\mu (\gamma + \lambda + \mu )} < 1 \Rightarrow R_{0} < 1\), therefore the system is locally asymptotically stable at worm free equilibrium point P 0 which proves the theorem.

Theorem 2

The system ( 2.2 ) is globally asymptotically stable if \(R_{0} \le 1\) at worm free equilibrium P 0 .

Proof

Consider the Lyapunov [15] function \(L(t):\Re^{4} \to \Re^{ + }\) defined by \(L\left( t \right)\text{ = }\omega i\).

Its derivative w.r.t t

$$\dot{L}(t) = \omega \frac{{{\text{d}}i}}{{{\text{d}}t}} = \omega \left( {\beta_{\text{si}} - (\gamma + \lambda + \mu )i} \right) \le \omega \left( {\frac{\beta \alpha }{\mu } - (\gamma + \lambda + \mu )} \right)i = \omega \left( {R_{0} - 1} \right)i,$$

It is clear that \(\frac{{{\text{d}}L(t)}}{{{\text{d}}t}} = 0\) only when i = 0. Therefore the maximum invariant \(\Gamma = \left\{ {(s,i,z,h) \in \Re_{ + }^{4} } \right\}\) is the singleton set. Therefore the global stability of worm free equilibrium P 0 when \(R_{0} \le 1\) from Lasalle invariance principle [15].

Theorem 3

The endemic equilibrium is locally asymptotic stable if \(R_{0} > 1\).

Proof

The Jacobian matrix associated with endemic equilibrium is

$$J(P_{0} ) = \left( {\begin{array}{*{20}c} { - \mu R_{0} } & { - \frac{\beta \alpha }{{\mu R_{0} }}} & 0 & 0 \\ {\mu (R_{0} - 1)} & 0 & 0 & 0 \\ 0 & \lambda & { - (\sigma + \mu + \rho )} & 0 \\ 0 & \nu & \sigma & { - (\delta + \mu + \phi )} \\ \end{array} } \right)$$
(4.2)

Eigenvalues of (4.2) are \(\omega_{1} = - (\mu + \delta + \phi ),\omega_{2} = - (\gamma + \lambda + \mu ),\omega_{3} = - (\sigma + \mu + \rho ),\) ω 4  = –μ(R 0  > 1). It is clear that \(\omega_{1} < 0,\omega_{2} < 0,\omega_{3} < 0,\omega_{4} < 0\), if R 0 > 1 therefore the system is locally asymptotically stable at endemic equilibrium point P *.

Theorem 4

The Endemic equilibrium is globally asymptotically stable.

Proof

Consider the suitable Lyapunov function

$$\begin{aligned} \dot{L} & = \left( {\frac{{s - s^{*} }}{s}} \right)\dot{s} + \left( {\frac{{i - i^{*} }}{i}} \right)i + \left( {\frac{{z - z^{*} }}{z}} \right)\dot{z} + \left( {\frac{{h - h^{*} }}{h}} \right)\dot{h} \\ & = \left( {\frac{{s - s^{*} }}{s}} \right)\left( {b - \beta (s - s^{*} )(i - i^{*} ) - \mu (s - s^{*} )} \right) + \left( {\frac{{i - i^{*} }}{i}} \right)\left( {\beta (s - s^{*} )(i - i^{*} )} \right. \\ & \quad \left. { - (\gamma + \lambda + \mu )(i - i^{*} )} \right) + \left( {\frac{{z - z^{*} }}{z}} \right)\left( {\lambda (i - i^{*} ) - (\sigma + \rho + \mu )(z - z^{*} )} \right) \\ & \quad + \left( {\frac{{h - h^{*} }}{h}} \right)\left( {\gamma (i - i^{*} ) - \sigma (z - z^{*} ) - (\delta + \mu + \phi )(h - h^{*} )} \right) \\ & = \left( {\alpha - \frac{{\alpha s^{*} }}{s}} \right) - \frac{{(s - s^{*} )^{2} }}{s}\left( {\beta (i - i^{*} ) + \mu } \right) + \frac{{(i - i^{*} )^{2} }}{i}\left( {\beta (s - s^{*} ) - (\gamma + \lambda + \mu )} \right) \\ & \quad - \frac{{(z - z^{*} )^{2} }}{z}(\sigma + \mu + \rho ) - (\delta + \mu + \phi )\frac{{(h - h^{*} )^{2} }}{h} + \lambda \left( {i - i^{*} - \frac{{z^{*} i}}{z} + \frac{{z^{*} i^{*} }}{z}} \right) \\ & \quad \gamma \left( {i - i^{*} - \frac{{h^{*} i}}{h} + \frac{{h^{*} i^{*} }}{h}} \right) + \sigma \left( {z - z^{*} - \frac{{h^{*} z}}{h} + \frac{{z^{*} h^{*} }}{h}} \right) \\ \end{aligned}$$
(4.3)

\(\Rightarrow \frac{{{\text{d}}L}}{{{\text{d}}t}} = P - Q\) where,

$$\begin{aligned} P & = \alpha + \frac{{\beta (s - s^{*} )^{2} i^{*} }}{s} + \frac{{\beta s(i - i^{*} )^{2} }}{i} + \lambda i + \frac{{\lambda z^{*} i^{*} }}{z} + \gamma i + \frac{{\gamma h^{*} i^{*} }}{h} + \sigma z + \frac{{\sigma z^{*} h^{*} }}{h} \\ Q & = \frac{{\alpha s^{*} }}{s} + \frac{{(s - s^{*} )^{2} }}{s}\left( {\beta i + \mu } \right) + \frac{{(i - i^{*} )^{2} }}{i}\left( {\beta s^{*} + (\gamma + \lambda + \mu )} \right) + (\sigma + \mu + \rho )\frac{{(z - z^{*} )^{2} }}{z} \\ & \quad (\delta + \mu + \phi )\frac{{(h - h^{*} )^{2} }}{h} + \lambda i^{*} + \frac{{\lambda iz^{*} }}{z} + \gamma i^{*} + \frac{{\gamma h^{*} i}}{h} + \sigma z^{*} + \frac{{\sigma h^{*} z}}{h} \\ \frac{{{\text{d}}L}}{{{\text{d}}t}} & = 0 \Leftrightarrow s = s^{*} ,i = i^{*} ,z = z^{*} ,h = h^{*} \\ \end{aligned}$$

If P < Q then we get \(\frac{{{\text{d}}L}}{{{\text{d}}t}} \le 0\), and \(\frac{{{\text{d}}L}}{{{\text{d}}t}} = 0\) iff \(s = s^{*} ,i = i^{*} ,z = z^{*} ,h = h^{*} ,\) therefore the largest compact invariant set \({\Gamma} = \left\{ {(s,i,z,h) \in \Re_{ + }^{4} :\frac{{\text{d}L}}{{\text{d}t}} = 0} \right\}\) is the singleton set {P *}. Hence by Lasalle’s invariance principle [15] P * globally asymptotically stable in Γ.

5 Simulation and Result

Figure 3 explain the dynamical behavior of susceptible (S), infective (I), treated (T), highly infected (H) and recovered (R) with respect to time (t). It has been observed that the number of susceptible and infected nodes takes non-negative values and approaches to steady state. In this situation the worms persist in the WSN. In this case R 0 > 1 this shows asymptotic behavior of endemic equilibrium.

Fig. 3
figure 3

Shows dynamical demeanor of the system for different classes under the condition (α = 0.35; β = 0.01; μ = 0.001; γ = 0.001; λ = 0.06; σ = 0.009; ρ = 0.01; δ = 0.08; φ = 0.01)

Full size image

It has been observed from Fig. 4, when treatment rate is high, initially infective nodes are removed quickly and after some time a treatment approach  is applied in a steady state.

Fig. 4
figure 4

Shows dynamical demeanor of the system for Treatment classes under the condition A α = 0.35; β = 0.01; μ = 0.001; γ = 0.001; λ = 0.06; σ = 0.009; ρ = 0.01; δ = 0.08; φ = 0.01; B α = 0.35; β = 0.01; μ = 0.001; γ = 0.001; λ = 0.09; σ = 0.009; ρ = 0.01; δ = 0.08; φ = 0.01; C α = 0.35; β = 0.01; μ = 0.001; γ = 0.001; λ = 0.1; σ = 0.009; ρ = 0.01; δ = 0.08; φ = 0.01

Full size image

Figure 5 demonstrates the analysis of susceptible class versus infective class by the variation of different parameters. Initially all nodes are susceptible and becomes infective after some time.

Fig. 5
figure 5

Shows dynamical demeanor of the system for susceptible versus infective under the condition A α = 0.35; β = 0.01; μ = 0.001; γ = 0.001; λ = 0.06; σ = 0.009; ρ = 0.01; δ = 0.08; φ = 0.01; B α = .38; β = 0.01; μ = 0.001; γ = 0.001; λ = 0.08; σ = 0.01; ρ = 0.01; δ = 0.08; φ = 0.01; C α = .4; β = 0.01; μ = 0.001; γ = 0.001; λ = 0.1; σ = 0.014; ρ = 0.01; δ = 0.08; φ = 0.01

Full size image

It has been observed from Fig. 6, when treatment rate is high, infective nodes get removed from the network quickly and elongate the lifetime of a network.

Fig. 6
figure 6

Shows dynamical demeanor of the system for infective versus treatment under the condition A α = 0.35; β = 0.01; μ = 0.001; γ = 0.001; λ = 0.06; σ = 0.009; ρ = .01; δ = 0.08; φ = 0.01; B α = 0.35; β = 0.01; μ = 0.001; γ = 0.001; λ = 0.09; σ = 0.009; ρ = 0.01; δ = 0.08; φ = 0.01; C α = 0.35; β = 0.01; μ = 0.001; γ = 0.001; λ = 0.1; σ = 0.009; ρ = 0.01; δ = 0.08; φ = 0.01

Full size image

6 Conclusion

We developed mathematical model to describe the spreading and controlling activities of malicious signals in WSN consisting of ordinary differential equations to study the effect of treatment dynamics of worm transmission. We derive the expression for basic reproduction R 0 for determining the dynamic behavior of worm transmission. The local and global stability of worm free equilibrium and endemic equilibrium are established by using the Jacobian matrix and Lyapunov function. It is establish that if R 0, is less than or equal to one, then worms can be eradicated and the system becomes globally stable and when R 0 > 1 the endemic equilibrium will be globally asymptotically stable. It is also observed that as the treatment rate increases the spreading of malicious signal decreases. It saves energy of the sensor nodes by operating in sleep and active modes and enhances the life of WSN.