Abstract
After several decades of rapid technological advancement and economic growth, alarming levels of pollutions and environmental degradation are emerging all over the world. Due to the geographical diffusion of pollutants, unilateral response on the part of one country or region is often ineffective. Though cooperation in environmental control holds out the best promise of effective action, limited success has been observed. Existing multinational joint initiatives like the Kyoto Protocol or pollution permit trading can hardly be expected to offer a long-term solution because there is no guarantee that participants will always be better off within the entire duration of the agreement. This Chapter presents collaborative schemes in a cooperative differential game framework and derives subgame consistent solutions for the schemes.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
After several decades of rapid technological advancement and economic growth, alarming levels of pollutions and environmental degradation are emerging all over the world. Due to the geographical diffusion of pollutants, unilateral response on the part of one country or region is often ineffective. Though cooperation in environmental control holds out the best promise of effective action, limited success has been observed. Existing multinational joint initiatives like the Kyoto Protocol or pollution permit trading can hardly be expected to offer a long-term solution because there is no guarantee that participants will always be better off within the entire duration of the agreement. This Chapter presents collaborative schemes in a cooperative differential game framework and derives subgame consistent solutions for the schemes.
Sections 13.1, 13.2, 13.3, and 13.4 of this Chapter give an integrated exposition of the work of Yeung and Petrosyan (2008) on a cooperative stochastic differential game of transboundary industrial pollution . The game formulation is provided in Sect. 13.1 and noncooperative outcomes are characterized in Sect. 13.2. Cooperative arrangements , subgame-consistent imputations and payment distribution mechanism are provided in Sect. 13.3. A numerical example is given in Sect. 13.4. In Sect. 13.5, an extension of the Yeung and Petrosyan (2008) analysis to incorporate uncertainties in future payoffs is presented. Section 13.6 contains the chapter appendices. Chapter notes are given in Sect. 13.7 and problems in Sect. 13.8.
1 Game Formulation
In this section we present a stochastic differential game model of environmental with n asymmetric nations or regions.
1.1 The Industrial Sector
Consider a multinational economy which is comprised of n nations. To allow different degrees of substitutability among the nations’ outputs a differentiated products oligopoly model has to be adopted. The differentiated oligopoly model used by Dixit (1979) and Singh and Vives (1984) in industrial organizations is adopted to characterize the interactions in this international market. In particular, the nations’ outputs may range from a homogeneous product to n unrelated products. Specifically, the inverse demand function of the output of nation \( i\in N\equiv \left\{1,2,\cdots, n\right\} \) at time instant s is
where P i (s) is the price of the output of nation i, q j (s), is the output of nation j, α i and β i j for \( i\in N \) and \( j\in N \) are positive constants. The output choice \( {q}_j(s)\in \left[0,{\overline{q}}_j\right] \) is nonnegative and bounded by a maximum output constraint \( {\overline{q}}_j \). Output price equals zero if the right-hand-side of (1.1) becomes negative. The demand system (1.1) shows that the economy is a form of differentiated products oligopoly with substitute goods. In the case when \( {\alpha}^i={\alpha}^j \) and \( {\beta}_j^i={\beta}_i^j \) for all \( i\in N \) and \( j\in N \), the industrial outputs resemble a homogeneous good. In the case when \( {\beta}_j^i=0 \) for \( i\ne j \), the n nations produce n unrelated products. Moreover, the industry equilibrium generated by this oligopoly model is computable and fully tractable.
Industrial profits of nation i at time s can be expressed as:
where is the tax rate imposed by government i on its industrial output at time s and c i is the unit cost of production. At each time instant s, the industrial sector of nation \( i\in N \) seeks to maximize (1.2). Note that each industrial sector would consider the information on the demand structure, each other’s cost structures and tax policies. In a competitive market equilibrium firms will produce up to a point where marginal cost of production equals marginal revenue and the first order condition for a Nash equilibrium for the n nations economy yields
With output tax rates being regarded as parameters by the industrial sectors (1.3) becomes a system of equations linear in \( q(s)=\left\{{q}_1(s),{q}_2(s),\cdots, {q}_n(s)\right\} \). Solving (1.3) yields an industry equilibrium with output in industry i being
where \( {\overline{\alpha}}^i \) and \( {\overline{\beta}}_j^i \), for \( i\in N \) and \( j\in N \), are constants involving the model parameters \( \left\{{\beta}_1^1,{\beta}_2^1,\cdots, {\beta}_n^1;{\beta}_1^2,{\beta}_2^2,\cdots, {\beta}_n^2;\cdots; {\beta}_1^n,{\beta}_2^n,\cdots, {\beta}_n^n\right\},\;\left\{{\alpha}^1,{\alpha}^2,\cdots, {\alpha}^n\right\} \) and \( \left\{{c}_1,{c}_2,\cdots, {c}_n\right\} \).
One can readily observe from (1.3) that an increase in the tax rate has the same effect of an increase in cost. Ceteris paribus, an increase in nation i’s tax rate would depress the output of industrial sector i and vice versa.
1.2 Local and Global Environmental Impacts
Industrial production emits pollutants into the environment. The emitted pollutants cause short term local impacts on neighboring areas of the origin of production in forms like passing-by waste in waterways, wind-driven suspended particles in air, unpleasant odour, noise, dust and heat. For an output of q i (s) produced by nation i, there will be a short-term local environmental impact (cost) of ε i i q i (s) on nation i itself and a local impact of ε i j q i (s) on its neighbor nation j. Nation i will receive short-term local environmental impacts from its adjacent nations measured as ε j i q j (s) for \( j\in {\overline{K}}^i \). Thus \( {\overline{K}}^i \) is the subset of nations whose outputs produce local environmental impacts to nation i. Moreover, industrial production would also create long-term global environmental impacts by building up existing pollution stocks like Green-house-gas, CFC and atmospheric particulates. Each government adopts its own pollution abatement policy to reduce the pollution stock. Let \( x(s)\subset {R}^{+} \) denote the level of pollution at time s, the dynamics of pollution stock is governed by the stochastic differential equation:
where σ is a noise parameter and z(s) is a Wiener process , a j q j is the amount added to the pollution stock by a unit of nation j’s output, u j (s) is the pollution abatement effort of nation j, b j u j (s)[x(s)]1/2 is the amount of pollution removed by u j (s) unit of abatement effort of nation j, and δ is the natural rate of decay of the pollutants.
Short term local impacts are closely related to the level of production activities and hence are characterized by a deterministic scheme. On the other hand, the accumulation of pollution stock like greenhouse gas often involves the interactions between the natural environment and the pollutants emitted and hence stochastic elements would appear. For instance, nature’s capability to replenish the environment, the rate of pollution degradation and climate change are subject to certain degrees of uncertainty. Hence a stochastic dynamic game is used to model the evolution of pollution stock (1.5). Finally the damage (cost) of the pollution stock in the environment to nation i at time s is h i x(s).
1.3 The Governments’ Objectives
The governments have to promote business interests and at the same time handle the financing of the costs brought about by pollution . In particular, each government maximizes the net gains in the industrial sector minus the sum of expenditures on pollution abatement and damages from pollution. The instantaneous objective of government i at time s can be expressed as:
where c a i [u i (s)]2 is the cost of employing u i amount of pollution abatement effort, and h i x(s) is the value of damage to country i from x(s) amount of pollution .
The governments’ planning horizon is [t 0, T]. It is possible that T may be very large. At time T, the terminal appraisal associated with the state of pollution is \( {g}^i\left[{\overline{x}}^i-x(T)\right] \) where \( {g}^i\ge 0 \) and \( {\overline{x}}^i\ge 0 \). The discount rate is r. Each one of the n governments seeks to maximize the integral of its instantaneous objective (1.6) over the planning horizon subject to pollution dynamics (1.5) with controls on the level of abatement effort and output tax.
By substituting q i (s), for \( i\in N \), from (1.4) into (1.5) and (1.6) one obtains a stochastic differential game in which government \( i\in N \) seeks to:
subject to
In the game (1.7 and 1.8) one can readily observe that government i’s tax policy is not only explicitly reflected in its own output but also on the outputs of other nations. This modeling formulation allows some intriguing scenario to arise. For instance, an increase of may just cause a minor drop in nation i’s industrial profit but may cause significant increases in its neighbors’ outputs which produce large local negative environmental impacts to nation i. This results in nations’ reluctance to increase or impose taxes on industrial outputs.
2 Noncooperative Outcomes
In this section we discuss the solution to the noncooperative game (1.7) and (1.8). Since the payoffs of nations are measured in monetary terms, the game is a transferable payoff game. Under a noncooperative framework, a feedback Nash equilibrium solution can be characterized as (see Basar and Olsder (1995)):
Definition 2.1
A set of feedback strategies \( \Big\{{u}_i^{*}(t)={\mu}_i\left(t,x\right),\kern0.24em {v}_i^{*}(t)={\phi}_i\left(t,x\right), \) for \( i\in N\Big\} \) provides a Nash equilibrium solution to the game (1.7 and 1.8) if there exist suitably smooth functions \( {V}^i\left(t,x\right):\;\left[{t}_0,T\right]\times R\to R,\;i\in N \), satisfying the following partial differential equations:
Performing the indicated maximization in (2.1) yields:
for \( t\in \left[{t}_0<T\right] \) and \( i\in N \).
System (2.4) forms a set of equations linear in \( \left\{{\phi}_1\left(t,x\right),{\phi}_2\left(t,x\right),\cdots, {\phi}_n\left(t,x\right)\right\} \) with \( \left\{{V}_x^1\left(t,x\right){e}^{r\left(t-{t}_0\right)},{V}_x^2\left(t,x\right){e}^{r\left(t-{t}_0\right)},\cdots, {V}_x^n\left(t,x\right){e}^{r\left(t-{t}_0\right)}\right\} \) being taken as a set of parameters. Solving (2.4) yields:
where \( {\widehat{\alpha}}^i \) and \( {\widehat{\beta}}_j^i \), for \( i\in N \) and \( j\in N \), are constants involving the constant coefficients in (2.4). Substituting the results in (2.3) and (2.5) into (2.1 and 2.2) we obtain game equilibrium expected payoffs of the nations as:
Proposition 2.1
where \( \left\{{A}_1(t),{A}_2(t),\cdots, {A}_n(t)\right\} \) satisfying the following set of constant coefficient quadratic ordinary differential equations:
where \( {C}_i^0={g}^i{\overline{x}}^i{e}^{-r\;\left(T-{t}_0\right)}-{\displaystyle \underset{t_0}{\overset{T}{\int }}}{F}_i(y){e}^{-r\left(y-{t}_0\right)} dy \)
Proof
See Appendix A. ■
The corresponding feedback Nash equilibrium strategies of the game (1.7 and 1.8) can be obtained as:
A remark that will be utilized in subsequent analysis is given below.
Remark 2.1
Let V (τ)i(t, x t ) denote the value function indicating the game equilibrium payoff of nation i in a game with payoffs (1.7) and dynamics (1.8) which starts at time τ. One can readily verify that \( {V}^{\left(\tau \right)i}\left(t,{x}_t\right)={V}^i\left(t,{x}_t\right){e}^{r\left(\tau -{t}_0\right)} \), for \( \tau \in \left[{t}_0,T\right] \). ■
3 Cooperative Arrangement
Now consider the case when all the nations want to cooperate and agree to act so that an international optimum could be achieved. For the cooperative scheme to be upheld throughout the game horizon both group rationality and individual rationality are required to be satisfied at any time. In addition, to ensure that the cooperative solution is dynamically stable, the agreement must be subgame-consistent . The cooperative plan will dissolve if any of the nations deviates from the agreed-upon plan.
3.1 Group Optimality and Cooperative State Trajectory
Consider the cooperative stochastic differential games with payoff structure (1.5) and dynamics (1.3). To secure group optimality the participating nations seek to maximize their joint expected payoff by solving the following stochastic control problem:
subject to (1.8).
Invoking Fleming’s (1969) technique in stochastic control in Theorem A.3 of the Technical Appendices a set of controls , for \( i\in N\left.\right\} \) constitutes an optimal solution to the stochastic control problem (3.1) and (1.8) if there exists continuously differentiable function \( W\left(t,x\right):\left[{t}_0,T\right]\times R\to R,\;i\in N, \) satisfying the following partial differential equations:
Performing the indicated maximization in (3.2) yields the optimal controls under cooperation as:
System (3.5) can be viewed as a set of equations linear in \( \left\{{\psi}_1\left(t,x\right),{\psi}_2\left(t,x\right),\cdots, {\psi}_n\left(t,x\right)\right\} \) with \( {W}_x\left(t,x\right){e}^{r\left(t-{t}_0\right)} \) being taken as a parameter. Solving (3.5) yields:
where \( {\widehat{\widehat{\alpha}}}^i \) and \( {\widehat{\widehat{\beta}}}^i \), for \( i\in N \), are constants involving the model parameters.
The expected joint payoff of the nations under cooperation can be obtained as:
Proposition 3.1
System (3.2 and 3.3) admits a solution
with
where \( {\Phi}^{*}(t)= \exp \left\{\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right.{\displaystyle \underset{t_0}{\overset{t}{\int }}\left[\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right.}{\displaystyle \sum_{j=1}^n\frac{b_j^2}{2{c}_j^a}}{A}_{*}^P+\left(r+\delta \right)\left.\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right]\kern0.5em dy\left.\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right\}, \)
Proof
See Appendix B. ■
Using (3.4), (3.6) and (3.7), the control strategy under cooperation can be obtained as:
for \( t\in \left[{t}_0<T\right] \) and \( i=1,2,\cdots, n \).
Substituting the optimal control strategy from (3.8) into (1.3) yields the dynamics of pollution accumulation under cooperation. Solving the stochastic cooperative pollution dynamics yields the cooperative state trajectory:
for \( t\in \left[{t}_0,T\right] \).
We use X * t to denote the set of realizable values of x*(t) at time t generated by (3.9). The term x * t is used to denote an element in the set X * t .
A remark that will be utilized in subsequent analysis is given below.
Remark 3.1
Let W (τ)(t, x t ) denote the value function indicating the maximized joint payoff of the stochastic control problem with objective (3.1) and dynamics (1.8) which starts at time τ. One can readily verify that \( {W}^{\left(\tau \right)}\left(t,{x}_t^{*}\right)=W\left(t,{x}_t^{*}\right){e}^{r\left(\tau -{t}_0\right)},\kern0.24em \mathrm{f}\mathrm{o}\mathrm{r}\;\tau \in \left[{t}_0,T\right]. \) ■
3.2 Individually Rational and Subgame-Consistent Imputation
An agreed upon optimality principle must be sought to allocate the cooperative payoff. In a dynamic framework individual rationality has to be maintained at every instant of time within the cooperative duration [t 0, T] given any feasible state generated by the cooperative trajectory (3.9). For \( \tau \in \left[{t}_0,T\right] \), let ξ (τ)i(τ, x * τ ) denote the solution imputation (payoff under cooperation) over the period [τ, T] to player \( i\in N \) given that the state is \( {x}_{\tau}^{*}\in {X}_{\tau}^{*} \). Individual rationality along the cooperative trajectory requires:
Since nations are asymmetric and the number of nations may be large, a reasonable solution optimality principle for gain distribution is to share the expected gain from cooperation proportional to the nations’ relative sizes of expected noncooperative payoffs. As mentioned before, a stringent condition – subgame consistency – is required for a credible cooperative solution . In order to satisfy the property of subgame consistency , this optimality principle has to remain in effect throughout the cooperation period. Hence the solution imputation scheme \( \Big\{{\xi}^{\left(\tau \right)i}\left(\tau, {x}_{\tau}^{*}\right) \); for \( i\in N\Big\} \) has to satisfy:
Condition 4.1
for \( i\in N,{x}_{\tau}^{*}\in {X}_{\tau}^{*} \) and \( \tau \in \left[{t}_0,T\right] \). ■
One can easily verify that the imputation scheme in Condition 4.1 satisfies individual rationality . Crucial to the analysis is the formulation of a payment distribution mechanism that would lead to the realization of Condition 4.1. This will be done in the next Section.
3.3 Payment Distribution Mechanism
To formulate a payment distribution scheme over time so that the agreed upon imputation (3.11) can be realized for any time instant \( \tau \in \left[{t}_0,T\right] \) we apply the techniques developed in Chap. 3. Let the vectors \( B\left(s,{x}_s^{*}\right)=\left[{B}_1\left(s,{x}_s^{*}\right),{B}_2\left(s,{x}_s^{*}\right),\cdots, {B}_n\left(s,{x}_s^{*}\right)\right] \) denote the instantaneous payment to the n nations at time instant s when the state is \( {x}_s^{*}\in {X}_s^{*} \). A terminal value of \( {g}^i\left[{\overline{x}}^i-{x}_T^{*}\right] \) is realized by nation i at time T.
To satisfy (3.11) it is required that
To facilitate further exposition, we use the term ξ (τ)i(t, x * t ) which equals
to denote the expected present value (with initial time set at τ) of nation i’s cooperative payoff over the time interval [t, T].
A theorem characterizing a formula for B i (τ, x * τ ), for \( \tau \in \left[{t}_0,T\right] \) and \( i\in N \), which yields Condition 4.1 is provided below.
Theorem 3.1
A distribution scheme with a terminal payment \( -{g}^i\left[{x}_T^{*}-{\overline{x}}^i\right] \) at time T and an instantaneous payment at time \( \tau \in \left[{t}_0,T\right] \) when \( x\left(\tau \right)={x}_{\tau}^{*} \):
yield Condition 4.1.
Proof
Since ξ (τ)i(t, x * t ) is continuously differentiable in t and x * t , using (3.13) and Remarks 2.1 and 3.1 one can obtain:
for \( i\in N \) and \( \tau \in \left[{t}_0,T\right] \),
where
\( \Delta {x}_{\tau }=\left[\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right.{\displaystyle \sum_{j=1}^n{a}_j\left[{\overline{\alpha}}^j+{\displaystyle \sum_{h\in N}{\overline{\beta}}_h^j}\kern0.5em {\psi}_h\left(\tau, {x}_{\tau}^{*}\right)\right]}-{\displaystyle \sum_{j=1}^n{b}_j{\varpi}_j\left(\tau, {x}_{\tau}^{*}\right)\Big(}{x}_{\tau}^{*}\Big){}^{1/2}-\delta\;{x}_{\tau}^{*}\left.\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right]\;\Delta\;t+\sigma\;{x}_{\tau}^{*}\Delta\;{z}_{\tau }+o\left(\Delta t\right), \) \( \Delta {z}_{\tau }=z\left(\tau +\Delta t\right)-z\left(\tau \right), \) and \( {E}_{\tau}\left[o\left(\Delta t\right)\right]/\Delta t\to 0 \) as \( \Delta t\to 0 \).
With \( \Delta t\to 0 \), condition (3.15) can be expressed as:
Taking expectation and dividing (3.16) throughout by Δt, with \( \Delta t\to 0 \), yields (3.14). Hence Theorem 3.1 follows. ■
When all nations are adopting the cooperative strategies the rate of instantaneous payment that nation \( \ell \in N \) will realize at time t with the state being x * t can be expressed as (see derivation in Appendix II):
Since according to Theorem 3.1 under the cooperative scheme an instantaneous payment to nation ℓ equaling B ℓ (t, x * t ) at time t with the state being x * t , a side payment of the value \( {B}_{\ell}\left(t,{x}_t^{*}\right)-{\Re}_{\ell}\left(t,{x}_t^{*}\right) \) will be offered to nation ℓ.
4 A Numerical Example
Consider a multinational economy which is comprised of 2 nations. At time instant s the demand functions of the output of nations 1 and 2 are respectively
The cost of production of a unit of output in nation 1 and nation 2 are respectively 2 and 1. Industrial profits of these nations at time s can be expressed as:
where is the tax rate imposed by the government of nation i on its industrial output.
An industry equilibrium can be obtained as:
The short-term local environmental impact (cost) of nation 1’s output on itself is 0.5q 1(s) and that on nation 2 is 0.4q 1(s). The short-term local environmental impact (cost) of nation 2’s output on itself is 0.8q 2(s) and that on nation 1 is 0.6q 2(s).
The dynamics of pollution stock is governed by the stochastic differential equation:
The damage (cost) of the pollution stock in the environment to nations 1 and 2 are respectively 4x(s) and 5x(s). The abatement costs are 0.5[u 1(s)]2 and [u 2(s)]2 for nations 1 and 2 respectively. The instantaneous objectives of the governments in nations 1 and 2 at time s are respectively:
and
At time \( T=5 \) (decades), the terminal value associated with the state of pollution is \( 2\;\left[100-x(T)\right] \) for nation 1 and \( 3\;\left[60-x(T)\right] \) for nation 2.
Substituting q i (s), for \( i\in \left\{1,2\right\} \), from (4.3) into (4.4, 4.5, and 4.6) one obtains a stochastic differential game in which government 1 seeks to:
and government 2 seeks to
subject to
Solving the game yields:
where
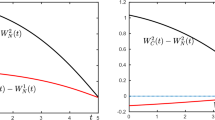
The values of A 1(t), A 2(t), C 1(t) and C 2(t) over the time interval [0, 5] are computed and presented in Figs. 13.1a, b.
Now consider the case when all the nations want to cooperate and agree to act so that an international optimum could be achieved. The instantaneous objective of the cooperative scheme is the sum of the individual objectives (4.5) and (4.6). The terminal value associated with the state of pollution is \( 2\;\left[100-x(T)\right]+3\;\left[60-x(T)\right] \).
To secure group optimality the participating nations seek to maximize their joint expected payoff by solving the following stochastic control problem:
subject to (4.9).
Solving the stochastic control problem (4.11) and (4.9) yields
where
The values of A(t) and C(t) over the time interval [0, 5] are computed and presented in Figs. 13.2a, b.
The cooperative strategies are:
Substituting the cooperative strategies into (4.13) yields the dynamics of pollution accumulation under cooperation as:
Sharing the expected gain from cooperation proportional to the nations’ relative sizes of expected noncooperative payoffs yields:
for \( i\in \left\{1,2\right\},{x}_{\tau}^{*}\in {X}_{\tau}^{*} \) and \( \tau \in \left[{t}_0,T\right] \).
Following Theorem 3.1, a subgame consistent payment distribution procedure consists of a terminal payment \( 2\;\left[100-{x}_T^{*}\right] \) to nation 1 and a terminal payment \( 3\;\left[60-{x}_T^{*}\right] \) to nation 2 at time T and an instantaneous payment at time \( \tau \in \left[{t}_0,T\right] \):
When both nations are adopting the cooperative strategies the rate of instantaneous payment that nation 1 will realize at time t with the state being x * t can be expressed as
Similarly, the rate of instantaneous payment that nation 2 will realize at time t with the state being x * t can be expressed as
A side payment of the value \( {B}_{\ell}\left(t,{x}_t^{*}\right)-{\Re}_{\ell}\left(t,{x}_t^{*}\right) \) will be offered to nation \( \ell \in \left\{1,2\right\} \). The values of B 1(t, x * t ), B 2(t, x * t ), ℜ 1(t, x * t ), ℜ 2(t, x * t ) together with the side payment nation 1 and nation 2 will receive at different time t with given x * t are given in Table 13.1 below.
5 Extension to Uncertainty in Payoffs
In this section we incorporate uncertainty in future payoffs into the cooperative environmental management presented in the previous sections. Uncertainties in future payoffs are prevalent in fast developing countries. This type of uncertainties often hinders the reaching of cooperative agreements in joint pollution control initiatives. Subgame consistent cooperative schemes provide an effective mean to resolve the problem.
5.1 Game Formulation and Non-cooperative Outcome
Consider a randomly furcating counterpart of the stochastic differential game of environmental management in Sect. 13.1 in which the future payoffs are not known with certainty. The game horizon is [t 0, T]. When the game commences at t 0, the demand structures, production costs and impacts of the pollution stock of the nations are known. In future instants of time \( {t}_k\ \left(k=1,\kern0.5em 2,\kern0.5em \cdots, \kern0.5em m\right) \), where \( {t}_0<{t}_m<T\equiv {t}_{m+1} \), the demand structures, production costs and pollution impacts in the time interval \( \left[{t}_k,{t}_{k+1}\right) \) are affected by a series of random events Θk. In particular, Θk for \( k\in \left\{1,\kern0.5em 2,\kern0.5em \cdots, \kern0.5em m\right\} \), are independent and identically distributed random variables with range {θ 1, θ 2, …, θ η } and corresponding probabilities {λ 1, λ 2, …, λ η }. Changes in preference, legal arrangements, technology and the physical environments are examples of factors which constitute to these uncertainties.
In the time interval \( \left[{t}_k,{t}_{k+1}\right) \) for \( k = \left(1,\kern0.5em 2,\kern0.5em \cdots, \kern0.5em m\right) \) if the random event \( {\theta}_{a_k} \) for \( {a}_k\in \left\{1,2,\cdots, \eta \right\} \) is realized the demand function of the output of nation \( i\in N\equiv \left\{1,2,\cdots, n\right\} \) at time instant s is \( {P}_i(s)={\alpha}_{\theta_{a_k}}^i-{\displaystyle \sum_{j=1}^n{\beta}_j^i{q}_j(s)} \), the unit cost of production is \( {c}_{i\left({\theta}_{a_k}\right)} \), and the value of damage to country i from x(s) amount of pollution is \( {h}_i^{\theta_{a_k}}x(s) \). When the game commences at t 0, the demand structures, production costs and pollution impact in the interval \( \left[{t}_0,{t}_1\right) \) are known to be \( {P}_i(s)={\alpha}_{\theta_1}^i-{\displaystyle \sum_{j=1}^n{\beta}_j^i{q}_j(s)},{c}_{i\left({\theta}_1\right)} \) and \( {h}_i^{\theta_1}x(s) \).
Industrial profits of nation i at time \( s\in \left[{t}_k,{t}_{k+1}\right) \) if \( {\theta}_{a_k} \) is realized can be expressed as:
where is the tax rate imposed by government i on its industrial output at time \( s\in \left[{t}_k,{t}_{k+1}\right) \).
In a competitive market equilibrium firms will produce up to a point where marginal cost of production equals marginal revenue and the first order condition for a Nash equilibrium for the n nations economy yields
With output tax rates being regarded as parameters by firms (5.2) becomes a system of equations linear in \( q(s)=\left\{{q}_1(s),{q}_2(s),\cdots, {q}_n(s)\right\} \). Solving (1.3) yields an industry equilibrium with output in industry i being
where \( {\overline{\alpha}}_{\theta_{a_k}}^i \) and \( {\overline{\beta}}_j^{i\left({\theta}_{a_k}\right)} \), for \( i\in N \) and \( j\in N \), are constants involving the model parameters \( \left\{{\beta}_1^1,{\beta}_2^1,\mathrm{\cdots},{\beta}_n^1;{\beta}_1^2,{\beta}_2^2,\mathrm{\cdots},{\beta}_n^2;\cdots; {\beta}_1^n,{\beta}_2^n,\mathrm{\cdots},{\beta}_n^n\right\},\kern0.24em \left\{{\alpha}_{\theta_{a_k}}^1,{\alpha}_{\theta_{a_k}}^2,\mathrm{\cdots},{\alpha}_{\theta_{a_k}}^n\right\}\kern0.24em \mathrm{and}\kern0.24em \left\{{c}_1^{\theta_{a_k}},{c}_2^{\theta_{a_k}},\mathrm{\cdots},{c}_n^{\theta_{a_k}}\right\} \)
The instantaneous objective of government i at time \( s\in \left[{t}_k,{t}_{k+1}\right) \) can be expressed as:
By substituting q i (s), for \( i\in N \), from (5.3) into (5.4) and (1.5) one obtains a randomly furcating stochastic differential game in which government \( i\in N \) seeks to maximize its payoff:
subject to
Invoking 1.1 in Chap. 4 a Nash equilibrium of the randomly furcating stochastic differential game (5.5 and 5.6) can be characterized by the following theorem.
Theorem 5.1
A set of feedback strategies \( \left\{\right.{u}_i^{(m){\theta}_{a_m*}}(t)={\mu}_i^{(m){\theta}_{a_m}}\left(t,x\right),{v}_i^{(m){\theta}_{a_m*}}(t)={\phi}_i^{(m){\theta}_{a_m}}\left(t,x\right), \) for \( t\in \left[{t}_m,T\right];\;{u}_i^{(k){\theta}_{a_k*}}(t)={\mu}_i^{(k){\theta}_{a_k}}\left(t,x\right),{v}_i^{(k){\theta}_{a_k*}}(t)={\phi}_i^{(k){\theta}_{\alpha_k}}\left(t,x\right), \) for \( t\in \left[{t}_k,{t}_{k+1}\right),k\in \left\{0,1,2,\cdots, m-1\right\} \) and \( i\in N\left.\right\} \), contingent upon the events \( {\theta}_{a_m}\in \left\{{\theta}_1,{\theta}_2,\kern0.5em \dots, {\theta}_{\eta}\right\} \) and \( {\theta}_{a_k}\in \left\{{\theta}_1,{\theta}_2,\kern0.5em \dots, {\theta}_{\eta}\right\} \) for \( k\in \left\{1,2,\cdots, m-1\right\} \) constitutes a Nash equilibrium solution for the game (5.5 and 5.6), if there exist continuously differentiable functions \( {V}^{i\left[{\theta}_{a_m}\right](m)}\left(t,x\right):\left[{t}_m,T\right]\times R\to R \) and \( {V}^{i\left[{\theta}_{\alpha_k}\right](k)}\left(t,x\right):\left[{t}_k,{t}_{k+1}\right]\times R\to R \), for \( k\in \left\{1,2,\cdots, m-1\right\} \) and \( i\in N \), which satisfy the following partial differential equations:
Proof
Follow the proof of Theorem 1.1 in Chap. 4. ■
Following the analysis in Sect. 13.2 we perform the indicated maximizations in (5.7 and 5.8) to obtain the game equilibrium strategies and the value functions:
for \( i\in N \) and \( k\in \left\{0,1,2,\cdots, m-1\right\} \),
where \( {A}_{k\left({\theta}_{a_k}\right)}^i(t) \) and \( {C}_{k\left({\theta}_{a_k}\right)}^i(t) \), for \( i\in N \) and \( k\in \left\{0,1,2,\cdots, m-1\right\} \) satisfy a set of constant coefficient quadratic ordinary differential equations similar to that in Proposition 2.1.
5.2 Cooperative Arrangement
Now consider the case when all the nations want to cooperate and agree to act so that an international optimum could be achieved. For the cooperative scheme to be upheld throughout the game horizon both group rationality and individual rationality are required to be satisfied at any time. In addition, to ensure that the cooperative solution is dynamically stable, the agreement must be subgame-consistent.
5.2.1 Group Optimality and Individual Rationality
To secure group optimality the participating nations seek to maximize their joint expected payoff
subject to (5.6)
Invoking Theorem 2.1 in Chap. 4 an optimal solution to the randomly furcating stochastic control problem (5.6) and (5.10) can be characterized by the theorem below.
Theorem 5.2
A set of control strategies \( \left\{\right.{u}_i^{(m){\theta}_{a_m*}}(t)={\varpi}_i^{(m){\theta}_{a_m}}\left(t,x\right),{v}_i^{(m){\theta}_{a_m*}}(t)={\psi}_i^{(m){\theta}_{a_m}}\left(t,x\right), \) for \( t\in \left[{t}_m,T\right];\;{u}_i^{(k){\theta}_{a_k*}}(t)={\varpi}_i^{(k){\theta}_{a_k}}\left(t,x\right),{v}_i^{(k){\theta}_{a_k*}}(t)={\psi}_i^{(k){\theta}_{\alpha_k}}\left(t,x\right), \) for \( t\in \left[{t}_k,{t}_{k+1}\right),\;k\in \left\{0,1,2,\cdots, m-1\right\} \) and \( i\in N\left.\right\} \), contingent upon the events \( {\theta}_{a_m}\in \left\{{\theta}_1,{\theta}_2,\kern0.5em \dots, {\theta}_{\eta}\right\} \) and \( {\theta}_{a_k}\in \left\{{\theta}_1,{\theta}_2,\kern0.5em \dots, {\theta}_{\eta}\right\} \) for \( k\in \left\{1,2,\cdots, m-1\right\} \) constitutes a Nash equilibrium solution for the game (5.5 and 5.6), if there exist continuously differentiable functions \( {W}^{\left[{\theta}_{a_m}\right](m)}\left(t,x\right):\left[{t}_m,T\right]\times R\to R \) and \( {W}^{\left[{\theta}_{\alpha_k}\right](k)}\left(t,x\right):\left[{t}_k,{t}_{k+1}\right]\times R\to R \), for \( k\in \left\{1,2,\cdots, m-1\right\} \) and \( i\in N \), which satisfy the following partial differential equations:
Proof
Follow the proof of Theorem 2.1 in Chap. 4. ■
Following the analysis in Sect. 13.3 we perform the indicated maximizations in Theorem 5.2 to obtain the game equilibrium strategies and the value functions:
for \( k\in \left\{0,1,2,\cdots, m-1\right\} \),
where \( {A}_{k\left({\theta}_{a_k}\right)}(t) \) and \( {C}_{k\left({\theta}_{a_k}\right)}(t) \), for \( k\in \left\{0,1,2,\cdots, m-1\right\} \) satisfy a set of ordinary differential equations similar to that in Proposition 3.1.
Assume that at time t 0 when the initial state is x 0 the agreed upon optimality principle assigns a set of imputation vectors contingent upon the events θ 1 and \( {\theta}_{a_k} \) for \( {\theta}_{a_k}\in \left\{{\theta}_1,{\theta}_2,\kern0.5em \dots, {\theta}_{\eta}\right\} \) and \( k\in \left\{1,2,\cdots, m\right\} \). We use
to denote an imputation vector of the gains in such a way that the share of the ith player over the time interval [t 0, T] is equal to \( {\xi}^{i\left[{\theta}_1\right](0)}\left({t}_0,{x}_0\right) \).
Individual rationality requires that
In a dynamic framework, individual rationality has to be maintained at every instant of time \( t\in \left[{t}_0,T\right] \) along the cooperative trajectory. At time t, for \( t\in \left[{t}_0,{t}_1\right) \), individual rationality requires:
At time t k , for \( k\in \left\{1,2,\cdots, m\right\} \), if \( {\theta}_{a_k}\in \left\{{\theta}_1,{\theta}_2,\kern0.5em \dots, {\theta}_{\eta}\right\} \) has occurred and the state is \( {x}_{t_k}^{*} \), the same optimality principle assigns an imputation vector \( \left[{\xi}^{1\left[{\theta}_{a_k}\right](k)}\left({t}_k,{x}_{t_k}^{*}\right),{\xi}^{2\left[{\theta}_{a_k}\right](k)}\left({t}_k,{x}_{t_k}^{*}\right),\cdots, {\xi}^{n\left[{\theta}_{a_k}\right](k)}\left({t}_k,{x}_{t_k}^{*}\right)\right] \) (in current value at time t k ). Individual rationality is satisfied if:
At time t, for \( t\in \left[{t}_k,{t}_{k+1}\right) \), individual rationality requires:
5.2.2 Subgame-Consistent Imputation
Finally , we would derive a set of imputation that would like to a subgame consistent solution. Invoking Theorem 3.1 in Chap. 4, a subgame consistent PDP can be derived with the theorem below.
Theorem 5.3
A PDP with a terminal payment \( {q}^i\left({x}_T^{*}\right)\Big) \) at time T and an instantaneous payment (in present value) at time \( \tau \in \left[{t}_k,{t}_{k+1}\right] \):
for \( i\in N \) and \( k\in \left\{1,2,\cdots, m\right\} \),
contingent upon \( {\theta}_{a_k}^k\in \left\{{\theta}_1,{\theta}_2,\kern0.5em \dots, {\theta}_{\eta}\right\} \) has occurred at time t k ,
yields a subgame-consistent cooperative solution to the randomly furcating stochastic differential game (5.1 and 5.2).
Proof
Follow the proof of Theorem 3.1 in Chap. 4. ■
Thus a subgame consistent cooperative solution is established.
6 Appendices
Appendix A: Proof of Proposition 2.1
Using (2.3), (2.5) and (2.6), system (2.1 and 2.2) can be expressed as:
For (6.1) and (6.2) to hold, it is required that
Equations (6.3, 6.4, 6.5, and 6.6) forms a block recursive system of differential equations with (6.3) and (6.4) being independent of (6.5) and (6.6).
Solving \( \left\{{A}_1(t),{A}_2(t),\cdots, {A}_n(t)\right\} \) in (6.3 and 6.4) and upon substituting them into (6.5) and (6.6) yield a system of linear first order differential equations:
Since C i (t) is independent of C j (t) for \( i\ne j,\;{C}_i(t) \) can be solved as:
Hence Proposition 2.1 follows. Q.E.D.
Appendix B: Proof of Proposition 3.1
Substituting (3.4) and (3.6) into (3.2) and using (3.7) one obtains:
For (6.11) and (6.12) to hold, it is required that
Equations (6.13, 6.14, 6.15, and 6.16) forms a block recursive system of differential equations with (6.13 and 6.14) being independent of (6.15 and 6.16). Moreover, (6.15 and 6.16) is a Riccati equation with constant coefficients which solution can be obtained by standard methods as:
where \( {\Phi}^{*}(t)= \exp \left\{\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right.{\displaystyle \underset{t_0}{\overset{t}{\int }}\left[\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right.}{\displaystyle \sum_{j=1}^n\frac{b_j^2}{2{c}_j^a}}{A}_{*}^P+\left(r+\delta \right)\left.\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right]\kern0.5em dy\left.\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right\}, \)
\( {\overline{C}}^{*}=\frac{-{\Phi}^{*}(T)}{\left({A}_{*}^P+{\displaystyle \sum_{j=1}^n}{g}^j\right)}+{\displaystyle \underset{t_0}{\overset{T}{\int }}}{\displaystyle \sum_{j=1}^n\frac{b_j^2}{2{c}_j^a}}{\Phi}^{*}(y) dy, \) and
\( {A}_{*}^P(t)=\left\{\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right.\left(r+\delta \right)\kern0.5em -\left[\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right.{\left(r+\delta \right)}^2+4{\displaystyle \sum_{j=1}^n\frac{b_j^2}{2{c}_j^a}}{\displaystyle \sum_{j=1}^n{h}_j}{\left.\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right]}^{1/2}\left.\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right\}/{\displaystyle \sum_{j=1}^n\frac{b_j^2}{c_j^a}} \) is a particular solution of the (6.13).
Upon substituting A*(t) above into (6.15), the system (6.15 and 6.16) becomes a system of linear first order differential equations:
Solving (6.18 and 6.19) yields:
where \( {C}_{*}^0={\displaystyle \sum_{j=1}^n}{g}^j{\overline{x}}^j{e}^{-r\;\left(\kern0.5em T-{t}_0\right)}-{\displaystyle \underset{t_0}{\overset{T}{\int }}}{F}^{*}(y){e}^{-r\left(y-{t}_0\right)} dy. \)
Hence Proposition 3.1 follows. Q.E.D.
7 Chapter Notes
Though cooperation in environmental control holds out the best promise of effective action, limited success has been observed because existing multinational joint initiatives fail to satisfy the property of subgame consistency . In this Chapter we present a cooperative stochastic differential game of transboundary industrial pollution with industries and governments being separate entities. In particular, industrial production creates two types of negative environmental externalities – a short-term local impact and a long-term global impact. Given these impacts the individual government tax policy has to take into consideration the tax policies of other nations and these policies’ intricate effects on outputs and environmental effects. A subgame consistent cooperative solution is derived in this stochastic differential game. A payment distribution mechanism is provided to support the subgame consistent solution under which the expected gain from cooperation is shared proportionally to the nations’ relative sizes of expected noncooperative payoffs. The incorporation of uncertainties in future payoffs in Sect. 13.5 enriches the analysis with consideration of a realistic concern.
Applications of noncooperative differential games in environmental studies can be found in Yeung (1992); Dockner and Long (1993); Tahvonen (1994); Stimming (1999); Feenstra et al. (2001) and Dockner and Leitmann (2001). Cooperative differential games in environmental control have been presented by Dockner and Long (1993); Jørgensen and Zaccour (2001); Petrosyan and Zaccour (2003); Fredj et al. (2004); Breton et al. (2005, 2006), Yeung (2007a, 2008), Yeung and Petrosyan (2007a, 2012c) and Li (2014).
8 Problems
-
1.
Consider an economy which is comprised of 2 nations and the planning horizon is [0, 4]. At time instant s the demand functions of the output of nations 1 and 2 are respectively
$$ {P}_1(s)=60-1.5{q}_1(s)-0.2{q}_2(s)\kern0.36em \mathrm{and}\kern0.24em {P}_2(s)=75-3{q}_2(s)-0.5{q}_1(s). $$The dynamics of pollution stock is governed by the stochastic differential equation:
$$ dx(s)=\left[\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right.{q}_1(s)+0.5{q}_2(s)-0.4{u}_1(s)x{(s)}^{1/2}-0.3{u}_2(s)x{(s)}^{1/2}-0.02\;x(s)\left.\begin{array}{c}\hfill \hfill \\ {}\hfill \hfill \end{array}\right]\;ds+0.04\kern0.1em x(s)dz(s),\kern0.36em x(0)=25. $$The damage (cost) of the pollution stock in the environment to nations 1 and 2 are respectively 3x(s) and 4x(s). The abatement costs are [u 1(s)]2 and 0.4[u 2(s)]2 for nations 1 and 2 respectively. The instantaneous objectives of the governments in nations 1 and 2 at time s are respectively:
\( \left[60-1.5{q}_1(s)-0.2{q}_2(s)\right]{q}_1(s)-2{q}_1(s)-{\left[{u}_1(s)\right]}^2-0.5{q}_1(s)-0.6{q}_2(s)-3x(s) \) and
$$ \left[75-3{q}_2(s)-0.5{q}_1(s)\right]{q}_2(s)-2{q}_2(s)-{\left[{u}_2(s)\right]}^2-0.8{q}_2(s)-0.4{q}_1(s)-4x(s). $$At terminal time 4, the terminal value associated with the state of pollution is \( 2\;\left[90-x(T)\right] \) for nation 1 and \( 2\;\left[70-x(T)\right] \) for nation 2.
Characterize a feedback Nash equilibrium solution for this fishery game.
-
2.
If these nations agree to cooperate and maximize their joint payoff, obtain a group optimal cooperative solution .
-
3.
Furthermore, if these nations agree to share their cooperative gain proportional to their expected payoffs, derive a subgame consistent cooperative solution .
References
Basar, T., Olsder, G.J.: Dynamic Noncooperative Game Theory, 2nd edn. Academic Press, London (1995)
Breton, M., Zaccour, G., Zahaf, M.: A differential game of joint implementation of environmental projects. Automatica 41, 1737–1749 (2005)
Breton, M., Zaccour, G., Zahaf, M.: A game-theoretic formulation of joint implementation of environmental projects. Eur. J. Oper. Res. 168, 221–239 (2006)
Dixit, A.K.: A model of duopoly suggesting a theory of entry barriers. Bell J. Econ. 10, 20–32 (1979)
Dockner, E.J., Leitmann, G.: Coordinate transformation and derivation of open-loop nash equilibria. J. Econ. Dyn. Control 110, 1–15 (2001)
Dockner, E.J., Long, N.V.: International pollution control: cooperative versus noncooperative strategies. J. Environ. Econ. Manag. 25, 13–29 (1993)
Feenstra, T., Kort, P.M., De Zeeuw, A.: Environmental policy instruments in an international duopoly with feedback investment strategies. J. Econ. Dyn. Control 25, 1665–1687 (2001)
Fleming, W.H.: Optimal continuous-parameter stochastic control. SIAM Rev. 11, 470–509 (1969)
Fredj, K., Martín-Herrán, G., Zaccour, G.: Slowing deforestation pace through subsidies: a differential game. Automatica 40, 301–309 (2004)
Jørgensen, S., Zaccour, G.: Time consistent side payments in a dynamic game of downstream pollution. J. Econ. Dyn. Control. 25, 1973–1987 (2001)
Li, S.: A differential game of transboundary industrial pollution with emission permits trading. J. Optim. Theory Appl. 163, 642–659 (2014)
Petrosyan, L.A., Zaccour, G.: Time-consistent Shapley value allocation of pollution cost reduction. J. Econ. Dyn. Control. 27, 381–398 (2003)
Singh, N., Vives, X.: Price and quantity competition in a differentiated duopoly. Rand J. Econ. 15, 546–554 (1984)
Stimming, M.: Capital accumulation subject to pollution control: open-loop versus feedback investment strategies. Ann. Oper. Res. 88, 309–336 (1999)
Tahvonen, O.: Carbon dioxide abatement as a differential game. Eur. J. Polit. Econ. 10, 685–705 (1994)
Yeung, D.W.K.: A differential game of industrial pollution management. Ann. Oper. Res. 37, 297–311 (1992)
Yeung, D.W.K.: Dynamically consistent cooperative solution in a differential game of transboundary industrial pollution. J. Optim. Theory Appl., 134, 143–160, (2007a)
Yeung, D.W.K.: Dynamically consistent solution for a pollution management game in collaborative abatement with uncertain future payoffs. In: Yeung, D.W.K., Petrosyan L.A. (Guest eds.) Special issue on frontiers in game theory: In honour of John F. Nash. Int. Game Theory Rev. 10(4), 517–538 (2008)
Yeung, D.W.K., Petrosyan, L.A.: Managing catastrophe-bound Industrial pollution with game-theoretic algorithm: The St Petersburg initiative. In: Petrosyan, L.A., Zenkevich, N.A. (eds.) Contributions to Game Theory and Managemen, pp. 524–538. St Petersburg State University, St Petersburg (2007a)
Yeung, D.W.K., Petrosyan, L.A.: A cooperative stochastic differential game of transboundary industrial pollution. Automatica 44(6), 1532–1544 (2008)
Yeung, D.W.K., Petrosyan, L.A.: Subgame consistent solution for a cooperative differential game of climate change control. Contrib. Game Theory Manag., 5, 356–386 (2012c)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer Science+Business Media Singapore
About this chapter
Cite this chapter
Yeung, D.W.K., Petrosyan, L.A. (2016). Collaborative Environmental Management. In: Subgame Consistent Cooperation. Theory and Decision Library C, vol 47. Springer, Singapore. https://doi.org/10.1007/978-981-10-1545-8_13
Download citation
DOI: https://doi.org/10.1007/978-981-10-1545-8_13
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-10-1544-1
Online ISBN: 978-981-10-1545-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)