Keywords

1 Introduction

The demand for designing efficient, reliable and robust numerical optimization techniques is very high because of their ability to tackle a number of real-life complex nonlinear optimization problems arising in the field of Engineering, Science, Industry and Finance, which may have constraints associated with them. There are a number of stochastic optimization techniques which are being used to solve complex optimization problems. Among these genetic algorithms (GA) are found to be very promising global optimizers. GAs are population-based heuristics which mimic the Darwin’s principal of “survival of fittest”. The concept of GA was given by Holland [1]. A detailed implementation of GA could be found in Goldberg [2]. The main attribute of GAs is their easy implementation nature, as they do not require any extra information such as continuity and differentiability about objective function and constraints. Although initial versions of GA use binary numbers for encoding of chromosomes, their major drawbacks such as lack of precision and existence of “Hamming-cliff” problem impel to look for another type of encoding scheme. To overcome these difficulties related to binary encoding of continuous parameter optimization problems, real encoding of chromosomes is used. GAs which make use of real encoding of chromosomes are termed as real-coded GA (RCGA).

In GAs crossover is considered to be main search operator. The crossover operator is used to thoroughly explore the search process. After the selection process, the population is enriched with better individuals. Selection makes clones of good strings but does not create new ones. Crossover operator is applied to the mating pool with the hope that it creates better offsprings. In crossover operator the genetic information between two or more individuals is blended to produce new individuals.

Though, along with crossover mutation operator is also essential for thorough search of the function landscape. The most important aspect of mutation operator is that it prevents premature convergence of an algorithm. Mutation operator provides random diversity in the population as described in [3].

A lot of effort has been put into the development of sophisticated real-coded crossover operators [4–8] to improve the performances of RCGAs for function optimization. Deep and Thakur [9] presented Laplace crossover operator which generates a pair of offspring solution from a pair of parent solutions using Laplace distribution. Tutkun [10] proposed a crossover operator based on Gaussian distribution. Kaelo and Ali [11] suggested integration of different crossover rules in the genetic algorithm and recommended some modifications in applying the crossover rules and localization of searches in their study. Recent development in RCGA includes [12].

In an endeavour to define new operators for real-coded genetic algorithms, in this paper, a new crossover operator called double distribution crossover (DDX) is presented. Combining DDX with power mutation (PM) [13], a new generational RCGA called DDX-PM is designed. It is compared with existing RCGA, LX-PM. In order to establish the strength of double distribution crossover computational analysis is performed and discussed.

The paper is organized as follows: the proposed double distribution crossover is defined in Sect. 2. In Sect. 3, new RCGAs based on double distribution crossover are discussed. In Sect. 4, the experimental setup of RCGAs is explained. The computational results and discussion is given in Sect. 5. Finally, in Sect. 6, the conclusions are drawn.

2 The Proposed Crossover Operator

In this section a new crossover operator based on the novel idea of merging of two existing crossover operators is proposed in such a way that it retains the strength of the operators from which it is obtained. The proposed crossover operator is called as double distribution crossover (DDX) as it makes use of two well-established crossover operators: Laplace Crossover (LX) [9] based on Laplace distribution and Weibull Crossover (WX) [14] based on Weibull distribution to produce two offsprings and hence named as double distribution crossover (DDX) operator.

Although DDX could be obtained by merging any two crossover operators, here WX and LX are used because they are well-established potentially effective crossover operators. In DDX two offsprings \( O_{1} \) and \( O_{2} \) are generated from a pair of parents \( P_{1} \) and \( P_{2} \) obtained after selection, in the following manner:

Generate a uniformly distributed random number \( u \in [0,1] \)

if \( u \le \frac{1}{2} \); then

$$ \begin{aligned} O_{1} = P_{1} + \mu d \hfill \\ O_{2} = P_{\,2} + \mu d \hfill \\ \end{aligned} $$
(1)

else

$$ \begin{aligned} O_{1} = P_{1} - \mu d \hfill \\ O_{2} = P_{2} - \mu d \hfill \\ \end{aligned} $$
(2)

where \( d = \left| {P_{1} - P_{2} } \right| \) is the distance between the parents and \( \mu \) is calculated as \( \mu = \frac{{r_{1} + r_{2} }}{2} \), where \( r_{1} \) is a random number following Laplace distribution and \( r_{2} \) is a random number following Weibull distribution. The density function of Weibull distribution is given as follows:

$$ f(x) = \left\{ {\begin{array}{*{20}l} {ab^{ - a} x^{a - 1} e^{{ - (x/b)^{a} }} } \hfill & {{\text{if}}\,\,x > 0} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$
(3)

and the distribution function is given by

$$ F(x) = \left\{ {\begin{array}{*{20}l} {1 - e^{{ - (x/b)^{a} }} } \hfill & {{\text{if}}\,\,x > 0} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$
(4)

where \( a > 0 \) is called shape parameter and \( b > 0 \) is called the scale parameter. And the density function of Laplace distribution is given as follows:

$$ f(x) = \frac{1}{2d}\exp \left( { - \frac{{\left| {x - c} \right|}}{d}} \right),\quad - \infty < x < \infty $$
(5)

the distribution function is given by

$$ F(x) = \left\{ {\begin{array}{*{20}l} {\frac{1}{2}\exp \left( {\frac{{\left| {x - c} \right|}}{d}} \right)} & {{\text{if}}\,\,x \le c} \\ {1 - \frac{1}{2}\exp \left( { - \frac{{\left| {x - c} \right|}}{d}} \right)} & {{\text{if}}\,\,x > c} \\ \end{array} } \right. $$
(6)

where \( c \in R \) is location parameter and \( d > 0 \) is termed as scale parameter.

DDX preserves the property of both the parent operators, i.e. for fixed values of the crossover index of DDX (which is a two-dimensional vector which includes the crossover indices of both WX and LX), the spread of offsprings is proportional to the spread of parents, i.e. if the parents are near to each other the offsprings are expected to be near to each other and if the parents are far from each other then offsprings are likely to be far from each other.

Also, from Eqs. 1 and 2 it is clear that both the offsprings are placed symmetrical with respect to the position of the parents and if DDX produces an offspring which is not within the bounds of the decision variable then that offspring is assigned a random value within its bounds.

3 The Proposed New RCGA

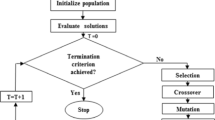
In this section a new RCGA namely DDX-PM is proposed, which combines the use of Laplace crossover with power mutation [13]. DDX-PM is compared with the existing LX-PM. Both the algorithms use tournament selection with tournament size three. In addition, both the RCGAs are elite preserving with elitism size one. The elitism operator helps to maintain fitness stability to increase the search performance of the proposed algorithm.

Both the RCGAs are terminated if either the pre-specified maximum number of generations (3000) is reached or the best solution obtained by the algorithm lies within specified accuracy (0.01) of known optimum, whichever occurs earlier. The algorithm is tested on standard benchmark problems taken from literature which includes five nonscalable test problems (Table 1) and five scalable test problems of size 30 (Table 2) of different levels of complexity and multimodality. The pseudocode of DDX-PM is given below:

Table 1 List of nonscalable benchmark functions
Full size table
Table 2 List of scalable benchmark functions
Full size table

4 Experimental Setup

The experimental setup used for both the RCGAs viz. DDX-PM and LX-PM is given in this section.

Parameter Setting: Population size is taken as 10 times the number of variables. The crossover index for DDX is fixed at (12, 0.20). The final parameter setting is presented in Table 3 where p c and p m represent the probabilities of crossover and mutation, respectively. Each GA runs at 100 times with same initial populations while each run is initiated using a different set of initial population.

Table 3 Parameter setting for DDX-PM and LX-PM
Full size table

All the algorithms are implemented in C++ and the experiments are done on a Core Duo Processor with 1.66 GHz speed and 1 GB RAM under WINXP platform.

Performance Evaluation Criteria: A run in which the algorithm finds a solution satisfying \( f_{\hbox{min} } - f_{\text{opt}} \le 0.01 \), where \( f_{\hbox{min} } \) is the best solution found when the algorithm terminates and \( f_{\text{opt}} \) is the known global minimum of the problem, is considered to be successful.

For each method and problem, the followings are recorded:

  • Success Rate \( \left( {\text{SR}} \right) = \frac{{{\text{Number}}\,{\text{of}}\,{\text{successful}}\,{\text{runs}}}}{{{\text{Total}}\,{\text{number}}\,{\text{of}}\,{\text{runs}}}} \times 100 \)

  • Average computational time (ACT) (in seconds).

  • Average number of function evaluations (AFE).

  • Average Error \( \left( {\text{AE}} \right) = \frac{{\sum\nolimits_{n} {\left( {f_{\hbox{min} } \,-\, f_{\text{opt}} } \right)} }}{n} \) where, n is the total number of runs.

5 Results and Discussion

The computational results of both the RCGAs are presented in this section.

Table 4 summarizes the computational results for both the algorithms. As the execution time for nonscalable problems is very less and hence insignificant in most of the cases, it is not included in Table 4. From Table 4 it can be easily observed that the proposed crossover operator DDX outperforms LX in terms of various performance criteria and thus indicates the efficiency of proposed crossover operator for providing suitable exploration for obtaining the global optimal solution.

Table 4 Computational results for nonscalable and scalable problems
Full size table

6 Conclusion

In this paper a new crossover operator called double distribution crossover (DDX) is introduced. By combining DDX with already existing operator, namely PM a new generational RCGA called DDX-PM is proposed. For an analogical comparison it is compared with the existing RCGA based on Laplace crossover and power mutation called LX-PM. Based on the numerical results it is clear that with respect to reliability, efficiency and accuracy measured in terms of success rate, function evaluation and average error, respectively, DDX-PM performed better than LX-PM, though they both use same mutation operator, which clearly signifies the role of crossover operators in the search process for locating global optima.

Thus DDX proved to be an efficient crossover operator when used with power mutation, but whether its performance will remain equally well, when used with other mutation operators for RCGAs, is the question whose answer is to be looked in future studies.