An Elitist Genetic Algorithm Based Extreme Learning Machine

Abstract

Extreme Learning Machine (ELM) has been proved to be exceptionally fast and achieves more generalized performance for learning Single-hidden Layer Feedforward Neural networks (SLFN). In this paper, a Genetic Algorithm (GA) is proposed to choose the appropriate initial weights, biases and the number of hidden neurons which minimizes the classification error. The proposed GA incorporates a novel elitism approach to avoid local optimum and also speed up GA to satisfy the multi-modal function. The experimental results indicate the superior performance of the proposed algorithm with lower classification error.

1 Introduction

Huang et al. [1] proposed a novel learning method called Extreme Learning Machine (ELM) to train Single-hidden Layer Feedforward Neural networks (SLFNs) faster than any other learning approaches. In case of classical learning algorithms, the learning process is done by iterative process which would be slower, however, the ELM simplifies the learning process in one step through a simple generalized inverse calculation [2]. Unlike other learning methods, ELM doesn’t requires any parameters to be tuned except network architecture. However, ELM has its own limitation that the random selection of input weights and biases might reduce the classification performance [3, 4]. Therefore, it is important to modify the ELM to overcome this inadequacy [5, 6]. Global searching methods such as Evolutionary Algorithms (EA) were used in the past decades for optimizing the weights and biases of the neural networks. In [7–11], Differential Evolution (DE) is adopted as a learning algorithm for SLFNs, but there is a chance that the DE algorithms may result in premature or slow convergence. Lahoz et al. [12] and Suresh et al. [13] used a Genetic Algorithm (GA) for optimizing the weights and number of hidden nodes.

This paper proposes a novel GA based learning for ELM. Genetic Algorithms (GAs) have proven useful in solving a variety of search and optimization problems. A major problem might occur in GA is that it might provide local optimum solution. The elitist strategy is widely adopted in the GAs’ search processes to recover the chance of finding the global optimal solution. Elitism is able to preserve promising individuals from one generation to the next and maintain the diversity of the population [14, 15]. A novel elitist strategy is proposed in this paper, which improves the performance of the GA towards improving the classification accuracy of ELM.

The rest of the paper is organized as follows: Sect. 2 describes the background terminologies about ELM and GA, and explains the proposed EGA-ELM subsequently. Section 3 discusses the databases and parameter settings used for the experiments. Section 4 brings out the results and analyzes the performance of the proposed system with the existing ELM algorithms. Section 5 concludes the paper.

2 Materials and Methods

2.1 Basic ELM

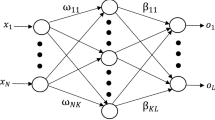
ELM reduces the learning time of SLFNs by finding the weights using a simple inverse generalization calculation. Consider N arbitrary training samples (x_i, t_i), where x_i are the decision attributes, x_i = [x_i1, x_i2, …, x_in]^T ∈ Rⁿ and ti are the target values or class attributes t_i = [t_i1, t_i2, …, t_im]^T ∈ R^m. A typical SLFNs with Ñ number of hidden nodes and activation function ƒ(x) are defined as

$$\sum\limits_{i = 1}^{{{\tilde{\text{N}}}}} {\alpha_{i} f_{i} \left( {x_{j} } \right)} = \sum\limits_{i = 1}^{{{\tilde{\text{N}}}}} {\alpha_{i} f\left( {w_{i \cdot } x_{j} + b_{i} } \right) = o_{j} , j = 1, \ldots , N}$$

(1)

where w_i = [w_i1, w₁₂, …, w_in]^T is the weight matrix between ith hidden and input nodes, α_i = [α_i1, α_i2, …, α_im]^T is the weight matrix between ith hidden and output nodes, and b_i is the bias value of the ith hidden node. w_i ∙ x_j denotes the inner product of w_i and x_j.

The classical learning algorithm repeats the learning process till the network error mean becomes zero, that is

$$\sum\limits_{j = 1}^{{{\tilde{\text{N}}}}} {\left\| {o_{j} - t_{j} } \right\| \cong 0}$$

(2)

The target value is the mapping between the weights and the activation function as defined below

$$\sum\limits_{i = 1}^{{{\tilde{\text{N}}}}} {\alpha_{i} f\left( {w_{i} \cdot x_{j} + b_{i} } \right) = t_{j} , j = 1, \ldots , N}$$

(3)

The above N equation could be simplified as Hα = T, where

$$H\left( {w_{1} , \ldots ,w_{{{\tilde{\text{N}}}}} ,b_{1} , \ldots ,b_{{{\tilde{\text{N}}}}} ,x_{1} , \ldots ,x_{N} } \right) = \left[ {\begin{array}{*{20}c} {f(w_{1} \cdot x_{1} + b_{1} )} & \cdots & {f(w_{{{\tilde{\text{N}}}}} \cdot x_{1} + b_{{{\tilde{\text{N}}}}} )} \\ \vdots & \cdots & \vdots \\ {f(w_{1} \cdot x_{N} + b_{1} )} & \cdots & {f(w_{{{\tilde{\text{N}}}}} \cdot x_{N} + b_{{{\tilde{\text{N}}}}} )} \\ \end{array} } \right]_{{N \times {\tilde{\text{N}}}}}$$

(4)

where H is called the hidden layer output matrix of the neural network [16, 17]; ith column of H is the ith hidden node output with respect to inputs x₁, x₂, …, x_N. If the activation function ƒ is infinitely differentiable we can prove that the required number of hidden nodes Ñ ≤ N. The main objective of any learning algorithms is to find the specific $\hat{w}_{i} , \hat{b}_{i} , \hat{\alpha }$ to reduce the network mean error, defined as

$$\left\| {H\left( {\hat{w}_{1} , \ldots ,\hat{w}_{{{\tilde{\text{N}}}}} ,\hat{b}_{1} , \ldots ,\hat{b}_{{{\tilde{\text{N}}}}} } \right)\hat{\alpha } - T} \right\| = \begin{array}{*{20}c} {\text{min}} \\ {w_{i} ,b_{i} ,\alpha } \\ \end{array} \left\| {H\left( {\hat{w}_{1} , \ldots ,\hat{w}_{{{\tilde{\text{N}}}}} ,\hat{b}_{1} , \ldots ,\hat{b}_{{{\tilde{\text{N}}}}} } \right)\hat{\alpha } - T} \right\|$$

(5)

This can be written as a cost function

$$E = \sum\limits_{j = 1}^{N} {\left( {\sum\limits_{i = 1}^{{{\tilde{\text{N}}}}} {\alpha_{i} f\left( {w_{i} \cdot x_{j} + b_{i} } \right) - t_{j} } } \right)^{2} }$$

(6)

The gradient-descent learning algorithms generally search for the minimum of $H\beta - T$, for that the weights and biases are iteratively adjusted as follows:

$$W_{k} = W_{k - 1} - \eta \frac{\partial E(W)}{\partial W}$$

(7)

Here η is a learning rate. BP is one of the popular learning algorithm for SLFNs, which has the following issues [18, 19]:

• The learning rate has to be carefully chosen, the minor η slows down the learning algorithm, and however, if it is too large then the learning becomes unstable.

• Training with more number of iteration leads to inferior performance.

• Gradient-descent based learning is very time-consuming in most applications.

According to Huang et al. [2] the w_i and b_i of SLFNs could be assigned with random values rather than iteratively adjusting them, and the output weights can be estimated as

$$\hat{\alpha } = H^{\dag } T$$

(8)

where $H^{\dag }$ is the Moore–Penrose (MP) generalized inverse [20] of the hidden layer output matrix H. There are several methods to calculate the MP generalized inverse of a matrix, among that the Singular Value Decomposition (SVD) is known for the best inverse and thus is used in most of the ELM implementations [18, 21]. The ELM can be summarized as follows:

2.2 Genetic Algorithm

Holland [22] introduces the basic principle of Genetic Algorithm (GA). GA is one of the best known search and optimization methods widely used to solve complex problems [23, 24]. The detailed description of the real coded GA is given in this section.

Initial Population. The initial population is a possible solution set P, which is a set of real values generated randomly, P = {p₁, p₂, …, p_s}.

Evaluation. A fitness function should be defined to evaluate each chromosome in the population, can be written as fitness = g(P).

Selection. After the fitness value is calculated, the chromosomes are sorted based on their fitness values, then the tournament selection method is widely used for parent selection.

Genetic Operators. The genetic operators are used to construct some new chromosomes (offspring) from their parents after the selection process. They include the crossover and mutation [25]. The crossover operation is applied to exchange the information between two parents, which are selected earlier. There are number of crossover operators are available, here we use arithmetical crossover. The crossed offspring will then apply with mutation operation, to change the genes of the chromosomes. Here we have used uniform mutation operation.

After the operations of selection, crossover and mutation, a new population is generated. The next iteration will continue with this new population and repeat the process. Each time the best chromosomes from the current or new population is selected and compared with the best from the previous population to maintain the global best chromosome. This iterative process could be stopped either the result converged or the number of iterations exceeds the maximum limit.

Elitism—The genetic operations such as crossover and mutation may produces weaker children than the parents. But the Evolutionary Algorithms (EA) could recover from this problem after consequent iterations but there is no assurance. Elitism is the known solution to solve this problem. The basic idea is to retain a copy of best parents from the previous population to the subsequent populations. Those parents are copied without changing them, helps to recover EA from re-discovering weaker children. Those elitist parents are still eligible to act as parents for the crossover and mutation operations [26]. Elitism can be implemented by producing only (s—ep) children in each generation, where ‘s’ is the population size and ‘ep’ is the user-defined number of elite parents. In this case, at each iteration, after the evaluation step, the parents are sorted based on their fitness values, and ‘ep’ number of best parents is selected for next generation, and only (s—ep) number of children are reproduced with genetic operations. Then the next iteration is continued with the population contains union of elitist parents and the children. The following pseudo code illustrates the elitist strategy.

2.3 The Proposed Elitism Strategy

In classical elitist strategy, the number of elites are fixed and continued till the genetic algorithm terminates. Our idea is to make ‘ep’ as a variable depends on the age of the population. And it is noted that, the elitist parents what we are assuming at the initial iterations may not the best parents globally, this point makes the proposed approach to keep increasing the number of elites while the iteration grows. Initially we started less number of elite parents (for example 10 % of the population size), over a period of time, the number of elites are gradually increased to reach up to 50 % of the population size. The increment is done with a constant value scheduled to happen at regular interval, say after some ‘q’ number of iterations.

2.4 Elitist Genetic Algorithm Based ELM

The proposed Elitist GA (EGA) strategy is applied to find the optimal weights between input and hidden layers and bias values. The weights has the bound of [−1, 1], so the lbound and ubound takes the values −1 and 1 respectively. The population dimension depends on the number of input variable to ELM. Initially a population is generated with a set of random numbers and these values are fed to ELM and find the classification accuracy as fitness for each chromosome. Then the genetic iteration is continued with the new population as discussed earlier with genetically optimized weights. After termination, the proposed algorithm will provide the optimum weights and bias values for the ELM.

3 Experimental Setup

The performance of the proposed EGA-ELM for SLFN is evaluated on the benchmark datasets described in Table 1, which includes five classification applications. The datasets are received from UCI machine learning repository. Table 2 summarizes the ELM and Elitist GA parameter values used for the experiments.

Table 1 The datasets used for performance evaluation

Table 2 Summary of Ex-ELM and elitist GA parameters settings

4 Results and Discussions

EGA-ELM performance is compared with the evolutionary based ELMs such as SaE-ELM [10], E-ELM [9], LM-SLFN [8], and compared with general Elitist GA based ELM (Elitist-ELM), also with traditional ELM [1], based on classification accuracy measure. Table 3 summarizes the classification accuracy received from each ELM algorithms on different datasets. The results clearly indicate that the proposed EGA-ELM outperforms other ELM approaches in terms of higher classification accuracy. Comparatively, only the EGA-ELM and the Elitist-ELM improves the classification accuracy consistently, the rest of the algorithms’ performance oscillates between a ranges, this way the proposed algorithm proves its stable performance.

Table 3 Summary of classification accuracy from ELM algorithms

5 Conclusions

Extreme Learning Machine (ELM) is one of the fastest learning algorithms used for classification and regression. One of the limitations of ELM is the random choice of input weights, might be results in lower prediction accuracy. Evolutionary algorithms have been implemented to optimize those weights. This paper proposed a novel Elitism based Genetic Algorithm (GA) based weight optimization strategy for ELM. The performance of the proposed algorithms is tested with five datasets from UCI machine learning repository against four other different evolutionary and traditional ELM algorithms. The result shows that the proposed EGA-ELM algorithm surpasses the other algorithms with superior classification accuracy in stable.