Keywords

1 Introduction

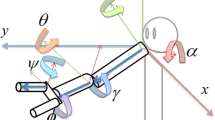
Since a few decades, brain science has been greatly developed, however, the mechanisms of advanced functions of brain have been still beyond our understanding. In these situations, there are people who think that recently discovered chaos in brain or biological systems could play an important role in their advanced functions [1–3]. Nara and Davis proposed that chaotic dynamics can occur in a recurrent neural network model by changing a system parameter, and they have studied that it can be applied to solving ill-posed problems, for example, memory search or synthesis, to solve maze (labyrinth) with use of chaotic roving robot, and so on [4–6]. In their opinion, chaotic dynamics with certain dynamical structures plays an important role in complex functions. In this paper, based on the same idea with them, and by computer experiment, we propose that chaos introduced into a recurrent neural network model can enable “complex arm control with simple rule(s)” under ill-posed situations [7, 8], and as an actual example, we show that an arm robot without having advanced visual processing function (see Figs. 1 and 2) can take an target object to a set position under ill-posed situations. Furthermore, we show behavioral interactions of two individual arm robots driven by independent chaos implemented into each arm control system using recurrent neural networks.

Fig. 1
figure 1

Our arm model in Euler angle scheme

Full size image
Fig. 2
figure 2

Firing pattern of 400 neurons & sub-vectors’ codings which correspond to incremental motions via Euler angles

Full size image

2 Method and Model

Our study works with an interconnected recurrent neural network model (abbreviated as RNNM hereafter) consisting of N binary neurons, and the updating rule is defined by

$$ {x}_i\left(t+1\right) = \mathrm{sgn}\left\{{\displaystyle \sum_{j\in {G}_i(r)}^N}{w}_{ij}{x}_j(t)\right\} $$
$$ \mathrm{sgn}(u)=\left\{\begin{array}{c}+1\quad\ u\ge 0 \\ {}-1\quad\ u<0 \end{array}\right. $$

where x i (t) = ±1 (i =1 ∼ N) is the firing state of a neuron specified by space site index i at time t, and w ij is connection weight from the neuron x j to the neuron x i . w ii is taken to be 0. r (0 < r < N) is fan-in number for neuron x i , named connectivity that is the most important system parameter in our work. G i (r) is a spatial configuration set of connectivity r for neuron x i., the number of which are N−1C r . Therefore, with full connectivity r = N − 1, determination of w ij by means of a kind of orthogonalized learning method enables us to embed a group of N dimensional state patterns (vectors) as cycle memory attractors in N dimensional state space. Let us employ our arm model as shown in Fig. 1, and introduce coding of sub-vectors of neuron firing pattern (vector) as increment of the Euler angles in arm motion. In our neural model system, attractor patterns consists of (K patterns per cycle) × L cycles, and each patterns has N neurons. In this work, we take K = 4, L = 8, and N = 400, where the firing states of N = 20 × 20 = 400 neurons are represented by black pixel or white pixel (see Fig. 2). Long time updating makes an initial pattern converge to one of the embedded cycle attractors.

Now, when we reduce connectivity r by blocking signal transfer from the other neurons, then attractors gradually become unstable, and the network state changes from attractor dynamics to chaotic dynamics, where we discard the detailed description of the destabilizing processes [5]. Let us describe actual arm motions and neural firing patterns (vectors). In the full connection state, when one of the embedded cycle attractors appears, then, at each time step, decoded quantities following the corresponding relations shown in Fig. 2 stationary give incremental Euler angles, so the generated motion by them is one of the definite motions shown in Fig. 4, whereas they are snap shots of the definite periodic motions of arm. It should be noted that, to display the results of computer experiment, we used the software “Insilico IDE” which is opened to the public on the web site “Physiome Platform”. Once connectivity is reduced to one order of magnitude smaller than full connection number, then dynamics of firing pattern becomes chaotic. Correspondingly, decoded motions indicate chaotic behaviors, in which fragmental motion of the embedded definite motions are coming out, vanishing, coming out vanishing, and repeating them chaotically.

Fig. 3
figure 3

The cycle attractor patterns

Full size image
Fig. 4
figure 4

The embedded four definite motions corresponding to the Fig. 3

Full size image

Now, we apply these two types of motions, definite motions and chaotic motions to realizing (a) catching a target object, (b) catching a target and taking it back to the set position, (c) catching a target and taking it back to the set position under the existence of unknown obstacles, (d) competitive catching a target object between two independent arm robots, where, in all cases, we assume that robot has no advanced ability of visual information processing, and only adaptive switching between attractor regime (full connection) and chaotic regime (small connection) depending on situations with including uncertainty (ill-posed situations) is used by means of simple rule. Figure 5 shows a schematic description of switching condition of connectivity and Fig. 6, the rough algorithm of this control system, where Figs. 7 and 8 are actual two examples of set situations (c) and (d) given above. All the computer experiments are successfully done and only about the case of (d), the result to evaluate the success rate with respect to connectivity is shown in Fig. 9.

Fig. 5
figure 5

A schematic description of the condition about connectivity switching. If the object is inside a certain cone the axis of which is an elongation of direction from the position of arm edge at time t-1 to the position of arm edge at time t, then r = N − 1, otherwise r = small.

Full size image
Fig. 6
figure 6

Control algorithm of connectivity switching at each time step, corresponding to Fig. 5

Full size image
Fig. 7
figure 7

Experiment of the situation (c) given in the text

Full size image
Fig. 8
figure 8

Experiment of the situation (d) given in the text

Full size image
Fig. 9
figure 9

Computer experiments of competitive taking of a target object between two arm robots, where evaluated success rate depending on connectivity is shown.

Full size image

One can recognize that chaos generated by rather small connectivity give better results, which means that chaos with having strong ruin of embedded attractors prevents the robots from generating various and/or adaptive motions in given environments. So, chaos having certain weak dynamical structures could be useful, however, optimization of dynamical structures is quite difficult problem and it would be big issues including learning of chaos in this scheme.

3 Concluding Remarks

  1. 1.

    Using Euler angle model of an arm robot having 6° (angles) of freedom, we made computer experiments to solve ill-posed problems using chaos in RNNM installed into the control systems of the robot, where the robot can obtain only information about target direction with uncertainty, and without any pre-knowledge about configurations of obstacles.

  2. 2.

    By the computer experiments, we were able to show that chaos realize autonomous and adaptive functions with use of simple rule(s)

  3. 3.

    The computer experiments in which the two robots competitively behave as taking off and back a target, show that functional performance strongly depends on dynamic structures of chaos generated by reducing connectivities in RNNM.