Keywords

1 Introduction

Oscillations are ubiquitous in the nervous system. Many experiments have shown that the complex interaction between neurons can induce various rhythmic activity in the nervous system [1]. Both the normal physiological function or abnormal physiological disorders (such as Parkinson’s disease, epilepsy and so on) are related to the synchronized neural activities with various frequency [2, 3]. Synchronized activity among neurons and the formation of neuronal clusters are considered as a fundamental mechanism for cognitive function and consciousness [4, 5]. Despite the ubiquity and importance of synchronized activity, the underlying mechanism and the key system parameters are not yet known, and little attention has been paid to investigating the dynamic response of an oscillator network to external stimuli. The phase response curve (PRC) represents how an external stimulus affects the timing of spikes immediately after the stimulus in repetitively firing neurons [6]. PRC describe the phase shift of the perturbed neuronal oscillator when a neural oscillator receive external input or synaptic input [7–9]. In order to explore the dynamic mechanism of synchronous activity in the nervous system, the phase response curve is an important and effective method [10–14]. In the nervous systems, cortical neurons undergo massive synaptic bombardment and ever-found perception information stimulation. To understand the response properties of neurons operating in this regime, we investigate a model neuron as a neuronal oscillator with non-instantaneous synaptic inputs represented by α − function, and external periodic stimulus.

2 Model

We consider a neural population composed of N neural oscillators, where neuronal oscillators are identical and globally coupled with each other, subject to a common external periodic force. The phase of jth oscillator θ j obeys the evolution equation:

$$ \frac{d{\theta}_j}{dt}=\omega +\frac{\varepsilon }{{\it NZ}(\theta_j)}{\displaystyle \sum_{k=1}^N{\displaystyle \sum_n\alpha \left(t-{t}_k^n\right)}}+c \sin \left(\omega t\right)Z\left({\theta}_j\right) $$
(1)

where \( \frac{\varepsilon }{N}{\displaystyle \sum_n\alpha \left(t-{t}_k^n\right)} \) is the input to the jth neuronal oscillator from the kth neuronal oscillator, ε is weak coupling constant, N is the total number of neuronal oscillators, t k n is the nth firing time of the kth neuronal oscillator, α(t) is a causal coupling function. θ j is the phase of jth neuronal oscillator, ω is the natural frequency of a neuronal oscillator, Z(θ) is a phase response curve of a neuronal oscillator, c sin(ω 0 t) is an external periodic force with a strength c and frequency ω 0.

We assume that the mutual interaction shift the frequency of the mean phase of these oscillators by εΩ from the natural frequency ω, and define the relative phase ψ j  = θ j  − (ω + εΩ)t. The relative phase ψ j changes slowly compared with and will hardly change during the oscillation period θ j . Therefore, we substituteψ j into Eq.(1), and average Eq. (1) over one period keeping ψ j constant, so the relative phase ψ j obeys the following equation:

$$ \begin{array}{ll}\frac{d{\psi}_j}{dt} & =-\varepsilon \Omega +\frac{\varepsilon }{NT}{\displaystyle {\int}_0^TZ\left({\psi}_j+\left(\omega +\varepsilon \Omega \right)t\right)}{\displaystyle \sum_{k=1}^N{\displaystyle \sum_n\alpha \left(t-{t}_k^n\right)}}\\ & \quad+ c \sin \left(\omega t\right)Z\left({\psi}_j+\left(\omega +\varepsilon \Omega \right)t\right) \end{array}$$
(2)

In order to investigate the dynamic response of neural population, we introduce complex order parameters describing synchronized phenomenon in the neuronal population

$$ {\mathrm{Re}}^{i\psi}=\frac{1}{N}{\displaystyle \sum_{j=1}^N{e}^{i{\psi}_j}} $$
(3)

where R is the amplitude of the order parameters describing the degree of synchronization of neuronal oscillators, 0 ≤ R ≤ 1, the bigger R show that synchronous activity is stronger, ψ is the average phase of the neuronal population.

3 Result

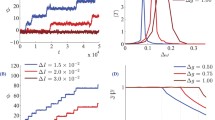
We investigate the response property of neuronal population to external periodic stimulus. The phase sensitivity function Z(θ) is considered as a sinusoidal sensitivity function sin(θ) as in Ref. [15]. As synaptic time constant τ is smaller, the neuronal population quickly synchronized in-phase (Fig. 1a); but with τ increased, periodic synchronization occurred, and as the synaptic time constant is larger, the synchronization become weaker (Fig. 1b, c); even more, synchronized activity can be lost (Fig. 1d). This shows that synaptic time constant is an important condition under which the global neural network synchronized.

Fig. 1
figure 1

Time evolution of the order parameter R by varying τ in the absence of stimulation. Parameters: ε = 0.01, ω = 3, Ω = 2π, T = 2.05, (a) τ = 0.4, (b) τ = 0.5, (c) τ = 0.7 (d) τ = 1.4

Full size image

Without stimulation, the neuronal population quickly tend to perfect synchronization (Fig. 2a); With a weak stimulation, the neuronal activity transition from the perfect synchronization to synchronized bursting occurred (Fig. 2b); As the stimulus intensity was increased, the synchronized bursting duration is prolonged (Fig. 2c); However, the synchronized bursting duration is shorten in the presence of stronger stimulus (Fig. 2d). As the stimulus frequency was increased, the neuronal activity transition from the perfect synchronization to synchronized bursting occurred (Fig. 3b); As the stimulus frequency was further increased, the synchronized bursting becomes stronger (Fig. 3c, d).

Fig. 2
figure 2

Time evolution of the order parameter R in the presence of stimulation. Parameters: ε = 0.01, ω = ω0 = 3, Ω = 2π, τ = 0.485, (a) c = 0, (b) c = 0.003, (c) c = 0.03 (d) c = 1.5

Full size image
Fig. 3
figure 3

Time evolution of the order parameter R in the presence of stimulation. Parameters: ε = 0.01, ω = ω 0 = 3, Ω = 2π, τ = 0.485, (a) ω 0 = 0.03, (b) ω 0 = 0.03, (c) ω 0 = 3 (d) ω 0 = 30

Full size image

4 Conclusions

In the present study, we have formulated the phase description of the neuronal oscillator with non-instantaneous synaptic inputs represented by α − function, and external periodic stimulus by using the phase sensitivity function. The synaptic time constant is an important parameter for perfect synchronization, periodic synchronization, synchronized bursting in the global neural network synchronized. The influence of external periodic stimulation on the neuronal population depends on stimulus intensity and frequency. With a stronger stimulation or a high frequency stimulation, synchronized bursting occurred.