Keywords

1 Introduction

Recent work has illustrated that scaling up arbitrarily selected ground motions to a specified spectral acceleration (Sa) level at period T can produce overly conservative structural responses, because a single extreme Sa(T) level of interest for engineering analysis does not imply occurrence of equally extreme Sa levels at all periods. The Conditional Mean Spectrum (CMS) and Conditional Spectrum (CS) have been developed to describe the expected response spectrum associated with a ground motion having a specified Sa(T) level (Baker and Cornell 2006; Baker 2011; Lin et al. 2013). The Conditional Mean Spectrum for a rare (i.e., positive ε) Sa(T) level has a relative peak at T and tapers back towards the median spectrum at other periods. The Conditional Spectrum differs from the Conditional Mean Spectrum in that it also considers the variability in response spectra at periods other than the conditioning period (which by definition has no variability).

The Conditional Spectrum approach for selecting and scaling ground motions requires the user to specify a conditioning period (denoted here as T*) that is used to compute corresponding distributions of spectral values at all other periods. Ground motions can then be selected to match these spectral values, and used as inputs to dynamic structural analysis, to compute Engineering Demand Parameters, or EDPs. When calculating Peak Story Drift Ratio (PSDR) in buildings, T* is often chosen to be the building’s elastic first-mode period (T 1). This is done because Sa(T 1) is often a “good” predictor of that EDP, so scaling ground motions based on this parameter can lead to reduced scatter in resulting response predictions and thus minimizes the required number of dynamic analyses (Shome et al. 1998).

There are situations where the application of the CS concept is not yet straightforward. One such situation is for prediction of EDPs which are not dominated by the first-mode structural response, due to contributions from higher modes, such as peak floor accelerations, or to longer periods associated with reduced-stiffness nonlinear response such as the onset of collapse (Haselton and Baker 2006). A second situation is for selection of ground motions prior to identification of a single conditioning period , because the structure is not yet designed or because multiple designs having multiple periods are being considered. In both cases, one is faced with the possibility of using a Conditional Spectrum that is not conditioned on Sa at the period that most efficiently predicts structural response. And even in cases where one does know an effective conditioning period for computing the CS, the question still arises as to whether a comparable-intensity Sa at some other conditioning period might produce a larger level of EDPs than the primary CS being considered.

Here we will demonstrate that, if the analysis objective is to compute the annual rate of the structure experiencing EDP > y, and if the ground motions are selected to match the Conditional Spectrum , then the resulting answer is relatively insensitive to the choice of conditioning period . While some researchers have previously suggested that the choice of conditioning period may not be critical to estimates of reliability (e.g., Abrahamson and Yunatci 2010; Shome and Luco 2010), those efforts did not perform a full risk-based assessment using nonlinear dynamic analyses, and did not consider spectral variability at periods other than the conditioning period . Here we do repeated risk-based assessments (i.e., compute the rate of EDP > y using nonlinear dynamic analysis at multiple Sa levels) to demonstrate this statement empirically. We also present theoretical arguments and intermediate results to support these findings.

2 Demonstration Analysis

To illustrate the effect of conditioning period , we first perform two parallel performance assessment s, using ground motions selected to match Conditional Spectra conditioned on two periods. We will later look at the effect of repeating the procedure using other conditioning period s. The test case and analysis procedure is described in this section.

2.1 Building Site and Structural Model

The structure being studied is assumed to be located in Palo Alto, California, approximately 10 km from the San Andreas Fault. The structure is a 20-story reinforced concrete special moment frame with the perimeter frame designed to resist lateral forces. This building was designed for the recent FEMA P695 project (Federal Emergency Management Agency 2009; Haselton and Deierlein 2007), and is denoted Building 1020 in that study. It is modeled in OpenSEES (2011), with strength deterioration (both cyclic and in-cycle) and stiffness deterioration that is believed to reasonably capture the responses up to the point of dynamic-instability collapse. The first three elastic modal periods are 2.6, 0.85 and 0.45 s. The building was designed per the ICC (2003), for a site with a slightly lower design ground motion level than the site being utilized in this study (by approximately 20 %). Estimating the annual rate of exceeding various thresholds of Peak Story Drift Ratio in this building is not trivial, as the PSDR is affected by multiple modes excited at multiple periods, and experiences effective period lengthening as it behaves nonlinearly up to the collapse level for high intensity ground motions.

2.2 Seismic Hazard Analysis and Ground Motion Selection

We perform seismic hazard analysis to obtain ground motion hazard curves for spectral accelerations at three periods (0.85, 2.6 and 5 s), corresponding to the first two modal periods of the building and a lengthened period that may be a good predictor of nonlinear response. For each spectral period and amplitude of interest, we obtain the rate of exceeding that amplitude and a deaggregation distribution providing the causal magnitudes, distances and ε values associated with spectral accelerations of that amplitude. All of this data comes from the U.S. Geological Survey online tools (USGS 2008). Ten rates of exceedance are considered for each conditioning period , ranging from 0.023 to 0.00005 per year (i.e., 50 % in 30 years to 1 % in 200 years probability of exceedance), as those are the exceedance rates for which the USGS provides the needed hazard and deaggregation information. Hazard curves and deaggregation results are not provided for exactly the conditioning period s used here, so interpolation between hazard results at adjacent periods is utilized.

Using the hazard curve and deaggregation information for a particular conditioning period , the Conditional Spectrum calculation is used to compute the mean and standard deviation of logarithmic response spectral values at all other periods, conditioned on an amplitude of Sa(T*). The mean and standard deviation of lnSa are given by the following equations (Baker and Cornell 2005a; Baker 2011)

$$ {\mu}_{\ln Sa\left({T}_i\right)| \ln Sa\left( T^{*}\right)}={\mu}_{\ln Sa}\left( M, R,{T}_i\right)+\rho \left({T}_i, T^{*}\right)\varepsilon \left( T^{*}\right){\sigma}_{\ln Sa}\left({T}_i\right) $$
(28.1)
$$ \sigma_{Sa\left({T}_i\right)| Sa\left( T^{*}\right)}={\sigma}_{\ln Sa}\left({T}_i\right)\sqrt{1-{\rho}^2\left({T}_i, T^{*}\right)} $$
(28.2)

where μ ln Sa (M, R, T i ) and σ ln Sa (T i ) are the predicted mean and standard deviation from a ground motion prediction model (Boore and Atkinson 2008 in this case), ρ(T i , T *) is the correlation between the spectral values at period T and the conditioning period T* (obtained from Baker and Jayaram 2008), and M, R and ε(T*) come from the deaggregation distributions described in the previous section. In this case the M, R and ε(T*) values used are the mean values from deaggregation at the given Sa(T*) level; this is an approximation relative to the use of the full distributions of potential M, R and ε(T*) values, and performing a more exact calculation is possible and important to do in some cases as discussed in detail by Lin (2012).

For each conditioning period and spectral amplitude, 40 recorded ground motions were selected and scaled such that their spectra matched the target mean and standard deviations computed using Eqs. 28.1 and 28.2. Figure 28.1 shows the target spectra and selected ground motions’ spectra for 0.85 and 2.6 s conditioning period s, at Sa amplitudes with 2 % probability of exceedance in 50 years. Ground motions were selected from the PEER NGA database (Chiou et al. 2008). No further constraints were placed on the ground motion selection (e.g., magnitudes and distances) other than limiting scale factors to less than four, with the primary selection focus being on the match of the ground motion spectra to the target spectra. This was done because the structure response parameter of interest in this case is thought to be most closely related to spectral values, and that earthquake magnitude and distance affect this structural response primarily as they relate to spectral values (which are accounted for directly through the Conditional Spectrum ) rather than other ground motion parameters such as duration. Details regarding the ground motion selection algorithm and its implications are provided by Jayaram et al. (2011).

Fig. 28.1
figure 1

Conditional spectra and spectra of selected ground motions for a site at Palo Alto, California, with spectral acceleration at the conditioning period having a 2 % probability of exceedance in 50 years, (a) conditioned on Sa(0.85 s) = 1.2 g, (b) conditioned on Sa(2.6 s) = 0.45 g

Full size image

2.3 Structural Analysis and Risk Assessment

With the selected ground motions (40 motions at each of 10 intensity levels, for a given conditioning period ), dynamic analysis of the structure described above was performed. Results are shown in Fig. 28.2 for the ground motions selected conditioned on two periods, and the fraction of ground motions causing collapse at each conditioning period and Sa level are shown in Fig. 28.3 (in this figure, results from ground motions with a third conditioning period of 5 s are also shown). A collapse fragility curve was obtained using a maximum likelihood approach to fit a lognormal fragility function to those observed fractions of collapse (Baker and Cornell 2005b, Appendix D).

Fig. 28.2
figure 2

Peak Story Drift Ratios from non-collapse dynamic structural analysis, and fitted probability distributions, for ground motions selected to match Conditional Spectra with (a) T* = 0.85 s and (b) T* = 2.6 s

Full size image
Fig. 28.3
figure 3

Observed fractions of analyses causing collapse from ground motions selected to match Conditional Spectra with three conditioning period s, and fitted fragility functions

Full size image

For our risk-based assessment the structural analysis results are combined with the hazard curve for the corresponding conditioning Sa, to compute the annual rate of exceeding a given PSDR level as follows:

$$ \lambda \left( PSDR> y\right)={\displaystyle \underset{x}{\int } P\left( PSDR> y| Sa\left( T^{*}\right)= x\right)| d\lambda \left( Sa\left( T^{*}\right)> x\right)|} $$
(28.3)

where dλ(Sa(T *) > x) is the derivative of the hazard curve for Sa(T*), P(PSDR > y|Sa(T *) = x) is the probability of Peak Story Drift Ratio exceeding y given a ground motion with Sa(T *) = x, and λ(PSDR > y) is the rate of Peak Story Drift Ratio exceeding y. The P(PSDR > y|Sa(T *) = x) term is computed as follows

$$ P\left( PSDR> y| Sa\left( T^{*}\right)\!=\! x\right)\!=\!P(C)+\left(1\!-\! P(C)\right)\left(1-\varPhi \left(\frac{ \ln y-{\mu}_{\ln P SDR}}{\beta_{\ln P SDR}}\right)\right) $$
(28.4)

where P(C) is the probability of collapse given Sa(T *) = x estimated from the collapse fragility function in Fig. 28.3, μ ln PSDR and β ln PSDR are the mean and standard deviation, respectively, of lnPSDR values given Sa(T *) = x in Fig. 28.2, and Φ( ) is the standard normal distribution cumulative distribution function. This approach assumes that all collapse cases exceed y, and fits a lognormal distribution to the non-collapse PSDRs, following procedures proposed elsewhere (e.g., Shome and Cornell 1999).

The calculation in Eq. 28.3 is referred to here as a risk-based assessment, though it is also referred to elsewhere as the first step of the “PEER Integral,” (Cornell and Krawinkler 2000), a “drift hazard” calculation (Krawinkler and Miranda 2004), or a “time-based assessment” (Applied Technology Council 2011). Equation 28.3 was evaluated using the three sets of hazard curves, ground motions and resulting structural responses associated with each of the considered T* values, and the resulting risk assessment results are shown in Fig. 28.4. The predictions of the rates of exceeding a given PSDR are very consistent regardless of the conditioning period .

Fig. 28.4
figure 4

Risk assessment results showing annual rates of exceedance for various Peak Story Drift Ratios, obtained using hazard curves and ground motions with three different conditioning period s

Full size image

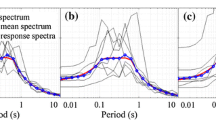
The relative consistency of results in Fig. 28.4 may be surprising at first, so let us examine the data underlying these results more closely. In Fig. 28.5a, b, we see the response spectra of the ground motions selected and scaled to match Sa(2.6 s) and Sa(0.85 s) at the ten amplitudes considered; we see the “pinched” shapes of the spectra at 0.85 and 2.6 s in Fig. 28.5a, b, respectively, at those ten conditioning amplitudes. At other periods, the spectra are more varied, as the amplitudes at other periods have variability even when Sa(T*) is known with certainty. But the careful way in which these ground motions were selected, to maintain proper conditional means and variances, ensures that the distributions of spectra at all periods are still consistent with all known hazard information for the site being considered. It is difficult to see this consistency visually in Fig. 28.5a, b, because there are 40 ground motions at each Sa amplitude, while the real site will have many more low-amplitude ground motions than high-amplitude motions (and Eq. 28.3 captures this by incorporating weights from the hazard curve).

Fig. 28.5
figure 5

(a) Response spectra of ground motions selected using T* = 0.85 s. (b) Response spectra of ground motions selected using T* = 2.6 s. (c) Rate of Sa(2.6 s) > y implied by each of the selected ground motion sets, plus the original ground motion hazard curve for reference. (d) Rate of Sa(5 s) > y implied by each of the selected ground motion sets, plus the original ground motion hazard curve for reference

Full size image

To make a quantitative comparison of the sets of response spectra, the rate of Sa exceeding a given amplitude y at an arbitrary period T, implied by the ground motions selected conditional on Sa(T*), is computing using an equation very similar to Eq. 28.3

$$ \lambda \left( Sa(T)> y\right)={\displaystyle \underset{x}{\int } P\left( Sa(T)> y| Sa\left( T^{*}\right)= x\right)| d\lambda \left( Sa\left( T^{*}\right)> x\right)|} $$
(28.5)

where P(Sa(T) > y|Sa(T *) = x) is the probability that a ground motion in the selected record set to have Sa(T*) = x has an Sa at period T that is greater than y. Here this probability is estimated as simply the fraction of the 40 ground motions with Sa(T*) = x that have Sa(T) > y. The multiplication of these probabilities by the derivative of the hazard curve reweights the results according to the rate of observing ground motions with Sa(T*) = x, as was done in Eq. 28.3.

Figure 28.5c shows the implied rate of Sa(2.6 s) > y for the ground motions in Fig. 28.5a, b, plus comparable ground motions with T* = 5 s. Additionally, the hazard curve for Sa(2.6 s) is plotted, as this is the correct answer from hazard analysis that we are trying to represent using a suite of ground motions. The ground motions selected using T* = 2.6 s have a stepped plot in Fig. 28.5c, due to the ten discrete Sa(2.6 s) amplitudes that were considered when selecting motions. The ground motions with other T* values have smoother curves, but all of the curves are in good general agreement, indicating that even though the other sets of ground motions did not scale ground motions to match Sa(2.6 s), they have the proper distribution of Sa(2.6 s) as specified by the hazard curve at that period. Thus, if Sa(2.6 s) is a good predictor of structural response, then the ground motions selected to match Sa(0.85 s) will still do a good job of capturing the distribution of structural response values that might be observed for the given site and structure considered. A similar plot is shown in Fig. 28.5d for the rate of exceeding Sa(5 s); in this case the ground motions with T* = 5 s have the stepped curve, and the other T* cases are smooth. Again the curves are in relatively good agreement with each other, and with the true ground motion hazard curve.

3 Discussion

In principle, Eq. 28.3 is correct regardless of the value used to quantify intensity, but a few assumptions inherent in the application of this equation place practical constraints on this evaluation. First, Eq. 28.3 assumes that P(PSDR > y|Sa(T *) = x) is not dependent upon other ground motion properties besides the one quantified by the intensity measure, although this is never true for structures other than elastic single-degree-of-freedom systems (Luco and Cornell 2007). Here we have addressed that problem by further accounting for the effect of spectral values at other periods through ground motion selection with Conditional Spectrum targets, such that spectral values at all periods in the selected ground motions are consistent with hazard curves for the site, regardless of the spectral period used for conditioning. Nonetheless, we have only considered spectral values and not other ground motion properties (e.g. velocity pulses not fully captured in the spectral acceleration values, duration, etc.). If non-spectral ground motion parameters were also deemed important for predicting the EDP of interest, the approach above can be generalized to account for those parameters (Bradley 2010).

Another limitation of the approach used here is that Eqs. 28.1 and 28.2 used for computing the target Conditional Spectra are approximate if only a single magnitude and distance value is input, or only a single ground motion prediction model is used, because the calculations that produced the hazard curves use multiple magnitudes, distances and ground motion prediction models. That approximation was reasonable for the cases considered here, but is known to be unreasonable for many other cases. More exact uses of Eqs. 28.1 and 28.2 are available in (Lin et al. 2013), and the impact of this refinement is the subject of more detailed discussion in (Lin 2012).

4 Conclusions

We have presented risk-based assessment results for Peak Story Drift Ratios in a 20-story concrete frame structure located in Palo Alto, California, using a structural model with strength and stiffness deterioration that is believed to reasonably capture the responses up to the point of dynamic-instability collapse. The assessment was performed three times, using ground motions selected and scaled to match Conditional Spectra at three conditioning period s from 0.85 to 5.0 s (i.e., the second-mode structural period up to twice the first-mode period). For each case, the risk-based assessment results were similar. This similarity stems from the fact that the careful record selection ensures that the distributions of response spectra at all periods are consistent with targets specified by hazard analysis, so the distribution of resulting story drifts should also be comparable (to the extent that response spectra describe the relationship between the ground motions and structural responses).

From these results, we observe if the analysis goal is to perform a full “risk assessment” calculation, then one should be able to obtain an accurate result using any conditioning period , as long as careful ground motion selection ensures proper representation of spectral values and other ground motion parameters of interest. Here “proper representation” refers to consistency with the site ground motion hazard curves at all relevant periods, and this is achieved by using the Conditional Spectrum approach to determine target response spectra for the selected ground motions. The reproducibility of the results with varying conditional periods then results from the fact that the ground motion intensity measure used to link the ground motion hazard and the structural response is not an inherent physical part of the seismic reliability problem we are considering; it is only a useful link to decouple the hazard and structural analysis. If this link is maintained carefully then one should get a consistent answer (the correct answer) for the risk assessment in every case. The consistency in risk assessments achieved here is in contrast to some previous speculation on this topic, because this study utilizes the recently developed Conditional Spectrum target for ground motion selection , and uses a newly available algorithm for selecting ground motions to match this target.

Is the choice of conditioning period still important? Choice of a “good” conditioning period does still serve several useful purposes. A good conditioning period helps because the spectral accelerations at the conditioning period will be a good predictor of structural response; this makes any inaccuracies in representing spectral values at other periods have a less severe impact on the resulting calculations. Additionally, use of a good conditioning period reduces the variability in structural responses and thus reduces the number of dynamic analyses that are required to accurately estimate distributions of structural response. Luco and Cornell (2007) referred to these two properties as “sufficiency” and “efficiency,” respectively. We take those concepts further here, acknowledge that there is no intensity measure with perfect efficiency and sufficiency, and so perform careful ground motion selection to compensate for shortcomings that are inherent in any intensity measure.

This document has presented a relatively simple illustration of the concept that hazard consistency in ground motions will lead to consistent risk-based assessment results. This work is part of a larger project on ground motion selection (NIST 2011), and the PhD thesis of Ting Lin (2012) provides a much more extensive set of analyses of this type, including studies of permutations on the target spectrum used, the EDP parameter of interest, and the type of structure being analyzed. Those results provide a more complete picture of the relationship between careful ground motion selection and robust structural response results.