Keywords

1 Introduction

In the last decade particle swarming optimization (PSO) has been applied in a plethora of fields such as social modeling, computer graphics, simulation and animation of natural flocks or swarms, pattern recognition, color image quantization and computational biology [1]. PSO has motivated considerable interest from the natural computing research, where important work has been enforced in the study of its convergence.

Fractional Calculus (FC) is a natural extension of the classical mathematics. Since the beginning of theory of differential and integral calculus, several mathematicians investigated the calculation of noninteger order derivatives and integrals. Nevertheless, the application of FC has been scarce until recently, but the recent scientific advances motivated a renewed interest in this field.

Bearing these ideas in mind, this work uses a fractional derivative to control the convergence rate of the PSO. The article is organized as follows. Section 2 introduces the FC. Section 3 presents the PSO and its working principles. Based on this formulation, Sect. 4 generalizes the PSO to a fractional order. Section 5 presents the results for the PSO with fractional velocity. Finally, Sect. 6 outlines the main conclusions.

2 Introduction to Fractional Calculus

FC goes back to the beginning of the theory of differential calculus. Nevertheless, the application of FC just emerged in the last two decades, due to the progresses in the area of nonlinear and complex systems that revealed subtle relationships with the FC concepts. In the field of dynamics systems theory some work has been carried out, but the proposed models and algorithms are still in a preliminary stage of establishment.

The fundamentals aspects of FC theory are addressed in [2–5]. Concerning FC applications research efforts can be mentioned in the area of viscoelasticity, chaos, fractals, biology, electronics, signal processing, diffusion, wave propagation, modeling, control and irreversibility [6–10].

FC is a branch of mathematical analysis that extends to real, or even complex, numbers the order of the differential and integral operators. Since its foundation, the generalization of the concept of derivative and integral to a non-integer order α has been the subject of distinct approaches. A formulation based on the concept of fractional differential, is the Grünwald–Letnikov definition given by the equation:

$$D^{\alpha}\left[x(t)\right]= \lim_{h\to 0}\left[\frac{1}{h^{\alpha}}\sum\limits_{k=0}^{+\infty} \frac{(-1)^k\Gamma(\alpha+1)x(t-kh)}{\Gamma(k+1)\Gamma(\alpha-k+1)}\right]$$
(1)

where \(\Gamma ()\) is the Euler function.

An important property revealed by expression (1) is that while an integer-order derivative just implies a finite series, the fractional-order derivative requires an infinite number of terms. Therefore, integer derivatives are ‘local’ operators in opposition with fractional derivatives which have, implicitly, a ‘memory’ of all past events.

Often, in discrete time implementations expression (1) is approximated by:

$$D^{\alpha}\left[x(t)\right]= \frac{1}{T^{\alpha}}\sum\limits_{k=0}^{r} \frac{(-1)^k\Gamma(\alpha+1)x(t-kT)}{\Gamma(k+1)\Gamma(\alpha-k+1)}$$
(2)

where T is the sampling period and r is the truncation order.

The \(\mathcal{Z}-\)transform formulation of a derivative of fractional order \(\alpha \in \mathbb{C}\) of the signal x(t), \(D^{\alpha}[x(t)]\), is a ‘direct’ generalization of the classical integer-order scheme yielding, for zero initial conditions:

$$\mathcal{Z}{\left\{{D^{\alpha} {\left[{x(t)} \right]}} \right\}} = \left(\frac{1-z^{-1}}{T}\right)^{\alpha} X(z)$$
(3)

where z is the \(\mathcal{Z}-\)transform variable.

The characteristics revealed by fractional-order models make this mathematical tool well suited to describe phenomena such as irreversibility and chaos because of its inherent memory property. In this line of thought, the propagation of perturbations and the appearance of long-term dynamic phenomena in a population of individuals subjected to an evolutionary process configure a case where FC tools fit adequately [11].

3 Particle Swarm Optimization Algorithm

Evolutionary algorithms have been successfully adopted to solve many complex optimization engineering applications. Together with genetic algorithms, the PSO algorithm, proposed by Kennedy and Eberhart [12], has achieved considerable success in solving optimization problems.

The PSO algorithm was proposed originally in [12]. This optimization technique is inspired in the way swarms behave and its elements move in a synchronized way, both as a defensive tactic and for searching food. An analogy is established between a particle and a swarm element. The particle movement is characterized by two vectors, representing its current position x and velocity v. Since 1995, many techniques were proposed to refine and/or complement the original canonical PSO algorithm, namely by analyzing the tuning parameters [13] and by considering hybridization with other evolutionary techniques [14].

In literature, some work embedding FC and PSO algorithms can be found. Pires et al. [15] studies the fractional dynamics during the evolution of a PSO. Reis et al. [16] propose a PSO, for logic and circuit design, where is implemented a proportional-derivative fitness function to guide the optimization. Pires et al. [17] study the convergence of a PSO with a fractional order velocity.

Algorithm 1 illustrates a standard PSO algorithm. The basic algorithm begins by initializing the swarm randomly in the search space. As it can be seen in the pseudo-code, were t and \(t + 1\) represent two consecutive iterations, the position x of each particle is updated during the iterations by adding a new velocity v term. This velocity is evaluated by summing an increment to the previous velocity value. The increment is a function of two components representing the cognitive and the social knowledge.

The cognitive knowledge of each particle is included by evaluating the difference between its best position found so far b and the current position x. On the other hand, the social knowledge, of each particle, is incorporated through the difference between the best swarm global position achieved so far g and its current position x. The cognitive and the social knowledge factors are multiplied by random uniformly generated terms ϕ 1 and ϕ 2, respectively.

Algorithm 1: Particle swarm optimization

figure a

PSO is a optimization algorithm that proves to be efficient, robust and simple. However, if no care is taken the velocities may attain large values, particularly when particles are far away from local and global bests. Some approaches were carried out in order to eliminate this drawback. Eberhat et al. [18] proposed a clamping function (4) to limit the velocity, through the expression:

$$v_{ij}(t+1)=\left\{\begin{array}{lcl} v_{ij}'(t+1) & \textrm{if} & v_{ij}'(t+1) < V_{\max\, j}\\V_{\max\, j} & \textrm{if} & v_{ij}'(t+1) \geq V_{\max\, j}\end{array}\right.$$
(4)

where \(v_{ij}'(t+1)\) is given by \(v_{ij}'(t+1)=v_{ij}(t)+\phi_1.(b-x)+\phi_2.(g-x)\) for the parameter j of particle i at iteration t + 1.

Later, a constant, the inertia weight, was introduced [13] to control the velocity from exploding (5). The inertia weight ω is very important to ensure convergence behavior over evolution by adopting the equation:

$$v_{t+1}=\omega. v_t+\phi_1.(b-x)+\phi_2.(g-x)$$
(5)

Some empirical and theoretical studies were made to determine the best inertia value [19] in order to obtain better PSO behavior.

Oliveira et al. [20] represent the PSO as a feedback control loop and establishing an analogy between the particle dynamics with a feedback control loop. They present a proportional and integral controller based on particle swarm algorithm, which does not require any parameter to regulate the swarm convergence over time.

4 Fractional PSO

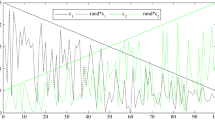
In this section the PSO is modeled through Z block diagram. Additionally, the local unit feedback of x t signal is replaced by a fractional one, represented by the pink block in Fig. 1.

Fig. 1
figure 1

PSO Diagram Block, \(e_{\textrm{l}}\)—local error, \(e_{\textrm{g}}\)—global error

Full size image

The position term b-x is substituted by a fractional version given in expression (5). In fact, considering the first r = 4 terms of the fractional derivative series, the b-x term is replaced by:

$$\begin{aligned} b-x_{t+1}=& b-\bigg[\alpha x_{t}+\frac{\alpha}{2}(1-\alpha)x_{t-1}+\frac{\alpha}{6}(1-\alpha)(2-\alpha)x_{t-2} \\ &+\frac{\alpha}{24}(1-\alpha)(2-\alpha)(3-\alpha)x_{t-3}\bigg] \end{aligned}$$
(6)

Therefore, the expression (5) can be rewritten as:

$$\begin{aligned} v_{t+1}=\;& v_t+\phi_1.\bigg[b-\alpha x_{t}-\frac{\alpha}{2}(1-\alpha)x_{t-1}-\frac{\alpha}{6}(1-\alpha)(2-\alpha)x_{t-2} \\ & -\frac{\alpha}{24}(1-\alpha)(2-\alpha)(3-\alpha)x_{t-3}\bigg]+\phi_2.(g-x_t) \end{aligned}$$
(7)

In the next section, several distinct values of r are tested.

5 Test Functions

This section introduces the optimization functions that are adopted during the tests of PSO with fractional velocity update (9). The objective consists in minimizing several well known functions [19]. These functions have n parameters, \(i=\{1,{\ldots},n\}\) and their global optimum value is \(f^{*}\). The algorithm adopts a real encoding scheme. In this line of thought are considered: (1) Rosenbrock’s valley (also known as Banana function), (2) Drop wave, (3) Easom and (4) Michalewicz’s, represented in the following expressions:

(1) Rosenbrock’s valley function:

$$f_1(x)= \sum\limits_{j=1}^{n-1} 100 \left(x_{i+1}-x_i^2 \right)^2$$
(8)

with \(x_i\in [-2.048,2.048]\), \(i=\{1,{\ldots},4\}\) and \(f^{*}(x)=0.0\).

(2) Drop wave function:

$$f_2(x)=-\frac{1+\cos\left(12\sqrt{x_1^2+x_2^2}\right)}{0.5 \left(x_1^2+x_2^2 \right)+2}$$
(9)

with \(x_i\in [-10,10]\), \(i=\{1,2\}\) and \(f^{*}(x)=-1.0\).

(3) Easom function:

$$f_3(x)=-\cos(x_1)\cos(x_2){\textrm{e}^{-(x_1-\pi)^2-(x_2-\pi)^2}}$$
(10)

with x 1, \(x_2\in [-100,100]\) and \(f^{*}(x)=-1.0\).

(4) Michalewicz’s function:

$$f_4(x)=\sum\limits_{j=1}^n -\sin(x_j)\left[\sin\frac{(j+1)x_j^2}{\pi}\right]^{2~m}$$
(11)

with n = 2, m = 1, \(x_i\in [0,\pi]\), \(i=\{1,2\}\) and \(f^{*}(x)=-1.84\).

6 Simulation Results

To study the influence of the fractional feedback effect in the algorithm, several tests are now developed. A 10–population size PSO is executed during a period of 200 iterations with \(\{\phi_1,\phi_2\}\sim U[0,1]\), where U represents the function that generates numbers with a uniform distribution in the specified range. The fitness evolution of the best global particle is taken as the system output.

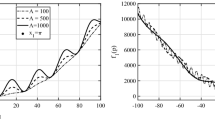
Since PSO is a stochastic algorithm, every time it is executed it leads to a different trajectory convergence. Therefore, a test group of 201 simulation was considered, and the median is taken as the final output, for each value in the set of fractional order \(\alpha=\{0,0.1,{\ldots},2.0\}\). In Figs. 2, 3, 4, and 5 are depicted results for the optimization functions f j , \(j=\{1,{\ldots},4\}\).

Fig. 2
figure 2

Rosenbrock’s function, evolution of the median of best PSO solution versus iteration for \(\alpha=\{0,0.1,\ldots,2.0\}\)

Full size image
Fig. 3
figure 3

Drop wave, evolution of the median of best PSO solution versus iteration for \(\alpha=\{0,0.1,\ldots,2.0\}\)

Full size image
Fig. 4
figure 4

Easom function, evolution of the median of best PSO solution versus iteration for \(\alpha=\{0,\ldots,1\}\)

Full size image
Fig. 5
figure 5

Michalewicz’s function, evolution of the median of best PSO solution versus iteration for \(\alpha=\{0,\ldots,1\}\)

Full size image

It can be verified that the convergence of the algorithm depends directly upon the fractional order α. Normally, values of \(\alpha=1.8\) reaches faster convergence results. One the other hand, for low values of α the algorithm reveals convergence problems. This is due to the local error, \(e_{\textrm{l}}=\phi_1[b-\alpha x_t-0.5\alpha(1-\alpha)x_{t-1}-{\ldots}]\simeq\phi_1 b\), that does not weights adequately the error between the particle actual position and the best position found so far by the particle. Therefore, the algorithm becomes inefficient and the algorithms takes more time to find the optimum.

7 Conclusions

Block diagram and \(\mathcal{Z}-\)transform are engineering tools that lead the designer to a better understanding of the PSO in a control perspective. On the other hand, FC is a mathematical tool that enables an efficient generalization of the PSO algorithm. Bearing these facts in mind, the fractional order position error was analyzed showing that it influences directly the algorithm convergence. Moreover, the results are consistent representing an important step towards understanding the relationship between the system position and the convergence behavior. In conclusion, the FC concepts open new perspectives towards the development of more efficient evolutionary algorithms.