Keywords

Introduction

The need for high-performance parallel processing is increasing because modern engineering and science application problems require many computations with real-time processing. A parallel processing system can connect thousands of processors with their own memory, or even more via an interconnection network enabling inter-processor communication by passing messages among processors through the network. An interconnection network can be depicted with an undirected graph. The most common parameters for evaluating the performance of interconnection networks are degree, connectivity, diameter, network cost, and broadcasting [1, 2].

In an interconnection network, degree (relevant to hardware cost) and diameter (relevant to message transmission time) are correlated. In general, the throughput of an interconnection network is improved with a higher degree because the diameter of the network is increased when its degree is increased. However, a parallel computer design increased the hardware costs of an interconnection network, because of the increased number of processor pins. An interconnection network with a lower degree can reduce hardware costs, but its latency and throughput are degraded because the message transmission time is increased. Due to such characteristics of interconnection networks, the network cost (= degree × diameter) is a typical parameter used to evaluate interconnection network performance [3].

The hypercube is a typical interconnection network topology and is widely used in both research and commercial fields due to its advantages that can easily provide a communication network structure as required in various application areas. The hypercube is node- and edge-symmetric with a simple routing algorithm, maximum fault tolerance, and simple recursive structure. Additionally, it can be easily embedded in various types of existing interconnection networks [4, 5]. However, it has the drawback of increasing network costs associated with the increased degree when the number of nodes increases. To improve this shortcoming, a number of variations of the hypercube have been proposed, such as multiple reduced hypercube [3], twisted cube [6], folded hypercube [7], connected hypercube network [8], and extended hypercube [9]. This paper proposes a new variation of the hypercube that reduces the hypercube degree by approximately half with the same number of nodes: the Half Hypercube (HH). We denote an n-dimensional half hypercube as HH n . To validate the effectiveness of the proposed HH, performance measurement parameters were analyzed, such as connectivity, routing, and diameter.

This paper is organized as follows. Section 2 presents the definition of the proposed HH and discusses its properties, including connectivity. Section 3 proposes and analyzes a simple routing algorithm and the diameter of the HH. Section 4 summarizes and concludes the paper.

Definition and Properties of the Proposed Half Hypercube

The hypercube Q n (n ≥ 2) is defined as an n-dimensional binary cube where the nodes of Q n are all binary n-tuples. Two nodes of Q n are adjacent to each other if and only if their corresponding n-tuples differ in one bit at exactly one position [10]. Q n is an n-regular graph with 2n nodes and its diameter is n. In this paper, \( \bar{S} \) indicates the complement of the binary string \( S\left( { = s_{n} s_{n - 1} \ldots s_{ 1} } \right) \); that is, it is obtained by inverting all the bits in the binary number (inverting 1’s for 0’s and vice versa).

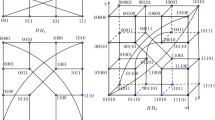
We denote an n-dimensional half hypercube as HH n and represent its node with n binary bits. Let the address of node S in HH n be \( s_{n} s_{n - 1} s_{n - 2} \ldots s_{i} \ldots s_{ 3} s_{ 2} s_{ 1} (n \ge 3) \). There are two types of edge in HH n : the h-edge, which connects node \( S( = s_{n} s_{n - 1} s_{n - 2} \ldots s_{i} \ldots s_{ 3} s_{ 2} s_{ 1} ) \) to a node that has the complement in exactly one h position of the bit string of node \( S( 1\le h \le \lceil n/ 2\rceil ) \), and the sw-edge (i.e., swap-edge), which connects node \( S( = s_{n} s_{n - 1} s_{n - 2} \ldots s_{h} s_{h - 1} \ldots s_{ 3} s_{ 2} s_{ 1} ) \) to a node in which the \( \lfloor n/ 2\rfloor \) leftmost bits of the bit string of S and the \( \lfloor n/ 2\rfloor \) bits on the right-side of S starting from the \( \lfloor n/ 2\rfloor \) bit are swapped \( (h = \lfloor n/ 2\rfloor ) \). For example, when n is even, node \( S( = s_{n} s_{n - 1} s_{n - 2} \ldots s_{ \lfloor n/ 2\rfloor + 1} s_{ \lfloor n/ 2\rfloor } s_{ \lfloor n/ 2\rfloor - 1} s_{ \lfloor n/ 2\rfloor - 2} \ldots s_{ 3} s_{ 2} s_{ 1} ) \) is connected to node \( (s_{ \lfloor n/ 2\rfloor } s_{ \lfloor n/ 2\rfloor - 1} s_{ \lfloor n/ 2\rfloor - 2} \ldots s_{ 3} s_{ 2} s_{ 1} s_{n} s_{n - 1} s_{n - 2} \ldots s_{ \lfloor n/ 2\rfloor + 1} ) \) in which \( (s_{n} s_{n - 1} s_{n - 2} \ldots s_{ \lfloor n/ 2\rfloor + 1} ) \) and \( (s_{ \lfloor n/ 2\rfloor } s_{ \lfloor n/ 2\rfloor - 1} s_{ \lfloor n/ 2\rfloor - 2} \ldots s_{ 3} s_{ 2} s_{ 1} ) \) of S are exchanged. When n is odd, node S is connected to node \( (s_{ \lfloor n/ 2\rfloor } s_{ \lfloor n/ 2\rfloor - 1} s_{ \lfloor n/ 2\rfloor - 2} \ldots s_{ 3} s_{ 2} s_{n} s_{n - 1} s_{n - 2} \ldots s_{ \lfloor n/ 2\rfloor + 1} s_{ 1} ) \) in which \( (s_{n} s_{n - 1} s_{n - 2} \ldots s_{ \lfloor n/ 2\rfloor + 1} ) \) and \( (s_{ \lfloor n/ 2\rfloor } s_{ \lfloor n/ 2\rfloor - 1} s_{ \lfloor n/ 2\rfloor - 2} \ldots s_{ 3} s_{ 2} ) \) of S are swapped. However, if two parts of \( \lfloor n/ 2\rfloor \) bits to exchange in the bit string of node S are the same, the node S connects to node \(s_{n} s_{n - 1} s_{n - 2} \ldots s_{{\left| {n/2} \right|+1}}s_{{\left| {n/2} \right|}}s_{{\left| {n/2 } \right|-1}} s_{{\left| {n/2} \right|-2}} \ldots s_{3} s_{2} s_{1} ,\) which is the one’s complement of the binary number of node S. Figure 1 shows an example of a 5-dimensional half hypercube (HH 5 ). The degree of HH n is \( \lceil n/ 2\rceil + { 1} \), which adds the number of h-edges \( ( 1\le h \le \lceil n/ 2\rceil ) \) and one of the sw-edges. Table 1 presents the degree of HH according to the dimension of HH graphs.

Fig. 1
figure 1

Example of a 5-dimensional half hypercube (HH 5 )

Full size image
Table 1 Degree of HHn according to its dimension
Full size table

Lemma 1

An HH n graph is expanded with recursive structures.

Proof

An HH n graph is constructed with the nodes of two (n-1)-dimensional HH n-1 graphs by adding one sw-edge or h-edge. The address of each node in an HH j graph is represented as j bit strings with binary numbers {0, 1} (i.e., with a binary number of length j). We denote \( HH_{j}^{0} \) when the bit at the j + 1 position of the address of a node (i.e., at the j + 1 position of the bit string of a node) is binary 0, and denote \( HH_{j}^{1} \) when it is binary 1. Let us examine the expansion of HH n by dividing it into two cases: when the dimension n is even and n is odd.

Case 1

When expanded from an odd-dimension (j) to an even-dimension (k), k = j + 1.

Let us construct an HH k graph by connecting a node of \( HH_{j}^{0} \) and a node of \( HH_{j}^{1} \) in HH j (k = j + 1). When expanded from an HH j graph to an HH k graph, the sw-edges in HH j will be replaced with new sw-edges in the expanded HH k graph. A node of \( HH_{j}^{0} \) the address bit of which is binary 1 at the \( n/ 2 \) position, will be connected to a node of \( HH_{j}^{1} \)through an sw-edge in HH k . When the bit is binary 0, the node will be connected to a node of \( HH_{j}^{0} \).

Case 2

When expanded from an even-dimension (k) to an add-dimension (l), l = k + 1.

We construct an HH l graph by connecting a node of \( HH_{k}^{0} \) and a node of \( HH_{k}^{1} \) in HH k . When expanded from an HH k graph to HH l , the sw-edges in HH k will be replaced with new sw-edges in the expanded HH l graph. A node of \( HH_{k}^{0} \), the address bit of which is binary 1 at the \( \lceil n/ 2\rceil \) position, will be connected to a node of \( HH_{k}^{1} \)via an sw-edge in HH l . When the bit is binary 0, the node will be connected to a node of \( HH_{k}^{0} \).

Lemma 2

There exist \( 2^{ \lfloor n/ 2\rfloor } \lceil n/ 2\rceil \) -dimensional hypercube structures in an HH n graph.

Proof

An h-edge of HH n connects node \( S( = s_{n} s_{n - 1} s_{n - 2} \ldots s_{h} \ldots s_{ 3} s_{ 2} s_{ 1} ) \) to a node, the address bit of which is the complement of the bit string of node S at exactly one h position \( ( 1\le h \le \lceil n/ 2\rceil ) \). The h-edge of HH n is equal to the edge of a hypercube. Therefore, the structure of a partial graph constructed from HH n via the h-edge is the same as the structure of a \( \lceil n/ 2\rceil \)-dimensional hypercube. Let us assume that a partial graph that has the same structure as an ⌈n/2⌉-dimensional hypercube is \( HH_{n}^{{\left[ {n/2} \right]}} \) in HH n and refer to it as a cluster. Here, the address of each node in a cluster is \( s_{h} \ldots s_{ 3} s_{ 2} s_{ 1} \). The number of clusters consisting of the HH n graph is \( 2^{ \lfloor n/ 2\rfloor } \) because the number of bit strings that can be configured by the bit string \( s_{n} s_{n - 1} s_{n - 2} \ldots s_{h} \) is \( 2^{ \lfloor n/ 2\rfloor } \) Node (or edge) connectivity is the minimum number of nodes (or edges) that must be removed to disconnect an interconnection network to two or more parts without duplicate nodes. If a given interconnection network remains connected with the removal of any arbitrary k-1 or fewer nodes, but the interconnection network becomes disconnected with the removal of any arbitrary k nodes, then the connectivity of the interconnection network is k. When the degree and node connectivity of a given interconnection network are the same, we say that the interconnection network has maximum fault-tolerance [3]. It has been proven that k (G) ≤  λ (G) ≤  d (G) where the node connectivity, edge connectivity, and degree of interconnection network G are denoted as k (G), λ (G), and d (G), respectively [6, 11]. Through the proving process of k (HH n ) =  λ (HH n ) =  d (HH n ) in Theorem 1, we will demonstrate that the proposed HH n has maximum fault-tolerance.

Theorem 1

The connectivity of \( {{HH}}_{n,\,k} ({{HH}}_{n} ) = \lceil n/ 2\rceil + { 1}(n \ge 3) \).

Proof

Let us prove that HH n remains connected even when n nodes are deleted from HH n . Through Lemma 2, we know that an HH n graph is composed of clusters, and all clusters in HH n are hypercubes and two arbitrary nodes are connected via an sw-edge. Assuming that X is a partial graph of HH n where |X| = n, it will be proven that \( _{k} ({\text{HH}}_{n} ) \ge \lceil n/ 2\rceil + { 1} \) by demonstrating that HH n remains connected even after the removal of X. This will be done by dividing two cases in accordance with the location of X. We denote the HH n in which X is deleted as HH n –X and a node of HH n as S.

Case 1

When X is located in one cluster of HH n :

The degree of each node in a cluster is \( \lceil n/ 2\rceil \). If \( \lceil n/ 2\rceil \) nodes adjacent to an arbitrary node S of the cluster are the same as the nodes to be deleted from X, HH n is divided into two components: an interconnection network HH n –X and a node S. However, all nodes in a cluster are linked to other clusters in HH n via sw-edges, and \( 2^{ \lfloor n/ 2\rfloor } - 1 \) clusters in which X is not located are also connected to other clusters via sw-edges. Therefore, HH n –X is always connected when X is included in only a cluster of HH n .

Case 2

When X is located across two or more clusters of HH n :

As the nodes of X to be deleted are included across two or more clusters of HH n , the number of nodes to be deleted from a cluster is at most \( \lceil {\text{n}}/ 2\rceil - 1 \). However, even if \( \lceil {\text{n}}/ 2\rceil - 1 \) nodes adjacent to an arbitrary node S of a cluster are deleted, the nodes of the cluster in which node S is included remain connected because the degree of a node in a cluster is \( \lceil n/ 2\rceil \). Although the other node to be removed is located in a different cluster, and not in the cluster that includes node S, it is still clear that HH n remains connected. Therefore, \( _{k} ({\text{HH}}_{n} ) \ge \lceil n/ 2\rceil + { 1} \) because HH n always remains connected after removing X from any clusters in HH n and \( _{k} ({\text{HH}}_{n} ) \le \lceil n/ 2\rceil + { 1} \) because the degree of HH n is \( \lceil n/ 2\rceil + { 1} \). Consequently, the connectivity of \( {\text{HH}}_{n,\,k} ({\text{HH}}_{n} ) = \lceil n/ 2\rceil + { 1} \).

Routing Algorithm and Diameter of HH n

This section analyzes a simple routing algorithm and diameter of HH n . We assume that an initial node S is \( s_{n} s_{n - 1} s_{n - 2} \ldots s_{n/2} \ldots s_{ 3} s_{ 2} s_{ 1} \) and a destination node T is \( t_{n} t_{n - 1} t_{n - 2} \ldots t_{n/2} \ldots t_{ 3} t_{ 2} t_{ 1} \). A simple routing algorithm can be considered in two cases depending on whether n is an even or an odd number.

Case 1

When n is an even number

If an initial node \( S( = s_{n} s_{n - 1} s_{n - 2} \ldots s_{n/2} s_{n/2 - 1} \ldots s_{ 3} s_{ 2} s_{ 1} ) \) is presented with two \( \lceil n/ 2\rceil \) bit strings \( A( = s_{n} s_{n - 1} s_{n - 2} \ldots s_{n/2} ) \) and \( B( = s_{n/2 - 1} \ldots s_{ 3} s_{ 2} s_{ 1} ) \), node S can be denoted as AB. In the same way, a destination node \( T( = t_{n} t_{n - 1} t_{n - 2} \ldots t_{n/2} t_{n/2 - 1} \ldots t_{ 3} t_{ 2} t_{ 1} ) \) can be denoted as CD where \( C\left( { = t_{n} t_{n - 1} t_{n - 2} \ldots t_{n/2} } \right) \) and \( D\left( { = t_{n/2 - 1} \ldots t_{ 3} t_{ 2} t_{ 1} } \right) \) (i.e., C is the \( \lceil n/ 2\rceil \) leftmost bits and D is the \( \lceil n/ 2\rceil \) rightmost bits in the bit string of node T).

Simple routing algorithm-even:

  1. (1)

    Convert the bit string of B in node S(= AB) with the bit string C in node T(= CD) using h-edge \( ( 1 { } \le h \le \lceil n/ 2\rceil ) \).

  2. (2)

    Exchange the bit string of \( A \) with that of C in node S(= AC) using sw-edge.

  3. (3)

    Convert the bit string of \( A \) in node \( S( = CA) \) with \( D \) of node \( T( = CD) \) using h-edge.

In Phases (1) and (3), the bit string B is converted with C and A is converted with D using the hypercube routing algorithm.

Corollary 1

When n is even, the length of the shortest path is \( 2\times \lceil n/ 2\rceil + 1= n + 1 \) by the above simple routing algorithm-even.

Case 2

When n is an odd number

Let the initial node be \( S( = s_{n} s_{n - 1} s_{n - 2} \ldots s_{ \lfloor n/ 2\rfloor + 1} s_{ \lfloor n/ 2\rfloor } s_{ \lfloor n/ 2\rfloor - 1} \ldots s_{ 3} s_{ 2} s_{ 1} ) \), the \( \lfloor n/ 2\rfloor \) leftmost bits of the bit string of S be \( A( = s_{n} s_{n - 1} s_{n - 2} \ldots s_{ \lfloor n/ 2\rfloor + 1} ) \) and the \( \lfloor n/ 2\rfloor \) bits on the right-side of S starting from the \( \lfloor n/ 2\rfloor \) bit be \( B( = s_{ \lfloor n/ 2\rfloor } s_{ \lfloor n/ 2\rfloor - 1} \ldots s_{ 3} s_{ 2} ) \). Then, node S can be denoted as (ABs 1 ). In the same way, a destination node \( T( = t_{n} t_{n - 1} t_{n - 2} \ldots t_{ \lfloor n/ 2\rfloor + 1} t_{ \lfloor n/ 2\rfloor } t_{ \lfloor n/ 2\rfloor - 1} \ldots t_{ 3} t_{ 2} t_{ 1} ) \) can be denoted as (CDt 1), where \( C( = t_{n} t_{n - 1} t_{n - 2} \ldots t_{ \lfloor n/ 2\rfloor + 1} ) \) and \( D( = t_{ \lfloor n/ 2\rfloor } t_{ \lfloor n/ 2\rfloor - 1} \ldots t_{ 3} t_{ 2} ) \).

Simple routing algorithm-odd:

  1. (1)

    Convert the bit string of B in node \( S( = ABs_{1} ) \) with the bit string \( C \) in node \( T( = CDt_{ 1} ) \) using h-edge \( ( 1 { } \le h \le \lfloor n/ 2\rfloor ) \).

  2. (2)

    Exchange the bit string of A with that of C in node S(= ACs 1 ) using sw-edge.

  3. (3)

    Convert the bit string of \( As_{1} \) in node \( S( = CAs_{1} ) \) with \( Dt_{ 1} \) of node \( T( = CDt_{ 1} ) \) using h-edge \( \left( { 1 { } \le h \le \lfloor n/ 2\rfloor } \right) \).

In Phases (1) and (3), the bit string B is swapped with C and \( As_{1} \) is swapped with \( Dt_{ 1} \) using the hypercube routing algorithm.

Corollary 2

When n is odd, the length of the shortest path is \( 2\times \lfloor n/ 2\rfloor + 2 \) by the above simple routing algorithm-odd.

Through the proposed simple routing algorithms, we can see an upper bound for the diameter of HH n , thus proving Theorem 2.

Theorem 2

The upper bound on the diameter of HH n is n + 1 when n is even and \( 2\times \lfloor n/ 2\rfloor + 2 \) when n is odd.

Conclusion

This paper proposed a half hypercube interconnection network HH n (a new variation of the hypercube) that reduced the degree by approximately half, n/2, even though it has the same number of nodes as a hypercube. To evaluate the effectiveness of the proposed half hypercube, we analyzed its connectivity and diameter properties. We also analyzed a simple routing algorithm of HH n and presented an upper bound for the diameter of HH n . These results demonstrate that the proposed half hypercube is an appropriate interconnection network for implementation in a large-scale system.