Average Unit Cell in Fourier Space and Its Application to Decagonal Quasicrystals

Abstract

This paper describes a new technique for solving the structure of quasicrystals. The technique is based on transformations between an average unit cell (AUC) and an envelope of diffraction peaks. For centrosymmetric structures like the Penrose tiling, the envelope makes it possible to determine the sign of the phase straight from the diffraction pattern. A Fourier transform of an envelope leads to a distribution of atomic positions within an AUC. Apart from theoretical and modeling aspects of the technique, the paper also presents the results of applying it to the well-known decagonal quasicrystal Al–Ni–Co.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

17.1 Introduction

The most commonly used techniques for recovering the phase of diffraction reflections are Low Density Elimination [12] and Charge Flipping [10]. Their comparison and efficiency in the examination of decagonal quasicrystalline structures were discussed in [4, 5]. The results of such analyses are entry points to a refinement process which uses a structure factor derived for a chosen structure model. The best-known structure model of 2D quasicrystals which proved to be an excellent starting point for the structure refinement of real decagonal quasicrystals is the Penrose tiling [1, 13–15]. Structure factors based on this tiling can operate in a higher-dimensional space—“cut-and-project” [2, 7, 9] method or solely in the physical space: average unit cell (AUC) approach [18]. In this paper, we use the AUC approach and, as the model structure, the Penrose tiling with rhombuses of the edge length equal to one. Based on those two, we developed a new technique for the phase recovery. It is achieved by using “envelope” curves. They allow us to determine the sign of the phase. The technique is still being developed but the initial results obtained on the widely studied alloy Al₇₂Ni₂₀Co₈ [8, 14–16] prove that the method is effective.

The paper is structured as follows: first, we define some basic terms we use in the diffraction analysis based on the average unit cell approach—among them, the structure factor and envelope function. Then, we show how we use the envelope function in the phase retrieval process and the reverse Fourier transform. Finally, we discuss an application of this method to Al₇₂Ni₂₀Co₈ alloy.

17.2 Average Unit Cell Approach

The Reference Grid

is a regular set of points r such that r _i =N _i λ, where N _i is an integer and λ denotes the vector of lengths between two neighboring points in the grid. For a 1D example, we simply have x _i =N _i λ _x . The vector λ defines also the elementary cell of a grid. The reduced coordinate u is the distance of an arbitrary position. For a 1D reference frame X, we have X _j =u _xj +N _xj ⋅λ _x . An average unit cell is a distribution of reduced coordinates P(u). The choice of λ is determined by the diffraction pattern that is studied and is associated with the base vectors of the reciprocal space λ=2π/k ₀, where k ₀ is the length of a chosen base vector.

It is shown [3, 11] that for the Fibonacci chain the average unit cell is non-zero only within a limited space where it assumes a constant value and the distribution becomes uniform. Similarly, in case of the Penrose tiling, the non-zero area of the AUC consists of four pentagonal areas within which the density is constant [17].

The Base Vectors of the Reciprocal Space

define the coordinate system of the reciprocal space. For a 1D grid, we have k=nk ₀+mq ₀, where k ₀ is called the main vector and q ₀ is the modulated vector, n and m are integers, q ₀=k ₀/τ and the value of $\tau =0.5 (1+\sqrt{5})\cong 1.618$.

Structure Factor

We can apply the definitions set above to a derivation of the structure factor:

The sum is over a very large set of points. In the first step of the derivation, we use reduced coordinates written in two reference grids u, v associated with the main and modulated vectors. In the second step, we exchange the sum for an integral over a density function P(u,v) of a 2D AUC.

v(u) Relationship

For both the Fibonacci chain and the Penrose tiling, this function assumes non-zero values only along a line segment defined by the equation v=−τ ²⋅(u−b)+b. For the Fibonacci chain b=0, and for the Penrose tiling b=j⋅λ/5 [6, 18].

Envelope Function

Let’s examine the implication of employing the v(u) relationship to the structure factor. For the Fibonacci chain, we have

$$F(w)=\int P(u)\cdot\exp\mathrm{i}(w\cdot u)\,\mathrm{d}u= \exp\mathrm{i}(-w\cdot u_{0})\cdot\frac{\sin(w\cdot u_{0})}{w\cdot u_{0}} $$

where w=k ₀(n−τ⋅m), u ₀=1/2τ, and the integral is over a uniform distribution limited by (0,u ₀). In general, the structure factor of the Fibonacci chain is a complex function. However, it is possible to cancel out the complex part of the function by introducing a shift in atomic positions Δu. This shift should result in moving the v(u) relationship to one of the symmetry points of the rectangular reference frame (u,v). It can be easily proved that if we choose as the main vector k ₀=2π/(3−τ) and at the same time we shift the whole chain by u ₀, we get

$$F(w)=\cos(m\cdot \pi)\cdot \frac{\sin(w\cdot u_{0})}{w\cdot u_{0}}. $$

Even though this is a special case for the Fibonacci chain and generally, for a freely decorated chain, it is impossible to make this sequence symmetric, the equation obtained above will prove very useful for a demonstration of a technique that allows us to establish the phases of the diffraction peaks for more symmetrical structures, such as decagonal, freely decorated Penrose tilings.

We can relate w to k by combining the definition of τ,v(u) relationship, and q=k/τ. As a result we obtain $w=k-m\sqrt{5}k_{0}$,

$$F(k)=\cos(m\cdot \pi)\cdot \frac{\sin(k-m\sqrt{5}k_{0}\cdot u_{0})}{k-m\sqrt{5}k_{0}\cdot u_{0}}. $$

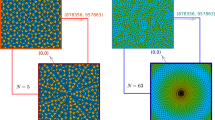
The structure factor can be used not only for the positions of peaks (k=nk ₀+mq ₀) but for any other continuous value of k. In such a case, it is called the envelope function. An envelope connects the tops of peaks that share the same value of m. For other peaks we observe a shift of an envelope by $m\sqrt{5}k_{0}$ (plus a reversion caused by the cosine factor for odd m’s); see Fig. 17.1 (bottom, left).

Fig. 17.1

Fibonacci chain analysis. Top, left: diffraction peaks; top, right: envelopes obtained from the peaks and the model; bottom, left: the diffraction peaks with phases retrieved from the envelops; bottom, right: the result of a Fourier reverse transform of the envelope curve

Note that for m=0 we obtain exactly the same equation as for F(w). This allows us to construct an envelope based on the experimental data. Namely, if we plot the function F(w) for the experimental peaks, the tops of those peaks will approximate the curve of the envelope function; see Fig. 17.1 (top, right).

Obviously, experimental data gives us little indication about the phase. For symmetrical structures, however, the relationship between theoretical envelops and envelops obtained from experimental data allows us to recover the phase. It is so because, firstly, those two types of envelops cross the k-axis at the same points and, secondly, because the phase is constant between two neighboring zeros of the function. After the phase is estimated and we have the model curve of the envelope function, we use the reverse Fourier transform to obtain the distribution of atoms within an AUC; see Fig. 17.1 (bottom, right)

$$P(u)=\int F(w)\cdot \exp\mathrm{i}(-w\cdot u)\,\mathrm{d}w. $$

A very similar reasoning can lead us to the envelope function for the Penrose tiling:

The integral over the pentagonal density functions has a simple closed-form solution. It is provided in [6]. The sum goes over all 4 distributions. The factor in front of the integral is a function of the diffraction peaks indices. An important property of function J is that it returns only integers. Consequently, the whole complex factor containing this function assumes only 5 different values. If, additionally, we take the symmetry into consideration this number reduces to only 3 values. As a result, for a given pair (w _x ,w _y ) we can find three different sets of indices that approximate this pair, and as a result, three different types of envelope functions. Figure 17.2 shows 2D maps of the Penrose tiling envelopes. Their cross-sections are presented in the bottom, right figure. Note that all high peaks belonging to one envelope have the same phase. The reverse Fourier transform over those envelopes gives the pentagonal distributions of atomic positions reduced to an AUC.

Fig. 17.2

Intensity maps of the three types of Penrose tiling envelopes (j=0: top, left; j=1: top, right; j=2: bottom left) and their cross-section along the X-axis (bottom, right)

17.3 Application—Al–Ni–Co Alloy

The technique described in the paper was applied to the widely discussed Al₇₂Ni₂₀Co₈ alloy [8, 14–16]. We used 264 unique reflections. Due to a low number of peaks available, it is not possible to show envelopes as in Fig. 17.2. Instead, we took advantage of an approximate radial symmetry of the envelopes and combined peaks into a radial function F(w _r ), where $w_{r}^{2}=w_{x}^{2}+w_{y}^{2}$. The results for the envelope indexed as j=0 (see Fig. 17.2 for a reference) are presented in Fig. 17.3 where the envelope obtained from the experimental data is compared to the combined envelope of the Penrose tiling. The curve proves that the envelope is present and that its zeros are very close to the zeros of the Penrose tiling envelope. It means we can use Penrose tiling envelopes as a source of the phase sign. After applying the signs to the experimental data, we calculated the initial distribution, and afterwards, we used the LDE algorithm to validate and correct the phase signs. It turned out that out of 264 peaks only 22 required further phase modification. Those were only very low peaks. The final results are presented in Fig. 17.4. The density and the shape of the distributions retrieved are in accordance to other analyses [4, 5, 15].

Fig. 17.3

2D envelopes (j=0) curves aggregated radially. A comparison of the experimental data and the Penrose tiling

Fig. 17.4

Distributions of atomic positions of the Al–Ni–Co alloy obtained as a result of a reverse Fourier transform and the technique described in the paper. Left: small pentagon; right: large pentagon

It is important to point out that those are initial results. There are some challenges to overcome. Firstly, the method assumes centrosymmetric structures. It is able to predict only the sign of the phase. Secondly, well-shaped envelopes appear only for structures that closely resemble the Penrose tiling. Additionally, the amplitudes of very low peaks do not form an envelope of clearly exposed zeros. And only by examining zeroes we can deduce the sign of a group of peaks. Currently, whenever we were uncertain, we used the phase obtained from the Penrose model. Finally, with only a few hundred peaks we were unable to reconstruct the whole envelope. Therefore, here we used only peaks and not continuous curves.

17.4 Conclusions

The paper presents a fast technique for the retrieval of the phase sign straight from the experimental diffraction data. The technique is based on the analysis of the envelope functions. The reverse Fourier transform performed on envelopes results in distributions of atomic positions written in boundaries of an average unit cell. We applied the technique to the experimental data for the Al₇₂Ni₂₀Co₈ alloy and obtained results that are in accordance with the generally accepted view of the structure of this alloy.