Rheology of Polymer Alloys and Blends

Abstract

This chapter presents an overview of some of the important principles and characteristics associated with the rheological behavior of polymer blends. Initially, the chapter reports the observations and the scientific laws that illustrate and govern the rheological behavior of classical suspensions and emulsions of simple non-polymeric liquids. It is indicated that one of the main characteristics that differentiates the rheological behavior of polymer blends from that of simpler liquids is the viscoelastic nature of polymers and their blends. The discussion also points out the relationship between blend morphology and rheology and the importance of surface energy effects, such as interparticle and interfacial interactions. The general rheological characteristics of miscible polymer systems are considered. However, since the majority of polymers are immiscible, the rheological behavior of immiscible polymer blends is considered in more detail, with allowance for both thermodynamic and morphological factors. The influence of flow on morphology, as in phase separation, drop deformation, breakup, and fiber formation are discussed. Both viscous and viscoelastic characteristics of blend behavior are described, under the influence of shear and elongational flow fields. Various examples are presented, based on the study of rheological behavior of blends in both rheological testing devices (parallel plate, rotational, steady state, oscillatory, capillary, elongational, etc.) and processing equipment (extruders, mixers, molds, dies, etc.). In many cases, the observed rheological behavior is compared to the predictions of theoretical, computational, or empirical models.

Leszek A. Utracki: deceased.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

1.1 Rheology of Multiphase Systems

The rheology of multiphase systems is an extension of the general rheological dependencies observed for single component fluids. Obviously, the basic definitions of rheological functions, e.g., viscosity, η, dynamic shear moduli, G′ and G″, dynamic shear compliance, J′ and J″, etc., are identical. However, owing to the numerous influences, viz., concentration, morphology, flow geometry, time scale, type of flow field, thermodynamic interactions between the phases, and many others, more complex relationships prevail between the measured rheological functions of multiphase system and the intrinsic physical properties of the constituent fluids.

Rheological measurements in multiphase systems should be designed so that the length scale of flow is significantly larger than the size of the flow element. This makes it possible to treat the multiphase system as being homogeneous, having an average, “specific” rheological behavior. For example, Brenner (1970) showed that magnitude of relative viscosity, η_r, of diluted spherical suspensions, measured in capillary flows, depends on the (d/D)² factor, where d is the sphere diameter and D is the diameter of the capillary – for D ≅ 10d, the error in η_r, was 1 %. Thus, if 1 % error is the acceptable limit, the size of the dispersion should be at least 10 times smaller than the characteristic dimension of the measuring device, viz., radius of a capillary in capillary viscometers, distance between stationary and rotating cylinders or plates in, respectively, the Couette or Weissenberg rheometer, etc. However, for many systems of industrial interest, the data are usually generated with a smaller factor, mainly for comparative purposes.

Another aspect of multiphase rheometry is related to the interrelations between the flow field and system morphology. In the present context, the term “morphology” will refer to the overall physical structure and/or arrangement of the components, usually described as a dispersed phase (particles or domains), co-continuous lamellae, fibrils, spherulites, etc. Furthermore, multiphase morphology deals with the distribution and orientation of the phases, the interfacial area, the volume of the interphase, etc. Flow may induce modifications of morphology, such as concentration gradients and orientation of domains.

Three types of flow are mainly used in rheological measurements: steady-state shearing, dynamic shearing, and elongation (Table 7.1). The three can be classified according to the strain, γ, vorticity, as well as uniformity of stress, σ, and strain within the measuring space.

Table 7.1 Characteristics of flow fields

Steady-state flows have a strong influence on the morphology, whereas dynamic flows have small influence. Extensional flows are characterized by uniform deformation with no vorticity; thus they are the most effective in changing the morphology and orientation of the system.

The rheological functions must be volume averaged (Hashin 1964). The averaged quantities are sometimes known as bulk quantities. For example, the bulk rate of strain tensor, $\left\langle {\dot{\upgamma}}_{ij}\right\rangle$, is expressed as

$$ \left\langle {\gamma}_{ij}\right\rangle =\frac{1}{2}\left(\left\langle \frac{\partial {v}_i}{\partial {x}_j}\right\rangle +\left\langle \frac{\partial {v}_{{}_j}}{\partial {x}_{{}_i}}\right\rangle \right)=\frac{1}{\Delta V}{\displaystyle \underset{\Delta \mathrm{v}}{\int }{\dot{\gamma}}_{ij}} dV $$

(7.1)

where $\left\langle \frac{\partial {v}_i}{\partial {x}_j}\right\rangle =\frac{1}{\Delta V}{\displaystyle \underset{\Delta V}{\int}\frac{\partial {v}_i}{\partial {x}_j}} dV$

The stress tensor, 〈σ_ij〉, in multiphase systems, is given by

$$ \left\langle {\sigma}_{ij}\right\rangle =-p{\delta}_{ij}+2{\eta}_0\left\langle {\dot{\gamma}}_{ij}\right\rangle +\frac{1}{\Delta V}{\displaystyle \sum \left({S}_{ij}-{x}_i{F}_j\right)} $$

(7.2)

In Eqs. 7.1 and 7.2, v_i is local velocity, x_i is local coordinate, ΔV is an elementary volume, p is pressure, δ_ij is unit tensor, η_o is viscosity of the continuous phase, while S_ij and F_i represent hydrodynamic and non-hydrodynamic forces acting on a particle. These two functionals are usually coupled, as the thermodynamic interactions affect the hydrodynamic forces and vice versa.

The first two terms on the right-hand side (rhs) of Eq. 7.2 are identical to those for a homogeneous fluid. For a multiphase system, they represent the stress tensor of the matrix liquid, while the third term describes the perturbing influences of the dispersed phase (Batchelor 1974, 1977). Owing to difficulties in deriving exact forms of the S_ij and F_i functions in the full range of concentrations, Eq. 7.2 is usually written as a power series in volume fraction, ϕ, of the suspended particles.

The rheological behavior of multiphase systems within the linear, dilute region (ϕ < 0.05) is relatively well described. For example, for dilute suspensions of spherical particles in Newtonian liquids, Eq. 7.2 reduces to Einstein’s formula for the relative viscosity, η_r:

$$ \begin{array}{l}\left\langle {\sigma}_{ij}\right\rangle =-p{\delta}_{ij}+2{\eta}_0\left[1+\left(5/2\right)\phi \right]{\dot{\gamma}}_{ij}\hfill \\ {}\mathrm{or}\ {\eta}_r=1+\left(5/2\right)\phi \hfill \end{array} $$

(7.3)

Equation 7.2 has been also solved for dilute suspension of anisometric particles (Hinch and Leal 1972), elastic spheres (Goddard and Miller 1967; Roscoe 1967), and emulsions (Oldroyd 1953, 1955; Barthès-Biesel and Chhim 1981). These works were reviewed by Barthès-Biesel (1988).

In the higher concentration range, where particle–particle interactions must be taken into account, Eq. 7.2 is often approximated by a second-order polynomial. However, even for hard-sphere suspensions, the theoretical extension of Eq. 7.3 has been found difficult:

$$ {\eta}_r=1+\left(5/2\right)\phi +K{\phi}^2+O\left({\phi}^3\right) $$

(7.4)

where the second-order coefficient was calculated as K = 5.2–7.6. Such theoretical predictions should be compared with experimental results. Thomas (1965) compiled relative viscosity data, η_r versus ϕ, measured in 16 laboratories for different types of hard-sphere suspensions, e.g., pollen in water, steel balls in oil, etc. After correcting the data (e.g., for the immobilized adsorbed layer of the suspending liquid), the results superimposed and were fitted to the following relation (valid within the experimentally explored range of concentration, ϕ ≤ 0.6):

$$ {\eta}_r=1+\left(5/2\right)\phi +10.05{\phi}^2+0.00273\kern0.4em \exp \left\{16.6\phi \right\} $$

(7.5)

Allowance for the last term in Eq. 7.5 yields K = 10.43 as the second-order coefficient of Eq. 7.4.

Owing to difficulties in deriving general constitutive equations for multiphase systems, rheologists had to resort to simplified theoretical or semiempirical dependencies derived for specific types of rheological tests and/or for specific multiphase systems. These, experimentally well-established relations, constitute the basic tools for the interpretation of rheological data for multiphase systems. They will be discussed in the following parts of the text.

1.2 Basic Concepts of Polymer Blends

The following standard definitions will be used (Utracki 1989a, 1991a; see also Nomenclature in Chap. 1, “Polymer Blends: Introduction” of this handbook).

1.2.1 Definitions

• (a) Polymer blend is a mixture of two or more polymers and/or copolymers, terpolymers, etc., containing at least 2 wt% of the dispersed phase.

• (b) Miscible blend is a blend with domain size comparable to the dimension of a macromolecular statistical segment, or in other words, whose free energy of mixing is negative, ΔG_m < 0, and its second derivative of concentration with volume, is positive: ${\partial}^2{\Delta \mathrm{G}}_{\mathrm{m}}/\partial {\upphi}^2>0$. Usually, miscibility is restricted to a relatively narrow range of independent variables, viz., molecular weight, composition, temperature, pressure, etc. Thus, immiscibility dominates.

• (c) Polymer alloy is an otherwise immiscible blend, which is compatibilized, with modified interphase and morphology.

Alloying involves several operations that must result in blends showing stable and reproducible properties. These processes comprise compatibilization, mixing, and stabilization. Compatibilization may be accomplished either by addition of a compatibilizer or by reactive processing. Its role is to facilitate dispersion, stabilization of the morphology, and enhancement of the interaction between phases in the solid state. Commercial alloys may comprise up to six polymeric ingredients. Development of such an alloy is complex, requiring knowledge of thermodynamics, rheology, and processing and their influences on morphology, thus performance.

If the rheology of suspensions and emulsions is difficult to describe theoretically and to determine experimentally, the difficulties increase substantially in the case of polymer blends. For example, both phases in polymer blends are likely to be viscoelastic, the viscosity ratio varies over a wide range, and morphology can be very complex. As a guide to characterization of the rheology of blends, it is useful to refer to the behavior of simpler systems, i.e., models that can offer important insight. The following systems (Table 7.2) are considered commonly. They will be treated in the following discussion.

Table 7.2 Rheological models for miscible and immiscible blends

1.2.2 Phase Co-continuity

When a small quantity of one polymer is intimately mixed with another polymer, the resulting system is a blend composed of a matrix (the major component) and the dispersed phase (the minor component). When the concentration of the dispersed phase is increased, the morphology may change from a discontinuous dispersion of nearly spherical drops to progressively interconnected drops, then rods, fibers, and sheets. At a certain concentration, labeled as the phase inversion volume fraction, ϕ_I, the distinction between the dispersed and matrix phases vanishes – the system morphology becomes co-continuous. Phase co-continuity is one of the most important aspects of blend morphology (Lyngaae-Jørgensen et al. 1999).

Since the morphology is strongly affected by large strain flow, it is expected that the method of specimen preparation influences the co-continuity. Both the phase inversion concentration and stability of the co-continuous phase structure depend on the strain and thermal history.

It has been reported that the onset of co-continuity occurs at an average volume fraction, ϕ_onset = 0.19 ± 0.09. In many branches of physics, the concept of percolation has been found useful. For example, when the concentration of conductive spheres in nonconductive medium exceeds the percolation threshold volume fraction, ϕ_perc, there is a sudden increase of electrical conductivity. For the three-dimensional case, 3D, theory predicts that ϕ_perc = 0.156, while for 1D it is ϕ_perc = 0.019. It has been postulated that the observed changes of morphology in polymer blends, when co-continuity occurs, belong to the group of percolation phenomena (Lyngaae-Jørgensen and Utracki 1991). Figure 7.1 depicts the variation of phase co-continuity in blends of high-density polyethylene with polystyrene, HDPE/PS. The data (obtained by selective extraction of the matrix phase) indicate that the onset of phase co-continuity occurred at ϕ_1perc = 0.16 and ϕ_2perc = 0.15, whereas ϕ_I = 0.64.

Fig. 7.1

For immiscible blends the onset of phase co-continuity should coincide with the percolation threshold. Theoretically, ϕ_perc = 0.156 for 3D flow of immiscible system. Experimentally, ϕ_2perc = 0.19 ± 0.09 was found (Lyngaae-Jørgensen and Utracki 1991)

Co-continuity contributes to synergism of properties, e.g., advantageous combination of high modulus and high impact strength in commercial blends. Therefore, it is of interest to determine the composition at which co-continuity can be formed. Practically, the breadth of the co-continuity composition range depends on the experimental concentration step size used during the selective extraction tests. The following simple equation was proposed to relate the phase inversion composition to volume fractions and viscosity ratio:

$$ \begin{array}{l}{\phi}_{I1}/{\phi}_{I2}={\eta}_1/{\eta}_2\equiv \lambda \kern0.75em \mathrm{or}\kern0.75em {\phi}_{I2}={\left(1+\lambda \right)}^{-1}\\ {}{\phi}_{I2}={\left(1+F\left(\lambda \right)\lambda \right)}^{-1}\end{array} $$

(7.6)

where

$$ F\left(\lambda \right)=1+2.25 \log \lambda +1.81{\left( \log \lambda \right)}^2 $$

(7.7)

Note that ϕ_I1 = 1 − ϕ_I2 and ϕ_I1 and ϕ_I2 are the volume fractions of liquids 1 and 2, respectively, at the phase inversion. Equation 7.6 is empirical, proposed by Paul and Barlow (1980) as a generalization of the experimental observations reported by Avgeropoulos et al. (1976). Equation 7.7 was derived from the filament instability equation by Metelkin and Blekht (1984). These relations are applicable to systems prepared at low stresses; thus in these equations, the viscosity ratio, λ, should correspond not to the ratio of the zero-shear viscosities, but to its value at the shear stress used to prepare the blends. The relations were found to describe the phase inversion for systems with nearly equal polymer viscosities, where λ → 1. As the viscosity ratio increases, these equations predict more rapid change of ϕ_I2.

To derive a more general relation for the phase inversion concentration, one may start by computing $\upeta \left(\mathrm{A}\right)={\upeta}_{\mathrm{B}}^{\mathrm{o}}{\upeta}_{\mathrm{r}}\left({\mathtt{\phi}}_{\mathrm{A}}\right)$ and $\upeta \left(\mathrm{B}\right)={\upeta}_{\mathrm{A}}^{\mathrm{o}}{\upeta}_{\mathrm{r}}\left({\mathtt{\phi}}_{\mathrm{B}}\right)$, where η_r is the relative viscosity. The latter dependence can be expressed as (Krieger and Dougherty 1959)

$$ {\eta}_r={\left[1-\left(\phi /{\phi}_m\right)\right]}^{-\left[\eta \right]{\phi}_m} $$

(7.8)

In Eq. 7.8, ϕ_m is the maximum packing volume fraction, and [η] is the intrinsic viscosity. The computed curves are shown in Fig. 7.2. To calculate these dependencies, ϕ_m = 0.8 and [η] = 2 were assumed. The six points of intersection represent the iso-viscous conditions for dispersion of liquid 1 in 2 and liquid 2 in 1, or in other words, the conditions for phase inversion.

Fig. 7.2

Concentration dependence of emulsion viscosity. Solid line represents η = η₁(ϕ₂) while the other lines the same dependence for η = η₂•η_r(ϕ₁). To calculate these dependencies [η] = 2 and ϕ_m = 0.8 were assumed. The intercepts correspond to the iso-viscous conditions defining the phase inversion concentration, ϕ_2I = 1 − ϕ_1I (Utracki 1991)

Based on Eq. 7.8, the iso-viscous point can be expressed as

$$ \lambda ={\left[\left({\phi}_m-{\phi}_{2I}\right)/\left({\phi}_m-{\phi}_{1I}\right)\right]}^{\left[\eta \right]{\phi}_m};\kern1em \mathrm{where}\kern1em {\phi}_m=1-{\phi}_{perc} $$

(7.9)

Equation 7.9 can be expanded into MacLaurin’s series, then truncated after the second term to give a simplified version, valid within the range −1 < ϕ_Ii/ϕ_m < 1:

$$ {\phi}_{I2}=\left[1-\left( \log \lambda \right)/\left[\eta \right]\right]/2 $$

(7.10)

Figure 7.3 shows the experimental dependence of λ on ϕ_2I for thermoplastic polymer blends. The horizontal and vertical lines represent the conditions between which the phase inversion took place. The straight line represents Eq. 7.10. For most polymer blends the values of parameters in Eq. 7.9: [η] ≅ 1.9; ϕ_m ≅ 1 − ϕ_perc = 0.84 provide good approximation.

Fig. 7.3

Experimental ϕ_2I versus λ dependence for mechanically prepared thermoplastics blends. The dotted, solid, and broken lines represent Eq. 7.6, 7.9, and Eq. 7.10, respectively; the values: [η] = 1.9 and ϕ_m = 0.84 were used (Utracki 1991)

It should be noted that the steady-state viscosity ratio should be taken at a constant stress (not deformation rate). The “sharpness” of the phase inversion peak depends on the distribution of stresses within the mixing device, as well as on the absolute magnitude of polymer viscosity – the wider the distribution of stresses and/or the higher the viscosity, the wider the range of concentrations at which the phase inversion takes place. Since many experiments are conducted using an internal mixer known to possess a wide range of flow conditions, instead of a single point, usually a range of concentrations for the phase co-continuity has been reported (see Fig. 7.3).

Another relation was proposed for predicting the phase inversion concentration. It assumes that, at the phase inversion, the morphology of both phases is fibrillar and that the rate of fiber disintegration is the same for both components (Metelkin and Blekht 1984). The validity of the model is limited to viscosity ratios ranging from 0.25 to 4 (Luciani 1993, 1996):

$$ \lambda \equiv {\eta}_1/{\eta}_2=\left[{\Omega}_2\left(\Lambda, \lambda \right)/{\Omega}_1\left(\Lambda, \lambda \right)\right]\left({R}_{0,1}/{R}_{0,2}\right)=\left[\Omega \left({\eta}_1/{\eta}_2\right)/\Omega \left({\eta}_2/{\eta}_1\right)\right]{\left({\phi}_1/{\phi}_2\right)}^{1/2} $$

(7.11)

The significance of the function Ω(Λ, λ) will be discussed in the Sect. 7.3.1.2, dedicated to emulsion microrheology. Steinmann et al. suggested that, at the phase inversion point, the shape relaxation times of domains of the components meet at a maximum (Steinmann et al. 2002).

Since these models do not always completely agree with phase inversion compositions found experimentally, melt elasticity effects were examined to verify if the observed deviations could be attributed to elasticity effects. A model was proposed, using the storage moduli and loss tangent ratios instead of viscosity ratios in Eq. 7.6 (Table 7.3) (Bourry and Favis 1998). Based on their results, the more elastic component tends to encapsulate the less elastic one. Therefore, the elastic contribution of the blends was found to be an important factor in determination of co-continuity.

Table 7.3 Summary of some available semiempirical phase inversion models

The validity of Cox–Merz rule should be verified by measuring G′ and tan δ at frequency ω corresponding to the shear rate γ_p. The use of the ratio of storage moduli for the experimental data evaluated at a constant matrix shear stress (Sarazin and Favis 2003; Shahbikian et al. 2011) and the loss tangent ratio for the data obtained at a constant shear rate (Shahbikian et al. 2011; Steinmann et al. 2001) yields better agreement with the predictions of the Bourry and Favis model.

It should be noted that phase inversion prediction models focus on only a single composition, whereas in reality, co-continuous structures are observed over a composition range. Considering the definition of co-continuous structure and equations based on the percolation theory, a model was proposed to correlate a continuity index (Φ _I ) with the volume fraction at onset of co-continuity (ϕ _cr ) (see Table 7.3) (Lyngaae-Jorgensen et al. 1999). Numerical simulation predicted ϕ _cr to be about 0.2 for classical percolation in three-dimensional systems (Dietrich and Amnon 1994; Potschke and Paul 2003).

The co-continuous structure and the final rheological properties of an immiscible polymer blend are generally controlled by not only the viscoelastic and interfacial properties of the constituent polymers but also by the processing parameters. For example, the effect of plasticizer on co-continuity development in blends based on polypropylene and ethylene-propylene-diene-terpolymer (PP/EPDM), at various compositions, was studied using solvent extraction. The results showed more rapid percolation of the elastomeric component in the presence of plasticizer. However, the same fully co-continuous composition range was maintained, as for the non-plasticized counterparts (Shahbikian et al. 2011). It was also shown that the presence of nanoclay narrows the co-continuity composition range for non-plasticized thermoplastic elastomeric materials (TPEs) based on polypropylene and ethylene-propylene-diene-terpolymer and influences their symmetry. This effect was more pronounced in intercalated nanocomposites than in partially exfoliated nanocomposites with improved clay dispersion. It seems that the smaller, well-dispersed particles interfere less with thermoplastic phase continuity (Mirzadeh et al. 2010). A blend of polyamide 6 (PA6) and a co-polyester of polylactide (BioFlex) was studied using scanning electron microscopy (SEM) and dynamic rheological measurements (Kucharczyk et al. 2012). SEM showed the formation of co-continuity for the blends containing 50–60 wt% of BioFlex. Rheological measurements and solvent extraction showed a broader co-continuity interval, even for blends with over 25 wt% BioFlex. All methods indicated maximum co-continuity at 60 wt% BioFlex. The best fit of experimental data was for the model including the contribution of elasticity to interfacial tension (Bourry and Favis 1998; Fig. 7.4).

Fig. 7.4

Co-continuity index versus BioFlex concentration (Kucharczyk et al. 2012)

1.2.3 The Interphase

Lattice theory predicts that the density profile across the interface follows the exponential decay function (Helfand and Tagami 1971, 1972):

$$ \begin{array}{l}\rho /{\rho}_o={y}^2/\left(1+{y}^2\right)\\ {}\mathrm{where}\kern1.25em y\equiv \exp \left\{{\left(6{\chi}_{AB}\right)}^{1/2}\left(x/b\right)\right\}\end{array} $$

(7.12)

In Eq. 7.12, χ_AB is the thermodynamic binary interaction between polymers A and B, and b is a lattice parameter. The dependence is shown in Fig. 7.5. The intercept of the tangential line at the place of the steepest decline (or incline for the other component) defines thickness of the interphase, Δl.

Fig. 7.5

Theoretical representation of the interface, with the definition of the interphase thickness; χ and b are, respectively, the binary interaction and the lattice parameters (Helfand and Tagami 1971)

The lattice theory of the interface predicts that there is a reciprocity between the interfacial tension coefficient and the interfacial thickness (Helfand and Sapse 1975):

$$ \begin{array}{l}{\nu}_{12}={k}_BT{a}^{-1}{\left(m{\chi}_{AB}\right)}^{1/2}\kern1em \mathrm{and}\kern1em \Delta l=2{\left(m/{\chi}_{AB}\right)}^{1/2}\\ {}\therefore \Delta \lambda \cdot {\nu}_{12}=2m{k}_BT/a\end{array} $$

(7.13)

where a, b, and m are lattice parameters. Notice that according to this theory, the product, ν ₁₂Δl, is independent of the thermodynamic binary interaction parameter, χ _AΒ . The theory leads to the conclusions that (i) surface free energy is proportional to the square root of χ _AΒ , (ii) the chain ends of both polymers concentrate at the interface, (iii) any small molecular weight third component will be repulsed to the interface, and (iv) interfacial tension coefficient increases with molecular weight to an asymptotic value: ν₁₂ = ν _∞ − a_oM ^{− 2/3}_n . These conclusions were found to offer good guidance for development of compatibilization strategies.

There are several other theories of the interface, some of which lead to quantitatively different results (Ajji and Utracki 1996, 1997). For example, Noolandi (1984) considered a binary system compatibilized by addition of a block copolymer. For χ_AΒN_cϕ_p ≤ 2 he derived:

$$ \begin{array}{l}{\nu}_{12}={\nu}_{o\Big|}+\Delta L{\phi}_c\left\{{\chi}_{AB}{\phi}_p/2+\left(1/{N}_c\right)\left[1- \exp \left\{{\chi}_{AB}{N}_c{\phi}_p/2\right\}\right]\right\}\\ {}\therefore \kern1em {\nu}_{12}\cong {\nu}_o-{a}_o\Delta L{\phi}_c+O\left({\phi}_c^2\right)\end{array} $$

(7.14)

where a_o is a numerical parameter, while ϕ_c, ϕ_p, and N_c are, respectively, volume fraction of copolymer, of polymer, and degree of polymerization of the copolymer. A semiempirical dependence of the interfacial tension coefficient on compatibilizer concentration can be derived from an analogy to titration of an emulsion with surfactants (Utracki 1992):

$$ \begin{array}{l}{\nu}_{12}=\left(\phi {\nu}_{\mathrm{CMC}}+{\phi}_{\mathrm{mean}}{\nu}_o\right)/\left(\phi +{\phi}_{\mathrm{mean}}\right)\\ {}\mathrm{where};\\ {}{\nu}_{\mathrm{CMC}}={\nu}_{12}\left({\phi}_c= CMC\right)\\ {}{\phi}_{\mathrm{mean}}=\left({\nu}_{\mathrm{CMC}}+{\nu}_o\right)/2\end{array} $$

(7.15)

where ν _o is the initial interfacial tension coefficient at zero concentration of copolymer, ν_CMC is the interfacial tension at saturation of the interface, and ϕ is the copolymer concentration. Eq. 7.15 adequately described the interfacial tension coefficient in the system polystyrene/polybutadiene compatibilized by addition of styrene-butadiene block copolymer; see Fig. 7.6 (Anastasiadis et al. 1988, 1989).

Fig. 7.6

Interfacial tension coefficient versus concentration of compatibilizer for polystyrene blends with polybutadiene, compatibilized with styrene-butadiene block copolymer. Data points (Anastasiadis and Koberstein 1988), line computed from Eq. 7.15

Recently an exponential decay relation was proposed (Tang and Huang 1994):

$$ {\nu}_{12}={\nu}_{CMC}+\left({\nu}_o-{\nu}_{CMC}\right) \exp \left\{- K\phi \right\} $$

(7.16)

where K is a parameter – from Eq. 7.14, its value should be proportional to K ∝ χ _AB N _c .

There have been several efforts to provide means for computation of the interfacial tension coefficient from characteristic parameters of the two fluids (Luciani et al. 1996). The most interesting relation was that found between the interfacial tension coefficient and the solubility parameter contributions that are calculable from the group contributions. The relation makes it possible to estimate the interfacial tension coefficient from the unit structure of macromolecules at any temperature. The correlation between the experimental and calculated data for 46 polymer blends were found to be good – the correlation coefficient R = 0.815 – especially when the computational and experimental errors are taken into account.

There are several methods for measuring the interfacial tension coefficient for low-viscosity liquids, e.g., spherical shape recovery after slight deformation, liquid thread breakup, rotating bubble or drop, pendant drop, sessile bubble or drop, du Nuouy ring, or light scattering. For high-viscosity polymeric melts, they can be used with decreasing reliability. The most recent and highly successful method involves spherical shape recovery of a drop deformed by about 15 % either in shear or (preferably) in elongation. Since the drop can be repetitively deformed and its shape recovery follows, this method is the only one that makes it possible to follow the time evolution of the interfacial tension coefficient. Furthermore, the method also makes it possible to examine whether, for a given polymer pair, the interfacial energy is symmetrical, i.e., if ν_αβ = ν_βα (Luciani et al. 1996).

There are fewer methods available to measure the interphase thickness, e.g., ellipsometry, microscopy, and scattering. For example, Ville et al. investigated the interphase in polyethylene (PE)/polyamide (PA) blends with nodular morphology, filled with modified montmorillonite, using morphological and rheological experimental techniques (Ville et al. 2012). The average interphase thickness was determined at several points (from more than 200 local interphase thickness measurements) by using an image analysis software. It was shown that the average interphase thickness increased with clay fraction, from about 7 nm at 1 % clay to about 20 nm at 4 % clay, which was expected since clay particles were localized exclusively at the interphase (Huitric et al. 2009; Khatua et al. 2004). However, based on rheological characterization, which showed not very long dominant relaxation times (nodule form relaxation time and interphase relaxation time), Ville et al. mentioned that using microscopy method to characterize the interphase is certainly insufficient due to the presence of a continuous rigid nanocomposite shell that misrepresents the physical reality of the interphase in these systems (Ville et al. 2012).

A summary of the measured Δl is given in Table 7.4. The temperature dependence of Δl in PMMA/SAN and PMMA/PS blends is presented in Fig. 7.7.

Table 7.4 Interphase thickness

Fig. 7.7

Interphase thickness versus temperature for polymethylmethacrylate blends with (from top) styrene-acrylonitrile copolymer and polystyrene (Kressler et al. 1993)

2 Rheological Models for Miscible Blends

By definition, miscible polymer blends are single-phase mixtures. Miscibility depends on the molecular weight, concentration, temperature, pressure, deformation rate, etc. Flow of these systems can be compared to that of solutions of low molecular weight, miscible components, or to flow of mixtures of polymeric fractions. Both models are far from perfect, but they serve to illustrate the basic behavior of miscible systems. In the first case one can learn about the effects of the thermodynamic interactions between chemically different components on the flow behavior. In the second case, it is the effect of molecular weight and molecular weight distribution that can be observed.

2.1 Solutions

For solutions (Glasstone et al. 1941):

$$ \ln \left[V{\eta}_0\right]={\displaystyle \sum_i{x}_i \ln}\left[{V}_i{\eta}_{0i}\right]-\underset{i}{\Pi}{x}_i\Delta {H}_m/2.45 RT $$

(7.17)

where V is the specific volume and x_i is the mole fraction. For miscible blends, ΔH_m < 0 and the above relations predict a positive deviation from the log-additivity rule, PDB. The latter rule, the log-additivity, was formulated by Arrhenius (1887):

$$ \ln {\eta}_0={\displaystyle \sum_i{x}_i \ln }\ {\eta}_{0i}+ \ln {\eta}^E $$

(7.18)

with the excess viscosity term, 1n η^E → 0.

There are several other blending rules for solution viscosity, e.g., (McAllister 1960):

$$ \begin{array}{c} \ln {\eta}_{k,b}={x}_1^3 \ln {\eta}_{k,1}+{x}_2^3 \ln {\eta}_{k,2}+3{x}_1^2{x}_2 \ln {\eta}_{k,12}\\ {}+3{x}_1{x}_2^2 \ln {\eta}_{k,21}+3{x}_1^2{x}_2 \ln \left[\left(2{M}_1+{M}_2\right)/3\right]\\ {}+3{x}_1{x}_2^2 \ln \left[\left({M}_1+2{M}_2\right)/3\right]+{x}_1^3 \ln {M}_1\\ {}+{x}_2^3 \ln {M}_2- \ln \left({x}_1{M}_1+{x}_2{M}_2\right)\end{array} $$

(7.19)

where η_k,i indicates the kinematic viscosity, M_i is the molecular weight, and the two kinematic viscosities with double subscripts are the empirical interaction viscosities. Equation 7.19 was derived from a three-body model of a miscible mixture comprising two low molecular weight liquids with two interaction viscosities.

2.2 Homologous Polymer Blends

The homologous macromolecular blends are simply mixtures of fractions of the same polymer having the same molecular constitutions. On the one hand, any commercial polymer may be treated as a homologous macromolecular blend, and on the other, blending narrow molecular weight distribution fractions provides important information on the rheological behavior of commercial materials. Since the zero-shear viscosity for narrow molecular weight distribution samples can be expressed as

$$ {\eta}_0=K{M}_w^{\alpha}\kern1em \mathrm{thus}\kern1em {M}_w={\left({\eta}_0/K\right)}^{1/\alpha } $$

(7.20)

(where K and α = 1 or 3.4 are parameters), but since

$$ {M}_w={\displaystyle \sum_i{w}_i{M}_i} $$

(7.21)

then it follows that (Friedman and Porter 1975)

$$ {\eta}_o={\left[{\displaystyle \sum_i{w}_i{\eta}_{o,i}^{1/\alpha }}\right]}^{\alpha } $$

(7.22)

For binary mixtures, Eq. 7.22 predicts that viscosity should show a positive deviation from the log-additivity rule, PDB.

There is a mounting evidence that PDB is not a rule for miscible polymer blends. Depending on the system and method of preparation, polymer blends can show a positive deviation, negative deviation, or additivity. Note that miscibility in polymeric systems requires strong specific interactions, which in turn affect the free volume, thus the rheological behavior. It has been demonstrated that Newtonian viscosity can be described by the relation (Utracki 1983, 1985, 1986)

$$ \ln {\eta}_0={a}_0+{a}_1/\left(f+{a}_2\right) $$

(7.23)

where a_i are equation parameters a_o ≡ ln η ^*_o with η ^*_o being the iso-free volume viscosity, a₁ is a function of the molecular architecture and polydispersity (a₁ = 0.79 was found for all paraffin’s and their mixtures), and a₂ = 0.07 is the linearization parameter. The key to Eq. 7.23 is the free volume fraction, f, computed from Simha’s statistical theory (Simha and Somcynsky 1969; Simha and Jain 1984). This approach was successful in describing pressure, temperature, and concentration dependence of the viscosities of solvents and polymer melts (Utracki 1983, 1985, 1986).

3 Model Systems for Immiscible Blends

Most polymer blends are immiscible. Their flow is complex not only due to the presence of several phases having different rheological properties (as it will be demonstrated later, even in blends of two polymers the third phase, the interphase, must be taken into account) but also due to strain sensitivity of blends’ morphology. Such a complexity of flow behavior can be best put in perspective by comparing it to flow of better understood systems, suspensions, emulsions, and block copolymers.

Flow of suspensions of solid particles in Newtonian liquids is relatively well understood, and these systems provide good model for flow of polymer blends, where the viscosity of dispersed polymer is much higher than that of the matrix polymer.

Flow of emulsions provides the best model for polymer blends, where the viscosity of both polymers is comparable. The microrheology of emulsions provides the best, predictive approach to morphological changes that take place during flow of polymer blends. The effect of emulsifiers on the drop size and its stability in emulsions has direct equivalence in the compatibilization effects in polymer blends.

Finally, the rheological behavior of block copolymers serves as a model for well-compatibilized blends, with perfect adhesion between the phases. The copolymers provide important insight into the effects of the chemical nature of the two components and the origin of the yield phenomena.

3.1 Suspensions

The dispersions of solid particles in viscous fluids can be found in a wide range of natural and industrial applications. There are some interactions determining the microstructure of the suspension, such as interactions arising from Brownian, interparticle, and flow-induced forces. In the equilibrium state, there is a balance between Brownian and interparticle forces. Under the influence of flow, hydrodynamic interactions become considerable, in comparison with thermal and interparticle forces.

The rheological properties of the suspension are strongly influenced by the spatial distribution of the particles. The relationship between microstructure and rheology of suspensions has been studied extensively (Brader 2010; Morris 2009; Vermant and Solomon 2005). Most of earlier studies dealt with the simplest form of suspensions, in which dilute hard-sphere suspensions are subjected only to hydrodynamic and thermal forces near the equilibrium state (i.e., Péclet number << 1) (Bergenholtz et al. 2002; Brady 1993; Brady and Vicic 1995). In shear flows of such suspensions, the structure is governed only by the particle volume fraction and the ratio of hydrodynamic to thermal forces, as given by the Péclet number.

The main problem in extending the microstructural theories to high Péclet number and volume fraction is related to the formulation of the many-body interactions. Recently, based on the Smoluchowski equation, Nazockdast and Morris (2012) developed a theory for concentrated hard-sphere suspensions under shear. The theory resulted in an integro-differential equation for the pair distribution function. It was used to capture the main features of the hard sphere structure and to predict the rheology of the suspension, over a wide range of volume fraction (≤0.55) for 0 < Pe ≤ 100 (Nazockdast and Morris 2012).

There are two reasons for discussing the solid-in-liquid dispersions in the chapter dedicated to flow of polymer blends (Utracki 1995). Historically, the first systematically studied multiphase systems were suspensions in Newtonian liquids, initially at infinite dilution (Einstein 1906, 1911), than at increasingly concentrated limits (Simha 1952). Knowledge of these derivations is fundamental to understanding the energy dissipation during flow in any multiphase system. Furthermore, the suspensions in viscoelastic matrix are good models for polymer blends having viscous polymer dispersed in a significantly less viscous matrix polymer.

3.1.1 Suspensions in Newtonian Liquids

The following assumptions are often used: (i) The size of a rigid particle is large in comparison to the suspending medium molecules, but small compared to the smallest characteristic diameter of the flow channel so the continuum theories are applicable. (ii) The flow is steady state, without inertia or sedimentation. (iii) The suspending medium perfectly adheres to the particles. Depending on the system (as well as the author), additional assumptions may be made, e.g., regarding interparticle interactions, orientation, etc.

Denisov et al. (1985) as well as Brady and Bossis (1985) reported on numerical simulation of suspension rheology. The first authors used the 6–12 Lennard-Jones potential with the usual meaning of ε* and σ* characteristic constants (with dimensions of energy and length, respectively) of the interacting species. Taking R_o as a measure of distance from the center of the particle at which action of the potential begins, the necessary conditions for dilatant behavior were: (i) R_o ≥ σ* and (ii) particle concentration exceeding a critical value dependent on the system. The Stokesian dynamic’s method was used by the other authors. The simulation provided valuable information on the influence of various microstructural elements on the macroscopic viscosity. The relative velocity of two particles in suspension provided the most important contribution to energy loss. As ϕ increased, the correlation of interparticle motion also increased. Hydrodynamic lubrication resulted in an increased number of particles acting as single agglomerate. The maximum packing volume fraction, ϕ_m, takes on a meaning as a percolation-like threshold for the viscosity to increase to infinity owing to the formation of infinite clusters.

Microstructural theories of suspensions appear to be particularly well suited to solve problems associated with time-dependent flows, thixotropy and rheopexy (anti-thixotropy) (Russel 1983; Utracki 1989, 1995).

3.1.1.1 Relative Viscosity of Suspensions

One of the most interesting derivations of the η versus ϕ dependence (covering the full range of concentration) was published by Simha (1952). He considered the effects of concentration on the hydrodynamic interactions between suspended particles of finite size. (Note that previously the particles were simply considered point centers of force that decayed with cube of the distance.) Simha adopted a cage model, placing each solid, spherical particle of radius a inside a spherical enclosure of radius b. At distances x < b, the presence of other particles does not influence flow around the central sphere and the Stokes relation is satisfied. This assumption leads to a modified Einstein (1906, 1911) relation

$$ {\eta}_r=1+\left(5/2\right)\lambda (y)\phi $$

(7.24)

where λ(y) is the modifying (or shielding) function of the relative cage size, y ≡ a/b:

$$ \begin{array}{l}\lambda (y)=\frac{4\left(1-{y}^7\right)}{4\left(1+{y}^{10}\right)-25{y}^3\left(1+{y}^4\right)+42{y}^5}\\ {}\mathrm{with}\kern2em y={\left[2{\left(1/\tilde{\phi}\right)}^{1/3}-1\right]}^{-1}\end{array} $$

(7.25)

In Eq. 7.25, ϕ_m is the maximum packing volume fraction. Thus, the magnitude of the shielding function λ(y) depends on the reduced volume fraction, $\tilde{\mathtt{\phi}}\equiv \mathtt{\phi}/{\mathtt{\phi}}_{\mathrm{m}}$. At low concentration, $\tilde{\mathtt{\phi}}\to 0$, the shielding factor vanishes and Einstein’s relation is recovered. However, at high concentration, $\tilde{\mathtt{\phi}}\to 1$, the shielding function and relative viscosity both go to infinity, λ(y), η_r → ∞. Substituting Eq. 7.25 into Eq. 7.24 and expanding it into power series make it possible to write simplified versions, valid respectively within the low (viz., Eq. 7.26) and high (viz., Eq. 7.27) concentration range:

$$ {\eta}_{sp}\equiv {\eta}_r-1=\left(5\phi /2\right)\left[1+\frac{25}{32}\tilde{\phi}-\frac{21}{64}{\tilde{\phi}}^{5/3}+\frac{625}{128}{\tilde{\phi}}^2+\dots \right] $$

(7.26)

and

$$ \underset{\phi \to {\phi}_m}{ \lim \kern0.5em {\eta}_r}=27\phi /20\left[\tilde{\phi}{\left(1-\tilde{\phi}\right)}^{-3}\right] $$

(7.27)

Two other semiempirical relations have been often used to describe the concentration dependence of suspension viscosity. The first was derived for the first time by Mooney (1951):

$$ \ln {\eta}_r=\left[\eta \right]/\left(1-\tilde{\phi}\right) $$

(7.28)

where [η]_s is the intrinsic viscosity. The subscript s indicates that the parameter refers to solid particles. The intrinsic viscosity is defined as

$$ \left[\upeta \right]=\underset{\upphi, \dot{\upgamma}\to 0}{ \lim \kern0.5em }\left(\upeta -{\upeta}_{\mathrm{o}}\right)/{\upeta}_{\mathrm{o}}\upphi =\underset{\upphi, \dot{\upgamma}\to 0}{ \lim \kern0.5em }\mathrm{d}\left({\upeta}_{\mathrm{r}}-1\right)/\mathrm{d}\upphi =\underset{\upphi, \dot{\upgamma}\to 0}{ \lim \kern0.5em }\mathrm{d}\kern0.3em \ln \kern0.3em {\upeta}_{\mathrm{r}}/\mathrm{d}\upphi $$

(7.29)

The second dependence is the already cited Eq. 7.8, derived by Krieger and Dougherty (1959). The relation belongs to a large group of dependencies of the type, discussed in detail a few years back (Utracki 1989):

$$ {\eta}_r={\left(1+\alpha \phi \right)}^{\beta } $$

(7.30)

In Eq. 7.30, the values of the semiempirical parameters, α and β, are usually constant, e.g., respectively 2.5 and 1, or −2.5 and −1, or −1.73 and −2.0, etc. However, in the Krieger–Dougherty relation, these two parameters depend on the system α = 1/ϕ_m and β = [η]ϕ_m.

In Fig. 7.8, the plots of η_r versus ϕ calculated from Simha’s Eq. 7.24, Mooney’s Eq. 7.28, and Krieger–Dougherty’s Eq. 7.8 are compared with the empirical curve-fitted relation, Eq. 7.5. For all the relations, the intrinsic viscosity [η]_s = 2.5 was used. However, to optimize the fit, different values for the maximum packing volume fraction, ϕ_m = 0.78, 0.91, and 0.62, respectively, had to be used. Detailed analysis of Thomas’ data made it possible to conclude that Simha’s relations provide the best fit with more realistic values of the physical parameters (Utracki and Fisa 1982).

Fig. 7.8

Relative viscosity of hard-sphere suspension in Newtonian fluid as a function of the volume fraction. Thomas curve represents the generalized behavior of suspensions as measured in 19 laboratories. The remaining curves were computed from Simha’s, Mooney’s, and Krieger–Dougherty’s relations assuming Einstein value for intrinsic viscosity of hard spheres, [η] = 2.5, but different values for the maximum packing volume fraction, ϕ_m = 0.78, 0.91, and 0.62, respectively

To summarize, the dependence of relative viscosity on the volume fraction of suspended particles can be expressed by any of several theoretical or semiempirical relations. These can be written in terms of the two parameters, [η] and ϕ_m; thus η_r = η_r([η], ϕ/ϕ_m). As it will be shown, the generality of this dependence extends beyond the monodispersed hard-sphere suspensions.

The relationships between η_r and ϕ have been derived for suspensions of monodispersed hard spheres in Newtonian liquids. However, most real systems are polydispersed in size and do not necessarily consist of spherical particles. It has been found that here also Simha’s Eq. 7.24, Mooney’s Eq. 7.28, or Krieger–Dougherty’s Eq. 7.8 are useful, provided that the intrinsic viscosity and the maximum packing volume fraction are defined as functions of particle shape and size polydispersity. For example, by allowing ϕ_m to vary with composition, it was possible to describe the η_r versus ϕ variation for bimodal suspensions (Chang and Powell 1994). Similarly, after values of [η] and ϕ_m were experimentally determined, Eq. 7.24 provided good description for the η_r versus ϕ dependence of several multiphase systems, e.g., PVC emulsions and plastisols, mica-reinforced polyolefins, and sealant formulations (Utracki 1988, 1989).

The problem of packing a maximum volume of solids into a given space is common to numerous branches of physics and technology. It suffices to note that the relative viscosity of suspensions is a function of the reduced volume fraction, $\tilde{\mathtt{\phi}}\equiv \mathtt{\phi}/{\mathtt{\phi}}_{\mathrm{m}}$, to realize the importance of ϕ_m. Experimentally, it was demonstrated that ϕ_m calculated from dry packing of solid particles agrees well with the value determined for a suspension.

Theoretically and experimentally polydispersity increases the ϕ_m value, for example, from 0.62 observed for random packing of uniform spheres to values exceeding 0.9. An interesting recipe for ϕ_m maximization requires four generations of nearly spherical particles with the diameter ratios 1:3:9:17. Blending them at the volume ratios 4:1:1:4 result in ϕ_m = 0.78. However, what was important, the suspensions were found to be nonsedimenting, and when dried they gave solid bed with uniform porosity (Ritter 1971; Lord 1971).

In industrial practice it may be important to use mixtures of filler particles not only of spheroidal shape (as discussed above) but also of different shapes, e.g., filling and reinforcing polymer with CaCO₃ particles and glass fibers. The theoretical basis for optimization of such systems was developed by Wieckowski and Streg (1966) and later by Milewski (Milewski 1973, 1977, 1978; Milewski and Katz 1987). These studies are also important for polymer blends where at concentrations exceeding the percolation threshold the morphology is complex, comprising spheres, fibers, and lamellas.

For anisometric particles it is useful to use the particle aspect ratio, p, defined as a ratio of two orthogonal axes. For prolate ellipsoids (fibers) p > 1 is the length-to-diameter ratio, whereas for oblate ellipsoids (plates) p < 1 is the thickness divided by the largest dimension of the plate. It was observed that both, the intrinsic viscosity, [η], and the inverse of the maximum packing volume fraction, 1/ϕ_m, increase linearly with p. Thus, the relative viscosity of suspensions of anisometric particles is higher than that observed for spheres. For example, Doi and Edwards predicted (1978) that for rods ${\upeta}_{\mathrm{r}}\propto {\mathtt{\phi}}^3$.

In the extensional, irrotational field, under the steady-state conditions, the particles remain oriented in the direction of stress. In uniaxial flow they align with the main axis in the flow direction, while in biaxial they lie on the stretch plane (Batchelor 1970, 1971). For dilute spherical suspensions in Newtonian liquid, the extensional viscosity follows the Trouton rule, i.e., η_E ≅ 3η. However, for anisometric particles the Trouton ratio η_E/η is a strong function of p. For example, at ϕ = 0.01 extensional viscosity of rods with aspect ratio p = 1,000 is 1,000 times higher than that for suspension of spheres.

3.1.1.2 Particle Orientation in Flow

The orientation of particles in flow is of particular interest to microrheology. To predict the macroscopic rheological properties of a multiphase system, a detailed description of each phase behavior is required. In this field, contributions from the Pulp and Paper Research Institute of Canada by Mason et al. and later by van de Ven and his coauthors are particularly valuable. The earlier results were summarized by Goldsmith and Mason (1967), the latter by Van de Ven (1989). The microrheology has been particularly well developed for infinitely dilute systems in Newtonian matrix – either solid particles or liquid drops. In the present part, only the former system will be summarized. More extensive discussion of microrheology of the liquid–liquid systems will be presented later, while considering the rheological behavior of polymer blends.

For suspension of solid particles in a liquid, the theoretical and experimental works indicate that the angle of orientation of a spheroid can be expressed as

$$ {\phi}_1= \arctan \left[p \tan \left(2\pi t/{t}_p\right)\right] $$

(7.31)

where the period of rotation of a particle with an aspect ratio, p, is given by

$$ {t}_p=2\pi \left(p+{p}^{-1}\right)/\dot{\gamma} $$

(7.32)

Accordingly, for rods, the maximum velocity of rotation occurs at t/t_p = 0, 1/2, 3/4, 5/4, …. For spheres with p = 1, ϕ₁ = 2π t/t_p, i.e., constant rotational velocity. In nonuniform shear fields, such as that observed during flow through a capillary (Poiseuille flow), the particles rotate with velocity predicted by Eqs. 7.31 and 7.32, according to the value of the shear rate existing at the radial location of the sphere in the capillary. Near the wall, for finite diameter spheres, the immobile layer of the suspending medium causes a reduction of rotational and translational velocity. The effect scales with the square of the sphere diameter.

The wall also causes a geometric exclusion effect, i.e., a lower-than-average concentration of particles near the wall and a retardation of their motion. The phenomena are complicated by the axial migration of particles, dependent on the Reynolds number, $\mathrm{Re}=\uprho \dot{\gamma}{\mathrm{d}}^2/{\upeta}_{\mathrm{o}}$, where ρ and d are the particle density and diameter, respectively.

To control the orientation of the fibers during composites manufacturing, it is helpful to have an insight about the relation between the suspension structure and rheological properties. Determination of the position, orientation history, and shape of fibers due to bending and twisting in a fluid are the main stream of the studies in this area (Joung et al. 2001; Schmid et al. 2000; Switzer Iii and Klingenberg 2003). There are a few studies about the role of the fiber flexibility. Recently, Keshtkar et al. (2009) investigated the effect of fiber flexibility on the rheological behavior and orientation of fibers suspended in a Newtonian fluid under simple shear flow using conventional rheometry and rheo-microscopy. The ability of the mesoscopic model of Rajabian et al. (2005) to predict the rheological behavior and orientation of the fibers was also examined (Keshtkar et al. 2010). The advantage of using the abovementioned mesoscopic model is related to the compatibility of thermodynamics with its equations. The results showed that by increasing the fiber flexibility, both the viscosity and first normal stress difference increased. The main conclusion based on rheo-microscopy of the various suspensions is that at low shear rates, the most rigid fibers are more easily oriented than flexible fibers. High shear rate data indicated negligible difference in the orientation state of the flexible and rigid fibers. However, the model predictions for the fiber orientation were qualitatively consistent with the experimental data; it was suggested that GENERIC model (Grmela and Öttinger 1997) should be extended to predict the formation of agglomerates in the fiber-filled suspensions (Keshtkar 2009).

3.1.1.3 Shear-Induced Particle Migration

There are at least two possible mechanisms for particle migration during shear flow, inhomogeneity of the stress field and strong interparticle interactions (Graham et al. 1991). In the first case, the particles tend to migrate to low shear stress regions, while in the second case the situation is more complex involving a coupled relationship between the thermodynamic and hydrodynamic forces.

The Newtonian behavior of suspensions in Newtonian liquids is limited to low concentrations. An exception seems to be the extensional flow of anisometric particles (irrotational flow field) where the rate of strain independent region extends to concentrations where strong non-Newtonian behavior would be expected in shear. This rate of deformation-dependent phenomena will be summarized below.

During the capillary flow of concentrated suspensions, the difference in velocities of particles located at different radial positions results in the formation of transient multiplets or stacks, behaving similarly to rods. Under these circumstances the rate of axial migration is accelerated, and the flow profile flattens. For example, experimentally, for ϕ = 1/3 suspensions of spheres flowing through a tube at the Reynolds number Re ≡ 2ρQ/πR₁ η = 0.056, a partial plug flow was observed. However, when Re reached the value of 0.112, a complete plug flow was observed – the flow was no longer Newtonian (Karnis et al. 1966; Vadas et al. 1973).

Matsumoto et al. (1986) reported that in the cone-and-plate geometry, the storage G′ and loss G″ shear moduli of uniform, nonrigid spheres decrease monotonically with test time (or number of shearing cycles). G′ and G″ were observed to decrease by four decades, but steady-state shearing for 15 s returned them to the initial values. Since the phenomenon depended on the rigidity as well as on the uniformity of shape and size, development of a structure during the dynamic test must be postulated.

In Couette flow the spheres migrate toward the outer cylinder. In shearing, a shear fractionation of spherical particles has been observed. For example, Giesekus (1981) observed that, during torsional shearing of binary sphere suspensions, the larger and the smaller spheres separated into two different annular volumes, i.e., for each sphere size a critical equilibrium radial distance had to be postulated. On the other hand, Prieve et al. (1984, 1985) reported that for each sphere diameter and speed of rotation there is a critical radius, r_c; in the parallel plate rheometer, a particle located at r < r_c was observed to migrate inward, whereas that placed at r > r_c migrated outward. There is no theoretical explanation for either observation.

In a wide-gap Couette rheometer, migration of spheres was followed by a nuclear magnetic resonance imaging (Abbott et al. 1991). Migration to the low shear rate region was found to be determined by the total strain, proportional to the shear rate and square of the particle diameter, but independent of the (Newtonian) viscosity of the matrix liquid. More recently, similar studies were undertaken for suspensions of rods with p = 2–18 and ϕ = 0.3 or 0.4 (Mondy et al. 1994). At the same ϕ, the composition gradient of rods of different aspect ratios was indistinguishable, the same as the one earlier reported for spheres. The rate of migration was found to increase with concentration.

Owing to the periodically accelerated rotation of fibers in a shear field, alignment of fibers in Couette flow is to be expected. Theory indicates that the shear field is about half as efficient at causing fiber alignment as extension. However, the shear field is rarely homogeneous, and during the flow fibers undergo breaking, bending, or coiling, which causes further reduction of alignment efficiency. Further details on various modes of orientation behavior of flowing suspensions can be found in reviews by Cox and Mason (1971), Batchelor (1974), and Leal (1980).

The evidence accumulated so far indicates that there is a full spectrum of structures, from a liquid-like where the yield stress, σ_y = 0, to a solid-like with large σ_y. For anisometric particles at ϕ > 1/p, yield may originate in mechanical interlocking of particles, but for spheres it stems from the interparticle interactions. When these interactions are weak, σ_y → 0 is observed, with the arrow indicating the time effect. If the experiment is conducted at low rates of shear, no yield behavior would be noted.

In uniaxial extensional (convergent) flow, there is evidence of spherical particles moving toward the center of the stream. Convergent flow of a dilute suspension of glass fibers, p = 200–800, in Newtonian liquids was studied by Murty and Modlen (1977). The fiber orientation angle (defined as an average angle between the fiber axis and flow direction) changed from 45° (random) to about 15°. The orientation started upstream from the convergence. For low viscosity liquids, jamming at the entrance region was responsible for as much as 60 % of fibers being “filtered out.”

At higher fiber loading, ϕ_p > 1, the rheological responses of aligned fiber suspensions resemble those of liquid crystals. Becraft and Metzner (1992) analyzed the rheological behavior and orientation of glass fibers (GF), in polyethylene (PE), and polypropylene (PP). The experimental data were interpreted using a modified Doi theory for liquid crystalline fluids, LCF (Doraiswamy and Metzner 1986). The kinetics of the distribution function, f, is given by

$$ \frac{Df}{Dt}=\nabla \cdot {\overline{D}}_r\nabla f+\nabla \cdot {\overline{D}}_r\frac{f\nabla V}{k_BT}-\nabla \cdot (uf) $$

(7.33)

where ${\overline{\mathrm{D}}}_{\mathrm{r}}$ is the rotational diffusivity of the rods and u denotes a unit vector corresponding to rod orientation. The first term on the rhs of Eq. 7.33 accounts for the contribution of Brownian motion to the orientation distribution function, the second for the effects of the liquid crystalline interaction potential between the rods, while the third term for the effects of flow.

Doraiswamy and Metzner noted that use of the LCF approach is permissible at concentrations above that which would correspond to the transition from isotropic to aligned morphology, ϕ > 8/p. The theory provided fair description of the stress–strain dependence for systems containing 10 wt% GF and excellent agreement for those with 40 wt% GF. Also, the approach gave good predictions of the diagonal terms of the second-order orientation tensor.

3.1.1.4 Aggregation and Yield Stress

One of the fundamental assumptions of the continuum theories is stability of structure (Newtonian behavior) or, alternatively, a well-defined process of structural changes (non-Newtonian behavior). However, as it was already mentioned, orientation effects in sheared layers of suspensions are responsible for either dilatant or pseudoplastic behavior, while strong interparticle interactions may lead to yield stress or a transient behavior. In short, there is an intimate relation between the liquid structure and its rheological response; change in one causes a corresponding change in the other. Some of these changes have been theoretically treated, viz., Eq. 7.32. The aggregation is the result of the attractive forces or the flow conditions. It could be categorized in two groups: flocculation which is the reversible aggregation and coagulation which is a fast irreversible aggregation (Larson 1999). A physical change in the system may cause flocculation. Flocculates can be re-dispersed in the suspension using mechanical processes such as shaking or stirring (deflocculation). Aggregation, agglomeration, and flocculation are structural phenomena ranging from transient rotating doublets observed within dilute region to a pseudo-solid-like behavior of flocculated suspensions with yield stress. Aggregation can occur due to thermodynamic interparticle interactions, chemical bonding, or geometric crowding. The latter type prevails in shear flows of suspensions of anisometric particles.

It was shown that even in the absence of attractive interparticle interactions, shear forces can make aggregates of the particles interacting by large friction forces (Switzer Iii and Klingenberg 2003). For example, flow-induced aggregation has been observed for stiff fibers (Schmid et al. 2000) and carbon nanotube suspensions (Khalkhal et al. 2011).

There are numerous theories based on structural models of suspensions (Mikami 1980). Wildemuth and Williams (1984) considered that the maximum packing volume fraction, ϕ_m, is a function of normalized shear stress, ${\tilde{\upsigma}}_{12}\equiv {\upsigma}_{12}/\mathrm{M}$, where M is a numerical parameter. The authors derived the relation

$$ {\phi}_m=\left({\phi}_{m,o}+{\phi}_{m,\mathit{\infty}}{\tilde{\sigma}}_{12}^m\right)/\left(1+{\tilde{\sigma}}_{12}^m\right) $$

(7.34)

where m = 1.00–1.17 is an experimental constant, while ϕ_m,o and ϕ_m∞ are values of the maximum packing volume fraction at ${\tilde{\upsigma}}_{12}$ and ${\tilde{\upsigma}}_{12}=\mathit{\infty}$, respectively. Defining the yield stress as ${\tilde{\upsigma}}_{12}$ when ϕ = ϕ_m, one can rearrange Eq. 7.34 to read

$$ {\tilde{\sigma}}_y=\left(\phi -{\phi}_{m,o}\right)/\left({\phi}_{m,\mathit{\infty}}-\phi \right) $$

(7.35)

Hoffman (1972, 1974) also reported that at low rates of shear and high solid content, ϕ > 0.54, the power law index $\mathrm{n}=\mathrm{d} \ln {\sigma}_{12}/\mathrm{d} \ln \dot{\upgamma}$ approaches zero.

For the system styrene-acrylonitrile (SAN) latex in ethylene glycol, addition of salt decreased n to zero. The experiment was performed to demonstrate that increased interparticle interaction causes the onset of dilatation to move to higher rate of shear. However, the work also demonstrated that at these high concentrations there is a yield stress, σ_y. Onogi and Matsumoto (1981) reported that in PS suspension with particles having strong attractive forces, the yield phenomenon was observed, while suspensions of PS particles having repulsive forces behaved like Newtonian liquids. Thus, the yield stress is associated with formation of a three-dimensional structure by interacting particles, resulting in a behavior similar to an elastic solid. Similarly, impact modification of PMMA by incorporation of 0–50 wt% of core-shell latex particles of poly(butylacrylate-co-styrene) demonstrated that the particles form a co-continuous network at ϕ ≤ 0.2 that result in a low frequency rubbery plateau. The high-frequency data were found independent of composition (Bousmina and Muller 1992). There are several methods for determining σ_y. Among these is the modified Casson equation (Utracki 1982):

$$ {F}^{1/2}={F}_y^{1/2}+a{F}_m^{1/2} $$

(7.36)

where F may be any rheological function (viz., shear stress σ₁₂, elongational stress σ₁₁, shear loss modulus G″, etc.), F_y indicates the yield value of F, F_m is the F-value of the matrix liquid at the same deformation rate as F, and a is a measure of the relative value of F. Another method requires a simultaneous fit of experimental data to a constitutive equation in which a parameter or parameters are related to σ_y (Utracki 1987).

Measurements of creep and elastic recovery also provide a sensitive, direct mean of detecting yield stress, either by simultaneous fit of time-dependent strain, γ(τ), at a constant stress, σ₁₂, to the compliance equation:

$$ J(t)\equiv {\gamma}_{12}(t)/{\sigma}_{12}={J}_0+{J}_e^0\Psi (t)+t/\eta $$

(7.37)

(where Ψ(t) is the retardation function), or by plotting the recoverable strain versus stress. In the latter case, the maximum value of stress below which the Hookean behavior is obtained gives the value of σ_y.

Polymer lattices and suspensions of carbon black in linseed oil and clay or calcium carbonate in aqueous media provide examples (Amari and Watanabe 1983). The values of σ_y determined from creep and those from shear viscosity were found to be in good agreement.

There are several direct methods of measurement of a yield stress. The constant stress rheometer is most frequently used to determine σ_y value in shear. Dzuy and Boger (1983, 1985) used a rotational vane viscometer. Yield stresses in compression can be calculated from the unrelaxed stress values in parallel plate geometry. Its value in elongation has been directly measured as the critical stress value below which no sample deformation was observed during 30 min of straining in an extensional rheometer.

Khalkhal and Carreau (2011) examined the linear viscoelastic properties as well as the evolution of the structure in multiwall carbon nanotube–epoxy suspensions at different concentration under the influence of flow history and temperature. Initially, based on the frequency sweep measurements, the critical concentration in which the storage and loss moduli shows a transition from liquid-like to solid-like behavior at low angular frequencies was found to be about 2 wt%. This transition indicates the formation of a percolated carbon nanotube network. Consequently, 2 wt% was considered as the rheological percolation threshold. The appearance of an apparent yield stress, at about 2 wt% and higher concentration in the steady shear measurements performed from the low shear of 0.01 s⁻¹ to high shear of 100 s⁻¹, confirmed the formation of a percolated network (Fig. 7.9). The authors used the Herschel–Bulkley model to estimate the apparent yield stress. As a result they showed that the apparent yield stress scales with concentration as τ_y ∼ φ_ν ^2.64±0.16 (Khalkhal and Carreau 2011).

Fig. 7.9

(a) Steady shear measurement of MWCNT suspensions at different concentrations. (b) Scaling behavior of the apparent yield stress obtained using the Herschel–Bulkley model with volume concentration of MWCNTs (Khalkhal and Carreau 2011)

For unoriented particle systems, the von Mises criterion for plastic flow of solids should be obeyed; the yield stress in elongation and compression should be equal to each other and larger by the factor of $\sqrt{3}$ than the yield stress in shear, σ_y. However, for highly concentrated suspensions of anisometric particles, von Mises criterion should not be used.

For suspensions, the concentration dependence of σ_y was found to follow either of the following two dependencies:

$$ {\sigma}_y={a}_1{\left(\phi -{\phi}_0\right)}^{a_2}\kern1em \mathrm{and}\kern1em {\sigma}_y={a}_3 \exp \left\{{a}_4\phi \right\} $$

(7.38)

where a_i are adjustable parameters. The exponent a₂ depends on the particle geometry as well as the interparticle interactions. For human blood σ_y = 26.87ϕ³ (mPa) was reported (Picart et al. 1998).

It has been observed that for many systems the value of yield stress depends on the time scale of the measurements. Setting all controversies aside, pragmatically it is advantageous to consider that in these systems there are aggregates of different size, characterized by the dynamic interparticle interactions. For a given system these interactions have specific strength, σ ^∞_y , and the aggregates have a characteristic relaxation time, τ_y. This model leads to the following relation:

$$ {\sigma}_y\left(\xi \right)={\sigma}_y^{\mathit{\infty}}{\left[1- \exp \left\{-{\tau}_y\xi \right\}\right]}^u;\kern1em \mathrm{for}\kern1em \xi =\omega, \overset{.}{\gamma}\kern0.5em \mathrm{or}\kern0.62em \overset{.}{\varepsilon } $$

(7.39)

where u = 0.2–1.0 characterizes polydispersity of the aggregates. Equation 7.39 was found to be easy to use, and the parameters computed from curve fitting of the experimental data, σ_apparent = σ _y + σ_true, agreed quite well with the independently determined values.

Leonov (1994) introduced kinetics of interactions into his rheological equation of state. The new relation can describe systems with a dynamic yield stress, without resorting to a priori introducing the yield stress as a model parameter (as it has been done in earlier models).

3.1.1.5 Time-Dependent Flows

Two types of flow are recognized: thixotropy, defined as a decrease of apparent viscosity under shear stress, followed by a gradual recovery when the stress is removed, and its opposite, anti-thixotropy, or rheopexy. Both are related to molecular or macroscopic changes in interactions. In thixotropic liquids, the aggregate bonding must be weak enough to be broken by flow-induced hydrodynamic forces. If dispersion is fine, even slight interactions may produce thixotropic effects. When the dispersion coarsens, larger forces are required to engender the same effects. In the case of suspensions of anisometric particles, the interactions are particularly strong, while for spheres, the effect can be controlled by changing the type and concentration of ionic groups on the surface. Similarly, in polymer blends the inter-domain interactions can be controlled by addition of a compatibilizer – its presence enhances the interphase interactions.

Breakup and recreation of the associated structure follow exponential decay kinetics. The simplest, single exponential relation representing thixotropic behavior is

$$ \eta (t)-{\eta}_{\mathit{\infty}}^t=\left({\eta}_0^t-{\eta}_{\mathit{\infty}}^t\right) \exp \left\{-t/{\tau}^{*}\right\} $$

(7.40)

where t is the shearing time, η ^t₀ and η ^t _∞ are values of shear viscosity at t = 0 and ∞, respectively, and τ* is the relaxation time of the system.

Time dependency also enters into the consideration of the rheological response of any viscoelastic system. In steady-state testing of materials such as molten polymers, the selected time scale should be sufficiently long for the system to reach equilibrium. Frequently, the required period, t > 10⁴ s, is comparable to that in thixotropic experiments. More direct distinctions between these two types of flow are the usual lack of elastic effects and the larger strain values at equilibrium observed for thixotropic materials (see Table 7.4). There is a correlation between these two phenomena, and theories of viscoelasticity based on thixotropic models have been formulated by Leonov (1972, 1994). Inherent to the concept of thixotropy is the yield stress. Both the microstructural and continuum theories postulate that the material behaves as a Bingham body at stresses below a critical value (Table 7.5).

Table 7.5 Definitions of viscoelastic and thixotropic systems

3.1.1.6 Steady-State Flows

There are three types of melt behavior in a simple shear flow: dilatant (D) (shear thickening); Newtonian (N), and pseudoplastic (P) (shear thinning). Similarly, in an extensional flow, the liquids may be stress hardening (SH), Troutonian (T), or stress softening (SS). By definition, the response considered here is taken at sufficiently long times to ensure steady state, and the yield effect, Y, is subtracted. In consequence, within the experimental range of stress or deformation rate, several types of behavior may be observed. There exist a great variety of flow curves observed for different materials.

3.1.1.6.1 Pseudoplastic Flows

For suspensions, the most common type is a pseudoplastic flow curve with the so-called upper, η_o, and lower, η_∞, Newtonian plateaux (Cross 1965, 1970, 1973):

$$ \eta -{\eta}_{\mathit{\infty}}=\left({\eta}_0-{\eta}_{\mathit{\infty}}\right)/\left(1+{a}_0{\dot{\gamma}}^{a_1}\right) $$

(7.41)

In this relation a_o is the parameter describing how fast the viscosity changes between the two plateaux. In viscoelastic systems, the lower plateau is several orders of magnitude smaller than the upper one, η_∞ << η_o, and it is frequently neglected.

Equation 7.41 resembles the one derived by Carreau (1972) for monodispersed polymer melts, which later was generalized for polydispersed systems (Utracki 1984, 1989):

$$ \eta ={\eta}_0{\left[1+{\left(\tau \dot{\gamma}\right)}^{m_1}\right]}^{-{m}_2} $$

(7.42)

In Eq. 7.42, τ is the relaxation time and m₁ and m₂ are polydispersity parameters, with a bound: n = 1 − m₁ m₂, where n is the power-law exponent in the relation:

$$ {\sigma}_{12}=K{\dot{\gamma}}^n $$

(7.43)

Equation 7.42 well describes the flow behavior of polymeric systems, and it was found useful for polymer blends. It should be stressed that Eqs. 7.41, 7.42, and 7.43 describe the flow behavior of fluids without yield stress or thixotropicity.

3.1.1.6.2 Dilatant Flows

Krieger and Choi (1984) studied the viscosity behavior of sterically stabilized PMMA spheres in silicone oil. In high viscosity oils, thixotropy and yield stress were observed. The former is well described by Eq. 7.41. The magnitude of σ_y was found to depend on ϕ, the oil viscosity, and temperature. In most systems, lower Newtonian plateau was observed for the reduced shear stress value: σ_r ≡ σ₁₂d³/RT > 3 (d is the sphere diameter, R is the gas constant, and T is the absolute temperature). However, when shear stress was further increased, dilatant behavior was observed. Dilatancy was found to depend on d, T, and silicone oil viscosity. The authors reported small and erratic normal stresses.

To describe the above behavior, the following relation was derived (Utracki 1989):

$$ \eta -{\eta}_{\mathit{\infty}}=\left({\eta}_0-{\eta}_{\mathit{\infty}}\right)\left[1+{a}_0 \exp {\left\{\tau \dot{\gamma}-{a}_1\right\}}^{2{a}_2}\right]\ {\left[1+{\left(\tau \dot{\gamma}\right)}^{m_1}\right]}^{-{m}_2} $$

(7.44)

where a_i are equation parameters. Excepting the assumptions that η _∞ ≠ 0 and insertion of the middle square bracket on the rhs of Eq. 7.44, the dependence is the same as Eq. 7.42.

Hoffman (1972, 1974), Strivens (1976), van de Ven (1984, 1985), Tomita et al. (1982, 1984), and Otsubo (1994) reported pseudoplastic/dilatant flow of concentrated suspensions of uniform and polydispersed spheres. A dramatic change in light diffraction pattern was systematically observed at the shear rate corresponding to the onset of dilatancy. Van de Ven and his collaborators demonstrated that, depending on concentration and shear rate, the distance between the sliding layers of uniform spheres in a parallel plate rheometer can vary by as much as 10 %.

The dilatant behavior of binary sphere suspensions in capillary flow was reported by Goto and Kuno (1982, 1984). At constant loading, dilatancy was observed only within a relatively narrow range of composition, 0.714 < x < 0.976, where x represents the fraction of larger spheres.

Suspensions, even in Newtonian liquids, may exhibit elasticity. Hinch and Leal (1972) derived relations expressing the particle stresses in dilute suspensions with small Peclet number, $\mathrm{Pe}=\dot{\upgamma}/{\mathrm{D}}_{\mathrm{r}}\sim 1$ (D_r is the rotary diffusion coefficient), and small aspect ratio. The origin of the elastic effect lies in the anisometry of particles or their aggregates. Rotation of asymmetric entities provides a mechanism for energy storage, Brownian motion for its recovery. For suspensions of spheres, this mechanism does not exist and the first normal stress, N₁, is expected to vanish. However, when at higher ϕ the spherical particles aggregate into anisometric clusters, the system may and does show a viscoelastic behavior. Indeed, large N₁ (Kitano and Kataoka 1981), Weissenberg rod climbing (Nawab and Mason 1958), and large capillary entrance–exit pressure drops were reported (Goto et al. 1986). On the other hand, owing to the yield stress, no extrudate swell was observed in suspensions of anisometric particles in Newtonian liquids (Roberts 1973).

Theoretically, interparticle interactions contribute directly to the elastic stress component of spherical suspensions as well as by modification of the microstructure (Batchelor 1977):

$$ \left\langle {S}^P\right\rangle N={\displaystyle \sum_{i=2}^N{\displaystyle \sum_{j<i}^N{r}_{ij}{F}_{ij}}} $$

(7.45)

where N is the number of particles and r_ij center-to-center separation of i and j particles with pairwise interparticle interaction force F_ij. Gadala-Maria (1979) reported that, for suspensions of PS spheres in silicone oil, N₁ linearly increased with σ₁₂. Other theories have been discussed by Van Arsdale (1982), Bibbo et al. (1985), Brady (1993), Becraft and Metzner (1994), and many others.

The dynamic mechanical testing of suspensions is particularly suitable for studying systems with anisometric particles with well-defined structures (Ganani and Powell 1985). The authors studied the dynamic behavior of spheres in Newtonian liquids. They reported that dynamic viscosity, η′, behaves similarly as the steady-state viscosity, η, while the storage modulus G′ ≅ N₁ ≅ 0.

3.1.1.7 Transient Effects

In system where the structure changes with time upon imposition of stress, transient effects are important. For example, semi-concentrated fiber suspensions in shear and extension show large transient peaks in the first and the second normal stress differences (Dinh and Armstrong 1984; Bibbo et al. 1985). It is interesting that the peaks appear at different times, first for N₂, then for N₁, and finally for σ₁₂.

3.1.2 Suspensions in Non-Newtonian Liquids

Filled and reinforced polymer melts belong in this category. There are numerous reviews on the topic (Chaffey 1983; Goettler 1984; Metzner 1985; Utracki 1987, 1988; Utracki and Vu-Khanh 1992). There is particularly strong interest in flow of polymeric composites filled with anisometric, reinforcing particles, with properties that strongly depend on the flow-induced morphology and distribution of residual stresses.

In the absence of interlayer slip, addition of a second phase leads to an increase of viscosity. The simplest way to treat the system is to consider the relative viscosity as a function volume fraction of the solids, ϕ, particle aspect ratio and orientation.

There is no difference between the flow of suspensions in Newtonian liquids and that of polymeric composites, when the focus is on the Newtonian behavior phase. The non-Newtonian behavior of suspensions originates either from the non-Newtonian behavior of the medium or from the presence of filler particles. The problems associated with this behavior can originate in interparticle interactions (viz., yield stress) and orientation in flow (Leonov 1990; Mutel and Kamal 1991; Vincent and Agassant 1991; Shikata and Pearson 1994).

3.1.3 Flow-Induced Orientation

The most efficient orientation fields are extensional. Using convergent and divergent flow one may control orientation of anisometric particles. Most of the work in this area has been done with fiber-filled materials, but the effects are equally important for flow of neat semicrystalline polymer melts or liquid crystal polymers (Goettler and Shen 1983; Goettler 1984). In extensional flow, platelets are less susceptible to orientation. Two-stage orientation mechanism was observed in converging flow (Utracki 1988).

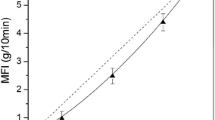
The nonlinear rheological behavior of platelet dispersions is a response to flow-induced rearrangements. Some methods have been developed to provide information on flow-induced orientation of platelets. These methods, generally, consist of performing in situ small-angle X-ray scattering (SAXS) (Bihannic et al. 2010) or small-angle neutron scattering (SANS) (Hanley et al. 1994; Kalman and Wagner 2009; Ramsay and Lindner 1993) experiments under shear flow applied in a Couette shear cell apparatus. For example, SAXS patterns obtained from radial and tangential incident beams relative to flow velocity field in a Couette apparatus showed biaxial orientation of natural clay particles (Bihannic et al. 2010). To correlate shear-induced particle orientation and the corresponding suspension viscosity, the effective volume fraction was first calculated based on parameters derived from SAXS patterns (using an orientation distribution function) for different shear rates. Then the viscosity was calculated using the model proposed by Quemada (Quemada 1977; Quemada and Berli 2002) that relates suspension viscosity to effective volume fraction. Figure 7.10 depicts the experimental and calculated viscosities for the clay suspension. It reveals that the proposed approach is successful in relating anisotropy of SAXS patterns to rheological behavior of the suspension.

Fig. 7.10

Comparison between experimental and calculated viscosities (Bihannic et al. 2010)

However, in shear-thinning dispersion, flow-induced orientation develops as shear rate increases. Moreover, the shape factor of the particles affects the orientational order. Evaluation of the shape factor effect on the orientation of particles and, consequently, the rheological properties of suspensions showed that the shape factor distribution provides more precise information than the median value of the shape factor, specially at high shear rates (>105 s⁻¹) (Lohmander and Rigdahl 2000). Comparing two suspensions prepared using particles with a broad shape factor distribution and a narrow one, with the same average value, showed higher viscosity for the latter due to the different orientational order.

The orientation affects flow profoundly, hence processability, as well as the product performance. It plays an important role in extrusion or injection molding where the anisometric particles may become oriented in a complex manner. Layered structures, weld lines, splice lines, swirls, and surface blemishes are well known. Mold geometry (e.g., inserts) and transient effects make predictions difficult. It has been theoretically and experimentally shown that, when designing a mold for composites with anisometric particles, the principles developed for single-phase melts do not apply (Crowson and Folkes 1980; Crowson et al. 1980, 1981; Folkes 1982; Vincent and Agassant 1986, 1991).

3.1.3.1 Yield Stress

Yield occurs as a result of structure formation due to physical crowding of particles, interparticle interactions, or steric–elastic effects of the medium. Depending on the stability of the structure, true or apparent (i.e., time-dependent) yield stress can be obtained. As a consequence, the magnitude of yield stress increases with aspect ratio of the particles, their rigidity, and concentration. The phenomenon is visible in steady-state shear, dynamic, or extensional flow, especially at low rates of deformation, where the slope of the flow curve, $\log \upeta \kern0.5em \mathrm{versus}\kern0.5em \log \dot{\gamma}$, is often $\partial \log \upeta /\partial \log \dot{\gamma}=-1$ (time-independent yield). Neglecting the yield stress may have serious consequences on interpretation of elasticity.

Yield stress and plug flow are interrelated. The viscous loss energy is dissipated in a relatively small volume of material, where the concentration of solids differs from average. This may lead to excessive shear heating (effects as large as ΔT ≥ 80 °C have been observed), degradation of polymeric matrix, strong change of skin morphology during polymer blends extrusion, as well as to attrition of anisometric particles, fibers, or flakes. Thus, the skin layer may not only have different concentration, but different chemical and physical composition as well. At high flow rates, this situation may lead to slip at the wall.

In capillary flow, slip velocity at the wall, s, can be calculated from (Reiner 1930, 1931)

$$ \begin{array}{l}\dot{\gamma}={\overset{.}{\gamma}}_N\left(3+1/n\right)-\left(s/R\right)\left({n}^{*}+3\right)\\ {}n\equiv \partial \ln {\sigma}_{12}/\partial \ln \overset{.}{\gamma}\\ {}{n}^{*}\equiv \partial \ln s/\partial \ln {\sigma}_{12}\\ {}s={s}_o{\left({\sigma}_{12}-{\sigma}_y\right)}^{s_1}\end{array} $$

(7.46)

where the first expression on the rhs of Eq. 7.46 is the well-known Rabinowitsch correction and the second expression represents the contribution of the slip. Here s is the slip velocity, R is the radius of the capillary, and s_i are parameters. Experimentally, it was observed that the slip velocity depends on the difference between shear stresses, σ₁₂ − σ _y . Exponent values as large as s₁ = 6.3 were determined for rigid PVC. Slip may occur in any large strain flow, in capillary, cone-and-plate, or parallel plate flow (Kalyon et al. 1993, 1998).

Further consequences of the yield stress (i.e., plug flow) are (i) a drastic reduction of the extrudate swell, B ≡ d/d_o (d is diameter of the extrudate, d_o that of the die) (see, e.g., Crowson and Folkes 1980; Utracki et al. 1984), and (ii) significant increase of the entrance–exit pressure drop, P_e (also known as Bagley correction). For single-phase fluids, these parameters have been related to elasticity by molecular mechanisms (Tanner 1970; Cogswell 1972; Laun and Schuch 1989). However, in multiphase systems, both B and P_e depend primarily on the inter-domain interactions and morphology, not on deformation of the macromolecular coils. Thus, in multiphase systems (i.e., blends, filled systems, or composites), only direct measures of elasticity, such as that of N₁, N₂, or G′ should be used. It is customary to plot the measure of the elastic component versus that of the shear components, viz., N₁ versus σ₁₂, or G′ versus G″, etc. For rheologically simple systems, the relationships are independent of temperature, but for the multiphase systems the viscoelastic time–temperature principle does not hold.

A viscoelastic–plastic model for suspensions of small particles in polymer melts was proposed (Sobhanie et al. 1997). The basic assumption is that the total stress is divided into that in the matrix and the network of immersed interacting particles. The model leads to nonlinear viscoelastic relations with the yield function, which is defined in terms of structure rupture and restoration.

Many parameters like the size, size distribution, and shape of the particles along with the particle–particle and particle–fluid interactions, viscoelastic properties of the suspending fluid, and the flow geometry complicate the modeling of suspension behavior. Chateau et al. proposed a homogenization approach to estimate the behavior of suspensions of noncolloidal particles in an incompressible yield stress fluids (Chateau et al. 2008). The study involve treats the non-Newtonian suspension as a continuous medium based on the properties of its constituents. The problem is simplified by using the secant method of Castañeda (1991) and Suquet (1993). According to Chateau et al., where Herschel–Bulkey law is valid, the yield stress (τ _c ^hom) of the suspension may be estimated as the product of the suspending fluid yield stress (τ _c ) and a function of solid volume fraction, φ: (τ _c ^hom/τ _c = ((1 − φ)g(φ))^½). Using the Krieger–Dougherty law (Krieger and Dougherty 1959) to determine the ratio of the macroscopic to the microscopic properties (g(φ)), it was found that the experimental results are in a good agreement with the simple law τ _c ^hom/τ _c = (1 − φ)^1/2(1 − φ/φ _m)^−1.25φm (Chateau et al. 2008). This means that as long as the noncolloidal particles are spherical, only the close packing density, yield stress, and power law index of the suspending medium are necessary to identify the macroscopic properties of these suspensions (Chateau et al. 2008).

3.1.3.2 Extensional Flows

The yield stress is also observed in extensional flows (Kamal et al. 1984a, b; Utracki 1988). Yield stress is manifested in two related ways: (i) as a vertical displacement in the stress growth function at decreasing strain rates, contrasting with the normal linear viscoelastic behavior of single-phase polymeric melts, and (ii) as a deviation from the relation $\underset{\dot{\upvarepsilon}\to 0}{ \lim }\ {\upeta}_{\mathrm{E}}\left(\dot{\upvarepsilon}\right)=3{\upeta}_0$.

In qualitative agreement with the von Mises criterion, σ_11,y/σ_12,y = 1.3 − 2.0 was reported (Utracki 1984). The Trouton ratio

$$ {R}_T\equiv \underset{\dot{\varepsilon}\to 0}{ \lim }{\eta}_E\left(\dot{\varepsilon}\right)/3{\eta}_0 $$

(7.47)

was found to decrease by half, as the concentration of glass beads in SAN increased (ϕ ≤ 0.37) (Martischius 1982). It was argued that in extensional flow only the liquid undergoes deformation; thus both the extensional strains and viscosities should be corrected for the “diluting” effect of the filler volume (Nicodemo et al. 1975).

The relative extensional viscosity of suspensions in a power-law liquid can be expressed as (Goddard 1978)

$$ {\eta}_{E,r}\equiv {\eta}_E\left(\phi, \dot{\varepsilon}\right)/{\eta}_E\left(0,\dot{\varepsilon}\right)=1+2\phi {R}_T{p}^{n+1}{\left\{\left(1/n-1\right)\left[1-{\left(\pi /\phi \right)}^{\left(1-1/n\right)/2}\right]\right\}}^{n/\left(2+n\right)} $$

(7.48)

Equation 7.48 described the extensional viscosity behavior of a PE/mica system well, after subtracting the yield stress using Casson’s equation (Utracki and Lara 1984).

3.2 Emulsion Rheology

Liquid-in-liquid systems can be divided into three categories: those in which both liquids are Newtonian, those in which both phases are viscoelastic, and those systems comprising one Newtonian and one viscoelastic liquid. The first of these categories refers to emulsions (E), the second to polymer blends (B), and the third class is used as models (M) to gain some insight into the effects of elasticity on the flow and morphology. Some polymer blends may also be classified as M. Several reviews are available on emulsion rheology (Sherman 1963, 1968; Barry 1977; Nielsen 1977; Utracki 1988, 1989; Pal 1996) and on emulsions containing high volume fraction of the dispersed phase, ϕ > 0.74 (Cameron and Sherrington 1996).

3.2.1 Newtonian Flow

Einstein’s treatment of suspensions was extended to emulsions by Taylor (1932, 1934) who derived the following expression for the relative viscosity of emulsions:

$$ \begin{array}{l}{\eta}_r=1+\left(5/2\right)\sigma \left[\lambda +2/5\right]/\left[\lambda +1\right]\\ {}\therefore {\left[\eta \right]}_e=\left(5/2\right)\sigma \left[\lambda +2/5\right]/\left[\lambda +1\right]\\ {}\mathrm{where}\kern0.75em \lambda \equiv {\eta}_d/{\eta}_{\mu}\end{array} $$

(7.49)

Oldroyd (1953, 1955) modified this theory by incorporating effects of the interface:

$$ \begin{array}{l}{\left[\eta \right]}_e=\left(5/2\right)\left[\Lambda +2/5\right]/\left[\Lambda +1\right]\\ {}\mathrm{where}\kern0.75em \Lambda \equiv \left({\eta}_d+{\eta}_i/5d\right)/{\eta}_m\\ {}\mathrm{and}\kern1.5em {\eta}_i=2{\eta}_{Si}+3{\eta}_{Ei}\end{array} $$

(7.50)

In Eq. 7.50 the interfacial viscosity, η _i , is expressed in terms of the interfacial shear (subscript Si) and extensional (subscript Ei) components. The plot of emulsion viscosity as a function of the dimensionless viscosity ratio, Λ, is shown in Fig. 7.11.

Fig. 7.11

Intrinsic viscosity of emulsion versus the viscosity ratio (defined in the Figure) (Oldroyd 1953, 1955)

Note that the upper bound of the emulsion intrinsic viscosity is Einstein’s value for hard-sphere suspension [η] = 2.5. This limit is observed for Λ > 100. For Λ = 1 (solutions), [η] = 1.75. The lower values are expected for emulsions of low viscosity liquids in highly viscous one – for Λ < 0.01, [η] ≈ 1. Equation 7.50 was found valid in a wide range of 1.3 < Λ < ∞.

Oldroyd (1953, 1955), Choi and Schowalter (1975), Oosterbroek et al. (1980, 1981), and many others considered the interphase between the dispersed phase and the matrix liquid to be a physical, three-dimensional entity endowed with its own specific rheological properties. These considerations led to calculations of two relaxation’s times for Newtonian emulsions (Choi and Schowalter 1975)

$$ \begin{array}{l}{\eta}_r=1+\phi \left[\left(5\lambda +2\right)/\left(2\lambda +2\right)\right]+\left(5/8\right){\left[\phi \left(5\lambda +2\right)/\left(\lambda +1\right)\right]}^2\\ {}{\tau}_1={\tau}_0\left[1+5\phi \left\{\left(19\lambda +16\right)/\left[4\left(\lambda +1\right)\left(2\lambda +3\right)\right]\right\}\right]\\ {}{\tau}_2={\tau}_0\left[1+3\phi \left\{\left(19\lambda +16\right)/\left[4\left(\lambda +1\right)\left(2\lambda +3\right)\right]\right\}\right]\\ {}{\tau}_0=\left({\eta}_2R/{v}_{12}\right)\left\{\left(19\lambda +16\right)\left(2\lambda +3\right)/\left[40\left(\lambda +1\right)\right]\right\}\end{array} $$

(7.51)

For the relative viscosity of emulsions, in the absence of deformation and coalescence, Eqs. 7.24, 7.25, 7.26, 7.27, 7.28, 7.29, and 7.30 may also be used, provided that the intrinsic viscosity is calculated from Eq. 7.50 and that the maximum packing volume fraction is treated as an adjustable parameter, dependent on the interphase. This pragmatic approach has been successfully used to describe [η] versus ϕ variation for such complex systems as industrial lattices (at various stages of conversion), plastisols, and organosols.

Industrial emulsions are usually prepared as concentrated systems, containing ϕ_m ≤ 0.94. Owing to interface interactions and deformability of droplets, these systems behave rather like elastic, soft solids without any sign of Newtonian behavior. Between the highly concentrated and dilute regions, there is a wide zone of structural change reflected in a spectrum of non-Newtonian behavior.

3.2.2 Emulsion Microrheology

3.2.2.1 Drop Deformability

When a neutrally buoyant, initially spherical droplet is suspended in another liquid and subjected to shear or extensional stress, it deforms and then breaks up into smaller droplets. Taylor (1932, 1934) extended the work of Einstein (1906, 1911) on dilute suspensions of solid spheres in a Newtonian liquid to dispersions of single Newtonian liquid droplet in another Newtonian liquid, subjected to a well-defined deformational field. Taylor noted that, at low deformation rates in both uniform shear and planar hyperbolic fields, the sphere deforms into a spheroid (Fig. 7.12).

Fig. 7.12

Deformation of drops in shear (a) and extensional (b) flow field (Taylor 1932, 1934)

At low stress in steady uniform shearing flow, the deformation can be described by three dimensionless parameters: the viscosity ratio, the capillary number, and the reduced time:

$$ \lambda \equiv {\eta}_1/{\eta}_2;\kern1em \kappa \equiv {\sigma}_{ij}d/{\nu}_{12}\kern1em \mathrm{and}\kern1em {t}^{*}=\gamma /\kappa $$

(7.52)

where η ₁ and η ₂ are the viscosities of the dispersed and the matrix phases, respectively, σ_ij is the stress (either in shear ij = 12 or in extension ij = 11), d is the initial drop diameter, ν₁₂ is the interfacial tension coefficient between two phases, and γ is the generated strain.

During shear or uniaxial extensional flow, the initially spherical drop deforms into a prolate ellipsoid with the long axis, a ₁, and two orthogonal short axes, a _2. It is convenient to define the drop deformability parameter, D, as

$$ \begin{array}{l}D\equiv \left({a}_1-{a}_2\right)/\left({a}_1+{a}_2\right)\\ {}\kern0.75em =\left\{{\left[1+{\gamma}^2/2+\left(\gamma /2\right){\left(4+{\gamma}^2\right)}^{1/2}\right]}^{3/4}-1\right\}/\left\{{\left[1+{\gamma}^2/2+\left(\gamma /2\right){\left(4+{\gamma}^2\right)}^{1/2}\right]}^{3/4}+1\right\}\\ {}\kern0.75em =\left[ \exp \left\{3\varepsilon /2\right\}-1\right]/\left[ \exp \left\{3\varepsilon /2\right\}+1\right]\end{array} $$

(7.53)

where γ and ε are shear and uniaxial extensional strains, respectively.

According to Taylor, the equilibrium deformability of drops is a complex function, which has simple solutions at two limits. On the one hand, at low stresses, when the interfacial tension effects dominate the viscous ones (low value of λ), the deformability D and the orientation angle α (see Fig. 7.12) of the droplet can be expressed as

$$ D=\left(\kappa /2\right)\left[\left(19\lambda +16\right)/\left(16\lambda +16\right)\right]\kern1em \mathrm{and}\kern1em \alpha =\pi /4 $$

(7.54a)

Since, for λ = 0 to ∞, the quantity in the square bracket ranges from 1.00 to 1.18, the drop deformability D ≅ 0.55κ. Thus, a small deformation of Newtonian drops in Newtonian matrix varies linearly with the capillary number. This proportionality was indeed demonstrated in Couette-type rheometer for a series of corn syrup/silicon oil emulsions (Elemans 1989).

On the other hand, when the interfacial tension is negligibly small in comparison to viscosity (high value of λ):

$$ D=\left(\kappa /2\right)\left[\left(19\lambda +16\right)/\left(16\lambda +16\right)\right]\kern1em \mathrm{and}\kern1em \alpha =\pi /4 $$

(7.54b)

Taylor predicted that droplet breakup will occur at D ≥ D _crit = 0.5.

Cox (1969) extended Taylor’s theory to systems with the full range of viscosity ratios:

$$ \begin{array}{l}D=\left(\kappa /2\right)\left[\left(19\lambda +16\right)/\left(16\lambda +16\right)\right]/{\left[{\left(19\lambda \kappa /40\right)}^2+1\right]}^{1/2}\\ {}\alpha =\left(\pi /4\right)+\left(1/2\right) \arctan \left\{19\lambda \kappa /20\right\}\end{array} $$

(7.55)

The above relations are valid for Newtonian systems undergoing small, linear deformation, smaller than that, which would lead to breakup. Furthermore, experimental data indicate that it takes time to reach the equilibrium deformation. It is convenient to use the reduced time scale (see Eq. 7.52), ${\mathrm{t}}_{{}_{\mathrm{d}}}^{*}\cong 25$ is required to reach the equilibrium deformation (Elemans 1989).

Taylor’s theory makes it also possible to predict the retraction of slightly deformed drops toward an equilibrium spherical form:

$$ \begin{array}{c}\mathrm{D}\left(\mathrm{t}\right)={\mathrm{D}}_{\mathrm{o}} \exp \left\{-\left[80\left(\uplambda +1\right)/\left(2\uplambda +3\right)\left(19\uplambda +16\right)\right]\left({\mathrm{t}\upnu}_{12}/{\upeta}_2\mathrm{d}\right)\right\}\\ {}={\mathrm{D}}_{\mathrm{o}} \exp \left\{-\mathrm{t}/{\uptau}_{\mathrm{ret}}\right\}\\ {}\mathrm{where}:\kern1em {\uptau}_{\mathrm{ret}}={\upeta}_{\mathrm{eq}}\mathrm{d}/{\upnu}_{12};\kern1em {\upeta}_{\mathrm{eq}}={\upeta}_2\left[\left(2\uplambda +3\right)\left(19\uplambda +16\right)/80\left(\uplambda +1\right)\right]\end{array} $$

(7.56)

where t is the retraction time and the relaxation time, τ_ret, is expressed as a ratio of the equivalent viscosity, η_eq, divided by the interfacial tension coefficient scaled by drop diameter. Thus, knowing the time evolution of D and the viscosity of the materials, one can calculate the interfacial tension coefficient. In principle, Eq. 7.56 is valid for Newtonian systems, but the method can also be used to characterize viscoelastic materials, provided that the following two conditions are valid: (1) the retraction rate is sufficiently slow to ensure that materials behave as Newtonian, and (2) the elastic relaxation of the materials after deformation is faster than the ellipsoidal droplet retraction, i.e., a clear separation of the two mechanisms is possible (Luciani et al. 1996).

The deformability of drops in a three-component Newtonian system (comprising 1.1 % PS and 1.7 % ethyl cellulose dissolved in benzene) was studied by Silberberg and Kuhn (1952, 1954). The authors reported that as the rate of shear increased, the spherical drops changed shape into prolate ellipsoids, with the long axis, a ₁, and two orthogonal short semiaxes, a ₂. The data are presented in Fig. 7.13. The observed maximum on the a ₁ curve may be associated with the rheological effect on solubility.

Fig. 7.13

Drop deformability versus shear rate (Silberberg and Kuhn 1954)

Owing to elasticity of the interphase, the first normal stress difference and the relaxation time can be calculated as (Schowalter et al. 1968)

$$ \begin{array}{l}{N}_1=\phi {\left({\sigma}_{12} d\kappa \right)}^2/40{v}_{12}\\ {}\mathrm{and}\kern1em {\tau}^{*}=\eta dD\kappa \left(2\lambda +3\right)/40{v}_{12}\end{array} $$

(7.57)

It is convenient to express the capillary number in its reduced form κ * ≡ κ/κ_cr, where the critical capillary number, κ_cr, is defined as the minimum capillary number sufficient to cause breakup of the deformed drop. Many experimental studies have been carried out to establish dependency of κ_cr on λ. For simple shear and uniaxial extensional flow, De Bruijn (1989) found that droplets break most easily when 0.1 < λ < 1, but do not break for λ > 4:

$$ \log \left({\kappa}_{cr}/2\right)={c}_1+{c}_2 \log \lambda +{c}_3{\left( \log \lambda \right)}^2+{c}_4\left( \log \lambda +{c}_5\right) $$

(7.58)

Parameters of Eq. 7.58 are listed in Table 7.6 (see also Fig. 7.45).

Table 7.6 Parameters of the critical capillary number for drop burst in shear and extension in Newtonian systems (R. A. de Bruijn 1989)

Note that in shear for λ = 1, the critical capillary number κ_cr = 1, whereas for λ > 1, κ_cr increases with λ and becomes infinite for λ > 3.8. This means that breakup of the dispersed phase in pure shear flow becomes impossible for λ > 3.8. This limitation does not exist in extensional flows.

The deformation of dispersed drops in immiscible polymer blends with viscosity ratio λ = 0.005–13 during extensional flow was studied by Delaby et al. (1994, 1995). The time-dependent drop deformation during start-up flow at constant deformation rate was derived. The model is restricted to small drop deformations.

Milliken and Leal (1991) used a computer-controlled four-roll mill to investigate the deformation of polymeric drops in an imiscible Newtonian fluid in planar extensional flow. They showed that deformation curves differ, based on the viscosity ratio. Steady drop shapes were observed only for emulsions with viscosity ratio higher than one. However, for the low-viscosity polymeric dispersed phase, the deformation of drops does not follow that of Newtonian fluids anymore, and the critical capillary number was significantly smaller. For both cases, the transient deformation and breakup of polymeric drops were found to be different from Newtonian drops (Milliken and Leal 1991). Other geometries, such as Couette, torsional parallel plate, torsional cone and plate, and rectilinear parallel plate, have been used extensively (Fischer and Erni 2007). Comparison between these experimental results and numerical data regarding the deformation behavior arising from shear or elongational flow of emulsions verifies the consistency of the Volume of Fluid (VoF) method (Renardy et al. 2002) and the Boundary Integral Method (BIM) (Feigl et al. 2003) for the simulation of concentrated emulsion flow.

3.2.2.2 Drop Breakup

With regard to drop deformation and breakup, there are four regions of reduced capillary numbers, κ*, both in shear and elongation:

• For −0.1 > κ*-droplets do not deform.

• For −0.1 < (κ*) < 1-droplets deform, but they do not break.

• For −1 < κ* < 2-droplets deform then split into two primary droplets.

• For −κ* > 2-droplets deform into stable filaments.

As for κ_cr, Fig. 7.14 shows that the critical time for drop breakup t_b* varies with λ.

Fig. 7.14

Effect of the viscosity ratio on the critical time to break (Huneault et al. 1994)

When values of the capillary number and the reduced time are within the region of drop breakup, the mechanism of breakup depends on the viscosity ratio, λ.

In shear, four regions have been identified (Goldsmith and Mason 1967):

• For −0.1 >> λ-small droplets are shed from sigmoidal drops – tip spinning.

• For −0.1 < λ < 1-drop breaks into two principal and odd number of satellite droplets.

• For −1 < λ < 3.8-drop deforms into fiber, which then disintegrates into small droplets.

• For −λ > 3.8-drops may deform, but they do not break.

Critical capillary numbers for elongational flows are lower than for shear flows. In other words, the elongational flow field is much more effective for droplet breakup in a dispersive mixing regime (Grace 1982).

3.2.2.2.1 Drop Fibrillation and Breakup

In addition to the previously discussed drop breakup into two principal drops (and an odd number of small satellite droplets), there is another mechanism for dispersing one liquid in another. This is based on the “capillarity instability principle” of long cylindrical bodies. For κ^∗ > 2, drops deform affinely with the matrix into long fibers. When subsequently the deforming stress decreases, causing the reduced capillary number to fall below two, κ^∗ < 2, the fibers disintegrate under the influence of the interfacial tension. The problem was theoretically treated by Rayleigh (1879), Taylor (1932, 1934), and Tomotika (1935, 1936). The latter author showed that the degree of instability can be described by the growth rate parameter of a sinusoidal distortion:

$$ q={v}_{12}\Omega \left(\Lambda, \lambda \right)/2{\eta}_m{R}_0 $$

(7.59)

where Λ is the distortion wavelength, Ω(Λ, λ) is a function tabulated by Tomotika, and R_o is the initial fiber radius. The hydrodynamic instability is characterized by a maximum for the dominant wavelength Λ_m that leads to thread breakup. For 0.01 ≤ λ ≤ 10:

$$ \Omega \left({\Lambda}_m,\lambda \right)= \exp \left\{{\displaystyle \sum_{i=0}^4{b}_i{\left( \log \lambda \right)}^i}\right\} $$

(7.60)

where b₀ = −2.588, b₁ = −1.154, b₂ = 0.03987, b₃ = 0.0889, and b₄ = 0.01154. The distortion amplitude α grows exponentially with time, t:

$$ \alpha ={\alpha}_0 \exp \left\{ qt\right\} $$

(7.61)

where α₀ is the distortion at t = 0. Assuming that the initial distortion is due only to thermal fluctuations, Kuhn (1953) estimated that

$$ {\alpha}_0=\left(21{k}_{\mathrm{B}}T\right){\left(8{\pi}^{3/2}{v}_{12}\right)}^{-1/2} $$

(7.62)

where k_B is Boltzmann constant and T is the absolute temperature. The thread breakup occurs when α = R ≅ 0.81R_o. The time required to reach this stage can be expressed as

$$ {t}_b^{*}\equiv {t}_b\dot{\gamma}/\kappa =2\left[ \ln \left(0.81{R}_0/{\alpha}_0\right)\right]/\Omega \left({\Lambda}_m,\lambda \right) $$

(7.63)

Thus, t ^*_b is an important parameter describing the breakup process for fibers subjected to lower stresses than those required for fibrillation, i.e., κ* < 2. The above indicates that breakup is less likely at low interfacial tension. Since the matrix viscosity appears in the left side of the equation (in the capillary number), one may expect shorter breakup times with lower matrix viscosity, but it is noteworthy that this term also changes the Tomotika function on the right side of the equation. Figure 7.15 shows the distortion growth rate at the dominant wavelength as a function of viscosity ratio. To obtain a low value of Ω(l, λ), thread viscosity should be high and the matrix viscosity has to be low (Potschke and Paul 2003).

Fig. 7.15

Distortion growth rate at dominant wavelength and dominant wave length versus λ (Potschke and Paul 2003)

In practice, one of the most serious obstacles for quantitative use of Timotika’s theory is estimation of the initial distortion, α₀.

The time corresponding to the complete breakup, t_b, was measured (Grace 1982; Elemans 1989). The data are presented in Fig. 7.14. Numerically they can be expressed as

$$ {t}_b^{*}\cong 84{\lambda}^{0.355}{\kappa}^{*^{-0.559}} $$

(7.64)

3.2.2.3 Coalescence

During mixing, the dispersed phase progressively breaks down until a minimum drop diameter is reached. As the drop diameter decreases, further breakup becomes increasingly difficult. For emulsions, the size of the smallest drop that can be broken can be calculated from Taylor’s theory, but experiments have shown that, in most cases, the equilibrium droplet size is larger than predicted. Furthermore, the deviation increases with concentration of the dispersed phase, ϕ_d − ϕ_o, where experimentally the smallest value for which the deviation occurs, ϕ_o ≈ 0.005 (Utracki and Shi 1992).

The fusion of the two or more droplets due to the local thinning and disruption of the matrix is called coalescence. Complete phase separation is expected as the limiting case of coalescence. Two types of coalescence must be recognized: the first is determined by equilibrium thermodynamics (e.g., liquid–liquid miscibility, interfacial tension coefficient, rheological conditions of the interphase, etc.); the second is determined by dynamics, and it is dominated by rheology and flow conditions. In the following text, only the second type will be discussed.

Utracki (1973) studied steady-state shear coagulation of PVC lattices for a wide range of variables. Assuming that the locus of coagulation is at the particle–matrix interface and that the rate of coagulation depends on the frequency of particle collisions, the critical time for coalescence was calculated as

$$ \begin{array}{l}{t}_c={a}_0{E}^{+}{d}^3/\left[{\rho}_d\left(1+{N}^{+}+{N}^0\right){\phi}_d^{8/3}{\dot{\gamma}}^2\right]\\ {}\mathrm{or}\kern1em {t}_c=2.940{E}^{+}\left({\phi}_m-{\phi}_d\right)/\left[{\eta}_m\left({V}_x/V\right){\phi}_d^{8/3}{\dot{\gamma}}^2\right]\end{array} $$

(7.65)

where a_o is a numerical parameter; E⁺ is the threshold energy of coagulation; N^o and N⁺ are the number of coagulating drops, respectively, initially and at t = t_o; V_x/V is the volume fraction of emulsion undergoing uniform shearing; and ρ_d is the drop density. Validity of these relations was confirmed on many lattices. In particular, ${\mathrm{t}}_{\mathrm{c}}\propto {\dot{\upgamma}}^{-2}$ and dt_c/dϕ_d < 0 (thus, coagulation rate increases with ϕ_d) were experimentally confirmed. Since the coagulation was assumed to be related to the projected area of the drop, $\mathrm{d}\propto {\mathtt{\phi}}_{\mathrm{d}}^{2/3}$ was implicitly assumed.

Fortelny et al. (1988, 1990) assumed that Brownian motion is the principal driving force for coalescence in polymer blends. Applying Smoluchowski’s theory, the authors obtained:

$$ S={S}_0{\left\{1+\left(2/3\pi \right){\left[{k}_BT/\left({\eta}_m{\phi}_d\right)\right]}^{1/2}{S}_0^{3/2}{t}^{1/2}\right\}}^{-2/3} $$

(7.66)

where S_o and S are the interface areas in the unit volume of the blend having monodisperse spherical particles, respectively, before and after coalescence. The experimental data confirmed the linearity of (S/S_o)^−3/2 as a function of t^1/2. However, it is to be noted that Brownian motion affects particles that usually are below the size of dispersions in polymer blends. Furthermore, coalescence should be independent of the stress field intensity and magnitude of the interfacial energy. The efficiency of particle collisions due to Brownian motion leading to coalescence should also be taken into account.

Coagulation is a result of collision between two spherical drops of diameter, d, that approach each other with certain velocity gradient to a distance smaller than their radius. Coalescence can occur only if the liquid remaining between two flattened drops will be removed sooner than the global velocity field will force the drops to separate. The instabilities in the layer of the entrapped film will break it when the separation between drops is smaller than the critical separation distance, h _c ≅ 5 nm, the critical coalescence time for systems with mobile interface is expected to follow the relation: ${\mathrm{t}}_{\mathrm{c}}=3\upkappa \left[ \ln \left(\mathrm{d}/4{\mathrm{h}}_{\mathrm{c}}\right)\right]/4{\dot{\gamma}}^2$ (Elmendorp 1986; Chesters 1991a). The relation was derived for isolated pairs of drops, and as such it does not take into account the concentration effect. It predicts that, in shear, the coalescence of two isolated drops is proportional to the exerted stress and it is easier for larger spheres with high surface energy. It was observed that ${\mathrm{t}}_{\mathrm{c}}\propto {\dot{\gamma}}^{-2}$, in agreement with Eq. 7.65. Experimentally, coalescence probability was found to rapidly decrease with increasing κ and d.

3.2.3 Non-Newtonian Flows

Only dilute emulsions or systems undergoing slow deformation show Newtonian, deformation rate-independent flow. As the concentration and deformation rate increases, the flow progressively changes into pseudoplastic. Since the rheological response is a reflection of the inner structure of the material, modifications of the emulsion morphology accompany such a change.

3.2.3.1 Morphology

Even in the dilute region, individual emulsion droplets rarely exist. In most cases, droplets are polydisperse in size, forming doublets, chain structures, or aggregates. Two types of emulsion morphology can be distinguished: (A) formed by the shear field (e.g., skin-core structures developed during flows through long tubes) and (B) formed by particle–particle interaction. Knowledge of type A structures is important for proper interpretation of the flow phenomena. Their formation is influenced by the differences in the flow behavior of the components, as well as by shear coagulation. Knowledge of type B structures is important for the utilization of suspension rheology in processing. Since the effective volume fraction of dispersed particles increases with increase of association, the relative viscosity of emulsion is strongly influenced by these variables.

By contrast with polymer blends, emulsions are prepared by carefully designing the interface system and by sequential addition of ingredients. Both elements are essential when 96 vol% of one liquid must be dispersed in 4 vol% of another. If, due to interactions of emulsifiers, the continuous phase becomes viscoelastic, the emulsion has high consistency or a body. There is gradual passage of structures, from rotating doublets in dilute systems to entrapment of the dispersed phase in a continuous network of interacting interfaces. Consequently, emulsions can show a Newtonian as well as a complex thixotropic and viscoelastic character (Nielsen 1977).

3.2.3.2 Theoretical Treatment

The theoretical treatment of two-phase flow was reviewed by Cox and Mason (1971), Leal (1980), and Barthès-Biesel (1988). As indicated before, dispersions of one Newtonian liquid in another result in systems that are characterized by elasticity and relaxation times, e.g., Eq. 7.57.

For dilute emulsions, with neither hydrodynamic interactions nor interfacial effects, Fröhlich and Sack (1946) developed the following time-dependent constitutive equation:

$$ \begin{array}{c}\left[1+{\tau}_1\left(d/ dt\right)\right]\tau =2\eta \left[1+{\tau}_2\left(d/ dt\right)\right]d\\ {}\mathrm{where}\kern1.25em \eta ={\eta}_m\left[1+\left(5\phi /2\right)+0\left({\phi}^2\right)\right],\\ {}{\tau}_1=\left[3{\eta}_m/2G\right]\left(1+5\phi /3\right),\\ {}{\tau}_2=\left[3{\eta}_m/2G\right]\left(1-5\phi /2\right)\end{array} $$

(7.67)

where G is the Hookean modulus of the elastic, dispersed spheres, while λ_i is the relaxation time of the emulsion. Thus, the theory considered viscoelasticity of dilute emulsions to originate in elastic deformability of the dispersed phase.

Nearly a decade later, Oldroyd (1953, 1955) proposed a constitutive model similar to that of Fröhlich and Sack, valid at small deformations. The model considered low concentration of monodisperse drops of one Newtonian liquid in another. The interfacial tension and the viscoelastic properties of the interfacial film were incorporated by means of convected derivatives. The model provided the following relation for the complex modulus:

$$\begin{array}{l}{\mathrm{G}}^{*}={\mathrm{G}}_{\mathrm{m}}^{*}\left[1+3\mathtt{\phi}\mathrm{H}\right]/\left[1-2\mathtt{\phi}\mathrm{H}\right]\\ {}H=\frac{\left(4/{\mathrm{R}}^{\prime}\right)\left(2{\mathrm{G}}_{\mathrm{m}}^{*}+5{\mathrm{G}}_{\mathrm{d}}^{*}\right)+\left({\mathrm{G}}_{\mathrm{d}}^{*}-{\mathrm{G}}_{\mathrm{m}}^{*}\right)\left(16{\mathrm{G}}_{\mathrm{m}}^{*}+19{\mathrm{G}}_{\mathrm{d}}^{*}\right)}{\left(40/{\mathrm{R}}^{\prime}\right)\left({\mathrm{G}}_{\mathrm{m}}^{*}+{\mathrm{G}}_{\mathrm{d}}^{*}\right)+\left(2{\mathrm{G}}_{\mathrm{d}}^{*}+3{\mathrm{G}}_{\mathrm{m}}^{*}\right)\left(16{\mathrm{G}}_{\mathrm{m}}^{*}+19{\mathrm{G}}_{\mathrm{d}}^{*}\right)}\\ {}{\mathrm{G}}_{\mathrm{i}}^{*}={\mathrm{G}}_{\mathrm{i}}^{*}\left(\omega \right);\mathrm{R}{\prime}=\mathrm{R}/{\nu}_{12}; \mathrm{thus}: \mathrm{H}=\mathrm{H}\left(\omega; {\mathrm{R}}^{\prime}\right)\end{array} $$

(7.68)

where ν₁₂ the interfacial tension coefficient, R is the drop radius, G ^* _i (ω) is the complex modulus, and subscripts i = m, d indicate matrix or disperse phase, respectively.

Oldroy’s model was extended by Palierne (1990) to emulsions with polydisperse spherical drops. The model considered viscoelastic liquids, the concentration range was extended up to that at which drop–drop interactions start complicating the flow field. However, the drops must be spherical, undergoing small deformation, and the interfacial tension coefficient was considered constant, independent of stress and the interfacial area. The following relation was derived for the complex modulus:

$$ \begin{array}{l}{G}^{*}={G}_m^{*}\left[1+3{\displaystyle \sum_{i=1}^n{\phi}_i{H}_i}\right]/\left[1-2{\displaystyle \sum_{i=1}^n{\phi}_i{H}_i}\right]\\ {}{H}_i=\frac{\left(4/{R_i}^{\prime}\right)\left(2{G}_m^{*}+5{G}_d^{*}\right)+\left({G}_d^{*}-{G}_m^{*}\right)\left(16{G}_m^{*}+19{G}_d^{*}\right)}{\left(40/{R_i}^{\prime}\right)\left({G}_m^{*}+{G}_d^{*}\right)+\left(2{G}_d^{*}+3{G}_m^{*}\right)\left(16{G}_m^{*}+19{G}_d^{*}\right)}\\ {}{G}_i^{*}={G}_i^{*}\left(\omega \right);\kern1em {R}_i\kern-0.2em ^{\prime }={R}_i/{\nu}_{12};\kern1em \mathrm{thus}\kern-0.3em :\kern1em {H}_i={H}_i\left(\omega; {R}^{\prime}\right)\end{array} $$

(7.69)

Here ϕ _i and R _i are, respectively, the volume fraction and the drop radius. The main feature of this model is the inclusion of a contribution from the interfacial tension to the viscoelastic properties and the inclusion of the effect of particle size polydispersity. For example, knowing G ^* _i (ω) of the two main components of the blend, one can predict the dynamic moduli of the emulsion (as well as dilute polymer blends) from the knowledge of the interfacial tension coefficient and distribution of drop sizes. This model has been used extensively to determine the interfacial tension or droplet size of emulsions (Guschl and Otaigbe 2003; Mekhilef et al. 2000; Xing et al. 2000; Yoo et al. 2010). It has been shown that the volume average droplet radius could be employed instead of R _i , as long as the ratio of volume to number average radius of an emulsion is less than two (Graebling et al. 1993a). The theory is applicable to low strains and to the concentration range where yield stress is absent (Graebling and Muller 1990, 1991; Graebling et al. 1993b).

Low-viscosity mixtures of PDMS and PI, with λ = 0.155, 0.825, and 4.02 were studied at room temperature (Kitade et al. 1997). The dynamic data were analyzed using Eq. 7.69. Good agreement was found. However, for the λ = 4.02 system, the drops were insensitive to the flow field. They neither broke nor coalesced. Similar observations were reported for PDMS/PIB system (Vinckier et al. 1996). The latter authors also observed that agreement with Palierne’s model becomes weaker for blends pre-sheared at higher shear rate, i.e., blends with finer drop dispersion.

Palierne emulsion model failed to describe the dynamic modulus of the PP/EPDM blends after radiation, because the viscosity ratio increased significantly and the rubber phase changed from deformed droplets to hard domains after radiation (Cao et al. 2007). Interconnections among inclusions of the dispersed phase (Shi et al. 2006) and the existence of multiple emulsion (emulsion-in-emulsion) structure exhibiting different relaxation domains in compatibilized systems are other factors contributing to the failure of Palierne’s model (Friedrich and Antonov 2007; Pal 2007).

Honerkamp and Weese (1990) reported on the use of Tikhonov’s regularization for the determination of material functions. This method of data treatment was found particularly useful for the computation of the relaxation and retardation spectra (Elster et al. 1991; Honerkamp and Weese 1993). It has also been used to compute the sphere-size distribution of the dispersed phase in binary blends (Gleisner et al. 1994a), as well as the ratio of the dispersed drop diameter divided by the interfacial tension coefficient, d/ν₁₂ (Gleisner et al. 1994b).

Friedrich et al. (1995) modified Palierne’s Eq. 7.69 by a continuous function:

$$ {G}^{*}\left(\omega \right)={G}_M^{*}\left(\omega \right)\left[1+3{\displaystyle {\int}_{-\mathit{\infty}}^{\mathit{\infty}}H\left(\omega, {R}^{\prime}\right)u\left({R}^{\prime}\right){R}^{\prime }d\kern0.2em \ln \kern0.1em {R}^{\prime }}\right]/\left[1-2{\displaystyle {\int}_{-\mathit{\infty}}^{\mathit{\infty}}H\left(\omega, {R}^{\prime}\right)u\left({R}^{\prime}\right){R}^{\prime }d\kern0.2em \ln \kern0.1em {R}^{\prime }}\right] $$

(7.70)

where R′ = R/ν₁₂ and u(R′) = ν₁₂v(R) is the scaled, volume-weighted distribution of sphere sizes. Using Tikhonov’s regularization method, the distribution function, u(R′), could be computed. The experimental data (storage and loss shear moduli, G′ and G″, respectively, within six decades of frequency and transmission electron microscopy, TEM) were determined for 2, 5, 10, and 20 wt% PS in the PMMA matrix. From the dynamic viscoelastic data of the neat components and the blends, the monomodal distribution of the distribution function u(R′) versus log R′ = log (R/ν₁₂) was computed and compared with data obtained from TEM. Excellent agreement was found for blends containing 2 and 5 wt%, fair for 10 wt%, and poor for 20 wt% PS. In the latter case, TEM showed a bimodal distribution (possibly resulting from coalescence), whereas a monomodal distribution was obtained from the rheological data. The interfacial tension coefficient computed from these results varied from ν₁₂ = 2.08 to 3.10 mN/m. The average value, ν₁₂ = 2.5 mN/m at 190 °C, is comparable to the literature data ν₁₂ = 0.8 to 1.8 mN/m at 200 °C (Luciani et al. 1996).

For infinitely dilute viscoelastic emulsions, the shear dependence of inherent viscosity was derived as (Barthès-Biesel and Acrivos 1973)

$$ {\eta}_{inh\equiv}\left({\eta}_{rel}-1\right)/\phi =\left[\left(5/2\right)\lambda +1\right]/\left[\lambda +1\right]-f\left(\lambda \right){\left({\sigma}_{12}/{E}_{\mathrm{int}}\right)}^2+0\left({\sigma}_{12}^3\right) $$

(7.71)

where f(λ) > 0 is a rational function of λ. The relation predicts that in dilute emulsions subjected to small deformations, the η_inh should decrease with the square of the shear stress. The effect of stress is moderated by interphase elasticity expressed as E_int. The theory was experimentally verified. Note the similarity of the first term on the rhs of Eq. 7.71 to the expression derived by Oldroyd for the intrinsic viscosity of emulsions, Eq. 7.50. Accordingly, Eq. 7.71 may be modified by replacing λ by Λ, as derived by Oldroyd.

Semi-concentrated emulsions were examined theoretically and experimentally only within the linear viscoelastic region (Oosterbroek and Mellema 1981; Oosterbroek et al. 1980, 1981; Eshuis and Mellema 1984). Recognizing that the interphase has a finite thickness (sometimes the total volume of the interphase is comparable to, or even exceeds, the volume of the dispersed phase), the authors postulated that the interphase should have two interfacial coefficients, ν′ and ν″ facing the two principal polymer domains. Then, two models of the interphase were evaluated: (i) a two-dimensional viscoelastic film and (ii) the interphase of finite thickness. Both led to at least two relaxation times:

$$ \begin{array}{l}{\tau}_1=\left\{{\left(1+R/\Delta L\right)}^2\eta \left(R+\Delta \mathrm{L}\right)\left(1/{\nu}^{\prime }+1/{\nu}^{{\prime\prime}}\right)\right\}\\ {}{\tau}_2=\left\{\eta \left(R+\Delta L\right)/\left({\nu}^{\prime }+{\nu}^{{\prime\prime}}\right)\right\};\mathrm{where}\kern0.5em {\nu}_{12}={\nu}^{\prime }+{\nu}^{{\prime\prime}}\end{array} $$

(7.72)

The experimental data employing dynamic testing in the kHz region for ionic emulsions was equally well described using either model. The emulsion elasticity was found to originate in droplet deformation. For nonionic emulsions, only one relaxation time was observed. The data were interpreted in terms of the second Oldroyd’s model in which the interfacial tension is more important than the viscoelasticity of the interphase. The steady-state viscosities of both ionic and nonionic systems at the volume fraction ϕ ≤ 0.2 were found to follow Simha’s Eq. 7.24.

For concentrated emulsions and foams, Princen (1983, 1985) proposed a stress–strain theory based on a two-dimensional cell model. Consider steady-state shearing of such a system. Initially, at small strains, the stress increases linearly as in an elastic body. As the strain increases, the stress reaches the yield value, then at still higher deformation, it catastrophically drops to negative values. The reason for the latter behavior is the creation of unstable cell structure that generates a recoil mechanism. The predicted dependencies for modulus and the yield stress were expressed as

$$ \begin{array}{l}G\equiv \sigma /\gamma \kern0.75em \propto \kern0.75em {\nu}_{12}{\phi}^{1/3}/d\\ {}\ \mathrm{and}\kern0.75em {\sigma}_y\propto G{\tilde{F}}_{\max}\left(\phi \right)\end{array} $$

(7.73)

where the function ${\tilde{\mathrm{F}}}_{\max}\left(\mathtt{\phi}\right)$ is the concentration-dependent, dimensionless contribution to stress per single drop. The theory was evaluated using a concentrated oil-in-water system.

Princen’s work was followed by (Reinelt 1993), who considered theoretical aspects of shearing three-dimensional, highly concentrated foams and emulsions. Initially, the structure is an assembly of interlocked tetrakaidecahedra (which have six square surfaces and eight hexagonal ones). An explicit relation for the stress tensor up to the elastic limit was derived. When the elastic limit is exceeded, the stress–strain dependence is discontinuous, made of a series of increasing parts of the dependence, displaced with a period of γ = 2^3/2.

The validity of Princen’s theory for concentrated water-in-oil emulsions was also investigated by Ponton et al. (2001), using the droplet size distribution determined by laser diffractometry based on the Mie theory model. Comparing the surface–volume diameter and the mass fractions of emulsions depicted an increase in the particle size with the volume fraction reduction. They showed that their experimental data (as obtained by oscillatory measurements and droplet-size distribution) corroborated the expression of the elastic shear modulus for the two-dimensional model proposed by Princen and Kiss (1986). In this model, G′ is proportional to (σ/R_SV)Φ_v ^1/3(Φ_v-Φ_c) where σ is the interfacial tension, R_SV is the volume–surface radius (as obtained by laser diffractometry), and Φ_v and Φ_C are the volume fraction and the critical volume fraction, respectively (Ponton et al. 2001). The latter was found to be 0.714 experimentally, which is close to the value obtained by Princen (∼0.712) (Ponton et al. 2001).

Paruta-Tuarez et al. (2011) analyzed the Princen and Kiss equation (Princen and Kiss 1986) associated with the linear form of the function E(Φ_v), (E(Φ_v) = A(Φ_v − Φ_c)). This function was proposed to take into account the experimental dependence of storage modulus (G′) on the dispersed-phase volume fraction (Φ_v). However, it was found that the Princen and Kiss equation underestimates the storage modulus values in some cases, due to the particular set of experimental data used for derivation of E(Φ_v). Thus, despite the applicability of the linear form of the function E(Φ_v) as proposed by Princen and Kiss, it is not universal and another choice of experimental data could lead to other mathematical functions (Paruta-Tuarez et al. 2011).

3.2.3.3 Experimental Data

Experimentally, there are three concentration regions of emulsion flow: (i) dilute for ϕ < 0.3, characterized by nearly Newtonian behavior; semi-concentrated at 0.3 < ϕ < ϕ_m with mainly pseudoplastic character; and concentrated at ϕ_m < ϕ < 1.0, showing solid-like properties with modulus and yield.

The necessary condition for non-Newtonian flow to occur is droplet deformation, expressed either by the deformability parameter, D = (a₁ − a₂)/(a₁ + a₂), or by the aspect ratio, p = a₁/a₂.

Figure 7.16 illustrates the effect of shear rate, initial drop diameter, and the viscosity ratio on the droplet aspect ratio, p. For low and high values of λ, a pseudoplastic dependence has been observed (Talstoguzov et al. 1974).

Fig. 7.16

Effect of the shear rate (top), the initial drop diameter (middle), and the viscosity ratio (bottom) on the drop aspect ratio for the systems: water–gelatin–dextran (W–G–D, circles) and water–gelatin–polyvinyl alcohol (W-G-P, squares) (Talstoguzov et al. 1974)

The shear viscosity of polymer-thickened oil-in-water emulsions was studied by Pal (1992). Addition of polyethyleneglycol, PEG, made it possible to vary the matrix liquid viscosity. The flow was pseudoplastic, following Ellis dependence:

$$ {\eta}_r=1/\left[1+A{\eta}_o{\sigma}_{12}^{\alpha -1}\right] $$

(7.74)

where A and α are equation parameters. The zero-shear viscosity, η_o, was found to follow a modified Mooney dependence (see Eq. 7.28):

$$ \ln {\eta}_r=2.5{K}_1\phi /\left[1-{K}_2\phi \right] $$

(7.75)

where K_i are equation parameters. It was observed that η_r of the thickened emulsions is lower than that for the emulsions without PEG.

In liquid–liquid systems, upon increase of concentration of the dispersed phase, at certain concentration suddenly the dispersed and continuous liquids exchange roles. This is known as a phase inversion. Salager et al. (1983) and Minana-Perez et al. (1986) reported two types of phase transition in ionic emulsions – in the first, viscosity goes through a minimum, whereas in the second it goes through a maximum. The first type of transition (normal) is associated with a decrease of the interfacial tension coefficient and formation of a microemulsion. The second (catastrophic) transition is associated with an inversion of unstable structure to a stable one.

The extensional viscosity of non-Newtonian emulsions, η_E, at the dispersed phase volume fraction ϕ = 0.3–0.8, was measured using the opposed nozzles configuration. For more diluted emulsions, ϕ < 0.6, the elongational viscosity, η_E, was found to decrease with the rate of elongation, $\dot{\varepsilon}$, mimicking the flow curves in a shear field, $\upeta \kern0.2em \mathrm{versus}\kern0.2em \dot{\gamma}$. Furthermore, the Trouton rule, η_E ≅ 3η, was found to be reasonably obeyed. However, for more concentrated emulsions, ϕ ≥ 0.7, owing to the presence of yield stress, η_E was found to depend on the test geometry, viz., nozzle diameters and their separation (Anklam et al. 1994). Since in more concentrated emulsions, the structure is engendered by close packing of interacting spheres, its destruction must depend on the type of imposed deformation as well as on strain. In consequence, the lack of correlation between the shear flow and extensional flow data was expected.

Compliance, J, of concentrated oil-in-water emulsions at 0.4 ≤ ϕ ≤ 0.7 was found to follow a two-retardation time process:

$$ J(t)-{J}_0+{J}_1 \exp \left\{-t/{\tau}_1^{*}\right\}+{J}_2 \exp \left\{-t/{\tau}_2^{*}\right\} $$

(7.76)

where J_o and J_i are, respectively, instantaneous compliance and retarded values, all three decreasing with concentration of the dispersed phase (Gladwell et al. 1986).

For a similar system, the shear viscosity was found to follow the power law model with yield (Pal et al. 1986). Owing to the presence of yield stress, the flow of concentrated emulsion was found to be facilitated by superposition of 10 Hz oscillation on the steady-state shear flow – up to 40 % energy saving was reported (Jezequel et al. 1985). More recently, the relative viscosity of emulsions was described in terms of scaling parameters (Pal 1997). Ten principal variables were incorporated into six dimensionless groups: λ, κ, reduced time, t_r = t/(η_md³/8 k_B T), relative density, ρ_r = ρ_d/ρ_m, Peclet number, $\mathrm{Pe}={\upeta}_{\mathrm{m}}\dot{\gamma}{\mathrm{d}}^3/8{\mathrm{k}}_{\mathrm{B}}\mathrm{T}$, and Reynolds number, $\mathrm{Re}={\uprho}_{\mathrm{m}}\dot{\gamma}{\mathrm{d}}^2/4{\upeta}_{\mathrm{m}}$. For the steady-state flow of well-stabilized emulsions, it was argued that the relative viscosity of emulsions should depend only on two parameters: volume fraction of the dispersed phase and Re, i.e., ${\upeta}_{\mathrm{r}}=\mathrm{f}\left(\mathtt{\phi},\mathrm{Re}\right)$. At constant composition, the experimental data for coarse and fine oil-in-water emulsions plotted versus the deformation rate, $\dot{\gamma}$, showed different dependencies (higher η_r for finer dispersion), but when plotted versus Re, a single dependence was found.

The understanding rheology of dilute and concentrated multiple emulsions is necessary to provide information related to mixing, processing, and storage of such systems. To predict the relative viscosity of multiple emulsions of type B, containing several small internal droplets, and type C, containing a large number of small internal droplets, four variables were introduced in the proposed viscosity models (Pal 2008) : K ₂₁(viscosity ratio of primary-emulsion matrix to multiple-emulsion matrix), K ₃₂ (viscosity ratio of internal droplet to primary-emulsion matrix), φ^PE (volume fraction of internal droplets within a multiple emulsion droplet), and φ^ME (volume fraction of total dispersed phase in the whole multiple emulsion). Based on experimental data and model predictions, it was shown that the viscosity generally increases with increase in any of these variables. Comparison between experimental data and predictions of various models showed that the model based on the Yaron and Gal-Or equation (Yaron and Gal-Or 1972) was reasonably in agreement with experimental data. However, the model based on the Oldroyd equation under predicted and the model obtained using the Choi–Schowalter equation (Choi and Schowalter 1975) overestimated the viscosity of multiple emulsion systems (Pal 2008).

3.2.4 Melt Flow of Block Copolymers

Block copolymers, BC, are macromolecular species in which long chains of one polymer are joined to long chains of another polymer. Thus, BCs are made of at least two chemically different chains arranged linearly, in form of multi-branch stars, combs, etc. Linear block copolymers are the most common – diblock, AB, triblock, ABA, or multiblock, A(BA)_n.

Commercial BCs are prepared from monomers that, upon polymerization, yield immiscible macromolecular blocks, one rigid and the other flexible, that separate into a two-phase system with “rigid” and “soft” domains. The concentration and molecular weights provide control of the size of the separated domains, thus the morphology and the interconnection between the domains. The existence of a dispersed rigid phase in an elastomeric matrix is responsible for its thermoplastic elastomer behavior. For symmetric block copolymers, Leibler (1980) showed that a sufficient condition for microphase separation is (χ_AΒN) = 10.5, where χ_AΒ is the binary thermodynamic interaction parameter and N is the degree of BC polymerization (Folkes 1985).

As in polymer blends, also in BC the phase transition is affected by flow. Theoretically it was predicted that homogeneous melt can be obtained at T < UCST, provided that the stress field exceeds the critical value for the phase demixing, σ₁₂ > σ_{12, crit} (Lyngaae-Jørgensen 1989).

For most BCs the phase diagram is characterized by the presence of an upper critical solution temperature, UCST, also known as an order–disorder transition temperature or a microphase separation temperature. Below UCST the block copolymers phase separate, while above it, an isotropic melt is obtained. Owing to the chemical link between the blocks, during phase separation in BCs, micro-domains instead of macroscopic phases are usually obtained. Furthermore, since the micromorphology depends on the concentration as well as on the temperature, the phase diagram is complex, similar to those of metallic alloys. Under thermodynamic equilibrium conditions, depending on the composition, magnitude of the interaction parameter, and temperature, spherical, cylindrical, lamellar, or some other structures are formed. There are three elements to BC morphology: domain size, domain shape, and the interfacial thickness – they lead to a wide variety of rheological responses (Inoue et al. 1969; Meir 1969; Hashimoto et al. 1980a,b; Krause 1980).

For A-B block copolymers, the thickness of the interphase, Δl, is theoretically derived by Helfand and Wasserman (1976, 1978, 1980):

$$ \begin{array}{l}\Delta l=2\sqrt{\left({\beta}_A^2+{\beta}_B^2\right)/2{\chi}_{AB}}\\ {}\mathrm{where}:\kern1em {\beta}_i^2=\left({\rho}_{oi}{b}_i^2\right)/6;\kern1em \mathrm{and}\kern1em {b}_i=<{R}_i^2>/{Z}_i\end{array} $$

(7.77)

where b _i is length of Kuhn’s statistical segment, Z _i is degree of polymerization, ρ _oi is density, and <R _i ²> is the radius of gyration of the block. For immiscible systems χ_AΒ ≥ 0; thus as the “antipathy” of the two types of blocks toward each other decreases and χ _AB → 0, the interphase thickness increases.

Recently, another theoretical expression for Δl was derived for symmetric diblock copolymer with N_A = N_B = N/2 with lamellar morphology (Spontak and Zielinski 1993):

$$ \Delta l=\Delta {l}_{\mathit{\infty}}{\left[1-\left(8 \ln 2\right)/\left({\chi}_{AB}N\right)\right]}^{-1/2} $$

(7.78)

where N is the degree of BC polymerization and Δl _∞ is the interface thickness when N → ∞. The dependence should only be used for χ _AB N ≥ 20. The theory predicts that as χ_ABN decreases, the thickness of the interphase increases – nearly three times more rapidly for block copolymers than for homopolymer blends.

Considering melt flow of BCs, it is usually assumed that the test temperature is UCST > T > T_gc, where T_gc stands for glass transition temperature of the continuous phase. However, at T_gc < T < T_gd (T_gd is T_g of the dispersed phase), the system behaves as a cross-linked rubber with strong viscoelastic character. At UCST > T > T_gd, the viscosity of BC is much greater than would be expected from its composition. The reason for this behavior is the need to deform the domain structure and pull filaments of one polymer through domains of the other. Viscosity increases with increase of the interaction parameter between the BC components, in a similar way as the increase of the interfacial tension coefficient in concentrated emulsions causes viscosity to rise (Henderson and Williams 1979).

In shear, the block copolymers exhibit time-dependent flow with yield stress (Liu et al. 1983):

$$ {\sigma}_{12}(t)={\sigma}_y+{\eta}_0\dot{\gamma}\left\{\beta +\left[\left(1-\beta \right)/\left(1+b{\dot{\gamma}}^m\right)\right]\left[1+b{\dot{\gamma}}^m \exp \left\{- kt\left(1/b={\dot{\gamma}}^m\right)\right\}\right]\right\} $$

(7.79)

where β represents the relative residual viscous dissipation parameter, b and m are parameters originating from the structural breakdown and reformation of structure, while k is the loss rate constant. The relation can describe multiple phenomena: yield, upper and lower Newtonian plateaus, pseudoplasticity, stress growth and overshoot, thixotropy, hysteresis, etc.

The multiplicity of rheological phenomena observed in BC is related to sensitivity of the melt structure to independent molecular and rheological variables. For example, for styrene-butadiene-styrene (SBS), the activation energy of flow ΔE_η = 80 or 160 kJ/mol for compositions containing less or more that 31 vol% of styrene. The difference originates in the structure; it is dispersed below 31 % and interconnected above (Arnold and Meier 1970).

Block polymers, owing to the tendency for formation of regular structures tailored by molecular design, are ideal models for compatibilized, two-phase polymer blends or alloys. Blends do show similar rheological behaviors, e.g., yield, pseudoplasticity, thixotropy, structural rearrangements, but since the morphology is more difficult to control, the interpretation of data could present serious difficulties.

4 Rheology of Miscible Blends

4.1 General Observations

Miscible polymer blends are less common that immiscible ones. The miscibility is usually confined to a specific range of independent variables, such as chain configuration, molecular weight, composition (viz., for alternate copolymers), temperature, pressure, etc. Nevertheless, Krause reported that 1680 two-, three, or four-component polymeric mixtures were identified as miscible in 780 publications (Krause 1980).

It is noteworthy that even in miscible polymers of similar molecular structure, viz., 1,4-polyisoprene with 1,2-polybutadiene, time–temperature superposition fails. With the glass transition temperatures separated by 60 °C, the polymers preserve their different dynamics in the blends (Kannan and Kornfield 1994). Thus, even miscible systems can be rheologically complex. The rheological behavior of blends in the vicinity of phase separation is of great fundamental importance. It will be discussed in Sect. 7.4.3.

PPE/PS mixtures are considered classical examples of miscible polymer blends. Within the accessible range of temperatures, single-phase melts have been observed with the size of homogeneity below 20 nm. Dynamic flow behavior of PPE/PS blends, with molecular weight ratio MW(PS)/MW(PPE) ≅ 1, was studied in a wide range of temperatures and compositions (Prest and Porter 1972). The authors assumed additivity of the free volumes of the components and characterized the blend flow behavior under iso-free volume conditions. Increasing PPE content resulted in higher values of the storage and loss shear moduli, G′ and G″. The same blends, but with MW(PS)/MW(PPE) = 100 were studied by Araujo and Stadler (1988).

Blends of atactic polymethylmethacrylate with polyethyleneglycol, PMMA/PEG, were reported miscible (Colby 1989). Their rheology, PMMA/PEG = 50/50 and 80/20 at T = 160–210 °C, was studied in a dynamic shear field (Booij and Palmen 1992). By contrast with homopolymers, the blends did not follow the time–temperature superposition. The deviation was particularly poor at low temperatures. The reason for the deviation is most likely based on the different temperature dependence of the relaxation functions. The authors concluded that in miscible blends, the temperature dependence of the relaxation times of individual macromolecules depends on composition. This leads to different degree of mutual entanglement and hence the rubber plateau moduli.

In contrast with PPE/PS blends, those of PS with PVME are known to have lower critical solution temperature, LCST, in the middle of the experimentally accessible temperature range, LCST = 100–180 °C (depending on composition and MW of the components). Rheology of these systems was studied within the miscible and immiscible as well as across the phase separation region. Within the miscible region, addition of PVME was reported to plasticize PS, thus shifting the terminal zone of G′ and G″ to higher frequencies (Schneider and Brekner 1985; Brekner et al. 1985; Yang et al. 1986). It was also reported that the time–temperature superposition principle for the blends breaks down as the temperature approaches the glass transition temperature, T_g (Cavaille et al. 1987). For the PS/PVME blends, with molecular weight ratio MW(PS)/MW(PVME) ≅ 40, separate relaxation times were found in the entanglement region (Stadler et al. 1988) (in homologous polymer blends having significantly different molecular weights, the relaxation spectra also show separate relaxation times for the components). Time–temperature superposition was obtained up to T = LCST + 40 °C (Stadler et al. 1988). For the PS/PVME blends, with molecular weight ratio MW(PS)/MW(PVME) ≅ 2, phase separation was found to increase G′ but not G″; thus the time–temperature superposition breaks down (Ajji et al. 1989; Ajji and Choplin 1991). For similar blends, with MW(PS)/MW(PVME) ≅ 0.8, total breakdown of the time–temperature superposition principle was reported for the phase-separated region. Large increases in both G′ and G″ were observed (Mani et al. 1992).

Sharma and Clarke (2004) reported experiments on a lower critical solution temperature blend of PSD and PVME, in order to determine the miscibility of the blend based purely on rheology. The investigation was done in the temperature range of T _g (glass-transition temperature) + 45 K to T _g + 155 K in which the blend morphology was expected to change from homogeneous to two-phase structure. Dynamic temperature sweep was found to be sensitive to the phase-separation temperature and the miscibility region. They suggested that the first change in the slope of the smoothly varying storage modulus is associated with the binodal temperature. Three different zones identified in the tan δ-temperature curve (peak zone and off-peak zones) were shown to correspond to the miscible, metastable, and phase-separated regions of the phase diagram (Sharma and Clarke 2004).

Time–temperature superposition works well in the homogeneous region of LCST (e.g., polystyrene and poly(vinyl methyl ether)) or UCST (e.g., polystyrene and poly(α-methylstyrene))systems. This suggests scaling behavior of G′ ∼ ω ² and G′′ ∼ ω ¹ at low frequencies. However, time–temperature superposition fails in the metastable region of these blends, which exhibit an increase in the magnitude of G′ in the terminal zone (Kim et al. 1998; Sharma and Clarke 2004). Figure 7.17 depicts clear deviation from scaling behavior of homogeneous blends of PSD/PVME, just after the rheologically determined binodal temperature (only the temperatures at which the time–temperature superposition failure occurs are listed in the fig., i.e., above 104 °C). It was suggested that the observed thermo-rheological complexity is related to the different morphologies formed by different coarsening kinetics. It seems that concentration fluctuation induced stress, which is mostly of elastic origin, causes storage modulus to be more sensitive to phase transitions than loss modulus (Kapnistos et al. 1996; Sharma and Clarke 2004).

Fig. 7.17

Master curves of storage modulus (G′) and loss modulus (G′′) for a 50:50 PSD/PVME blend, as a function of frequency ω (Sharma and Clarke 2004)

The investigation of the Han plots, which is the log–log plot of storage modulus versus loss modulus, is another effective method to determine the onset of phase separation. This method is more sensitive to concentration fluctuations than data obtained from time–temperature superposition. The Han plot of homogeneous phases shows two main features: temperature independence and terminal slope of two (Han et al. 1990, 1995). Deviations from these two criteria were reported only for Han plots above the LCST and below the UCST (Kim et al. 1998; Sharma and Clarke 2004). Therefore, it has been suggested to use this method to infer the phase-separation (binodal) temperature rheologically.

There are other fingerprints that may be used to track the critical point of the phase transition in polymer blends, using the linear regime of rheological experiments. One method is the so-called Cole–Cole diagram showing the relationship between the dynamic viscosity (η′) and the loss viscosity (η″). For example, Ajji et al. (1988a) used the Cole–Cole representations to estimate the phase-transition temperature of the 80:20 PS/PVME blend, as shown in Fig. 7.18 at different temperatures. The characteristic of the Cole–Cole plot for homogeneous blends is the presence of only one circular arc. Therefore, the temperature at which a second circular arc begins to appear is the phase-transition temperature of the system. Close to this temperature on the right-hand side of the first arc, a tail develops and forms a second arc. Phase-transition temperature was found to be about 140 °C by this technique, which was close to the value of 138 °C found by cloud point measurements (Ajji et al. 1988a,b). Phase separation of polymer blends can be also identified in the relaxation spectrum H(τ) of polymer blends in the form of an additional relaxation (Bousmina et al. 2002; Zuo and Zheng 2006).

Fig. 7.18

Cole–Cole plot of the 80:20 blend at different temperatures (Ajji et al. 1988a)

According to Onuki (1987), the shear viscosity increases in phase-separating fluids near the critical point. However, Sharma and Clarke (2004) claimed that Onuki’s prediction of features specific to the transition from a homogeneous to a two-phase regime was not observed for PSD/PVME blends.

Blends of tetramethyl polycarbonate, TMPC, with PS were reported miscible (Wisniewsky et al. 1984). Couchman (1996) demonstrated that the concentration dependence of η_o at 230 °C can be predicted from the characteristic parameters of the two components, assuming absence of specific interactions.

In miscible blends, flow behavior depends on free volume, entanglements, and specific interactions. From Doolittle’s equation, assuming additivity of the occupied volume and non-additivity of the free volume, Steller and Zuchowska (1990) derived:

$$ \begin{array}{l} \ln {\eta}_b={\displaystyle \sum_{i=1}^n{\phi}_i} \ln {\eta}_i=\frac{{\displaystyle \sum_{i=1}^n{w}_i\left[\left({\delta}_i-1\right)/\left({\delta}_{i+1}\right)\right]{V}_i}}{2{\displaystyle \sum_{i=1}^n{w}_i{V}_i/\left({\delta}_i+1\right)}}-\left(1/2\right){\displaystyle \sum_{i=1}^n{\phi}_i\Big({\delta}_i-1}\Big)\\ {}\delta \equiv {\left[1-4\left(\partial \ln \eta /\partial T\right)/\left(\partial \ln V/\partial T\right)/B\right]}^{1/2}=\left(2{V}_0+{V}_f\right)/{V}_f\end{array} $$

(7.80)

where w _i and V _i are, respectively, weight fraction and specific volume of i-th component, while V _o and V _f are the occupied and free volume, respectively. Since the parameter δ can be determined experimentally (from the temperature gradient of the viscosity and specific volume – see Eq. 7.80), the dependence is fully predictive, as shown in Fig. 7.19.

Fig. 7.19

The experimental (points) and computed from Eq. 7.80 relation between viscosity and composition for polypropylene blends with styrene-ethylene-butene-styrene block copolymer (Steller and Zuchowska 1990)

The reptation model provides simple mixing rules for miscible systems (Doi and Edwards 1986):

$$ {G}_N^o={\displaystyle \sum {G}_{Ni}^o{\phi}_i;\kern1em {\eta}_o={\displaystyle \sum {\eta}_{oi}{\phi}_i;\kern1em {J}_e^o{\eta}_o^2={\displaystyle \sum {J}_{ei}^o{\eta}_{oi}^2}}}{\phi}_i $$

(7.81)

where G ^o _N is the plateau modulus, η _o is the zero-shear viscosity, and J ^o _e is the recoverable shear compliance. This “single reptation model” neglects the thermodynamic interactions and constraints release. Viscoelasticity of miscible polymer blends was also analyzed by Tsenoglou (1988). The “double reptation model” resulted in the following mixing rules for the miscible blends:

$$ \begin{array}{l}{G}_N^o={\left[{\displaystyle \sum_{i=1}^2{\left({G}_{Ni}^o\right)}^{1/2}{\phi}_i}\right]}^2\\ {}{\eta}_o={\eta}_{o1}{\phi}_1^2+{\eta}_{o2}{\phi}_2^2+4{\left({G}_{N1}^o{G}_{N2}^o\right)}^{1/2}{\phi}_1{\phi}_2{\left[\left({G}_{N1}^o/{\eta}_{o1}\right)+\left({G}_{N2}^o/{\eta}_{o2}\right)\right]}^{-1}\\ {}{J}_e^o{\eta}_o^2={J}_{e1}^o{\eta}_{o1}^2{\phi}_1^2+{J}_{e2}^o{\eta}_{o2}^2{\phi}_2^2+8{\phi}_1{\phi}_2{\left[\frac{{\left({G}_{N1}^o/{G}_{N2}^o\right)}^{1/4}}{{\left({J}_{e1}^o{\eta}_{o1}^2\right)}^{1/2}}+\frac{{\left({G}_{N2}^o/{G}_{N1}^o\right)}^{1/4}}{{\left({J}_{e2}^o{\eta}_{o2}^2\right)}^{1/2}}\right]}^{-1}\;\end{array} $$

(7.82)

Validity of Eqs. 7.81 and 7.82 was examined for mixtures of entangled, nearly monodisperse blends of poly(ethylene-alt-propylene) with head-to-head PP (Gell et al. 1997). The viscoelastic properties, compared at constant distances from the respective glass transition temperatures of each component, were found to obey the time–temperature superposition principle. The data agreed better with the predictions of Eq. 7.82 than Eq. 7.81. However, for blends of linear and branched PE, the relations were found valid only when MW and rheological properties of the two components were similar (Groves et al. 1996).

The double reptation model was used to evaluate viscoelastic behavior of metallocene-catalyzed polyethylene and low-density polyethylene blends by Peon et al. (2003). They compared their results with those obtained for HDPE/BPE blends prepared under similar conditions. Since this model assumes miscibility between the mixed species, the experimental viscosity of HDPE/BPE blends showed only small deviation compared to that expected according to the reputation miscible model. However, the model underestimated the compositional dependence of the zero-shear viscosity for mPE/LDPE blends, especially at intermediate levels. The enhanced zero-shear viscosity in immiscible blends such as PETG/EVA, PP/EVA, or EVA/PE blends was found to be more abrupt than it is for mPE/LDPE blends (Lacroix et al. 1996, 1997; Peon et al. 2003).

The enhanced viscoelastic functions are attributable to additional relaxation processes that occur at low frequencies associated with deformation of the dispersed phase. Therefore, for cases such as mPE/LDPE, where partial miscibility at high LDPE content and the extremely different relaxation times of the phases in the blends rich in mPE are observed, a hybrid model including the double reptation approach for the matrix and the linear Palierne approach for the whole system could successfully explain the viscoelastic response of these blends (Peon et al. 2003).

Yu et al. (2011) studied rheology and phase separation of polymer blends with weak dynamic asymmetry ((poly(Me methacrylate)/poly(styrene-co-maleic anhydride)). They showed that the failure of methods, such as the time–temperature superposition principle in isothermal experiments or the deviation of the storage modulus from the apparent extrapolation of modulus in the miscible regime in non-isothermal tests, to predict the binodal temperature is not always applicable in systems with weak dynamic asymmetry. Therefore, they proposed a rheological model, which is an integration of the double reptation model and the self-concentration model to describe the linear viscoelasticity of miscible blends. Then, the deviation of experimental data from the model predictions for miscible blends determines the binodal temperature. This method was successfully applied in PMMA/SMA blend with weak dynamic asymmetry (Yu et al. 2011).

4.2 Relaxation Spectrum and Linear Viscoelasticity

Substituting Eq. 7.42 into Gross frequency relaxation spectrum, H_G, results in the following expression:

$$ \begin{array}{c}\hfill {\tilde{\mathrm{H}}}_{\mathrm{G}}{\equiv \mathrm{H}}_{\mathrm{G}}/{\eta}_0=\left(2/\pi \right){\mathrm{r}}^{-{\mathrm{m}}_2} \sin \left({\mathrm{m}}_2\Theta \right)\hfill \\ {}\hfill \mathrm{r}=\Big[1+2{\left(\omega \tau \right)}^{{\mathrm{m}}_1} \cos \left({\mathrm{m}}_1\pi /2\right)+{\left(\omega \tau \right)}^{{2\mathrm{m}}_1}{\left)\right.}\Big]^{{{\raise0.7ex\hbox{$1$} \mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace}\lower0.7ex\hbox{$2$}}}}\hfill \\ {}\hfill \Theta \equiv \mathrm{arc} \sin \left\{{\left(\omega \tau \right)}^{{\mathrm{m}}_1}{\mathrm{r}}^{-1} \sin \left({\mathrm{m}}_1\pi /2\right)\right\}\hfill \end{array} $$

(7.83)

Thus, once the four parameters of Eq. 7.42 are known, the relaxation spectrum and then any linear viscoelastic function can be calculated. For example, the experimental data of the dynamic storage and loss shear moduli, respectively G′ and G″, or the linear viscoelastic stress growth function in shear or uniaxial elongation can be computed from the following relations (Utracki and Schlund 1987):

$$ \begin{array}{l}{G}^{\prime}\left(\omega \right)={\displaystyle \underset{-\mathit{\infty}}{\overset{+\mathit{\infty}}{\int }}\left\{s{H}_G(s)/\left[1+{\left(s/\omega \right)}^2\right]\right\}}d \ln s\\ {}{G}^{{\prime\prime}}\left(\omega \right)={\displaystyle \underset{-\mathit{\infty}}{\overset{+\mathit{\infty}}{\int }}\left\{\omega {H}_G(s)/\left[1+{\left(\omega /s\right)}^2\right]\right\}}d \ln s\\ {}{\eta}_E^{+}(t)={\displaystyle \underset{-\mathit{\infty}}{\overset{+\mathit{\infty}}{\int }}\left\{{H}_G\left(\omega \right)\left[1- \exp \left(-\omega t\right)\right]\right\}}d \ln \omega \end{array} $$

(7.84)

Since Gross frequency relaxation spectrum can be computed from η′, i.e., from the loss modulus, G″ = η′ω, the agreement between the computed and measured G′ values provides good means of verifying both the computational and experimental procedures. It has been found that Eqs. 7.83 and 7.84 are useful to evaluate the rheological performance of systems that obey linear viscoelastic principles.

According to the definition of the reduced relaxation spectrum, the integral:

$$ {\displaystyle \underset{-\mathit{\infty}}{\overset{+\mathit{\infty}}{\int }}{\tilde{H}}_G(s)d \ln s}\equiv 1 $$

(7.85)

Thus, the coordinates of the maximum, ${\tilde{\mathrm{H}}}_{\mathrm{G}, \max };{\upomega}_{\max }$, are related respectively to the system polydispersity and molecular weight. However, if the system is miscible, these functions are fully predictable from the composition, polydispersity, and molecular weight of the components. Note that in miscible blends, the general relation between the relaxation spectrum of a mixture and its composition follows the third-order blending rule:

$$ H\left(\tau \right)={\displaystyle \sum {w}_{ijk}{H}_{ijk}\left(t/{\tau}_{ijk}\right)} $$

(7.86)

The dependence can be significantly simplified, when all fractions are either entangled or not (the situation that exists in most polymer blends):

$$ {H}_G\left(\omega \right)={\displaystyle \sum {w}_i}{H}_{Gi}\left(\omega \right) $$

(7.87)

Thus, for miscible polymer blends, the relaxation spectrum is a linear function of the relaxation spectra of the components and their weight fractions, w_i. Hence, one may use rheological functions to detect miscibility/immiscibility of polymer blends. An example is presented in Fig. 7.20 (Utracki and Schlund 1987).

Fig. 7.20

Coordinates of the maximum of the Gross frequency relaxation function, ${\tilde{\mathrm{H}}}_{\mathrm{G}, \max }$ (top), and, ω_max (bottom), versus, respectively, the polydispersity index, M_w/M_n, and the zero shear viscosity, η_o, a measure of the molecular weight (Utracki and Schlund 1987)

Two principles can be used for the rheological methods of miscibility detection:

• 1. Effect of polydispersity on the rheological functions

• 2. Effect of the inherent nature of the two-phase flow

The first principle makes it possible to draw conclusions about miscibility from, e.g.:

• Coordinates of the relaxation spectrum maximum (Utracki and Schlund 1987)

• Cross-point coordinates (G_x, ω_x) (Zeichner and Patel 1981)

• Free volume gradient of viscosity: α = d(lnη)/df

• Initial slope of the stress growth function: S ≡ dlnη ⁺_E /d ln t (Schlund and Utracki 1987)

• The power-law exponent $\mathrm{n}\equiv \mathrm{d} \ln {\upsigma}_{12}/\mathrm{d} \ln \dot{\upgamma}\cong \mathrm{S}$

The second principle involves evaluation of, e.g.:

• Extrudate swell parameter, B = D/Do

• Strain (form) recovery

• Yield stress

These effects, associated with immiscibility, will be discussed in later in this chapter.

4.3 Phase Separation and Flow

The phase behavior of polymer blends under flow was reviewed by Kammer et al. (1993).

For most polymer blends, the phase diagram is characterized by the presence of the lower critical solution temperature, LCST. Thus, as the temperature increases, miscible polymer blends may phase-separate. Theoretically, the miscibility region stretches up to the binodal. However, as the system approaches the binodal, there is strong mutual interaction between the rheology and thermodynamics (Rangel-Nafaile et al. 1984; Larson 1992).

For systems of small molecules, the phase diagram does not change by the kinetic energy. However, due to the viscoelastic nature of polymer blends, a part of the flow energy could be stored as the free elastic energy. This influences the Gibbs free energy of the blend. Therefore, the phase diagram and miscibility would change. Various studies attempted to correlate this energy to the properties and the conditions of flow. One approach involves modification of the free energy of the system by the addition of the elastic free energy, which is expressed in terms of the viscosity and the shear modulus. Berrayah and Maschke (2011) considered the effects of shear on the phase diagram of binary polymer blends of poly(styrene acrylonitrile) copolymer and poly(methyl methacrylate) characterized by a lower critical solution temperature (LCST). Using the above theoretical formulism, they showed that predictions are in good agreement with cloud point data of the PSAN/PMMA blend in the quiescent state and the miscibility was enhanced with increasing shear rate (Fig. 7.21) (Berrayah and Maschke 2011).

Fig. 7.21

The equilibrium phase diagram of PSAN/PMMA under shear flow at several shear rates. Symbols represent the cloud point data of the system PSAN/PMMA in the quiescent (Berrayah and Maschke 2011)

The interaction between stress and composition in single-phase polymer solutions and blends is of theoretical and experimental concern. Flow-induced encapsulation has been known for a long time. Recently, the focus has shifted to miscible systems of nonuniform compositions placed in a nonuniform stress field. Two mechanisms have been proposed: the first postulating that long chains migrate to lower stress regions to decrease the elastic energy stored by deformation of the macromolecular coil (Metzner et al. 1979), the second assumes that long chains can support stress more than the short ones, creating imbalance of stresses and relative motion of the components (Doi and Onuki 1992). The latter theory makes it possible to calculate the concentration gradients in sheared blends. For example, in cone-and-plate geometry, the theory predicts migration of the high molecular weight fractions toward the center. Phenomenologically, the effect may be considered to originate from the hoop stress created in shearing of the larger polymeric chains that force them to migrate toward the center, engendering what is known as Weissenberg effect. The effect is related to the normal stress, σ_N = N₁ + 2 N₂, and the osmotic pressure gradient, dπ/dϕ, while the diffusion time is determined by the ratio (l/D_m), where l is the diffusion length scale and D_m is the mutual diffusion coefficient – the process is rather slow.

4.3.1 Influence of Thermodynamics on Rheology

For linear viscoelastic functions near phase separation at low strains, Larson and Fredrickson (1987) derived:

$$ \left.\begin{array}{l}{G}^{\prime}\left(\omega \right)={\omega}^2{\Delta}^{-5/2};\kern0.75em {\psi}_1={\psi}_2={\Delta}^{-5/2}\\ {}{G}^{{\prime\prime}}\left(\omega \right)=\omega {\Delta}^{-3/2};\kern0.75em \eta \left(\dot{\upgamma}\right)={\Delta}^{-3/2}\end{array}\right\} $$

(7.88)

where Δ = 2((χN)_s − (χN)) is a measure of thermodynamic distance from the spinodal. The theory indicates that, at spinodal, the linear viscoelastic functions go to infinity or, in other words, the system becomes rheologically nonlinear. Numerically, near the spinodal, the theory predicts that the ratio Ψ₂/Ψ₁ ≅ −1.35, instead of the usual Ψ₂/Ψ₁ = −0.05 to −0.20. All the data for diverse liquid systems indicate that when approaching phase separation, the viscosity should increase with the correlation length, but the rate of the increase and the absolute magnitude may vary from one system to another. The effect depends on the deformation rate and is more pronounced in high molecular weight systems.

This prediction was found qualitatively valid for blends of low density polyethylene, LDPE, with linear low density polyethylene, LLDPE. At about 20 wt% of LDPE, a sharp peak in the plot of a₁ ≡ dlnη/dlnY (where Y = 1/(f + 0.07) with f being the free volume fraction) versus composition. This behavior was associated with the phase separation in the blends (Utracki and Schlund 1987).

In contrast to the predictions of Eq. 7.88, the effective viscosity at the spinodal was described by the fluidity additivity relation (Onuki 1994, 1997):

$$ \begin{array}{l}1/{\upeta}_{\mathrm{eff}}={\mathtt{\phi}}_1/{\upeta}_1+{\mathtt{\phi}}_2/{\upeta}_2;\kern1em {\mathrm{N}}_1\propto \dot{\gamma}\left({\mathtt{\phi}}_1{\upeta}_2/{\mathtt{\phi}}_2\right)\\ {}\mathrm{at}\kern0.5em \mathrm{SD}:\kern1em {\mathtt{\phi}}_1/{\upeta}_1\approx {\mathtt{\phi}}_2/{\upeta}_2;\kern1em \mathrm{where}\kern1em {\mathtt{\phi}}_1=1-{\mathtt{\phi}}_2\end{array} $$

(7.89)

Similarly, the first normal stress difference, N₁, is also predicted to be proportional to the shear stress. The phase co-continuity condition was derived from the equal shear stress principle between two phase-separating phases. The dependence is the same as empirically derived by Paul and Barlow – see Eq. 7.6.

The effect of phase separation on the dynamic shear flow of PS/PVME blends was frequently studied (Schneider and Brekner 1985; Brekner et al. 1985; Yang et al. 1986; Cavaille et al. 1987; Stadler et al. 1988; Ajji et al. 1989; Ajji and Choplin 1991; Mani et al. 1992). The results seem to differ, depending on the relative magnitude on the molecular weight, MW(PS)/MW(PVME). When the ratio was large, PVME acts as a plasticizer. When the ratio was about 2, a passage through the phase-separation region affected the dynamic storage shear modulus, G′, but not the loss modulus, G″. Finally, for ratios less than one, it was reported that neither the storage nor loss dynamic shear modulus, G′ and G″, respectively, indicated any significant change near the phase separation region, but upon entering the phase separation region both functions increased. By measuring the fluorescence intensity, the authors were able to map the phase separation region well. The time–temperature superposition principle was found to be valid only within the miscible blends region (Mani et al. 1992).

Dynamic shear flow within the linear viscoelastic region was used to determine binodal and spinodal temperatures (T_b and T_s, respectively) in LCST-type blends (Vlassopoulos 1996). The system of interest was PMMA (containing 12 wt% ethyl acrylate) with 10–60 wt% SMA. The demixing temperature was determined in temperature sweeps, by plotting log G′ versus T – departure from a straight line was taken as T_b. Determination of T_s involved plotting [G″(ω)]²/[TG′(ω)]^2/3 versus 1/T. Again, linear extrapolation was used to determine T_s. The rheologically determined data were found to correspond reasonably well to those determined by turbidity and light scattering.

The viscoelastic properties of model blends with UCST were studied in dynamic and steady-state shearing (Vlassopoulos et al. 1997). Low molecular weight PS and poly(methyl phenyl siloxane), PMPS, were used – the neat resins showed Newtonian behavior. The equilibrium phase diagram was determined by optical means. Within the miscible region, blend viscosity followed the log-additivity rule, provided that the concentration was corrected for the difference in the surfaces (Mertsch and Wolf 1994):

$$ \begin{array}{l} \ln \eta ={w}_1 \ln {\eta}_1+{w}_2 \ln {\eta}_2+\left\{ \ln \left({\eta}_1/{\eta}_2\right)\frac{\varsigma {w}_1{w}_2}{1+\varsigma {w}_1}\right\}\\ {}\mathrm{where}:\kern1em \varsigma \left(\mathrm{Bondi}\right)={\left.\frac{S_1/{S}_2}{V_1/{V}_2}\right|}_{\mathrm{Bondi}}-1\;\end{array} $$

(7.90)

where w_i is the weight fraction of polymer i. The correcting factor, ς, can either be treated as a fitting parameter (ς = −0.54 was determined for PS/PMPS system) or it can be calculated using Bondi’s values of the surface, S_i, and volume, V_i, for each component (ς = −0.5 was calculated). The phase separation resulted in rheologically complex behavior. However, the rapid increases of the rheological functions near SD, predicted by Eq. 7.88, were not observed.

4.3.2 Influence of Rheology on Thermodynamics

The response of heterogeneous systems to a stress field allows them to be placed in two categories: (i) those in which stress induces irreversible changes (e.g., precipitation, denaturation of protein, crystallization, etc.) and (ii) those in which the changes are reversible. The classification is not perfect, as the type and magnitude of stress field can be crucial, but it provides a guide: in most cases, miscibility in systems (i) is reduced by stress, while in systems (ii) it is increased. In other words, if a system can be irreversibly modified by rheological means, its solubility will be reduced. An excellent review on the phase transition in shear flow has been published (Onuki 1997).

Microrheology indicates that drops burst when the capillarity parameter κ ≈ 1 (see Eq. 7.52). Thus, in shear, the equilibrium drop diameter d ∝ ν₁₂/σ₁₂ – the higher is the shear stress in the matrix or the lower is the interfacial tension coefficient, the smaller is the drop size. In other words, it is natural to expect that shearing improves dispersion. When the drop diameter becomes comparable to the radius of gyration of the macromolecules, miscibility is achieved (Silberberg and Kuhn 1952; Wolf 1980, 1984).

The above argument is correct for infinitely diluted systems. In the practical case at finite concentrations, drop coalescence may limit the dispersion process. However, when shearing takes place near the critical point, phase separation can only occur when the rate of shear is smaller than 1/τ_c, where τ_c is the thermodynamic relaxation time for the concentration fluctuations.

Strain compatibilization at low, steady-state stress was considered by Lyngaae-Jørgensen (1985):

$$ {\upsigma}_{\mathrm{cr}}^2\cong {\mathrm{a}}_{\mathrm{o}}\mathrm{T}\left({\mathrm{T}}_{\mathrm{s}}-\mathrm{T}\right);\kern1em \mathrm{T}\le {\mathrm{T}}_{\mathrm{s}} $$

(7.91)

where a _o is a material parameter. Subjecting block copolymers to above-critical stresses at low deformation rates made it possible to change T_s by ΔT = 29 °C. For systems with lower critical solution temperature, LCST, the spinodal was shifted to higher temperatures. The values a_o = 0.26 and 0.53 (kPa/K)² were calculated, for block copolymers and poly(styrene-co-acrylonitrile)/poly(methyl methacrylate) blends, respectively. Equation 7.91 is in qualitative agreement with experimental observations that, in polystyrene/polybutadiene/dioctylphthalate systems, the critical point shifted as according to ${\Delta \mathrm{T}}_{\mathrm{o}}\left(\dot{\upgamma}\right)\approx {\mathrm{a}}_{\mathrm{o}}{\mathrm{T}}_{\mathrm{o}}{\dot{\upgamma}}^{1/2}$, where a_o is a numerical (Hashimoto et al. 1990).

A thermodynamic theory of strain demixing was proposed (Horst and Wolf 1991, 1992, 1994). The authors postulated that the Gibbs free energy of mixing for flowing blends can be expressed as a sum of the equilibrium thermodynamic free energy of mixing, ΔG_m, and the flow-induced stored energy term ΔE_S:

$$ \Delta {G}_{\dot{\gamma}}=\Delta {G}_m-\Delta {E}_s=\left({\displaystyle \sum_{i=1}^n{x}_i{V}_i}\right)\left\langle {J}_e^o\right\rangle {\left[\left\langle {\eta}_o\right\rangle \dot{\gamma}\right]}^{2n} $$

(7.92)

where the averaged values of the zero-shear viscosity and the steady-state shear compliance can be calculated from, respectively

$$ \begin{array}{l}\left\langle {\eta}_o\right\rangle ={\left({\displaystyle \sum_{i=1}^n{w}_i{\eta}_i^{1/3.4}}\right)}^{3.4}\\ {}\left\langle {J}_e^o\right\rangle {\left\langle {\eta}_o\right\rangle}^{4.4/3.4}={\displaystyle \sum_{i=1}^n{w}_i{J}_{ei}^o{\eta}_i^{4.4/3.4}}\end{array} $$

(7.93)

The theory was found to predict complex behavior near the phase-separation conditions. As the rate of shear increases, first, the system undergoes homogenization, then demixing, followed by another homogenization and demixing. At high rates of shear, the system should behave similarly as in the quiescent state. These predictions were found to be in qualitative agreement with experimental data, e.g., for blends of ethylene-vinyl acetate copolymer with chlorinated polyethylene, EVAc/CPE, or polystyrene with poly(vinylmethylether), PS/PVME (Hindawi et al. 1992; Fernandez et al. 1993a, 1995).

The first observation of shear-induced increase of the LCST was reported for PS/PVME by Mazich and Carr (1983). The authors concluded that shear stress can enhance miscibility by 2–7 °C. Larger effects, ΔT ≤ 12 °C, were reported for the same system in hyperbolic flow (Katsaros et al. 1986). In a planar extensional flow at $\dot{\upvarepsilon}=0.012-26\kern0.5em {\mathrm{s}}^{-1}$, the phase-separated PS/PVME was homogenized at temperatures 3 to 6 °C above T_s. The critical parameter of homogenization was found to be the extensional strain, $\upvarepsilon =\dot{\upvarepsilon}\kern0.2em {\mathrm{t}}_{\mathrm{c}}=44\pm 14$, where t_c is the critical time to achieve miscibility at various levels of ϕ, T, and $\dot{\upvarepsilon}$. The constancy of ε_c indicates that the main mechanism of flow-induced miscibility is related to deformation; after cessation of flow, the deformation dissipates and the homogenized blend phase separates within 20–70 s. By contrast, large stresses can cause demixing in colloidal (e.g., denaturation of proteins) and polymeric systems. In the latter case, precipitation from poor solvent solution, shear crystallization, and stress-related phase separation, are known. For example, PS/PVME under planar stresses at σ₁₁ < 10 MPa shows the previously discussed strain compatibilization, whereas at σ₁₁ ≥ 30 MPa it exhibits stress demixing (Katsaros et al. 1986). The demixing may be related to differences in the rheological behavior of the two blend components.

The correlation between rheology and thermodynamics in polymer blends is not straightforward. The concept of stored energy is useful in describing the interaction of rheology with thermodynamics in partially miscible polymer blends (Soontaranum et al. 1996). Flow-induced stored energy determines the deviation of the stored energy of the blend from the linear additivity rule (ΔE_S = E_s (ϕ₁Ε₁ + ϕ₂Ε₂). It is reasonable to consider that the miscibility region of the system is extended when flow-induced stored energy is negative (ΔGγ = ΔG_m + ΔΕ_s). This is called flow-induced mixing (shear-induced mixing) and has been observed in a number of systems, such as PS/PIB blends exhibiting UCST (Wu et al. 1992), PSAN-PMMA blends exhibiting LCST (Kammer et al. 1991), and PSAN-PMMA blends in which the spinodal curve is shifted upward upon imposition of shear (Soontaranum et al. 1996). In contrast, positive deviation of the flow-induced stored energy from additivity leads to flow-induced phase separation (de-mixing) (Fernandez et al. 1993b).

For true shifting of the critical point to occur, the suppression of long-range concentration fluctuation must be anisotropic. This has not been observed in PS/PVME blends. Using neutron scattering, it was demonstrated that shearing suppresses the fluctuations only parallel to the flow, leaving the concentration gradients in other directions unchanged (Nakatani et al. 1990). Viscoelastic effects (caused by the presence of a high-MW polymer) during the early stage of spinodal decomposition (SD) were discussed (Clarke et al. 1997). The data were verified using PVME blended with PS having MW = 1,610 kg/mol. Good agreement was observed.

The relation between rheology and morphology during late stages of SD in PS/PVME blends was investigated by means of several techniques (Polios et al. 1997). The results were interpreted using Doi-Ohta (1991) theory.

Shear-induced mixing was reported for polystyrene/polyisobutylene, PS/PIB, blends (Wu et al. 1992). Optical measurements indicated that shearing within the miscible blend region did not cause demixing, while shearing within the two-phase region reduced turbidity. The latter observation was interpreted as most probably resulting from the shear-induced mixing of the blends.

Blends of PI with PB were dynamically sheared at large amplitude (γ_o = 0.8) and frequency ω = 0.63 and 6.3 rad/s (Matsuzaka et al. 1997). After a temperature jump, the spinodal decomposition (SD) was in situ observed at the lower frequency, but not at the higher frequency. In the latter case, after stopping the oscillation, a modified SD pattern emerged. The authors postulated that the dynamic flow induced a structure in the miscible system, quite different from that which exists in the non-sheared specimens.

5 Rheology of Immiscible Blends

5.1 Rheological Equation of State

Based on the principles of the flow behavior of simpler systems, viz., suspensions, emulsions, and block copolymers, as well as an understanding of the mutual interactions between rheology and thermodynamics near phase separation, it may be possible to consider the flow of more complex systems where all these elements may play a role. Evidently, any constitutive equation to describe flow of immiscible polymer blends should combine three elements: (i) the stress-induced effects on the concentration gradient, (ii) an orientation function, and (iii) the stress–strain description of the systems, including the flow-generated morphology. The first steps toward a theory of blend flow behavior were proposed by Helfand and Fredrickson (1989), then by Doi and Onuki (1992). A greatly simplified constitutive equation for immiscible 1:1 mixture of two Newtonian fluids having the same viscosity and density was also derived (Doi and Ohta 1991). The derivation considered time evolution of the area and orientation of the interface in flow, as well as the interfacial tension effects. The relation predicted scaling behavior for the stress and the velocity gradient tensors:

$$ \begin{array}{l}\sigma \left(t,\left[\tilde{\kappa}(t)\right]\right)= c\sigma \left( ct,\left[\kappa (t)\right]\right)\kern1em \mathrm{and}\kern1em \tilde{\kappa}(t)= c\kappa (ct)\\ {}\sigma \left(c\dot{\gamma}\right)= c\sigma \left(\dot{\upgamma}\right);\kern1em {\sigma}_{12}\propto \dot{\gamma}\kern1em \mathrm{and}\kern1em \left({\sigma}_{11}-{\sigma}_{22}\right)\propto \dot{\gamma}\end{array} $$

(7.94)

Experimental verification of Eqs. 7.94 indicated that the scaling relationships are valid, but the shape of the experimental transient stress curves, after a step-change of shear rate, did not agree with Doi-Ohta’s theory (Takahashi et al. 1994). Similar conclusions were reported for PA-66 blends with 25 wt% PET (Guenther and Baird 1996). For steady shear flow, the agreement was poor, even when the strain-rate dependence of the viscosities of the components was incorporated. Similarly, the recovery of the overshoot (or that of undershoot for step-down experiments) and the shear thinning were not predicted by that theory. However, the theory could predict the extra stress arising from the interfacial tension. Also, the transients (η and N₁) at the start-up of steady-state flow agreed qualitatively with the theory. Doi-Ohta’s theory was also compared to the experimental data of semi-concentrated mixtures of PIB in PDMS (Vinckier et al. 1997). The theory described reasonably well the transient effects at the start-up of steady-state shearing. The scaling laws were also obeyed by these slightly viscoelastic blends.

Following the work of Doi and Ohta, a more general theory was derived for immiscible polymer blends by Lee and Park (1994). A constitutive equation for immiscible blends was proposed. The model and the implied blending laws were verified by comparison with dynamic shear data of PS/LLDPE blends in oscillatory shear flow. This new approach considered the influence of morphology in determining the rheological behavior in a given flow field. Thus, instead of formulating a single droplet problem, as microrheology does for the dilute dispersions, the authors considered the complex interfaces formed between two phases of immiscible fluids created by deformations, breakup, and coalescence of drops (caused by flow and interfacial tension). A semi-phenomenological kinetic equation was derived that described the time evolution of the interfacial area per unit volume, Q, and its anisotropy in a given flow field, q_ij:

$$ Q=\left(1/V\right){\displaystyle \int ds;\kern1em {q}_{ij}=\left(1/V\right){\displaystyle \int \left[{n}_i{n}_j-\left(1/3\right){\delta}_{ij}\right] ds}} $$

(7.95)

where n _i denotes the unit normal vector to the interfaces, V the total system volume, and dS an interface element. The time evolutions of Q and q_ij are affected by the flow that deforms the interface to an anisotropic state:

$$ \begin{array}{l} dQ/ dt=-{d}_{ij}{q}_{ij}\\ {}d{q}_{ij}/ dt=-{q}_{ik}{d}_{kj}-{q}_{jk}{d}_{ik}+\left(2/3\right){d}_{ij}{d}_{lm}{q}_{lm}-\left(Q/3\right)\left({d}_{ij}+{d}_{ji}\right)+\left({q}_{lm}{d}_{lm}\right)/Q{q}_{ij}\;\end{array} $$

(7.96)

where d_ij = ∂u_i/∂x_j is the macroscopic velocity gradient tensor. For a mixture of fluids with equal viscosity, the stress tensor may be expressed as

$$ {\sigma}_{ij}={\eta}_m\left({d}_{ij}+{d}_{ji}\right)-{\nu}_{12}{q}_{ij}-P{d}_{ij};\kern1em {d}_{ij}\equiv d{u}_i/d{x}_j $$

(7.97)

where η_m is the matrix viscosity and ν₁₂ is the interfacial tension coefficient. In Eq. 7.97, the excess shear stress is proportional to the spatial anisotropy of the interfaces, q _ij , and the structure of the interface distorted by the competition between flow and interfacial tension.

The resulting constitutive equation can be used not only for arbitrary volume fractions but also for arbitrary flow fields. It is advantageous to consider that the time evolution of Q and q _ij originates in the external flow as well as in the interfacial tension:

$$ \begin{array}{l} dQ/ dt={\left( dQ/ dt\right)}_{\mathrm{flow}}+{\left( dQ/ dt\right)}_{\mathrm{interf}.\mathrm{tens}.}\\ {}d{q}_{ij}/ dt={\left(d{q}_{ij}/ dt\right)}_{\mathrm{flow}}+{\left(d{q}_{ij}/ dt\right)}_{\mathrm{intenf}.\mathrm{tens}.}\end{array} $$

(7.98)

For concentrated systems, dimensional analysis of the retraction caused by interfacial tension makes it possible to express the second terms in Eq. 7.98 as

$$ dQ/ dt=-{c}_1{c}_2\left({\nu}_{12}/{\eta}_m\right){Q}^2-{c}_1{c}_3\left({\nu}_{12}/{\eta}_m\right){q}_{ij}{q}_{ij} $$

(7.99)

$$ d{q}_{ij}/ dt=-{c}_1\left({\nu}_{12}/{\eta}_m\right)Q{q}_{ij}-{c}_1{c}_3\left({\nu}_{12}/{\eta}_m\right)\left({q}_{lm}{q}_{lm}/Q\right){q}_{ij} $$

(7.100)

where the dimensionless parameters, c _i , are, respectively, the total relaxation, the size relaxation, and the breakup and shape relaxation. They all depend on the volume fraction ϕ.

The macroscopic stress tensor for the two-phase fluid can be expressed as σ_ij = (pressure term) + η_m(d_ij + d_ji) + (viscosity ratio term) + (morphology-dependent term) or respectively

$$ {\sigma}_{ij}=-P{\delta}_{ij}+\left[1+3\phi \left(\lambda -1\right)/5\left(\lambda +1\right)\right]{\eta}_m\left({d}_{ij}+{d}_{ji}\right)-{\nu}_{12}{q}_{ij} $$

(7.101)

To complete the constitutive equation, contributions originating from flow must be incorporated. These are expressed as

$$ dQ/ dt=-{d}_{ij}{q}_{ij} $$

(7.102)

$$ d{q}_{ij}/ dt=-{q}_{ik}{d}_{kj}-{q}_{jk}{d}_{ki}+\left(2/3\right){\delta}_{ij}{d}_{lm}{q}_{lm}-\left(Q/3\right)\left({d}_{ij}+{d}_{ji}\right)+\left({q}_{lm}{d}_{lm}/Q\right){q}_{ij} $$

(7.103)

Substitution of Eqs. 7.99, 7.100, 7.102, and 7.103 into the two dependencies in Eq. 7.98 provides two relations that, when combined with Eq. 7.101, form the rheological equation of state. Note that at t = 0: Q = Q_o and q_ij = q_ijo. For dynamic oscillatory flow, the relationships between the complex shear moduli G* = iωη* can be written as

$$ {G}_b^{*}=\left\{1+\left[6\phi \left({G}_i^{*}-{G}_m^{*}\right)/10\left({G}_i^{*}+{G}_m^{*}\right)\right]{G}_m^{*}+{G}_{\mathrm{int}}^{*}\right\} $$

(7.104)

where G_b*, G_m*, and G_i* are the complex moduli of the blend, the matrix, and the dispersed phase, respectively. The term G_int* is the complex modulus attributed to the interfaces. Imposition of sinusoidally varying strain, γ(ω) = γ_o sin(ωt) results in frequency-dependent stress at the interface ν₁₂q_ij. The latter also sinusoidally changes with the stress amplitude, δ_int, and is out of phase with the strain. The interfacial stress amplitude σ_int and its phase lag by δ_int can be calculated by solving Eqs. 7.102, and 7.103 assuming the initial values of Q_o, q_ijo as well as of the parameters, c_i. The interfacial moduli G_int*, G′_int, and G″_int can be expressed as

$$ {G}_{\mathrm{int}}^{*}\left( i\omega \right)={G}_{\mathrm{int}}^{\prime}\left(\omega \right)+i{G}_{\mathrm{int}}^{{\prime\prime}}\left(\omega \right) $$

(7.105)

$$ {G}^{\prime }=\left({\sigma}_{\mathrm{int}}/{\gamma}_0\right) \cos \left({\delta}_{\mathrm{int}}\right) $$

(7.106)

$$ {G}^{{\prime\prime} }=\left({\sigma}_{\mathrm{int}}/{\gamma}_0\right) \sin \left({\delta}_{\mathrm{int}}\right) $$

(7.107)

where γ_o is the strain amplitude.

The effects of shear flow on the PS/LLDPE morphology were investigated by observing the structure of quenched samples under the scanning electron microscope, SEM. Predictions based on the constitutive equations were compared with observations from the dynamic shear experiments at 200 °C (see Fig. 7.22). The frequency variations of G_b′, G_b″, and η_b* were found to be in good agreement with computations based on Eqs. 7.101, 7.102, and 7.103. However, to get such agreement, seven parameters (viz., ν₁₂, ϕ, initial value of the anisotropy parameter, q_ijo, initial size of the dispersion, and three dimensionless equation parameters) were required (Lee and Park 1994).

Fig. 7.22

Comparison of model predictions with experimental results for (a) 10 wt% and (b) 30 wt% of PS in LLDPE (After Lee and Park 1994)

It should be noted that the Doi and Ohta theory predicts only an enhancement of viscosity, the so-called emulsion-like behavior that results in the positive deviation from the log-additivity rule, PDB. However, the theory does not have a mechanism that may generate an opposite behavior that may result in a negative deviation from the log-additivity rule, NDB. The latter deviation has been reported for the viscosity versus concentration dependencies of PET/PA-66 blends (Utracki et al. 1982). The NDB deviation was introduced into the viscosity–concentration dependence of immiscible polymer blends in form of an interlayer slip caused by steady-state shearing at large strains that modify the morphology (Utracki 1991).

A complete set of governing relationships was derived from the requirements of the compatibility of dynamics and thermodynamics (Grmela and Ait-Kadi 1994, 1998; Grmela et al. 1998). The authors developed a set of equations governing the time evolution of the functions Q and q_ij (see Eqs. 7.95), as well as the extra stress tensor expressed in their terms. The rheological and morphological behavior was expressed as controlled by two potentials: thermodynamic and dissipative. Under specific conditions for these potentials, the Lee and Park formalism can be recovered.

Lacroix et al. (1997, 1998) attempted to evaluate three approaches (those of Palierne, Lee and Park, and Grmela and Aït-Kadi). They are capable in describing the experimental data of different types of polymer blends, viz., PS/PE, PETG/EVAc, PP/EVAc, and PP with EVAc and poly(ethyl methacrylate) (PEMA). Since EVAc is miscible with PEMA, the latter blend is also a two-phase blend with PP being the matrix. All blends were prepared within the concentration range that assured dispersed morphology. The Palierne model was found to describe well the linear viscoelastic behavior, whereas the model of Lee and Park was found useful for describing the rheological behavior under large strains. In the later paper, it was shown that the overshoot at the start-up of shearing was described well using either the Lee and Park or Grmela and Aït-Kadi model.

Based on the morphological features, the proposed models can be divided into two categories (Yu and Zhou 2007). The first group is based on local coarse-grained morphology such as the models of Doi and Ohta, Lee and Park, and Grmela. The second group includes the models based on droplet morphology, such as the models proposed by Maffettone and Minale (1998), Jackson and Tucker Iii (2003), and Yu and Bousmina (2003).

The first group used a statistical area tensor or interfacial anisotropic tensor to explain the complex interface by applying some modification on the Doi and Ohta model. The general advantage of these models is their ability to describe the blends with co-continuous structure or irregular phase morphology. On the other hand, the main drawback is attributed to the model parameters that can be used for a specific system and are non-generalizable. More quantitative morphological studies should be done to extend their applications.

The second group involves an ellipsoidal shape tensor representing the shape of the droplets. They lead to good description of droplet deformation, droplet relaxation, and rheological properties, along with the ability to incorporate the viscoelastic effects of components (Maffettone and Greco 2004; Yu et al. 2004; Yu et al. 2005). However, they fail to describe the systems that undergo droplet breakup and coalescence phenomena. To overcome this problem, Dressler and Edwards (2004) assumed that the variable droplet distribution can be considered in terms of two thermodynamic variables: the droplet shape tensor and the number density of representative droplets. They used a single time scale for breakup and coalescence to track droplet numbers. However, while this approach worked well for the PIB/PDMS blend, it was suggested that more quantitative rheological and morphological studies are needed to compare model predictions and experiments, especially for systems in which the breakup process dominates (e.g., transient process under large step shear) (Yu and Zhou 2007).

As another approach to predict the rheological behavior of immiscible blends, Almusallam et al. (2003) and Zkiek et al. (2004) constructed “hybrid” models based on local coarse-grained morphology by casting Tomotika’s theory to consider thread breakup under quiescent conditions. Yu and Zhou (2007) proposed a simple constitutive equation for immiscible blends. The theory predicts the overshoot in the first normal stress difference in the transient start-up of shear and morphology of droplets under varying shear histories. This model is based on the ellipsoidal description of droplets and includes the breakup and coalescence processes. The main assumption is that the discrete droplet breakup/coalescence process can affect droplet size only and it can be approximated by a continuous dynamic equation. A simple mapping approach was suggested to unify the variation of droplet volume due to the breakup/coalescence process and the conservation of droplet volume during the deformation (Yu and Zhou 2007).

5.2 Morphology of Immiscible Blends

In immiscible blends, the properties are related to the interface as well as to the size and shape of the dispersed phase. The morphology is controlled by both equilibrium and nonequilibrium thermodynamics, as well as by the flow field. As discussed in Sect. 7.1.2.2, at equilibrium and within the region of low volume fraction of the dispersed phase, ϕ < ϕ_perc = 0.16, droplets are expected, while at ϕ > ϕ_perc = 0.16 a co-continuous morphology, e.g., fibers or lamellae, are usually observed.

When the polymers are miscible under one set of conditions (e.g., within a specified range of concentration (ϕ), pressure (P), and temperature (T)), but immiscible under other conditions, the nonequilibrium morphology depends on the quench depth and time scale. Shallow quenching into the metastable region (between the binodal and spinodal curves) results in nucleation of the dispersed drops, followed by their growth. The mechanism of this phase separation is appropriately called nucleation and growth, NG. By contrast, deep quenching into the spinodal region results in spinodal decomposition, SD. Here there is an instantaneous generation of regularly spaced co-continuous structures, with progressive increase of the concentration difference between the two adjacent regions and increased spacing. The co-continuity of structures has been reported for scales varying from a few nanometers to hundreds of micrometers.

Both the NG and SD morphologies are transient, progressively coarsening. At a late stage, both NG and SD mechanisms follow similar ripening patterns, leading to an appropriate equilibrium morphology. Without compatibilization, the two phases may totally separate into two layers. In the case of well-compatibilized blends, the action of a compatibilizing agent is similar to that of surfactants in emulsions – one may assign specific surface area coverage per single molecule of the compatibilizer. However, dimensions of the dispersed, compatibilized phase do change with time after cessation of flow. By contrast, addition of a stabilizing agent (e.g., a third polymer immiscible in the two others) may prevent coalescence, preserving the degree of dispersion (but not the orientation) generated during the flow.

5.3 Microrheology of Polymer Blends

In this part, the breakup of polymer drops will be discussed, initially dealing with diluted systems (isolated drops) and subsequently with concentrated dispersions where coalescence is of equal importance. Dispersion in Newtonian systems was discussed in Sect. 7.3.2.2.

The mechanisms governing deformation and breakup of drops in Newtonian liquid systems are well understood. The viscosity ratio, λ, critical capillary number, κ_crit, and the reduced time, t*, are the controlling parameters. Within the entire range of λ, it was found that elongational flow is more effective than shear flow for breaking the drops. However, it is always important to realize that both rheological and thermodynamic considerations play an important role in the development of morphology in polymer blends. The role of thermodynamics is illustrated in the following example. Ravati and Favis (2013) reported three completely different interfacial tension-driven structures for the ternary blends: partial wetting for PBS/PLA/PCL, complete wetting tri-continuous morphology for PBS/PLA/PBAT, and combined partial-complete wetting cases for the PBS/PBAT/PCL blend. The variety of structures was achieved since the interfacial tensions between the phases were very low and the spreading coefficients were close to zero. Simply replacing one component with another changed the sign of the spreading coefficient and led to a different wetting behavior, as shown in Fig. 7.23. The observed partial and complete wetting cases were supported by Harkins theory of the spreading of liquids (Harkins 1941).

Fig. 7.23

Micrographs and schematics of combined partial-complete wetting morphology for ternary PBS/PBAT/PCL blends showing the effect of composition. (a, b) 25%PBS/25%PBAT/50%PCL after extraction of the PCL phase by acetic acid and annealing; (c) schematic of 25%PBS/25%PBAT/50%PCL; (d) schematic of 10%PBS/40%PBAT/50%PCL; (e, f) 10%PBS/40%PBAT/50%PCL after extraction of PCL phase by acetic acid and annealing. The white bar indicates 10 μm except for (b) which is 1 μm (Ravati and Favis 2013)

5.3.1 Deformation and Breakup of Viscoelastic Drops

The shear deformation of viscoelastic drops in a Newtonian medium has been the subject of several studies. Gauthier et al. (1971) found higher values of the critical capillary number than those determined for Newtonian drops. Prabodh and Stroeve (1991) observed that, during shearing, some drops are greatly extended and only break when the flow is stopped. The authors concluded that, at λ < 0.5, the drop elasticity has a stabilizing effect, but for λ > 0.5 the opposite is true. Interestingly, the experimental observations of De Bruijn (1989) seem to contradict the latter conclusion. He found that the critical capillary number for the viscoelastic droplets is always higher (sometimes much higher) than for the Newtonian drops, whatever the λ-value. De Bruijn concluded that drop elasticity always hinders drop breakup.

For Newtonian drops suspended in a viscoelastic fluid, Flumerfelt (1972) reported the existence of a minimum drop size below which breakup cannot be achieved. The author pointed out that the elasticity of the medium tends to increase this minimum value for breakup, that is, to stabilize the droplets.

In the case when both the droplets and the suspending medium are viscoelastic liquids, Wu (1987) reported that drops can break up during extrusion even when λ > 4. However, owing to the complex nature of the deformation during flow through an extruder, it was difficult to even speculate on the origin of this phenomenon. Van Oene (1978) studied the mechanisms of two-phase formation in a mixture of two viscoelastic fluids. He pointed out that, besides the viscosity ratio and the equilibrium interfacial tension of the two liquids, the elasticity of the liquids plays an important role in deformability of drops. Thermodynamic considerations led to the following relation for the dynamic interfacial tension coefficient:

$$ {\nu}_{12}={\nu}_{12}^0+\left({d}_0/12\right)\left[{\left({\sigma}_{11}-{\sigma}_{22}\right)}_d-{\left({\sigma}_{11}-{\sigma}_{22}\right)}_m\right] $$

(7.108)

where v ⁰₁₂ is the interfacial tension in a quiescent polymer blend, d_o is the initial diameter of the dispersed drop, and (σ₁₁ − σ₂₂)_i is the first normal stress difference of the dispersed (i = d) and of the matrix (i = m) phase, respectively. For (σ₁₁ − σ₂₂)_d > (σ₁₁ − σ₂₂)_m the dependence predicts that higher elasticity of the dispersed than the continuous phase results in more stable drops. On the other hand, for (σ₁₁ − σ₂₂)_d < (σ₁₁ − σ₂₂)_m Eq. 7.108 predicts that ν₁₂ < ν ^o₁₂ ; thus the flow tends to enhance the dispersing process (flow compatibilization). Note that ν₁₂ cannot be negative; for large differences of the normal stress difference and for large drop diameters (thus, for higher concentration of the dispersed phase), this translates into co-continuous morphology, for which the above relation is no longer valid.

Since flow affects miscibility of blends near the spinodal, the interfacial tension coefficient must also change with the flow conditions. This theory leads to ${\upnu}_{12}\left(\dot{\upgamma}\right)={\upnu}_{12}^o{\left[1-{\mathrm{a}\upkappa}^{1/3b}\right]}^{2\mathrm{b}}$, where a and b are parameters (Onuki 1986).

Han and Funatsu (1978) studied droplet deformation and breakup for viscoelastic liquid systems in extensional and nonuniform shear flow. The authors found that viscoelastic droplets are more stable than the Newtonian ones; in both Newtonian and viscoelastic media, they require higher shear stress for breaking. The critical shear rate for droplet breakup was found to depend on the viscosity ratio; it was lower for λ < 1 than for λ > 1. In a steady extensional flow field, the viscoelastic droplets were also found less deformable than the Newtonian ones. In the viscoelastic matrix, elongation led to large deformation of droplets (Chin and Han 1979).

Bousfield et al. (1986) studied the surface-tension-driven breakup of Newtonian and viscoelastic filaments. The authors found that disturbances grow more rapidly in viscoelastic filaments than in the Newtonian ones but that there is a retardation of the growth and stabilization at long times, resulting from large extensional stresses (see Fig. 7.24). The formation of satellite drops was found to be retarded by the elasticity. The authors analyzed the problem using the Galerkin finite element method, as well as a one-dimensional theory for viscoelastic filaments. Their findings were successfully used to interpret existing experimental data on Newtonian and viscoelastic jet disintegration, where the initial disturbance was imposed by nozzle vibration. For viscoelastic jets, an asymptotic solution was offered for the later stages of the process:

Fig. 7.24

Computed radius at the neck for disintegrating jet stream of Newtonian (solid line) and Maxwell fluid (dashed line) (Bousfield et al. 1986)

$$ \ln \left(R/{R}_0\right)={a}_0-t/3\tau; \kern1em \mathrm{for}\kern1.25em t>>\tau $$

(7.109)

where a_o and τ are, respectively, the numerical constant and the relaxation time. This work should have direct bearing on disintegration of viscoelastic filaments in a Newtonian matrix, but application of these findings to polymer blends is more difficult.

Lyngaae-Jørgensen et al. (1993) developed a predictive model of morphology variation during simple shear flow of diluted polymer blends. The model considers the balance between the rate of breakup and the rate of drop coalescence. It was assumed that (i) the viscosity and elasticity of the dispersed phase are significantly lower than those of the matrix, (ii) only the cylindrical, large drops (defined by the long and short semiaxes a₁ and a₂) are able to break and form small drops, and (iii) the coalescence can occur between all types of the dispersed entities. The dynamics of drop formation and breakup can be described by

$$ \begin{array}{l}d{N}_S/ dt={N}_b{R}_{Lb}-2{R}_{\mathrm{SSC}}-{R}_{\mathrm{LSC}}\\ {}d{N}_L/ dt={R}_{\mathrm{SSC}}-{R}_{Lb}-{R}_{\mathrm{LSC}}\\ {}d{a}_2/ dt={\left({a}_2/ dt\right)}_{V,\mathrm{flow}}+{\left({a}_2/ dt\right)}_{\mathrm{coalescense}}\end{array} $$

(7.110)

where dN_S/dt, dN_L/dt, and da₂/dt are the rates of change of the numbers of small drops and large drops and the rate of change of drop dimension correspondingly; R_Lb is the rate at which the number of small drops, N_b, are produced by breakage of the large drops; R_LSC and R_SSC are the number rates at which small drops are destroyed by coalescence with large and small drops, respectively; R_LSC is the number rate of coalescence between large drops. The first term on the right side of the last relation in Eq. 7.110 describes the contribution due to the flow process, and the second reflects that the average thickness of the large domains increases during coalescence.

The theory makes it possible to compute the drop aspect ratio, p = a₁/a₂, a parameter that can be directly measured in either a transient or steady-state flow. Following the derivation by Hinch and Acrivos (1980), the flow-induced changes to the drop aspect ratio were assumed to be proportional to the first normal stress coefficient of the matrix fluid. The coalescence was assumed to follow the Silberberg and Kuhn (1954) mechanism. These assumptions substituted into Eq. 7.110 gave a simple dependence for the aspect ratio:

$$ p=4{\phi}_d{p}_r{\eta}_m\dot{\gamma}/\pi {a}_1{\left({\sigma}_{11}-{\sigma}_{12}\right)}_m-{a}_2 $$

(7.111)

where a_i are adjustable parameters.

A special unit, equipped for light-scattering measurements, was attached to a Rheometrics Mechanical Spectrometer with cone and plate to follow the transitional events during shearing of polymer blend melts. The predictions of p obtained by the proposed model were found to be in a reasonable agreement with the experimental observations for poly(methyl methacrylate) blends with either 8 or 10 wt% polystyrene, PMMA/PS. The most interesting finding that came out of this work was that, both theoretically and experimentally, under steady-state flow conditions, the aspect ratio plotted versus shear stress showed a sharp peak at the stresses corresponding to transition of PMMA viscosity from the Newtonian plateau to the power-law flow, i.e., to the onset of the elastic behavior. The dependence is presented in Fig. 7.25.

Fig. 7.25

Deformability of PS drops in PMMA during steady-state shear flow at 180 °C. The points are experimental; the line is to guide an eye (Lyngaae-Jørgensen et al. 1993)

Mighri and Huneault (2002) investigated the drop deformation and breakup mechanisms in Boger fluid in PDMS as a viscoelastic model fluid system and PPS/PE and EPR/PP polymer blends under high shear rate conditions. Flow visualization was carried out in a transparent Couette shearing setup. Two non-Newtonian deformation and breakup mechanisms were presented. The first one was attributed to normal force buildup in the droplet. It was manifested in contraction of the dispersed droplet in the flow direction and its elongation in the vorticity direction at high deformation rates. The second deformation/breakup mechanism was the erosion mechanism. Erosion at the drop surface would occur only in highly viscous molten polymer systems, in which shear stresses could reach the required level. It was suggested that the ends of highly elongated particles would be located in different planes due to flow disturbance. Consequently, clouds of very small ribbons and sheets were formed around the drop, which then elongated and broke into very small droplets (Mighri and Huneault 2002). They also mentioned that the breakup process for the high interfacial tension PS/PE blends was very similar to that of low interfacial tension the EPR/PP system, probably due to the fact that viscosity ratio of both blends was very high.

Aggarwal and Sarkar (2008) used a three-dimensional front-tracking finite-difference method to study the effects of matrix viscoelasticity on viscous and viscoelastic drop deformation in shear flow. They used the Oldroyd-B constitutive equation to model the viscoelasticity of the system and to predict numerically the drop deformation and orientation. It was observed that increasing matrix viscoelasticity changed the drop inclination angle with the flow direction significantly. Also the steady-state drop deformation first decreased and then increased with increasing Deborah number. The change in drop orientation angle along with localized stretching of the polymer molecules at the drop tips was shown to play a critical role in the observed non-monotonic behavior. It was mentioned that the breakup of a viscous drop in a viscoelastic matrix is more pronounced for high De and restricted at smaller De. They showed that polymer to total viscosity ratio (β) affects the drop inclination angle through the combined parameter βDe, pointing out the effect of the first normal stress difference in a steady shear (N₁ = 2βDe) (Aggarwal and Sarkar 2008).

In another attempt, Sirivat et al. (2011) investigated the effects of three different parameters on droplet oscillatory deformation and breakup in polystyrene/high-density polyethylene by using a flow cell mounted on an optical microscope: (i) the effect of time scale ratio (4.0, 16.6, 33.2, and 63.8), (ii) the effect of viscosity ratio (0.58, 0.12, and 0.06), and (iii) the effect of droplet elasticity. The authors defined a modified deformation parameter as Def* = (a* − c)/(a* + c) where a* and c denote the apparent drop principal axes and the minor axes of the droplets as obtained from the droplet image projected onto the flow-vorticity plane from the time series of images. The difference between the maximum and minimum values of Def* divided by two (as a measure of amplitudes of deformation parameters) showed the linear correlation with small capillary numbers, whereas the dependences became nonlinear at large capillary numbers. The increase in critical capillary number was considerable with increasing viscosity ratio, but capillary number changed slightly with the time scale ratio. On the other hand, at a fixed capillary number, amplitudes of deformation parameters increased with decreasing the droplet elasticity (Sirivat et al. 2011) which is in agreement with the main conclusion of the previous studies showing the elasticity of the droplet suppresses droplet deformation and breakup (Lerdwijitjarud et al. 2003, 2004). Furthermore, Sirivat et al. suggested two different drop breakup patterns for PS/HDPE blends; (i) the nonsymmetric one-end tearing pattern that forms many smaller drops for the high-viscosity ratio system and (ii) the two-end stretching and twisting pattern that makes only few satellite drops at each end for the lower-viscosity ratio blend (Sirivat et al. 2011). Lee et al. (2009, 2010) studied the effect of steady shear on the phase separation in LCP/PC blends, using a shear stage, in conjunction with polarized light microscopy (Linkam stage). The phase diagram was divided into three regions with two phase-separation temperatures, Tsp1 and Tsp2, as the internal boundaries. Below Tsp1, phase separation can hardly occur. Between Tsp1 and Tsp2, phase separation can occur to a small extent. Above Tsp2, phase separation in the blends can proceed to a large extent. At low shear rates, both Tsp1 and Tsp2 are shifted to a lower position (relative to the quiescent conditions) on the phase diagram, indicating that the LCP/PC blends exhibited shear-induced phase-separation behavior. The phase-separated morphology of the blends showed significant changes under shear. For low LCP contents (10 wt%), the blends did not form the droplet-type morphology under shear, as was observed under quiescent conditions. Instead, the blends formed interconnected-type structure, and the network-like LCP-rich domains were transformed to short and thick fragments, due to the breakup of the network. For moderate LCP contents (20–30 wt%), the blends exhibited interconnected structure. However, the LCP-rich domains were thicker and shorter than those formed under quiescent conditions. For high LCP content (40–60 wt%), the blend exhibited droplet-type morphology, with the PC-rich phase appearing as dispersed domains. However, these dispersed domains were not distributed uniformly spatially. The effect of shear, at a shear rate of 0.40 s⁻¹, on the temporal morphological development in 50 wt% LCP/PC blends at 290 °C was examined and compared to the situation under quiescent conditions. Both cases showed that phase separation started quickly and then slowed down at the later stages of the process. The speed and magnitude of phase separation in the blend was enhanced significantly under shear, because of the shift of the phase diagram.

The dynamic mechanical shear behavior of several blends, viz., PS with PMMA, PDMS with PEG, and PS with PEMA, were studied by Graebling et al. (1989, 1993b). The linear viscoelastic behavior of these blends with the volume fraction of the dispersed phase ϕ ≤ 0.15 was found to follow predictions of Palierne’s emulsion model, which makes use of the viscoelastic behavior of component polymers and a single parameter that characterizes the interface, i.e., the ratio of the interfacial tension coefficient and drop radius, ν₁₂/R. The values of the interfacial tension coefficient determined from the viscoelastic measurements were found to be in good agreement with results obtained from the pendant drop method. However, the theory seems to break down for polymer blends with ϕ ≥ 0.2. The observed agreement between the experimental data and the theory means that the emulsion model can indeed be used for interpretation of the viscoelastic behavior of polymer blends. The noted deviations at higher concentration range are not in conflict with the basic premises of the approach. They originate from the imposed limitations of the model (see Sect. 7.3.2.3.2).

5.3.2 Coalescence of Viscoelastic Drops

For diluted Newtonian systems, the size of the smallest drop that can be broken is calculable from Taylor’s theory. However, for polymer systems, many studies have shown that equilibrium drop size is usually larger than predicted and the deviation increases with concentration of the dispersed phase, ϕ₁ − ϕ_o, where ϕ₁ is the volume fraction of the dispersed phase and ϕ_o ≈ 0.005 is the smallest concentration for which the deviation occurs. Roland and Bohm (1984) studied the shear-induced coalescence in two-phase polymeric fluids by small-angle neutron scattering. The coalescence rate was high, dependant on the rheological properties of the two phases and the flow field.

Coalescence occurs in shear as well as quiescent systems. In the latter case, the effect can be caused by molecular diffusion to regions of lower free energy, by Brownian motion, dynamics of concentration fluctuation, etc. Diffusion is the mechanism responsible for coalescence known as Ostwald ripening. The process involves diffusion from smaller drops (high interfacial energy) to the larger ones. Shear flow enhances the process (Ratke and Thieringer 1985):

$$ {\left(d/{d}_0\right)}^n=1+{a}_0t,\kern0.75em n=n(y)=3/2\kern0.5em \mathrm{to}\kern0.5em 3 $$

(7.112)

where d_o is the drop diameter at the moment of imposition of stress and a_o is a constant. The exponent n decreases from the classical value of 3, for quiescent systems, to 3/2 at high shear rates.

Flow-induced coalescence is accelerated by the same factors that favor drop breakup, e.g., higher shear rates, reduced dispersed-phase viscosity, etc. Most theories start with calculation of probabilities for the drops to collide, for the liquid separating them to be squeezed out, and for the new enlarged drop to survive the parallel process of drop breakup. As a result, at dynamic equilibrium, the relations between drop diameter and the independent variables can be derived.

Tokita (1977) calculated the total number of collisions per unit volume and time. The author assumed that coalescence is proportional to this number and to the number of particles. The latter was assumed to increase with mixing time, being proportional to the shearing energy, $\dot{\upgamma}{\upsigma}_{12}$, and inversely proportional to the interfacial tension coefficient, ν₁₂. At equilibrium, the rates of coalescence and breakup are equal. Thus, the equilibrium drop size can be expressed as

$$ d=\left(24/\pi \right){p}_r{\nu}_{12}{\phi}_1/\left[{\sigma}_{12}\dot{\gamma}-\left(4/\pi \right){p}_rE{\phi}_1\right] $$

(7.113)

where p_r is the probability of collision and E is the macroscopic bulk breaking energy. In agreement with experimental findings, the relation predicts that the equilibrium drop diameter increases with concentration and the interfacial tension coefficient, but it decreases with shear stress. At the low concentration limit, ϕ₁ ≤ ϕ_o, Eq. 7.113 also agrees with the conclusions of Taylor’s theory, but for ϕ_d→0, it predicts an unrealistic limit, d → 0.

Under steady-state flow conditions, the morphology is fully defined by the dynamic breakup and coalescence processes. However, behind is an implicit assumption that the flow conditions are strong enough to erase the initial morphology. The presence of the critical value of shear rate, ${\dot{\upgamma}}_{\mathrm{cr}}$, has been documented (Minale et al. 1997). The authors reported that the unique morphology was observed only above ${\dot{\upgamma}}_{\mathrm{cr}}$. Below this limit, multiple pseudo-steady-state structures were observed for the model PDMS/PIB system. No attempt was made to generalize this observation. In principle, the phenomenon should be related to the critical value of the capillary number, κ_cr, and a ratio of the polymer(s) relaxation time to the rate of shearing. The presence of ${\dot{\upgamma}}_{\mathrm{cr}}$ can also be used to explain observations on morphology evolution of PDMS/PIB blends (Grizzuti and Bifulco 1997).

Following a procedure similar to that of Tokita (1977), for equilibrium drop diameter in steady simple shear flow, the following dependence was proposed (Fortelny et al. 1988, 1990):

$$ d={d}_T+\left[\left({\nu}_{12}{p}_r{\phi}_1\right)/{\eta}_2f\left(\kappa \right)\right] $$

(7.114)

where d_T is Taylor’s equilibrium diameter (e.g., calculable from Eq. 7.52) and f(κ) is a function of the capillary number and the rheological properties of the system. Equation 7.114 predicts that as ϕ_1→0, the drop diameter is determined by the Taylor breakup conditions. As the concentration increases, d becomes proportional to the expression in square bracket. The authors reported that, in the system PP/EPDM, coalescence was more intense than predicted by the dependence.

A theory for the dynamic equilibrium drop diameter also started from separate calculations of the drop breakup and coalescence during steady-state shearing. The rate of particle generation was taken to be determined by microrheology, viz., Eq. 7.52, (Huneault et al. 1995a):

$$ {\left(d{N}_d/ dt\right)}_{\mathrm{break}\hbox{-} \mathrm{up}}=\overset{.}{\gamma }{N}_d/{\kappa}_{cr}{t}_b^{*} $$

(7.115)

Since the dispersed phase volume is constant, the number of drops, N_d, can be related to the volume fraction of the dispersed phase, ϕ, and to the drop diameter, ${\mathrm{N}}_{\mathrm{d}}=6\mathtt{\phi}\mathrm{V}/{\uppi \mathrm{d}}^3$. The coalescence rate is a function of the collision probability and the dynamics of the collision process. From Eq. 7.65 coalescence rate can be written as

$$ {\left(d{N}_d/ dt\right)}_{\mathrm{coalescence}}=-C\overset{.}{\gamma }{N}_d{\phi}^{8/3}/{d}^2 $$

(7.116)

where C is a coalescence constant. At equilibrium, the diameter rate of change is zero.

From Eqs. 7.115, and 7.116, the dynamic drop diameter is

$$ {d}_{eq}={d}_{eq}^0+{\left(6C{\kappa}_{cr}{t}_b^{*}{\phi}^{8/3}\right)}^{1/2} $$

(7.117)

where d_eq is the equilibrium drop diameter (at steady-state shearing), in a blend with the volume fraction of the dispersed phase, ϕ, mixed under a given set of processing conditions, while d ^o_eq = d_T is its value extrapolated to zero concentration. The only unknown in Eq. 7.117 is the coalescence constant, C. Its value can be determined from a plot of d_eq versus ϕ (Fig. 7.26).

Fig. 7.26

Equilibrium drop diameter as a function of polyethylene volume fraction in polystyrene matrix. The blend was compounded for 5 min in an internal mixer at 200 °C – line is theoretical, Eq. 7.117, the points are experimental (Huneault et al. 1995)

Domingues et al. (2010) developed a model to predict the morphology of immiscible systems in a single screw extruder. This model considers the stretching, breakup, and coalescence phenomena. The authors followed the approach proposed by Chesters (1991b) and Delamare and Vergnes (1996). They assumed that coalescence occurs by collision of two identical spherical drops in a shear flow, while the polymer film between them will be excluded and flow into the main stream. Therefore, the probability of the coalescence was defined as the product of the probability for expulsing the film separating the drops (P_exp) and the probability of the two drops colliding (P_col). P_col increases exponentially with the local residence time (t_loc), the volume fraction of the dispersed phase (ϕ), and shear rate. On the other hand, the probability for expulsing the liquid film depends on the viscosity ratio determining the type of interface. As seen in Table 7.7, P_exp is expressed differently using h*, the critical value for the breaking of the liquid film, the viscosity ratio (λ), capillary number (κ), the droplet radius (R), and the interfacial tension (ʋ₁₂). Finally the new particle size after coalescence, R*, was computed from volume conservation to develop a model of morphology evolution (Delamare and Vergnes 1996).

Table 7.7 Expressions for the probabilities of collision and expulsion h* and the new particle size after coalescence R* (Delamare and Vergnes 1996)

The coarsening of the phase structure due to the matrix crystallization process is an important issue to be considered. Dimzoski et al. (2013) attempted to clarify the coalescence of dispersed phase particles induced by crystallizing matrix domains during the cooling of an immiscible polymer blend in the quiescent state. The study was carried out using PP/EPR blends for which the coalescence during annealing in the quiescent state was studied in detail (Dimzoski et al. 2011). It is known that changes in the size of the rubber particles, during the cooling of the melt mixed blend, determine the effectiveness of EPR in the toughening of the PP matrix. Therefore, the authors investigated the possible changes in blend morphology during the crystallization of PP via the rejection of the EPR domains from the spherulites growth front, which consequently could lead to collision and coalescence. They suggested that molecular forces and/or coalescence induced by the Brownian motion caused a primary coarsening of the phase structure before reaching the temperature of PP crystallization. The contribution of crystallization to coalescence of the dispersed phase particles was found to be largest at a finite rate of cooling. This was explained by the rejection energy required to exclude particle from the growing spherulite (Dimzoski et al. 2013).

5.3.3 Predicting Drop Size Changes During Processing

Mohr et al. (1957) analyzed the degree of mixing in a single screw extruder (SSE), using the concept of striation thickness suggested by Spencer and Wiley (1957). The amount of shear strain experienced by an element of fluid in the extruder screw channel was calculated for a number of flow paths. Decreased helix angle, increased ratio of pressure flow to drag flow, and an increased flight height were predicted to improve mixing. The ratio of the viscosities of the minor and matrix phases significantly influenced the degree of mixing.

Schrenk et al. (1963) analyzed the degree of mixing in a simple annular mixer, which might be helpful for understanding mixing in a SSE. To evaluate the mixedness of the two-component polymers, the striation thickness was measured, when the inner shaft was rotated and the outer cylinder was stationary. Near the shaft, the thickness was substantially reduced, but only slightly near the external cylinder.

Bigg and Middleman (1974) studied the transverse flow in a rectangular cavity, similar to that in an SSE. They used the Marker and Cell technique to calculate the degree of mixing, which was described by the interfacial perimeter per cavity width. As the viscosity ratio decreased, the degree of mixing was enhanced.

Chella and Ottino (1985) studied the degree of mixing in an SSE by theoretical analysis of the kinematics of mixing. They evaluated the degree of mixing as a function of the ratio of screw length to height of flight, helix angle, the ratio of pressure flow and drag flow, and the direction of the shearing plane. The stretch of the minor phase increased with axial distance. Mixing was relatively insensitive to the initial feed conditions. The results of the studies on the dependence of mixing on extruder dimensions and operating conditions were in qualitative agreement with Mohr’s analysis (Mohr et al. 1957).

The initial morphology generated during the melting and mixing stages in an extruder is important in the development of the final morphology of the extrudate. Lindt and Ghosh (1992) suggested that an abrupt morphological change occurs during the simultaneous melting and striation formation in the melting zone in an SSE. Within a fraction of a second, the scale of mixing drops by several orders of magnitude. High stress in the thin molten film in the melting zone causes a reduction of striation thickness of the minor phase. The lamellar layers may be developed when the minor component pellets melt at the interface between the melt film and the solid bed. The layers could become threads as they undergo breakup. Finally, the threads change into droplets, as they are broken.

Scott and Macosko (1991) proposed a mechanism of morphology development based on experiments carried out in a batch mixer. When the minor component pellet melts, sheets or ribbons of the dispersed phase are formed, due to dragging of the pellets on the hot surface of the mixing equipment. Next, holes are formed in the sheets or ribbons of the dispersed phase, as the interfacial instability starts, and sheet or ribbon morphology changes into a lace structure. Then, the lace breaks into irregularly shaped pieces with diameters equal to the ultimate sphere morphology.

The above two proposed mechanisms incorporate concepts involving distributive and dispersive mixing. Layer or sheet morphology development is mainly due to distributive mixing. Distributive mixing refers to the physical process of blending two fluids such that the physical separation distances are reduced to a scale where diffusion or a chemical reaction can occur (Bigio and Conner 1995). Breakup of layers into threads, laces, or spheres could be attributed to dispersive mixing which is related to instability of the minor phases.

Other studies attempted to develop a model describe morphology evolution during polymer blending in a twin screw extruder. The first model (Shi and Utracki 1992) was based on a simplified flow analysis, and the microrheological considerations of the dispersed-phase drop disintegration. The effects of coalescence were neglected. A later model comprised more refined flow analysis, two mechanisms of dispersion (the fibrillation mechanism and a drop splitting mechanism for low supercritical capillary numbers, with the choice of breakup mechanism based on locally computed microrheological criteria), as well as coalescence effects (Huneault et al. 1995a). The latter effects were taken into account by determining the coalescence constant in Eq. 7.117 from the plot shown in Fig. 7.26. Thus, this model was self-consistent, fully predictive, without any adjustable parameters. The validity of the theoretical assumptions was evaluated by comparing the two model predictions with the experimentally measured drop diameters at different axial positions in the twin screw extruder. Experimentally, after the extrusion reached steady state, the screw rotation was stopped and the molten blend was quenched within a specially designed extruder barrel. It was estimated that the PS/PE blends were quenched within 7–10 s. The second model yielded reasonable predictions of morphology evolution of non-compatibilized blends of PS in PE and of PE in PS.

Based on microrheology, it is possible to expect that (i) the drop size is influenced by the following variables: viscosity and elasticity ratios, dynamic interfacial tension coefficient, critical capillary number, composition, flow field type, and flow field intensity; (ii) in Newtonian liquid systems subjected to a simple shear field, the drop breaks most easily when the viscosity ratio falls within the range 0.3 < λ < 1.5, while drops having λ ≥ 3.8 do not break under shear; (iii) droplet breakup is easier in an elongational flow field than in a shear flow field; the relative efficiency of the elongational field dramatically increases for large values of λ ≥ 1; (iv) drop deformation and breakup in viscoelastic systems seems to be more difficult than that observed for Newtonian systems; (v) when the concentration of the minor phase exceeds a critical value, ϕ_d > ϕ_c ≈ 0.005, the effect of coalescence must be taken into account; (vi) even when the theoretical predictions of droplet deformation and breakup are limited to infinitely dilute, monodispersed Newtonian systems, they can be successfully used for predicting the development of blend morphology during compounding in twin-screw extruders.

Other experiments were conducted in a corotating, intermeshing twin-screw extruder using the same PE/PS system as described above (Huneault et al. 1995b). The screw geometry consisted of five zones: melting, melt conveying (no pressure), mixing (kneading), pumping, and flow through a die. The specimens were scooped from three ports and quenched within a second. After dissolution of the matrix, the dispersed phase was divided into fibers and droplets, characterized separately. Immediately after melting, the dispersed phase formed into fibers and droplets, both with diameters below 10 μm. Contrary to the previous model assumptions, fibers did not break in the unfilled conveying region that followed the melting section. Instead, they were mainly destroyed in the kneading section. Fibers were present after melting even at concentrations of the dispersed phase as low as 2 wt%. The effect of increasing the concentration was not only to increase the final diameter of droplets but also to increase the fiber content. The observations indicated that coalescence was not limited to drops. However, near the die, the average drop diameter did decrease to about d ≅ 1 μm range (as observed earlier).

Cho and Kamal (2002) derived equations for the affine deformation of the dispersed phase, using a stratified, steady, simple shear flow model. It includes the effects of viscosity ratio and volume fraction. According to the equation, for viscosity ratio > 1, the deformation of the dispersed phase increases with the increase of the dispersed phase fraction. For compatibilized PE/PA-6 blends at high RPM (i.e., 100, 150, and 200 RPM) in the Haake mixer, the particle size decreases with concentration of the dispersed phase up to 20 wt%. This occurs because the total deformation of the dispersed phase before breakup increases as the volume fraction increases, and coalescence is suppressed. The increase of the particle sizes between 20 and 30 wt% results from the increase of coalescence due to the high dispersed phase fractions. The data for 1 wt% blends suggest that mixing in the Haake mixer follows the transient deformation and breakup mechanism, and that shear flow is dominant in the mixer.

Clearly, the microrheology of polymeric systems is more complex than the classical microrheology of Newtonian, low viscosity liquids. Near the liquefaction point (either T_m or T_g) the viscosity is of the order of 10¹² Pas, and the relaxation time is of the order of 100 s (Angell 1997). As temperature increases along the barrel, these values decrease according to the Vogel–Tamman–Fulcher relation:

$$ \begin{array}{l}\eta ={\eta}_o \exp \left\{B/\left(T-{T}_o\right)\right\}\\ {}\tau ={\tau}_o \exp \left\{B/\left(T-{T}_o\right)\right\}\\ {}\mathrm{where}:\kern1em {T}_o\approx {T}_g+50\;\end{array} $$

(7.118)

The long relaxation times are responsible for nonequilibrium structures, generated by the mechanical action of the compounding equipment that is not taken into account by microrheology. The microrheological model provided good agreement with the experimental data obtained after 7–10 s quenching. However, these data were on purpose collected from the second half of the TSE barrel, where the temperature was reasonably stable (isothermal model). Evidently, evolution of blend morphology is more complex than a simple, “steady-state” model can predict. The rapid variations of morphology will be particularly important for computations of reactive compatibilization.

The evolution of morphology along the extrusion direction, in a twin screw extruder, for thermoplastic vulcanizates (TPVs) and TPV nanocomposites at high EPDM content during dynamic vulcanization was studied by Mirzadeh et al. (2013). Figure 7.27 shows that the coarse co-continuous morphology in the first mixing zone changed to droplet matrix structure, as a result of cross-linking of the rubber phase. The breakup of highly elongated threads observed in the second mixing zone led to a line of small rubber droplets in the third mixing zone. It seems that the TPV nanocomposites reach this morphological state sooner due to the faster cross-linking reaction. Morphology evolution continued by the transition of the droplets into a network made by irregular rubber particles in the second and third mixing zones. The SEM micrographs of the samples taken from the die exit showed the coexistence of a small number of rubber droplets in the vicinity of the smaller irregular rubber particles connected to each other by some rubber fibrils. The existence of irregular shape rubber particles was also observed by Shahbikian et al. using the AFM technique (Shahbikian 2010). The evolution of morphology in this case is in agreement with the conceptual mechanism of morphology evolution in thermoplastic vulcanizates proposed by Bhadane et al. (2006). They suggested that a network (namely, β-network) forms due to the viscosity mismatch between the non-cross-linked rubber (in the center of rubber domains) and cross-linked rubber (at the outer envelope of the rubber phase), during the dynamic cross-linking. Again, it is obvious that the drop size changes during processing in the case of reactive blends are also complex.

Fig. 7.27

SEM micrographs of TPV (X1; the first row) and TPV nanocomposite (X2:the second row) for the samples taken at the first mixing zone (a), the second mixing zone (b), the third mixing zone (c), and the die exit (d) (Mirzadeh et al. 2013)

Different morphological changes during blending were reported by Sundararaj et al. (1992, 1995). Similar morphological features were observed for reactive or nonreactive blends in an extruder, internal mixer, or a miniature cup-and-rotor mixer. Initially, during melting, the polymers were stretched into sheets and ribbons, which broke into fibers, then in turn into drops. However, the two studies reported different morphologies, most likely due to differences in the concentration of the dispersed phase (5 % and 20 %, respectively).

5.3.4 Mixing and Blending in Extensional Flow Field

Most works on liquid mixing in the extensional flow field considered convergent flow of a Newtonian liquid from a reservoir to a capillary (Tsebrenko et al. 1974, 1976; Ablazova et al. 1975; Krasnikova et al. 1978; Han and Funatsu 1978; Chin and Han 1979, 1980; Han 1981; Han and Yu 1981; Suzaka 1982; Vinogradov et al. 1982; Utracki et al. 1986). A device capable of mixing polymeric liquids (having widely ranging viscosity ratios) in an extensional field was constructed (Nguyen and Utracki 1995). The extensional flow mixer, EFM, was designed incorporating the following principles, based on the microrheological analysis:

• 1. The blend must be exposed to the extensional flow fields and to semi-quiescent zones.

• 2. The convergences and divergences should be of progressively increasing intensity.

• 3. The convergent–divergent flow should be generated in the radial not axial direction.

• 4. To reduce the pressure drop, and to prevent blockage, slit restrictions should be used.

• 5. The extensional flow mixer must be adjustable.

• 6. The rate of flow, upstream from the plates, should be approximately constant.

In EFM, the material flows from the rim between two facing each other circular convergent–divergent plates with ridges, toward the opening in the center of the lower plate. To assess the relative merit of the extensional mixing, EFM was attached to an SSE. For comparison, the blends were also prepared in a corotating, intermeshing TSE. The same temperature profiles were used for SSE + EFM as for TSE. In all cases the dispersed phase was significantly more viscous than the matrix, λ ≥ 4. The efficiency was judged considering:

• 1. The degree of dispersion in PS/PE blends of PS with either 5 or 10 wt% HDPE. At the exit from SSE + EFM, either fibrillar or nodular morphology was observed. The number average fiber diameter decreased with pressure across the c–d plates from d_n = 1.2–0.7 μm to d = 0.2–3 μm, at respectively P = 10.3 to 18.6 MPa. The blends prepared in a TSE showed much coarser morphology, containing mainly infinitely long HDPE fibers with diameter varying from d = 1 to 10 μm.

• 2. The results of PP impact strength improvement by incorporation of EPR are summarized in Fig. 7.28. As evident, impact strength at room temperature increased with EPR content. Clearly, SSE + EFM compounding resulted in higher impact strength (points) than that obtained from TSE (broken line).

• 3. The ability to homogenize resins with widely different molecular weight can be exemplified by UHMWPE/HDPE blends. Addition of high MW polymer is expected to increase G′, G″, η, and the first normal stress coefficient, Ψ₁. For the linear polymers, these parameters at low deformation rates, η_o and Ψ_1ο, are proportional to M_w ^3.5 and M_w ⁷, respectively. Thus, the elasticity is more sensitive to the high MW fractions. For this reason, the frequency dependence of the storage modulus ratio G′(blend)/G′(PE), at 200 °C, for HDPE and its blends with 3 wt% UHMWPE was measured. The blends prepared in TSE had the worst performance: G′ at ω = 0.01 rad/s increased by 90 %, while in EFM + SSE the increase was up to 210 % at P = 18.6 MPa.

• 4. Elimination of gel particles in the reactor powder. The gel particles can form during polymerization of EVAc or TPO. Since they may be considered very high molecular weight fractions of the same resins, SSE + EFM was used to eliminate or reduce the blemishes and improve the mechanical performance. On both counts, the performance was found at least equivalent to that obtained using a TSE.

Fig. 7.28

Effect of EPR addition on PP’s notched impact strength at room temperature. The specimens were prepared either in a TSE (horizontal lines) or in an SSE/EFM with c–d plates #2. In the latter case the results depended on the pressure drop across EFM (Utracki and Luciani 1996)

One may calculate the pressure drop, ΔP, in EFM starting with well-known expressions (Cogswell 1972; Binding 1988; Tremblay 1989). An expression derived from Binding’s theory was found to provide excellent prediction (no adjustable parameters) of the pressure across EFM.

Historically, the counterrotating TSEs were known as “calendaring” extruders, with high stresses existing between the two screws and low stresses outside this region. Owing to the high calendering pressures, the screws could rub against the barrel causing premature wear. Thus, slower speeds (up to 150 rpm) and large intermeshing gaps were recommended. One of the advantages of these counterrotating machines has been the presence of the elongational flow field within the calendering zone. The machines have been successfully used in numerous applications requiring high dispersive stresses.

The analysis of TSE performance resulted in modification of the screw profiles (higher free volume of the process), as well as in development of new mixing (or kneading) elements. The increased free volume (thus slender screw profile) resulted in lowering the average shear rate; thus the screw speeds needed to be increased. New kneading and mixing elements have been designed to improve either the distributive or dispersive mixing. The kneading blocks (mono- and bi-lobal, to be used either in co- or counterrotating TSE, the tri- and hexa-lobal only in counterrotating TSE) were designed to maximize the extensional flow field within the lobal pools and reduce the shear field in the intermeshing and overflight regions. These designs improved mixing capabilities greatly, even for polymeric systems having large differences in the rheological flow parameters (Thiele 1995).

The influence of these complex flow fields on morphology development in blends of HDPE/PA6 (Wang 2005) and also immiscible polymer blends of PS/PMMA (Mours et al. 2003) was investigated. Droplet formation, breakup, and coalescence in these flows were studied by different microscopic techniques. The results showed that drop deformation and breakup were sensitive to both shear and extensional flow fields. However, extensional flow was more effective than shear flow in generating well-developed laminar phase. The main conclusion of these attempts points out the significant effect of the elongational flow fields on the final morphology. Therefore, it should be emphasized that the description of shear flow alone is insufficient for modeling purposes in processing machines (Mours et al. 2003).

5.4 Flow-Imposed Morphology

In this part, focus will be on the changes of morphology imposed by different flow fields and on the influence of variations in morphology on flow behavior. It must be evident that the degree of dispersion and the type of structure strongly relate to the type and intensity of imposed stresses during flow. Note that both concentrated suspensions and emulsions show yield stress and time-dependent flow. These macroscopic observations are related to the structural changes occurring on the microscale. Similar behavior of polymer blends is to be expected. One has to keep in mind that, during polymer processing, neither the thermodynamic miscibility, the macromolecular configuration (e.g., entanglement), nor the morphology is in an equilibrium state.

Most models of the morphological changes in polymer blends assume that an average response (e.g., an average size drop is being broken, or average size drops coalesce) provides good representation of the whole system. This assumption should be reasonably correct for blends with narrow distribution of drop sizes. However, there are reports in which (e.g., during the initial stages of blending in a twin-screw extruder) the domain sizes may differ by three orders of magnitude. Here the “average size” response may not be valid. A kinetic theory of structure development in moderately concentrated polymer blends was proposed (Patlazhan and Lindt 1996). The breakup and coalescence under steady-state shearing were considered, assuming a temporal population balance. This development provides a framework for incorporation of the elementary phenomena of drop breakup and coalescence to an overall model.

The effect of flow on miscibility of polymer blends is another area of industrial importance. There is evidence that during processing, the imposed stresses can change the critical temperature by at least 60 °C, causing miscibility inside the processing equipment. The blends, upon release of pressure, may undergo spinodal decomposition that results in superior performance (Inoue 1993).

Flow may also result in mechanochemical degradation processes that generate reactive sites, viz., radicals, peroxides, acids, etc. Furthermore, transesterification and ester–amide exchange reactions are well documented. These reactions affect the phase equilibrium as well as the regularity of the chain structure, thus dispersion in the blend and its crystallinity.

Blend morphology refers to the spatial arrangement of the blend components forming either a dispersed, a stratified (e.g., lamellar or a sandwich-type), or a co-continuous structure. Generation of morphology depends on the viscosity and elasticity ratios of the polymeric blend components (at constant stress). Both ratios vary with the type and the intensity of the flow field. While the viscosity ratio seems to control the ease of dispersing the component, thus the degree of dispersion, the elasticity ratio contributes to shaping the phases – the type of morphology. Two other pertinent parameters are the concentration and the level of interfacial interactions. To modify the interfacial energy, blends are usually compatibilized either by the addition of compatibilizer or by reactive blending. Once formed, the morphology needs to be stabilized against a possible destruction during the forming steps.

The rheological properties of a two-phase system depend not only on the rheological behavior of the components but also on the size, size distribution, and the shape of the discrete phase droplets dispersed in the continuous matrix phase. Flow affects morphology in two different ways:

• It changes the degree and type of dispersion at the local level, viz., drop breakup and coalescence.

• It causes migration of the dispersed phase, thus imposing global changes of morphology in the formed parts, viz., skin-core structures, weld lines, blush lines, etc.

In consequence, the flow-imposed morphologies can be classified as (i) dispersion (mechanical compatibilization), (ii) fibrillation, (iii) lamellae formation, (iv) coalescence, (v) interlayer slip, (vi) encapsulation, etc. These types will be discussed below under appropriate headings.

There is a reciprocal relation between morphology and flow behavior. Plochocki (1978, 1983) defined the particular rheological composition (PRC) most frequently observed in polyolefin blends. At PRC the η = η(ϕ) function reaches a local maximum or minimum. The existence of the maximum is related to a change of the dispersed phase, e.g., from spherical to fibrillar or from dispersed to co-continuous, while that of the minimum is related to a reciprocal change and/or to variation of the specific volume.

Table 7.8 provides a partial reference to studies on the effects of flow on the morphology of polymer blends (Lohfink 1990; Walling 1995). The dispersed phase morphology development has been mainly studied in a capillary flow. To explain the fibrillation processes, not only the viscosity ratio but also the elasticity effects and the interfacial properties have to be considered. In agreement with the microrheology of Newtonian systems, an upper bound for the viscosity ratio, λ, has also been reported for polymer blends – above certain value of λ (which could be significantly larger than the Newtonian value of 3.8) the dispersed phase could not be deformed. By contrast, lower bounds of λ were not established for polymer blends.

Table 7.8 Studies of flow field effects on polymer blends morphology

Incorporation of compatibilizers (a third phase) into immiscible blends improves the adhesion between blend phases and helps to achieve mechanical properties comparable to those of homopolymers. The formation of lamellar structures with specifically designed arrangement of the dispersed phase in the matrix phase could provide barrier properties comparable to those achieved in multilayer parts.

5.4.1 Dispersion

Microrheology can provide information regarding the temporal evolution of the drop diameter, d, under steady-state shearing, in the absence of coalescence. Assume that drops breakup occurs only if the shearing time at each appropriate shear stress exceeds the required time to break, t > t_b (for shearing times t < t_b the average drop remains unchanged). Then, Eq. 7.115 yields the following expression for the relative change of drop diameter as

$$ \begin{array}{l} \ln \left({d}_o/d\right)=\overset{.}{\gamma}\left(t-{t}_b\right)/3{\kappa}_{cr}{t}_b^{*}=\left[\left(\gamma /{\gamma}_b\right)-1\right]/3\\ {}\mathrm{since}:\kern1em {\gamma}_b\cong 2\kern1em \to \kern1em \therefore d={d}_o \exp \left\{\left(1-\gamma /2\right)/3\right\}\;\end{array} $$

(7.119)

Since derivation of this relation considered only the drop-splitting mechanism and neglected coalescence, its validity may be limited to small capillary numbers, κ* = 1–2, and low concentrations.

The drop diameter usually decreases with an increase of shear rate (see Fig. 7.29). However, microrheology indicates that there are different mechanisms operating in different flow types (e.g., shear and elongation) or at different field intensity. Furthermore, there is usually a difference in the quench time between the outer layer and the core of specimen. The data in Fig. 7.29 were obtained using capillary flow. The morphology was affected by the extensional flow field upstream from the die, shear flow (and flow-induced encapsulation) inside the die, and slower cooling in the center than at the core of the extrudate. After such complex morphological changes, empirically the drop diameter decreases with logarithm of the deformation rate, $\mathrm{d}/{\mathrm{d}}_{\mathrm{o}}=1-{\mathrm{a}}_{\mathrm{o}} \ln \dot{\upgamma}$, where a_o ≅ 0.3–0.6 is a material parameter.

Fig. 7.29

Reduced drop diameter versus rate of shear at 250 °C. The blend comprising 10 wt% PA-6 in HDPE was extruded through a capillary with the L/D = 40 (Utracki et al. 1986)

Huang et al. (2008) simulated the effect of three different screw geometries on morphology development of an immiscible polymer blend based on polypropylene/polyamide-6 (PP/PA 6). Samples collected from four different points along the extruder using a specially designed sampling device during blending by conventional screw elements, a fluted mixing element, and also by pineapple mixing element. Morphology evolution was evaluated using scanning electron microscopy, and it was interpreted considering the flow fields occurring along screw elements. The coarsest and most nonuniform morphology at the exit of the extruder was produced with the screw with conventional screw elements, whereas the finest and most uniform morphology was produced using the screw with a fluted mixing element. The chaotic mixing characteristic of the pineapple mixing element produced thin laminar layers of dispersed phase (Huang et al. 2008).

5.4.2 Fibrillation

The mechanism responsible for formation of fibers or fibrils is extensional, e.g., at the entrance to a capillary. Once inside the capillary, the blend undergoes shear flow, with intensity dependent on the radial position. The evolution of morphology of PMMA blends with core-shell elastomeric latex particles, poly(butylacrylate-co-styrene) was studied (Bousmina and Muller 1996). It was found that, within the plug flow region, the particles were randomly distributed, but in the outer part of the extrudate the particles were aligned into straight pearl strings. Had coalescence been possible, these would form fibers. The authors proposed a mechanism for string formation within the steady-state shear zone of the flow field. It is possible to postulate that there are at least two possible fibrillation mechanisms: the extensional flow at the entrance to capillary and the “stringing” process described by Bousmina and Muller.

Stress-induced fibrillation occurs under steady-state shearing or elongation when κ > 2. Under these conditions, the dispersed phase is co-deformational with the matrix. Since the capillary parameter is proportional to diameter (viz., Eq. 7.52), it is easier to fibrillate coarser dispersions at concentrations exceeding a limited value: ${\mathtt{\phi}}_{\mathrm{limit}}\approx {\mathrm{a}\uplambda}^b$, where the numerical values of a, b depend on the blend (Krasnikova et al. 1984).

Fibrillation is also affected by the presence of a compatibilizer. From the perspective of the capillary parameter, κ, addition of a surface tension modifier has two effects: it lowers the interfacial tension coefficient (thus increasing κ) and decreasing the initial drop diameter (thus increasing κ) – the net result is difficult to predict. An illustration is provided in Fig. 7.30. Here PP drops in PA-6 matrix were observed during shearing in a cone-and-plate geometry, without and with an acrylic compatibilizer, AA. For both systems, the dimensions (long and short axes of a prolate ellipsoid) were approached a plateau at shear stress σ₁₂ ≥ 10 kPa. Evidently, the plateau value of the long axis, a₁ = L, was higher for the system without AA than that with it. However, the rate of elongation indicates that AA facilitated the fibrillation process (Søndergaard et al. 1992).

Fig. 7.30

Stress-dependent values of the orthogonal axis of deformed polypropylene drops in shear at 250 °C. The blend comprised PP/PA-6 = 1:5, with and without an acrylic compatibilizer, AA (Søndergaard et al. 1992)

Tsebrenko et al. (1976) reported on fibrillation of POM in a copolyamide (CPA) matrix as a result of flow through a capillary. Fine fibrils with diameters of about 20 μm and length 3.2 mm were obtained during extrusion at T = T_m(POM) + 6 °C. The low extrusion temperature facilitated stress-induced crystallization of the POM fibers, preserving the morphology engendered at the entrance to the spinneret.

As evident from data in Table 7.9, fibrillation of POM in poly(ethylene-co-vinyl acetate), PEVAc, strongly depended on the viscosity ratio, λ (Tsebrenko et al. 1982). These data also indicate that for low-viscosity dispersed phase, the coalescence that results in formation of plate-like objects complicates the blend morphology. Furthermore, since the diameter of the fibrils remains virtually constant, low-viscosity ratios result in short fibers. On the other hand, for λ ≥ 1.7, the diameter drops again and platelets were detected. In short, for the best results λ ≅ 1 is preferred.

Table 7.9 Effect of viscosity ratio on fibrillation of POM in POM/PEVAc = 20/80 (Tsebrenko et al. 1982)

Polymer blends were prepared comprising a poly(etheresteramide) block copolymer, PEBA, with liquid crystalline copolymers, LCP (Champagne et al. 1996). The minor component was deformed into fibrillar-type morphology that enhanced the mechanical properties in the draw direction, in a manner comparable to unidirectional continuous-fiber reinforced composites. Films prepared using a single screw extruder were melt drawn on calendering rolls. The storage modulus of blends containing 30 wt% LCP increased with draw ratio, DR ≤ 12, nearly 50-fold in comparison to neat PEBA (from 18 MPa to almost 1 GPa). The blend morphology was characterized by dissolving the PEBA matrix, followed by gravimetric and microscopic analysis of the LCP phase. As expected, the average fiber diameter decreased as a function of DR^−0.5. It was noted that only relatively large drops were deformed into fibers, leaving nearly 50 % of LCP in the form of small dispersed nodules. The fiber content as a function of DR followed a trend parallel to that of the mechanical properties. Longitudinal and transverse moduli followed the Halpin-Tsai predictions for unidirectional fiber composites. Properties of compression-molded specimens prepared from these blends compared favorably with glass fiber composites.

Drop deformation in shear that leads to fibrillation was examined using microscopy, light scattering, and fluorescence (Kim et al. 1997). They selected systems near the critical conditions of miscibility, thus where the flow affects miscibility and reduces the value of ν₁₂. The drop aspect ratio, p, plotted as a function of the capillary number, κ, showed two distinct regimes. For κ < κ_cr, p was directly proportional to κ, whereas for κ > κ_cr, p followed more complex behavior, with an asymptote that corresponds to flow-induced homogenization.

5.4.3 Lamellar Morphology

Lamellar morphology occurs in flow regimes where the dispersed phase undergoes two dimensional stretching with the formation of multilayers. In immiscible blends, such a structure may enhance barrier properties when the dispersed phase is a barrier material (e.g., PA, EVAl) and the matrix phase is a commodity polymer (e.g., PE, PP, etc.). Well-developed lamellas increase the length of the pathway for permeants diffusing through the blend. The longer path causes a lowering of the concentration gradient across the blend material, thus reducing the mass flux or permeability.

Subramanian (1985, 1987) was the first to develop a method for generating lamellar morphologies in polymer blends during melt processing. The method has been used to impart permeability barriers to low-cost polyolefins, PO, using small amounts of a barrier polymer. For example, blending under controlled conditions HDPE and a modified polyamide, either PA-6 or PA-66, led to compositions that during the subsequent blow molding or film blowing, generated lamellar PA dispersions. In particular, the lamellar morphology blends of PE and PA-6 were produced in a blow-molding machine. The product exhibited good barrier properties. The optimum performance was obtained using 18 wt% PA. The work resulted in commercialization of the Selar™ technology.

PP/EVAl blends with lamellar morphology were produced either in a single screw extruder with a specially designed die (Lohfink and Kamal 1993), using the injection molding machine (Walling 1995; Walling and Kamal 1996), or in an extruder with an annular blown film die (Lee and Kim 1997). To produce PP/EVAl sheets with lamellar morphology, Lohfink and Kamal (1993) designed and constructed a biaxially stretching slit die, which had converging and diverging sections to achieve the desirable extensional flow. In the PP matrix, EVAl lamellae were formed in the sheet core. The optimum barrier performance for oxygen transmission was obtained using 25 wt% EVAl. The barrier properties of the blends were superior to those obtained later in the blow molding process (Walling and Kamal 1996). During the injection molding of PP/EVAl blends, a complex morphology was obtained. In the core region, small relatively undeformed EVAl particles were found. By contrast, in the high shear zone near the skin, lamellas were present. Formation of the lamellar structure was enhanced by increasing EVAl concentration, compatibilization, and reduced mold thickness (Walling 1995; Walling and Kamal 1996).

The study by Kamal et al. (1995) showed that it is possible to control the flow-induced morphology to generate discontinuous overlapping platelets of PA-6 or EVOH dispersed phase in a polyolefin matrix phase. They considered the effects of feeding order, melt temperature, composition, compatibilizer level, die design, screw type, and cooling conditions. The results confirmed that screw type and processing conditions are key factors in developing a laminar morphology. For example, the combination of metering screw, 1.0 mm die exit gap, and 270 °C die temperature results in a laminar morphology. However, a mixing screw, 0.5 mm die exit gap, and 250 °C die temperature lead only to an alignment of the PA-6 domains in the flow direction without well-developed laminar morphology. For the optimized case, the toluene permeability of extruded ribbons of HDPE/PA-6 blends was found to be in the range of values obtained only with multilayer systems (Kamal et al. 1995).

In another attempt, the effects of processing conditions, such as different screw speeds, screw geometries, metering and mixing screws, on the morphology of the extruded ribbons of HDPE/PA-6 blends prepared by single screw extruder equipped with a convergent die were studied by Huang et al. (2005). The results showed that, in contrast to previous studies, even with a viscosity ratio larger than one, a laminar morphology with an aspect ratio of about 100 could be generated by appropriate combination of the screw type and shear intensity. Also, the formation of well-developed laminar PA-6 phase is more effective using an extensional flow field rather than shear flow (Huang et al. 2005).

Morphology of blends is strongly influenced by the mixing mechanism. Well-developed lamellar morphology is produced when deformation of the minor phase is high, and its breakup is minimized. Coalescence of the deformed minor phase could also contribute to lamellar morphology (Lohfink and Kamal 1993). Thus, from the microrheological point of view, the best results are to be expected from systems where (1) the domain size of the dispersed phase is relatively homogeneous, with d ≅ 50 μm; (2) the viscosity of the dispersed phase is lower than that of the matrix, i.e., λ < 1 (which is not in agreement with the work done by Huang et al. (2005)); (3) the dispersed phase shows a strain hardening behavior. Breakup of the minor phase has been discussed in detail in the former sections.

5.4.3.1 Kinematics of Mixing

Spencer and Wiley (1957) found that the deformation of an interface, subject to large unidirectional shear, is proportional to the imposed shear and that the proportionality factor depends on the orientation of the surface prior to deformation. Erwin (1978) developed an expression, which described the stretch of area under deformation. The stretch ratio (i.e., deformed area to initial area) is a function of the principal values of the strain tensor and the orientation of the fluid. Deformation of a plane in a fluid is a transient phenomenon. So, the Eulerian frame of deformation that is traditionally used in fluid mechanical analysis is not suitable for the general analysis of deformation of a plane, and a local Lagrangian frame is more convenient (Chella 1994).

A general equation for the kinematics of distributive mixing was developed in a Lagrangian frame. The degree of mixing was described in terms of inter-material area density, or striation thickness, which could be obtained experimentally. Using an ideal laminar mixing model, the thickness of an individual particle of the minor phase was expressed as ${\updelta}_{\mathrm{d}}=2{\mathtt{\phi}}_1/{\mathrm{a}}_{\mathrm{v}}$, where ϕ₁ is the volume fraction of the minor phase and a_v is the interfacial area density (Ottino et al. 1981). As a result of deformation, the lamellar thickness and the interfacial area density change with the local strain, γ_l, viz., δ_d = δ ^o_d /γ_l; a_v = a ^o_v γ_l, where the symbols with upperscript “o” indicate the initial conditions. For simple shear flow deformation, when the deforming interface has the same direction as the flow, the local area strain is related to the linear strain of the flow field, $\upgamma =\overset{.}{\mathrm{t}\upgamma}$:

$$ {\updelta}_{\mathrm{d}}={\updelta}_{\mathrm{d}}^{\mathrm{o}}{\left[1+{\left(\mathrm{t}\overset{.}{\upgamma}\right)}^2\right]}^{-1/2} $$

(7.120)

The above equation could be used for the interpretation of lamellar morphology development, when breakup of the minor phase is excluded, and the interfacial tension coefficient is vanishingly small.

5.4.3.2 Parameters Determining Lamellar Morphology Development

Distributive lamellar mixing depends on the deformation rate, deformation time, and the initial direction of the interface. The degree of mixing increases as the deformation rate and time increase. The initial direction of the interface, favorable for maximum mixing, is also needed for achieving a high degree of mixing (Ottino et al. 1981).

Lohfink and Kamal (1993) observed that, in single screw extrusion through a flat die, an increase of die gap size yielded fewer, but thicker layers. On the other hand, a smaller die gap size resulted in an increased number of stacked thin layers. Higher screw rpm produced a more pronounced lamellar structure. In real mixing equipment, such as an SSE, deformation time (residence time) could be limited by the deformation rate (screw speed). Lee and Kim (1997) reported that an increase in screw speed reduced the degree of mixing, because the residence time decreased and the minor phase melting was insufficient.

The viscosity ratio, λ, is one of the major parameters in determining the deformation of the minor phase layer. When the viscosity ratio varies from zero to infinity, Taylor’s Eq. 7.49 predicts that deformability of a small drop would change from 1.0λ to 1.18λ. For viscoelastic systems, Gonzalez-Nunez et al. (1993) and Lee and Kim (1997) obtained higher deformation for lower viscosity ratio, when they changed the viscosity ratio by changing the viscosity of matrix material.

Lamellar morphology development also depends on the volume fraction of the minor phase. The individual thickness of EVAl phase in PP matrix phase decreased when the concentration of EVAl phase decreased from 30 to 20 vol% (Kamal et al. 1995). In the experiment, for the processing conditions the viscosity ratio was λ > 1.

The minor phase layers become thinner as interfacial tension coefficient, ν₁₂, decreases (Kamal et al. 1995; Lee and Kim 1997). This confirms that the decrease of ν₁₂ results in a more efficient transfer of stress from the matrix to the minor phase layer (Gopalakrishnan et al. 1995). As the ν₁₂ is reduced further, the layers of minor phase transform into fibers (Kamal et al. 1995). These results are in agreement with the morphology development mechanisms (Ottino et al. 1981; Lindt and Ghosh 1992; Scott and Macosko 1991).

5.4.4 Coalescence

Droplet–droplet coalescence was already discussed in Part 9.4.2.2. Here, the effects of coalescence on morphology will be summarized. Under normal circumstances, there is a dynamic equilibrium between coalescence and dispersion processes; thus it is difficult to assign a particular effect as due to coalescence. However, during flow at temperatures near the melting point, the effects of coalescence dominate the final morphology. For example, blends of HDPE with up to 30 wt% of PA-6 were extruded using a capillary viscometer at T = 150, 200 and 250 °C. All the extrudates contained PA-6 fibrils, independently at T below or above the melting point of PA-6, T_m = 219 °C (Utracki et al. 1986). Judging by the diameter of the resulting PA-6 domains and their internal structure, the fibrillation originated mainly from the flow-induced coalescence.

For capillary flow at 150 °C, the extensional stress, σ₁₁ = 50–800 kPa, at the entrance to capillary was calculated from (Cogswell 1972)

$$ \begin{array}{l}\eta /{\eta}_E=2{ \tan}^{\kern-0.2em -2}\alpha; \kern0.75em \alpha = \arctan \left(2\dot{\varepsilon}/\dot{\gamma}\right);\\ {}{\sigma}_{12}\dot{\gamma}=2{\sigma}_{12}\dot{\varepsilon}\end{array} $$

(7.121)

Since the tensile yield stress for “solid” PA-6 at 150 °C was determined as σ_y = 15 kPa, independent of the rate of straining, the extensional stress in the capillary entrance was more than sufficient to deform the amorphous part of PA-6. Owing to crystallization, the elongated structures, once created, could neither disintegrate nor elastically retract to spherical shapes.

Similarly, at T > T_m, coalescence of semicrystalline dispersed domains combined with stress-induced crystallization leads to formation of long fibers. This effect was explored for the improvement of performance of blends comprising liquid crystal polymers, LCP (La Mantia 1993).

Velankar et al. (2001) conducted shear-induced coalescence experiments on immiscible polymer blends with a droplet–matrix morphology. The study was carried out on model blends of polyisobutylene (PIB) and polydimethylsiloxane (PDMS), with various amounts of a PIB–PDMS diblock copolymer as a compatibilizer. This kind of compatibilizer promotes intimate mixing of thermodynamically immiscible homopolymers through their effect on the interfacial tension between them. The authors determined the mean capillary number of the droplets using dynamic mechanical measurements. The results showed that increasing the amount of a surface-active compatibilizer increased the steady shear capillary number of droplets to values well above the Ca_cr required for breakup of uncompatibilized droplets. This suggests that a simple decrease in interfacial tension is not the only effect of adding the compatibilizer to these immiscible blends. The hydrodynamic stress required for breakup of uncompatibilized blends, based on interfacial tension arguments, is lower than that required for breaking compatibilized droplets. Previous simulations by Stone and Leal (1990) and Li and Pozrikidis (1997) indicated the flow-induced gradients in the concentration of the compatibilizer on the droplet surface. Therefore, Valenkar et al. explained their results by assuming the existence of gradients in interfacial tension induced by the gradients of compatibilizer concentration due to flow. Microscopy experiments were in agreement with this interpretation (Velankar et al. 2001).

5.4.5 Interlayer Slip

The interlayer slip originates in the low entanglement density region at the interface (Helfand and Tagami 1971, 1972). There is a preponderance of chain ends and the low molecular weight species in the interphase. This leads to the low viscosity – in binary PS/PMMA blends, the interphase viscosity was determined as η_Interph ≈ 90 Pas, hence three orders of magnitude smaller than viscosities of the two comprised polymers (Valenza et al. 1991). The net result of the interlayer slip is a drastic reduction of viscosity for mixtures of two immiscible liquids. The phenomenon, first observed for mixtures of low molecular weight liquids, was empirically described, using the fluidity additivity equation. The latter dependence was first derived by Bingham (1922):

$$ \begin{array}{c}1/\upeta =\left({\mathrm{w}}_1/{\upeta}_1\right)+\left({\mathrm{w}}_2/{\upeta}_2\right)\\ {}\mathrm{or}\kern0.5em \mathrm{general},\kern1em 1/\upeta ={\displaystyle \sum_{1=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{i}}/{\upeta}_{\mathrm{i}}}\end{array} $$

(7.122)

where w_i and η_i are the volume or weight fraction and the viscosity of the component i, respectively (see Fig.. 7.31).

Fig. 7.31

Concentration dependence of shear viscosity of PP/LCP blends; dotted line represents the fluidity equation, Eq. 7.122 (Data from Ye et al. 1991)

The dependence was re-derived later for a telescopic flow of two polymers through a pipe (Heitmiller et al. 1964). The two liquids formed a large number of concentric layers, each of the same cross-sectional areas. The fundamental condition that leads to the fluidity additivity relation was the continuity of the shear stress across the multi-stratified structure. Lin (1979) followed this derivation with an additional assumption that the shear stress of each layer can be modified by the presence of an additional frictional stress, Z = (β − 1)(RΔP/2L), where R is the capillary radius, ΔP is the pressure drop, and β is a characteristic material parameter (interlayer slip factor) in

$$ 1/\eta =\beta \left[\left({w}_1/{\eta}_1\right)+\left({w}_2/{\eta}_2\right)\right] $$

(7.123)

For a mixture of two liquids having the same viscosity, η₁ = η₂, Eq. 7.122 predicts additivity, while Eq. 7.123 with β > 0 predicts a negative deviation form additivity (NDB). For β = 1 Bingham’s relation is recovered. However, there are serious reservations about the fundamental consequences of the frictional extra stress Z (Bousmina et al. 1999). In a rigorous derivation for a telescopic flow with the interfacial slip, the following dependence was obtained:

$$ \begin{array}{l}1/\eta =\left({w}_1/{\eta}_1\right)+\left({w}_2/{\eta}_2\right)+\theta \sqrt{\phi_1{\phi}_2}\\ {}\mathrm{where}:\kern1em \theta \propto 1/\Delta \mathrm{l}{\eta}_{\mathrm{Interphase}}\end{array} $$

(7.124)

Equations 7.123 and 7.124 predict a negative deviation from the log-additivity rule.

The material parameter θ in Eq. 7.124 governs the NDB behavior. It was shown that its value is inversely proportional to the thickness of the interphase, Δl, and its viscosity, η_Interphase (Bousmina et al. 1999). Theoretically, the same molecular mechanism should be responsible for both factors, viz., better miscibility, better interdiffusion, thus higher Δl and η_Interphase. However, the low molecular weight components of the blend, that are forced by the thermodynamics to diffuse to the interphase, may not change much the former parameter, but drastically reduce the latter. For immiscible blends, Δl is small, typically 2–6 nm. Thus θ is large, and interlayer slip takes place. For compatibilized blends, the macromolecules of the two phases interact and interlace, which increases both factors; thus, the slip effects are negligible. Measured or calculated values of the interphase viscosity are listed in Table 7.10.

Table 7.10 Calculated viscosity of the interphase

Interlayer slip creates a tree-ring structure in extrusion, e.g., observed in samples containing 30 wt% PA-6 in HDPE matrix, extruded at T = 250 °C. The HDPE/PA-6 capillary viscosities at 250 °C followed Lin’s Eq. 7.123 (Utracki et al. 1986). The simplest fluidity equation, Eq. 7.122, may be useful in describing steady-state viscosity of antagonistically immiscible polymer blends, such as PP/LCP shown in Fig. 7.31. When the volume of the interphase is known, the general form of the Bingham formula in Eq. 7.122 can be used to calculate the interphase viscosity. This indeed has been done, in the case of shear flow of a multilayer PS/PMMA sandwich (Lyngaae-Jørgensen et al. 1988).

Yang et al. (2003) investigated the rheological behavior of PBT/LLDPE and PBT/LLDPE-g-acrylic acid, using a capillary rheometer. They used an equation proposed by Utracki (1991) successfully to depict the viscosity–composition dependence of the blends at low shear stresses. Morphological studies showed a droplet–matrix morphology at low shear rates. On the other hand, at high shear rates, the droplet–matrix morphology at the center of the extruded bar was observed in vicinity of a stratified PBT phase (co-continuous morphology) which contributed to lowering the viscosity of the blending system. This also caused the above equation to fail to predict the rheological behavior of these two systems. It was concluded that the parameter β (interlayer slip factor) in the equation (see Eqs. 7.123 and 7.125) was related not only to the shear stress but also to the elasticity difference of the two components of the blend, the composition, and the interactions of the blend components at high shear stresses (Yang et al. 2003).

5.4.6 Encapsulation

Shear-induced segregation of polymer domains is related to differences in the magnitudes of the rheological properties of blend components. During large strain flow, segregation takes place not only in immiscible blends, in which the viscosities and elasticity of the two phases differ, but also in miscible blends comprising components of different MW. In the latter case, it is the difference in chain lengths that causes an imbalance of stresses and relative motion of the components (Doi and Onuki 1992).

Migration of the low viscosity component toward the high stress regions results in flow encapsulation of one phase by another. The effect has been well documented and successfully explored in polymer processing. For example, this mechanism is responsible for the lubricated, high-throughput flow of POs upon addition of either fluoro- or siloxane polymers. Similarly, enhancement of flow of engineering and specialty resins by incorporation of low viscosity (when molten) LCP is attributed to flow segregation (Utracki 1987, 1988, 1989).

5.5 Shear Flows

The easiest way to discuss flow of polymer blends is to compare them to simpler, low molecular weight homologues, viz., Sect. 7.3. For immiscible blends, the best model is that of emulsions. Like blends, emulsions comprise one liquid dispersed in another. The emulsion morphology is stabilized by addition of a surfactant or an emulsifier, similarly as immiscible blend is stabilized by addition of a compatibilizer. Both systems, emulsions and blends, show phase inversion, viz., Sect. 7.3.2. In emulsions, the phase inversion concentration, ϕ_Ι1, depends mainly on the type and concentration of emulsifier, while in blends it is dominated by relative rheological properties of the two polymers. In emulsion technology, by carefully selecting surfactants and the sequence of liquid addition, it is possible to generate (at the same concentration) two emulsions having different morphologies, viscosities, and other properties (Utracki 1989).

5.5.1 Concentration Dependence of Viscosity

In miscible blends, where the free energy of mixing is negative, ΔG_m < 0, experimental data indicate that, in most system, either the log-additivity rule (see Eq. 7.18) or small positive deviations from it are generally observed. Near the phase separation region, where ΔG_m ≈ 0, the rheological response is complex as the free energy of mixing is precariously balanced by the term describing the energy input by the flow. Finally, in immiscible systems, where ΔG_m > 0, five different types of behavior have been identified. In Fig. 7.32, curves 1–5 represent, respectively, (i)) positively deviating blend (PDB), (ii) negatively deviating blends (NDB), (iii) log-additivity, (iv) PNDB, and (v) NPDB (Utracki 1991). To understand the origins of these types of behavior, it is necessary first to evaluate morphology and flow-imposed morphology in polymer blends.

Fig. 7.32

Five types of the relation between shear viscosity and concentration for immiscible polymer blends: 1. PDB, 2. NDB, 3. additivity, 4. PNDB, and 5. NPDB (Utracki 1991)

From the discussion of phase inversion in Sect. 7.1.2, the emulsion model predicts that immiscible blends should show positive deviation, PDB, from the log-additivity rule: ln η = ∑ w_i ln η_i. However, while PDB has been found in about 60 % of such blends, the remaining four types (see Fig. 7.32) must also be accounted for. This means that at least one other mechanism must be considered when modeling the viscosity–concentration dependence of polymer blends. This second mechanism should lead to the opposite effect, which is to the negative deviation from the log-additivity rule, NDB.

The simplest mechanism that explains the NDB behavior is interlayer slip, which leads to derivation of Eq. 7.123 and Eq. 7.124. One may postulate that at constant stress, the net η versus ϕ dependence can be written as a sum of two contributions: the interlayer slip, expressed by η_Λ (calculated from either Eq. 7.123 or Eq. 7.124), and the emulsion-like viscosity enhancement given by an excess term, Δlog η^Ε (Utracki 1991):

$$ \begin{array}{l} \ln \eta = \ln {\eta}_L+\Delta \ln {\eta}^E\\ {}\Delta \ln {\eta}^E={\eta}_{\max}\left\{1-\left[{\left({\phi}_1-{\phi}_{1I}\right)}^2/\left({\phi}_1{\phi}_{2I}^2+{\phi}_2{\phi}_{1I}^2\right)\right]\right\}\end{array} $$

(7.125)

As mentioned in Sect. 7.1 for polymer blends, the relation between the steady-state shear viscosity and concentration can be quite complex. In the following discussion, the constant stress (not the constant rate) viscosity, corrected for the yield and time effects, will be considered. To illustrate flexibility of Eq. 7.125 to describe (and thus to facilitate interpretation of the rheological results) η versus ϕ, dependence examples of computations are shown in Figures 7.33, 7.34, 7.35, 7.36, 7.37, 7.38, 7.39, and 7.40.

Fig. 7.33

Concentration dependence of blend viscosity at five levels of shear stress (from top: σ₁₂ = 10¹ to 10⁵), indicating a gradual change of dominant flow mechanism from emulsion-type to interlayer slip

Fig. 7.34

Concentration dependence of blend viscosity for polymer-1/polymer-2 blends; three different molecular weight grades of polymer-2 were used. For the lowest molecular weight PDB, whereas for the highest NDB behavior is to be expected

Fig. 7.35

Concentration dependence of shear viscosity of PS/PMMA blends. Points are experimental (Lyngaae-Jørgensen 1983), while the lines were computed from Eq. 7.125

Fig. 7.36

Concentration dependence of zero shear viscosity of polypropylene blends with two linear low density polyethylenes at 190 °C. Points are experimental with error bars indicating the standard deviation (Dumoulin 1988). Lines are computed from Eq. 7.125

Fig. 7.37

Concentration dependence of η′ and η, shear viscosities of LLDPE/PC blends at 245 °C and at constant stresses: G″ = 1, 10 and 100 kPa and σ₁₂ = 100 kPa, respectively. Points – experimental; error bars of measurements ± 2 % (Utracki and Sammut 1990)

Fig. 7.38

Concentration dependence of zero shear viscosity at 260, 280, and 300 °C of polyethylene terephthalate blended with polyamide-6,6. Points are experimental with the error bars indicating the error of measurements ± 2 % (Utracki et al. 1982)

Fig. 7.39

Concentration dependence of zero shear viscosity of PS/PMMA blends at 180 and 210 °C. Points are experimental (Valenza et al. 1991); solid lines are computed from Eq. 7.125

Fig. 7.40

Concentration dependence of zero shear viscosity at 200 °C of PS/LDPE blends without (solid line) and with (broken line) 5 wt% SEB. Points – experimental; error bars of measurement ±3 % (Ausin et al. 1987)

The numerical values of the phase inversion concentration, ϕ_2I, as well as the two material parameters that enter Eq. 7.125 are listed in Table 7.11.

Table 7.11 Parameters used for curve fitting of viscosity versus concentration data to Eqs. 7.9 and 7.123 (Utracki 1991)

5.5.2 Dynamic Flow

Blend structure changes with flow conditions. Therefore, the observed rheological responses must be sensitive to method of measurement. Since modification of structure is related to strain, responses measured at high and low strain values will be different. For this reason, the selected type of test procedure should reflect the final use of the data. When simulation of flow through a die is considered, large strain capillary flow is useful. On the other hand, if material characterization is important, low strain dynamic testing should be used. Because of morphology sensitivity to test conditions, there is a serious disagreement between predictions of the continuum-based theories and experiments. This is summarized in Table 7.12.

Table 7.12 Comparison of continuum-based predictions for simple fluid with experimental observations for polymer blends

A study using confocal Raman spectrometry was carried out to determine the concentration profile within the extrudate of rubbery particles in a polyethylene matrix during capillary flow (Chartier et al. 2010). Chartier et al. reported that the effect of the concentration of particles on the apparent viscosity of polymer melts measured using capillary flow was the opposite of that based on observations made using linear dynamic viscosity measurements (Fig. 7.41). Shear-induced migration can be detected from the concentration profile of the components of the blends inside the material. They discovered that the lowest viscosity component migrates toward the capillary wall. The addition of a compatibilizers inhibited this migration.

Fig. 7.41

(top) the dynamic viscosity versus frequency and (bottom) apparent capillary viscosity of various concentrations of rubber in uncompatibilized PE/Sunigum blends at 180 °C (Chartier et al. 2010)

Dynamic testing of polymer blends at small amplitude is a relatively simple and reliable procedure. The resulting storage and loss shear moduli, G′ and G″, respectively, should be first corrected for yield stress then the loss data can be fitted to Eq. 7.42 to determine the value of the four parameters, η_o, τ, m₁, and m₂. Once these parameters are known, the Gross frequency relaxation spectrum, and as a result all linear viscoelastic functions, can be calculated (see Eqs. 7.85, 7.86, and 7.87).

The dependence of rheological functions of liquid mixtures on the content and the rheological functions of neat ingredients has been discussed, to some extent, in Sect. 7.3.2.3. A summary of these results is given in Table 7.13.

Table 7.13 Blend viscoelasticity from emulsion models (Graebling and Muller 1991)

The last entry in Table 7.13 refers to the theory by Palierne (1990). The theory is based on the following assumptions: (i) the system consists of two viscoelastic liquids; (ii) the concentration of the dispersed phase is moderate; (iii) the drops are spherical, polydisperse, and deformable; (iv) the drop deformation is small, so the blend behavior is linear viscoelastic; and (v) the interfacial tension coefficient, ν₁₂, is constant, independent of stress and interfacial area. The theoretical analysis leads to Eq. 7.70. Note that the ratio ν₁₂/d is the only parameter of the equation. The model was found to provide good description of the dynamic behavior for several blends, supporting the idea that the long relaxation times in blends originate from geometrical relaxation of droplets (Graebling et al. 1989, 1993b).

5.5.3 Compatibilization Effects

Most immiscible polymer blends require compatibilization to reduce the interfacial tension. This helps to increase the degree of dispersion to stabilize the morphology developed during compounding against extensive damage during high stress and strain processing (e.g., during injection molding) and to enhance adhesion between the phases in the solid state, facilitating the stress transfer and improving the mechanical properties of the product. Compatibilization is achieved either by addition of a small quantity, 0.5–2 wt%, of a precisely tailored (usually) block copolymer; an addition of a multipurpose core-shell copolymer, ≤35 wt%, that also improves toughness of the blend; or by reactive processing.

Compatibilization strategy for either addition or reactive blending requires that the copolymer migrates to the interface, thus, on the one hand, lowering the thermodynamic immiscibility barrier between the two phases, and, on the other, engendering formation of the third phase, the interphase.

From the point of view of blend morphology in the molten state, compatibilization enhances the dispersion, increases the total apparent volume of the dispersed phase, rigidifies the interface, and increases interaction not only between the two phases, but also between the dispersed drops. Furthermore, reactive compatibilization may involve chemical bonding between the two polymer macromolecules, resulting in significant increase of the molecular weight at the interface.

The rheological consequences of these changes can be predicted from a model system. The emulsion model indicates that making the interface more rigid causes the intrinsic viscosity of the emulsion to increase (see Eq. 7.50). Similarly, an increase of the apparent volume of the dispersed phase causes the relative viscosity to increase (see Eqs. 7.24 and 7.25). Furthermore, enhanced interactions between the phases will reduce the possibility of the interlayer slip and increase formation of associative network formation, which may result in the yield stress. In short, compatibilization is expected to increase melt viscosity, elasticity, and the yield stress.

There are two mechanisms that may invalidate this prediction: (i) In spite of the best efforts of researchers and technologist the added copolymer may prefer to form micelles inside one of the polymeric phases than to migrate to the interphase. This has been frequently observed in blends with block copolymers, e.g., for blends of PS with PE, “compatibilized” by addition of a hydrogenated styrene-butadiene block copolymer, SEBS (Utracki and Sammut 1988, 1990). (ii) Depending on the blend composition, an addition of compatibilizer may affect the total free volume of the system. These changes are difficult to predict. An increase of the free volume (evidenced by reduction of melt density) is expected to result in increased fluidity of the system.

Effects of addition of hydrogenated styrene-butadiene di-block copolymers (one strictly di-block and the other tapered) on properties of HDPE/HIPS blends were investigated (Brahimi et al. 1991). The rheological behavior of the blends, especially in the low-frequency region, was sensitive to the copolymer content. However, at high frequencies, the copolymer only slightly affected the flow. Furthermore, addition of a small amount of compatibilizer reduced the zero-shear viscosity, η_o, while higher loading had an opposite effect. This behavior was interpreted as due to the change in the copolymer state in the blend, i.e., saturation of the interface followed by micelle formation.

The results were compared with prediction of Palierne model, viz., Eq. 7.39. For diluted, uncompatibilized blends, PS/PE = 10/90 or 90/10, relatively good agreement was found. The agreement was poor for blends containing 3 wt% of the tapered di-block copolymer. In the latter case, the reduction of storage and loss shear moduli, especially at low frequencies, could not be explained by the emulsion model. The effect of the interfacial tension and particle size over a relatively wide range did not significantly affect the model predictions. These observations confirmed an earlier report for the same system (Aït-Kadi et al. 1992). Since, at low frequencies, slip is less likely to occur than at high frequencies, low values of G′ and G″ could not be explained by this mechanism. The most likely explanation is an increase of the free volume by incorporation of the copolymer. The nonlinear variation of specific volume as a function of composition has been frequently observed for systems with limited miscibility.

Blends of PS with LDPE were compatibilized by addition of di- and tri-block copolymers, Kraton™ G 1701 and G 1605 (Pascault et al. 1994). A continuous decrease of PS-drop size and an increase of shear viscosity with addition of copolymer were reported.

Blends of PP with a polyamide (PA-6, PA-66, or PA-12) were the object of intensive studies. Linear viscoelastic shear moduli were measured for PP/PA-6 blends comprising different amount of PP-g-PA-6 copolymer. It was reported that, in spite of the expected reduction of the particle size with increase of the compatibilizer content, no qualitative effect of the flow was observed (Scholz et al. 1989).

In a thorough study, PP, PA-6, and their compatibilized blends were studied at 225–250 °C, in steady-state and dynamic shear, as well as extensional flow conditions (Utracki and Sammut 1992). The dynamic flow curves for the blend were significantly higher than what could be predicted from the component flow behavior. The blends showed a regular, pseudoplastic flow behavior, without yield stress. By contrast, capillary flow was found to be insensitive to temperature, suggesting a major modification of morphology during these large strain tests. Similarly, the extensional viscosity of the blends was one order of magnitude higher than what could be expected from the component polymer behavior. During extensional flow, the blends showed strain hardening, absent for either PP or PA-6. This could be explained by postulating that reactive compatibilization significantly increased the molecular weight of the system – strain hardening is to be expected for highly entangled, high MW systems. It was also reported that the measured elongational viscosity, η_E, for two homopolymers agreed quite well with the value calculated from the entrance pressure drop in capillary flow, P_e. However, for the blend, the calculated value of η_E was one order of magnitude higher than measured.

Reactive compatibilization in a specially designed twin-screw extruder was carried out during compounding maleated polypropylene, PP-MA (0–0.14 wt% MA), with PA-6. During the reaction a di-block copolymer was formed at the interface. As the copolymer content increases from zero to 20 wt%, the number average diameter of PA-6 drops decreased from the initial value d_o = 20 to d = 0.14 μm at 20 wt% copolymer. The concentration dependence of shear viscosity also changed with compatibilization from negative deviation from the log additivity rule, NDB, to positive deviation, PDB (Nishio et al. 1992).

The effect of compatibilization on the shear flow of PP/PA-6 and PP/PA-12 blends was also studied (Germain et al. 1994). Here the copolymer flow curve was one order of magnitude lower than that of PA. The authors reported that, at low deformation rates, emulsion-type morphology dominated the flow, whereas, at higher rates, concentric layered-type morphology, with appropriate flow behavior, was observed. At low shear rates, the blend viscosity was higher than the viscosity of the matrix, while at high shear rates the contrary was observed. The low shear rate behavior was analyzed by means of Palierne theory, assuming that the copolymer is located at the interface. Good agreement was obtained for the low-concentration blends. For high stress (and strain) deformation, a model of lamellar telescopic flow for power-law fluid was derived. The skin-core model represented the flow of blends well. Thus, it can be postulated that, in blends with low MW copolymeric compatibilizers, the stress may cause its disentanglement from at least one phase, forming a layered morphology, and resulting in flow lubricated by the presence of the low molecular weight compatibilizer.

Effects of addition of a compatibilizing block copolymer, poly(styrene-b-methyl methacrylate), P(S-b-MMA) on the rheological behavior of an immiscible blend of PS with SAN were studied by dynamic mechanical spectroscopy (Gleisner et al. 1994a). Upon addition of the compatibilizer, the average diameter of PS particles decreased from d ≅ 400 to 120 nm. The data were analyzed using weighted relaxation-time spectra. A modified emulsion model, originally proposed by Choi and Schowalter (1975), made it possible to correlate the particle size and the interfacial tension coefficient with the compatibilizer concentration. It was reported that the particle size reduction and the reduction of ν₁₂ occur at different block copolymer concentrations.

In another attempt, TPVs based on ENR/PP blends were prepared by melt mixing via dynamic vulcanization, using two different types of compatibilizers: phenolic-modified polypropylene (Ph-PP) and graft copolymer of maleic anhydride on polypropylene molecules (PP-g-MA) (Nakason et al. 2006). A high compatibilizing effect was found because of the chemical interaction between the polar groups in ENR and Ph-PP or PP-g-MA. The TPVs prepared from ENR/PP with Ph-PP as a compatibilizer showed the highest rheological and mechanical properties, while those based on ENR/PP exhibited the lowest values. Moreover, the TPV, compatibilized with Ph-PP, showed smaller rubber particles dispersed in the PP matrix, compared to the corresponding TPV based on ENR/PP-g-MA (Nakason et al. 2006).

Huitric et al. (2007) studied the effect of different concentrations of polyethylene-graft-maleic anhydride on the morphology evolution of blends of low density polyethylene and nylon 12, using a method based on quenching following deformation of the samples, which were kept between the parallel plates of a rheometer. They determined droplet size and transient viscosity of the blends as functions of the total strain. The results revealed that the droplet size was governed by coalescence at low strain values. Due to the important interfacial coverage of the interface by the grafted copolymer chains, a significant coalescence inhibition was observed for the blends with high concentration of compatibilizer. In that case, the intensity of the coalescence did not change by the applied shear rate. On the contrary, increasing shear rate favored the coalescence for the blends without compatibilizer or with low compatibilizer concentration. The authors introduced an additional parameter for non-affine deformation (slip parameter) in a modified version of the Lee and Park model. The results showed great improvement in the predictions of droplet size evolution by this adjustment.

Kordjazi and Ebrahimi (2010) investigated the rheological properties and morphology of compatibilized and noncompatibilized PP/PET blends, using SEBS-g-MA as a compatibilizer. They suggested that the behavioral changes of rheological properties by increasing the compatibilizer are related to the aggregation of the dispersed particles encapsulated with elastomeric shell, which is responsible for the failure of Palierne’s model predictions. Based on frequency sweep and step strain experiments in the linear region, after pre-shearing using various shear rates, the authors also suggested that the aggregated structure was destroyed and replaced by an alignment in the flow direction (Kordjazi and Ebrahimi 2010).

DeLeo et al. (2011) considered the formation of a compatibilizer between two multifunctional reactive polymers that leads to a cross-linked copolymer at the interface. The study was conducted on model blends PDMS/PI. In this case a chemical reaction between amine-functional PDMS and maleic anhydride-functional PI formed the compatibilizer. The effects of interfacial cross-linking on rheological behavior and morphological characteristics were found to be highly asymmetric for the samples with PI:PDMS ratio of 30:70 or 70:30. The PI-continuous blends showed unusual features including drop clusters, nonspherical drops, and “gel-like” behavior, which increased by increasing reactive compatibilizer loading. Contrarily, PDMS-continuous blends displayed typical droplet–matrix morphology with round drops and showed liquid-like behavior that was qualitatively similar to that of compatibilizer-free blends. The authors speculated that the asymmetry of the compatibilizer architecture on the two sides of the interface is the factor causing the structural and rheological asymmetry (DeLeo et al. 2011).

Entezam et al. (2012) studied the effect of interfacial activity and micelle formation on rheological behavior and microstructure of reactively compatibilized PP/PET blends. They used different interfacial modifiers, i.e., PTW or PP-g-MAH. They also used dynamic and start-up shear flow experiments as well as their subsequent recovery. Reactive compatibilization, in concentrations close to the critical micelle concentration, at which the interface is saturated with the compatibilizer, changed the rheological behavior from emulsion to solid-like behavior due to the interconnectivity between dispersed phase domains. They suggested that PTW micelles in the bulk phase of the blend favored physical network-like structure formation and enhanced the time and intensity of the relaxation process. However, the PP-g-MAH micelles restricted interconnectivity between the dispersed domains. The analysis of fractional Zener models (FZMs) showed nonzero value of G _e (the elastic modulus of spring element of FZM) for the compatibilized blends with network-like structure. It was suggested that the increase of G _e with formation of PTW micelles and its zero value for the blends consisting of PP-g-MAH micelles indicate a dual role for micelles influencing rheological and morphological properties of PP/PET blends (Entezam et al. 2012).

5.5.4 Time–Temperature Superposition

The time–temperature superposition principle, t-T, has been a cornerstone of viscoelastometry. It has been invariably used to determine the viscoelastic properties of materials over the required 10 to 15 decades of reduced frequency, ωa_T (Ferry 1980). Measuring the rheological properties at several levels of temperature, T, over the experimentally accessible frequency range (usually two to four decades wide), then using the t-T shifting, has made it possible to construct the complete isothermal function.

As demonstrated before, the shifting involves three shift factors, one horizontal, usually expressed as a_T = b_Tη_o(T)/η_o(T_o), where b_T = ρ_oT_o/ρT is the first vertical shift factor that originates in the thermal expansion of the system (ρ is density). The subscript o indicates the reference conditions, defined by the selected reference temperature T_o, usually taken in the middle of the explored T-range. For homopolymer melts as well as for amorphous resins, the two shift factors, a_T and b_T, are sufficient. However, for semicrystalline polymers the second vertical factor v_T has been found necessary – it accounts for variation of the crystallinity content during frequency scans at different temperatures (Ninomiya and Ferry 1967; Dumoulin 1988).

Only when all the relaxation times in a given system are multiplied by the same factor, when the temperature is changed, the t-T principle can be observed. In single-phase homologous polymer blends, the relaxations are mainly controlled by the segmental mobility; thus the t-T superposition has been observed in a wide range of conditions. Similarly, for polymers filled with high modulus particles, the filler is responsible for enhancement of modulus without affecting the relaxation spectrum, and as a consequence t-T superposition is obeyed. However, in rheologically complex heterogeneous systems, individual polymeric components contribute to the relaxation and since their activation energies are usually different, a change of temperature affects them differently – lack of t-T is a result.

Fesko and Tschoegl (1971) demonstrated that the simplest form of the time–temperature superposition relation for a function G(t, T) = G[t, a(T)] is

$$ \begin{array}{l}{\left[\partial G\left(t,T\right)/\partial T\right]}_t=\left\{\left[\partial G\left(t,T\right)\right]/{\left[\partial \ln t\right]}_T\right\}\left\{d\left[ \ln a\left(t,T\right)\right]/ dT\right\}\\ {}\kern0.1em d\left[ \ln a\left(t,T\right)\right]/ dt={\displaystyle \sum_i{N}_i(t)}d\left[ \ln {a}_i(T)\right]/ dT;i=1,\dots, n\\ {}\kern3.6em {N}_i(t)={\phi}_i{L}_i\left(t,{T}_0\right)/{\displaystyle \sum_i{\phi}_i{L}_i\left(t,{T}_0\right)}\\ {}\kern2.5em {L}_i\left(t,{T}_0\right)=\partial {G}_i\left[\left( \ln t\right),{T}_0\right]/\partial \ln t\end{array} $$

(7.126)

where the summation extends over every species in the system. Equation 7.126 assumes that the effects of time and temperature can be separated, G(t, T) = G[t·a(t, T)]. Similar derivation was published by Goldman et al. (1977).

There is growing evidence that t-T superposition is not valid even in miscible blends well above the glass transition temperature. For example, Cavaille et al. (1987) reported lack of superposition for the classical miscible blends – PS/PVME. The deviation was particularly evident in the loss tangent versus frequency plot. Lack of t-T superposition was also observed in PI/PB systems (Roovers and Toporowski 1992). By contrast, mixtures of entangled, nearly monodispersed blends of poly(ethylene-alt-propylene) with head-to-head PP were evaluated at constant distance from the glass transition temperature of each system, homopolymer or blend (Gell et al. 1997). The viscoelastic properties were best described by the “double reptation model,” viz., Eq. 7.82. The data were found to obey the time–temperature superposition principle.

The explanation proposed by Ngai and Plazek (1990) was based on the postulate that the number of couplings between the macromolecules varies with concentration and temperature of the blend. The number of couplings, n, can be calculated from the shift factor, a_T = [ς_o(T)/ς_o(T_o)]^{1/(1 − n)}, where ς_o(T) is the Rouse friction coefficient. Thus, in miscible, single-phase systems, as either the concentration or temperature changes, the chain mobility changes and relaxation spectra of polymeric components in the blends show different temperature dependence, i.e., the t-T principle cannot be obeyed. Similar conclusions were reached from a postulate that the deviation originates from different temperature dependence of the relaxation functions of the blend components (Booij and Palmen 1992).

In immiscible blends, the t-T principle does not hold. For immiscible amorphous blends, it was postulated that two processes must be taken into account: the t-T superposition and the aging time (Maurer et al. 1985). On the other hand, in immiscible blends, at the test temperature, the polymeric components are at different distances from their respective glass transition temperatures, T − T_g1 ≠ T − T_g2. In blends of semicrystalline polymers, such as PE/PP, the superposition is limited to the molten state, within a narrow, high temperature range (Dumoulin 1988).

As an alternative to t-T superposition, plot of the elastic stress tensor component as a function of the viscous one has been used, e.g., (σ₁₁ − σ₂₂) versus σ₁₂ or G′ versus G″. For systems in which the t-T is obeyed, such plots provide a temperature-independent master curve, without the need for data shifting and calculating the three shift factors. Indeed, from Doi and Edwards tube model, the following relation was derived:

$$ \ln {G}^{\prime }=2 \ln {G}^{{\prime\prime} }+ \ln \left(6{M}_e/5\rho RT\right) $$

(7.127)

where M_e is the entanglement molecular weight (Han and Kim 1993). The dependence suggests that a plot of G′ versus G″ should be insensitive to temperature. Indeed, good superposition was obtained for several blends where the structure remained unchanged within the range of independent variables, e.g., in such miscible systems as PS/PVME and PEO/PMMA, or even in some immiscible blends whose components have similar glass transition temperature, viz., PS/PMMA. However, lack of superposition was noted in other systems, where the structure did change, viz., PS/PVME heated across the binodal, block copolymer across the microphase separation temperature, LCP across the nematic transition temperature, etc.

5.5.5 Steady-State Versus Dynamic Viscosities

For most blends, the morphology changes with the imposed strain. Thus, it is expected that the dynamic low strain data will not follow the pattern observed for steady-state flow. One may formulate it more strongly: in polymer blends, the morphology and the flow behavior depend on the deformation field; thus under different flow conditions, different structures are being tested. Even if low strain dynamic data can be generalized using the t-T principle, those determined in steady state will not follow the pattern.

Chuang and Han (1984) reported that, for miscible and immiscible blends at constant composition, the plots of N₁ versus σ₁₂ and G′ versus G″ are independent of T. However, while for single phase systems, the two dependencies are approximately parallel, the steady-state relation may be quite different from the dynamic one for immiscible blends, such as PS/PMMA.

The agreement can be improved by means of the Sprigg’s theory (1965). The general theory leads to the conclusion that

$$ \begin{array}{l}\eta \left(\dot{\gamma}\right)={\eta}^{\prime}\left(\omega \right),\kern1em \mathrm{or}\kern1em {\sigma}_{12}\left(\dot{\gamma}\right)={G}^{{\prime\prime}}\left(\omega \right)/C\\ {}{\psi}_1\left(\dot{\gamma}\right)=2{G}^{\prime}\left(\omega \right)/{\omega}^2,\kern1em \mathrm{or}\kern1em {N}_1\left(\dot{\gamma}\right)=2{G}^{\prime}\left(\omega \right)/{C}^2\end{array} $$

(7.128)

where $C\equiv \omega /\dot{\gamma}={\left[\left(2-2e-{e}^2\right)/3\right]}^{1/2}$ and e is a model parameter. For a series of PMMA/ABS blends, the plot of C versus composition was nonlinear, with C = 1 found only for PMMA homopolymer. Variation of this structural parameter seems to be related to differences of morphology existing in dynamic and steady-state flow fields (Utracki 1989).

Capillary flow of EPDM with poly(vinylidene-co-hexafluoropropylene), Viton™, showed a sixfold reduction of shear viscosity upon addition of about 2 % of the other component (Shih 1976, 1979), whereas in dynamic tests, the complex viscosity behavior of EPDM and EPDM with 5 % Viton™ was similar over a wide range of frequency and strain (Kanu and Shaw 1982). The latter authors postulated accumulation of the second component at the capillary entrance, which periodically feeds into the capillary, lubricating the main stream by a sort of roll bearing effect. In this particular case, the difference is related not only to material properties but also to a flow segregation enhanced by the geometry of the measuring device. Since the effect is strongly affected by flow geometry, the data obtained in capillary flow have little value for process design requirements.

The phenomenon of flow segregation has been exploited commercially. For example, high viscosity engineering resin that has poor resistance to solvents, e.g., polycarbonate or polyetheretherketone (PC or PEEK, respectively), can be blended with low melt viscosity liquid crystal polymer, LCP. Extruding such a blend through die with long enough land forces LCP to migrate toward the high stress surface, thus lubricating die flow and in addition engendering a protective layer on the surface of PC or PEEK. The reduction of viscosity of a polymer melt upon addition of LCP was originally described in 1979, in a patent deposition from ICI (Cogswell et al. 1981, 1983, 1984). The rheological behavior of LCP blends with polyether imide Ultem™ was studied by Nobile et al. (1990) in steady-state capillary and dynamic mechanical modes of deformation. The flow of LCP was reported to be sensitive to pressure; thus the flow of blends was carried out using a short capillary.

Another, more common commercial use of the phenomenon is addition of fluoropolymers to polyolefins. In this case, a small amount of fluoropolymer progressively migrates to the die surface, reducing the die pressure drop and making it possible to extrude the resin at high throughput without melt fracture. It has been shown that this approach also works for other polymers, viz., PEEK. Thus blends of PEEK with polytetrafluoroethylene, 1–5 wt% PTFE, were extruded. The pressure drop across the die was reported to decrease with time to an equilibrium value, P_lim. The value of P_lim depended on PTFE content, whereas the time to reach it depended on the rate of extrusion – the higher was the rate, the shorter was the saturation time (Chan et al. 1992).

Over the years, dynamic testing has become the preferred method of testing the rheological behavior of the multiphase systems. For example, Nishi et al. (1981) carried out careful studies on the dynamic behavior of PS/PVME. The specimens were cast at temperatures either below or above the lower critical solution temperature, LCST ≅ 95 °C. While those prepared at T < LCST (single-phase system) showed superimposition of dynamic data onto a master curve, those that were cast at T > LCST did not.

5.5.6 Blend Elasticity

Four measures of melt elasticity are commonly used: in steady-state shearing, the first normal stress difference (N₁₎; in dynamic tests, the storage modulus (G′); and the two indirect and controversial ones, namely, entrance–exit pressure drop (Bagley correction) (P_e) and the extrudate swell (B). In homogeneous melts, the four measurements are in qualitative agreement. More complex behavior is expected for blends. If the blend can be regarded as an emulsion, without interlayer slip the PDB behavior for the elastic measurements is to be expected. On the other hand, in systems where the dispersed phase is difficult to deform (as in suspensions), extrudate swell should be small. Deformation and recovery of the dispersed phase shape provides a potent mechanism for the elastic energy that result in large elastic response – this does not have anything to do with the molecular energy storage.

The direct measurements of N₁ and σ₁₂ indicate a parallel dependence of both these functions plotted versus ϕ, even when they have a sigmoidal form. Considering the steady shear flow of a two-phase system, it is generally accepted that the rate of deformation may be discontinuous at the interface, and it is more appropriate to consider variation of the rheological functions at constant stress than at constant rate, i.e., N₁ = N₁ (σ₁₂). Using a similar argument for the dynamic functions, it should be concluded that G′ = G′(G″) should be used. Note that, as discussed above, the steady-state and dynamic data for polymer blends rarely superimpose.

Another method for estimating the elasticity contribution is through the Bagley entrance–exit pressure drop correction, P_e. For single-phase systems, the plot of P_e versus σ₁₂ is independent of capillary diameter, temperature, and molecular weight, but rather sensitive to changes in flow profile (Utracki 1985). The plot was found to be useful for interpretation of the stress, temperature, and composition-dependent morphological changes in immiscible polymer blends (Dumoulin et al. 1985). However, it could not be used to estimate the elasticity of blends.

Extrudate swell, B, has been used to calculate the recoverable shear strain, γ_R, for single-phase materials (Utracki et al. 1975). Introduction of the interface negates the basic theoretical assumptions on which the calculation of γ_R was based. In addition, presence of the yield stress, frequently observed in multiphase systems, prevents B from reaching its equilibrium value required to calculate γ_R and then N₁. Nevertheless, B is used as a qualitative measure of blend elasticity.

Note that the presence of the dispersed, deformable phase leads to form recovery, i.e., shrinkage of the prolate ellipsoids motivated by the interfacial energy, which results in unduly large enhancement of B. The phenomenon has little to do with deformability of macromolecular coil – the postulated mechanism of swelling in single-phase polymeric system. The main origin of blend swelling is the elastic recovery of domains extended during the convergent flow in the capillary entrance. The observed form swelling of blends could be large, giving strain recovery, γ_R ≤ 6.5.

It is worth pointing out that strain recovery can be nonsymmetrical as far as the blend composition is concerned. In the case when the viscosity ratio at low deformation rate exceeds the limiting value λ_cr = 3.8, there is a significant difference in the mechanism of dispersion. During compounding in a twin-screw or twin-shaft instrument, the material undergoes stretching in shear and extensional flow fields. Depending on the composition, the stretched forms undergo different recovery. For blends with λ > λ_cr the prolate ellipsoids cannot be broken; thus they slowly retract into large spheres. For blends with λ < 1/λ_cr the prolate ellipsoids will disintegrate by the capillarity instability mechanism (El Khadi et al. 1995).

Similar observations were reported for PMMA/PS blends (Gramespacher and Meissner 1995). The elastic creep compliance for PMMA/PS = 16/84 behaved regularly, similar to what has been observed for single-phase polymers. However, when the composition was reversed, i.e., PMMA/PS = 84/16, the recovery creep compliance showed a maximum at which the recovery direction was reversed. The authors attributed the dissymmetry of behavior to different retardation times of the blend components.

5.6 Elongational Flows

Owing to experimental difficulties, there are but few publications on uniaxial deformation of blends. To prepare specimens for testing, samples usually are transfer molded and relaxed, both operations requiring relatively long heating time, during which only well-stabilized blends will not coarsen.

It is convenient to distinguish two contributions to the tensile stress growth function, η ⁺_E , one due to the linear viscoelastic response, η ⁺_EL , and the other originating in the structural change of the specimen during deformation, η ⁺_ES . The first can be calculated from any linear viscoelastic response, while the second (which originates in either intermolecular interactions or entanglements) depends on both the total strain, $\upvarepsilon =\dot{\upvarepsilon}\mathrm{t}$, and either strain rate $\dot{\upvarepsilon}$ or straining time t. Owing to the industrial importance of strain hardening (SH), a large body of literature focuses on the optimization of blend composition to maximize SH. Since SH depends on the entanglements, blending branched polymers usually affects SH even in the low concentration range.

Most of the work on uniaxial extensional flow of immiscible polymer blends has focused on the behavior of systems containing PE. The main reason is the need for better, easier-to-process film resins, moreover for a relative stability of polyolefin blend morphology. Film blowing conceptually involves two different engineering operations, extrusion and blowing. For most production lines the latter limits productivity. For low density LDPE resins, strain hardening provides a self-regulating, self-healing mechanism. For HDPE and LLDPE, only small SH can be obtained for the high MW and MWD resins. As a result, most LLDPE resins on the market are blends with LDPE, rubbers, copolymers, or another type of LLDPE. SH was also found to be an important resin characteristic for wire coating. Here the surface finish and uniformity of the deposited layer were superior for blends with high strain hardening and low shear viscosity (Utracki 1988).

Among biodegradable polymers, poly(lactic acid) (PLA) is a popular candidate for a wide variety of packaging applications because of its excellent gloss and clarity, high tensile strength, good heat sealability, and low coefficient of friction. However, drawbacks, including a low melt strength and brittleness, limit its end-use applications. Eslami and Kamal (2012) examined three different potential approaches to overcome these limitation by proper rheological and mechanical experiments: (i) the blending of PLA with poly((butylene succinate)-co-adipate) (PBSA) as another biodegradable polymer, (ii) the modification of the clay by formation of a blend/clay nanocomposite (Eslami and Kamal 2013b), and (iii) the introduction of by branching using chain extender (Eslami and Kamal 2013a). In the first approach, a series of blends based on poly(lactic acid) (PLA) and biodegradable poly((butylene succinate)-co-adipate) (PBSA) and their nanocomposites with nanoclay (PLA/PBSA/Clay ternary nanocomposites) were prepared using a twin-screw extruder. The morphology and structure of the blends and the nanocomposites were examined using field emission scanning electron microscopy, transmission electron microscopy, and X-ray diffraction. Rheological properties of the blends, nanocomposites, and pure components were also studied in dynamic oscillatory shear measurements and elongational mode at different Hencky rate.

The authors calculated the strain hardening intensity values as a measure of melt strength using the ratio of η_E,nonlinear/η_E,linear (λ_n). The slope of log λ_n versus Hencky strain defines the strain hardening intensity. As seen in Fig. 7.42 (a), effective improvements in melt strength required over 50 wt% PBSA which decreases the tensile modulus.

Fig. 7.42

(a) Rheological properties of PLA/PBSA blends without chain extender (b) with chain extender (Eslami and Kamal 2013a, b)

It was mentioned that the incorporation of nanoclay had only a minor effect on melt strength; however it increased the tensile modulus. On the other hand, Cole–Cole plot of the melts showed that the chain extender can promote the development of chain branching by time. The use of an epoxy based multifunctional chain extender resulted in significant enhancement of the melt strength and processability of the blends even at 30 wt% PBSA (Fig. 7.39b). These blends also exhibited interesting mechanical properties (Eslami and Kamal 2013a).

Blends of LLDPE/PP = 50:50, with or without compatibilizing ethylene-propylene copolymer, EPR, was studied by Dumoulin et al. (1984a, b, c). In spite of the expected immiscibility, the blends showed additivity of properties with good superposition of the stress growth functions in shear and elongation, as well as with the zero deformation rate Trouton ratio, R_T ≅ 1. In earlier work, blends of medium density PE (MDPE) with small quantities of ultra-high molecular weight polyethylene (UHMWPE) were studied in shear and extension. Again, SH and R_T ≅ 1 was observed.

It has been shown that the stress growth function, in uniaxial extension, provides three important pieces of information on the polymer. The initial slope of the stress growth function

$$ {S}_i=\underset{t\to 0}{ \lim }d \ln {\eta}_E^{+}/d \ln t $$

(7.129)

was found to correlate with polydispersity of the molecular weights, M_z/M_n, where M_z and M_n are respectively z- and number average molecular weights (Schlund and Utracki 1987). The observation agrees with Gleissle’s principle (1980):

$$ \begin{array}{l}\eta \left(\dot{\gamma}\right)={\eta}^{+}(t)\kern0.75em \mathrm{for}\kern0.75em \dot{\gamma}=1/t\\ {}\therefore \kern0.75em \underset{t\to 0}{ \lim}\partial \ln {\eta}^{+}(t)/\partial \ln t=\underset{t\to 0}{ \lim}\partial \ln \eta \left(\dot{\gamma}\right)/\partial \ln \dot{\gamma}=n-1\end{array} $$

(7.130)

The plateau or equilibrium value provides information on the weight average molecular weight, M_w, and the stress hardening part, η ⁺_ES (t) on the entanglements, i.e., branching, association, etc. The parameter S_i could provide information regarding blend miscibility. Solubility usually broadens the width of the MW distribution, causing S_i to increase. By contrast, immiscibility causes separation of high molecular weight fractions and narrowing MWD. The miscibility can also be reflected in a maximum strain at break, ε_b. In “antagonistically” immiscible blends of PA-6 in LLDPE, a sharp decrease of ε_b was observed. However, in blends with co-continuous morphology ε_b may increase to an average value, with negative deviations on both sides (Min 1984).

Li et al. (1990) studied the elongational viscosity of specially prepared blends of styrene-acrylonitrile copolymer, SAN, with different loadings of cross-linked polybutadiene, BR, particles having diameter, d = 170 nm. At higher rates of extension, the SAN showed strong strain hardening behavior. As the volume of rubber particles in the system increased, the strain hardening became less evident. By contrast, the low deformation rate elongational viscosity was shown to increase with BR loading, and as its content increased, the system progressively showed increased sensitivity to strain.

Delaby et al. (1994) attempted to experimentally examine the relation between droplet deformability and the extensional viscosity ratio, D_E = D_E(λ_Ε). The authors demonstrated that the theories proposed by Taylor (1932, 1934) and Palierne (1990) predict the same dependence:

$$ \left({\gamma}_d-1\right)/\left({\gamma}_m-1\right)=5/\left(2{\lambda}_E+3\right) $$

(7.131)

where γ_d and γ_m are respectively strain of the dispersed phase (defined as a ratio of the long axis to the original drop diameter) and the matrix. Only for λ_E = 1 co-deformation of drop is to be expected. The dependence is shown in Fig. 7.43. The experiments show good agreement with the behavior predicted by Eq. 7.131 in the full range of the viscosity ratios used in the studies, λ_E = 0.005 to 13. Drop deformability computed in 2D, using the boundary element method, resulted in higher value than 5/3, given for 3D by Eq. 7.131; independently, two research teams found the limit for λ_E → 0 to be 2 (Khayat et al. 1996; Stradins and Osswald 1996).

Fig. 7.43

Relative deformation of the dispersed phase versus the viscosity ratio (Delaby et al. 1994)

Convergent flow at the die entrance provides strong elongational flow. Laun and Schuch [1989 derived the following relation between the entrance pressure drop in capillary flow and the shear stress at the capillary wall:

$$ {P}_e=1.89{\left({\eta}_E/\eta \right)}^{1/2}{\sigma}_{12}/\left(n+1\right) $$

(7.132)

For Newtonian liquids Eq. 7.132 predicts P_e ≈ 1.64σ₁₂, This proportionality is shown in Fig. 7.44 along with the experimental values determined for ORGALLOY™, PP, and PA-6. Evidently, Eq. 7.132 provides satisfactory approximation for the homopolymers, but for the blend, the prediction is again about one decade too low. Similarly, as for the shear flows, here also the elongational properties of blends show a different behavior under different extensional flow field conditions.

Fig. 7.44

Entrance–exit pressure drop in capillary flow of polypropylene, polyamide-6, and commercial PP/PA-6 blend, Orgalloy at 230 °C – line computed from Eq. 7.132

Extensional flow is important for the dispersion process. As the microrheology indicates, the minimum of the κ versus λ curve is very narrow for the shear flow, but very broad (and lower) for the extensional flow (see Fig. 7.45). This suggests that it should be much easier to disperse fluids in extensional than in shear flow fields. In particular, the benefits are obvious for high and low values of the viscosity ratio. It has been demonstrated theoretically and experimentally that drops can be deformed but not broken by shear flow if λ > 3.8. This is not the case for the inverse ratio, but the drop spinning mechanism in this region is slow, which makes the dispersion process inefficient. These theoretical findings have been confirmed by constructing an extensional flow mixer, EFM, and performing experiments with polymer blends having large difference of viscosity (Luciani and Utracki 1996; Utracki and Luciani 1996).

Fig. 7.45

Critical capillary number versus viscosity ratio is shear flow (solid lines) and extension (dash line)

6 Concluding Remarks

The rheological behavior of polymer blends is a complex phenomenon that is not only an extension of the rheological behavior of simple multicomponent systems, such as solutions, emulsions, and suspensions. Also, it is not the combination of the rheological behavior of the individual polymeric components or additive. However, the rheological behavior of polymer blends is governed by the same general rules of thermodynamics, mechanics, surface science, and other physical and chemical principles that govern the behavior of all materials, when they respond to stress or strain or forces that produce a rheological response.

In this chapter, we have attempted to provide some of the fundamental background regarding the behavior of simpler systems and to indicate how polymer blends behave similarly to these systems in some respects, while in many other respects they behave in a much more complex manner. Much of our discussion related to simple two-component blend systems. However, there are many multicomponent systems that are of commercial interest in many applications. Even more complex blends, such as those involving biosystems and systems involving natural polymers, are gaining interest. The understanding of the flow and rheological behavior of these systems is certainly very difficult. However, in the final analysis, these materials must obey the same laws of physics and chemistry. Complex as they might be, it is certain that the modern tools of science and technology will deal with the relevant issues.

It should be apparent from the aspects covered in this chapter that the rheological behavior of polymer blends, as many aspects of the behavior of polymer systems, cannot be understood or explained in terms of fundamentals and observations associated with rheology alone. Many aspects of polymer and blend behavior are involved. Therefore, we suggest to the reader to refer to other chapters in this handbook for a more complete understanding of the issues involved.

7 Cross-References

Compounding Polymer Blends

Interpenetrating Polymer Networks

Interphase and Compatibilization by Addition of a Compatibilizer

Miscible Polymer Blends

Morphology of Polymer Blends

Polymer Blends Containing “Nanoparticles”

Thermodynamics of Polymer Blends

Notation and Abbreviations

a, b, k, K, n, u, β

Equation constants

a_v

Interfacial area density

B_AB

Reduced binary thermodynamic interaction parameter, B_AB = χ_ABRT/V

B

Droplet width

b_i

Segment length

c_i

Lee and Park relaxation parameters

D

Deformation

d

Droplet diameter

d*

Equilibrium droplet diameter

D, D_M, D_s

Diffusion, inter diffusion and self diffusion coefficient, respectively

D_p

Particle diffusion coefficient

E⁺

Threshold energy of coagulation

E_DK

Macroscopic bulk breaking energy

F

Intrinsic thermodynamic function

f

Frequency

G*, G′, G″

Complex, storage and loss shear modulus, respectively

H(τ)

Relaxation time spectrum

$\tilde{\mathbf{H}}\left(\boldsymbol{\upomega} \right)$

Reduced frequency relaxation spectrum

${\tilde{\mathbf{H}}}_{\mathbf{G}}\left(\boldsymbol{\upomega} \right)$

Gross’ frequency relaxation spectrum

H_max

Maximum of the relaxation spectrum

h_c

Critical separation distance

k_B

Boltzmann constant

L

Droplet length

M

Onsager-type mobility factor

M_n, M_w, M_z

Number, weight and z-average molecular weight, respectively

N₁ = σ₁₁ − σ₂₂

First normal stress difference

N_o,N

Initial and final number of particles respectively

N^o, N⁺

Number of coagulating drops, initially and at t = t_c

N_T

Total number of collisions per unit time

n

Number of particles

n_i

Number of moles unit volume

P

Pressure

Pe

Peclet number

p_r

Probability that two particles that have collided result in coalescence

q

Wave vector, or sinusoidal distortion

R

Ideal gas constant

Re

Reynolds number or real part of a complex function

R(q)

Fluctuation function

$\overline{\mathbf{r}}$

Reduced drop radius

〈r ²_Θ 〉^1/2

Unperturbed, average radius of gyration

rad

Radian

r_N

Radius of the critical nucleus

S(q), S₀

Virtual structure function

S_o, S

Interfacial area per unit volume of the blend for monodispersed spherical particles before and after coalescence, respectively

s

Spinodal

T

Absolute temperature

T_g

Glass transition temperature

t

Time

t_b

Necessary time for breakup of droplets

t_b*

Dimensionless breakup time

t_c

Coalescence time

UCST

Upper critical solubility temperature

V

Volume

V_x/V

Volume fraction of emulsion undergoing uniform shear

z

Reduced frequency, f · τ

α

Orientation angle

α_o

The distortion at t = 0

β₁₂

Interlayer slip factor

χ_AΒ

Binary thermodynamic interaction parameter between polymers A and B

Δ

Thermodynamic distance from the spinodal; Δ ≡ 2((χ_AΒN)_s− (χ_AΒN)

ΔΕ

Activation energy, e.g., of flow: ΔΕ_η

ΔG_m

Gibbs free energy of mixing

ΔH_m, ΔS_m

Enthalpy and entropy of mixing, respectively

ε, $\dot{\boldsymbol{\upvarepsilon}}$

Hencky strain and Hencky strain rate in extension, respectively

ϕ₁, ϕ₂

Volume fraction of dispersed and matrix phase, respectively

ϕ_c

Volume fraction of the cross-linked monomer units

ϕ_i

Volume fraction of phase i at phase inversion

ϕ_m

Maximum packing volume fraction

ϕ_perc

Percolation threshold

γ, $\dot{\boldsymbol{\upgamma}}$

Shear strain and rate of shearing, respectively

η

Viscosity

η_o

Zero-shear viscosity

η_r

Relative viscosity

[η]

Intrinsic viscosity

η′

Dynamic viscosity

η*

Complex viscosity

η₁, η₂

Viscosity of dispersed and matrix phase, respectively

κ = σ_ιφd/ν₁₂

Capillary number

κ_crit

Critical capillary number

Λ

Distortion wavelength

λ = η₁/η₂

Viscosity ratio

λ_s

Wavelength

ν ^o₁₂

Interfacial tension in a quiescent blends

ν₁₂

Interfacial tension coefficient between phase 1 and 2

ρ

Density

ρ_d

Droplet density

σ

Stress

σ₁₁

Extensional stress

σ₁₁ − σ₂₂ = N₁

First normal stress difference

σ₁₂

Shear stress

s_m

Stress in the matrix phase

σ_y

Yield stress

σ_y ^o

Permanent yield stress

τ

Relaxation time

t*

Mean relaxation time

Ω(Λ, λ)

Tabulated function for capillary instability

ω

Angular frequency

ω_max

Frequency at which $\tilde{H}\left(\omega \right)$ is maximum

ω_x

Crossover frequency

ψ₁, ψ₂

First and second normal stress difference coefficient, respectively

ABS

Acrylonitrile-butadiene-styrene

EFM

Extensional flow mixer

EPDM

Ethylene-propylene-diene terpolymer

EPR

Ethylene-propylene rubber

EVAc

Ethylene-vinyl acetate copolymer

HDPE

High density polyethylene

HIPS

High impact polystyrene

IPN

Interpenetrating networks

LDPE

Low density polyethylene

LLDPE

Linear low density polyethylene

NG

Nucleation and growth

NR

Natural rubber

PA

Polyamide

PAA

Polyacrylic acid

PB

Polybutadiene

PC

Polycarbonate

PCL

Polcaprolactone

PE

Polyethylene

PEO

Polyethylene oxide (or polyethyleneglycol, PEG)

PEMA

Poly(ethyl methacrylate)

Phenoxy

Polyhydroxyether of bis-phenol A

PMMA

Polymethylmethacrylate

PnBA

Poly(n-butyl)acrylate

PP

Polypropylene

PPE

Polyphenyleneether

PS, PSD

Polystyrene, deuterated PS

PSF

Polysulfone

PVC

Polyvinyl chloride

PVME

Polyvinylmethylether

RMS

Rheometrics Mechanical Spectrometer

RSR

Rheometrics Stress Rheometer

SBR

Styrene-butadiene rubber

SBS

Styrene-butadiene-styrene three block copolymer

SD

Spinodal decomposition

SEBS

Styrene-ethylene/butene-styrene three block copolymer

SEC

Size exclusion chromatography

SIN

Simultaneous interpenetrating polymer networks

SSE

Single-screw extruder

TP

Thermoplastic resin

TS

Thermoset resin

TSE

Twin-screw extruder