Keywords

1 Introduction

Suspension bridges under wind of constant velocity are subjected to oscillating vertical external force due to vortex shedding by the separation of the wind along the deck of the bridge. In the case of suspension bridges with thin decks aeroelastic instability can appear above a critical wind velocity and dangerously damage the structure. The use of control devices, by means of passive nonlinear absorbers and targeted energy transfer, to prevent from these instabilities, could be a powerful solution. These range of absorber have been studied theoretically/numerically by Gendelman and Manevitch (2001) and Vakakis and Gendelman (2001) and experimentally to control linear modes of a building reduce model by  Gourdon et al. (2007) and Gourdon and Lamarque (2007, 2005). Their application have been also studied by Lee et al. to suppress linear instability of system: the instability suppression in the Van Der Pol oscillator (Lee et al. 2005), and in an aircraft wing (Lee et al. 2006, 2007) have been considered. This study focuses on the aeroelastic instability of a suspension bridge and investigates the efficiency of a single degree of freedom passive nonlinear absorber introduced in the bridge deck. We study the suppression mechanisms of the bridge aeroelastic instability by mean of this nonlinear absorber. This study introduces an original analytical approach based on the concept of Limiting Phase Trajectories (LPT) to predict the asymptotic behavior of the controlled system. The Limiting Phase Trajectories have been introduced by Manevitch et al., that showed in Manevitch (2007), Manevitch et al. (2007), Manevitch and Musienko (2009), Manevitch and Musienko (2008), Manevitch et al. (2009), Manevitch and Manevitch (2009a,b) and Manevitch (2009) that the energy exchange in systems of weakly coupled oscillators or oscillatory chains can be efficiently described introducing the concept of Limiting Phase Trajectories (LPT). Contrary to normal modes (NM), LPT corresponds to complete energy exchange between weakly coupled elements of the system. In appropriates coordinates LPT can be simply described in terms of non-smooth basic functions introduced in Pilipchuk (1985), Vakakis et al. (1996) and Manevitch et al. (1989) for solution of problems close to vibro-impact ones. It turns out, however, that the most adequate area for using these techniques is the problem of intensive energy transfer in linear and nonlinear oscillatory chains. The analytical approach of the aeroelastic instability problem throughout the LPTs concept gives a better understanding of energy pumping triggering mechanisms and how the system variables such as initial conditions or absorber nonlinearity interact during the control.

In Sect. 2 we introduce a two degrees of freedom model of a suspension bridge coupled with a purely cubic nonlinear absorber. In Sect. 3 this three degrees of freedom system is reduced to a single nonlinear oscillator. The more relevant resonance case is considered and the concept of LPT is used to predict analytically the asymptotic behavior of the whole system in Sect. 4. Finally Sect. 5 exhibits numerical simulations with good agreement with the analytical prediction, and show that the absorber is able to control the aeroelastic instability of the bridge.

2 Dynamics of the System

We investigate the response of a two DOF suspension bridge model from Blevins (1977). This model takes into account the coupling between aerodynamical actions on the structure and its elastic response. Considering only the torsional and flexional natural modes the equations of motion representing the wind induced aeroelastic instability can be written as follows:

$$\begin{array}{rcl} \ddot{\varphi } + \frac{{m}_{0}} {m} {\omega }_{0}\dot{\varphi } + {\omega }_{1}^{2}\varphi -\frac{{m}_{0}} {m} {\omega }_{0}^{2}\theta = 0& & \\ \end{array}$$
$$\begin{array}{rcl} \ddot{\theta } + \frac{{m}_{1}{l}^{2}} {2m{r}^{2}}{\omega }_{0}\dot{\theta } + \left ({\omega }_{2}^{2} - \frac{{m}_{0}{l}^{2}} {2m{r}^{2}}{\omega }_{0}^{2}\right )\theta + \frac{{m}_{0}{l}^{2}} {2m{r}^{2}}{\omega }_{0}\dot{\varphi } = 0& &\end{array}$$
(1)

with the following variables:

These equations illustrate the aeroelastic instability of the bridge, this linear system exhibits linear instability for a critical value of wind velocity V.

Table 1
Full size table

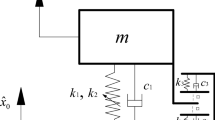
We consider in this paper the solution of adding a SDOF NES, coupled along the bending direction on the elastic axis. This coupling is represented in Fig. 1.

Fig. 1
figure 1

Two DOF bridge deck coupled with a SDOF NES on the elastic axis

Full size image

The NES characteristics are in the previous nomenclature. Taking into account this nonlinear coupling equation (1) can be rewritten as a three DOF system:

$$\begin{array}{rcl} \ddot{\varphi } + \frac{{m}_{0}} {m} {\omega }_{0}\dot{\varphi } + {\omega }_{1}^{2}\varphi -\frac{{m}_{0}} {m} {\omega }_{0}^{2}\theta + \frac{{\lambda }_{\epsilon }} {m} (\dot{\varphi } -\dot{ z}) + \frac{{k}_{\epsilon }} {m} {(\varphi - z)}^{3} = 0& & \\ \end{array}$$
$$\begin{array}{rcl} \ddot{\theta } + \frac{{m}_{1}{l}^{2}} {2m{r}^{2}}{\omega }_{0}\dot{\theta } + \left ({\omega }_{2}^{2} - \frac{{m}_{0}{l}^{2}} {2m{r}^{2}}{\omega }_{0}^{2}\right )\theta + \frac{{m}_{0}{l}^{2}} {2m{r}^{2}}{\omega }_{0}\dot{\varphi } = 0& & \\ \end{array}$$
$$\begin{array}{rcl}{ m}_{\epsilon }\ddot{z} + {\lambda }_{\epsilon }(\dot{z} -\dot{ \varphi }) + {k}_{\epsilon }{(z - \varphi )}^{3} = 0& &\end{array}$$
(2)

The terms involving \({\omega }_{0}\dot{\varphi }\) and \({\omega }_{0}\dot{\theta }\) cannot be ignored, as they are produced by wind loading ω0. For simplicity, these terms are assumed small compared to all other terms of order 1. Considering the smallness of parameters it is reasonable to rewrite (2) as:

$$\begin{array}{rcl} \ddot{\varphi } + {\epsilon }^{2}{\gamma }_{ 1}\dot{\varphi } + {\Omega }_{1}^{2}\varphi - \epsilon k\theta - {\epsilon }^{2}\lambda \dot{\Psi } - {\epsilon }^{2}K{\Psi }^{3} = 0& & \\ \end{array}$$
$$\begin{array}{rcl} \quad \ddot{\theta } + {\epsilon }^{2}{\gamma }_{ 2}\dot{\theta } + {\Omega }_{2}^{2}\theta + {\epsilon }^{2}{\gamma }_{ 3}\dot{\varphi } = 0& & \\ \end{array}$$
$$\begin{array}{rcl} \qquad \ddot{\varphi } +\ddot{ \Psi } + \lambda \dot{\Psi } + K{\Psi }^{3} = 0& &\end{array}$$
(3)

where Ψ = z − φ is the internal displacement between the NES and the bridge deck.

3 Reduction of the System to a Single Oscillator and Resonance Oscillations

In this Section we study the system under 1:1 resonance using complexification, multiple scales methods and limit phase trajectory approach (Manevitch and Musienko 2009; Manevitch et al.). First we will reduce the three DOF system to a single oscillator considering the bridge behavior as an external forcing applied to the NES.

Table 2
Full size table

We solve the bridge equations without damping terms to reduce the bridge motion to an external forcing. We have to solve the following system:

$$\begin{array}{rcl} \ddot{\varphi }& +& {\Omega }_{1}^{2}\varphi - \epsilon k\theta = {\epsilon }^{2}K{\Psi }^{3}, \\ \end{array}$$
$$\begin{array}{rcl} \ddot{\theta }& +& {\Omega }_{2}^{2}\theta = 0,\end{array}$$
(4)

with initial conditions:

$$\begin{array}{rcl} \varphi (0) = \epsilon {q}_{10},& & \ \dot{\varphi }(0) = \epsilon {\Omega }_{1}{v}_{10},\ \theta (0) = {q}_{20}, \\ \end{array}$$
$$\begin{array}{rcl} \dot{\theta }(0) = {\Omega }_{2}{v}_{20},& & \ z(0) = 0,\ \dot{z}(0) = \end{array}$$
(0.)

Solution θ(t),φ(t) is:

$$\begin{array}{lll} \theta (t) & =&{Y }_{2}\sin ({\Omega }_{2}t + {\phi }_{2}) \\ \varphi (t)& =&\epsilon {\Phi }_{1}\sin ({\Omega }_{1}t + {\phi }_{1}) + \epsilon k{\Phi }_{2}\sin ({\Omega }_{2}t + {\phi }_{2}) + {\epsilon }^{2}{K}_{1}I(t) \end{array}$$
(5)

with the following parameters:

Finally we obtain the external forcing applied on the NES:

$$\ddot{\varphi }(t) = -\epsilon {Q}_{1}\sin ({\Omega }_{1}t + {\phi }_{1}) - \epsilon k{Q}_{2}\sin ({\Omega }_{2}t + {\phi }_{2}) + {\epsilon }^{2}K{\Psi }^{3}(t) - {\epsilon }^{2}K{\Omega }_{ 1}I(t)$$

According to Eq. (3) we have:

$$\begin{array}{l} \ddot{\Psi } + \lambda \dot{\Psi } + K{\Psi }^{3} = -\ddot{\varphi } \\ \text{ with} -\ddot{ \varphi } = \epsilon F(t) - \epsilon {K}_{1}I(t) \\ \text{ and}F(t) = {Q}_{1}\sin ({\Omega }_{1}t + {\phi }_{1}) + k{Q}_{2}\sin ({\Omega }_{2}t + {\phi }_{2}),\text{ ${K}_{\epsilon } = \epsilon K{\Omega }_{1}$} \end{array}$$
(6)
Table 3
Full size table

We investigate the 1:1 resonance of the system. For this reason we introduce parameter ω corresponding to the resonant pulsation of the system under 1:1 resonance assumption. We will determine later the vicinity of this parameter according to the bridge modal parameters. As a result Eq. (6) can be rewritten as follows:

$$\ddot{\Psi } + {\omega }^{2}\Psi + \epsilon \mu [\lambda \dot{\Psi } + K{\Psi }^{3} - {\omega }^{2}\Psi ] = \epsilon F(t) - \epsilon {K}_{ \epsilon }I(t)$$
(7)

with \(\mu = \frac{1} {\epsilon }\). For parameter μ to be considered as independent from variable ε the sum in the square brackets must be small compared to the other terms of order 1. This means that we have to verify the following relation:

$$[\lambda \dot{\Psi } + K{\Psi }^{3} - {\omega }^{2}\Psi ] = o(1)$$
(8)

In Eq. (7) the term in Ψ 3 appears at first of higher order but we must consider that the integral term I(t), under some special resonant cases can be of order ε − 1 and must be taken into account for the asymptotic analysis. We will expand Eq. (6) using complexification and multiple scale expansions with ω near Ω 1 and ω near Ω 2 considering primary resonance only.

In order to describe the system evolution we introduce a complex valued transformation, with variables Φ and Φ  ∗ , such that:

$$\begin{array}{lcl} \Phi =\dot{ \Psi } + i\omega \Psi ,&&\qquad {\Phi }^{{_\ast}} =\dot{ \Psi } - i\omega \Psi ,\\ & & \\ \dot{\Psi } = \frac{\Phi + {\Phi }^{{_\ast}}} {2} , &&\qquad \Psi = \frac{\Phi - {\Phi }^{{_\ast}}} {2i\omega } \end{array}$$
(9)

where \(i = \sqrt{-1}\) and the asterisk denotes complex conjugate. Introducing these new variables in (6) we obtain:

$$\dot{\Phi }-i\omega \Phi +\epsilon \frac{\mu \lambda } {2} (\Phi -{\Phi }^{{_\ast}})-\epsilon \frac{3i\mu K} {8\omega } {(\Phi -{\Phi }^{{_\ast}})}^{3}+\epsilon \mu \frac{i\omega } {2} (\Phi -{\Phi }^{{_\ast}}) = \epsilon F(t)-\epsilon {K}_{ \epsilon }I(t)$$
(10)

Then we apply a multiple scale method to construct an approximate solution of (10) as an ε expansion:

$$\begin{array}{l} \Phi (t,\epsilon ) = {\Phi }_{10}({T}_{0},{T}_{1}) + \epsilon {\Phi }_{11}({T}_{0},{T}_{1}) + \ldots \\ \frac{d} {dt} = \frac{\partial } {\partial {T}_{0}} + \epsilon \frac{\partial } {\partial {T}_{1}} + {\epsilon }^{2} \frac{\partial } {\partial {T}_{2}} + \end{array}$$
(11)

with T j  = εj t,  j = 0, 1, 2, …. We can substitute expression (11) in (10). Equating the different power of ε we obtain:

$$\begin{array}{rcl}{ \epsilon }^{0} : \frac{\partial {\Phi }_{10}} {\partial {T}_{0}} - i\omega {\Phi }_{10} = 0 \Rightarrow {\Phi }_{10}({T}_{0},{T}_{1}) = {\varphi }_{10}({T}_{1}){e}^{i\omega {T}_{0} }& &\end{array}$$
(12)
$$\begin{array}{rcl}{ \epsilon }^{1} : \frac{\partial {\Phi }_{10}} {\partial {T}_{1}} + \frac{\partial {\Phi }_{11}} {\partial {T}_{0}} - i\omega {\Phi }_{11} + \frac{\mu \lambda } {2} ({\Phi }_{10} - {\Phi }_{10}^{{_\ast}})& & \\ \end{array}$$
$$\begin{array}{rcl} \quad -\frac{3i\mu K} {8{\omega }^{3}} {({\Phi }_{10} - {\Phi }_{10}^{{_\ast}})}^{3} + \frac{i\mu \omega } {2} ({\Phi }_{10} - {\Phi }_{10}^{{_\ast}}) = F(t) - {K}_{ \epsilon }I(t)& &\end{array}$$
(13)

Suppressing secular terms from (13) we obtain:

$$\begin{array}{rcl} \frac{\partial {\varphi }_{10}} {\partial {T}_{1}} + \frac{\mu \lambda } {2} {\varphi }_{10}-\frac{3i\mu K} {8{\omega }^{3}} {\varphi }_{10}^{2}{\varphi }_{ 10}^{{_\ast}}+\frac{i\omega \mu } {2} {\varphi }_{10} = \frac{{Q}_{1}} {2i} ({e}^{i({\Omega }_{1}-\omega ){T}_{0}+i{\phi }_{1} } - {e}^{-i({\Omega }_{1}+\omega ){T}_{0}+i{\phi }_{1} })& & \\ \end{array}$$
$$\begin{array}{rcl} +\ k\dfrac{{Q}_{2}} {2i} ({e}^{i({\Omega }_{2}-\omega ){T}_{0}+i{\phi }_{2} } - {e}^{-i({\Omega }_{2}+\omega ){T}_{0}+i{\phi }_{2} })& & \\ \end{array}$$
$$\begin{array}{rcl} -\ {C}_{\epsilon }(t)& &\end{array}$$
(14)
$$\begin{array}{ccc} &\\{C}_{\epsilon } ({T}_{0 } ) = \epsilon K \frac{i} {8{\omega }^{3}}{e}^{-i\omega {T}_{0} }{ \int \nolimits \nolimits }_{0}^{{T}_{0} }\sin ({\Omega }_{1}({T}_{0} - s)){({\varphi }_{10}(s){e}^{i\omega s} - {\varphi }_{10}^{{_\ast}}(s){e}^{-i\omega s})}^{3}\,\mathrm{d}s& \end{array}$$
(15)

In order to calculate C ε it is convenient to introduce function:

$$ G(\omega ,{\Omega }_{1}) = \epsilon K \frac{1}{16{\omega }^{3}}{e}^{-i\omega {T}_{0} }{ \int \nolimits \nolimits }_{0}^{{T}_{0} }{e}^{i{\Omega }_{1}{T}_{0} }{e}^{i(\omega -{\Omega }_{1})s}\mathrm{d}s $$
(16)

The integral C ε can be expressed in function of G:

$$ \begin{array}{rcl}{C}_{\epsilon }({T}_{0}) = {\varphi }_{10}G(3\omega ,{\Omega}_{1})-{\varphi }_{10}G(3\omega ,-{\Omega }_{1}) + {\varphi }_{10}^{{_\ast}}G(-3\omega ,{\Omega }_{1})-{\varphi }_{10}^{{_\ast}}G(-3\omega ,-{\Omega }_{1})& & \\\end{array} $$
$$\begin{array}{rcl}+3\vert {\varphi }_{10}{\vert }^{2}{\varphi }_{10}G(\omega ,{\Omega }_{1}) - 3\vert {\varphi }_{10}{\vert }^{2}{\varphi }_{10}G(\omega ,-{\Omega }_{1})& & \\ \end{array} $$
$$\begin{array}{rcl}+3\vert {\varphi }_{10}{\vert }^{2}{\varphi }_{10}^{{_\ast}}G(-\omega ,{\Omega }_{1}) - 3\vert {\varphi }_{10}{\vert }^{2}{\varphi }_{10}^{{_\ast}}G(-\omega ,-{\Omega }_{ 1})& & \\ \end{array}$$
(17)

These equations should be studied in the vicinity of different system pulsation ω.For the sake of simplicity and considering numerical evidence of Sect. 4 we will focus on the resonant case ω ≈ Ω 2, which involves that Ω 1does not generate resonant terms.

3.1 Case ω ≈ Ω 2, Ω 1 Does Not Generate Resonance Terms

Let us consider ω ≈ Ω 2, in this particular case Ω 1 does not generate resonance terms which involves that C ε(T 0) is not a resonance term. Secular terms give:

$$\begin{array}{rcl} \frac{\partial {\varphi }_{11}} {\partial {T}_{0}} + \frac{\partial {\varphi }_{10}} {\partial {T}_{1}} + \frac{\mu \lambda } {2} {\varphi }_{10} -\frac{3i\mu K} {8{\omega }^{3}} {\varphi }_{10}^{2}{\varphi }_{ 10}^{{_\ast}} + \frac{i\omega \mu } {2} {\varphi }_{10} =\tilde{ f}({T}_{0})& & \\ \end{array}$$
$$\begin{array}{rcl} \tilde{f}({T}_{0}) = k\frac{{Q}_{2}} {2i} ({e}^{i({\Omega }_{2}-\omega ){T}_{0}+i{\phi }_{2} } - {e}^{-i({\Omega }_{2}+\omega ){T}_{0}+i{\phi }_{2} }) + \text{ non-secular terms}& &\end{array}$$
(18)

Considering Ω 2 = ω − εσ2 secular terms permit to write \(\tilde{f}({T}_{0})\) as:

$$\tilde{f}({T}_{0}) = -k{Q}_{2} \frac{i} {2}{e}^{-i({\sigma }_{2}{T}_{1}-\phi 2)}+\text{ non-secular terms} =\tilde{ {f}_{ 2}}({T}_{0})+\text{ non-secular terms}$$
(19)

We finally get the reduction to a single oscillator for Ω 2 = ω − εσ2:

$$\frac{\partial {\varphi }_{10}} {\partial {T}_{1}} + \frac{\mu \lambda } {2} {\varphi }_{10} -\frac{3i\mu K} {8{\omega }^{3}} {\varphi }_{10}^{2}{\varphi }_{ 10}^{{_\ast}} + \frac{i\omega \mu } {2} {\varphi }_{10} = -k{Q}_{2} \frac{i} {2}{e}^{-i({\sigma }_{2}{T}_{1}-\phi 2)}$$
(20)
Fig. 4
figure 4

K = 2. 5 N.m − 3, (a) Numerical integration of variable a from (2), (b) Hamiltonian of Eq. (22) with LPT in large line

Full size image

3.2 Single Oscillator Differential System

We consider the ε-order equations of Sect. 3.1 and introduce the polar representation of complex variable φ10 = ae iγ into Eq. (20) and separate real and imaginary parts to get an amplitude-phase differential system. We obtain the following differential system for variables a and Δ :

$$\left \{\begin{array}{lcl} \frac{\partial a} {\partial {T}_{1}} & =&\frac{-\mu \lambda } {2} a - F\sin \Delta \\ a \frac{\partial \gamma } {\partial {T}_{1}} & =&\frac{-\mu \omega } {2} a + \frac{3\mu K} {8{\omega }^{3}} {a}^{3} - F\cos \Delta \end{array} \right.$$
(21)
$$\Delta = \gamma + {\sigma }_{2}{T}_{1} - {\phi }_{2}F = \frac{1} {2}k{Q}_{2}$$
$$\left \{\begin{array}{l} \frac{\partial a} {\partial {T}_{1}} = \frac{-\mu \lambda } {2} a - F\sin \Delta \\ a \frac{\partial \Delta } {\partial {T}_{1}} = \mu a(-s + \alpha {a}^{2}) - F\cos \Delta \\ \end{array} \right.$$
(22)
$$\alpha = \frac{3K} {8{\omega }^{3}}s = \frac{\omega } {2} -\frac{{\sigma }_{2}} {\mu }$$

In the next section differential system (22) is studied. The fixed points of the system are first investigated and then the Hamiltonian of the undamped (22) system, corresponding to λ = 0 is considered.

4 Analytical Study of the Nonlinear SDOF Oscillator

In this part we will consider the differential system (22) in the damped (λ≠0) and undamped case (λ = 0). This analysis is mainly based on the analysis of Manevitch and Manevitch (2009b).

4.1 Fixed Points

Stationary points of the phase portraits correspond to periodic vibrations and can be found from conditions:

$${F}^{2} = {\mu }^{2}{a}^{2}\left (\frac{{\lambda }^{2}} {4} + {(\alpha {a}^{2} - s)}^{2}\right )$$
(23)

This equation is a cubic equation in the variable X = a 2, and (25) can be rewritten as:

$${X}^{3} -\frac{2s} {\alpha } {X}^{2} + \frac{{\lambda }^{2} + 4{s}^{2}} {4{\alpha }^{2}} X - \frac{{F}^{2}} {{\mu }^{2}{\alpha }^{2}} = 0$$
(24)

Equation (24) gives the fixed points of system (22), taking the bridge damping into account. To understand the general behavior of the system it is easier to get rid of damping. Let us consider system (22) without damping, which means for λ = 0.

Equating the system to zero we obtain:

$$\left \{\begin{array}{lcl} \sin \Delta = 0 &&\\ \mu a(\alpha {a}^{2 } - s) = F\cos \Delta &&\end{array} \right.$$
(25)

Let us consider a range − π ≤ Δ ≤ π, then Δ =  ± π [2π] and amplitudes a for stationary vibrations satisfy the equation:

$$\mu a(\alpha {a}^{2} - s) = \pm F$$
(26)

where + F and − F correspond to Δ = 0 and Δ = π respectively. Discriminant of Eq. (26) is R:

$$R = \frac{1} {{\alpha }^{2}}\left [\frac{{F}^{2}} {{\mu }^{2}} - \frac{4} {27} \frac{{s}^{3}} {\alpha } \right ]$$
(27)

If R < 0 system (22) has three real roots: a nonsensical negative one and two positive roots corresponding to saddle point and quasilinear center of the system.

If R > 0 system (22) has one single real root that corresponds to the nonlinear resonance center.

4.2 Analytical Study of the LPT

Equation (22), for the undamped oscillator, has the following Hamiltonian:

$$H = \mu \left (\frac{\alpha {a}^{4}} {4} -\frac{s{a}^{2}} {2} \right ) - aF\cos \Delta $$
(28)

Let us consider Eq. (22) for the LPT (H = 0), Δ = 0{ or}Δ = π.

$$\begin{array}{lcr} \frac{\mu \alpha } {2} {a}^{3} - \mu sa \pm 2F = 0&&a = \end{array}$$
(29)

This is a cubic equation of discriminant Q:

$$Q = \frac{16} {{\alpha }^{2}}\left (\frac{{F}^{2}} {{\mu }^{2}} - \frac{2{s}^{3}} {27\alpha }\right )$$
(30)

We will observe qualitative transformation of the phase plane for:

$$\alpha = {\alpha }_{c} = \frac{2{\mu }^{2}{s}^{3}} {27{F}^{2}}$$
(31)

While α < α c the LPT encircles the non-resonance quasilinear center at Δ =  − π.

If α > α c the LPT does not encircle the quasilinear center, but the LPT encircles the resonance center at Δ = 0.

If α > 2α c then quasilinear center and saddle point coincide and ‘annihilate’. That can be explained studying the discriminant R of Eq. (26).

There are no other important transformations of the phase plane, for α > 2α c we get one single stationary point that decreases with the rise of parameter α.

5 Numerical Simulations in the Case ω ≈ Ω 2

For the numerical simulations we fix the bridge parameters as :

$$\begin{array}{lcllll} V = 27.5\,\mathrm{m.{s}^{-1}} & & & \qquad \qquad \frac{{m}_{0}} {m} = \frac{{m}_{1}} {m} = \frac{1} {50} &&\qquad \qquad {\omega }_{1}^{2} \approx 0.72 \\ l = 6\,\mathrm{m} &&&\qquad \qquad \sigma = 0.5 &&\qquad \qquad {\omega }_{2}^{2} \approx 2{\omega }_{1}^{2} \\ \frac{{l}^{2}} {2{r}^{2}} = 1 &&&\qquad \qquad {\epsilon }^{2} = 0.1 &&\qquad \qquad \lambda = \end{array}$$
(32)

And initial conditions to:

$$\begin{array}{lll} \varphi (0) = 0 &\dot{\varphi }(0) = 0.3&\theta (0) = 0 \\ \dot{\theta }(0) = 0.3&z(0) = 0 &\dot{z}(0) = \end{array}$$
(33)

Under these initial conditions and choosing nonlinear parameter K = 2. 5 N.m − 3 we observe that the NES is able to control the bridge instability. Figure 2 shows that both variables θ and φ are controlled. The dashed line represents the linear instable system whereas the solid line represents the system under the NES control (to display correctly the control the plot has been cut, and only the part | φ(t) |  < 2 and | θ(t) |  < 2 is presented).

Fig. 2
figure 2

Displacements of bridge variables φ and θ with and without nonlinear coupling with K = 2. 5 N.m − 3 and initial conditions (33) (— with coupling, …without coupling)

Full size image

We now observe the different types of behavior that can occur for different values of K.

We choose to work under the assumption of a ω ≈ Ω 2 resonance. This assumption is numerically verified as shown in Fig. 3a, the main harmonic of the signal correspond to frequency Ω 2, nevertheless the other resonance approximations give only small shift in the results, mainly because frequencies Ω 2 and Ω 1 are very close to each other.

Fig. 3
figure 3

(a) K = 2. 5 N.m − 3 Frequency analysis of variable Ψ; (b) K = 0. 01 N.m − 3, (c) K = 2. 5 N.m − 3, (d) K = 500 N.m − 3 Displacements of variables φ and z for different value of K,φ in solid line and z in dotted line

Full size image

We focus on parameter K to study the influence of the NES design, and specially the NES nonlinear stiffness, on the quality of the control. Investigating numerically the behavior of the bridge we can determinate three very different kind of behavior depending on the nonlinearity of the NES. These curves presented Fig. 3 show the displacements in time of variables φ and z. We can separate three very different types of behavior. Nevertheless they are linked together by the nonlinear beating that characterizes the nonlinear control that asymptotically occurs. When the stiffness is too low system displacements grow up until a critical value for the nonlinear beating and the control to start (see Fig. 3b), this is the first case: a long time before nonlinear control starts, and a control that occurs at very high displacements. On the contrary when the stiffness is too strong system displacements decrease until a critical value for the nonlinear control to start (see Fig. 3d), the bigger the stiffness is, the longer is the decrease. The control resulting from this case is very efficient (the displacement reduction is huge), but takes a long time to start.

If we choose a good balance between the two previous cases the nonlinear beating starts quickly enough, and reduces significantly the system vibrations (see Fig. 3c). These different cases underline a range of efficiency for the NES system.

5.1 Behavior of the Hamiltonian

Let us consider the case of initial conditions (33) and K = 2. 5 N.m − 3, under the assumption of an ω ≈ Ω 2 resonance. We perform numerical simulation on the general system (2) and on the reduce system (22), checking that assumption (8) is numerically confirmed.

In Fig. 4a the numerical integration of variable a(t) from general system (2) is presented. This Figure shows a good agreement with Fig. 4b which represents the Hamiltonian of the associated single oscillator of system (22) with the numerical integration of variable a from this system. The LPT is highlighted with a large black line. It results that the concept of LPT allows predicting the asymptotic behavior of the controlled system. These numerical integrations show good agreement with the prediction made using the single oscillator approximation and its Hamiltonian.

It is also interesting to study the evolution of the Hamiltonian with the nonlinearity parameter α. According to Eq. (31) we obtain α c  ≈ 0. 147 N.m − 3. The evolution of the Hamiltonian (28) around the critical value α c is plotted in Fig. 5a–d.

Fig. 5
figure 5

Evolution of the Hamiltonian with the stiffness of the NES, the LPT is underlined in large line. (a) α < α c , (b) α ≈ α c , (c) α > α c , (d) α > 2α c

Full size image

The numerical simulations of Fig. 5a–d are in good agreement with the analytical predictions of Sect. 4.2. These figures correspond to the different cases α < α c , α ≈ α c , and α > α c . They are similar to the results obtained in Manevitch et al.,Manevitch and Musienko (2009), and Manevitch and Musienko (2008).

6 Conclusion

This study demonstrates that a NES (Nonlinear Energy Sink) can control the aeroelastic instability of a structure using targeted energy transfer. The example chosen was a two degree of freedom bridge under a constant wind excitation. Numerical and analytical calculations underline two different behaviors for the system, around a critical constant depending on the nonlinear stiffness and system initial conditions. The energy exchange in the system gives a good understanding of these behaviors.

The analytical approach gives approximate solutions under the assumption of 1:1:1 resonance using the concept of LPT (Limiting Phase Trajectories). The procedure applied in our study permits to reduce the Bridge/NES three degrees of freedom model to a single forced oscillator, and then allows us to construct the limiting phase trajectories and approximate the steady state of the resulting system. We have shown that LPT-concept provides efficient solution to the aeroelastic instability control problem. This method shows good agreement with numerical integration and gives elements to understand how the nonlinear stiffness and the initial conditions govern the system.