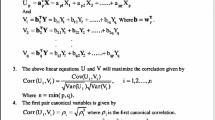Keywords

1 Introduction

Knowledge of Independent Component Analysis (ICA) has a great importance for potential speech signal processing, brain signal processing, feature extraction, and acoustic processing. Defined ICA is very closely related to the method called Blind Source Separation (BSS). ICA problem arises in many application domains, such as speech separation, array antenna processing, multi-sensor biomedical records and financial data analysis [1]. Blind Source Separation was using a two stage sparse representation approach and presented an algorithm for estimating the mixing matrix [2]. The over-complete were introduced that the source separation problem consist of estimating the original sources, the observed signals, then were introduced the over-complete source separation case where there are the mixture less than source signals [3]. A novel BSS algorithm for de-mixing under-determined presented anechoic mixtures [4].

In this paper, we proposed a new method to find the number of columns in the mixing matrix and estimated the value of each element. The remainder of this paper has the following structure. Section 2 describes the problem with constraints. Section 3 focuses on the main idea and the detail of the proposed algorithms. The experimental result is presented in Sect. 4. Section 5 concludes the paper.

2 Problem Statement

Under-determined ICA is considered in this paper. Let \( {\mathbf{S = [s}}_{{\mathbf{1}}} ,s_{2} , \ldots ,s_{N} {\mathbf{]}}^{T} \in R^{m \times T} \) and \( {\mathbf{X}} = \left[ {x_{1} ,x_{2} , \ldots ,x_{M} } \right]^{T} \in {\mathbf{R}}^{n \times M} \) be the source signals of n dimensions and observed signals of m dimensions, respectively. Each observed signal xi is computed by using a mixing matrix \( {\mathbf{A}} = \left[ {a_{1} ,a_{2} , \ldots ,a_{m} } \right] \in {\mathbf{R}}^{n \times m} \) for n < m as follows.

$$ {\text{X}} = {\text{AS}} $$
(1)

The source signals are based on the sparseness assumption [5]. The problem of how to recover the source signals after estimating the mixing matrix will not be considered here. However, we adopted the recovering method from [6].

3 Main Concept and Algorithms

Our method to find the columns of mixing matrix A is based on this simple observation. Let X = [xi,1, xi,2,…,x i,3]T be an observed signal i for 1 <= i <= n in a p-dimensional space. The mixing matrix A maps each incoming signal si to a new location considered as an observed signal xi in lower dimensions. An observed signal can be viewed as a vector. These observed vectors are clustered along each new independent basis represented by each column vector of mixing matrix A. Therefore, to compute each column vector of A, a new similarity measure for all observed vectors clustered at any column must be introduced. Our method consists of the following main steps.

  1. 1.

    Computing the direction of each observed vector \( x_{i} \) in terms of radian degrees.

  2. 2.

    Grouping all observed vectors based on their directions computed from Step 1.

  3. 3.

    Finding the direction of each group and use it as a column vector of the mixing matrix A.

In this paper, we consider only the case where the observed vectors are in two dimensions. Hence, Xi = [xi,1, xi,2]T. The detail of the first two steps is given in the following Algorithm.

3.1 Grouping Observed Vectors Algorithm

Variable group in the algorithm is for counting the total number of groups. After grouping the observed vectors according to their radian degrees, the actual direction of each group will be derived and used as the column vector in mixing matrix A. Not every group generated by Grouping Observed Vectors Algorithm is feasible enough to derive a column vector in mixing matrix A. Only the group with high density of clustering will be selected. The detail of how to find the actual column of mixing matrix A is the following.

3.2 Finding Actual Column Algorithm

Steps 4 and 5 are used to measure the density of clustering of each group. The eigenvectors extracted from steps 10 in Finding Actual Column Algorithm above are used as column vectors in mixing matrix A. Figure 1 shows an example as the result of the above algorithms. Figure 1a is the observed vectors. After being grouped by Grouping Observed Vectors Algorithm, Fig. 1b is obtained. The actual column vectors of the mixing matrix are shown in Fig. 1c.

Fig. 1
figure 1

An example of the result from the proposed algorithm. a The given synthetic observed vectors. b The result after grouping. c The computed eigenvectors which are used as column vectors in the mixing matrix

Full size image

4 The Experimental Results

The algorithms are tested with a real speech as shown in Fig. 2a. There are three sources of signals and two observed signals. The source signals are mixed by using the following mixing matrix.

$$ {\mathbf{A}} = \left[ \begin{array}{lll} 0. 7 0 7 1 & -0.4 4 7 2 & -0.9 4 8 7 \\ 0.7 0 7 1 & 0.8 9 4 4 & 0.3 1 6 2 \\ \end{array} \right] $$
(2)
Fig. 2
figure 2

The tested data. a Three given source signals. b Two observed signals. c The distribution plot of observed vectors

Full size image

The wave form of each observed signal is shown in Fig. 2b. The distribution of both observed vectors are plotted as shown in Fig. 2c. After applying Grouping Observed Vectors Algorithm to all observed vectors, three groups are obtained as shown in Fig. 3a. The direction of each eigenvector in each group is computed and illustrated in Fig. 3b. Our result was compared with the results produced by AICA method [7] and the Information Index Removal and Perturbed Mean Shift Algorithm [8]. To measure the accuracy of the estimated mixing matrix, Algebraic Matrix-Distance Index (AMDI) [7] was used. The following matrix is the result from our algorithms. Table 1 summarizes the accuracy of each method.

$$ {\hat{\mathbf{A}}} = \left[ \begin{array}{lll} -0.9 4 8 7 & 0.7 0 7 1 & -0.4 4 7 2 \\ 0.3 1 6 2 & 0.7 0 7 1 & 0.8 9 4 4 \\ \end{array} \right] $$
(3)
Fig. 3
figure 3

The result from our algorithm. a Groups of observed vectors in the experiment obtained after applying Grouping Observed Vectors Algorithm. b The direction of each eigenvector in each group

Full size image
Table 1 The comparison of the estimated mixing matrix by different methods
Full size table

5 Conclusions

This paper presents a new approach for de-mixing mixtures under-determined Independent Component Analysis. This technique is based on the observation that the observed vectors usually clustered along the direction of column vectors in the mixing matrix. Our algorithms can find the correct number of column vectors in the mixing matrix with the lowest AMDI value. However, a further modification must be studied to scope with higher dimensional signals.