Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

This chapter is adapted from a description of the PDF method described in Chapter 16 of “Powder Diffraction: Theory and Practice” [1]. Increasingly, materials that are under study for their interesting technological or scientific properties are highly complex. They are made of multiple elements, have large unit cells and often low dimensional or incommensurate structures [2]. Increasingly also, they have aperiodic disorder: some aspect of the structure that is different from the average crystal structure. In the case of nanoparticles the very concept of a crystal is invalid as the approximation of infinite periodicity is no longer a good one. Still we would like to study the structure of these materials. Powder diffraction is an important method for characterizing these materials, but we have to go beyond the Bragg equation and crystallographic analysis.

The “total scattering” approach treats both the Bragg and diffuse scattering on an equal basis [3]. Powder diffraction data are measured in much the same way as in a regular powder measurement. However, explicit corrections are made for extrinsic contributions to the background intensity from such things as Compton scattering, fluorescence, scattering from the sample holder, and so on. The resulting coherent scattering function I(Q) is a continuous function of Q, the magnitude of the scattering vector,

$$ Q = \left| \user2{Q} \right| = 2k \sin \theta = \frac{{4\pi \sin \theta }}{\lambda } $$
(17.1)

with sharp intensities where there are Bragg peaks, and broad features in between, the diffuse scattering. In general we like to work with a normalized version of this scattering intensity, S(Q). This is the intensity normalized by the incident flux per atom in the sample. S(Q) is the total-scattering structure function. It is a dimensionless quantity and the normalization is such that the average value, \( \langle \) S(Q) \( \rangle \) = 1. Despite the tricky definition, it is worth remembering that S(Q) is nothing other than the powder diffraction pattern that has been corrected for experimental artifacts and suitably normalized.

To get a good resolution in real-space, the S(Q) must be measured over a wide range of Q-values. The coherent intensity (the features) in S(Q) die out with increasing Q due to the Debye-Waller factor which comes from thermal and quantum zero-point motion of the atoms, as well as any static displacive disorder in the material. By a Q-value of 30–50 Å−1 (depending on temperature and stiffness of the bonding) there are no more features in S(Q) and there is no need to measure it to higher-Q. Still, this is much higher than conventional powder diffraction experiments using laboratory x-rays or reactor neutrons. The maximum Q attainable in back-scattering from a copper-K α tube is around 8 Å−1 and from a Mo-K α tube 16 Å−1.Routine total-scattering measurements can be made using laboratory sources with Mo or Ag tubes; however, for the highest real-space resolution, and the smallest statistical uncertainties, synchrotron data are preferred. In the case of neutron scattering, spallation neutron sources are ideal for this type of experiment.

Total scattering S(Q) functions appear different to standard powder diffraction measurements because of the Q-range studied, but also because of an important aspect of the normalization: the measured intensity is divided by the total scattering cross-section of the sample. For neutrons, this scattering cross-section is simply \( \langle \) b \( \rangle \) 2, where b is the coherent neutron scattering length of the atoms of the material in units of barns. The angle brackets denote an average. The scattering length, b, is constant as a function of Q and so is just part of the overall normalization coefficient. However, in the case of x-ray scattering, the sample scattering cross-section is the square of the atomic form-factor, \( \langle \) f(Q) \( \rangle \) 2, which becomes very small at high-Q. Thus, during the normalization process the data at high-Q are amplified (by being divided by a small number). This has the effect that even rather weak intensities at high-Q, which are totally neglected in a conventional analysis of the data, become rather important in a total-scattering experiment. Because the signal at high-Q is weak it is important to collect the data in that region with good statistics. This is illustrated in Fig. 17.1.

Fig. 17.1
figure 1

Comparison of raw data and normalized reduced total scattering structure function F(Q) = Q[S(Q)−1]. The sample is a powder of 2 nm diameter CdSe nanoparticles and the data are x-ray data from 6ID-D at the Advanced Photon Source at Argonne National Laboratory. The raw data are shown in the left panel. The high-Q data in the region Q > 9 appear smooth and featureless (left panel). However, after normalizing and dividing by the square of the atomic form-factor, important diffuse scattering is evident in this region of the diffraction pattern (right panel)

Full size image

Thus, the value added of a total scattering experiment over a conventional powder diffraction analysis is the inclusion of diffuse scattering as well as Bragg peak intensities in the analysis, and the wide range of Q over which data are measured. In fact, the total scattering name comes from the fact that all the coherent scattering in all of Q-space is measured.

Total scattering data can be analyzed by fitting models directly in reciprocal-space (i.e., the S(Q) function is fit). However, an interesting and intuitive approach is to Fourier transform the data to real-space to obtain the atomic pair distribution function (PDF), which is then fit in real-space. The reduced pair distribution function, G(r), is related to S(Q) through a Sine Fourier transform according to

$$ G(r) = \frac{2}{\pi}\int\limits_{{Q\min }}^{{Q\max }} {Q[S(Q) - 1]\sin \left( {Qr} \right)dQ} *{-2pt}$$
(17.2)

Examples of a G(r) functions are shown in Fig. 17.2.

Fig. 17.2
figure 2

PDFs in the form of G(r) from bulk CdSe, and from a series of CdSe nanoparticles. The blue curve at the bottom is the PDF obtained from the data shown in Fig. 17.1. The thick lines are from the data, with thin lines on top from models of the local structure in these nanoparticles. Offset below are difference curves between the model and the data (Figure adapted from [4]) (color figure online)

Full size image

It has peaks at positions, r, where pairs of atoms are separated in the solid with high probability. For example, there are no peaks below the nearest neighbor peak at ∼2.5 Å which is the Cd-Se separation in CdSe [4]. However, in addition to the nearest-neighbor information, valuable structural information is contained in the pair-correlations extending to much higher values of r. In fact, with high Q-space resolution data, PDFs can be measured out to tens of nanometers (hundreds of angstroms) and the structural information remains quantitatively reliable.

There are now many classes of problems that have been studied using total scattering analysis. Traditionally it was used for liquids [5] and amorphous materials, more recently for the study of disorder in crystalline materials, and now with increasing popularity it is used to study nanostructured materials. A number of recent reviews [3, 6, 7] give examples of modern applications of the PDF method.

2 Theory

The basis of the total scattering method is the normalized, measured, scattering intensity from a sample, total scattering structure function, S(Q) [3, 8, 9]. The wavevector, Q, is a vector quantity and in general the intensity variation, S(Q), will depend on which direction one looks in Q-space. However, when the sample is isotropic, for example, a powder, it depends only on the magnitude of Q and not its direction.

Similarly, the Fourier transform of the scattered intensity, in the form of S(Q), yields the reduced atomic pair distribution function, G(r), defined by Eq. 17.2. This is strictly correct when the sample is made of a single element. We will discuss an approximate extension that works excellently in practice, to the more interesting case of multiple elements.

The inverse transformation of Eq. 17.2 can be defined and it yields the structure function S(Q) in terms of G(r),

$$ S(Q) = 1 + \frac{1}{Q}\int_0^{\infty } {G(r)\sin \left( {Qr} \right)dr}.*{-2pt} $$
(17.3)

There are a number of similar correlation functions related to G(r) by multiplicative and additive constants. They contain the same structural information but are subtly different in some detail. G(r) is the function obtained directly from the Fourier transform of the scattered data. The function oscillates around zero and asymptotes to zero at high-r. It also tends to zero at r = 0 with the slope −4πρ 0 , where ρ 0 is the average number density of the material. From a practical point of view G(r) is attractive because the random uncertainties on the data (propagated from the measurement) are constant in r [3]. This means that fluctuations in the difference between a calculated and measured G(r) curve have the same significance at all values of r. Thus, for example, if the observed fluctuations in the difference curve decrease with increasing r this implies that the model is providing a better fit at longer distances (perhaps it is a model of the average crystallographic structure). This inference cannot be made directly from a difference curve to ρ(r) or g(r). A further advantage of the G(r) function is that the amplitude of the oscillations gives a direct measure of the structural coherence of the sample. In a crystal with perfect structural coherence, oscillations in G(r) extend to infinity with a constant peak-peak amplitude [10]. In the G(r) from a real crystal the peak-peak amplitude of the signal gradually falls off due to the finite Q-resolution of the measurement, which is then the limitation on the spatial coherence of the measurement rather than the structural coherence itself. A higher Q-resolution results in data extending over a wider range of r. In samples with some degree of structural disorder, the signal amplitude in G(r) falls off faster than dictated by the Q-resolution and this becomes a useful measure of the structural coherence of the sample. For example, it can be used to measure the diameter of nanoparticles.

Another function often denoted g(r) is called the pair distribution function. It is normalized so that, as r → ∞, g(r) → 1 and has the property that for r shorter than the distance of closest approach of pairs of atoms g(r) becomes zero. It is closely related to the pair density function, ρ(r) = ρ 0 g(r). Clearly, ρ(r) oscillates about, and then asymptotes to, the average number density of the material, ρ 0 at high-r and becomes zero as r → 0. The relationship between these correlation functions is given by

$$ G(r) = 4\pi r\left( {\rho (r) - {{\rho}_0}} \right) = 4\pi {{\rho}_0}r(g(r) - 1) *{-2pt}$$
(17.4)

Finally we describe the radial distribution function, R(r) given by

$$ R(r) = 4\pi {{r}^2}\rho (r) *{-2pt}$$
(17.5)

which is related to G(r) by

$$ G(r) = \frac{{R(r)}}{r} - 4\pi r{{\rho}_0} *{-2pt}$$
(17.6)

The R(r) function is important because it is the most closely related to the physical structure since R(r)dr gives the number of atoms in an annulus of thickness dr at distance r from another atom. For example, the coordination number, or the number of neighbors, N C , is given by

$$ {{N}_C} = \int_{{{{r}_1}}}^{{{{r}_2}}} {R(r)dr} $$
(17.7)

where r 1 and r 2 define the beginning and ending positions of the RDF peak corresponding to the coordination shell in question. This suggests a scheme for calculating PDFs from atomic models. Consider a model consisting of a large number of atoms situated at positions r ν with respect to some origin. Expressed mathematically, this amounts to a series of delta functions, δ(r – r ν). The RDF is then given as

$$ R(r) = \frac{1}{N}\sum\limits_{\nu } {\sum\limits_{\mu } {\delta (r - {{r}_{{\nu \mu }}})} } $$
(17.8)

where r νμ  = |r ν – r μ | is the magnitude of the separation of the ν-th and μ-th ions and the double sum runs twice over all atoms in the sample. Later we address explicitly samples with more than one type of atom, but for completeness we give here the expression for R(r) in this case:

$$ R(r) = \frac{1}{N}\sum\limits_{\nu } {\sum\limits_{\mu } {\frac{{{{b}_{\nu }}{{b}_{\mu }}}}{{{{{\left\langle b \right\rangle }}^2}}}} } \delta (r - {{r}_{{\nu \mu }}}) $$
(17.9)

where the b terms are the Q-independent coherent scattering lengths for the νth and μth atoms and \( \langle \) b \( \rangle \) is the sample average scattering length. In the case of x-rays, the b terms are replaced with atomic number, Z.

3 Experimental Methods

Total scattering measurements have basically the same requirements as any powder diffraction measurement. Special requirements for high-quality total scattering data are the following:

  1. 1.

    Data measured over a wide Q-range. This requires wide scattering angles and/or short-wavelength incident radiation.

  2. 2.

    Good statistics, especially at high-Q where the scattering signal is weak.

  3. 3.

    Low background scattering. It is important to measure weak diffuse scattering signals accurately which is difficult on top of high backgrounds.

  4. 4.

    Stable set-up and accurate incident intensity monitoring. The data are normalized by incident intensity. It is important that the incident beam and detector characteristics do not change in an uncontrolled way during the course of the experiment, or that this can be corrected, for example, by monitoring the incident beam intensity as is done at synchrotron x-ray and spallation neutron measurements.

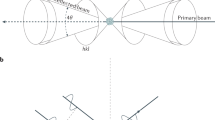
X-ray experiments can be carried out using laboratory diffractometers with Mo or Ag sources which give Q-ranges up to Q max ∼14 and 20 Å−1, respectively. These are less than optimal values for Q max , but acceptable for straightforward characterization of nanostructured materials at room temperature. Optimally, x-ray experiments are carried out at x-ray synchrotron sources using high incident energy x-rays. These can be done with incidence energies in the vicinity of 30–45 keV in conventional Debye-Scherrer geometry (for instance using be beamlines such as X31 at ESRF or 11BM at APS that are constructed for regular powder diffraction). However, more common, these days, is to use the rapid acquisition PDF mode (RAPDF) in which data for a PDF is collected in a single-shot using a planar 2D detector [11]. This is illustrated in Fig. 17.3.

Fig. 17.3
figure 3

Schematic of the rapid acquisition RAPDF x-ray data collection method

Full size image

Dedicated beamlines have been constructed at APS for this purpose (11ID-B and 11ID-C) with similar beamlines under construction at NSLS (X17A), ESRF and NSLS-II. In this geometry, incident x-rays of energy 60–150 keV are fired through a sample and collected on a large area image-plate detector placed behind the sample. The experiment consists of ensuring the incident beam is perpendicular and centered on the detector and the sample, then exposing the image plate. Depending on the strength of scattering and the sensitivity of the detector, exposures for good PDFs in excess of Q max  = 30 Å−1 can be obtained in as little as 100 ms, and typically a few seconds to minutes. This compares to data collection times of 8–12 h with conventional non-parallel counting approaches, even at the synchrotron. The RAPDF measurement is ideal for time-resolved and parametric measurements, of local structure through phase transitions for example. The Q-resolution of these measurements is very poor because of the geometry, and this limits the r-range of the resulting data from crystalline materials. However, most modeling is carried out over rather narrow ranges of r and this represents a very good tradeoff. Where a wide r-range is necessary for the measurement (to study some aspect of intermediate range order on length-scales of 5–10 nm for, example) the Debye-Scherrer geometry diffractometers can be used.

In the case of neutron measurements, the requirement of short-wavelengths really limits experiments to time-of-flight spallation neutron sources. Reactor sources with hot moderators would give good quality data for PDF studies, but are in short supply. The requirements for a spallation neutron powder diffractometer are laid out in the list of experimental requirements above. Normal time-of-flight powder diffractometers can be used provided the length of the flight-path and frequency of operation are such to allow good fluxes of neutrons with short wavelength (0.2–0.4 Å). Currently neutron guides do not propagate these short-wavelength neutrons effectively so shorter flight-path diffractometers with or without guides give the best data. Currently the instruments of choice are NPDF at the Lujan Center at Los Alamos National Laboratory in the USA and GEM at ISIS, Rutherford Laboratory, in the UK. The former was upgraded with PDF experiments in mind and has excellent stability on a water moderator and low backgrounds, though data collection time is not quite at the level of GEM. New powder diffractometers are coming on line at the Spallation Neutron Source at Oak Ridge National Laboratory (NOMAD and POWGEN) that will give unprecedented data-rates and will be suitable for PDF studies.

A number of data correction programs are available for free download and these take care of the corrections and normalizations needed to obtain PDFs from raw data. These can be browsed at the ccp14 software website [12]. Commonly used, and generally easy to use, programs are Gudrun [13] and PDFgetN [14] for spallation neutron data and PDFgetX2 [15, 16] for x-ray data. PDFgetX2 has the corrections implemented for accurate analysis of RAPDF data. Details of the corrections are beyond the scope of this article, but can be found in some detail in “Underneath the Bragg peaks: structural analysis of complex materials” by Egami and Billinge [3].

4 Extracting Structural Information from Total Scattering

Here we confine ourselves to real-space modeling whereby the PDF of the model is calculated and compared to an experiment. Fitting the PDF is generally done with models described by a small number of atoms in a unit cell (which may or may not be the crystalline unit cell) and yields information about the very local structure.

Information can be extracted directly from the PDF in a model-independent way because of its definition as the atom-pair correlation function. The position of a peak in the PDF indicates the existence of a pair of atoms with that separation. There is no intensity in R(r) for distances less than the nearest-neighbor distance, r < r nn and a sharp peak at r nn . This behavior is very general and true even in atomically disordered systems such as glasses, liquids and gasses. In crystals, because of the long-range order of the structure, all neighbors at all lengths are well defined and give rise to sharp PDF peaks. The positions of these peaks give the separations of pairs of atoms in the structure directly and the width contains information about thermal motion of the atoms, or static disorder. In general, it is not possible to tell directly from the data whether a PDF peak broadening is static or dynamic in nature, though this can sometimes be inferred by fitting temperature dependence to a dynamical model such as the Debye model.

When a well-defined PDF peak can be observed, we can determine information about the number of neighbors in that coordination shell around an origin atom by integrating the intensity under that peak, as shown in Eq. 17.7. In the case of crystalline Ni there are four Ni atoms in the unit cell (fcc structure). Each nickel ion has 12 neighbors at 2.49 Å [17]. When we construct our PDF we will therefore place 48 units of intensity at position r = 2.49 Å (the weighting factor, bmbn/<b>2, is unity since there is only one kind of scatterer) and divide by N = 4 since we put 4 atoms respectively at the origin. Thus, integrating the first peak will yield 12 which is the coordination number of Ni. The same information can be obtained from multi-element samples if the chemical origin of the PDF peak, and therefore the weighting factor, is known. If, as is often the case, PDF peaks from different origins overlap this process is complicated. Information can be extracted by measuring the chemical specific differential or partial-PDFs directly [18], by fitting the peaks with a series of Gaussian functions, or better, by full-scale structural modeling.

Atomic disorder in the form of thermal and zero-point motion of atoms, and any static displacements of atoms away from ideal lattice sites, give rise to a distribution of atom-atom distances. The PDF peaks are therefore broadened resulting in Gaussian shaped peaks. The width and shape of the PDF peaks contain information about the real atomic probability distribution. For example, a non-Gaussian PDF peak may suggest an anharmonic crystal potential.

Modeling the data reveals much more information that straight model independent analysis. The most popular approach for real-space modeling is to use PDFfit, and its replacement PDFfit2 and PDFgui [19, 20], a full-profile fitting method analogous to the Rietveld method [21] but where the function being fit is the PDF.

Parameters in the structural model, and other experiment-dependent parameters, are allowed to vary until a best-fit of the PDF calculated from the model and the data derived PDF is obtained, using a least-squares approach. The sample dependent parameters thus derived include the unit cell parameters (unit cell lengths and angles), atomic positions in the unit cell expressed in fractional coordinates, anisotropic thermal ellipsoids for each atom and the average atomic occupancy of each site.

We highlight here the similarities and differences with conventional Rietveld. The main similarity is that the model is defined in a small unit cell with atom positions specified in terms of fractional coordinates. The refined structural parameters are exactly the same as those obtained from Rietveld. The main difference from conventional Rietveld is that the local structure is being fit which contains information about short-range atomic correlations. There is additional information in the data, which is not present in the average structure, about disordered and short-range ordered atomic displacements. To successfully model these displacements it is often necessary to utilize a “unit cell” which is larger than the crystallographic one. It is also a common strategy to introduce disorder in an average sense without increasing the unit cell. For example, in the example where an atom is sitting in one of two displaced minima in the atomic potential, but its probability of being in either well is random, can be modeled as a split atomic position with 50% occupancy in each well. This is not a perfect, but a very good, approximation of the real situation and is very useful as a first order attempt at modeling the data.

This “Real-space Rietveld” approach is proving to be very useful and an important first step in analyzing PDFs from crystalline materials. This is because of two main reasons. First, its similarity with traditional Rietveld means that a traditional Rietveld derived structure can be compared quantitatively with the results of the PDF modeling. This is an important first step in determining whether there is significant evidence for local distortions beyond the average structure. If evidence exists to suggest that local structural distortions beyond the average structure are present, these can then be incorporated in the PDF model. The second strength of the real-space Rietveld approach is the simplicity of the structural models making it quick and straightforward to construct the structural models and making physical interpretations from the models similarly quick and straightforward. The most recent version of the PDFfit code comes with a user-friendly graphical user interface facilitating many tasks in the data analysis, called PDFgui and PDFfit2 [19].

PDFfit was originally designed to study disorder and short-range order in crystalline materials with significant disorder such as nanoporous bulk materials. It has also found extensive use in studying more heavily disordered materials such as nanocrystalline materials and nanoporous materials and this looks set to increase in the future.

5 Conclusions

This chapter contains a brief account of the theory behind the PDF method and the basic methods for obtaining suitable data, analyzing it and extracting nanostructural information from it. Interest in the technique is growing rapidly as the quality of structural information obtainable from it improves due to methodological advances, and as more and more researchers seek to make and characterize materials on the nanoscale.