An Edge-Based Smoothed Finite Element Method for Primal-Dual Shakedown Analysis of Structures Under Uncertainties

Abstract

This paper deals with the application of a new algorithm of probabilistic limit and shakedown analysis for 2D structures, in which the loading and strength of the material are to be considered as random variables. The procedure involves a deterministic shakedown analysis for each probabilistic iteration, which is based on the primal-dual approach and the edge-based smoothed finite element method (ES-FEM). The limit state function separating the safe and failure regions is defined directly as the difference between the obtained shakedown load factor and the current load factor. A Sequential Quadratic Programming (SQP) is implemented for finding the design point. Sensitivity analyses are performed numerically from a mathematical model and the probability of failure is calculated by the First Order Reliability Method. Because of use of constant smoothing functions in the ES-FEM, only one Gaussian point is required for each smoothing domain ensuring that the total number of variables in the resulting optimization problem is kept to a minimum compared with standard finite element formulation. Numerical examples are presented to show the validity and effectiveness of the present method.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Recent trends consider the combination of the limit state analysis with the probabilistic approach to safety as a promising point of view, in order to take rational decisions in structural design. For limit state analysis, it has been recognized that the plastic collapse limit and the shakedown limit have to be accounted in an advanced approach since they define the real limit states of structures. Handling with such kind of problems, well-known direct plasticity methods such as limit and shakedown analysis becomes a powerful and effective tool. The upper bound shakedown analysis is based on Koiter’s kinematic theorem to determine the minimum load factor for non-shakedown, see e.g. [9, 15]. The strategy of computation is initiated from the unsafe region to calculate the exterior approximation of the shakedown load domain by supposing a kinematically admissible failure mechanism. On the contrary, the lower bound shakedown analysis is based on Melan’s static theorem, and the strategy of computation is begun from the safe region by supposing a statically admissible stress field to determine the maximum load factor for shakedown, see e.g. [2, 4]. Duality between these two bounds was proved by the flow rule including two main points: (1) the strain rate vector is proportional to the gradient of the yield function and (2) the plastic multiplier can be non-negative only at points where the yield function equals to zero.

In fact, no established design standard is able to definitely exclude any occurrence of structural malfunctions. All that can be successfully done is to recognize that both strength of the material and loading have an essential random nature, that therefore they are described as random variables or processes, and to keep the probability that such malfunctions occur as small as possible. Structural reliability analysis deals with these random variables in a rational way. An effective method of structural reliability analysis is probabilistic limit and shakedown analyses, which is based on the direct computation of the load-carrying capacity or the safety margin. Most important, this approach makes the problem time-invariant and therefore reduces considerably the needs for uncertain technological input data and computing costs.

The submitted contribution based on a new algorithm of probabilistic limit and shakedown analysis for 2D structures, in which the loading and strength of the material are to be considered as random variables. The procedure involves a deterministic shakedown analysis for each probabilistic iteration, which is based on the primal-dual approach and the edge-based smoothed finite element method (ES-FEM). The limit state function separating the safe and failure regions is defined directly as the difference between the obtained shakedown load factor and the current load factor. A Sequential Quadratic Programming (SQP) is implemented for finding the design point. Sensitivity analyses are performed numerically from a mathematical model and the probability of failure is calculated by the First Order Reliability Method. Because of use of constant smoothing functions in the ES-FEM, only one Gaussian point is required for each smoothing domain ensuring that the total number of variables in the resulting optimization problem is kept to a minimum compared with standard finite element formulation.

2 The Formulation of the ES-FEM

In engineering practice, the 3-node linear triangular element (FEM-T3) and the 4-node linear quadrilateral element (FEM-Q4) are preferred by many engineers due to their simplicity, robustness, lesser demand on the smoothness of the solution, and efficiency of adaptive mesh refinements for solutions of desired accuracy. However, the FEM models using FEM-T3 or FEM-Q4 elements still possess inherent drawbacks such as the overestimation of the system stiffness matrix which leads to poor accuracy of the solution and they are subjected to locking effects for incompressible materials. Moreover, mesh distortion due to large deformations may lead to a severe convergence problem of the analysis.

In order to avoid these drawbacks, Liu et al. [5] have combined the strain smoothing technique used in meshfree methods with the FEM to formulate a so-called smoothed finite element method (S-FEM or CS-FEM). In the S-FEM, they subdivide each FE element into smoothing cells and do not use the compatible strain fields. The strain field is projected (smoothed) onto a constant field or set of constant fields based on local smoothing cells (domains) and the domain integration becomes integration along the boundary of the domain. The derivatives of the shape functions are not used to calculate the strain matrix, which accordingly reduces the requirements on the smoothness of the shape functions.

Very recently, Liu et al. [6] also proposed an edge-based smoothed finite element method (ES-FEM) for static, free and forced vibration analyses of solid 2D mechanics problems using triangular elements (T3). Intensive numerical results have demonstrated that ES-FEM possesses the following excellent properties: (1) ES-FEM-T3 is much more accurate than the FEM using linear triangular elements (FEM-T3) and often found even more accurate than those of the FEM using quadrilateral elements (FEM-Q4) with the same sets of nodes; (2) there are no spurious non-zeros energy modes found and hence the method is also temporally stable and works well for vibration analysis and (3) no penalty parameter is used and the computational efficiency is much better than the FEM using the same sets of elements. The ES-FEM was then extended successfully to primal-dual limit and shakedown analysis of structures made of elastic-perfectly plastic material [11].

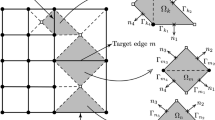
Suppose that the entire problem domain is discretized by finite elements. In the ES-FEM, the compatible strains ε=∇ _s u are smoothed over local smoothing domains Ω ^(k) associated with edges of the elements by the following operation

$$ \tilde{\boldsymbol{\varepsilon}}_{k} = \int _{\varOmega^{(k)}} \boldsymbol{\varepsilon} (\mathbf{x})\varPhi_{k}( \mathbf{x})d\varOmega= \int_{\varOmega^{(k)}} \nabla_{s} \mathbf{u}(\mathbf{x})\varPhi_{k}(\mathbf{x})d\varOmega, $$

(1)

where Φ _k (x) is a given smoothing function that satisfies the unity property

$$ \int_{\varOmega^{(k)}} \varPhi_{k}(\mathbf {x})d\varOmega = 1. $$

(2)

The local smoothing domains Ω ^(k) are constructed based on edges of elements such that they cover the entire problem domain $\varOmega = \bigcup_{k = 1}^{N_{e}} \varOmega^{(k)}$ and Ω ⁽ⁱ⁾∩Ω ^(j)=∅ for i≠j, in which N _e is the total number of edges (sides) in the entire problem domain. If triangular elements are used, the smoothing domain Ω ^(k) associated with edge k is created by connecting two endpoints of the edge to two centroids of two adjacent elements, see Fig. 1. For the mesh consisting of n-sided polygonal elements, the construction of smoothing domains is straightforward.

Fig. 1

Division of domain into triangular elements and smoothing cells Ω ^(k) connected to edge k of triangular elements

Using the constant smoothing function

$$ \varPhi_{k}(\mathbf{x}) = \begin{cases} 1/A^{(k)},& \mathbf{x} \in\varOmega^{(k)}, \\ 0,& \mathbf{x} \notin\varOmega^{(k)}, \end{cases} $$

(3)

where A ^(k) is the area of the smoothing domain Ω ^(k), the smoothed strains $\tilde{\boldsymbol{\varepsilon}}_{k}$ in (1) and therefore the stresses are constant in the smoothing domain. Let x _k stand for x∈Ω ^(k). In terms of nodal displacement vectors d _I , the smoothing strains can be written as

$$ \tilde{\boldsymbol{\varepsilon}}_{k} = \sum _{I = 1}^{N_{n}^{(k)}} \tilde{\mathbf{B}}_{I}( \mathbf{x}_{k})\mathbf{d}_{I} , $$

(4)

where $N_{n}^{(k)}$ is the total number of nodes of elements containing the common edge k. For inner edges (see Fig. 1) $N_{n}^{(k)} = 4$, for boundary edges $N_{n}^{(k)} = 3$. $\tilde{\mathbf{B}}_{I}(\mathbf{x}_{k})$ is the smoothed strain matrix on the domain Ω ^(k) which is calculated numerically by an assembly process similarly as in the standard FEM

$$ \tilde{\mathbf{B}}_{I}(\mathbf{x}_{k}) = \frac{1}{A^{(k)}}\sum_{j = 1}^{N_{e}^{(k)}} \frac{1}{3}A_{e}^{(j)}\mathbf{B}_{j} , $$

(5)

in which $N_{e}^{(k)}$, $A_{e}^{(j)}$, B _j are the number of elements, the area and the strain matrix of the jth element around the edge k, respectively. For inner edges (see Fig. 1) $N_{e}^{(k)} = 2$, for boundary edges $N_{e}^{(k)} = 1$. The matrix B _j is exactly the strain matrix of the T3 element in the standard FEM. When linear elements are used, the entries of B _j and therefore of $\tilde{\mathbf{B}}_{I}(\mathbf{x}_{k})$ are also constants.

In general, the smoothed strain matrix for 2-dimensional problems consisting of n-sided polygonal elements can be calculated as follows

(6)

in which

$$ \tilde{b}_{Ih}(\mathbf{x}_{k}) = \frac{1}{A^{(k)}}\sum_{i = 1}^{N_{s}} N_{I}\bigl(\mathbf{x}_{i}^{GP} \bigr)n_{ih}^{(k)}l_{i}^{(k)},\quad (h = x,y) , $$

(7)

where N _s is the total number of the boundary segments $\partial\varOmega_{i}^{( k )}$ of the domain Ω ^(k), $N_{I}(\mathbf{x}_{i}^{GP})$ is the shape function value at Gaussian point (midpoint) $\mathbf{x}_{i}^{GP}$ on $\partial\varOmega_{i}^{( k )}$ and $n_{ih}^{(k)}$, $l_{i}^{(k)}$ are the outward unit normal and the length of boundary segment $\partial\varOmega_{i}^{( k )}$.

The smoothed domain stiffness matrix is then calculated by

$$ \tilde{\mathbf{K}}_{(k)} = \int_{\varOmega^{(k)}} \tilde{\mathbf{B}}_{I}^{T}\mathbf{E}\tilde{\mathbf{B}}_{I}d \varOmega= A^{(k)}\tilde{\mathbf{B}}_{I}^{T}\mathbf{E}\tilde {\mathbf{B}}_{I}, $$

(8)

where E is the matrix of elastic material constants. The global stiffness matrix $\tilde{\mathbf{K}}$ is then assembled over all domain stiffness matrices $\tilde{\mathbf{K}}_{(k)}$ by a similar process as in the FEM.

3 A Primal-Dual Shakedown Algorithm Based on the ES-FEM

Let us restrict ourselves to the case of homogeneous material, where the yield limit σ _y is the same at every point of the structure. Then we always can write σ _y =Yσ ₀ where σ ₀ is a constant reference value and Y is a random variable. Consider a convex polyhedral load domain and a special loading path consisting of all load vertices $\hat{P}_{i}$ (i=1,…,m) of . According to Koiter’s theorem, the upper bound shakedown limit, which is the smaller one of the low cycle fatigue limit and the ratcheting limit, may be found by the following minimization

(9)

in which $D^{p}(\dot{\tilde{\boldsymbol{\varepsilon}}}_{ik})$ is the plastic dissipation power per unit domain, σ ^E is the fictitious elastic stress vector, $\Delta\dot{\tilde{\boldsymbol{\varepsilon}}}$ is the vector of accumulated strain rates over a load cycle and $\dot{\mathbf{u}}$ is the vector of nodal velocities. The fictitious elastic stress vector σ ^E and the starting value of the strain rate vector $\dot{\tilde{\boldsymbol{\varepsilon}}}_{ik}$ are calculated by solving the global system of equations with the global stiffness matrix $\tilde{\mathbf{K}}$ derived from Eq. (8). The third constraint (Eq. (9d)) ensures that the incompressibility condition is satisfied on all smoothing domains Ω ^(k) and at all load vertices i. For plane strain problems, D _v assumes the form

(10)

It is noted that only the first row in Eq. (9d) is necessary to ensure the incompressibility. However, we write D _v as a square matrix since it will help to formulate our optimization procedure conveniently, for example in Eq. (14). By discretizing the entire problem domain into smoothing domains, applying the strain smoothing technique described in Sect. 2 and introducing some new notations such as

$$ \dot{\mathbf{e}}_{ik} = A^{(k)} \mathbf{D}^{1/2}\dot{\tilde{\varepsilon}}_{ik},\qquad \mathbf{t}_{ik} = \mathbf{D}^{ - 1/2}\sigma_{ik}^{E},\qquad \hat{\mathbf{B}}_{k} = A^{(k)}\mathbf{D}^{1/2}\tilde{\mathbf{B}}_{k}, $$

(11)

we obtain a simplified version for the upper bound shakedown analysis (primal problem)

(12)

where $\varepsilon_{0}^{2}$ is a small positive number to ensure the objective function to be differentiable everywhere. It has been proved that the numerical result is not sensitive to $\varepsilon_{0}^{2}$ if it is smaller than 10⁻¹⁴ [14]. D is a diagonal square matrix and has the following form for two-dimensional problems

(13)

Note that the second constraint in (9) is omitted here since it will be automatically fulfilled by the shape functions. The Lagrangian associated with the primal problem (12) can be written as follows

(14)

where γ _ik , β _k , α are Lagrange multipliers. The dual problem of (12) which can be proved by dual theory takes the form [14]

(15)

The form (15) is also exactly the discretized form of the lower bound shakedown limit which is formulated by Melan’s static theorem. Since the stresses are constant in each smoothing domain, the two constraints in (15) are satisfied at all points in the entire problem domain. It follows that the lower bound shakedown limit obtained in (15) dual to the upper bound obtained in (12), for $\varepsilon_{0}^{2} \to0$, will have a strict bounding characteristic. It is noted that when m=1, the formulations (12) and (15) reduce to those of limit analysis.

Dealing with the nonlinear constrained optimization problem (12), an iterative primal-dual algorithm is developed to calculate simultaneously the upper bound and lower bound of the shakedown limit. Details of this iterative algorithm can be found in [11].

4 Probabilistic Algorithm

Denote by X=(X ₁,X ₁,…,X _n ) an n-dimensional random vector characterizing uncertainties in the structure and load parameters. The limit state function g(x)=0, which is based on the comparison of a structural resistance (threshold) and loading, defines the limit state hyper-surface ∂S which separates the failure region S={x|g(x)<0} from the safe region. The probability of failure P _f is the probability that g(X) is non-positive, i.e.

$$ P_{f} = P \bigl( g(\mathbf{X}) \le0 \bigr) = \int _{S} f_{X}(\mathbf{x})dx , $$

(16)

where f _X (x) is the n-dimensional joint probability density function. In general, it is not possible to calculate P _f analytically since the form of the limit state surface is very complex. Therefore, approximation approaches should be used. In the First-Order Reliability Method (FORM), an approximation to the probability of failure is obtained by linearizing the limit state function at the “design point” (the most likely failure point or β _HL -point). This is the point on the limit state surface that is nearest to the origin in the space of standard normal random variables. The failure probability P _f is thus approximated by

$$ P_{f} = \varPhi( - \beta_{HL}) = \frac{1}{\sqrt{2\pi}} \int_{ - \infty}^{ - \beta_{HL}} e^{ - 0.5z^{2}}dz , $$

(17)

where β _HL =∥u ^∗∥, Φ(.) is the standard normal cumulative distribution function and u ^∗ is found from a nonlinear constrained optimization problem as follows

$$ \everymath{\displaystyle} \begin{aligned}[c] & \text{minimize:}&&f(\mathbf{u}) = \frac{1}{2}\| \mathbf{u} \|^{2} \\[6pt] &\text{s.t.}&& g(\mathbf{u}) \le 0. \end{aligned} $$

(18)

The main computational task for a reliability analysis problem is to locate the design point u ^∗, i.e. to solve the optimization problem (18). Staat and Heitzer [8], Heitzer and Staat [3] and Bjerager [1] got good results in probabilistic limit analyses with a simple gradient search algorithm, which is based on a linearization of the limit state function at each step. However, this algorithm is only guaranteed to converge towards a locally most likely failure point in each sequence of points on the failure surface if the safe region is quasi-convex or concave. A more general algorithm is the Sequential Quadratic Programming (SQP). This method has proved to be suitable for tasks in the area of the reliability theory [7]. Details of an SQP method stabilized by a simple line search procedure subject to a suitable merit function for solving the optimization problem (18) can be found in [10]. Details of the definition of the limit state function and its gradients can be found in [12].

5 Validations

In the following, a number of examples are presented to demonstrate the capabilities of the proposed algorithm. In all cases, structures are made of elastic-perfectly plastic material and the 3-node triangular elements (FEM-T3) are applied for structural discretization.

5.1 Square Plate with a Hole

The first example concerns a square plate with central hole as shown in Fig. 2b. The plate is subjected to a pressure p which can vary within a range p∈[0,p _max]. The geometrical data and material properties are chosen as those used in [14]: E=200 GPa, ν=0.3, σ _y =10 MPa. Both plane strain and plane stress hypotheses are analyzed using 500 T3 elements as shown in Fig. 2a.

Fig. 2

FE-mesh and geometrical dimensions of square plate in mm

If both material strength and load (stress) random variables are supposed to be normally distributed with means μ _r ,μ _s and standard deviations σ _r ,σ _s respectively, then the analytical reliability index may be given [8]

$$ \beta_{HL} = \frac{ ( 1 - \alpha)\mu_{r} - \mu _{s}}{\sqrt{ ( 1 - \alpha)^{2}\sigma_{r}^{2} + \sigma_{s}^{2}}} $$

(19)

where α=p _lim/σ _y is the load factor. From the deterministic numerical analysis [13], we got the limit load factor α=0.5573 and the shakedown load factor α=0.3626 for the case of plane stress. For plane strain, they are 0.6895 and 0.4331, respectively.

The numerical probabilities of failure for limit and shakedown analysis and for both plane stress and plane strain cases are presented in Tables 1 and 2, compared with the semi-analytical solutions, which are calculated by substituting α in (19). Both random variables have the same standard deviations σ _r,s =0.1μ _r,s . The present solutions are very close to the semi-analytical ones for both cases. It is worth to note that the shakedown probabilities of failure are considerably smaller than those of limit analysis. Thus, the loading conditions should be considered carefully when assessing the load-carrying capacity of the structure.

Table 1 Failure probabilities for normal distributions, plane stress

Table 2 Failure probabilities for normal distributions, plane strain

5.2 Simple Frame

In the second example, we consider a simple frame subjected to a load as shown in Fig. 3a. Two different boundary conditions are considered: (a) only the horizontal displacement on the left boundary is free and (b) both vertical and horizontal displacements on both boundaries are fixed. The load domain, geometrical data and material properties are chosen analogously as: p∈[0,p _max], E=2⋅10⁵ GPa, ν=0.3, σ _y =10 MPa. The frame is discretized by 1600 T3 elements as shown in Fig. 3b.

Fig. 3

FE-mesh and geometrical dimensions of simple frame in mm

For case (a), numerical deterministic analyses lead to the limit load factor α=0.8474 and the shakedown load factor α=0.8232. For case (b), they are 1.3487 and 0.9187, respectively. Numerical probabilities of failure for limit and shakedown analyses for normal distributions are presented in Tables 3 and 4, compared with corresponding semi-analytical solutions by (19). Both random variables have standard deviations σ _r,s =0.1μ _r,s . The numerical error results only from reliability analysis. It is shown that the present numerical results are very close to the exact ones, even in the case of very small probabilities.

Table 3 Failure probabilities for normal distributions, case (a)

Table 4 Failure probabilities for normal distributions, case (b)

6 Conclusions

The paper has presented the application of a numerical procedure for probabilistic limit and shakedown analyses of 2D structures made of elastic-perfectly plastic materials using a novel ES-FEM. The procedure involves a deterministic limit and shakedown analysis for each probabilistic iteration, which is based on the primal-dual approach and the use of the von Mises yield criterion. A mesh of three-node linear triangular elements and constant smoothing functions are used to construct the ES-FEM formulation. The probabilistic formulation considers the loading and the material strength as random variables. A nonlinear optimization was implemented, which is based on the Sequential Quadratic Programming for finding the design point and the probabilities of failure were calculated by FORM. Numerical examples were tested demonstrating that the proposed method appears to be powerful and effective for evaluating of the probabilities of failure of 2D structures. The extension for 3D structures using the face-based smoothed finite element method (FS-FEM) is straightforward.