Application of Density Matrix Methods to Ultrafast Processes

Abstract

The density matrix method is a powerful theoretical technique to describe the ultrafast processes and to analyze the femtosecond time-resolved spectra in the pump-probe experiment. The dynamics of population and coherence of the system can be described by the evolution of density matrix elements. In this chapter, the applications of density matrix method on internal conversion and vibrational relaxation processes will be presented. As an example, the ultrafast internal conversion process of ππ* → nπ* transition of pyrazine will be presented, in which case the conical intersection is commonly believed to play an important role. A treatment with Q-dependent nonadiabatic coupling will be applied to deal with the internal conversion rate. Another important ultrafast process, vibrational relaxation, which usually takes place in sub-ps and ps range, will be treated using adiabatic approximation. Then the vibrational relaxation in water dimer and aniline will be chosen to demonstrate the calculation.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Pump-probe experiment is an efficient approach to detect the ultrafast processes of molecules, clusters, and dense media. The dynamics of population and coherence of the system can be theoretically described using density matrix method. In this chapter, for ultrafast processes, we choose to investigate the effect of conical intersection (CI) on internal conversion (IC) and the theory and numerical calculations of intramolecular vibrational relaxation (IVR). Since the 1970s, the theories of vibrational relaxation have been widely studied [1–7]. Until recently, the quantum chemical calculations of anharmonic coefficients of potential-energy surfaces (PESs) have become available [8–10]. In this chapter, we shall use the water dimer (H₂O)₂ and aniline as examples to demonstrate how to apply the adiabatic approximation to calculate the rates of vibrational relaxation.

The CI of the adiabatic PESs is a common phenomenon in molecules [11–13]. The singular nonadiabatic coupling (NAC) associated with CI is the origin of ultrafast non-Born-Oppenheimer transitions. For a number of years, the effects of CI on IC (or other nonadiabatic processes) have been much discussed and numerous PESs with CIs have been obtained [11, 12] for qualitative discussion. Actual numerical calculations of IC rates are still missing. In this chapter, we shall calculate IC rate with Q-dependent nonadiabatic coupling for the pyrazine molecule as an example to show how to deal with the IC process with the effect of CI. Recently, Suzuki et al. have researched the ππ* state lifetimes for pyrazine in the fs time-resolved pump-probe experiments [13]. The population and coherence dynamics are often involved in such fs photophysical processes. The density matrix method is ideal to describe these types of ultrafast processes and fs time-resolved pump-probe experiments [14–19].

This chapter is organized as follows: In Sect. 4.2, the theory of density matrix method is introduced. In Sect. 4.3, we use a theoretical model to manifest the condition of nonexponential decay. In Sect. 4.4, conical intersection in the IC process will be dealt with. In Sect. 4.5, the vibrational relaxation process in the framework of adiabatic approximation will be discussed. And at last, we will give a conclusion in Sect. 4.6.

2 Density Matrix Method

The dynamics of an isolated (or total) system is governed by the Liouville equation [14–21]

$$ \frac{{{\text{d}}\hat{\sigma }}}{{{\text{d}}t}} = - \frac{i}{\hbar }{ [}{\hat{H}_{\text{t}}},\hat{\sigma }] = - i{\hat{L}_{\text{t}}}\hat{\sigma } $$

(4.1)

Here, ${\hat{H}_{\text{t}}}$ is the Hamiltonian of the total system. The subscript “t” here refers to the “total system”. ${\hat{H}_{\text{t}}}$ can be written as

$$ {\hat{H}_{\text{t}}} = {\hat{H}_{\text{s}}} + {\hat{H}_{\text{b}}} + \hat{H}^\prime $$

(4.2)

where ${\hat{H}_{\text{s}}}$, ${\hat{H}_{\text{b}}}$, and $\hat{H}^\prime$ are the Hamiltonians of the system, heat bath, and the interaction between the system and the heat bath, respectively. The symbol $\hat{\sigma }{ }$in Eq. (4.1) denotes the density operator of the total system. ${\hat{L}_{\text{t}}}$ represents the Liouville operator corresponding to ${\hat{H}_{\text{t}}}$. The time-dependent behavior of the system is described by the reduced density matrix $\hat{\rho }$, which can be obtained by eliminating the heat bath variables:

$$ {\rho_{mn}} = \sum\limits_\alpha {{\sigma_{m\alpha, n\alpha }}} $$

(4.3)

That is,

$$ \hat{\rho } = {\text{T}}{{\text{r}}_{\text{b}}}\left[ {\hat{\sigma }} \right] $$

(4.4)

Define project operator $\hat{D}$

$$ {\hat{\sigma }_1} = \hat{D}\hat{\sigma }{,}\quad {\hat{\sigma }_2} = (1 - \hat{D})\hat{\sigma } $$

(4.5)

where the matrix elements of $\hat{D}$ can be represented as [21]

$$ D_{m\alpha, n\beta }^{m^\prime\alpha ^\prime,n^\prime\beta ^\prime} \equiv {\delta_{\alpha \alpha ^\prime}}{\delta_{mm^\prime}}{\delta_{nn^\prime}}{\delta_{\beta \beta ^\prime}}{\delta_{\alpha \beta }} $$

(4.6)

$\hat{D}$ can project the density matrix elements onto the diagonal matrix elements of the bath. Apply Laplace transformation to density operator $\hat{\sigma }$:

$$ \hat{\sigma }(p) = \int_0^\infty {{e^{ - pt}}\hat{\sigma }(t){\text{d}}t} $$

(4.7)

Insert Eq. (4.7) into Eq. (4.1):

$$ p{\hat{\sigma }_1}(p) - {\hat{\sigma }_1}(0) = - i\hat{D}{\hat{L}_{\text{t}}}{\hat{\sigma }_1}(p) - i\hat{D}{\hat{L}_{\text{t}}}\frac{1}{{p + i\left( {1 - \hat{D}} \right){{\hat{L}}_t}}}{\hat{\sigma }_2}(0) - \hat{M}(p){\hat{\sigma }_1}(p) $$

(4.8)

Here, $\hat{M}(t)$ or $\hat{M}(p)$ denotes the memory kernel:

$$ \hat{M}(p) = \hat{D}{\hat{L}_t}\frac{1}{{p + i\left( {1 - \hat{D}} \right){{\hat{L}}_{\text{t}}}}}\left( {1 - \hat{D}} \right){\hat{L}_t} $$

(4.9)

It follows that

$$ \frac{{{\text{d}}\hat{\rho }}}{{{\text{d}}t}} = - i\bar{L}\hat{\rho } - \int_0^t {\bar{M}{(}\tau {)}\hat{\rho }(t - \tau ){\text{d}}\tau } $$

(4.10)

where

$$ \bar{L} = {\text{T}}{{\text{r}}_{\text{b}}}\left[ {\hat{D}{{\hat{L}}_{\text{t}}}{{\hat{\rho }}^{({\text{b}})}}} \right] $$

(4.11)

and

$$ \bar{M}{(}\tau {)} = {\text{T}}{{\text{r}}_b}\left[ {\hat{M}{(}\tau {)}{{\hat{\rho }}^{({\text{b}})}}} \right] $$

(4.12)

Applying Markoff approximation, Eq. (4.10) becomes

$$ \frac{{{\text{d}}\hat{\rho }}}{{{\text{d}}t}} = - i\bar{L}\hat{\rho } - \hat{\Gamma }\hat{\rho } $$

(4.13)

That is, the evolution of population dynamics is described by

$$ \begin{aligned} \frac{{{\text{d}}{\rho_{nn}}}}{{{\text{d}}t}} = & - \Gamma_{nn}^{nn}{\rho_{nn}} - \sum\limits_m {^\prime \Gamma_{nn}^{mm}{\rho_{mm}}} - \frac{i}{\hbar }{\left[ {{{\hat{H}}_{\text{s}}},\hat{\rho }} \right]_{nn}} \\ = & \sum\limits_m {\left( {\Gamma_{mm}^{nn}{\rho_{nn}} - \Gamma_{nn}^{mm}{\rho_{mm}}} \right)} - \frac{i}{\hbar }{\left[ {{{\hat{H}}_{\text{s}}},\hat{\rho }} \right]_{nn}} \\ \end{aligned} $$

(4.14)

where

$$ \Gamma_{nn}^{mm} = - \frac{{2\pi }}{\hbar }\sum\limits_\alpha^{\alpha \ne \beta } {\sum\limits_\beta {^\prime \rho_{\beta \beta }^{({\text{b}})}{{\left| {{{H^\prime}_{m\alpha, n\beta }}} \right|}^2}\delta \left( {{E_{m\alpha }} - {E_{n\beta }}} \right)} } $$

(4.15)

represents the rate constant for m → n transition, and

$$ \Gamma_{nn}^{nn} = - \sum\limits_m {^\prime \Gamma_{mm}^{nn}} $$

(4.16)

represents the total transition rate constant of state n. Similarly, the coherence (or phase) dynamics is described by

$$ \frac{{{\text{d}}{\rho_{mn}}}}{{{\text{d}}t}} = - \Gamma_{mn}^{mn}{\rho_{mn}} - \frac{i}{\hbar }{\left[ {{{\hat{H}}_{\text{s}}},\hat{\rho }} \right]_{mn}} $$

(4.17)

$$ \Gamma_{mn}^{mn} = \frac{1}{2}\left( {\Gamma_{mm}^{mm} + \Gamma_{nn}^{nn}} \right) + \Gamma_{mn}^{mn}(d) $$

(4.18)

and

$$ \Gamma_{mn}^{mn}(d) = \frac{\pi }{{{\hbar^2}}}\sum\limits_\alpha {\sum\limits_\beta {^\prime \rho_{\alpha \alpha }^{({\text{b}})}} } {\left( {{{H^\prime}_{m\alpha, m\beta }} - {{H^\prime}_{n\alpha, n\beta }}} \right)^2}\delta ({\omega_{\alpha \beta }}) $$

(4.19)

In the presence of an optical interaction $\hat{V}(t)$, the Liouville equation becomes

$$ \frac{{{\text{d}}\hat{\rho }}}{{{\text{d}}t}} = - \frac{i}{\hbar }\left[ {{{\hat{H}}_{\text{s}}},\hat{\rho }} \right] - \frac{i}{\hbar }\left[ {\hat{V}(t),\hat{\rho }} \right] - \hat{\Gamma }\hat{\rho } $$

(4.20)

This equation can be applied to study the dynamics of the systems with $\hat{V}(t) = 0$, linear and nonlinear optics, and pump-probe experiments, etc.

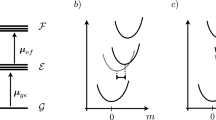
In femtosecond experiments, as shown in Fig. 4.1, the pump-probe methods are most commonly used to study the dynamic processes in chemical compounds or materials. It should be noted that for probing, one can use the optical excitation, photoionization up-conversion, and stimulated emission [18]. From the uncertainty principle, $\Delta E \Delta t \approx \hbar /2$, we can see that ΔE depends on the pumping-pulse duration Δt. For short Δt, both population and coherence (or phase) can be created. In other words, in this case, both population and coherence dynamics have to be treated. Thus, the density matrix method is ideal for this purpose. In pump-probe experiments, the Liouville equation takes the form

$$ \begin{aligned} \frac{{{\text{d}}\hat{\rho }}}{{{\text{d}}t}} = & - i{{\hat{L}}_0}\hat{\rho } - \frac{i}{\hbar }\left[ {\hat{V}(t),\hat{\rho }} \right] - \hat{\Gamma }\hat{\rho }{ } = - i{{\hat{L}^\prime}_0}\hat{\rho } - i\hat{L}^\prime(t)\hat{\rho } \\ = & - \frac{i}{\hbar }[{{\hat{H}}_s},\hat{\rho }] - \frac{i}{\hbar }\left[ {\hat{V}(t),\hat{\rho }} \right] - \hat{\Gamma }\hat{\rho } \\ \end{aligned} $$

(4.21)

where $\hat{V}(t) = - \vec{\mu } \cdot \vec{E} (t)$, $\vec{\mu }$ is the dipole operator, and $\hat{V}(t)$ describes the interaction between the system and the pumping (or probing) laser.

Fig. 4.1

Sketch of pump-probe experiment process

For the probing experiment, applying the perturbation method, the first-order solution of Eq. (4.21) is given by

$$ \rho_{nm}^{(1)}(t) = - \frac{1}{\hbar }\sum\limits_{n^\prime} {\rho {{(\Delta t)}_{nn^\prime}}} \frac{{{{\vec{\mu }}_{n^\prime m}}}}{{\omega + {{\omega ^\prime}_{n^\prime m}} - i/{T_P}}} \cdot {\vec{E}_0}( - \omega ){e^{it\omega }}{L_0}(t) $$

(4.22)

where $\Delta t = t - {t_i}$ and ${T_p}$ represents the duration of the probing laser. Here, $\hat{V}(t)$ is denoted by

$$ \hat{V}(t) = - \vec{\mu } \cdot \left[ {\vec{E}(\omega ){e^{ - it\omega }} + \vec{E}( - \omega ){e^{it\omega }}} \right]{L_0}(t) $$

(4.23)

and ${L_0}(t)$ denotes the laser-pulse shape function. Next, we calculate the polarization $\vec{P}(t)$

$$ \vec{P}(t) = {\vec{P}^{(1)}}(t) = {\text{Tr}}\left[ {\vec{\mu }{{\hat{\rho }}^{(1)}}(t)} \right] = \sum\limits_n {\sum\limits_m {{{\vec{\mu }}_{nm}}\rho_{nm}^{(1)}(t)} } $$

(4.24)

or

$$ \vec{P}(t) = - \frac{1}{\hbar }\sum\limits_n {\sum\limits_{n^\prime} {\sum\limits_m {\rho {{(\Delta t)}_{nn^\prime}}} } } \frac{{{{\vec{\mu }}_{mn}}{{\vec{\mu }}_{n^\prime m}}}}{{\omega + {{\omega ^\prime}_{n^\prime m}} - i/{T_P}}} \cdot {\vec{E}_0}( - \omega ){e^{it\omega }}{L_0}(t) $$

(4.25)

and the linear optical susceptibility

$$ \chi (\omega ) = - \frac{1}{\hbar }\sum\limits_n {\sum\limits_{n^\prime} {\sum\limits_m {\rho {{(\Delta t)}_{nn^\prime}}} } } \frac{{{{\vec{\mu }}_{n^\prime m}}{{\vec{\mu }}_{mn}}}}{{\omega + {\omega_{nm}} + i{\gamma_{nm}} + i/{T_P}}} $$

(4.26)

As shown from Eq. (4.26), the dynamics of both population $\rho {(\Delta t)_{nn}}$ and coherence $\rho {(\Delta t)_{nn^\prime}}$ $(n \ne n^\prime)$is involved in the time-resolved experiment (the probe experiment here), and Eq. (4.26) can be applied to optical absorption and stimulated emission. Furthermore, we recover the ordinary linear response theory where ${\rho_{nn^\prime}} = 0$ and ${\rho_{nn}}$ represents the Boltzmann distribution. In other words, Eq. (4.26) denotes the generalized linear response theory (GLRP). Pumping experiments can be treated similarly by using Eq. (4.21). With a short-pulse pumping laser, both population and coherence excitations can be created and the nonadiabatic processes such as photoinduced electron transfer take place afterward. With a similar derivation as shown above, we obtain the coherence created by the pumping laser with electric field ${\vec{E}_{\text{pu}}}$ and frequency ${\omega_{\text{pu}}}$ as

$$ {({\hat{\rho }_i})_{nn^\prime}} = \frac{{\tau_{\text{pu}}^2}}{{{\hbar^2}}}\left[ {{{\vec{\mu }}_{\text{ng}}} \cdot {{\vec{E}}_{\text{pu}}}({\omega_{\text{pu}}})} \right]\left[ {{{\vec{\mu }}_{gn^\prime}} \cdot {{\vec{E}}_{\text{pu}}}( - {\omega_{\text{pu}}})} \right]{\hat{\rho }_0} $$

(4.27)

where ${\tau_{pu}}$ denotes the pump-laser pulse duration and ${\hat{\rho }_0}$ is the density matrix of the system before the arrival of the pump laser. It is assumed that initially only the g state is populated. Here ${({\hat{\rho }_i})_{nn^\prime}}$by setting $n^\prime = n$, we obtain the population ${({\hat{\rho }_i})_{nn}}$. Other pumping conditions can be treated similarly by using Eq. (4.21).

3 Application to a Case of Bixon-Jortner Model

In intermediate or small systems, their population dynamic behaviors often exhibit nonexponential decay or even oscillatory decay like the vibrational relaxation of C₆H₅NH₂ in Sect. 5.2. To show how the density matrix method can be applied to study these systems, the Bixon-Jortner model is considered in this section. For this purpose, we consider the following model (see Fig. 4.2). $\left| 0 \right\rangle$ and $\left| i \right\rangle (i = 1,n)$ are the eigenstates of the Hamiltonian ${\hat{H}_0}$. For simplicity, we assume that only the perturbation matrix elements between $\left| 0 \right\rangle$ and $\left| i \right\rangle$ states are nonzero. That is,

Fig. 4.2

Bixon-Jortner model for decay from $\left| 0 \right\rangle$ state

$$ \begin{aligned} H^\prime_{00} &= 0 \\ H^\prime_{0i} & = H_{i0}^{\prime *} \quad = E^\prime \ne 0 \\ H^\prime_{ij} & = 0,\qquad i,j \geqslant 1 \\ \end{aligned} $$

(4.28)

The state of the system driven by the Hamiltonian $\hat{H} = {\hat{H}_0} + \hat{H^\prime}$ at time t can be expanded by $\left| 0 \right\rangle$ and $\left| i \right\rangle$ states:

$$ \left| {\Psi (t)} \right\rangle = {C_0}(t)\left| 0 \right\rangle + \sum\limits_i {{C_i}(t)\left| i \right\rangle } $$

(4.29)

Then, the population of state $\left| 0 \right\rangle$ can be expressed as

$$ {\rho_{00}}(t) = {\left| {{C_0}(t)} \right|^2} $$

(4.30)

The density operator will evolve according to the Liouville equation

$$ \frac{{{\text{d}}\hat{\rho }}}{{{\text{d}}t}} = - \frac{i}{\hbar }\left[ {\hat{H},\hat{\rho }} \right] - \hat{\Gamma }\hat{\rho } $$

(4.31)

In order to simulate the damping process of states $\left| i \right\rangle$ (i = 1, n), the imaginary energies have been added:

$$ {E_i} \to {E_i} - i{E_\eta } $$

(4.32)

Define

$$ \lambda \equiv \frac{{{{H^\prime}_{0i}}}}{\varepsilon } = \frac{{E^\prime}}{\varepsilon } $$

(4.33)

where ε denotes the energy interval between the eigenstate $\left| i \right\rangle$ and $\left| {i + 1} \right\rangle$. For this model, we set $n = 100$, which means that $n + 1$ eigenstates including $\left| 0 \right\rangle$ have been involved in this evolution process. We set the damping parameter ${E_\eta } = 20\;{\text{c}}{{\text{m}}^{ - 1}}$ and the energy interval $\varepsilon = 20\;{\text{c}}{{\text{m}}^{ - 1}}$. Assuming that at the beginning, ${C_0}(0) = 1$ and ${C_i}(0) = 0$ for $i \geqslant 1$, and then the population of state $\left| 0 \right\rangle$, ${\rho_{00}}(t)$, is calculated and plotted in Fig. 4.3. When $\lambda = 1$, $E^\prime = \varepsilon$, the decay of ${\rho_{00}}(t)$ appears near exponential character. With the increasing of perturbation $E^\prime$, the population ${\rho_{00}}(t)$ decays rapidly, and the oscillation appears. The reason of this phenomenon is due to the increasing of the perturbation speeding up the dynamics between $\left| 0 \right\rangle$ and $\left| i \right\rangle$ states, which results in the nonexponential decay.

The purpose of this section is to show how to employ the density matrix method to study the population dynamics of a system. From the model shown in Fig. 4.2, we can see that due to the fact that there is only one “system” state, there is no system coherence (or phase). However, quantum beat may be observed under certain conditions. It should be noticed that the master equations of this model can be solved exactly and analytically. Likewise, its Schrödinger equation can also be solved exactly and analytically.

Fig. 4.3

The population ${\rho_{00}}(t)$ of the state $\left| 0 \right\rangle$. Set the damping parameter ${E_\eta } = 20\;{\text{c}}{{\text{m}}^{ - 1}}$ and the energy interval $\varepsilon = 20\;{\text{c}}{{\text{m}}^{ - 1}}$. Different value of $\lambda$ corresponds to different perturbation $E^\prime$

Fig. 4.4

The experimental results of pyrazine from Ref. [13]. Ultraviolet photoabsorption spectra of (a) S ₁, S ₂, and S ₃ of pyrazine-h4 vapor (thin solid line) and pyrazine-d4 vapor (thin dashed line) at room temperature. The spectra of their pump (264 nm, 4.70 eV) and probe (198 nm, 6.26 eV) pulses are also shown in solid lines. (b) Schematic energy diagram of pyrazine

4 A Model of Conical Intersection

Recently, the pump-probe experiment for studying the ultrafast dynamics ππ* → nπ* of pyrazine has been carried out by Suzuki et al. [13]. Figure 4.4 shows the absorption spectra, pump and probe beam profiles, and energy level diagram. The adiabatic electronic excitation energies are taken from the Refs. [22–26]. It should be noted that the photoionization method has been employed for probing. Due to the particular use of pumping and probing lasers, the probing signals contain the dynamics information of S ₂ and S ₃ states. Employing the 22-fs duration lasers, Suzuki et al. obtained the lifetimes for pyrazine as τ(S ₂) = 22 ± 2 fs and τ(S ₃) = 40–43 fs. Their experimental results of temporal profiles of total photoelectron signals are shown in Fig. 4.5. For the equalization discussion of their experimental results, the potential surfaces obtained by Domcke et al. [27] have been used (see Fig. 4.6).

Fig. 4.5

Temporal profiles of total photoelectron signals in (1 + 1′) REMPI of (a) pyrazine-h₄ and (b) pyrazine-d₄ from Ref. [13]. The observed data (solid circles with error bars) are well explained by three components: the single-exponential decay of S ₂ (dotted line), the corresponding increase in S ₁ (dashed line) in the positive-time delay, and the single-exponential decay of S ₃ (dash-dotted line) in the negative-time delay. The fitting result is shown as a solid line

Fig. 4.6

A cut through the potential-energy surfaces of pyrazine along the normal coordinate ${Q_{6a}}$ from Ref. [27]. The vertical energy differences and shifts are drawn on scale. The shaded areas symbolize the ionization continua. The arrows on the right-hand side indicate a possible two photon transition (Reprinted with permission from Ref. [27] Copyright (1991), American Institute of Physics)

Next, we shall propose a treatment of IC ππ* → nπ* with conical intersection. This model can be commonly used to describe the CI of ππ* and nπ* electronic states of the pyrazine molecule. Near the bottom of the two potential surfaces, the two electronic states in the “diabatic” approximation are described by $\Phi_1^{\text{d}}$(nπ*) and $\Phi_2^{\text{d}}$(ππ*). The adiabatic approximation $\Phi_1^{\text{ad}}$ and $\Phi_2^{\text{ad}}$ will be employed to describe the electronic states in the CI region. Thus,

$$ \Phi_1^{\text{d}} = \cos \theta { }\Phi_1^{\text{ad}} + \sin \theta { }\Phi_2^{\text{ad}} $$

(4.34)

and

$$ \Phi_2^{\text{d}} = - \sin \theta { }\Phi_1^{\text{ad}} + \cos \theta { }\Phi_2^{\text{ad}} $$

(4.35)

The adiabatic PESs of $\Phi_1^{\text{ad}}$ and $\Phi_2^{\text{ad}}$ are given by [12]

$$ {U_1} = \frac{{\left( {{H_{11}} + {H_{22}}} \right) + {{\left[ {{{\left( {{H_{11}} - {H_{22}}} \right)}^2} + 4H_{12}^2} \right]}^{\frac{1}{2}}}}}{2} $$

(4.36)

and

$$ {U_2} = \frac{{\left( {{H_{11}} + {H_{22}}} \right) - {{\left[ {{{\left( {{H_{11}} - {H_{22}}} \right)}^2} + 4H_{12}^2} \right]}^{\frac{1}{2}}}}}{2} $$

(4.37)

where

$$ \tan 2\theta = \frac{{2{H_{12}}}}{{{H_{11}} - {H_{22}}}} $$

(4.38)

Here, the ${H_{ij}}$ ($i,j = 1,2$) are the Hamiltonian matrix elements in the diabatic representation [12]. To analyze the nonadiabatic dynamic data of pyrazine reported by Suzuki et al. [13] and to use the PESs of Domcke et al. [27], we use the dimensionless normal coordinate

$$ {Q_j} = \sqrt {{\frac{{{\omega_j}}}{\hbar }}} \sum\limits_i {{L_{ij}}M_i^{\frac{1}{2}}{q_i}} $$

(4.39)

where ${\omega_j}$ is the angular frequency of the $j{\text{th}}$ mode. ${L_{ij}}$ represents the element of eigenvector matrix of Hessian matrix. ${q_i}$ is the Cartesian coordinate, and ${M_i}$ is the corresponding nuclear mass, respectively. Apply the linear coupling approximation [12]

$$ {H_{11}} - {H_{22}} = \bar{\kappa }\left( {{Q_{\text{t}}} - {{\bar{Q}}_{\text{t}}}} \right),\quad {H_{12}} = \bar{\lambda }{Q_{\text{c}}} $$

(4.40)

where ${Q_{\text{t}}}$ and ${Q_{\text{c}}}$ denote the totally symmetric mode (i.e., an accepting mode or tuning mode), describing the displacement between the ππ* surface and nπ* surface, and the vibronic coupling mode (i.e., the promoting mode), respectively. The point $({Q_{\text{t}}},{Q_{\text{c}}}) = ({\bar{Q}_{\text{t}}},0)$ is just the crossing point of the ππ* surface and nπ* surface (i.e., ${U_1} = {U_2}$). Notice that

$$ {\left( {{H_{11}} - {H_{22}}} \right)^2} + 4H_{12}^2 = {\bar{\kappa }^2}{\left( {{Q_{\text{t}}} - {{\bar{Q}}_{\text{t}}}} \right)^2} + 4{\bar{\lambda }^2}Q_{\text{c}}^2 $$

(4.41)

At the points other than $({Q_{\text{t}}},{Q_{\text{c}}}) = ({\bar{Q}_{\text{t}}},0)$, ${U_1}$ and ${U_2}$ represent conical surfaces.

Next, we discuss the calculation of the IC rate of ππ* → nπ* transition. The IC rate for the electronic transition a → b based on the breakdown of the Born-Oppenheimer adiabatic approximation

$$ {\Psi_{av}} = \Phi_a^{\text{ad}}\Theta_{av}^{\text{ad}}{,}\quad {\Psi_{bu}} = \Phi_b^{\text{ad}}\Theta_{bu}^{\text{ad}} $$

(4.42)

can be expressed as

$$ {W_{av}} = \frac{{2\pi }}{\hbar }\sum\limits_u {{{\left| {\left\langle {\Theta_{bu}^{\text{ad}}\left| { - \sum\limits_i {\hbar {\omega_i}\left\langle {\Phi_b^{\text{ad}}\left| {\frac{\partial }{{\partial {Q_i}}}} \right|\Phi_a^{\text{ad}}} \right\rangle } } \right|\frac{{\partial \Theta_{av}^{\text{ad}}}}{{\partial {Q_i}}}} \right\rangle } \right|}^2}} D\left( {{E_{bu}} - {E_{av}}} \right) $$

(4.43)

where $D\left( {{E_{bu}} - {E_{av}}} \right)$ denotes the line-shape function. In this case, it could be the Lorentzian function:

$$ D\left( {{E_{bu}} - {E_{av}}} \right) = \frac{1}{\pi } \cdot \frac{{{\Gamma_{bu,av}}}}{{{{\left( {{E_{bu}} - {E_{av}}} \right)}^2} + \Gamma_{bu,av}^2}} $$

(4.44)

${Q_{\text{c}}}$in Eq. (4.40) and ${Q_i}$ in Eq. (4.43) represent the promoting mode (i.e., the coupling mode for the pyrazine case). Notice that

$$ \left\langle {\Phi_b^{\text{ad}}\left| {\frac{\partial }{{\partial {Q_i}}}} \right|\Phi_a^{\text{ad}}} \right\rangle = \frac{{\left\langle {\Phi_b^{\text{ad}}\left| {\frac{{\partial V}}{{\partial {Q_i}}}} \right|\Phi_a^{\text{ad}}} \right\rangle }}{{{U_a} - {U_b}}} $$

(4.45)

For the pyrazine case, the molecule is optically pumped from the ground electronic state to the diabatic state $\Phi_2^{\text{d}}$; in this case, we have

$$ \left\langle {\Phi_2^{\text{d}}\left| {\frac{\partial }{{\partial {Q_{\text{c}}}}}} \right|\Phi_1^{\text{d}}} \right\rangle = \frac{{\left\langle {\Phi_2^{\text{d}}\left| {\frac{{\partial V}}{{\partial {Q_{\text{c}}}}}} \right|\Phi_1^{\text{d}}} \right\rangle }}{{{H_{11}} - {H_{22}}}} $$

(4.46)

And to avoid the divergence of Eq. (4.46), we change the basic set from ($\Phi_2^{\text{d}}$, $\Phi_1^{\text{d}}$), the “diabatic” approximation, to ($\Phi_2^{\text{ad}}$, $\Phi_1^{\text{ad}}$), the adiabatic approximation. Substituting Eqs. 4.34 and 4.35 into 4.46 yields

$$ \left\langle {\Phi_2^{\text{d}}\left| {\frac{\partial }{{\partial {Q_{\text{c}}}}}} \right|\Phi_1^{\text{d}}} \right\rangle = \frac{{\partial \theta }}{{\partial {Q_{\text{c}}}}} + \frac{{\left\langle {\Phi_2^{\text{ad}}\left| {\frac{{\partial V}}{{\partial {Q_{\text{c}}}}}} \right|\Phi_1^{\text{ad}}} \right\rangle }}{{{U_1} - {U_2}}} $$

(4.47)

According to the Eq. (4.38),

$$ \frac{{\partial \theta }}{{\partial {Q_{\text{c}}}}} = \frac{{\bar{\lambda }{{\cos }^2}2\theta }}{{{H_{11}} - {H_{22}}}} = \frac{{\bar{\lambda }\left( {{H_{11}} - {H_{22}}} \right)}}{{{{\left( {{H_{11}} - {H_{22}}} \right)}^2} + 4H_{12}^2}} $$

(4.48)

For practical calculations, we use the following relation:

$$ \left\langle {\Phi_2^{\text{ad}}\left| {\frac{{\partial V}}{{\partial {Q_{\text{c}}}}}} \right|\Phi_1^{\text{ad}}} \right\rangle = \cos 2\theta \left\langle {\Phi_2^{\text{d}}\left| {\frac{{\partial V}}{{\partial {Q_{\text{c}}}}}} \right|\Phi_1^{\text{d}}} \right\rangle $$

(4.49)

Using the calculated ππ* and nπ* surfaces obtained by Domcke et al., we obtain

$$ \left\langle {\Phi_2^{\text{d}}\left| {\frac{\partial }{{\partial {Q_{\text{c}}}}}} \right|\Phi_1^{\text{d}}} \right\rangle = \frac{{2\bar{\lambda }\bar{\kappa }\left( {{Q_{\text{t}}} - {{\bar{Q}}_{\text{t}}}} \right)}}{{{{\bar{\kappa }}^2}{{\left( {{Q_{\text{t}}} - {{\bar{Q}}_{\text{t}}}} \right)}^2} + 4{{\bar{\lambda }}^2}Q_{\text{c}}^2}} $$

(4.50)

The surface properties of the electronic states obtained by Domcke et al. are shown in Tables 4.1 and 4.2. The gradients of the excitation energies of the S ₁ and S ₂ are coming from Ref. [12], where

$$ {\kappa_j} = {\left. {\frac{{\partial {U_j}}}{{\partial {Q_{\text{t}}}}}} \right|_0} $$

(4.51)

and

$$ \bar{\kappa } = \Delta \kappa = {\kappa_2} - {\kappa_1} $$

(4.52)

and we assume that

Table 4.1 Harmonic vibrational frequencies (in cm⁻¹) of A _g and B _1g normal modes of pyrazine in the electronic ground state from Ref. [12]

Table 4.2 Gradients of the excitation energies of the S ₁ and S ₂ states of pyrazine with respect to the totally symmetric normal coordinates defined at the reference geometry in MRCI (including the Davidson correction) method, from Ref. [12]

$$ \bar{\lambda } = \lambda = {\left. {\frac{{\partial {U_j}}}{{\partial {Q_{\text{c}}}}}} \right|_0} $$

(4.53)

Then, Huang-Rhys factor S can be obtained from the following formula:

$$ S = \frac{1}{2}{\left( {\frac{{\Delta \kappa }}{{\hbar \omega }}} \right)^2} $$

(4.54)

The vibronic coupling constant ${\lambda_{10a}}$ is set to 1,472 cm⁻¹ according to Ref. [12] in MRCI method. We then obtain the Q-dependent nonadiabatic coupling IC rate as

$$ \begin{aligned} {W_{a0}} = & \pi \hbar \omega_{\text{c}}^2\sum\limits_{{u_{\text{t}}}} {\sum\limits_{\left\{ {{u_j}} \right\}} {{{\left| {\left\langle {{\chi_{b{u_{\text{t}}}}}{\chi_{b{1_{\text{c}}}}}\left| {\frac{{\left( {{Q_{\text{t}}} - {{\bar{Q}}_{\text{t}}}} \right)}}{{{A_{\text{t}}}{{\left( {{Q_{\text{t}}} - {{\bar{Q}}_{\text{t}}}} \right)}^2} + {A_{\text{c}}}Q_{\text{c}}^2}}} \right|{\chi_{a{0_{\text{t}}}}}{\chi_{a{0_{\text{c}}}}}} \right\rangle } \right|}^2}} } { } \\ \times & \prod\limits_{j\left( { \ne {\text{t,c}}} \right)} {{{\left| {\left\langle {{{\chi_{b{u_j}}}}} \mathrel{\left | {\vphantom {{{\chi_{b{u_j}}}} {{\chi_{a{0_j}}}}}} \right. } {{{\chi_{a{0_j}}}}} \right\rangle } \right|}^2}D\left( {{E_{a0}} - {E_{bu}}} \right)} \\ \end{aligned} $$

(4.55)

where

$$ {A_{\text{t}}} \equiv \frac{{\Delta \kappa }}{{2\bar{\lambda }}},{ }{A_{\text{c}}} \equiv \frac{{2\bar{\lambda }}}{{\Delta \kappa }} $$

(4.56)

In the Condon approximation at equilibrium geometry of ground state, the Q-independent nonadiabatic coupling IC rate is

$$ {W_{a0}} = \pi \hbar \omega_{\text{c}}^2{\left| {\frac{\lambda }{{{E_{\text{Vert}}}}}} \right|^2}\sum\limits_{\left\{ {{u_j}} \right\}} {\prod\limits_{j\left( { \ne {\text{c}}} \right)} {{{\left| {\left\langle {{{\chi_{b{u_j}}}}} \mathrel{\left | {\vphantom {{{\chi_{b{u_j}}}} {{\chi_{a{0_j}}}}}} \right. } {{{\chi_{a{0_j}}}}} \right\rangle } \right|}^2}\delta \left( {{E_{a0}} - {E_{bu}}} \right)} } $$

(4.57)

Next, we define the ${I_{{u_{\text{t}}}}}$ and $I_{{u_{\text{t}}}}^{\text{CI}}$ to compare the difference between the Franck-Condon factor without and with conical intersection:

$$ {I_{{u_{\text{t}}}}} \equiv {\left| {\left\langle {{{\chi_{b{u_{\text{t}}}}}}} \mathrel{\left | {\vphantom {{{\chi_{b{u_{\text{t}}}}}} {{\chi_{a{0_{\text{t}}}}}}}} \right. } {{{\chi_{a{0_{\text{t}}}}}}} \right\rangle } \right|^2} $$

(4.58)

$$ I_{{u_{\text{t}}}}^{\text{CI}} \equiv {\left| {\frac{{{E_{\text{Vert}}}}}{\lambda }\left\langle {{\chi_{b{u_{\text{t}}}}}{\chi_{b{1_{\text{c}}}}}\left| {\frac{{\left( {{Q_{\text{t}}} - {{\bar{Q}}_{\text{t}}}} \right)}}{{{A_{\text{t}}}{{\left( {{Q_{\text{t}}} - {{\bar{Q}}_{\text{t}}}} \right)}^2} + {A_{\text{c}}}Q_{\text{c}}^2}}} \right|{\chi_{a{0_{\text{t}}}}}{\chi_{a{1_{\text{c}}}}}} \right\rangle } \right|^2} $$

(4.59)

It should be noted that the IC lifetime should depend on the line-shape function (see 4.43). The formula (4.59) is calculated numerically. The nonradiative lifetime versus broadening Γ has been plotted in Fig. 4.7. The vertical excited energy changes from 0.50 to 1.00 eV. In Fig. 4.7, it shows that when the vertical excited energies are 0.50 or 0.70 eV, and when the broadening parameter Γ tends to 0, the lifetime tends to about 50 fs. From Fig. 4.7, we can see that the nonadiabatic transition rates depend on Γ and the energy gap.

Fig. 4.7

Lifetimes of S ₂ state of pyrazine versus broadening parameter Γ, with equal different vertical excitation energy from 0.50 to 1.00 eV

The main purpose of using the dynamics of the ππ* → nπ* transition of pyrazine as an example is to show how to treat the effect of CI on IC. Suzuki et al. have employed the 22-fs laser pulse for pumping in their studies of the ππ* → nπ* dynamics of pyrazine. In this case, the dynamics of both population and coherence should be considered. Using the notations of bu and av to describe the vibronic states of ππ* and nπ*, we obtain

$$ \frac{{{\text{d}}{\rho_{bu,bu^\prime}}}}{{{\text{d}}t}} = - \left( {i{\omega_{bu,bu^\prime}} + \Gamma_{bu,bu^\prime}^{bu,bu^\prime}} \right){\rho_{bu,bu^\prime}} - \frac{i}{\hbar }{\left[ {\hat{V}(t),\hat{\rho }} \right]_{bu,bu^\prime}} - \frac{i}{\hbar }{\left[ {{{\hat{H}}_{{{s^\prime}}}}(t),\hat{\rho }} \right]_{bu,bu^\prime}} $$

(4.60)

for the coherence, and

$$ \frac{{{\text{d}}{\rho_{bu,bu}}}}{{{\text{d}}t}} = - \frac{i}{\hbar }{\left[ {\hat{V}(t),\hat{\rho }} \right]_{bu,bu}} - \frac{i}{\hbar }{\left[ {{{\hat{H}}_{{{s^\prime}}}}(t),\hat{\rho }} \right]_{bu,bu}} $$

(4.61)

for the population. ${\hat{H}_{{{s^\prime}}}}$ describes the dynamics of IC, and $\hat{V}(t)$ describes the pumping process. In the pyrazine case, since its lifetime is also 22 fs, both pumping and decay should be considered simultaneously.

From the discussion of the fs pump-probe experiments, when the fs laser pulse is used for pumping, from the uncertainty principle ΔωΔt ∼ 1, one can expect that when the pulse duration of Δt is employed, the coherence corresponding to $\Delta \omega \sim 1/\Delta t$ will be created, and the corresponding quantum beat will be observed. This can indeed be seen from Fig. 4.5 for the pyrazine case. In this case, $\Delta \omega \sim 560{\text{ c}}{{\text{m}}^{ - 1}}$ is corresponding to the mode ${v_{6a}}$, which has the largest Huang-Rhys factor and can be most effectively pumped.

For the analysis of the ππ* → nπ* dynamics, the potential surfaces of Domcke et al. have been commonly used (including Suzuki et al.). However, recently, we have shown that their surfaces are imperfect because in pyrazine there are two nπ* states, but Domcke et al. have only considered one nπ* surface. Recently, we have calculated the location of the second nπ* state and its effect on the spectra of pyrazine [28].

The purpose of Fig. 4.7 is to show the effect of electronic energy gap and dephasing (or damping) constant on the nonadiabatic transition rate by using the surface of Domcke et al.

The dephasing (or damping) constants involved in the nonadiabatic processes like IC of ππ* → nπ* of pyrazine are mainly due to vibrational relaxation and dephasing of the nπ* state (see Eq. 4.44).

5 Vibrational Relaxation

In this section, we shall propose to the intramolecular vibrational relaxation. We shall first describe the problem associated with the harmonic approximation of molecular vibration. In the harmonic oscillator approximation, we have

$$ T = \sum\limits_i {\frac{1}{2}\dot{Q}_i^2}, \quad U = \sum\limits_i {\frac{1}{2}\omega_i^2Q_i^2}, \quad E = T + U $$

(4.62)

and

$$ \frac{{{\text{d}}E}}{{{\text{d}}t}} = \sum\limits_i {{{\dot{Q}}_i}\left( {{{\ddot{Q}}_i} + \omega_i^2{Q_i}} \right)} = 0 $$

(4.63)

This indicates that the energy conservation holds for each individual mode. That is, energy exchange between different normal modes is impossible. Taking the anharmonic coupling into account, the anharmonic potential-energy function can be expressed as

$$ U = \sum\limits_i {\frac{1}{{2!}}{{\left( {\frac{{{\partial^2}U}}{{\partial Q_i^2}}} \right)}_0}Q_i^2} + \sum\limits_{ijk} {\frac{1}{{3!}}{{\left( {\frac{{{\partial^3}U}}{{\partial {Q_i}\partial {Q_j}\partial {Q_k}}}} \right)}_0}{Q_i}{Q_j}{Q_k}} + \cdots $$

(4.64)

Cross terms can lead to energy flow from one mode to another.

Recently, developments in quantum chemical calculations have made it possible to perform the calculations of the potential surfaces expressed in the form of Eq. (4.64) for polyatomic PESs [10]. The anharmonic potential can modify the energy level spacing, produce a maximum quantum number for a vibrational mode, and introduce mode-mode coupling. These make the IR spectra exhibit not only fundamental transition bands but also overtone and combination bands, side bands, and often new bands.

Next, we consider the solution of the Schrödinger equation of vibrational motion with the anharmonic PESs

$$ \hat{H}\Psi = E\Psi $$

(4.65)

where $\hat{H}$ is the molecular Hamiltonian, and

$$ \hat{H} = \hat{T} + U $$

(4.66)

Two methods will be presented in this chapter, the self-consistent field (SCF) method and the adiabatic approximation method [29–31]; for demonstration, we shall apply these methods to the example

$$ \hat{H} = - \frac{1}{2}\frac{{{\partial^2}U}}{{\partial Q_i^2}} + \frac{1}{2}\omega_i^2Q_i^2 - \frac{1}{2}\frac{{{\partial^2}U}}{{\partial q_\alpha^2}} + \frac{1}{2}\omega_\alpha^2q_\alpha^2 + V\left( {{Q_i},{q_\alpha }} \right) $$

(4.67)

where

$$ V\left( {{Q_i},{q_\alpha }} \right) = \lambda \left( {Q_i^2{q_\alpha } + \eta q_\alpha^3} \right) $$

(4.68)

We shall first consider the SCF method. Notice that

$$ \Psi = {\varphi_\alpha }({q_\alpha }){\varphi_i}({Q_i}) $$

(4.69)

$$ W = \frac{{\left\langle {\Psi \left| {\hat{H}} \right|\Psi } \right\rangle }}{{\left\langle {\Psi } \mathrel{\left | {\vphantom {\Psi \Psi }} \right. } {\Psi } \right\rangle }} $$

(4.70)

$$ \left\langle {\Psi } \mathrel{\left | {\vphantom {\Psi \Psi }} \right. } {\Psi } \right\rangle = 1,\quad \left\langle {{{\varphi_\alpha }}} \mathrel{\left | {\vphantom {{{\varphi_\alpha }} {{\varphi_\alpha }}}} \right. } {{{\varphi_\alpha }}} \right\rangle = 1,\quad \left\langle {{{\varphi_i}}} \mathrel{\left | {\vphantom {{{\varphi_i}} {{\varphi_i}}}} \right. } {{{\varphi_i}}} \right\rangle = {1} $$

(4.71)

According to the variational method, we have

$$ \hat{H} = {\hat{H}_\alpha } + {\hat{H}_i} + V({q_\alpha },{Q_i}) $$

(4.72)

$$ {\hat{H}_\alpha } = {\hat{T}_\alpha } + \frac{1}{2}\omega_\alpha^2q_\alpha^2 $$

(4.73)

$$ {\hat{H}_i} = {\hat{T}_i} + \frac{1}{2}\omega_i^2Q_i^2 $$

(4.74)

$$ W^\prime = \left\langle {\Psi \left| {\hat{H}} \right|\Psi } \right\rangle + {\varepsilon_\alpha }\left( {1 - \left\langle {{\varphi_\alpha }\left| {{\varphi_\alpha }} \right.} \right\rangle } \right) + {\varepsilon_i}\left( {1 - \left\langle {{\varphi_i}\left| {{\varphi_i}} \right.} \right\rangle } \right) $$

(4.75)

and

$$ \begin{aligned} \delta W^\prime = & \left\langle {\delta {\varphi_\alpha }\left| {{{\hat{H}}_\alpha } + {E_i} + \left\langle {{\varphi_i}\left| {V\left( {{q_\alpha },{Q_i}} \right)} \right|{\varphi_i}} \right\rangle } \right|{\varphi_\alpha }} \right\rangle \\ + & \left\langle {\delta {\varphi_i}\left| {{{\hat{H}}_i} + {E_\alpha } + \left\langle {{\varphi_\alpha }\left| {V\left( {{Q_\alpha },{q_i}} \right)} \right|{\varphi_\alpha }} \right\rangle } \right|{\varphi_i}} \right\rangle \\ + & {\varepsilon_\alpha }\left( { - \left\langle {\delta {\varphi_\alpha }\left| {{\varphi_\alpha }} \right.} \right\rangle } \right) + {\varepsilon_i}\left( { - \left\langle {{\varphi_i}\left| {{\varphi_i}} \right.} \right\rangle } \right) + {\text{c}}{\text{.c}}{.} \\ = & 0 \\ \end{aligned} $$

(4.76)

where

$$ {E_i} = \left\langle {{\varphi_i}\left| {{{\hat{H}}_i}} \right|{\varphi_i}} \right\rangle {,}\quad {E_\alpha } = \left\langle {{\varphi_\alpha }\left| {{{\hat{H}}_\alpha }} \right|{\varphi_\alpha }} \right\rangle $$

(4.77)

From Eq. (4.76), we obtain

$$ \left( {{{\hat{H}}_\alpha } + {E_i} + \left\langle {{\varphi_i}\left| V \right|{\varphi_i}} \right\rangle } \right){\varphi_\alpha } = {\varepsilon_\alpha }{\varphi_\alpha } $$

(4.78)

and

$$ \left( {{{\hat{H}}_i} + {E_\alpha } + \left\langle {{\varphi_\alpha }\left| V \right|{\varphi_\alpha }} \right\rangle } \right){\varphi_i} = {\varepsilon_i}{\varphi_i} $$

(4.79)

Equations (4.78) and (4.79) have to be solved in the SCF manner.

Next, we consider the adiabatic approximation model, which is similar to the Born-Oppenheimer approximation model for molecules, that is, electronic motion corresponding to ${Q_i}$, nuclear motion corresponding to {${q_\alpha }$}, UV-visible spectra corresponding to IR vibrational spectra, and IC corresponding to vibrational relaxation. It follows that to solve

$$ \hat{H}{\Psi_{av}}(Q,q) = {E_{av}}{\Psi_{av}}(Q,q) $$

(4.80)

where

$$ \hat{H} = {\hat{T}_Q} + {\hat{T}_q} + V = {\hat{T}_q} + {\hat{H}_Q} $$

(4.81)

we first solve

$$ {\hat{H}_Q}{\Phi_a}(Q;q) = {U_a}(q){\Phi_a}(Q;q) $$

(4.82)

and then solve

$$ \left[ {{{\hat{T}}_q} + {U_a}(q)} \right]{\Theta_{av}}(q) = {E_{av}}{\Theta_{av}}(q) $$

(4.83)

and

$$ {\Psi_{av}}(Q,q) = {\Phi_a}(Q;q){\Theta_{av}}(q) $$

(4.84)

Here, semicolon means that q is regarded as parameter in ${\Phi_a}(Q;q)$. Numerical results for this model are shown in Table 4.3 [31]. The performance for these cases for the adiabatic approximation is acceptable.

Table 4.3 Comparison of uncoupled harmonic oscillator (HO), exact quantum (EQ) [32–35], semiclassical (SC) [34], self-consistent field (SCF) [30], adiabatic approximation (AA), and NA eigenvalues

Next we consider the general case with adiabatic approximation

$$ \hat{H} = {\hat{T}_Q} + {\hat{T}_q} + V(q,Q) $$

(4.85)

$$ {\hat{T}_Q} = - \sum\limits_n {\frac{{{\hbar^2}}}{2}} \frac{{{\partial^2}}}{{\partial Q_n^2}} $$

(4.86)

$$ {\hat{T}_q} = - \sum\limits_i {\frac{{{\hbar^2}}}{2}} \frac{{{\partial^2}}}{{\partial q_i^2}} $$

(4.87)

$$ V(Q,q) = {V_{\text{H}}}(Q) + {V_{\text{L}}}(q) + {V_{{\rm int} }}(Q,q) $$

(4.88)

$$ {V_{\text{H}}}(Q) = \sum\limits_{\text{I}} {\frac{1}{2}} \omega_{\text{I}}^2Q_{\text{I}}^2 + \sum\limits_{\text{IJK}} {{{\bar{V}}_{\text{IJK}}}{Q_{\text{I}}}{Q_{\text{J}}}{Q_{\text{K}}}} + \sum\limits_{\text{IJKL}} {{{\bar{V}}_{\text{IJKL}}}{Q_{\text{I}}}{Q_{\text{J}}}{Q_{\text{K}}}{Q_{\text{L}}}} + \cdots $$

(4.89)

$$ {V_{\text{L}}}(q) = \sum\limits_i {\frac{1}{2}} \omega_i^2q_i^2 + \sum\limits_{ijk} {{{\bar{V}}_{ijk}}{q_i}{q_j}{q_k}} + \sum\limits_{ijkl} {{{\bar{V}}_{ijkl}}{q_i}{q_j}{q_k}{q_l}} + \cdots $$

(4.90)

$$ \begin{aligned} {V_{{\rm int} }}\left( {Q,q} \right) = & \sum\limits_{{\text{IJ}}i} {{{\bar{V}}_{{\text{IJ}}i}}{Q_{\text{I}}}{Q_{\text{J}}}{q_i}} + \sum\limits_{{\text{I}}ij} {{{\bar{V}}_{{\text{I}}ij}}{Q_{\text{I}}}{q_i}{q_j}} + \sum\limits_{{\text{I}}ijk} {{{\bar{V}}_{{\text{I}}ijk}}{Q_{\text{I}}}{q_i}{q_j}{q_k}} \\ + & \sum\limits_{{\text{IJ}}ij} {{{\bar{V}}_{{\text{IJ}}ij}}{Q_{\text{I}}}{Q_{\text{J}}}{q_i}{q_j}} + \sum\limits_{{\text{IJK}}i} {{{\bar{V}}_{{\text{IJK}}i}}{Q_{\text{I}}}{Q_{\text{J}}}{Q_{\text{K}}}{q_i}} + \cdots \\ \end{aligned} $$

(4.91)

where $\bar{V}$ are the anharmonic expansion coefficients of the PES. In Eq. (4.91), for example,

$$ {V_{{\text{IJ}}i}} \equiv {\left( {\frac{{{\partial^3}V}}{{\partial {Q_{\text{I}}}\partial {Q_{\text{J}}}\partial {q_i}}}} \right)_0} $$

(4.92)

$$ {\bar{V}_{{\text{IJ}}i}} \equiv \frac{1}{{3!}}{V_{{\text{IJ}}i}} $$

(4.93)

Vibrational IR spectra can be then calculated according to

$$ \alpha \left( \omega \right) = \frac{{4{\pi^2}\omega }}{{3\hbar c}}\sum\limits_{vn} {\sum\limits_{v^\prime n^\prime} {{P_{vn}}{{\left| {\left\langle {{\Psi_{v^\prime n^\prime}}(Q;q)\left| {{{\vec{\mu }}_{aa}}} \right|{\Psi_{vn}}(Q;q)} \right\rangle } \right|}^2}} } D({\omega_{v^\prime n^\prime,vn}} - \omega ){ } $$

(4.94)

where

$$ {\vec{\mu }_{aa}} = {\vec{\mu }_{aa}}(0) + \sum\limits_i {{{\left( {\frac{{\partial {{\vec{\mu }}_{aa}}}}{{\partial {Q_i}}}} \right)}_0}{Q_i} + \cdots } $$

(4.95)

and P _vn denotes the Boltzmann distribution function. Fundamental, overtone, combination, and side bands based on the adiabatic approximation method can then be calculated.

In the B-O approximation, the IC a → b can be expressed as

$$ {W_i} = \frac{{2\pi }}{\hbar }\sum\limits_u {\sum\limits_v {{P_{av}}} } {\left| {\left\langle {{\Theta_{bu}}\left| { - {\hbar^2}\left\langle {{\Phi_b}\left| {\frac{\partial }{{\partial {Q_i}}}} \right|{\Phi_a}} \right\rangle } \right|\frac{{\partial {\Theta_{av}}}}{{\partial {Q_i}}}} \right\rangle } \right|^2}D({E_{av}} - {E_{bu}}) $$

(4.96)

$$ W = \sum\limits_i {{W_i}} $$

(4.97)

$$ \left\langle {{\Phi_b}\left| {\frac{\partial }{{\partial {Q_i}}}} \right|{\Phi_a}} \right\rangle = {{\left\langle {{\Phi_b}\left| {\frac{{\partial V}}{{\partial {Q_i}}}} \right|{\Phi_a}} \right\rangle } \mathord{\left/{\vphantom {{\left\langle {{\Phi_b}\left| {\frac{{\partial V}}{{\partial {Q_i}}}} \right|{\Phi_a}} \right\rangle } {\left[ {{U_a}(Q) - {U_b}(Q)} \right]}}} \right.} {\left[ {{U_a}(Q) - {U_b}(Q)} \right]}} $$

(4.98)

For vibrational relaxation in the adiabatic approximation, the above equation can be used by changing (a, b) into the vibrational quantum numbers of high-frequency modes and by changing (u, v) into the quantum numbers of low-frequency modes. For example, the coupling becomes

$$ \frac{{\partial V}}{{\partial {q_k}}} = 6\sum\limits_l {{{\bar{V}}_{{\text{I}}lk}}} {Q_{\text{I}}}{q_l} + \cdots = \sum\limits_l {{V_{{\text{I}}lk}}} {Q_{\text{I}}}{q_l} + \cdots $$

(4.99)

We consider the relaxation of ${Q_{\text{I}}}$ mode. Notice that {${q_l}$} consist of the promoting modes and the accepting modes. The displacement of low-frequency mode ${q_j}$ comes from the anharmonic coupling term ${\bar{V}_{{\text{II}}j}}$ in first-order perturbation theory

$$ {U_{{N_{\text{I}}}}}({q_j}) = \frac{1}{2}\omega_j^2q_j^2 + \left\langle {{N_{\text{I}}}\left| {3{{\bar{V}}_{{\text{II}}j}}Q_{\text{I}}^2{q_j}} \right|{N_{\text{I}}}} \right\rangle \equiv \frac{1}{2}\omega_j^2{\left[ {{q_j} + {d_j}({N_{\text{I}}})} \right]^2} + \cdots $$

(4.100)

where

$$ {d_{nj}}({N_{\text{I}}}) = \frac{{3{{\bar{V}}_{{\text{II}}j}}({N_{\text{I}}} + (\frac{1}{2}))\hbar }}{{\omega_j^2{\omega_{\text{I}}}}} $$

(4.101)

represents the displacement of mode j for the specific vibrational state $\left| {{N_{\text{I}}}} \right\rangle$ of high-frequency mode. Then, we define the displacement between $\left| {{1_{\text{I}}}} \right\rangle$ and $\left| {{0_{\text{I}}}} \right\rangle$ as

$$ \Delta {d_{{\text{I}}j}} \equiv {d_{{\text{I}}j}}(1) - {d_{{\text{I}}j}}(0) = \frac{{3{{\bar{V}}_{{\text{II}}j}}\hbar }}{{\omega_j^2{\omega_{\text{I}}}}} $$

(4.102)

and the corresponding Huang-Rhys factor is

$$ {S_{{\text{I}}j}} = \frac{{{\omega_{\text{I}}}}}{{2\hbar }}\Delta d_{{\text{I}}j}^2 $$

(4.103)

Similar to IC, the vibrational relaxation rate formula can be expressed as

$$ W_{{\text{I}}lk}^0 = \frac{{\omega_l^2}}{4}R_{{\text{I}}lk}^2\int_{ - \infty }^\infty {{\text{d}}t\exp \left\{ {it\left( {{\omega_{\text{I}}} - {\omega_l} - {\omega_k}} \right) - \sum\limits_{j( \ne l,k)} {{S_{{\text{I}}j}}(1 - {{\text{e}}^{ - it{\omega_j}}})} } \right\}} $$

(4.104)

and the total decay rate is given by

$$ W_{\text{I}}^0 = \sum\limits_{l \leqslant k} {W_{{\text{I}}lk}^0} $$

(4.105)

where

$$ {R_{{\text{I}}lk}} = \frac{{{V_{{\text{I}}lk}}}}{{\hbar {\omega_{\text{I}}}}} $$

(4.106)

and

$$ {V_{{\text{I}}lk}} = \frac{{{\partial^3}V}}{{\partial {Q_{\text{I}}}\partial {q_l}\partial {q_k}}}\sqrt {{\frac{{{\hbar^3}}}{{{\omega_{\text{I}}}{\omega_l}{\omega_k}}}}} $$

(4.107)

5.1 Vibrational Relaxation of Water Dimer

As an example to apply the adiabatic approximation theory of vibrational relaxation, the hydrogen-bonded water dimer (H₂O)₂ will be studied in this work. The structure of (H₂O)₂ was optimized using Gaussian 09 program [36] with DFT method and CAM-B3LYP/6-311++g(d,p) long-range corrected version of B3LYP functional. The optimized structure is shown in Fig. 4.8.

Fig. 4.8

Structure of water dimer, calculated in Gaussian 09, DFT/CAM-B3LYP/6-311++g(d,p) long-range corrected version of B3LYP functional

The point group of water dimer is C _S . There are eight symmetric modes and four antisymmetric modes. The frequencies have been listed in Table 4.4.

Table 4.4 The symmetries and harmonic frequencies of water dimer

Employing Eq. (4.103), Huang-Rhys factors ${S_{{\text{I}}j}}$can be calculated and listed in Table 4.5. The Huang-Rhys factor is related with mode displacement in Eq. (4.101), which is determined by the anharmonic expansion coefficient ${V_{{\text{II}}j}}$. I and j are the indexes of high-frequency mode and low-frequency mode, respectively. According to group theory, ${V_{{\text{II}}j}}$ with antisymmetric low-frequency mode j is vanished. This means that only symmetric low-frequency mode can contribute to the Huang-Rhys factor, which can be obviously observed in Table 4.5.

Table 4.5 Huang-Rhys factors of water dimer in adiabatic approximation

Overall vibrational relaxation rates for modes 7–12 are calculated according to Eq. (4.105) and listed in Table 4.6, while detailed vibrational relaxation rates are listed in Table 4.7. From these tables, we can see that the fastest vibrational relaxation rate is 1.93 × 10¹⁰ s⁻¹ for the mode 9. The rates are consistent with the experimental data of Miller et al. [37], estimating from the spectral bandwidth. An important feature is that the detailed relaxation rates like ${W_{11,8,8}}$, ${W_{11,7,7}}$, ${W_{10,8,8}}$, ${W_{10,7,7}}$,${W_{9,8,8}}$, ${W_{9,7,7}}$, ${W_{8,6,6}}$, and ${W_{7,6,6}}$ play important roles in the vibrational relaxation of (H₂O)₂.

Table 4.6 The overall vibrational relaxation rate

Table 4.7 Vibrational relaxation paths. ${\hbox{Accepting energy}} = {\omega_n} - {\omega_l} - {\omega_k}$

Another vibrational energy flow pathway is due to the vibrational energy transfer through the dipole-dipole interaction:

$$ \left\langle {{\Phi_b}\left| {\hat{H}^\prime\left| {{\Phi_a}} \right.} \right.} \right\rangle = \left\langle {{\Phi_b}\left| {\frac{1}{{R_{{D_1}{D_2}}^3}}\left[ {{{\vec{\mu }^\prime}_{{D_1}}} \cdot {{\vec{\mu }^\prime}_{{D_2}}} - \frac{{3\left( {{{\vec{\mu }^\prime}_{{D_1}}} \cdot {{\vec{R}}_{{D_1}{D_2}}}} \right)\left( {{{\vec{\mu }^\prime}_{{D_2}}} \cdot {{\vec{R}}_{{D_1}{D_2}}}} \right)}}{{\vec{R}_{{D_1}{D_2}}^2}}} \right]} \right|{\Phi_a}} \right\rangle\\ $$

(4.108)

where

$$ {\vec{\mu }^\prime_{{D_1}}} \equiv {\left( {\frac{{\partial {{\vec{\mu }}_{{D_1}}}}}{{\partial {Q_8}}}} \right)_0};{ }{\vec{\mu }^\prime_{{D_2}}} \equiv {\left( {\frac{{\partial {{\vec{\mu }}_{{D_2}}}}}{{\partial {Q_7}}}} \right)_0} $$

(4.109)

for example.

It should be noted that our attempt to calculate vibrational relaxation for clusters and complex systems should be regarded as a preliminary attempt because the anharmonic potential function, themselves, are approximate and their performance should be carefully examined by calculating IR spectra in addition to vibrational relaxation.

5.2 Intramolecular Vibrational Relaxation of Aniline

IVR is one of the most important dynamics of the vibrationally excited polyatomic molecules. In most cases, IVR is the first dynamical step prior to chemical reactions [6, 38, 39]. The IVR of the NH₂ symmetric and antisymmetric stretching vibrations of jet-cooled aniline has been investigated by picosecond time-resolved IR-UV pump-probe spectroscopy [40, 41]. Aniline has two NH₂ stretching modes (see Fig. 4.9): symmetric stretching vibration (v _s) with the frequency of 3,423 cm⁻¹ and antisymmetric stretch (v _a) with 3,509 cm⁻¹ [42]. In the picosecond pump-probe experiment, the IVR of the NH₂ stretch is described by two-step tier model as shown in Fig. 4.10. The symmetric or antisymmetric stretching mode is initially excited to the vibrational excited state. In the first step, the energy flows into the doorway states [43, 44]. Then in the second step, the energy is further redistributed to dense base states. By fitting the transient (1 + 1) REMPI spectra of aniline, the IVR rates of NH₂ symmetric and antisymmetric stretching vibrations are summarized as follows [41]:

Fig. 4.9

IR spectra of aniline in a supersonic beam from Ref. [41]. The upper trace was obtained by IR-UV double-resonance spectroscopy with the use of the nanosecond laser system. The inset shows the expanded spectrum in the CH stretch region. The lower trace is the ionization gain IR spectrum obtained with the picosecond laser system (Reprinted with permission from Ref. [41]. Copyright (2005), American Institute of Physics)

Fig. 4.10

The two-step tier model of IVR from Ref. [41]. V _anh1 and V _anh2 indicate the anharmonic coupling matrix elements in each step, and k ₁ and k ₂ are the rate constants (Reprinted with permission from Ref. [41]. Copyright (2005), American Institute of Physics)

• 1. v _s (3,423 cm⁻¹) : k ₁ = 5.6 × 10¹⁰ s⁻¹, and k ₂ = (0.1–5) × 10¹⁰ s⁻¹

• 2. v _a (3,509 cm⁻¹) : k ₁ = 2.9 × 10¹⁰ s⁻¹, and k ₂ = (0.1–2) × 10¹⁰ s⁻¹

In this chapter, we calculate the IVR rates of NH₂ symmetric and antisymmetric stretching vibrations of aniline and compare the results with the first vibrational state k ₁.

The structure of aniline was optimized using Gaussian 09 program [36] with DFT method and B3LYP/6-311++g(d,p). The optimized structure is shown in Fig. 4.11. Tables 4.8 and 4.9 list the vibrational relaxation paths for symmetric and antisymmetric stretching vibrational modes, which IVR rates are larger than 1 × 10⁹ s⁻¹. The theoretical results of IVR rates, v _s = 10.11 × 10¹⁰ s⁻¹ and v _a = 1.59 × 10¹⁰ s⁻¹, are as the same orders of magnitude as the experimental values. It also shows that the IVR rate of symmetric mode is larger than that of antisymmetric mode. Due to selection rule, the NH₂ scissoring and C–C stretching symmetric modes 28 and 29 can accept relaxation energy from symmetric mode 35 at the same time. This makes that the accepting energy for symmetric mode 35 be smaller than that for antisymmetric mode 36 and then enhances the IVR rate according to energy gap law. It should be noted that, in Yamada’s work [41], it is thought that the doorway states consist of the CH stretching modes because the deuterium substitution of the CH group significantly reduces the IVR rate constant of the first step. However, the theoretical study shows that modes 28 and 29 may be the doorway states in this study. Considering the cubic anharmonic coupling (see Eq. 4.99) between NH₂ stretching modes and CH stretching modes, the CH stretching modes may also be the doorway states.

Fig. 4.11

Structure of aniline, calculated in Gaussian 09, DFT/B3LYP/6-311++g(d,p)

Table 4.8 Vibrational relaxation paths for symmetric stretching mode of NH₂ (mode 35)

Table 4.9 Vibrational relaxation paths for antisymmetric stretching mode of NH₂ (mode 36)

The main reason for choosing the treatment of vibrational relaxation of (H₂O)₂ and C₆H₅NH₂ is to show that the quantum chemistry programs can now provide the anharmonic vibrational potentials so that the first-principle calculation of vibrational relaxation has become possible. Their dynamical behaviors may be described by the density matrix method through the Bixon-Jortner model (see Sect. 4.3).

6 Discussion

The aim of this chapter is to show how to apply the density matrix method for ultrafast dynamics of the systems and fs time-resolved experiment, such as pump probes, and to show the applications. Two important examples, the effect of CI on the IC ππ* → nπ* of pyrazine and intramolecular vibrational relaxation of water dimer and aniline, are presented. This chapter consists of five parts. The first part is the general introduction to the purpose and contents of this chapter. The second part concerns with the derivation of the general master equation resulted from the reduced density matrix. The third part is an application of the density matrix method to study the dynamical behavior of the system. We have solved the master equation for a system state coupled with a group of bath states and shown the condition of nonexponential decay. We have shown that the density matrix method can treat a whole experiment including pump and probe processes. We are concerned with the use of fs pump-probe experiment to study fs nonadiabatic processes. In other words, the density matrix method can describe not only the fs pump-probe experiments but also the fs processes. A distinct feature in this case is that due to the use of fs time-resolved laser for pumping, both population and coherence excitations are created and hence their dynamics have to be treated. Since the diagonal elements of the density matrix can provide the time-dependent information of the population of the system and the off-diagonal elements of the density matrix can provide the time-dependent information of coherence (or phase) of the system, the density matrix method is an ideal method for treating ultrafast dynamical processes.

In the fourth part, we study the effect of CI on IC. It was applied to study the ππ* → nπ* transition of the pyrazine molecule. In this nonadiabatic process, the CI of the ππ* and nπ* PESs is believed to play a major role in the nonadiabatic fs transition. In fact, the CI has been widely proposed to play the key factor in an IC, and quantum trajectory calculations have been used to calculate the IC rates [45]. However, this method cannot properly take into account of the initial conditions of the population and coherence of the system created by the fs pumping laser. In this chapter, we propose to develop a method to calculate the IC with conical intersections. It should be known that for the IC between S ₁ and S ₀ in most molecules (in these cases, the energy gap between S ₁ and S ₀ is of several eV), the surface crossings do not take place due to the anharmonic effect in the two PESs. Thus, the CI should not play any role in these cases. We have proposed one method to calculate the IC rate of ππ* → nπ* of the pyrazine molecule. The experimental measurement of its ππ* state lifetime is determined to be ~22 fs. In their determination of this lifetime, Suzuki et al. [13] have employed the calculated potential surfaces obtained by Domcke et al. It should be noted that in pyrazine, there should exist two nπ* states [28]. But they only include one nπ* state in their treatments of nonadiabatic processes. The work in progress is to calculate the lifetime of ππ* by using the new set of PESs of pyrazine.

In the fifth part of this chapter, we reported our theoretical studies of vibrational relaxation, which can be applied to that in isolated molecules, molecular cluster, and dense media. In other words, the type of vibrational relaxation studied in this chapter is mainly due to anharmonic couplings among different vibrational modes. This type of potential surfaces has become available in recent quantum chemistry programs. Although theories of vibrational relaxation have been proposed, its numerical calculations have only become possible recently. The vibrational relaxation under consideration depending on the size of the system takes place in the time range of sub-picoseconds to picoseconds. In this chapter, we have chosen the water dimer (H₂O)₂ as the system for investigation. The PES includes the harmonic and cubic anharmonic contributions. In this case, the vibrational relaxation will be similar to IC. That is, in our treatment of vibrational relaxation, we will also have “promoting” modes and “accepting” modes; it follows that there are usually several paths of vibrational relaxation. In the case of (H₂O)₂, the fastest vibrational relaxation rate is of order 10² ps.

Another system aniline C₆H₅NH₂ has also been studied. We found that the vibrational relaxation rates of symmetric and antisymmetric stretching modes of NH₂ take in the ps range in good agreement with experiment.

In this chapter, we only apply the first-order perturbation theory to the adiabatic approximation to deal with the vibrational relaxation process. This will be improved in the next step.