Novel Ultrasound Imaging Applications

Abstract

Routine applications of ultrasound imaging combine array technology and beamforming (BF) algorithms for image formation. Although BF is very robust, it discards a significant proportion of the information encoded in ultrasonic signals. Therefore, BF can reconstruct some of the geometrical features of an object but with limited resolution due to the diffraction limit. Inverse scattering theory offers an alternative approach to BF imaging that has the potential to break the diffraction limit and extract quantitative information about the mechanical properties of the object. High-resolution, quantitative imaging is central to modern diagnostic technology to achieve cost-effective detection through high sensitivity and limited false positive rate. This chapter lays out a framework encompassing theoretical and experimental results, and in which inverse scattering and modern array technology can be combined together to achieve super-resolution, quantitative imaging.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

5.1 Introduction

Whether the aim is to detect a cancer mass in the human body, a precursor of damage in a metal, or to monitor CO₂ sequestration in an oil reservoir, the complexity of the host medium can result in a very challenging process. As an example, the different spatial scales that characterize the structure of the human body from molecular to organ system level and which in turn determine life functions, result in an extraordinarily complex system where discriminating between a state of disease, especially at an early stage, and normal function, poses a fundamental challenge.

The extent of the detection challenge is better understood by considering the final stage of the detection process when the diagnosis is formulated. In this context, the most basic form of detection is based on the analysis of signals such as the one shown in the diagram in Fig. 5.1(a). To illustrate the underpinning principles we consider the problem of damage detection in NDE although similar observations apply to other fields. This signal contains a signature that is related to the presence of damage and some nuisance signatures that do not bear any direct relationship to damage and arise from the complexity of the host medium. Here, we refer to the nuisance signatures as noise. The key challenge in diagnostics is to decide whether a particular signature is due to noise or to the feature of interest. For this purpose an inspector sets a threshold level, Fig. 5.1(b), and decides that damage is present if somewhere in the signal the amplitude of one of the signatures rises above the threshold. Since the choice of the threshold level is somehow arbitrary, this approach is reliable only if the amplitude of the signature from damage is larger than the amplitude of noise, i.e. the signal to noise ratio (SNR) is high. In fact, if the damage is smaller in size, the amplitude of its signature can drop below the threshold and the flaw would go undetected. To detect the smaller flaw it is then necessary to lower the threshold, Fig. 5.1(c); however, now also noise intersects the threshold level leading to a false positive when damage is not present, Fig. 5.1(d).

Fig. 5.1

The detection problem. (a) A signal contains signatures due to noise and features of interest; (b) to differentiate between noise and features a detection threshold is introduced; (c) lowering the threshold enables the detection of smaller features (d) but leads to false positives; (e) typical trends of probability of detection (POD) and false positives (PFP) as a function of feature size

The tradeoff between the detection of weak signatures, hence small features, and the occurrence of false positives is very important when assessing the cost-effectiveness of a diagnostic technology. In particular, the cost associated with false positives can be far more important than the direct cost of the diagnostic test. For instance, x-ray based mammography is the gold standard for breast cancer detection. However, it is known that in dense breast it leads to a 80 % false positive rate which results in unnecessary biopsies [22]. As a result, most of the more than $ 2 billion spent annually on biopsies and follow up ultrasound in the USA is spent on benign lesions.

To characterize the cost-effectiveness of a diagnostic method two key metrics are used: sensitivity and specificity [43]. The former refers to the rate of true positives whereas the latter gives the rate of true negatives. In NDE, sensitivity is more often referred to as probability of detection (POD). Under ideal conditions, a detection technology should achieve 100 % sensitivity and 100 % specificity. However, real values of sensitivity and specificity tend to be lower and vary depending on the characteristics of the feature of interest. Figure 5.1(e) illustrates typical trends of the POD and probability of false positive (PFP) as a function of damage size for a typical NDE inspection technique (PFP = 1-specificity). As damage size decreases the POD decreases while the PFP increases due to the need for lowering the detection threshold. The POD and PFP curves can be combined in a single curve resulting in the Receiver-Operating Characteristic (ROC) which summarizes the performance of a diagnostic system [43].

Detection of small features is becoming increasingly more important in a number of fields. Examples include early stage detection of cancer, which is known to reduce mortality rates, and detection of damage precursors that allows life extension of complex engineering systems such as jet engines.

Imaging technology offers the potential to improve the sensitivity of diagnostic methods whilst limiting or even lowering the PFP. This is possible because an image is the synthesis of the information contained in multiple measurements recorded by sensors deployed at different positions along an aperture. This spatial diversity yields complementary information that enhances the SNR of individual signals when they are combined together to form an image.

Although image-based detection could use threshold levels applied to the image, in a similar fashion to conventional detection (Fig. 5.1), thresholding would not make full use of the information available in the image. In fact, an image provides geometrical information about the structures within an object which allows target features to be discriminated from other nuisance features, thus detecting a target even in the presence of a highly complex background.

The metric used for quantifying the amount of information contained in an image is resolution. As an example Fig. 5.2 shows the high and low resolution versions of a photograph of the hieroglyphics on a sarcophagus. From the high resolution image it is possible to conclude that the sarcophagus contains a hieroglyphic that resembles the number 9 (pointed to by the arrow). On the other hand, the same conclusion cannot be reached from the low resolution image, thus illustrating how a loss of resolution results in a loss of information.

Fig. 5.2

Images of a photograph of the hieroglyphics on a sarcophagus in the British Museum: (a) High and (b) low resolution. The arrows point at a feature shaped like the number 9, as resolution decreases it is no longer possible to detect individual features

While resolution is important to discriminate between the different geometrical features of an image, it is not sufficient to characterize the full amount of information that is contained in the image. For instance, Fig. 5.3 shows two experimental images of a complex three-dimensional breast phantom. Figure 5.3(a) is obtained using ultrasound based sonography and is characterized by a granular appearance due to the speckle phenomenon [1]. Thanks to the speckle contrast it is possible to detect two circular dark inclusions inside the phantom. Next, is an ultrasound tomography image of the same phantom obtained with the method introduced in [37]. The image shows how the speed of sound, which is related to the mechanical properties of the materials in the phantom, varies in space with each grey level corresponding to a numerical value of sound speed. While the sonogram provides a structural image containing geometrical information, the tomogram in Fig. 5.3(b) is a quantitative image that blends together the geometrical and material properties of the probed object. Importantly, thanks to the sound-speed contrast in Fig. 5.3(b) it is possible to observe that the two inclusions are different in nature whereas, they appear to be the same on the sonogram. The sound-speed information is critical to increase specificity (lower the PFP). As an example, in human tissue it is known that cancer masses tend to be stiffer and have higher sound-speed than healthy tissue [17]. As a result, by examining the image in Fig. 5.3(b) it would be possible to conclude that the bright inclusion, which has high sound speed, is a cancer mass while the dark one could be a cyst of simply fat. Therefore, although the two images in Fig. 5.3 have comparable level of spatial resolution, the quantitative image yields additional information that leads to higher specificity and hence to a superior diagnostic technology.

Fig. 5.3

Comparison between a structural (a) and a quantitative image of a three-dimensional object. (a) Features can be detected thanks to speckle contrast; (b) grey levels provide a spatial map of sound speed throughout the object

To meet the requirements of high sensitivity and specificity of modern diagnostics, imaging methods have to provide quantitative information with high spatial resolution. However, the resolution of classical imaging methods is dictated by the diffraction limit that leads to a minimum resolvable size of the order of the wavelength, λ, of the probing wave (see, for instance, Ref. [16]). This has important practical implications in subsurface imaging. In fact, to achieve high resolution short wavelengths need to be propagated. However, as λ decreases the penetration depth of the probing wave decreases due to increasing absorption and scattering. As a result, the higher the resolution the shallower the volume of the object that can be imaged, this being the major limitation of conventional ultrasonic imaging systems.

This chapter provides an overview of recent progress on acoustic imaging methods that can break the diffraction limit to achieve super resolution as well as reconstructing spatial maps of material properties. Therefore, the imaging problem is formulated in Sect. 5.2 which also introduces the classical diffraction limit. Section 5.3 links acoustic scattering to the imaging problem using a general wave-matter interaction model. Section 5.4 introduces beamforming that is used in routine ultrasound imaging and shows its connection to diffraction tomography. Section 5.5 presents the approach to subwavelength resolution imaging which is based on nonlinear inverse scattering as discussed in Sect. 5.6. To support the inverse scattering approach, experimental results are presented in Sect. 5.7 which is followed by conclusions in Sect. 5.8.

5.2 The Imaging Problem

Modern imaging technology builds on recent progress in solid state electronics and micromachining that have led to the rapid development of ultrasound arrays.

Scattering experiments can be performed with sensors arranged under different configurations. If the entire surface of the volume is accessible, they can be distributed in a full-view configuration (Fig. 5.4(a)) whereas in the limited view case, data can be collected by using an array interrogating the accessible surface (Fig. 5.4(b)). Array elements can be excited individually, launching a wave which propagates in the background medium and is scattered by the features contained in it. The scattered field is detected by all the transducers and recorded individually. Therefore, for an array with N elements, N ² signals can be measured.

Fig. 5.4

Diagram of typical transducer arrangements for acoustic imaging. Signals are collected for each permutation of transmitter and receiver element pairs in the array: (a) full view; (b) limited view

The general imaging problem can be formulated in terms of reconstructing the spatial distribution of one or more physical parameters characterizing the structure of an object from a set of scattering experiments performed with an array. Let us assume that scattering can be described by a scalar wavefield, ψ, solution to

(5.1)

where $\widehat{H}$ is the Helmholtz operator, (∇²+k ²), k is the background wavenumber (2π/λ), ${\hat{\mathbf{r}}}_{0}$ specifies the direction of the incident plane wave which illuminates the object and ω is the angular frequency. The object is described by the Object Function, O(r,ω), of support D corresponding to the volume occupied by the object

(5.2)

where, c ₀ is the sound speed in the homogeneous background and c(r), and ρ(r) are the local sound speed and mass density inside the object [27]. The analysis performed in the rest of this chapter will consider monochromatic wavefields, therefore the explicit dependence on ω is omitted.

Equations (5.1) and (5.2) provide an accurate representation of the acoustic scattering problem where elastic effects can be neglected. Therefore, while this model is suitable to describe the propagation of ultrasound in human tissue it is less accurate when studying ultrasonic NDE of solids or seismic wave scattering in the earth. Despite these limitations, the acoustic model underpins most of the imaging methods used in NDE and seismic imaging, therefore it will be adopted as the basic model for the theory presented in the following sections.

To obtain a quantitative image of the object, the spatial function O(r) needs to be reconstructed from the set of scattering experiments. Spatial maps of sound speed and density can then be obtained by inverting (5.2) [23]. Structural imaging on the other hand, only reconstructs the boundaries of sudden variations of O(r) as in the case of the sonogram shown in Fig. 5.3(a).

Even with the most advanced quantitative imaging method, it is not possible to reconstruct O(r) exactly as this would require unlimited resolving power. A rigorous definition of resolution can be based on the representation of the object function in the spatial frequency domain, Ω, obtained by performing the three-dimensional Fourier transform of O(r)

(5.3)

The resolution of an imaging system is then determined by the largest spatial frequency, |Ω|, that the system can reconstruct.

5.2.1 The Diffraction Limit

While a homogeneous medium does not support the propagation of monochromatic wavefields oscillating over a spatial scale smaller than λ, subwavelength oscillations can occur on the surface and within the interior of the probed object [16]. The subwavelength oscillations are described by evanescent fields that are trapped on the object’s surface and do not radiate energy into the far field. The interplay between radiating and evanescent fields can be seen by considering the scattering of a plane wave incident on a planar surface. Let ψ ^s(r _∥,0) be the resulting complex scattered field, measured along an aperture close (≪λ) to the surface. By means of the angular spectrum method [16], the spectrum of the field along a parallel aperture at distance z from the first is $\tilde{\psi}^{s}(k_{\|},z)=\tilde{\psi}^{s}(k_{\|},0)\exp(\textit {i}k_{\bot}z)$ where $\tilde{\psi}^{s}(\textbf{k}_{\|},0)$ is the spectrum of ψ ^s(r _∥,0) and k _∥ and k _⊥ are related to the medium wavenumber, k

(5.4)

The condition, |k _∥|≤k, corresponds to propagating waves that can travel from the object to a remote detector placed in the far field. In this case, k _∥ and k _⊥ are the projections of the wavenumber vector k along the plane of the aperture and in the direction perpendicular to it. Since |k _∥|≤k, propagating waves oscillate over a spatial scale larger than λ (k=2π/λ). In contrast, |k _∥|>k corresponds to evanescent waves that decay exponentially in the direction perpendicular to the aperture, thus making their detection increasingly more difficult as the detector moves away from the surface of the object. Evanescent waves can oscillate over a subwavelength scale along the surface of the object and the smaller their spatial period, the more rapid their exponential decay is. As a result, if detectors are placed many wavelengths away from the object, the contribution from the evanescent fields is negligible and the wavefield is effectively bandlimited with bandwidth  [16].

Classical imaging methods, from microscopy to sonography, are based on a linear, one-to-one mapping between the spatial frequencies contained in a radiating wavefield and the spatial frequencies, Ω, of the object function $\widetilde{O}(\varOmega)$ [4]. Since the wavefield is bandlimited to 2k, the largest object bandwidth that can be retrieved is also 2k leading to the classical Rayleigh limit [16].

In 1928 Synge suggested that subwavelength resolution could be achieved by probing the evanescent fields directly. The premise of this approach is that evanescent waves encode information about the subwavelength properties of the object due to their super-oscillatory behavior. Synge’s original idea has led to the development of Near-field Scanning Optical Microscopy (NSOM) where resolution in the order of λ/100 has been reported (for an overview of the topic see [11]). However, a major limitation of NSOM is that to access the evanescent fields a probe has to be scanned close (<λ) to the surface to be imaged. This is not feasible in a number of subsurface imaging problems where the surface or volume of interest are many wavelengths away from the sensors. This chapter explores the possibility of achieving super resolution when all the sensors are in the far field (≫λ).

5.3 Acoustic Scattering and the Far-Field Operator

The link between the spatial frequencies of the object function and those of the radiating scattered field is dictated by the scattering mechanism describing how waves interact with matter. In this section this link is considered further based on the theory of acoustic scattering. For this purpose, it can be observed that the potential ψ in (5.1) is also a solution to the Lippman-Schwinger equation

(5.5)

where $\exp({{\mathit{i}k{\hat{\mathbf{r}}}_{0}\cdot{\mathbf{r}}}})$ is an incident plane wave and G(r,r′) is the free-space Green’s function solution to $\widehat{H}G({\mathbf{r}},{\mathbf{r}}')=-4\pi\delta(|{\mathbf{r}}-{\mathbf{r}}'|)$. Using the far-field approximation, |r−r′|→r[1−(r⋅r′)/r ²], (5.5) leads to the asymptotic expression of ψ

(5.6)

where $f(k{\hat{\mathbf{r}}},k{\hat{\mathbf{r}}}_{0})$ is the scattering amplitude defined as

(5.7)

We now introduce the T-matrix or transition amplitude [41]

(5.8)

so that $T(\alpha{\hat{\mathbf{u}}},k{\hat{\mathbf{r}}}_{0})=f(k{\hat{\mathbf{r}}},k{\hat{\mathbf{r}}}_{0})$ for $\alpha{\hat{\mathbf{u}}}=k{\hat{\mathbf{r}}}$. As shown in [32] the scattering amplitude can be related to the spectral representation of the object function $\widetilde{O}({\varOmega})$ and the transition matrix according to

(5.9)

where ε is an infinitesimal introduced to remove the singularity at k=α. Equation (5.9) links the spectrum of O(r) to the measurements and is central to super resolution imaging as explained in Sect. 5.5.

5.3.1 Born Approximation

Under the Born approximation, the total field under the integral sign in (5.5) is approximated to the incident field which causes the integral term in (5.9) to vanish [32]. As a result, the Born approximation leads to a one-to-one mapping between the measured scattering amplitude $f(k{\hat{\mathbf{r}}},k{\hat{\mathbf{r}}}_{0})$ and $\widetilde{O}(\varOmega)$ at the spatial frequency $\varOmega=k({\hat{\mathbf{r}}}-{\hat{\mathbf{r}}}_{0})$, i. e.

(5.10)

To illustrate the physical implications of the one-to-one mapping, Fig. 5.5 depicts a two-dimensional scattering problem. If the object is probed with a circular array consisting of N transducers, the scattering amplitude can be measured for N ² combinations of the illumination, θ, and scattering, ϕ, angles through (5.6). The measurements can be arranged into a N×N matrix, known as the multistatic matrix, whose i–j entry is the scattering amplitude measured under the scattering angle ϕ _i when the object is illuminated in the direction θ _j . Due to (5.10), the entries of the multistatic matrix map into a subset of the Ω-space which coincides with a disk (sphere in 3-D) of radius 2k known as the Ewald limiting disk [4]. This also implies that under the Born approximation, measurements are independent of the spatial frequencies of the object larger than 2k or in other words the spatial periodicities of the object function that vary over a spatial scale shorter than λ/2 do not affect the far-field measurements. Therefore, since the measurements are independent of the sub-λ/2 structures, any imaging method consistent with the Born approximation will not be able to achieve sub-λ/2 resolution.

Fig. 5.5

(a) Diagram of scattering experiments showing a transmitter, T _x , launching a plane wave and a receiver, R _x detecting the scattered field. (b) The multistatic matrix—a discrete representation of the T _∞ operator. (c) The spatial frequency domain showing how measurements map onto the Ewald limiting disk

For the Born approximation to be valid the object should have low contrast relative to the background. Moreover, its size should be comparable to λ so that the phase delay accumulated by the incident field as it travels inside the object is less than π [19]. These are very stringent conditions for most practical applications and are in common with other linear approximations such as Rytov [24]. Finally, it is observed that the Born approximation violates energy conservation [18].

5.3.2 Factorization of the Far-Field Operator T _∞

Here, we follow the approach proposed by Kirsch [20, 21]. Central to any imaging method is the far-field operator, $T_{\infty}: L^{2}(\mathbb{S})\rightarrow L^{2}(\mathbb{S})$ defined as

(5.11)

where we have made use of the Dirac notation¹ and $\mathbb{S}$ is the unit shell in ℝ³. The physical significance of T _∞ can be understood by observing that T _∞|g〉 is the far-field pattern of the scattered field, |u _s 〉, due to a linear combination of incident plane waves, $\exp({{\mathit{i}k{\hat{\mathbf{r}}}_{0}\cdot{\mathbf{r}}}})$, with relative complex amplitude $g(k{\hat{\mathbf{r}}}_{0})$, i.e.

(5.12)

Therefore, T _∞ describes how any arbitrary incident field is scattered by the object. From a functional analysis perspective, T _∞ maps the space of the functions |g〉 that define the incident field into the space of the far-field scattering patterns |u _s 〉.

The definition of T _∞ allows the scattering process to be expressed as the combination of three consecutive events: 1) the propagation of an incident field from the far-field (or array of transducers) to the object; 2) the interaction of the incident field with the object physical properties and the resulting local perturbation to the incident field; 3) the radiation of the perturbation from the object to the far field.

The three scattering events can be described by three separate mathematical operators that combined together result in T _∞. To show this, let us introduce the illumination operator $H : L^{2}(\mathbb{S})\rightarrow L^{2}(D)$ which maps the illumination functions |g〉 into the incident field |ϕ〉 inside the object

(5.13)

Similarly, it is possible to define a radiation operator $H^{\dag}:L^{2}(D) \rightarrow L^{2}(\mathbb{S})$ that maps a continuous distribution of point sources in D with strength defined by the continuous function |σ〉 into the radiated far-field pattern

(5.14)

By definition H ^† is the adjoint operator of H. Crucially, both H and H ^† depend on the geometry of the scatterer but are independent of its mechanical properties.

Finally we introduce the interaction operator S:L ²(D)→L ²(D) that transforms the incident field inside the object, |ϕ〉, into the source distribution |σ〉 characterizing the perturbation to the incident field. This operator accounts for the wave-matter interaction and can take different forms depending on the scattering model under consideration. As an example, under the Born approximation it is assumed that each point inside the scatterer acts as an independent point scatterer. Therefore, the equivalent source distribution coincides with the incident field multiplied by the object function and S is a diagonal operator defined as

(5.15)

The expression of S in the case of multiple scattering can be found in [21].

We are now able to decompose the far-field operator into the three main steps of the scattering process. In particular, from the diagram in Fig. 5.6 it is clear that |u _s 〉=T _∞|g〉=H ^† SH|g〉, which leads to the factorization

(5.16)

The factorization of T _∞ suggests a formal approach to imaging. In particular, we have already observed that only S depends on O(r). Therefore, to reconstruct O(r) from T _∞, it is necessary to isolate the contribution of S from H and H ^†.

Fig. 5.6

The mapping of the space of the illumination laws |g〉 into the space of scattered fields |u _s 〉 can be described by three operators. In anticlockwise order: the space of illumination functions |g〉 maps onto the space of incident fields inside the object |ϕ〉 via H. The space of incident fields then maps onto the space of secondary sources |σ〉 through S. Finally the secondary sources radiate into the space of the scattered fields |u _s 〉 as described by H ^†

5.4 Beamforming and Diffraction Tomography

Beamforming (BF) is the image formation method underpinning current commercial imaging technology. Fields of application include: sonar [3], medical diagnostics [42], and non-destructive testing [13].

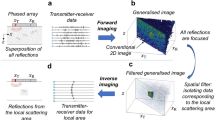
Although several hardware and software implementations of BF have been proposed, the general working principle consists of two stages as illustrated in Fig. 5.7. In the first stage and for each point in the image space, z, a focal law is defined. This sets the relative time delays between the input signals fed into each array transducer so that the acoustic waves excited by the array elements interfere coherently with each other only when they reach z. For this purpose, the transducer that is at the greatest distance from z is fired first while the closest transducer is fired last. The field resulting from the superposition of the waves radiating from the array elements is an acoustic beam focused at z. If a point scatterer is present at z, the beam is scattered into a spherical wave radiating from z. The scattered wave is subsequently detected by the array elements that measure wavepackets arriving at different times depending on the element relative distance from z. The signals are again time shifted using the same focal law used in transmission and summed coherently. This ensures that maximum weight is given to the energy scattered from z and represents the second stage of BF imaging. This two-stage process shares the same physical principle used in confocal microscopy where two separate lenses are used to achieve the two focusing stages. To form an image, the BF process is repeated for all points in the volume to be imaged assuming that the scattering event at a particular location z is independent of the scattering events occurring at neighboring points, i.e. multiple scattering effects are neglected. Therefore, BF makes use of the Born approximation.

Fig. 5.7

The two stages of beamforming imaging. In the transmission stage, the array elements are phased according to a delay law that results in a focused beam at a prescribed point z. In the reception stage, the signals received by different array elements are again time shifted with the same delay law to isolate the energy scattered from z. For illustration purposes two separate arrays are shown; however, in practice the two operations are performed by a single array

The two stages of the BF process aim at isolating the interaction operator S from H and H ^† in the factorization of T _∞. To illustrate this, we first consider an ideal scenario where it is possible to focus a beam at a point in space, z, with unlimited resolution, or in other words there exists an illumination law |g _z 〉 such that

$$ H\vert g_z\rangle=\delta\bigl(|\textbf{r}-\textbf{z}|\bigr). $$

(5.17)

By reciprocity, this also means that it is possible to ‘see’ a secondary source at the same position z with unlimited resolution

$$ \langle g_z \vert H^{\dag}\vert\sigma\rangle= \sigma(\textbf{z}). $$

(5.18)

Using properties (5.17) and (5.18) and the factorization of T _∞ in (5.16) one obtains

$$ \langle g_z \vert T_\infty\vert g_z\rangle=S(\textbf{z},\textbf{z}). $$

(5.19)

Under the Born approximation, (5.15) and (5.19) then lead to

$$ \langle g_z \vert T_\infty\vert g_z\rangle=O(\textbf{z}), $$

(5.20)

which is the object function reconstructed with unlimited resolution. However, the ideal focusing in (5.17) and (5.18) is not physically possible. Symmetry considerations imply that in a homogeneous medium with transmitters placed far away from the focal point, the sharpest acoustic beam is obtained by using the focal law

$$ |g_{\mathbf{z}}\rangle=\exp{({-\mathit{i}k{\hat{\mathbf{r}}}_0\cdot{\mathbf{z}}})}, $$

(5.21)

which is also known as the steering function. This function produces a relative phasing between the sources that is equivalent to the time delays between the elements of an array in BF imaging. Therefore, properties (5.17) and (5.18) now become

(5.22)

(5.23)

where j ₀ is the zero-order spherical Bessel function of the first kind. Under the Born approximation, the finite spatial extent of the focal spot now implies that the object function reconstructed with BF, R _BF (z), is²

$$ R_\mathit{BF}(\textbf{z})=\langle g_z \vert T_\infty\vert g_z\rangle= \int_D dr^3\, O(\textbf{r})h_\mathit{BF}\bigl(|\textbf{r}-\textbf{z}|\bigr), $$

(5.24)

which is the spatial convolution of the object function with the point spread function (PSF) h _BF (|r−z|) defined as

$$ h_\mathit{BF}\bigl(|\textbf{r}-\textbf{z}|\bigr)=\langle g_z \vert I \vert g_z\rangle =16\pi^2 j_0^2\bigl(k|\textbf{r}-\textbf{z}|\bigr). $$

(5.25)

In the spatial frequency domain the convolution in (5.24) is equivalent to

$$ \widetilde{R}_\mathit{BF}(\varOmega) = \widetilde{O}(\varOmega)\tilde{h}_\mathit{BF}(\varOmega), $$

(5.26)

where, $\tilde{h}_{\mathit{BF}}(\varOmega)$ is the Fourier transform of (5.25)

(5.27)

From (5.26) and (5.27) it follows that the BF process leads to a reconstruction of the object function which is a low-pass filtered version of O(r) with a cutoff at 2k consistent with the diffraction limit. However, BF also introduces a distortion caused by the factor 1/|Ω| in (5.27) which tends to amplify the low spatial frequencies of the object at the expense of the higher ones. Because of this distortion, the use of BF is limited to structural imaging as in the case of sonography. Diffraction tomography (DT) algorithms rectify the distortion while retaining the same resolution level producing a PSF with a flat spectrum $\tilde{h}_{\mathit{DT}}(\varOmega)=1$ within the ball |Ω|<2k and zero outside it [4]. The reconstructed object function is therefore low-pass filtered

$$ \widetilde{R}_{\mathit{\mathit{DT}}}(\varOmega) = \widetilde{O}(\varOmega)\tilde{h}_\mathit{DT}(\varOmega), $$

(5.28)

with

(5.29)

where, j ₁(⋅) is the spherical Bessel function of the first order.

From (5.26) and (5.28) it is clear that the DT image can be obtained from the BF image by deconvolving the latter with the BF PSF in (5.27). Similar considerations apply to the two dimensional problem [33].

5.5 Subwavelength Imaging

Equation (5.9) describes the encoding of subwavelength information into the far field. In fact, the integral term in (5.9) which is due to multiple scattering, links the entire spectrum of O(r) to a single scattering measurement $f(k{\hat{\mathbf{r}}},k{\hat{\mathbf{r}}}_{0})$ since the integral spans the entire ℝ³ domain rather than being limited to a point inside the Ewald limiting sphere. Therefore, far-field measurements are sensitive to the spatial frequencies larger than 2k and hence to the subwavelength structures of the object. This is a key observation because if the measurements are sensitive to the subwavelength structure of the object then it should be possible to retrieve them. The encoding mechanism for the simple case of two point scatterers has been studied in [29, 36].

In order to extract this information from the far field, the inverse scattering problem needs to be solved. While the forward scattering problem predicts the scattered field for a prescribed object function [solving (5.1)], the inverse problem attempts to retrieve O(r) from the measured T _∞. The former is well posed whereas the latter is ill-posed in the sense of Hadamard, because although the solution exists and is unique (at least under full view conditions), it is unstable [9].

From a mathematical perspective, the uniqueness of the solution to the inverse problem implies that the object function could be reconstructed with unlimited resolution, since only the exact object function is the solution to the inverse problem. However, the problem is also unstable, which means that small measurement errors (e.g. noise) can be amplified in the reconstructed image leading to significant artifacts or even causing the non-existence of the solution. As a result, central to the imaging problem is the solution of the inverse scattering problem in a stable fashion.

The solution of the inverse problem is further complicated by its nonlinear nature. In fact, while the forward problem is linear with respect to the incident field, it is nonlinear relative to the object function due to the presence of multiple scattering. On the other hand, under the Born approximation the problem becomes linear because multiple scattering is neglected. As a result, DT and hence BF are solutions to the linearized inverse scattering problem. This implies that even if real measurements are affected by multiple scattering, both DT and BF are not able to decode the subwavelength information that is encoded by multiple scattering.

To extract subwavelength information it is therefore necessary to account for the actual physical mechanism that describes the interaction of the incident field with the object and solve the fully nonlinear inverse problem.

5.5.1 The Information Capacity of Noisy Measurements

Before discussing methods to solve the inverse scattering problem it is important to consider the extent of information available in noisy measurements. According to the definition introduced in Sect. 5.2 a super resolved image of O(r), R(r), is characterized by a spatial bandwidth B>4/λ. Since the bandwidth of R(r) will be finite, a complete representation of R(r) can be obtained by calculating R(r) at the nodes of a regular grid where the nodes are spaced 1/B apart. If the object is contained in a cubic field of view with dimensions L, R(r) is fully characterized by N _R =(1+LB)³ nodal values; here, we refer to N _R as the number of degrees of freedom (DOF) of the reconstruction. The N _R nodal values of R(r) are obtained by solving the inverse scattering problem which uses as an input the discrete number of measurements contained in the matrix representation of T _∞. On the other hand, if the measurements are performed with an array with N transducers, the number of independent measurements after performing all the possible transmit-receive experiments is M=N(N+1)/2, since some of the measurements are redundant by reciprocity. If the number of measurements is kept constant, the inverse problem becomes increasingly more ill-posed as we try to increase resolution—a larger number of DOF needs to be determined from the same number of measurements, M. This would suggest that to increase resolution whilst limiting ill-posedness one should increase the number of measurements, e.g. by increasing the number of transducer elements. However, in the presence of noise only a finite number of measurements are truly independent. To show this, let us consider an object contained in a ball of radius R ₀ probed with an ideal spherical array of radius R≫R ₀ concentric with the ball. The scattered field measured by the array when one transducer is excited is

(5.30)

where the position of the receiving array element is expressed in spherical coordinates {r,θ,ϕ}. The coefficients $a_{mn}(k{\hat{\mathbf{r}}}_{0})$ depend on the distribution of the scattered field over the sphere of radius R ₀, vary with the illumination direction ${\hat{\mathbf{r}}}_{0}$, and encode information about the properties of the object. Even if the field does not contain evanescent waves, the coefficients a _nm can be non-zero for any order.³ The functions $h_{n}^{(1)}$ are the spherical Hankel functions of the first kind and order n representing outgoing waves, $Y_{n}^{m}(\theta,\phi)$ are the spherical harmonics of order n and degree m [2]. By considering the asymptotic case r→∞, $h_{n}^{(1)}(kr)\approx(-\textit{i})^{n+1}\exp(\textit{i}kr)/r$, the scattering amplitude can be written as

(5.31)

Equation (5.31) shows that any order n of the scattered field on the sphere of radius R ₀ radiates into the far field. All the spherical waves decay at the same rate, 1/r; therefore, the possibility of measuring a particular a _mn coefficient depends on the efficiency with which the corresponding spherical wave radiates from the object. This is determined by the factor $1/h_{n}^{(1)}(kR_{0})$ in (5.31) which for n≫kR ₀ has the asymptotic form

(5.32)

From this expression it is clear that for high order spherical waves n≫kR ₀, the radiation efficiency rapidly decays as the order n increases. In other words, the radiation mechanism leads to a greater attenuation of the higher order spherical waves, thus making their detection more challenging. In particular, there exists an upper bound to the maximum order, n _max , of the spherical waves that can be detected by an array system. This is dependent upon the noise characteristic and dynamic range of the array system. The latter refers to the capability of the detector to measure large signals, as well as small ones and is defined as where S _min is the amplitude of the smallest signal that can be detected.

Assuming that all the coefficients a _mn have comparable magnitude, the amplitude of the corresponding spherical waves reaching the detectors would only be dependent on their radiation efficiency which for n>kR ₀ decays according to (5.32). As a result, for large orders (n>kR ₀) the minimum dynamic range, , required to detect the orders up to n _max is

(5.33)

Figure 5.8 shows the dynamic range for increasing orders n when kR ₀=10. For n>kR ₀, the dynamic range increases rapidly with the order to be detected.

Fig. 5.8

Required dynamic range as a function of the order of the spherical harmonics to be detected when kR ₀=10. If the dynamic range of the array system is , only harmonics up to n _max can be detected

Since any detector will have a finite dynamic range, the wavefield is bandlimited by the maximum order that the system can sense, i.e. B=n _max where B is the effective bandwidth. The spatial sampling criterion for a bandlimited field sampled over a spherical surface was given by Driscoll and Healy [14] and states that the wavefield can be represented by B ² sampling points distributed over an equiangular grid of points (ϕ _i ,θ _j ), i,j=0,…,2B−1, where ϕ _i =πi/2B and θ _j =πj/B. Therefore, the number of sampling points is $n_{\mathit{max}}^{2}$; a larger number of detectors would yield redundant information. For detectors with low dynamic range, it can be assumed that the maximum order is kR ₀; therefore it is sufficient to sample the field with an array that contains

(5.34)

elements [5, 34]. By reciprocity, it can be shown that the number of independent illumination directions is also limited by the dynamic range of the array system and the number of independent scattering experiments is still M=N(N+1)/2, where N is limited by the effective bandwidth as discussed earlier.

So far it has been assumed that scattering experiments are performed at a single frequency. However, ultrasound imaging utilizes broadband signals from which it is possible to extract measurements at different frequencies by means of Fourier analysis. Therefore, it can be expected that measurements at different frequencies yield complementarity information. From an information theory perspective, this is understood in terms of information capacity of an imaging system. As an example, in an optical system such as a microscope, the number of DOF necessary to describe the wavefield in the image plane is

(5.35)

where B _x and B _y are the spatial bandwidth determined by the optics of the system, L _x and L _y are the widths of the rectangular image area in the x and y directions, respectively. T is the observation time and B _T is the temporal bandwidth of the signals, and the factor 2 accounts for two possible states of polarization. According to the invariance theorem [25] and in the absence of noise, one of the spatial bandwidths in (5.35) can be extended at the expense of the others—provided that N _F remains constant. The invariance theorem can be extended to the case of noisy measurements by introducing the concept of information capacity defined as

(5.36)

where and are the average signal and noise power. By applying the invariance theorem to N _C , it is possible to extend the spatial bandwidth at the expense of other parameters, including the noise level, provided that some a priori knowledge is available [12]. For the acoustic problem considered throughout this chapter it is realistic to assume that the object to be imaged is finite in size and that its properties do not vary with time. The latter assumption implies that the spatial bandwidths can be extended at the expense of the temporal bandwidth whilst maintaining the same SNR and leads to so-called time multiplexing [30]. We now observe that an ultrasonic array can be thought of as the image plane of a particular optical system without lenses, therefore the spatial bandwidths in (5.36) correspond to the spatial bandwidth B of the array (as determined by its characteristic dynamic range). As a result, in principle it is possible to increase B from B _T , or in other words to increase the number of independent data by using measurements at different frequencies.

5.6 Nonlinear Inverse Scattering

Since the introduction of regularization methods for ill-posed problems by Tikhonov, the nonlinear inverse scattering problem has attracted considerable interest across a number of disciplines. It is possible to discriminate between two main streams of research depending on whether the inversion is performed directly or by means of multiple iterations.

Iterative inverse scattering methods fall within the category of optimization methods and nonlinear filters. A variety of methods have been therefore proposed and the reader is referred to [8] for a general overview. Common to all iterative techniques is the use of a forward model that allows the output of scattering experiments to be predicted if the object function is known. The key idea of these methods is then to update the object function in the forward model until a cost function defined by the residual between the measured and predicted scattered field is minimized. The use of numerical solvers for the forward problem allows for accurate wave-matter interaction models to be used. In particular, it is possible to model multiple scattering effects that are central to achieving super resolution. Iterative techniques require an initial model for the object function to be assumed at the beginning of the iterations. This is a very critical step because if the model is not sufficiently close to the true object function, several iterations are required to achieve convergence and most importantly the iterations could converge to a local rather than the global minimum. To address this problem, frequency hopping techniques can be used. The key idea is to perform a frequency sweep, using the image produced at a lower frequency as the initial model for the next higher frequency. The premise is that at lower frequencies the resolution is lower and therefore the accuracy of the initial model is less critical. In addition, the use of multiple frequencies allows the limited bandwidth of the detection system to be expanded from the temporal one. This method has been implemented in geophysics [28] and optical and microwave imaging leading to the experimental super-resolved reconstructions in [6, 7].

Although iterative methods are extremely versatile they do not allow a direct representation of the link between measurements and reconstruction. Therefore, direct inverse scattering methods are considered in greater detail next.

5.6.1 Sampling Methods

Here, the nonlinear inverse problem is replaced with a linear integral equation of the first kind whilst still accounting for multiple scattering. However, while the iterative methods can reconstruct the object function, these methods can only reconstruct its support D, i.e. the shape of the object.

The sampling methods are based on the factorization of T _∞ and use two main results: 1) If the H ^† operator is known, the shape of the object can be reconstructed exactly; 2) H ^† can be characterized from T _∞ by means of the factorization in (5.16).

It can be shown [9] that if we select a point z in the image space and consider the far-field pattern of a point source at z, $g_{z}=\exp{(-\textit{i}k\hat{\textbf{r}}\cdot\textbf{z})}$, the solution to

(5.37)

exists if and only if z∈D. In other words, if z belongs to D there exists a continuous source distribution, |a〉 inside D that produces a far-field pattern equal to the pattern of a single point source at z. On the other hand, such a source distribution does not exist if z is outside D. Therefore, the shape of the object is the locus of all points z for which (5.37) is solvable. In functional analysis this condition (solvability) is expressed by saying that g _z is in the range of the operator H ^†.

The second result is based on the fact that the range of H ^† can be evaluated from T _∞ without knowing H ^†. In particular, Kirsch [20, 21] has demonstrated that the range of H ^† is equal to that of the operator $\sqrt{T_{\infty}}$. As a result, the condition of existence of the solution to (5.37) can be assessed by considering the equation

(5.38)

The condition can be verified by using the singular value decomposition of T _∞ {μ _n ,|p _n 〉,|q _n 〉} where μ _n are the singular values (real) so that

(5.39)

According to Picard’s theorem, the solution to T _∞|x〉=|y〉 exists if and only if

(5.40)

By Silvester’s theorem the singular value decomposition of $\sqrt {T_{\infty}}$ is $\{\sqrt{\mu_{n}}, \vert p_{n}\rangle,\allowbreak \vert q_{n}\rangle\}$; therefore, the condition of existence in (5.37) via (5.40) leads to the central result of the sampling methods

(5.41)

which means that the series converges only inside the scatterer. An image of the shape of the object can be formed by plotting the functional

(5.42)

which is non-zero inside the object and vanishes outside it. Equation (5.42) defines the Factorization Method (FM) [20]; slightly different expressions have been given for the Linear Sampling Method [8] and Time Reversal and MUSIC [26].

In the absence of noise, condition (5.41) leads to the reconstruction of the object shape with unlimited resolution since the condition is exact. However, in the presence of noise the resolution degrades. In fact, T _∞ is a compact operator with a countable number of singular values accumulating at zero. In other words, when n→∞, μ _n →0 with the singular values following a similar trend to that shown in Fig. 5.8 with a cutoff order at n=kR ₀ [10]. Therefore, as the order of the terms in the series in (5.41) increases, errors in the estimation of the singular functions |q _n 〉 are amplified by the small singular values at the denominator.

The limited resolution of BF can also be explained in terms of the singular value decomposition of T _∞ [33]

(5.43)

Due to the rapid decay of the singular values of orders larger than kR ₀ only the first n≈kR ₀ terms in the series contribute to R _BF . As a result, the information contained in the higher order singular functions is lost due to the small weight given by the corresponding singular values μ _n .

5.7 Experimental Examples

To illustrate how the inverse scattering approach is applied to experimental data this section outlines methods and results that have been reported in previous communications. We start with full-view experiments that have been performed with a prototype array system for breast ultrasound tomography (BUST) [15]. BUST produces tomographic slices of the breast using ultrasound rather than the ionizing radiation used in CT. The basic measurement setup is shown in Fig. 5.9(a). The patient lies prone on a table with a breast suspended in a water bath through an aperture in the table. A toroidal ultrasound array encircles the breast and scans it vertically from the chest wall to the nipple region. The array consists of 256 transducers, which are mounted on a 200 mm diameter ring, and can measure the multistatic matrix in around 0.1 seconds. A total of 65536 signals is recorded within this time and the data is stored in around 100 MBytes of RAM. Similar systems with more array elements have been built, e.g. [40].

Fig. 5.9

Example of quantitative imaging under a full-view configuration. (a) Diagram of the BUST setup for cancer detection; (b) amplitude and (c) phase of the multistatic matrix at 750 kHz; (e) X-ray CT of a complex 3-D breast phantom showing density distribution; (f) sound-speed map obtained with the inverse scattering approach; (g) BF reconstruction representative of sonography

The signals are wideband therefore, the i–j entry of the multistatic matrix at a particular frequency ω, is obtained by performing the Fourier transform of the i–j signal and selecting the complex value of the spectrum at the frequency ω. This leads to the amplitude and phase of the multistatic matrix shown in Fig. 5.9(b), (c) which have been measured for the complex three-dimensional breast phantom shown in the CT image in Fig. 5.9(d) at 750 kHz.

Figure 5.9(e) is the sound-speed map obtained from the data shown in Fig. 5.9(b), (c) with the inverse scattering approach introduced in [37]. The sound-speed reconstruction shows striking similarities with the CT image revealing, for instance, the irregular contour of the bright inclusion on the right. Some artifact outside the phantom boundary is due to aliasing caused by spatial undersampling.⁴

Another important characteristic of the reconstruction in Fig. 5.9(e) is that it is relatively free of speckle. Speckle is instead dominant in the reflection image shown in Fig. 5.9(f) which is obtained with BF [38]. Thanks to speckle contrast, the irregular outline of the glandular tissue and three of the four inclusions are revealed. At the same time, speckle masks the presence of the smallest inclusion, thus affecting the sensitivity of BF to the smaller lesions. These results show that current ultrasound array technology is sufficiently mature to achieve high resolution tomographic images of complex 3-D objects, comparable to those obtained with X-ray CT.

The super resolving capabilities of the inverse scattering approach can be demonstrated using the sampling methods. As an example Fig. 5.10 refers to an experiment performed with two 0.25 mm diameter nylon wires immersed in the water bath perpendicularly to the plane of the array (the experimental setup is detailed in [35]). Due to the small diameter of the wires compared to λ, the reflected signal is very weak as can be seen from Fig. 5.10(a). The reflections are buried in the background noise and the SNR is lower than 0 dB.

Fig. 5.10

(a) Pulse-echo signals showing the reflection (between 120 and 140 μs) from two 0.25 mm diameter nylon wires immersed in water; (b) monochromatic image obtained with the FM at 1 MHz (λ=1.5 mm); (c) monochromatic image at 1 MHz obtained with BF

Figure 5.10(b) is a monochromatic image of the wires obtained at 1 MHz (λ=1.5 mm) with the FM over an area λ×λ around the wires; the BF image is shown in Fig. 5.10(c) for comparison. While BF cannot resolve the two wires, FM clearly resolve them despite of their λ/4 spacing. Moreover, FM provides a well defined reconstruction of the shape of the scatterers revealing features which are even smaller than λ/4. Note that the diameter of the wires is λ/6. This is a remarkable result given the low SNR and the large distance between the wires and the sensors, ∼70λ.

Finally we consider a limited view configuration [Fig. 5.4(b)] in which a mild steel block is probed with a 32 element linear array. The block contains two parallel through-thickness holes 1 mm diameter, 1.5 mm apart, and at a 46 mm depth from the array (see, for more details, [31]). Figure 5.11(a) is a BF image of the two holes at 2 MHz obtained with a commercial BF system from Technology Design. The image reveals the presence of the scatterers but is not able to resolve them. This is better shown in Fig. 5.11(b) which is a cross section of Fig. 5.11(a) along the direction joining the two hole centers. The lack of resolution is predicted by the Rayleigh criterion [16] which, for the aperture of the array and the depth of the holes, predicts a minimum resolvable distance d=0.61λ/sin(θ)=1.32λ. Since λ=3 mm, d=4 mm which is well above the actual distance between the holes (1.5 mm).

Fig. 5.11

Experimental demonstration of super resolution imaging under limited view. The images show an area of 15×15 mm centered in between two holes in a block of steel, the circles representing the position and actual size of the holes. (a) Image obtained with commercial BF technology; (b) cross-section of (a); (c) super resolved image obtained with the methods; (d) cross-section of (c)

Figures 5.11(c), (d) show the reconstructions obtained with the sampling methods at 2 MHz [31]. By contrast with BF the two holes are completely resolved and the image is very sharp as better seen in Fig. 5.11(d). The resolved distance is more than 2.5 times smaller the minimum resolvable distance predicted by the Rayleigh criterion. This means that in order to achieve the same resolution with BF, a frequency of 5 MHz would be required, thus resulting in a much higher attenuation (in metals the attenuation due to grain scattering increases with the square of the frequency).

5.8 Conclusion

The detection of small features in complex background media is a recurrent problem across a number of application areas, medical diagnostics and non-destructive testing being two important examples. In this context, imaging techniques offer significant potential for achieving cost-effective detection through high sensitivity and limited false positive rate. However, to fully realize this potential, it is crucial to extract all the information encoded in the physical signals that are used to form the image. Current, off-the-shelf ultrasound imaging technology is underpinned by the beamforming (BF) method, which although very robust, discards a significant proportion of the information carried by ultrasonic signals. Therefore, BF reconstructs some of the geometrical features of the object but with a resolution limited by the wavelength of the probing signals according to the diffraction limit.

This chapter has introduced the notion that scattering measurements encode more information about the object’s structure than BF can extract. In particular, the distortion experienced by the probing wavefield as it travels within the object and which is caused by multiple scattering, encodes information about the subwavelength features of the object in the far-field pattern of the scattered wave. To unlock this information, it is necessary to approach image formation from an inverse scattering perspective. By accounting for multiple scattering effects when solving the inverse problem, it is then possible to obtain subwavelength resolution beyond the diffraction limit. Moreover, the inverse scattering approach introduces a shift of paradigm from the structural imaging of BF that is limited to the geometrical features of an object, to quantitative imaging that reveals complementary information about the mechanical properties of the object.

The use of advanced inverse scattering techniques is now possible thanks to progress in computer power and advances in ultrasound array technology and the front-end electronics used to drive them. These technologies enable a fast and accurate mapping of the perturbation to the free propagation of ultrasound induced by the presence of an object. The dynamic range of the array system, which measures the ability of the system to detect large signals as well as small ones, is a limiting factor in measurement accuracy. Importantly, the maximum achievable resolution is dictated by the dynamic range of the detector and is not an intrinsic physical limitation of wave propagation and scattering mechanisms.