Abstract
The characterisation of the excited state of a molecule implies the determinations of the different quantum yields and lifetimes. Additionally, complex kinetic systems are frequently observed and need to be solved. In this contribution, we give our particular way of studying systems of organic molecules where we describe how a quantum yield of fluorescence (in fluid or rigid solution, or in film), phosphorescence, singlet oxygen and intersystem crossing can be experimentally determined. This includes a brief description of the equipments routinely used for these determinations. The interpretation of bi- and tri-exponential decays (associated with proton transfer, excimer/exciplex formation in the excited state) with the solution of kinetic schemes (with two and three excited species), and consequently the determination of the rate constants is also presented. Particular examples such as the excited state proton transfer in indigo (2-state system), the acid–base and tautomerisation equilibria in 7-hydroxy-4-methylcoumarin (3-state system), together with the classical examples of intramolecular excimer formation in 1,1’-dipyrenyldecane (2-state system) and 1,1’-dipyrenylpropane (3-state system) are given as illustrative examples.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
15.1 General Jablonski Diagram: What parameters are needed to fully describe the excited state of a molecule?
The investigation of the excited state relaxation processes is one of the experimental key determinations to the interpretation of correlations between reactivity, stability and molecular structure. Prior to electronic excitation a molecule is usually in its ground electronic state. One of the few exceptions is molecular oxygen whose ground state is a triplet. Upon electronic excitation (1 fs) to any state above the first singlet excited state (S1), deactivation occurs through internal conversion to the S1 state, and here after vibrational relaxation to the lowest vibronic state of S1, the molecule further decays to its ground electronic state through several slower deactivation processes: radiative (fluorescence and phosphorescence) and radiationless (internal conversion and intersystem crossing), see Scheme 15.1. Photochemistry can compete with all the foregoing processes, including vibrational relaxation. This last process will be discussed in the context of the so-called vibronic effect, which will be described later in this chapter.
Jablonski-type diagram schematising the overall set of deactivation processes occurring upon excitation. vr vibrational relaxation; IC internal conversion; ISC interystem crossing. In addition, the vibronic effect is illustrated in red, where k V and k PC are the vibrational relaxation constant and the photochemistry rate constant, respectively. This model for the fate of quanta absorbed into any vibrational level of any excited electronic singlet state excludes the occurrence of intersystem crossing
The general processes and deactivation mechanisms in Scheme 15.1 have been already described in Chap. 1. In this chapter, we will be mainly concerned with aspects associated with the experimental determinations of these parameters (energies, lifetimes, quantum yields and rate constants) and with particular emphasis on the determination of rate constants of reactions occurring in the excited states. These reactions include the formation of additional species (2, 3 and 4-state systems) or particular competition between deactivation processes—see the vibronic effect—and their dependence on the experiment conditions (solvent, temperature etc.).
15.2 Characteristics of an Excited State
The lifetime of an excited state of a molecule is one of its fundamental characteristics; the others being its energy, quantum yields of decay processes and their respective rate constants. After generation of an excited population of molecules of concentration c 0 in the lowest vibronic state of S1, the concentration c(t) at the time t after excitation decreases exponentially with time, according to the law \( c(t) = c_{0} e^{{ - t/\tau_{0} }} \), where τ 0 is the reciprocal of the sum of the rate constants of all the decay processes available for this state. When the time t is equal to τ 0, the concentration c has fallen to 1/e of its initial value. The value of τ 0 is defined as the lifetime of the excited state (Eq. 15.1). When the excited state is luminescent, the most common method to measure the lifetime consists in recording the luminescence decay. Since the luminescence intensity I(t) is proportional to c(t), it follows that \( I(t) = I_{0} e^{{ - t/\tau_{0} }} \), with,
where k F, k IC and k ISC are the rate constants for respectively the fluorescence, internal conversion and intersystem crossing. It is worth noting here that the foregoing exponential law does not hold when higher vibronic levels are excited and the decay includes the time region (fs-ps) where vibrational redistribution and relaxation occurs. In this time region, redistribution leads to oscillating functions and relaxation leads to additional negative exponential terms (rise times). These features become important in the particular case of competition between vibrational redistribution/relaxation and photochemistry. When fluorescence (or phosphorescence) is the only deactivation process, the value of τ is commonly designated as τ F (or τ P) with the meaning of radiative lifetime.
Additional excited state reactions add new pathways for energy dissipation, and consequently additional rate constants in (the denominator of) Eq. (15.1). Among these, we can find processes leading to the formation of new species (for example excimer formation, electron transfer or proton transfer) and/or quenching (e.g., energy transfer). Oxygen, present in all solvents in equilibrium with air, acts as a very efficient quencher, which is due to energy transfer to the triplet ground state of oxygen to generate singlet molecular oxygen (1270 nm, ≈1 eV), see Scheme 15.1. Obviously, the efficiency of diffusional oxygen quenching depends on the lifetime of the probe being quenched, and particularly on the nature and energy of the quenched state.
In the case of triplet states, due to their longer lifetimes, rigid matrices (frozen solutions or glasses for example) can be used to prevent diffusional collision between molecular oxygen and the probe, thus avoiding quenching. In the case of the singlet state, molecules with long lifetimes are highly sensitive to the presence of oxygen, whereas those with short lifetimes are only slightly affected. An important example of long-lived probes is pyrene, whose measured fluorescence lifetime (> 100 ns) critically depends on the oxygen content of the media; in contrast, compounds with lifetimes shorter than 1 ns can generally be considered to be insensitive to the presence of oxygen. This can be easily explained with he Stern–Volmer equation (Eq. 15.2) [1].
In liquid solutions at room temperature, the fluorescence of aromatic hydrocarbons or derivatives is known to be quenched by oxygen with a nearly diffusion-controlled rate constant. Values of k q for more than 100 aromatic compounds in common solvents can be found in Ref. [2], as well as the concentration values of dissolved oxygen at 1 atm for ca. 70 common solvents. Let us take as an example 9,10-diphenylanthracene (DPA), whose lifetime is equal to 7.44 ns and k q = 1.7 × 1010 mol−1 dm3 s−1, in cyclohexane at 20 °C, ([O2] = 2.4 × 10−3 mol dm−3). Substitution of these values in Eq. 15.2 yields τ 0/τ = 1.30. This means that, if oxygen is not removed from a solution of 9,10-diphenylanthracene, a significant difference will be observed in the lifetime of the probe, as shown in Fig. 15.1. However, suppose now that the lifetime is 1 ns. Now the ratio τ 0/τ = 1.02 and the effect of oxygen can be considered to be essentially negligible.
Fluorescence emission decays for DPA (with λ ex = 373 nm) obtained in a previously degassed with nitrogen and sealed solution of cyclohexane and b in air-saturated solution of cyclohexane. The autocorrelation functions (AC), weighted residuals and χ 2 values, are also shown. The blue line is the pulse instrumental response
For fluorescent molecules with lifetimes ranging from 10 ns up to 500 ns, the influence of oxygen is even more relevant. For example, for pyrene (one of the most used, and probably most long-lived fluorescence probe), lifetimes values ranging between 382 and 650 ns can be found in the literature for the same solvent [2, 3].
One other way to observe this effect is by obtaining the rate constant for oxygen quenching from reorganisation of Eq. 15.2, leading to Eq. 15.3, and then compare the obtained values with those in the literature:
The values for pyrene and other aromatic hydrocarbons lifetimes are presented in Table 15.1. Note that the most dramatic change in the decay time values in the presence (for 0.21 atm pO2) and absence of oxygen is displayed for pyrene. This is a clear consequence of its long lifetime, making it particularly sensitive to the presence of the oxygen quencher. Applying Eq. 15.2, and using the fluorescence lifetimes of common aromatic hydrocarbons provide rate constants for singlet state quenching by oxygen (k q), which can be compared with those found in the literature [2] (see Table 15.1).
15.3 Quantum Yields and Energies
15.3.1 Quantum yields
From the Jablonski diagram, the different deactivation processes and the associated quantum yields and lifetimes are easily visualised. For all the deactivation processes the quantum yield is defined as the absolute ratio quanta out/quanta in. In the case of the fluorescence process:
However, experimentally, room temperature fluorescence quantum yields (ϕ F) can be determined by comparison with standards of known quantum yield (\( \phi_{\text{F}}^{\text{ref}} \)). The emission quantum yields of these reference compounds should be independent of the excitation wavelength and the absorption and emission range of the sample (cp) and reference (ref) compound should match as much as possible. In practice, the quantum yield is determined by comparison of the integrated area under the emission spectra of optically matched solutions of the samples (\( \int {I(\lambda )^{\text{cp}} d\lambda } \)) and that of the suitable reference compound (\( \int {I(\lambda )^{\text{ref}} d\lambda } \)). The absorbance values should be kept as low as possible to avoid inner filter effects. In these conditions, using the same excitation wavelength, the unknown fluorescence quantum yield (\( \phi_{\text{F}}^{\text{cp}} \)) is calculated using Eq. 15.5 [4],
where n x is the refractive index of the solvents in which the compounds and the reference were respectively dissolved; ODref and ODcp are the optical densities of the reference (ref) and compound (cp) at the excitation wavelength used. Since these experiments are done under usual laboratory conditions (room temperature and atmospheric pressure) and oxygen is present and dissolved in the solvent. In these conditions, oxygen must be removed ideally under several freeze-pump-freeze cycles. However, this is usually not practical. An alternative and more straightforward approach consists in the introduction of a correction factor, \( f_{\text{des}}^{\text{x}} \), that represents the degassing factor for the sample and reference compound, which is given by the ratio between the integrated area under the emission spectra in the absence and presence of oxygen. In general, the most used reference compound is quinine bisulfate [5], which ensures a good reliability in terms of the absolute value of the determined quantum yield (0.546 in 1 mol dm−3 aqueous H2SO4). However, because it is critical to guarantee the same absorption of sample and reference at the excitation wavelength, the required match of absorption spectra may not be possible with quinine bisulfate. A detailed list of other fluorescence standards can be found in Refs. [6, 7].
15.3.1.1 Fluorescence Quantum Yields at Low Temperature (77 K)
The fluorescence quantum yields at 77 K can be obtained by comparison with the spectrum at 293 K run under the same experimental conditions. Equation (15.6) is then applied [8],
where \( \int {I(\lambda )^{\text{x}} d\lambda } \) is the integrated area under the emission of the sample at 77 and 293 K, \( \phi_{\text{F}}^{293\text{K}} \)is the fluorescence quantum yield at 293 K and \( f_{c} \) is the factor that considers the “shrinkage” of the solvent volume (V) upon cooling, given by V 77K/V 293K.
15.3.1.2 Solid-State Fluorescence Quantum Yields
The solid-state fluorescence quantum yields in thin films can be obtained with the help of an integrating sphere, using the method outlined by de Mello et al. [9] and developed by Palsson and Monkman [10]. Equation (15.7) is used to determine the solid-state fluorescence quantum yields (\( \phi_{\text{F}}^{\text{Solid}} \)),
where \( \int {^{\text{cp}} I(\lambda )d\lambda } \) is the integrated area under the emission of the sample compound in the thin film (which excludes the integration of Rayleigh peak), \( \int {^{\text{SA}} I(\lambda )d\lambda } \) is the integrated area under the Rayleigh peak of a sample containing only the quartz or sapphire disc support and \( \int {^{\text{SS}} I(\lambda )d\lambda } \) is the integrated area under the Rayleigh peak in the emission spectra of the compounds under investigation in thin films. Since the emission from the samples is much weaker than the scattered excitation light (Rayleigh peak), the spectra are recorded with a filter that attenuates the emission intensity at the excitation wavelength. This is considered in Eq. 15.7 by \( 10^{{\Updelta {\text{OD}}(\lambda_{\text{ex}} )}} \), the filter transmittance at the excitation wavelength.
15.3.1.3 Phosphorescence Quantum Yields
Phosphorescence measurements (spectra and decays, see Fig. 15.2) can be carried out in glasses at 77 K using a spectrometer equipped with a phosphorimeter unit (and an appropriate light source which can be a pulsed xenon lamp or a laser). The phosphorescence spectra should also be corrected for the wavelength response of the system.
Phosphorescence emission spectrum (a) and phosphorescence decay (b) for an oligothienyl-imidazole in ethanol glass at 77 K. (Reproduced with permission from Ref. [94], Copyright 2010, the American Chemical Society)
Phosphorescence quantum yields (ϕ Ph) are obtained by collecting the phosphorescence emission spectra from optically matched solutions (at the excitation wavelength) of the samples and the reference compound and by applying the following equation,
where \( \int {I(\lambda )^{\text{x}} d\lambda } \) is the integrated area under the phosphorescence emission of the samples and the reference and \( \phi_{\text{Ph}}^{\text{ref}} \) is the phosphorescence quantum yield of the reference compound. When possible, the phosphorescence quantum yields are determined using benzophenone (ϕ Ph = 0.84 in ethanol) as standard [2]. It is worth noting that, as with fluorescence (Eq. 15.5), in the determination of phosphorescence quantum yields, the same solvent should be used for the standard and sample. However, in the case that different solvents have to be used the correction introduced by the refractive index, n, in Eq. (15.5) is not necessary since the phosphorescence quantum yields are obtained in rigid matrices and the properties of the solvent can be considered to be roughly identical.
15.3.1.4 Room-Temperature Singlet Oxygen Phosphorescence
Room-temperature singlet oxygen phosphorescence can be detected at 1,270 nm with the help of an appropriate detector (e.g., Hamamatsu R5509-42 photomultiplier cooled to 193 K in a liquid nitrogen chamber), and following laser excitation (at 266, 355 or 532 nm) of aerated solutions of the samples in a laser flash photolysis spectrometer [11]. In addition, the interposition of a 600-line diffraction grating, instead of the standard spectrometer grating (1,200-line), is needed to extend spectral response to the infrared.
In cases where the singlet oxygen phosphorescence emission intensity is sufficiently strong, measurements can be performed in a spectrofluorimeter using the Hamamatsu R5509-42 photomultiplier previously reported [12]. In both cases the use of a filter (Schott RG1000 for example), placed between the sample and the emission monochromator is essential to eliminate the first harmonic contribution of the sensitiser emission in the region below 850 nm. A characteristic singlet oxygen phosphorescence emission spectrum is shown in Fig. 15.3.
Sensitised emission spectra of singlet oxygen in aerated toluene solutions of 1H-phenalen-1-one and a bis(naphthalene)-oligothiophene at 293 K. Reproduced with permission from Ref. [12], Copyright 2009, the Royal Society of Chemistry
15.3.1.5 Singlet-Oxygen Formation Quantum Yields
When using the laser flash photolysis apparatus, the singlet oxygen formation quantum yields (ϕ Δ) are obtained by direct measurement of the phosphorescence at 1,270 nm following irradiation of aerated solutions of the compounds. The ϕ Δ values are determined by plotting the initial emission intensity for optically matched solutions as a function of the laser energy (Fig. 15.4) and comparing the slope with that obtained upon sensitisation with the reference compound (see Eq. 15.9). Biphenyl in cyclohexane (λ ex = 266 nm, ϕ Δ = 0.73 [13]), 1H–phenalen-1-one in toluene (λ ex = 355 nm, ϕ Δ = 0.93) or Rose Bengal in methanol (λ ex = 532 nm, ϕ Δ = 0.76) are generally used as standards [14].
Plots of the initial phosphorescence of singlet oxygen at 1,270 nm as a function of laser intensity for 1H-phenalen-1-one and an oligothiophene derivative in air-saturated toluene solutions at 293 K. Reproduced with permission from Ref. [95], Copyright 2006, the American Chemical Society
In a spectrofluorimeter, the sensitised phosphorescence emission spectra of singlet oxygen from optically matched solutions of the samples and that of the reference compound should be obtained in identical experimental conditions (see Fig. 15.3). The singlet oxygen formation quantum yield is then determined by comparing the integrated area under the emission spectra of the samples solutions (\( \int {I(\lambda )^{\text{cp}} d\lambda } \)) and that of the reference solution (\( \int {I(\lambda )^{\text{ref}} d\lambda } \)) and applying Eq. 15.10,
with \( \phi_{\Updelta }^{\text{ref}} \) the singlet oxygen formation quantum yield of the reference compound.
15.3.1.6 Triplet–Triplet Transient Absorption Spectra
The transient triplet–triplet absorption spectra are collected by monitoring the optical density change at intervals of 5–10 nm over the range 250–850 nm and averaging at least 10 decays at each wavelength. First-order kinetics should be observed above the μs time range for the decays of the lowest triplet state. Special care should be taken in order to have low laser energy (≤2 mJ) to avoid multiphoton and triplet–triplet annihilation effects. All solutions should be degassed using the freeze-pump-thaw technique, or by bubbling with argon or nitrogen for ≈20 min, and sealed. The earlier is more accurate; however, for routine determinations, and for systems containing polymers, biomolecules, surfactants, etc., it is preferably to degas gently, which leads to the second method.
15.3.1.7 Triplet–Triplet Molar Absorption Coefficients Measurements
15.3.1.7.1 Singlet Depletion Method
This technique uses flash photolysis excitation and involves comparing the observed loss of ground state absorption with the gain in triplet absorption (see Fig. 15.5). The triplet molar absorption coefficients (ε T) are determined according to the well-known relationship [4, 15],
Generic transient differential absorption spectrum
where ΔODS and ΔODT are the changes in optical density due to singlet depletion and to triplet absorption in the differential transient absorption spectra, respectively, and ε S is the singlet molar extinction coefficient. Since assumptions have to be made concerning the absence of absorption of the triplet state in the region of the ground state absorption, where the depletion is being monitored, this method is frequently associated with 50 or more percent error [16].
15.3.1.7.2 Energy Transfer Method
The energy transfer method is the most generally applicable method and involves sensitisation of the triplet state of the unknown compound (acceptor) by an appropriate energy donor in the triplet state (see Scheme 15.2). When using the flash photolysis technique, the unknown triplet–triplet molar absorption coefficient of the acceptor molecule can be obtained by comparison with that of the donor compound (with known molar absorption coefficient) by applying Eq. (15.12) [4].
Schematic representation of the energy transfer method used for determination of the triplet molar absorption coefficient in the laser flash photolysis apparatus
where ΔODD is the maximum absorbance from the transient triplet–triplet absorption spectra of the donor in the absence of acceptor and ΔODA is the maximum absorbance of the acceptor triplet when both the donor and acceptor are present (see Fig. 15.6). For determination of ΔODA, additional corrections were taken into account, in particular, when the decay rate constant of the acceptor k 3 is not negligible. For this situation Eq. (15.13) should be applied [4];
Illustrative example of the shape of the triplet–triplet absorption decay obtained at the wavelength maxima of the transient absorption spectra of the acceptor in the presence of the donor
where k 2 is the donor decay rate constant in the presence of acceptor and \( \Updelta {\text{OD}}_{\text{obs}}^{\text{A}} \) is taken from the maximum observed in the triplet–triplet difference spectra of the acceptor in the presence of donor.
The decay in Fig. 15.6 clearly shows that the acceptor is being formed (by energy transfer from the donor) at the expense and during the decay of the donor (which occurs with a rate constant of k 2 = 4 × 105 s−1) and then decays with a rate constant of k 3 = 2 × 104 s−1.
Experimentally the samples under study are dissolved in solutions of relatively high concentrations of the donor compounds (10−2–10−4 mol dm−3 solutions), while the concentration for the samples with unknown ε T should be of ~10−5 mol dm−3.
15.3.1.8 Intersystem Crossing Quantum Yield Determinations
The singlet–triplet intersystem crossing quantum yields (ϕ ISC) for the compounds with unknown values, \( \phi_{\text{ISC}}^{\text{cp}} \), but known triplet molar absorption coefficient, \( \varepsilon_{\text{T}}^{\text{cp}} \), can be obtained by comparing the \( \Updelta {\text{OD}}_{\text{T}}^{\text{cp}} \), in the triplet–triplet absorption maximum of the compounds, with the \( \Updelta {\text{OD}}_{\text{T}}^{\text{ref}} \) in the triplet wavelength absorption maximum of a reference compound with known intersystem crossing quantum yield, \( \phi_{\text{ISC}}^{\text{ref}} \), and triplet molar absorption coefficient, \( \varepsilon_{\text{T}}^{\text{ref}} \), using Eq. (15.14) [17].
Care must be taken in order to have diluted solutions of the compounds and the reference optically matched at the laser excitation wavelength. Typically, we should have standards to obtain the \( \phi_{\text{ISC}}^{\text{ref}} \) value for the three available wavelengths of a Nd:YAG laser: 266, 355 and 532 nm. Optical parametric amplifiers can be used to tune other wavelengths, but these are not always available and always reduce the laser intensity reaching the sample. Therefore, the ϕ T values are generally determined using as standards naphthalene in ethanol (ε T = 24,500 mol−1 dm3 cm−1 at 415 nm, ϕ T = 0.8) when the laser excitation is with the fourth harmonic (λ ex = 266 nm) of a Nd:YAG, benzophenone in benzene (ε T = 7,220 mol−1 dm3 cm−1 at 530 nm, ϕ T = 1) with λ ex = 355 nm and tetraphenyl-porphyrin in toluene (ε T = 6,000 mol−1 dm3 cm−1 at 790 nm, ϕ T = 0.82) for λ ex = 532 nm [2, 15].
15.3.1.9 Photoacoustic Calorimetry
An alternative method to evaluate the intersystem crossing quantum yield is the photoacoustic calorimetry (PAC) technique, which requires previous knowledge of the triplet energy (see below). In a PAC experiment, the fraction of heat released following excitation with a laser pulse is measured by way of the resulting sound wave [18]. Using knowledge of the energies of the excited states involved (S1 and T1), and the quantum yield of fluorescence (ϕ F), it is possible to determine the quantum yields for the non-radiative processes [18]. Moreover, it is also possible to split the relative contributions of the radiationless processes (heat released) into two components occurring in different time ranges: a fast and slow step (ϕ 1 and ϕ 2 respectively). The fast component results from the internal conversions, S n ~> S1 and S1 ~> S0, and the intersystem crossing to the triplet manifold, and lasts a few ns. The slower component is associated with radiationless processes originating from the lowest triplet state, thus occurring on a much longer time scale (> 10 μs). Longer lived processes are not detected using appropriate PAC transducers. Therefore, the process is considered ‘blocked’ at that energy level, and thus the deactivation of the system (as seen from PAC) stops in the triplet manifold. In this situation, it can be showed that the product of the singlet–triplet intersystem crossing yield (ϕ ISC) and energy (E T) is given by Eq. (15.15), [18, 19] where \( E_{{\bar{\nu }\hbox{max} }} \) is the energy of fluorescence (more correctly, the energy at the maximum fluorescence intensity taken as the Gaussian centre of the fluorescence band), and \( E_{h\nu } \) is the energy of the laser.
The photoacoustic calorimetry technique together with the triplet–triplet energy transfer method (see below) has been used to characterise the non-emissive triplet excited state of indigo, that is, to evaluate the intersystem crossing quantum yield and triplet energy values for this compound [20].
A value of ϕ 1 = 0.9952 was obtained for indigo, and based on the triplet energy of indigo, 134.7 kcal mol−1 (1.05 eV), and the values of ϕ F = 0.0023 [21], together with the energy of the singlet state 43.78 kcal mol−1 (\( E_{{\bar{\nu }\hbox{max} }} \)), a value of ϕ ISC = 0.0065 was obtained [20]. In addition, this value was found in agreement with the value obtained for ϕ Δ = 0.0012 [22], which validates the obtained ϕ ISC value.
15.3.2 Triplet Energy Measurements
As mentioned before, the energy of the first triplet state T1 can be taken from the 0–0 vibronic of the T1 → S0 transition (or from the S0 → T1 transition when induced by the external heavy atom effect [23]), or from the band onset. This is illustrated in Fig. 15.7 for naphthalene, which also includes the transient triplet–triplet absorption of this compound.
Total electronic spectra including absorption (S0 → S1,2), fluorescence (S1 → S0), phosphorescence (T1 → S0) and transient triplet–triplet absorption spectra for naphthalene in methylcyclohexane. The absorption, fluorescence and transient triplet–triplet spectra were acquired at 293 K, whereas the phosphorescence spectrum was recorded at 77 K
In the absence of phosphorescence, the triplet state energy can be obtained by the triplet–triplet energy transfer method as described in the next section [4, 24, 25].
15.3.2.1 Triplet–Triplet Energy Transfer
The absorption spectra of triplet states can also be obtained by the pulse radiolysis technique (see Chap. 8), which briefly consists of using 200 ns–2 μs high-energy electron pulses from a 12 MeV linear accelerator, which is passed through solutions in a 2.5 cm optical path-length quartz cuvette attached to a flow system [26–28]. Optical spectra are normalised for the radiation dose and recorded using a spectrometer consisting of a xenon arc lamp, monochromator, photomultiplier and appropriate filters [27]. In the absence of appropriate sensitisers, pulse radiolysis of benzene solutions containing organic molecules can produce excited states and radical ions (see Sect. 8.2.1.4) [29–32]. However, upon pulse radiolysis of an argon-saturated solution of a donor D (in the sense that it can further transfer energy to an acceptor if present, for example 1 × 10−2 mol dm−3 solutions of biphenyl) in benzene, the only significant species seen by transient absorption spectroscopy (within the time resolution used in this type of experiments; i.e. a few ns) is the triplet state of the donor (biphenyl). On this basis, triplet states of an acceptor (A), for example, a conjugated organic polymer or oligomer, can be selectively produced by energy transfer from appropriate donors which act as triplet sensitisers (S) following pulse radiolysis of benzene solutions as illustrated in Scheme 15.3 [33, 34].
Schematic representation of the pulse radiolysis energy transfer technique applied to the characterisation of the triplet state (triplet energy determination)
The experiments are subject to the kinetically demanded concentration ratio [Bz] ≫ [S] ≫ [A]. This technique was applied to characterise the triplet state of conjugated oligomers and polymers where the concentrations of these were 10−5 mol dm−3 (in terms of repeating units for the polymers), and they were dissolved in benzene solutions of biphenyl and degassed [11, 34–36].
This technique also allows the determination of the triplet energy of the compounds and is known as the triplet–triplet energy transfer method which was developed by Bensasson and Land [4, 24, 25]. Briefly, the procedure is as follows: the compound, with an unknown triplet level, is excited in the presence of a given compound whose triplet energy is known (see Table 15.2).
If the unknown triplet is quenched, then its triplet energy level should lie above that of the standard, whereas if it is not quenched its level lies below that of the standard. By this way, it is often possible to fix upper and lower limits to the lowest triplet levels of the compound under study. The method is based on the finding that when the triplet levels of two compounds differ by more than 0.08–0.12 eV, then the triplet energy will be transferred from the compound with the higher triplet level to the compound with the lower triplet level with a rate constant approaching the diffusion-controlled limit [4]. As an example, indigo quenches the triplets of biphenyl (2.84 eV), perylene (1.53 eV), TPP (1.42 eV) and rubrene (1.14 eV). Assuming that these all involve energy transfer and since indigo is known to sensitise single oxygen (0.94 eV), this puts the triplet somewhere above 0.94 but below 1.14 eV, i.e., 1.0 plus or minus 0.1 eV (see Scheme 15.3).
15.4 The Vibronic Effect
Exceptions to Kasha’s rule can not only be found with azulene and other compounds [37], where emission from S2 is observed (typically because the energetic difference between the S2 and S1 states is sufficiently large to reduce the S2–S1 internal conversion to values close to the S2–S0 radiative rate), but also when there is competition between vibrational relaxation and photochemistry, the so-called vibronic effect. This is an important concept that has been recently developed contrasting with the general wisdom in photochemistry, that only very few exceptions to Kasha’s rule exist. The foundations of the vibronic effects were found in 1966 when Ralph Becker and Joseph Michl noticed that the fluorescence excitation spectrum of a photochromic compound, 2,2-diethylchromene (see Scheme 15.4), was significantly different from the absorption spectrum [38].
Some of the molecules, described in the text, where the vibronic effect was found and investigated
In 1969, a further development of the phenomenon was made [39] in which the relative quantum yields of fluorescence, \( \phi_{\text{F}}^{{{\text{re}}1}} \), were obtained for excitation of all the vibronic levels in the first two electronic excited states of 2,2-diethylchromene (I in Scheme 15.4). It was there found that \( \phi_{\text{F}}^{{{\text{re}}1}} \)showed variation as a function of (a) the electronic state, (b) the vibrational mode and (c) the vibrational level that was being excited. Comparison was made to a molecule of similar structure to 2,2-diethylchromene except the O atom was replaced by –CH2 (1,2-dihydronaphthalene, II in Scheme 15.4). In this case, excitation over 15 wavelengths, between 296 and 250 nm (first entire transition), did not result in any deviation (± 5 %) of \( \phi_{\text{F}}^{{{\text{re}}1}} \) and no photochemistry was observed over irradiation times comparable to that used for the chromene. Indeed, in that work the \( \phi_{\text{F}}^{{{\text{re}}1}} \) values for 2,2-diethylchromene changed, within the first absorption band, from \( \phi_{\text{F}}^{{{\text{re}}1}} \) at 329 nm, to \( \phi_{\text{F}}^{{{\text{re}}1}} \)= 0.33 at 303 nm and in the second electronic absorption band from \( \phi_{\text{F}}^{{{\text{re}}1}} \)= 0.51 at 278 nm, to \( \phi_{\text{F}}^{{{\text{re}}1}} \)= 0.10 at 257 nm [39].
Very surprisingly, these findings had no impact or repercussion during more than 30 years until 1999, when further work with another photochromic compound (Flindersine, III in Scheme 15.4) was published [40]. An improved mechanism was developed to understand the strong dependence of \( \phi_{\text{F}}^{{{\text{re}}1}} \) on the particular vibronic level excited for molecules that underwent photochromism. It is worth noting that in order to validate this model, and equations, no triplet state can be formed, which was validated on the absence of phosphorescence [41, 42] and triplet transients with chromenes and benzochromenes, except for a small amount (~0.1 %) for molecules having a 7,8-benzochromene core. This means that photochemistry should, in these molecules, be considered uniquely in competition with vibrational relaxation at every vibronic level. With this premise, the fraction of molecules that relax from an upper (n) to a lower (n-1) vibronic level (within a given mode) is given by [39–41]:
where k V is the vibrational relaxation constant (in the one of the pioneering works [39] k V was identified as k IC) and k PC is the photochemistry rate constant. The subsequent model is valid in the absence of vibrational redistribution, as it is implicit in Scheme 15.1 and Eqs. 15.16 through 15.22. Considering n vibronic levels one gets:
Applying logarithms to this equation shows that a plot of log \( \phi_{\text{F}}^{{{\text{re}}1}} (n) \) versus n should give a straight line with a slope equal to \( \log [k_{\text{V}} /(k_{\text{V}} + k_{\text{PC}} )] \) and consequently from this, the ratio of k V/k PC can be obtained. This, by itself, showed that, for these molecules, the quantum yield was changing with energy, which was in contradiction with the known wisdom, Kasha’s–Vavilov’s rule.
In order to obtain all the rate constants, and to fully solve the kinetic scheme, one would need to also evaluate the dependence of ϕ PC as a function of n, which was established in the 1999 work where the absolute ϕ PC and ϕ F values for Flindersine were experimentally determined [40]. This led to improved equations to obtain ϕ F, particularly because ϕ F(n) was considered as the experimentally absolute quantum yield of fluorescence as a function of the vibronic level (n) and state that is excited and:
with ϕ F(0) the quantum yield of fluorescence (from n = 0) of S1 and k NR includes k ISC if any triplet is formed [from S1(0) to Tn]. Furthermore, an equation for ϕ PC was given (expansion in series) which allowed the evaluation of ϕ PC(n) and its dependence on ϕ V and the vibronic or state level excited.
with
where ϕ V is the vibrational relaxation quantum yield (in the absence of triplet formation). The ϕ V can be considered a measure of the efficiency of relaxation from one vibronic level to another, in competition with photochemistry within a given mode. It is worth noting that the concept of a vibrational relaxation quantum yield was new and had never been considered before in photochemistry or photophysics. Note also that such as the fluorescence quantum yield at the zero level (Eq. 15.18) has a different expression relative to \( \phi_{\text{F}}^{{{\text{re}}1}} (n) \) (Eq. 15.17), and the same occurs with the photochemistry quantum yield, \( \phi_{\text{PC}} (0) \):
where k NR includes k ISC if triplet states are formed and since ϕ PC is given by:
this means that for n = 0, \( \phi_{\text{PC}} (0) = k_{\text{PC}} (0)/[k_{\text{PC}} (0) + k_{\text{NR}} + k_{\text{F}} ] \), for n = 1, \( \phi_{\text{PC}} (1) = \phi_{\text{PC}} (0)\phi_{\text{V}} + \phi_{\text{PC}} \) and for n = 2, \( \phi_{\text{PC}} (2) = \phi_{\text{PC}} (0)\phi_{\text{V}}^{2} + \phi_{\text{PC}} (1 + \phi_{\text{V}} ). \)
15.5 Absorption and Emission: Avoiding Experimental Pitfalls
The way light interacts with matter and is observed in solution can be summarised in four different manners: absorption, transmission, emission and scattering (Fig. 15.8). The first two are related through the relation of absorbance (A) with transmittance (T) (A = −log10 T). Considering as T = I/I 0 and I abs = I 0−I, that is the difference between the incident light (I 0) and the emerging light (I), the intensity of light absorbed is given by \( I_{\text{abs}} = I_{0} - I = I_{0} - I_{0} T = I_{0} (1 - 10^{ - A} ) \). This expression can be further developed in terms of series of terms,
Typical ways light interacts with matter in a cuvette. The eye in the emission represents the detector location
which, for sufficiently low values of A, reduces to \( I_{\text{abs}} = I_{0} (1 - 10^{ - A} ) \cong 2.303I_{0} \varepsilon cl \).
The intensity of emission, I em, is proportional to the number of molecules in solution and therefore \( I_{\text{em}} = I_{\text{abs}} \times \phi_{\text{F}} \) and consequently \( I_{\text{em}} = I_{0} [2.303\varepsilon cl]\phi_{\text{F}} \) or \( I_{\text{em}} = I_{ 0} \times A \times \phi_{\text{F}} \). However, this stands only for diluted solutions, typically with A ≤ 0.01. When this is not the case, the light that excites the molecules does not reach the centre of the cuvette, where the photomultiplier ‘eye’ is set to observe the emitted light, and in extreme cases no emission is observed even for solutions of a highly fluorescent compound.
When recording the emission spectra of a fluorophore other considerations/observations should be taken into account. The excitation, also known as the Rayleigh, and the Raman peaks is commonly observed in the emission (and excitation) spectra (see Fig. 15.9). For several reasons, people tend to avoid collecting the excitation (Rayleigh) peak when acquiring the emission spectra. However, this can be sometimes critical. The so-called scatter peak should be centred at the wavelength of excitation and this gives a good indication of the monochromator position; any departure from this can indicate that the spectrofluorimeter is somehow misaligned.
Illustrative representation of the Rayleigh and Raman peaks observed in the fluorescence emission spectrum
The intensity of the Rayleigh scattering (I RS) is proportional to the size of the solute particles (r) and to the excitation wavelength (λ ex) through the relationship \( I_{\text{RS}} \propto r^{6} /\lambda_{\text{ex}}^{ 4} \). Moreover, the Raman peak is also present in the emission spectra when the solutions are very dilute or display very low fluorescence quantum yields. Indeed, this transition results from the fact that part of the excitation energy is subtracted by the active vibrational modes of the solvent molecules. For example, with water or other hydroxylic solvents the dominant vibrational mode is the O–H stretching mode at ~3,300 cm−1. When collecting an emission spectrum, this Raman peak (λ RA) will be observed at a wavelength that should be energetically lower by 3,300 cm−1 than the excitation (Rayleigh peak), λ ex(λ RS); which is easily mirrored from the relationship: 1/λ RA = 1/λ ex–0.00033. Taking into consideration that the usual units when tracing an emission spectrum in a spectrofluorimeter are nm, if one excites with λ ex = 290 nm one gets λ RA = 320.69 nm (a difference of 30.69 nm), whereas when the same solution is excited with λ ex = 300 nm one gets λ RA = 333 nm (a difference of 33 nm). Indeed, this difference should be identical and would constitute a proof that what we are observing is a Raman peak. This, indeed, is true when we considered energetic units: λ ex = 290 nm (33,482.76 cm−1) and λ RA = 320.69 nm (31,182.76 cm−1); λ ex = 300 nm (33,333.33 cm−1) and λ RA = 333 nm (30,030 cm−1); in both situations an identical energetic difference of 3,300 cm−1 is obtained.
15.6 Fluorescence Lifetimes. Decay Times. Fluorescence Lifetime Standards in the ns and ps Time Scales
Fluorescence decays are generally measured using the time-correlated single photon counting (TCSPC) technique [43, 44], although the ‘phase-shift’ [45] method has been also used (see Chap. 14). A brief description of TCSPC apparatus with nanosecond and picosecond time resolution is given below in order to illustrate the essential components and requirements for each time resolution.
15.6.1 Fluorescence Decays with Nanosecond Time Resolution
The light source is either a pulsed flash lamp (e.g., the IBH 5000 coaxial flashlamp, typically filled with N2, D2, H2 or mixtures of these gases), or pulsed NanoLEDs. The excitation wavelength is selected with interference filters or a monochromator (e.g., a Jobin–Yvon H20, with a UV-blazed grating), and focused on the sample. The sample emission is passed through a second monochromator (Vis-blazed grating) and detected with a high gain photomultiplier, such as the Philips XP2020Q. The electric signals from the light source and from the photomultiplier are supplied to a TCSPC board (Becker & Hickl or PicoQuant) in a computer as start and stop signals. The TCSPC board integrates two discriminators, a time-to-amplitude converter, and a multichannel analyser where the histogram of counts as a function of time is recorded. Since the measurement time can be long, alternate collection of pulse (recorded with a scattering solution) and sample is usually made [46–48]. If the controlling software allows alternate measurements (1,000 counts per cycle) of the pulse and sample profiles to be performed, a typical experiment is made until 5 × 104 to 20 × 104 counts at the maximum intensity are reached.
With this equipment solid-state fluorescence decays can also be measured with samples in a Horiba–Jobin–Yvon integrating sphere [49]. For these experiments the pulse profile, at the excitation wavelength, is obtained by collecting the pulse with a sapphire blank disc inside the integrating sphere. In this way, it is possible to produce the pulse profile with the instrumental response function (IRF) as generated within the integrating sphere, that, as seen from Fig. 15.10 is significantly different from the IRF obtained with a scattering Ludox solution. In the case of our laboratories, the fluorescence decays are usually analysed using the modulating functions method to evaluate the decay times [6], which are then optimised [50].
Fluorescence decays for a polythiophene derivative in toluene solution at 293 K and in thin film. The dashed lines in the decays are the pulse instrumental response functions in solution (obtained with a Ludox solution) and in the solid state (obtained with a blank sapphire disc inside the Horiba-Jobin–Yvon integrating sphere). Autocorrelation functions (AC.), weighted residuals and Chi square values (χ2) are also present as insets. Reproduced with permission from Ref. [49], Copyright 2007, the American Chemical Society
15.6.2 Fluorescence Decays with Picosecond Time Resolution
A TCSPC apparatus with ps-time-resolution requires three changes with respect to the previous equipment: the light source, the emission photomultiplier and several details in the optical path. An example of a simple home-built picosecond TCSPC apparatus is shown in Scheme 15.5 [35, 51]. The excitation source consists of a picosecond mode-locked Ti:Sapphire laser (Tsunami, Spectra Physics, tuning range 700–1,000 nm, 82 MHz), pumped by a diode-pump YAG Laser (Millennia® Pro-10s, Spectra Physics). A harmonic generator is used to produce the second and third harmonic from the Ti:Sapphire output. The pulse frequency of the excitation beam is reduced with a pulse-picker unit whenever decays longer than 2 ns are present. Samples are measured using the second (horizontally polarised) or the third (vertically polarised) harmonic output beam from the GWU that is first passed through a depolariser (WDPOL-A) and after by a Glan–Thompson polariser (POL1) with vertical polarisation. Emission at 90° geometry is collected at magic angle polarisation (POL2) and detected through a double monochromator (Mono) by a microchannel plate photomultiplier (MCPMT, Hamamatsu R3809U-50). Special care with focusing, and keeping the diameter of the emission beam as small as possible is recommended. Signal acquisition and data processing are performed employing a Becker and Hickl SPC-630 TCSPC module. The full width at half maximum (FWHM) of the IRF ranges from 17 to 22 ps and is highly reproducible within identical system setups. Again, deconvolution of the fluorescence decay curves is performed using the method of modulating functions [50].
Time-correlated single photon counting experimental setup: SHG/THG, second and third harmonic generator; ND, neutral density filter; WDPOL-A, depolariser; POl1, vertically aligned polariser; POL2, polariser at magic angle; F2, lenses; PD, photodiode; Mono, monochromator; MCPMT, microchannel plate photomultiplier; PA, pre-amplifier; CFD, constant fraction discriminators; TAC, time-to-pulse height converter; ADC, analog-to-digital signal converter
The verification of good calibration of the ps-TCSPC system is performed, when possible, with standard compounds that are easily obtained/purified and exhibit a single exponential decay independent of excitation and emission wavelength in a solvent of good spectral grade. In general, depending on the excitation wavelength, p-terphenyl (p-terp) in cyclohexane [52] and 2,2′:5′,2′′:5′′,2′′′-quaterthiophene (α4) in methylcyclohexane are used as standards for calibration of our system (see Fig. 15.11 and Table 15.3). However, 2,5-diphenyloxazole (PPO), 9,10-diphenylanthracene (DPA) and coumarin 153 (C153) are also commonly used standards for calibration of pico- and nanosecond TCSPC, see Table 15.3 [52, 53].
Fluorescence decays showing monoexponential fits of the reference compounds (obtained for the calibration of the ps time-resolution apparatus) a 2,2′:5′,2′′:5′′,2′′′-quaterthiophene in methylcyclohexane (λ ex = 425 nm) and b p-terphenyl in cyclohexane (λ ex = 296 nm). For better judgment of the quality of the fits, autocorrelation functions (AC.), weighted residuals (W.R.) and χ 2 values are also presented as insets. The shorter pulse is the instrumental response
15.7 Excited-State Kinetics
15.7.1 Analysis of Two-State Systems
As mentioned before, an electronically excited molecule A* can undergo a number of (intramolecular or intermolecular) reactions, from which another excited molecule B*, emitting (or not) at a different wavelength, results. This may be called a two-state system, for which, in the most general case, the fluorescence decays of both A* and B* follow a sum of two exponential terms.
We will briefly describe the kinetics of the two-state system, and then apply the result to some common examples of inter and/or intramolecular reactions: excimer formation, charge transfer (leading to an exciplex), electron transfer (leading to radical ions), proton transfer or isomerisation. Scheme 15.6 is a condensed representation of the two-state system.
Kinetic scheme involving two excited state species (A* and B*) formed at the expense of a single ground-state species (A)
15.7.1.1 Dynamic Approach
The time evolution of the concentrations of A* and B* [A(t) and B(t)] is given by Eq. (15.24), where k 1, k -1, k A and k B represent the rate constants of the four processes involved (Scheme 15.6). k X = k 1 + k A is the decay constant of A and k Y = k -1 + k B is that of B.
The solution of Eq. (15.24) predicts double exponential decays for the two species, A and B, (Eq. 15.25),
where the reciprocal decay times λ j = 1/τ j are the eigenvalues of the characteristic polynomial (Eq. 15.26),
and the pre-exponential coefficients a i,j are linear combinations of the eigenvectors of the rate constants matrix k that satisfies the initial conditions (see below).
Substitution of Eqs. (15.25) and (15.26) provides an expression of the rate constants matrix k as a function of the pre-exponential coefficients (a i,j) matrix a and the reciprocal decay time (λ j = 1/τ j) matrix λ (Eq. 15.27, or abbreviated as k = aλa −1).
However, because the pre-exponential coefficients a i,j (concentrations) must be evaluated from the experimental pre-exponential coefficients A i,j (fluorescence intensities at a given wavelength, depending on the experimental setup and number of accumulated counts), it is easier, in the case of the two-state system, to evaluate the rate constants using the procedure first introduced by John Birks [54] to solve the kinetics of excimer formation (the relation between a i,j and A i,j will be discussed latter for three-state or four-state systems [55]).
In the Birks’ method the two reciprocal decay times are expressed as functions of the rate constants by Eq. (15.28) (which also results from Eq. (15.26)).
The pre-exponential coefficients can also be expressed as functions of the rate constants after definition of the initial conditions. If only A has been excited, then the normalised concentration of A* at t = 0 is unity, i.e., A(0) = a 1,1 + a 1,2 = 1 and that of B* is equal to zero, i.e., B(0) = a 2,1 + a 2,2 = 0. Note that the last equation implies a 2,1 = −a 2,2.
The problem of relating the pre-exponential coefficients a i,j to the experimental pre-exponential coefficients A i,j is solved here by using the ratios of the coefficients (because A i,j = S i a i,j , being S i a constant for a given measurement, a i,1 /a i,2 = A i,1 /A i,2 ). However, this solution leaves us with only three experimental values, the two decay times and the A 1,1 /A 1,2 ratio (the A 2,1 /A 2,2 ratio equals −1, i.e., Eqs. 15.31 and 15.32 are not independent), for the four unknowns (rate constants). There are several methods to obtain the fourth piece of information, the most common being the measurement of the lifetime of A* in the absence of reaction (1/k A ), when possible. From the A 1,1 /A 1,2 ratio one obtains,
and from rearrangement of Eq. (15.33) we obtain the value of k X ,
which, with the value of τ A and from \( k_{X} = k_{1} + 1/\tau_{A} \), provides the value for k 1.
Because \( k_{X} + k_{Y} = \lambda_{1} + \lambda_{2} \) (from Eq. 15.28) we obtain the following relationships:
and
Simple manipulation of Eqs. (15.36) and (15.37) leads to:
and finally, from \( \tau_{B} = 1/(k_{Y} - k_{ - 1} ) \), we obtain τ B.
Despite its mathematical simplicity, the foregoing procedure may present some experimental difficulties, which normally result from: (1) small values of some pre-exponential coefficients in the decays of A* and/or B*, (2) too close decay times (differing by less than a factor of two) that mix, or (3) insufficient time resolution. In most cases, these difficulties can be overcome by changing the experimental conditions (temperature, solvent viscosity and/or polarity, and concentration among others, e.g. pressure)Footnote 1 and/or by coupling the results from time-resolved fluorescence with those obtained from steady-state experiments (Stern–Volmer [1] and/or Stevens-Ban [56] plots).
15.7.1.2 Steady-State Approach
Under steady-state conditions (continuous irradiation), the concentrations of A and B do not change with time,
and, if only A is excited, Eq. (15.24) reads:
where I ss is the mole of quanta absorbed by A, per litre and per second and A ss and B ss are the steady-state concentrations of A and B, respectively. Rearranging Eq. (15.40) [57], one obtains,
and, because the (wavelength) integrated fluorescence intensities of A and B are proportional to their respective steady-state concentrations and radiative rate constants (ϕ A = k FA A ss and ϕ B = k FB B ss), the following relationship between the fluorescence intensities and rate constants holds:
15.7.1.3 Stevens–Ban plots: Determination Of Thermodynamic Parameters Associated with an Excimer Formation Reaction
Equation (15.42) is the basis of Stern–Volmer and Stevens–Ban plots. The Stevens–Ban plot [56] is a representation of ln(ϕ B/ϕ A), given by Eq. (15.43), versus the reciprocal temperature, T −1:
For exothermic reactions, these plots have a characteristic parabolic like shape (see Fig. 15.12) where two limits are reached: the high (HTL) and the low temperature limits (LTL). In the LTL, k −1 ≪ k B, while the reverse condition (k −1 ≫ k B) defines the HTL. In these limits, Eq. (15.43) reads:
Generic Stevens–Ban plot showing the high (HTL) and low temperature limits (LTL), the transition temperature between these two regimes (T*), the enthalpy (ΔH) and the activation energy of excimer formation (E1), together with the δ parameter (see text for further details)
Considering that the ratio of the radiative rate constants is approximately independent of temperature (the dependence of the radiative rates on the solvent refractive index, which depends on temperature, cancels), and the dependence of k B on temperature is often weak, the LTL slope of the Stevens–Ban plot (Eq. 15.44) provides an approximate value for the activation energy of the forward reaction (E 1), and the HTL slope (Eq. 15.45) is equal to the reaction enthalpy (ΔH * = E 1 − E −1).
By comparing Eqs. (15.44) and (15.45), it is seen that the LTL and HTL straight lines cross at a temperature at which k −1 = k B (see Fig. 15.12). At this temperature, the difference δ between the crossing point and the full function (Eq. 15.43) is equal to ln 2.
When the fluorescence intensity of A in the absence of reaction \( \phi_{\text{A}}^{ 0} \) (\( \phi_{\text{A}}^{ 0} = k_{\text{FA}} {\mathbf{A}}_{\text{SS}}^{ 0} \), with \( {\mathbf{A}}_{\text{SS}}^{ 0} = I_{\text{SS}} /k_{\text{A}} \)) can be measured, the \( \phi_{\text{A}}^{ 0} /\phi_{\text{A}} \) ratio (Eq. 15.46) provides an alternative method to analyse the steady-state data.
Classical Stern–Volmer plots are normally used when the back reaction is negligible (k −1 ≪ k B) and the forward reaction in Scheme 15.6 is bimolecular, and consequently k 1 is a pseudo-first-order rate constant of the form \( k_{1} = k_{\text{q}} [\text{Q}] \). Under these conditions, the representation of the \( \phi_{\text{A}}^{ 0} /\phi_{\text{A}} \) ratio as a function of [Q] is linear with intercept = 1, and slope k SV = k 1/k A (= k q τ A).
However, Eq. (15.46) can be useful in many other ways. For example, the representation of \( (\phi_{\text{A}}^{0} /\phi_{\text{A}} - 1)k_{\text{A}} \) as a function of the reciprocal temperature, T −1 provides a modified Stevens–Ban plot, which has, at least, three advantages over the classic Stevens–Ban plot. First, it does not require B to be fluorescent. Second, it avoids the assumption that k FB /k FA is independent of temperature. Third, from the LTL (k −1 ≪ k B), the value of k 1 is obtained, besides that of E 1. Finally, when both \( \phi_{\text{B}} /\phi_{\text{A}} \) and \( \phi_{\text{A}}^{ 0} /\phi_{\text{A}} \) are available the \( k_{\text{FB}} /k_{\text{FA}} = \phi_{\text{B}} /\phi_{\text{A}} - \phi_{\text{A}}^{ 0} /\phi_{\text{A}} \) ratio can be obtained (Eqs. 15.43 and 15.46).
As mentioned, the formalism derived here is valid for any excited state system involving two species. We will next describe the required adaptations for the most common reactions.
15.7.1.4 Excimer Formation
Aromatic hydrocarbons such as pyrene, naphthalene, perylene or other related compounds are known to undergo excimer formation reactions in the excited state. For intermolecular excimer formation, the kinetics fall in the category of two-state systems (Scheme 15.7), as well as for the intramolecular case when the interconnecting chain is sufficiently long. With short connecting chains, two excimer conformations may occur, leading to three excited state species (three-state system, see below).
Kinetic scheme for intermolecular excimer formation
It is worth noting that Scheme 15.6 is equivalent to Scheme 15.7, with k 1 = k a[M], where k a is the bimolecular association rate constant (diffusion controlled in most excimer formation reactions) and [M] is the concentration of monomer in the ground state (k −1 is the dissociation rate constant, which is usually denoted k d).
From the above-mentioned aromatic hydrocarbons, pyrene is for sure the most widespread excimer forming fluorescent probe. The fluorescence spectra of pyrene are known to display the characteristic vibronically resolved pyrene band with a maximum at ≈375 nm, together with a structureless long-wavelength band (ca. 480 nm). Typically, only at concentrations of pyrene above ca. 10−3 mol dm−3, intermolecular excimer formation is clearly observed. For intramolecular excimer formation (concentration independent kinetics) the long-wavelength emission band can be observed for concentrations as low as 10−7 mol dm−3.
Due to the fact that the two emission bands of pyrene (monomer and excimer) are well separated, the monomer and excimer decays can be measured without mutual interference, and analysed with the two-state model (Eqs. 15.33–15.38). For the intermolecular case, the monomer lifetime is measured with pyrene at very low concentration (< 10−7 mol dm−3), but for the intramolecular case a model compound (an alkylpyrene) is required [58, 59]. For short interconnecting chains this procedure may also be problematic [60]. Excimer formation with pyrene has also been measured as function of temperature, using both time-resolved and steady-state fluorescence (Stevens–Ban plots), in order to evaluate the energy parameters of the reaction.
In Fig. 15.13, the fluorescence decays of 1,1’-dipyrenyldecane [1Py(10)1Py] in n-decane, are presented. In this compound, the two pyrene units are connected by a saturated carbon chain of 10 carbons, in this case only one excimer (more stable and non-parallel conformation) and one monomer exist; this leads to a bi-exponential decay in which the sum of pre-exponential factors at the emission wavelengths of the excimer cancel out.
Fluorescence decays of 1Py(10)1Py in n-decane at 293 K obtained with λ ex = 339 nm and collected at 375 nm (monomer) and 480, 520 nm (excimer). At 375 nm an additional exponential of 259 ns (with a pre-exponential factor of 0.028) is needed to fit the decay. This most likely results from un-reacted pyrene; a similar situation has been reported elsewhere [89, 96] for 1Py(3)1Py. For a better judgment of the quality of the fits, autocorrelation functions (AC.), weighted residuals (W.R.) and χ 2 values are also present as insets. The short pulse line in the first channels is the pulse instrumental response
15.7.1.5 Charge Transfer and Electron Transfer Exciplexes
There is some parallelism between charge/electron transfer and excimer formation. They both are two-state systems (in the simplest case), and both can occur either intra- or intermolecularly [61–69]. In this case, Scheme 15.6 is slightly modified as for excimer formation (Scheme 15.8). The major difference between charge transfer (Scheme 15.8a) and electron transfer (Scheme 15.8b) reactions lies on the reaction product: an exciplex (more or less fluorescent), resulting from partial charge transfer, and a non-fluorescent, solvent-separated radical-ion pair from (full) electron transfer, respectively.
a exciplex formation and b full electron transfer. The excited molecule can be either the electron acceptor A or donor D
For a given acceptor–donor system, charge transfer can switch to electron transfer by increasing solvent polarity. Potentially, the kinetic analysis of electron transfer can be more complex than charge transfer for a number of reasons. First, the reaction product is non-fluorescent (less information is available from fluorescence techniques). Second, electron transfer can occur at distances larger than the collisional distance, leading to distance-dependent rate ‘constants’, i.e., to non-exponential decays. Third, the geminate radical-ion pair can count as a third species (leading to a three-state system), except when either the dissociation rate constant k diss (leading to the solvent-separated radical-ion pair) or the recombination rate constant k rec (to give the ground states of acceptor and donor) is much larger than recombination to the excited state of either the acceptor or donor (which is frequently true). In this case k −1 = 0 and thus a 1,1 = 0 (Eq. 15.27), leading to a single exponential decay of the fluorophore. Thus, only the electron transfer rate constant is accessible from fluorescence studies, being the sequent processes accessible only from time-resolved absorption (flash photolysis and/or pump probe). Note that for intramolecular electron transfer, the full dissociation of the geminate radical-ion pair is hindered.
For charge transfer leading to a fluorescent exciplex, all rate constants can be evaluated from the fluorescence decays, but particular attention should be paid to the possibility of occurrence of (1) transient effects, (2) the harpoon mechanism [70] (the electron goes first and then the exciplex is formed) and (3) ground-state charge-transfer complexes. All these phenomena lead to deviations from double-exponential decays and/or differences between Stern–Volmer plots obtained from time-resolved (τ 0/τ vs [Q]) and steady-state (I0/I vs [Q]) measurements.
In conclusion, for the analysis of fluorescence data in systems where charge or electron transfer reactions occur, the availability of both time-resolved and steady-state fluorescence data, as a function of solvent polarity and temperature, has particular importance. Moreover, experimental (or theoretical) oxidation and reduction potentials of A and D are also important to rationalise the results.
15.7.1.6 Proton Transfer
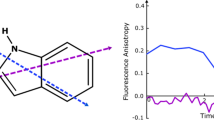
It is well-known that aromatic alcohols become stronger acids in the excited state (less negative charge on the hydroxyl oxygen), while aromatic acids or ketones become stronger bases (more negative charge on the carbonyl oxygens) [51, 71–74]. Therefore, electronic excitation triggers a proton transfer reaction (usually to or from water). When an aromatic molecule possesses both acid and base moieties in appropriate locations, intramolecular proton transfer can occur in a few ps or faster as with 3-hydroxyflavothione [75]. A classical example of intermolecular proton transfer to water is β-naphthol shown in Scheme 15.9, where N is the neutral (acidic) form, and A is the anionic (base) form [73].
Two examples of proton transfer in the excited state. The top (with β-naphthol, [73]) is illustrative of an intermolecular proton transfer (to the solvent) process whereas the bottom (with indigo, [22]) is illustrative of an intramolecular proton transfer. In the two cases the kinetic scheme (in the middle) applies with a single ground-state species; however in the case of indigo, the back-proton transfer reaction in the excited state is unlikely
Scheme 15.9 is once again similar to Scheme 15.6 except that the protonation back reaction is bimolecular. Thus, the two-state formalism is applicable with some changes concerning the determination of the fourth unknown. Because the lifetime of N in the absence of reaction, \( \tau_{\text{N}} = 1/k_{\text{FN}} \), cannot be reliably measured with N even at very low pH values, it has to be obtained with a parent compound, with which the proton transfer reaction does not occur (in this case, 2-methoxynaphthalene). However, the implicit assumption of the procedure, that the lifetime measured with the methoxylated compound would be equal to τ N, may be dangerous with the strongly hydrogen bonding solvent water (the most common solvent for proton transfer).
Alternatively, τ A may be evaluated independently at sufficiently high pH values such that A is present in the ground state and can be selectively excited. This provides a single exponential decay with the lifetime, τ A. Another, perhaps safer, solution is to profit from the fact that the back reaction is bimolecular, \( k_{ - 1} = k_{\text{p}} [{\text{H}}^{ + } ] \) and we can vary [H+]. Thus, k p can be obtained, [51, 55], from the slope the plot of \( \lambda_{1} + \lambda_{2} = k_{\text{X}} + k_{\text{Y}} \) as a function of [H+], because all the remaining rate constants are pH independent.
15.7.2 Three-State Systems
Excited state processes involving three species (three-state systems) are now commonly observed. These can be found in excimer formation (oligomers and polymers containing pyrene, naphthalene and carbazole), proton transfer [76], charge transfer, etc.
The most general kinetic scheme for a three-state system is the so-called photokinetic triangle (Scheme 15.10), described by Eqs. (15.48–15.50) (these are simple extensions of Eqs. (15.24–15.26). The decays are sums of three exponential terms (Eq. 15.49), and the kinetics involves nine unknowns (six reaction rate-constants and three reciprocal lifetimes).
Kinetic scheme involving three species
with k X = k A + k 1 + k 2, k Y = k B + k −1 + k −3, and k Z = k C + k -2 + k 3.
In this case the extension of the algebraic analysis of Birks is too complex and the rate constants are better evaluated with Eq. (15.51) (see also Eq. 15.27), which relates the experimental pre-exponential coefficients A i,j to a i,j, as previously discussed.
Let us first consider that only the species A is excited, and that the fluorescence decays of A, B and C can be measured in independent experiments (the presence of emission overlap will be discussed latter). Then, each of the three rows of the experimental pre-exponentials matrix A is affected by a constant depending on: (1) the number of counts accumulated, (2) the fraction of the total emission collected at the measurement wavelength and (3) the instrumental response at that wavelength, i.e. A i,j = S i a i,j . The relation between matrixes A and a is given by Eq. (15.52), and its substitution in Eq. (15.51) yields the explicit relation of the rate constants matrix to the experimental matrixes of rate constants λ and pre-exponential coefficients, A (Eq. 15.53).
This adds three unknowns (S 1 , S 2 and S 3 ) to the initial nine unknowns giving a total number of 12 unknowns, which are larger than the number of independent equations provided by the three decays (3 reciprocal decay times plus 7 = 3 + 2 + 2 pre-exponential coefficients). Therefore, the solution of Eq. (15.53) requires additional information.
As discussed for the two-state systems, there are several possibilities, depending on the system, to obtain such information. These are: (1) independent measurement of k A, k B or k C, (2) changing the concentration of quencher (when a bimolecular reaction is involved) and (3) using steady-state fluorescence data (Eqs. 15.55 and 15.56).
Under steady-state conditions, the integrated fluorescence intensities of A, B and C are given by Eq. (15.54) (an extension of Eq. 15.42),
and the ratios of fluorescence intensities are given by Eqs. (15.55) and (15.56).
Two examples, illustrating the foregoing possibilities to obtain the additional information will be described below.
15.7.2.1 Excimer Formation
A classic example of a three-state system is the intramolecular excimer formation with 1,1’-dipyrenylpropane [1Py(3)1Py], a dipyrenyl oligomer with three carbon atoms connecting the two pyrenes (see Fig. 15.14). Three species are observed: one monomer and two excimers (sandwich-like and twisted conformations). It is worth noting that in the case of 2,2’-dipyrenylpropane [2Py(3)2Py] only one monomer and one excimer (less stable with a parallel sandwich-like geometry and decay time of 150 ns, [59]) are present, because the C2 symmetry of the pyrene-chain bond axis allows only one excimer conformation. Also, with the longer (ten carbon atoms chain) of 1,1’-dipyrenyldecane [1Py(10)1Py], see Fig. 15.13 above, only one monomer and one excimer are present, because the longer chain is sufficiently flexible to allow relaxation to the most stable conformation of the excimer (two-state system).
Chemical structure of 1Py(3)1Py, together with the drawings of the two excimers [97] (E1 and E2) conformations
The short propane chain of [1Py(3)1Py] does not allow direct interconversion from E 1 to E 2 or E 2 to E 1 without excimer dissociation, i.e., k 3 and k −3 are equal to zero (Scheme 15.11), thus reducing the number of unknowns to seven. Additionally, k M can be measured with a parent compound (e.g., 1-propylpyrene).
Kinetic scheme for the formation of two distinct and non-interconverting excimers E 1 and E 2
Despite the simplification to a number of six unknowns (smaller than the seven equations obtained from the fluorescence decays), there are still problems, because the fluorescence decays of the two excimers cannot be measured independently from each other (due to strong overlap of the emission spectra of E 1 and E 2 ). Thus, the pre-exponential coefficients of the excimer decays are linear combinations of A 2,j and A 3,j, and their splitting implies knowledge of the emission spectra and the radiative rate constants of the two excimers (see below). The splitting is not simple because the emission spectra of E 1 and E 2 nearly overlap, and thus the fluorescence decays of [1Py(3)1Py] do not substantially change along the excimer band (see pre-exponential coefficients at 480 and 520 nm in Fig. 15.15).
Fluorescence decays of 1Py(3)1Py in n-heptane at 313 K obtained with λ ex = 339 nm and collected at 375 nm (monomer) and 480, 520 nm (excimer). Autocorrelation functions (A.C.), weighted residuals (W.R.) and χ2 values are also presented as insets
This limitation leaves us with only five pieces of information from the fluorescence decays (three decay times and two ratios of pre-exponential coefficients from the monomer decay), for the six unknowns.
The kinetics were successfully solved, using an extension of the Birks’ method, by measuring the decays as a function of temperature, and globally fitting the data, under a number of reasonable assumptions on the temperature dependence of the rate constants [58].
15.7.2.2 Proton Transfer and Tautomerisation
Another representative example of a three-state system has been observed with 7-hydroxy-4-methylcoumarin (7H4MC) in water, where three excited species are present: the neutral N*, anionic A* and tautomeric T* forms of 7H4MC (see Fig. 15.16 [77]).
Emission spectra of 7H4MC in water as a function of the pH. The spectra display three bands: N*(380 nm), A*(450 nm), T*(480 nm). The structures of N, A and T are depicted in the picture
Figure 15.17 illustrates a typical decay at pH = 1.6 (obtained with ps time resolution) and the overall decay time dependence on pH (obtained with ns-time resolution). There is good agreement of the ns and ps data, as attested by the values obtained at [H+] = 0.025 mol dm−3 (ps-time resolution) which match the extrapolated values in the left-hand panel obtained with ns time resolution.
Left: decay time values dependence with [H+], obtained with ns-time resolution, for 7H4MC in a dioxane–water mixture 1:4, [77]. Right: fluorescence decays of 7H4MC in a dioxane–water mixture 1:4, [H+] = 0.025 M, obtained at 293 K and at three different emission wavelengths: 370 nm (N*), 450 nm (A*) and 530 nm (T*), with ps-time resolution. The arrows in the left-hand panel indicate the [H+] value at which the decay times values in the right hand panel were obtained
The fluorescence decays and steady-state data (see below) indicated that all the prototropic reactions shown in Scheme 15.12 had to be considered (six rate constants plus three reciprocal lifetimes).
Photokinetic triangle for 7H4MC [77]
An additional difficulty to solving the kinetics results from the fact that the fluorescence decay of A * cannot be obtained without contribution from those of N * and T *, and that of T * will always have some contribution of A * (see Fig. 15.16). When the decays of A * and T * are measured at 450 and 530 nm, respectively, the equation that relates the pre-exponential matrixes a and A is given by Eq. (15.57),
where \( \alpha = \frac{{f_{\text{N}} (450)}}{{f_{\text{A}} (450)}},\;\;\beta = \frac{{f_{\text{T}} (450)}}{{f_{\text{A}} (450)}},\;\gamma = \frac{{f_{\text{A}} (530)}}{{f_{\text{T}} (530)}} \), and \( f_{i} (\lambda ) = k_{\text{Fi}} \frac{{I_{\text{i}} (\lambda )}}{{\int\limits_{0}^{\infty } {I_{\text{i}} (\lambda )d\lambda } }} \) is the fraction of the fluorescence intensity of the species i (= N, A or T) that is emitted at wavelength λ. Therefore, the determination of the rate constants using Eq. (15.53) involves five additional unknowns (S 1, S 2, α, β and γ), i.e., a total of 14 unknowns for the 10 pieces of information provided by the fluorescence decays (three lifetimes and seven pre-exponential coefficients).
Let us see for this case how the four missing pieces of information can be obtained. First, the fluorescence lifetime and quantum yield of N * can be measured with the parent compound 7-methoxy-4-methylcoumarin, thus providing the values of k N and k FN. The same measurements can be carried out for the anion, by measuring 7H4MC at basic pH, to evaluate the values of k A and k FA. At this stage, the number of unknown rate constants has been reduced to seven (k N and k A are known), and the values of f N(λ) and f A(λ) can be evaluated from the radiative constants and emission spectra (after spectral decomposition, shown in Fig. 15.16), yielding the value of α. Now, by guessing a value for k FT, f T(λ) can also be evaluated to obtain estimated values for β and γ (depending only on the guessed k FT). This reduces the number of the additional unknowns to three (S 1 , S 2 and k FT), i.e., a total number of unknowns (7 + 3 = 10) equal to the number of pieces of information provided by the fluorescence decays. However, because of the propagation of the experimental errors in the calculations, this equality is not sufficient.
Let us now analyse the information that can be extracted from steady-state fluorescence data. First we note that the matrix of rate constants k (Eq. 15.57) contains two pseudo-unimolecular rate constants, k -1[H+] and k -3[H+] (Eq. 15.58, where \( k_{\text{X}} = k_{\text{N}} + k_{1} + k_{2} \), \( k_{\text{Y}} = k_{\text{A}} + (k_{ - 1} + k_{ - 3} )[{\text{H}}^{ + } ] \) and \( k_{\text{Z}} = k_{\text{T}} + k_{ - 2} + k_{3} \)).
Second, by adapting Eqs. (15.55) and (15.56) (replacing A, B and C with N, A and T) one obtains Eqs. (15.59) and (15.60), which predict that ϕ N/ϕ A and ϕ T/ϕ A are linear functions of [H+], a prediction that has been experimentally observed [77].
Thus, the intercepts and slopes of ϕ N/ϕ A and ϕ T/ϕ A versus [H+] gives four additional values related to the rate constants, which complete and exceed the required information.
The data analysis can be carried out by calculating the matrix of rate constants k with an initial guess of S 1, S 2 and k FT and optimising these values by minimisation of the differences between the experimental and calculated values of k N, k A, which result of intercepts 1 and 2 and slopes 1 and 2 in Eqs. (15.59) and (15.60).
Other examples of three-state systems can be found with the β-carboline harmine [78, 79], poly(acrylic acid) labelled with pyrene [80] or naphthalene [81], polyphenylsiloxanes [82], poly(N-vinylcarbazole) [83, 84], etc. The solution of a four-state system has also been carried out [55].
15.7.3 Other Models: Lifetime Distributions, Stretched Exponential and Transient Effects
15.7.3.1 Lifetime Distributions
The analysis of time-resolved fluorescence decay curves, using a sum of discrete exponential functions to fit the experimental data, is based on a simple assumption: the number of different exponential terms used has to be equal to the number of kinetically different excited state species present in the molecular system. While this assumption has the advantage of providing a clear physical meaning for the fitting parameters, decay times and pre-exponential coefficients, the identification of the different kinetic species is frequently not evident, particularly in more complex systems like polymers and proteins, and this approach has been questioned [85].
The possibility of using alternative kinetic schemes to rationalise the same fitting parameters, and the fact that in general a distribution of lifetimes can be fitted successfully by a sum of discrete exponential terms are the main reasons against the multi-exponential approach [86]. However, this difficulty can be overcome when narrow and well-separated time distributions can be identified, and data obtained from other techniques can be used as a functional block to help on the model selection.
Lifetime distributions can be expected in different situations: molecules incorporated in micelles and cyclodextrins, polymers—in solution and films, solid solutions, complex biological molecules—as for example proteins with several residuals located within different environments, which make impossible the use of the multi-exponential approach [45, 85, 87, 88].
In such cases, the individual pre-exponential amplitudes (a i) are substituted by distribution functions a i(τ), and the intensity decay component, associated with a time constant τ, is given by \( I(\tau ,t) = a(\tau )e^{ - t/\tau } \). The entire decay law will then be described by the sum of the individual decay components, weighted by the amplitudes: \( I(t) = \int\limits_{0}^{\infty } {a(\tau )e^{ - t/\tau } d\tau } \), with \( \int\limits_{0}^{\infty } {a(\tau )d\tau = 1} \) [45, 85].
In the absence of a physical model, describing the underlying physics that leads to the appearance of a distribution of lifetimes in the molecular system, the best way to analyse the data is to use a method that does not require the assumption of a particular distribution shape to describe the a(τ) values, as for example the maximum entropy method (MEM) [6].
While still being criticised by some for subjectivity on the specification of the fitting parameters, MEM is thought not to introduce more components than those necessary to fit the data, and has the advantage of giving a smooth a(τ) plot, that reveals the shape of the distribution. However, the instability of the distribution recovered has been reported for repeated experiments, even under exactly the same experimental conditions [63, 89, 90].
The MEM analysis of time-resolved fluorescence decays of several copolymers is shown in Fig. 15.18a. For the homopolymer PF2/6, only a narrow distribution is observed around 360 ps. However, for copolymers PF/FLx, with different fractions of fluorenone residues, distributed randomly along the polymer chain, the distribution at 360 ps is accompanied by two additional peaks. These are observed around 20 and 100 ps as a result of quenching of polyfluorene emission, due to energy transfer from the fluorene to the fluorenone sinks. Figure 15.18b shows the fluorescence decay of the copolymer labelled with 25 % of fluorenone groups, analysed with a sum of three exponential functions. Note the good agreement between MEM and multiexponential analysis [91].
Maximum entropy method (MEM) analysis of PF2/6 and PF/FLx copolymers fluorescence decays a, and fluorescence decay of PF/FL0.25, with emission collected at 415 nm, analysed with a sum of three exponential functions, decay times (τ i), amplitudes (A 415 nmi ) and χ2 are also given in b. Reproduced with permission from Ref. [90], Copyright 2006, the American Chemical Society
15.7.3.2 Dipole–Dipole Energy Transfer and Stretched Exponential
Dipole–dipole (Förster) energy transfer depends on the distance and relative orientation of the donor and acceptor dipoles. For the simplest case of transfer from a donor to an isotropic three-dimensional distribution of energy acceptors, the fluorescence decay of the donor is given by Eq. (15.61), where \( A = (4/3)\pi^{3/2} R_{0}^{3} c_{\text{A}} \) is proportional to the cubic power of the Förster radius R 0 and to the acceptor concentration c A, and β is equal to 1/2.
For other distributions and/or dimensionalities the donor decay becomes more complex with β assuming values equal to 1/6 and 1/3 for one and two dimensional systems, respectively [85, 86]. In many cases, such as photon-harvesting polymer systems, where a distribution of relaxation times is expected, due to intrachain donor–acceptor energy transfer steps, either the distributions and/or the dimensionality are difficult to define a priori. Thus the use of a stretched exponential (Eq. 15.61, where 0 < β < 1 is an empirical parameter) has been proposed.
Equation 15.61 predicts two time regimes for 0 < β < 1 (see Fig. 15.19, where A was set equal to 1). The non-exponential behaviour is more pronounced for small values of β and becomes almost imperceptible when β approaches unity.
Stretched exponential decay curves for several values of β. For small β values, the curve decays faster for t < τ 0, and is followed by a slower tail afterwards
In the particular case of conjugated polymers, the situation can be even more complex due to the presence of both Dexter and Förster energy transfer mechanisms (the former being dominant at short distances), and the possibility of interchain energy transfer steps; these are favoured in polymer solid films due to a closer proximity between chains.
Energy migration is strongly dependent on the number of neighbour chromophores that a given excitation can ‘hop’ to and in conjugated polymers this is particularly evident. These long molecules can be looked as being formed by an array of different chromophores (conjugated segments) of close energy, separated by chemical and conformational defects. Since shorter segments have higher energies than the longer ones, an energy funnelling from shorter to longer segments occurs every time an excitation is created at sufficiently higher energies.
At early times, after an excitation has been created, there are a large number of acceptors available, and migration proceeds in a sub-ps time scale, after some hops, as the excitation moves to lower energy sites, the number of acceptors decreases, and the rate of migration slows down. This initial regime of migration is described by a time-dependent rate constant and is referred to as dispersive migration.
After reaching the lower energy sites available in the polymer density of states, energy migration can only proceed via dynamical thermal fluctuations of the polymer backbone that dynamically alter the polymer energy landscape. Such fluctuations can break and form new energy sites very close in energy that allows migration to proceed with a constant rate. This regime, occurring in solution on a time window that goes typically up to a hundred of picoseconds, is referred to as non-dispersive migration.
The analysis with a stretched exponential (Eq. 15.61) of the fluorescence decay of a fluorene copolymer labelled with 25 % of fluorenone groups is shown in Fig. 15.20. Table 15.4 shows the results obtained from the analysis of fluorescence decays of PF2/6 and several PF/FLx copolymers in toluene solution with Eq. (15.61) [91].
Stretched exponential analysis of PF/FL0.25 copolymer fluorescence decay, with emission collected at 415 nm. Reproduced with permission from Ref. [91], Copyright 2006, the American Chemical Society
Apart from the identification of different physical kinetic species, the picture that emerges from the data analysis with Eq. (15.61) (see Table 15.4) agrees with the interpretation obtained from analysis with a sum of three exponential functions, showing that with the increase on the fluorenone fraction in the copolymer backbone, the decay times associated with the quenching of the copolymer emission are becoming faster, in agreement with a more efficient energy transfer from fluorene to fluorenone moieties [91]. At higher fluorenone fractions the local concentration of acceptors increases, giving larger A values; the importance of the fast component in the overall decay also increases with the fluorenone fraction, giving smaller β values. However, the physical meaning of parameters τ 0 and β is not so clear; actually the former increases with the fluorenone fraction, assuming a value of 487 ps for PF/FL0.25, about 120 ps longer than the polyfluorene lifetime.
However, even in the absence of a physical model, which would justify the use of a particular model, sum of exponentials or stretched exponential functions, relevant information can be obtained from time-resolved fluorescence decays of complex systems. For example, Fig. 15.21 shows the temperature dependence of the migration rate constant (obtained using a sum of exponential functions) in the non-dispersive regime for a polyfluorene copolymer film. At room temperature, the migration shows an activated regime with an energy barrier of 23 meV, turning over to a non-activated regime below 200 K. Above this temperature transition, migration is a thermally assisted process, with indication that the thermal energy value (k B T) is larger than the average energy difference between two close segments, and both “downhill” and “uphill” exciton jumps in energy are possible. Below 200 K, the thermal energy value, kBT, becomes smaller than the average energy difference between two close segments and thermal assisted around Uphill and downhill with in a non-activated way and at slower rate, since the number of energy acceptors available has also decreased [92]. The behaviour identified in Fig. 15.21 was confirmed by fluorescence steady-state experiments, giving similar energy barrier in the activated region and turn-over temperature.
Energy migration rate constant plotted against the reciprocal of temperature, for a fluorene copolymer containing dibenzothiophenedioxide and benzothiadiazole units. Both activated and barrier-less temperature regimes are observed. Reproduced with permission from Ref. [92], Copyright 2009, Wiley–VCH
15.7.3.3 Transient Effects
An additional source of non-exponential emission decays is the transient effect that might appear at short times following excitation. This effect is frequently found in collisional quenching controlled by diffusion. In this situation, the quenching rate depends on the encounter probability between the fluorophore and the quencher, which is obviously also dependent on the diffusion coefficient and on quencher accessibility; at early times, fluorophores that have quenchers located at short distances will react almost ‘immediately’, leaving behind just those that have to diffuse to encounter a quencher centre. The phenomenon is going to be perceived as a quenching rate that is time dependent at early times, and results in a faster decay component of the fluorophore emission [93].
While important, transient effects often pass unnoticed due to limited time resolution of the experimental apparatus or due to the small magnitude of the effect; in fact, the phenomenon is more easily detected on slow diffusion processes in viscous media and long fluorescence lifetimes. The non-exponential intensity decay, resulting from a transient effect is described by Eq. (15.62), where a and b depend on diffusional parameters (diffusion coefficient and collision distance) and quencher concentration.
Such decays can also be fitted by an infinite sum of exponential terms, but those components cannot be assigned to different populations of excited state species, i.e., in the case of a transient effect, it is the single fluorophore population that gives origin to a non-exponential decay.
There are thus several different models able to describe time-resolved fluorescence decays, all of them equally valid but giving origin to different physical meanings of the fitting parameters. The choice of an appropriate model is crucial and should rely on our knowledge of the system under investigation and the underlying physical phenomena involved.
15.8 Conclusions
In this chapter, we have described the fundamental parameters that should be obtained when characterising an electronic, singlet or triplet, excited state and how to determine them experimentally including methodologies and required equipment. These characteristics include electronic energy, quantum yields, lifetimes and number and type of species in the excited state. Within this last context, i.e., when excited state reactions give rise to additional species in the excited state we have explored several excited state kinetic schemes, found to be present when excimers, exciplexes are formed and (intra and intermolecular) proton transfer occurs. This includes a complete formalism (with equations) for the steady-state and dynamic approaches for two and three-state systems, from where all the rate constants can be obtained. Additionally, we have explored additional recent developments in photophysics: the competition between vibrational relaxation and photochemistry, and the non-discrete analysis (stretched-exponential) of fluorescence decays.
Notes
- 1.
As a general rule, the credibility of the results obtained from the analysis of fluorescence decays should be (with few exceptions) assessed, by checking the interconsistency of results obtained under different experimental conditions (temperature, solvent viscosity and/or polarity and concentration, among others, e.g. pressure). Changing temperature provides Arrhenius plots of the rate constants, which should be linear. Otherwise, something is wrong with the experiments, or something interesting/new is happening. Changing solvent viscosity (η) provides log–log plots of diffusion-dependent rate constants versus η, which should also be linear (slope = –1) for diffusion-controlled processes (deviations are also interesting) [56–59]. Solvent polarity strongly affects charge and electron transfer processes in a well-known way. For inter-molecular processes, changing the concentration [Q] provides linear plots of the pseudo-unimolecular rate constant k 1 = k bimol[Q] and an accurate value for the bimolecular rate constant, k bimol.
Finally, coupling results from time-resolved fluorescence with those obtained from steady-state experiments are essential in some cases (complex kinetics or low time resolution), and advisable in most other cases. For example, the rate constants obtained from time-resolved experiments can be used to evaluate Stern–Volmer or Stevens–Ban plots (see below) and compare them to those obtained from steady-state experiments. Agreement tells us that everything is alright, while disagreement means that something else is happening, as for example, undetectable short components in the decays (e.g., static quenching and transient effects, see below).
References
Stern O, Volmer M (1919) Über die Abklingzeit der Fluoreszenz. Physikalische Zeitschrift 20:183–188
Murov S, Charmichael I, Hug GL (1993) Handbook of photochemistry. M Dekker Inc, New York
Karpovich DS, Blanchard GJ (1995) Relating the polarity-dependent fluorescence response of pyrene to vibronic coupling. Achieving a fundamental understanding of the py polarity scale. J Phys Chem 99:3951–3958
Bensasson RV, Land EJ, Truscott TG (1993) Excited states and free radicals in biology and medicine. Oxford Science Publications, Oxford
Rusakowi R, Testa AC (1968) Comparison of quinine bisulfate and 9,10-diphenylanthracene as fluorescence standards. J Phys Chem 72:793–796
Valeur B (2002) Molecular fluorescence: principles and applications. Wiley-VCH, Weinheim
Montalti M, Credi A, Prodi L, Gandolfi M (2006) Handbook of photochemistry. 3rd edn. CRC Presss, Boca Raton
Parker CA, (1968) Photoluminescence of solutions. Elsevier, Amsterdam
deMello JC, Wittmann HF, Friend RH (1997) An improved experimental determination of external photoluminescence quantum efficiency. Adv Mater 9:230–233
Palsson LO, Monkman AP (2002) Measurement of solid-state photoluminescence quantum yields using a fluorimeter. Adv Mater 14:757–758
Pina J, Seixas de Melo J, Burrows HD et al (2008) Excited state properties of oligophenyl and oligothienyl swivel cruciforms. J Phys Chem B 112:1104–1111
Pina J, Seixas de Melo J (2009) A comprehensive investigation of the electronic spectral and photophysical properties of conjugated naphthalene–thiophene oligomers. Phys Chem Chem Phys 11:8706–8713
Kristiansen M, Scurlock RD, Iu KK, Ogilby PR (1991) Charge-transfer state and singlet oxygen (1Δg O2) production in photoexcited organic molecule-molecular oxygen complexes. J Phys Chem 95:5190–5197
Martinez CG, Neumer A, Marti C et al (2003) Effect of the media on the quantum yield of singlet oxygen (O2(1Δg)) production by 9H-fluoren-9-one: solvents and solvent mixtures. Helv Chim Acta 86:384–397
Carmichael I, Hug GL (1986) Triplet-triplet absorption spectra of organic molecules in condensed phases. J Phys Chem Ref Data 15:1–250
Becker RS, Seixas de Melo J, Maçanita AL, Elisei F (1996) Comprehensive evaluation of the absorption, photophysical, energy transfer, structural, and theoretical properties of α-oligothiophenes with one to seven rings. J Phys Chem 100:18683–18695
Kumar CV, Qin L, Das PK (1984) Aromatic thioketone triplets and their quenching behavior towards oxygen. J Chem Soc-Faraday Trans II 80:783–793
Seixas de Melo J, Silva LM, Arnaut LG, Becker RS (1999) Singlet and triplet energies of α-oligothiophenes: a spectroscopic, theoretical, and photoacoustic study: extrapolation to polythiophene. J Chem Phys 111:5427–5434
Pineiro M, Gonsalves A, Pereira MM et al (2002) New halogenated phenylbacteriochlorins and their efficiency in singlet-oxygen sensitization. J Phys Chem A 106:3787–3795
Seixas de Melo J, Serpa C, Burrows HD, Arnaut LG (2007) The triplet state of indigo. Angew Chem Int Ed 46:2094–2096
Seixas de Melo J, Moura AP, Melo MJ (2004) Photophysical and spectroscopic studies of indigo derivatives in their keto and leuco forms. J Phys Chem A 108:6975–6981
Seixas de Melo J, Rondão R, Burrows HD et al (2006) Spectral and photophysical studies of substituted indigo derivatives in their keto forms. Chem Phys Chem 7:2303–2311
Becker RS (1969) Theory and interpretation of fluorescence and phosphorescence. Wiley-Interscience, New York
Land EJ (1968) Extinction coefficients of triplet–triplet transitions. Proc Royal Soc Lond A 305:457–471
Bensasson R, Land EJ (1971) Triplet-triplet extinction coefficients via energy transfer. Trans Faraday Soc 67:1904–1915
Keene JP (1964) Pulse radiolysis equipment. J Sci Instrum 41:493–496
Butler J, Hodgson BW, Hoey BM et al (1989) Experimental studies of some moderately fast processes initiated by radiation. Radiat Phys Chem 34:633–646
Monkman AP, Burrows HD, Miguel MD et al (2001) Triplet state spectroscopy of conjugated polymers studied by pulse radiolysis. Synth Met 116:75–79
Cooper R, Thomas JK (1968) Formation of excited states in the nanosecond-pulse radiolysis of solutions of benzene and toluene. J Chem Phys 48:5097–6002
Candeias LP, Wildeman J, Hadziioannou G, Warman JM (2000) Pulse radiolysis—optical absorption studies on the triplet states of p-phenylenevinylene oligomers in solution. J Phys Chem B 104:8366–8371
Hoofman R, de Haas MP, Siebbeles LDA, Warman JM (1998) Highly mobile electrons and holes on isolated chains of the semiconducting polymer poly(phenylene vinylene). Nature 392:54–56
Grozema FC, Siebbeles LDA, Warman JM et al (2002) Hole conduction along molecular wires: σ-bonded silicon versus π-bond-conjugated carbon. Adv Mater 14:228–231
Burrows HD, Seixas de Melo J, Serpa C et al (2001) S1∼>T1 intersystem crossing in π-conjugated organic polymers. J Chem Phys 115:9601–9606
Monkman AP, Burrows HD, Miguel MD et al (1999) Measurement of the S0–T1 energy gap in poly(2-methoxy,5-(2′-ethyl-hexoxy)–p-phenylenevinylene) by triplet–triplet energy transfer. Chem Phys Lett 307:303–309
Pina J, Seixas de Melo J, Burrows HD et al (2009) Alternating binaphthyl—thiophene copolymers: synthesis, spectroscopy, and photophysics and their relevance to the question of energy migration versus conformational relaxation. Macromolecules 42:1710–1719
Fonseca SM, Pina J, Arnaut LG et al (2006) Triplet-state and singlet oxygen formation in fluorene-based alternating copolymers. J Phys Chem B 110:8278–8283
Maciejewski A, Steer RP (1993) The photophysics, physical photochemistry, and related spectroscopy of thiocarbonyls. Chem Rev 93:67–98
Becker RS, Michl J (1966) Photochromism of synthetic and naturally occurring 2H-chromenes and 2H-pyrans. J Am Chem Soc 88(5931):5933
Becker RS, Dolan E, Balke DE (1969) Vibronic effects in photochemistry- competition between internal conversion and photochemistry. J Chem Phys 50:239–245
Becker RS, Pelliccioli AP, Romani A et al (1999) Vibronic quantum effects in fluorescence and photochemistry. Competition between vibrational relaxation and photochemistry and consequences for photochemical control. J Am Chem Soc 121:2104–2109
Becker RS, Favaro G, Romani A et al (2005) Vibronic effects in pathways of photochemistry and vibrational relaxation. Chem Phys 316:108–116
Lenoble C, Becker RS (1986) Photophysics, photochemistry and kinetics of photochromic 2H-pyrans and chromenes. J Photochem 33:187–197
Demas JN (1983) Excited state lifetime measurements. Academic Press, Inc, London
O’Connor DV, Phillips D (1984) Time-correlated single photon counting. Academic Press, London
Lakowicz JR (2006) Principles of fluorescence spectroscopy, 3rd edn. Kluwer Academic, New York
Zachariasse KA, Busse R, Schrader U et al (1982) Intramolecular siglet and triplet excimers with diphenanthrylpropanes. Chem Phys Lett 89:303–308
Seixas de Melo J, Fernandes PF (2001) Spectroscopy and photophysics of 4- and 7-hydroxycoumarins and their thione analogs. J Mol Struct 565:69–78
Maçanita AL, Costa FP, Costa S et al (1989) The 9-anthroate chromophore as a fluorescent probe for water. J Phys Chem 93:336–343
Pina J, Seixas de Melo J, Burrows HD et al (2007) Spectral and photophysical studies of poly[2,6-(1,5-dioctylnaphthalene)]thiophenes. J Phys Chem C 111:7185–7191
Striker G, Subramaniam V, Seidel CAM et al (1999) Photochromicity and fluorescence lifetimes of green fluorescent protein. J Phys Chem B 103:8612–8617
Lima JC, Abreu I, Brouillard R, Maçanita AL (1998) Kinetics of ultra-fast excited state proton transfer from 7-hydroxy-4-methylflavylium chloride to water. Chem Phys Lett 298:189–195
Boens N, Qin WW, Basaric N et al (2007) Fluorescence lifetime standards for time and frequency domain fluorescence spectroscopy. Anal Chem 79:2137–2149
Lampert RA, Chewter LA, Phillips D et al (1983) Standards for nanosecond fluorescence decay time measurements. Anal Chem 55:68–73
Birks JB (1970) Photophysics of aromatic molecules. Wiley, London
Freitas AA, Quina FH, Fernandes AC, Maçanita AL (2010) Picosecond dynamics of the prototropic reactions of 7-hydroxyflavylium photoacids anchored at an anionic micellar surface. J Phys Chem A 114:4188–4196
Stevens B, Ban MI (1964) Spectrophotometric determination of enthalpies and entropies of photoassociation for dissolved aromatic hydrocarbons. Trans Faraday Soc 60:1515–1523
Boyce WE, DiPrima RC (1986) Elementary differential equations and boundary value problems, 4th edn. Wiley, New York
Zachariasse KA, Busse R, Duveneck G, Kühnle W (1985) Intramolecular monomer and excimer fluorescence with dipyrenylpropanes: double-exponential versus triple-exponential decays. J Photochem 28:237–253
Zachariasse KA, Duveneck G, Kühnle W (1985) Double-exponential decay in intramolecular excimer formation: 1,3-di(2-pyrenyl)propane. Chem Phys Lett 113:337–343
Zachariasse KA, Maçanita AL, Kühnle W (1999) Chain length dependence of intramolecular excimer formation with 1, n-bis(1-pyrenylcarboxy)alkanes for n = 1–16, 22, and 32. J Phys Chem B 103:9356–9365
Serpa C, Gomes PJS, Arnaut LG et al (2006) Temperature dependence of ultra-exothermic charge recombinations. Chem Phys Chem 7:2533–2539
Gordon M, Ware WR (1975) The exciplex. Academic Press, New York
Waluk J (2000) Conformational analysis of molecules in excited states. Wiley-VCH, New York
Becker HD (1993) Unimolecular photochemistry of anthracenes. Chem Rev 93:145–172
Chandross EA, Thomas HT (1971) Intramolecular exciplex formation in naphthylalkylamines. Chem Phys Lett 9:393–396
Hinatu J, Masuhara H, Mataga N et al (1978) Absorption spectra of inter- and intramolecular exciplex systems of pyrene and N, N-dimethylaniline in alcoholic solutions. Bull Chem Soc Jpn 51:1032–1036
Itoh M, Mimura T, Usui H, Okamoto T (1973) Intramolecular exciplex and charge transfer complex formations in (9,10-dicyanoanthracene)-(trimethylene)-(naphthalene) systems. J Am Chem Soc 95:4388–4392
Leinhos U, Kühnle W, Zachariasse KA (1991) Intramolecular charge transfer and thermal exciplex dissociation with p-aminobenzonitriles in toluene. J Phys Chem 95:2013–2021
Swinnen AM, Vanderauweraer M, De Schryver FC et al (1987) Photophysics of the intramolecular exciplex formation in omega-(1-pyrenyl)-alpha-(dimethylamino)alkanes. J Am Chem Soc 109(321):330
Fajardo ME, Withnall R, Feld J et al (1988) Condensed phase laser induced harpoon reactions. Laser Chem 9:1–3
Douhal A, Lahmani F, Zewail AH (1996) Proton-transfer reaction dynamics. Chem Phys 207:477–498
Arnaut LG, Formosinho SJ (1993) Excited-state proton transfer reactions I. Fundamentals and intermolecular reactions. J Photochem Photobiol A-Chem 75:1–20
Laws WR, Brand L (1979) Analysis of two-state excited-state reactions. The fluorescence decay of 2-naphthol. J Phys Chem 83:795–802
Nunes RMD, Pineiro M, Arnaut LG (2009) Photoacid for extremely long-lived and reversible pH-jumps. J Am Chem Soc 131:9456–9462
Aloisi GG, Latterini L, Maçanita AL et al (2003) Singlet and triplet state properties of substituted flavothiones. Phys Chem Chem Phys 5:69–3464
Costa T, Pina J, de Seixas Melo J (2009) Photophysical processes in polymers and oligomers. Spec Period Rep Photochem 37:44–71
Seixas de Melo J, Maçanita AL (1993) Three interconverting excited species: experimental study and solution of the general photokinetic triangle by time-resolved fluorescence. Chem Phys Lett 204:556–562
Dias A, Varela AP, Miguel MD et al (1996) β-Carbolines. 2. Rate constants of proton transfer from multiexponential decays in the lowest singlet excited state of harmine in water as a function of pH. J Phys Chem 100:17970–17977
Dias A, Varela AP, Miguel MD et al (1992) β -Carboline photosensitizers. 1. Photophysics, kinetics and excited-state equilibria in organic solvents, and theoretical calculations. J Phys Chem 96:10290–10296
Seixas de Melo J, Costa T, Francisco A et al (2007) Dynamics of short as compared with long poly(acrylic acid) chains hydrophobically modified with pyrene, as followed by fluorescence techniques. Phys Chem Chem Phys 9:1370–1385
Costa T, Miguel MG, Lindman B et al (2005) Dynamics and energetics of the self-assembly of a hydrophobically modified polyelectrolyte: naphthalene-labeled poly(acrylic acid). J Phys Chem B 109:11478–11492
Dias FB, Lima JC, Pierola IF et al (2001) Internal dynamics of poly(methylphenylsiloxane) chains as revealed by picosecond time resolved fluorescence. J Phys Chem A 105:10286–10295
Masuhara H, Tamai N, Mataga N et al (1983) Excimer formation in poly(N-vinylcarbazole) and its model compounds as revealed by picosecond time-resolved absorption spectroscopy. Chem Phys Lett 95:471–475
Vandendriessche J, Palmans P, Toppet S et al (1984) Configurational and conformational aspects in the excimer formation of bis(carbazoles). J Am Chem Soc 106(8057):8064
Berberan-Santos MN, Bodunov EN, Valeur B (2005) Mathematical functions for the analysis of luminescence decays with underlying distributions 1. Kohlrausch decay function (stretched exponential). Chem Phys 315:171182
Webber SE (1990) Photon-harvesting polymers. Chem Rev 90:1469–1482
Noronha M, Lima JC, Paci E et al (2007) Tracking local conformational changes of ribonuclease A using picosecond time-resolved fluorescence of the six tyrosine residues. Biophys J 92:4401–4414
Noronha M, Santos R, Paci E et al (2009) Fluorescence lifetimes of tyrosine residues in cytochrome c′′ as local probes to study protein unfolding. J Phys Chem B 113:4466–4474
Zachariasse KA, Striker G (1988) Three and only three excited-state species (one monomer and two excimers) in 1,3-di(1-pyrenyl)propane. Chem Phys Lett 145:251
Liu YS, Ware WR (1993) Photophysics of polycyclic aromatic hydrocarbons adsorbed on silica gel surfaces. 1. Fluorescence lifetime distribution analysis: an ill-conditioned problem. J Phys Chem 97:5980–5986
Dias FB, Knaapila M, Monkman AP, Burrows HD (2006) Fast and slow time regimes of fluorescence quenching in conjugated polyfluorene—fluorenone random copolymers: The role of exciton hopping and Dexter transfer along the polymer backbone. Macromol 39:1598–1606
Dias FB, Kamtekar KT, Cazati T et al (2009) Exciton diffusion in polyfluorene copolymer thin films: kinetics, energy disorder and thermally assisted hopping. Chem Phys Chem 10:2096–2104
Lakowicz JR, Johnson ML, Joshi N et al (1986) Transient effects in quenching detected by harmonic-content frequency-domain fluorometry. Chem Phys Lett 131:343–348
Pina J, Seixas de Melo J, Batista RMF et al (2010) Synthesis and characterization of the ground and excited states of tripodal-like oligothienyl-imidazoles. J Phys Chem B 114:4964–4972
Pina J, Seixas de Melo J, Burrows HD et al (2006) Spectral and photophysical studies on cruciform oligothiophenes in solution and the solid state. J Phys Chem B 110:15100–15106
Zachariasse KA, Kühnle W, Leinhos U et al (1991) Time-resolved monomer and excimer fluorescence of 1,3-di(1-pyrenyl)propane at different temperatures: no evidence for distributions from picosecond laser experiments with nanosecond time resolution. J Phys Chem 95:5476–5488
Zachariasse KA, Duveneck G, Kühnle W et al (1991) Multicomponent fluorescence decay analysis in intramolecular excimer formation with dipyrenylalkanes. In: Honda K (ed) Photophysical processes in organized molecular systems. Elsevier, Amsterdam, pp 83
Seixas de Melo J (2005) The influence of oxygen on the lifetime of luminescence probes. A simple device for degassing solutions for fluorescence experiments. Chem Educ 10:29–35
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Seixas de Melo, J.S., Pina, J., Dias, F.B., Maçanita, A.L. (2013). Experimental Techniques for Excited State Characterisation. In: Evans, R., Douglas, P., Burrow, H. (eds) Applied Photochemistry. Springer, Dordrecht. https://doi.org/10.1007/978-90-481-3830-2_15
Download citation
DOI: https://doi.org/10.1007/978-90-481-3830-2_15
Published:
Publisher Name: Springer, Dordrecht
Print ISBN: 978-90-481-3829-6
Online ISBN: 978-90-481-3830-2
eBook Packages: Chemistry and Materials ScienceChemistry and Material Science (R0)