Abstract
The set of solutions of a parameter-dependent linear partial differential equation with smooth coefficients typically forms a compact manifold in a Hilbert space. In this paper we review the generalized reduced basis method as a fast computational tool for the uniform approximation of the solution manifold.
We focus on operators showing an affine parametric dependence, expressed as a linear combination of parameter-independent operators through some smooth, parameter-dependent scalar functions. In the case that the parameter-dependent operator has a dominant term in its affine expansion, one can prove the existence of exponentially convergent uniform approximation spaces for the entire solution manifold. These spaces can be constructed without any assumptions on the parametric regularity of the manifold—only spatial regularity of the solutions is required. The exponential convergence rate is then inherited by the generalized reduced basis method. We provide a numerical example related to parametrized elliptic equations confirming the predicted convergence rates.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Greedy Algorithm
- Proper Orthogonal Decomposition
- Proper Orthogonal Decomposition Mode
- Approximation Space
- Exponential Convergence
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Reduced order models (ROMs) are a crucial ingredient of many applications of increasing complexity in scientific computing related e.g. to parameter estimation, sensitivity analysis, optimal control, and design or shape optimization. In this paper we consider the reduced basis method for the numerical approximation of parameter-dependent partial differential equations (μ-PDEs). The set of solutions of such an equation depends on a finite-dimensional vector of parameters related e.g. to physical coefficients, geometrical configuration, source terms, and boundary conditions. Solving the μ-PDE for many different values of the parameters entails the exploration of the manifold of solutions, and is not affordable if each μ-PDE requires an expensive numerical approximation, such as the one built over the finite element method. Suitable structural assumptions about the parametrization enable one to decouple the computational effort into two stages. A (very expensive) pre-processing step that is performed once (“offline”)—consisting in the construction of a reduced basis for the representation of the manifold of solutions, followed by very inexpensive calculations performed “online” for each new input-output evaluation required. In the reduced basis method, numerical solutions for certain parameters values are computed offline by a classical discretization technique. These solutions give a basis for approximating online the PDE solution (for a large number of new parameter values) as a linear combination of the basis elements. The rational of this approach stands on the very fast (often exponential) convergence—with respect to the number of basis—is exhibited by approximation spaces. We point out that in the real-time or many-query contexts, where the goal is to achieve a very low marginal cost per input-output evaluation, we can accept an increased “offline” cost—not tolerable for a single or few evaluations—in exchange for greatly decreased “online” cost for each new/additional input-output evaluation. In previous works (see e.g. [18–20]) a priori exponential convergence with respect to the number of basis functions is proved in the case of elliptic PDEs depending on one-dimensional parameters; several computational tests shown e.g. in [28] provide a numerical assessment of this behavior, also for larger parameter space dimensions. Several new results, such as the ones presented in [4], address an a priori convergence analysis in the more general case where a greedy algorithm is employed to build the reduced space in an automatic, adaptive way. A further improvement has been proposed in [3], where an error estimate for the greedy algorithm has been developed in terms of the Kolmogorov n-width. After recalling the basic features of a generalized version of the reduced basis method, and the main convergence results in this field, the goal of this paper is to provide both a convergence analysis for the greedy algorithm and a numerical proof of this behavior, in order to extend the a priori convergence results presented in [19, 20]. To do this, we rely on the introduction of a fundamental basis, a suitable error representation formula and an upper bound estimate for the n-width of the solution set of an elliptic parametric PDE under suitable assumptions on its parametric form.
We proceed to describe the functional setting of our problems. Let Ω⊂ℝd, d∈{1,2,3}, be a bounded domain and X=X(Ω) a Hilbert space of functions defined on Ω with inner product (⋅,⋅)
X
and induced norm \(\| \cdot \|_{X} = \sqrt{(\cdot{,}\cdot)_{X}}\). We consider the following problem: given a vector of parameters  from a compact parameter set
from a compact parameter set  , find u(μ)∈X s.t.
, find u(μ)∈X s.t.
where the parameters can enter in the bilinear form a(⋅,⋅;μ) in several possible ways: as variable coefficients, as coefficient entering in the parametrization of the domain Ω⊂ℝd of the problem, in the definition of the right-hand side f that account for either forcing terms and/or boundary conditions. We denote the P-manifold of solutions

in the space X. In many applications  is a differentiable manifold. We also allow the case of a manifold that is not locally smooth at some isolated points, e.g. the parametric Helmholtz equation ∇⋅(a(⋅;μ)∇u)+u=0, which has a smooth solution manifold except at the eigenvalues of the parametric Laplacian, −∇⋅(a(⋅;μ)∇u)=λ(μ)u. We considered this problem in [17]. A typical objective in applications is to provide a numerical approximation \(\widetilde{u}(\mu)\) for
is a differentiable manifold. We also allow the case of a manifold that is not locally smooth at some isolated points, e.g. the parametric Helmholtz equation ∇⋅(a(⋅;μ)∇u)+u=0, which has a smooth solution manifold except at the eigenvalues of the parametric Laplacian, −∇⋅(a(⋅;μ)∇u)=λ(μ)u. We considered this problem in [17]. A typical objective in applications is to provide a numerical approximation \(\widetilde{u}(\mu)\) for  that is uniform
Footnote 1 over the entire manifold
that is uniform
Footnote 1 over the entire manifold  . To fulfill this request, a necessary condition is that, for any ε>0, we find a linear subspace X
N
⊂X of dimension N s.t.
. To fulfill this request, a necessary condition is that, for any ε>0, we find a linear subspace X
N
⊂X of dimension N s.t.

where the dimension N is as small as possible. The question is: how small can we expect N to be?
To address this question, we introduce e.g. the finite element (FE) approximation of problem (1): given a vector of parameters  , find u
h,p
(μ)∈X
h,p
=X
h,p
(Ω) s.t.
, find u
h,p
(μ)∈X
h,p
=X
h,p
(Ω) s.t.
where X h,p ⊂X is a conforming FE subspace spanned by piecewise polynomial shape functions of degree p defined on a quasi-uniform mesh of maximum element size h. Due to classical a priori error estimates such an approximation will eventually approximate well all the solutions on the manifold as the dimension N:=dim(X h,p ) increases, but only for quite large N we can expect a uniformly small error in the approximation. When X=H 1(Ω) is the standard Sobolev space, the classical a priori estimates for piecewise polynomial approximations are as follows [2]:
where s>1 denotes the number of weak derivatives of u(μ), and δ>0 is arbitrarily small. If the solution u is analytic (s=∞), one obtains exponential convergence as a result of p-refinement, i.e.
and this leads to the study of spectral methods. It should be cautioned that even if a spectral approximation can obtain in theory exponential convergence across the entire parameter range, the constants in front depend on both the dimension d and the number of parameters P of the problem. The assumption of analyticity of solutions is also often violated.
An efficient method for the approximation of the parametric manifold  should (i) provide exponential convergence in the dimension N of the approximation space; (ii) have the same convergence rate irrespective of the number of parameters P; and (iii) entail a computational cost that scales only moderately in N. Exploiting the structure of the manifold
should (i) provide exponential convergence in the dimension N of the approximation space; (ii) have the same convergence rate irrespective of the number of parameters P; and (iii) entail a computational cost that scales only moderately in N. Exploiting the structure of the manifold
 is key to finding uniform approximations that satisfy (i)–(iii). Our technique for proving exponentially convergent approximation estimates for the manifold of solutions relies on a series expansion of the solution u(μ). Series expansion solutions, either by separation of variables or by power series expansion for PDEs with analytical coefficients, are classical tools for existence proofs. Analytical power series expansions, such as the decomposition method of Adomian [1], are not competitive against good numerical approximation schemes in actually providing approximate solutions to PDEs, but they do provide an interesting approach to constructing convergence estimates. The novel contribution of this work is to consider the power series expansion method forparameter-dependent PDEs by searching for solutions in a parametrically separable form
is key to finding uniform approximations that satisfy (i)–(iii). Our technique for proving exponentially convergent approximation estimates for the manifold of solutions relies on a series expansion of the solution u(μ). Series expansion solutions, either by separation of variables or by power series expansion for PDEs with analytical coefficients, are classical tools for existence proofs. Analytical power series expansions, such as the decomposition method of Adomian [1], are not competitive against good numerical approximation schemes in actually providing approximate solutions to PDEs, but they do provide an interesting approach to constructing convergence estimates. The novel contribution of this work is to consider the power series expansion method forparameter-dependent PDEs by searching for solutions in a parametrically separable form
where the Ψ k do not depend on μ and the scalar functions Θ k (μ). The expansion (4) together with standard estimates for convergent power series then provides a construction of approximation spaces that are uniformly exponentially convergent over the entire parameter range. In order to achieve separation w.r.t. to the parameters, we must make suitable structural assumptions on the PDE. A typical assumption is that of affine dependence on the parameter, i.e. problem (1) is assumed to be of the form
where every a
q
:X×X→ℝ and f
q
:X→ℝ are parameter-independent bilinear and linear forms respectively, whereas  and
and  are scalar coefficient functions depending only on the parameter (but not necessary in a smooth way). We shall next describe the generalized reduced basis method (GRBM) that, given assumption (5), satisfies (i)–(iii). We then discuss some recent theoretical approximation results linking the best possible approximation space for
are scalar coefficient functions depending only on the parameter (but not necessary in a smooth way). We shall next describe the generalized reduced basis method (GRBM) that, given assumption (5), satisfies (i)–(iii). We then discuss some recent theoretical approximation results linking the best possible approximation space for  with the convergence rate obtained by the GRBM, and exhibit a model problem where, at least in the case we have Q
a
=2 and some additional special structure on bilinear forms a
q
, we indeed observe in practice the exponential convergence predicted by theory.
with the convergence rate obtained by the GRBM, and exhibit a model problem where, at least in the case we have Q
a
=2 and some additional special structure on bilinear forms a
q
, we indeed observe in practice the exponential convergence predicted by theory.
2 Generalized Reduced Basis Method for Uniform Approximation of μ-PDEs
It is clear that the FE approximation u
h,p
(μ) of (1) can be made arbitrarily accurate for all possible parameters  , but this usually require a considerable computational cost. In order to overcome this (sometimes unaffordable) difficulty, a possible idea is to instead consider the manifold of discrete solutions u
h,p
(μ) given by
, but this usually require a considerable computational cost. In order to overcome this (sometimes unaffordable) difficulty, a possible idea is to instead consider the manifold of discrete solutions u
h,p
(μ) given by

as a surrogate for  , and then to look for approximations of
, and then to look for approximations of  that converge exponentially fast (see Fig. 1 for a graphical sketch). Specifically, we consider subspaces X
n
⊂X
h,p
(for n≪N) that are constructed by using information coming from the snapshot solutions u
h,p
(μ
i
) computed at well-chosen points μ
i
, i=1,…,n. More precisely, X
n
is the span of the snapshot solutions u
h,p
(μ
i
), i=1,…,n. This leads to the Reduced Basis (RB) method [27, 28], which is, in brief, a Galerkin projection on an n-dimensional approximation space relying on the parametrically induced manifold
that converge exponentially fast (see Fig. 1 for a graphical sketch). Specifically, we consider subspaces X
n
⊂X
h,p
(for n≪N) that are constructed by using information coming from the snapshot solutions u
h,p
(μ
i
) computed at well-chosen points μ
i
, i=1,…,n. More precisely, X
n
is the span of the snapshot solutions u
h,p
(μ
i
), i=1,…,n. This leads to the Reduced Basis (RB) method [27, 28], which is, in brief, a Galerkin projection on an n-dimensional approximation space relying on the parametrically induced manifold  . Assuming that the solutions u
h,p
satisfy the a priori convergence estimate (3) and that the approximation u
n
(μ) converges exponentially to u
h,p
(μ), we can write the total error of the reduced solution as
. Assuming that the solutions u
h,p
satisfy the a priori convergence estimate (3) and that the approximation u
n
(μ) converges exponentially to u
h,p
(μ), we can write the total error of the reduced solution as

and for N sufficiently large the exponential term in n dominates the error. The additional strength of this method is that in the best case we only need to solve n times the FE problem for u h,p , and that the solution for u n (μ) can be done with complexity depending on n but not N after some initial preprocessing steps, so that indeed N can be chosen fairly large in order to obtain highly accurate reduced order solutions.
For notational simplicity we present here the case P=1 and formulate the RB method in a slightly more general form than usually given. It can be expressed in three distinct steps:
-
(i)
Choice of the reduced subspace. The basic idea of every reduced basis method is to choose a finite training sample
 , |Ξ
train|=M, in the parameter space and to use the information contained in the corresponding solutions u
h,p
(μ) for each μ∈Ξ
train (called snapshots) to find a representative subspace for the approximation of the manifold
, |Ξ
train|=M, in the parameter space and to use the information contained in the corresponding solutions u
h,p
(μ) for each μ∈Ξ
train (called snapshots) to find a representative subspace for the approximation of the manifold  . The reduced subspace X
n
of dimension n is found by solving [28]
. The reduced subspace X
n
of dimension n is found by solving [28]
 (6)
(6)where X train:=span{u h,p (μ):μ∈Ξ train} is the space containing all the snapshots, and the function
 measures the distance between any subspace X
∗⊂X and the manifold
measures the distance between any subspace X
∗⊂X and the manifold  and is defined by
and is defined by

Since the exact distance of the subspace to the manifold is usually unknown, we must resort to computable surrogates to solve (6). Nonetheless, we mention that the exact distance is used in the so-called strong greedy algorithm introduced in [3] for the theoretical analysis of convergence rates of reduced basis methods. Thus we replace (6) with
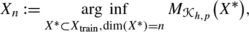 (7)
(7)where
 is an approximate distance between any subspace X
∗⊂X and the manifold
is an approximate distance between any subspace X
∗⊂X and the manifold  . The choice of the function
. The choice of the function  to be used for the approximation of δ(⋅,⋅;⋅) defines which algorithm we use to choose the subspace. This is by far the most common way of constructing reduced subspaces, and we call these approaches Lagrange ROMs. In the GRBM we consider also the parametric sensitivities up to a suitable order, say K−1 (with K≥1) as part of the snapshot set
$$ X_{\mathrm{train}} := \mbox{span} \biggl\{ \frac{\partial^k u_{h,p}}{\partial \mu^k}(\mu) : \mu \in \varXi_{\mathrm{train}}, \ k=0,\ldots,K-1 \biggr\} , $$
to be used for the approximation of δ(⋅,⋅;⋅) defines which algorithm we use to choose the subspace. This is by far the most common way of constructing reduced subspaces, and we call these approaches Lagrange ROMs. In the GRBM we consider also the parametric sensitivities up to a suitable order, say K−1 (with K≥1) as part of the snapshot set
$$ X_{\mathrm{train}} := \mbox{span} \biggl\{ \frac{\partial^k u_{h,p}}{\partial \mu^k}(\mu) : \mu \in \varXi_{\mathrm{train}}, \ k=0,\ldots,K-1 \biggr\} , $$giving a total number of MK snapshots. They can be computed from the discrete sensitivity equation(s): find \(w_{k}(\mu) = \frac{\partial^{k} u_{h,p}}{\partial \mu^{k}}(\mu) \in X_{h,p}\) s.t.
 (8)
(8)for all k=1,…,K. Only the right-hand side of the system changes with k and thus any preconditioners or matrix decompositions used for the primal problem can be reused. The information contained in these snapshots is then used to build the reduced space X n with dimension dim X n =n≪MK in what can also be understood as a data compression problem. If K=2 and M>1 we have a Hermite ROM,Footnote 2 and if K>1 and M=1 we have a Taylor ROM.Footnote 3
Two standard choices for
 are:
are: -
1.
the proper orthogonal decomposition (POD), where
 (9)
(9)and \(\varPi_{X_{n}} : X \to X_{n}\) is the orthogonal projection w.r.t. the inner product of X. In this case, we choose the basis by minimizing the ℓ 2(Ξ train) error in parameter space. It turns out that the optimal bases are hierarchical and are spanned by the leading n eigenvectors of the correlation matrix
$$\mathbb{C}_{ij} = \frac{1}{M} \bigl(u_{h,p}( \mu_j) -\bar{u}, u_{h,p}(\mu_i) -\bar{u} \bigr)_X, \quad 1 \leq i,j \leq M, $$where we have subtracted the mean of the snapshots
$$\bar{u} = \frac{1}{M} \sum_{i=1}^{M} u_{h,p}(\bar{\mu}). $$The eigenpairs \(({\lambda}_{j}, \boldsymbol{\psi}_{j})_{j=1}^{M}\) of ℂ (with the eigenvalues ordered in the decreasing order) are the solutions of
$$\mathbb{C} {\boldsymbol{\psi}}_j = \lambda_j { \boldsymbol{\psi}}_j, \quad j=1,\ldots,|\varXi_{\mathrm{train}}|. $$Then, the optimal basis for the n-th dimensional space X n generated by minimizing (9) is given by
$$\chi_0 = \bar{u}, \qquad \quad \chi_j = \sum _{i=1}^{M} [\boldsymbol{\psi}_j]_i \bigl(u_{h,p}(\mu_i) - \bar{u}\bigr), \quad 1 \leq j \leq n, $$being [ψ j ] i the i-th component of the j-th eigenvector. Extensions of the standard POD basis to incorporate parametric sensitivities (8) were presented in [6, 12, 13] and are not discussed in detail here;Footnote 4 , Footnote 5
-
2.
the greedy algorithm, where
 (10)
(10)i.e. minimization of the ℓ ∞(Ξ train) error in parameter space. In practice no efficient algorithm exists to solve (6) for large-scale problems, so we approximate it by its relaxation
 (11)
(11)where \(\varDelta _{n}(\widetilde{u}(\mu))\) is a computationally inexpensive a posteriori error estimator for the quantity \(\| u_{h,p}(\mu) - \widetilde{u}(\mu)\|_{X}\) that should satisfy
 (12)
(12)for some constants C 1>0, C 2≥1. This corresponds to the approximate minimization of the ℓ ∞(Ξ train) error in parameter space. In this case we have a weak greedy algorithm as defined in [3].
Note that while conceptually the POD and the greedy algorithms can be cast in a similar framework, their practical implementations are quite different. The training set
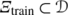 needs to be reasonably dense in the parameter space for
needs to be reasonably dense in the parameter space for  to be a good approximation of the true distance
to be a good approximation of the true distance  for all subspaces X
∗⊂X. In the POD one needs to compute the FE approximations u
h,p
(μ) for all the points in Ξ
train, which amounts to a considerable computational undertaking. In contrast, the weak greedy algorithm only needs to compute the exact solutions (and their parametric derivatives) at the n snapshots comprising the RB and only the computationally inexpensive a posteriori estimator Δ
n
(u
n
(μ)) needs to be evaluated over the entire training set. The difference in the norms used (ℓ
∞ for the greedy vs. ℓ
2 for the POD) also results in slightly different approximation behavior of the resulting bases. Typically the POD basis needed to reach a given tolerance is smaller in size but tends to be not as robust far away from the snapshots (see e.g. [28, 29]).
for all subspaces X
∗⊂X. In the POD one needs to compute the FE approximations u
h,p
(μ) for all the points in Ξ
train, which amounts to a considerable computational undertaking. In contrast, the weak greedy algorithm only needs to compute the exact solutions (and their parametric derivatives) at the n snapshots comprising the RB and only the computationally inexpensive a posteriori estimator Δ
n
(u
n
(μ)) needs to be evaluated over the entire training set. The difference in the norms used (ℓ
∞ for the greedy vs. ℓ
2 for the POD) also results in slightly different approximation behavior of the resulting bases. Typically the POD basis needed to reach a given tolerance is smaller in size but tends to be not as robust far away from the snapshots (see e.g. [28, 29]). -
1.
-
(ii)
(Petrov-)Galerkin projection of the equations. In the second step we perform projection of the original problem onto the reduced trial subspace X n using the reduced test subspace Y n to obtain the reduced basis approximation: find u n (μ)∈X n s.t.
$$ a\bigl(u_n(\mu),v_n; \mu\bigr) = f(v_n;\mu) \quad \mbox{for all } v_n \in Y_n, $$(13)where \(X_{n} = \mbox{span} \{ \varphi_{j} \}_{j=1}^{n}\) and \(Y_{n} = \operatorname{span} \{ \psi_{j} \}_{j=1}^{n}\). If Y n =X n this is a pure Galerkin method, otherwise it is a Petrov-Galerkin method. The Petrov-Galerkin approach is adopted if the underlying system is either nonsymmetric or noncoercive and can be interpreted as a form of stabilization of the ROM. Applying the assumption (5) to (13) leads to the discrete system
$$ \sum_{q=1}^{Q_a} \varTheta_q^a(\mu) A^n_q U^n = \sum_{q=1}^{Q_f} \varTheta_q^f(\mu) F^n_q $$(14)where the matrices and vectors
$$ \bigl[\mathop{A_q^n}_{n \times n} \bigr]_{i,j} := a_q(\varphi_j, \psi_i), \quad \bigl[\mathop{F_q^n}_{n \times 1} \bigr]_{i} := F_q(\psi_i), \quad \mathop{U^n}_{n \times 1} \mbox{ the reduced solution}, $$(15)are dense but only of dimension n and more importantly can be assembled once and then stored. The system (14) is then assembled by evaluating the coefficient functions \(\varTheta_{q}^{a}\), \(\varTheta_{q}^{f}\) and summing together the weighted contributions from all the parts of the decomposition, and solving one small dense linear system. Assuming all the FE degrees of freedom are nodal, we can write the discrete projectors
$$ {}[\mathop{\mathbb{X}_n}_{N \times n}]_{i,j} := \varphi_j(x_i), \qquad [\mathop{\mathbb{Y}_n}_{N \times n}]_{i,j} := \psi_j(x_i) $$(16)where x i are the nodal points in the full space X N . The discrete matrices and vectors (15) can then be obtained as
$$A_q^n = \mathbb{Y}_n A_q \mathbb{X}_n^T, \qquad F_q^n = \mathbb{Y}_n F_q, $$and the approximation of the solution u N (μ) is obtained as \(u_{n}(x_{i}) = [\mathbb{X}_{n}^{T} U_{n}]_{i}\) for i=1,…,N. From here on we use mainly the discrete forms of the equations.
-
(iii)
Certification of the ROM with error bounds. A posteriori error bounds are used to both (i) certify the GRBM solution during the online stage, and (ii) construct the reduced space by means of the weak greedy algorithm. For the sake of simplicity we treat the case of linear, elliptic and coercive μ-PDEs—extensions to noncoercive and nonlinear problems can be found in [5, 8, 11, 21, 30]. Our error bounds rely on two basic ingredients: the dual norm of the residual and a lower bound of the stability factor (in this case, of the parameter-dependent coercivity constant). The residual \(r(v;\mu) \in X_{h,p}'\) is defined as
$$ r(v;\mu) \equiv f(v;\mu) - a\bigl(u_n(\mu),v;\mu\bigr), \quad \forall v \in X_{h,p} $$(17)so that exploiting (2) and the bilinearity of a(⋅,⋅;μ) we have the error representation for e(μ)=u h,p (μ)−u n (μ)∈X h,p given by
$$ a\bigl(e(\mu),v;\mu\bigr) = r(v; \mu), \quad \forall v \in X_{h,p}. $$(18)As a second ingredient, we need a positive lower bound \(\alpha_{h}^{LB}(\mu)\) for the (discrete) coercivity constant α h (μ):
 (19)
(19)whose efficient evaluation as a function of μ is made possible thanks to the so-called successive constraint method (see e.g. [14, 15, 17] for a general description of this procedure). By combining (18) with 19 and using the Cauchy-Schwarz inequality, the following a posteriori error estimate in the energy norm holds (see [28] for a proof):
 (20)
(20)so that expression (12) is now made explicit, being

3 Approximation Theoretical Basis for the Generalized Reduced Basis Method
We now turn to the convergence analysis of approximations in the reduced subspaces that are obtained by (7) and the choice (11) for  . We recall some recent theoretical results and provide an extension through an exponential convergence result. To do this, we rely on the introduction of a fundamental basis and on an intuitive error representation formula, which will be exploited in the numerical example discussed in the following section. We define the best approximation error of
. We recall some recent theoretical results and provide an extension through an exponential convergence result. To do this, we rely on the introduction of a fundamental basis and on an intuitive error representation formula, which will be exploited in the numerical example discussed in the following section. We define the best approximation error of  obtained by the greedy algorithm (6) as
obtained by the greedy algorithm (6) as

A priori convergence estimates for reduced basis approximations have been demonstrated in simple cases, such as in [19], where it was found that for a specific problem exponential convergence was achieved

Recently much interest has been devoted to understanding why the weak greedy method (11) is able to give an approximation space X
n
that exhibits exponential convergence in n. To express how well we are able to uniformly approximate a given manifold of solutions  with a finite-dimensional subspace, we recall the notion of n-width [22, 26] that is used to measure the degree in which we can uniformly approximate a subset of the space X using finite-dimensional subspaces X
n
. The Kolmogorov n-width is defined as
with a finite-dimensional subspace, we recall the notion of n-width [22, 26] that is used to measure the degree in which we can uniformly approximate a subset of the space X using finite-dimensional subspaces X
n
. The Kolmogorov n-width is defined as

where the first supremum is taken over all linear subspaces X
n
⊂X of dimension n. We also define the discrepancy between the subspace X
n
and the manifold  as
as

The subspace X
n
is said to be optimal if  . In general, the optimal subspace w.r.t. the Kolmogorov n-width (21) is not spanned by elements of the set
. In general, the optimal subspace w.r.t. the Kolmogorov n-width (21) is not spanned by elements of the set  being approximated, so that possibly
being approximated, so that possibly  . In the recent work [3] it was shown that
. In the recent work [3] it was shown that

and that this estimate cannot in general be improved. However, it was also shown that if the n-width converges at an exponential rate, say  for all n>0 and some \(\widetilde{C},c > 0\), then
for all n>0 and some \(\widetilde{C},c > 0\), then

A tighter estimate was proved for the case of algebraic convergence: if  for all n>0 and some M,α>0, then also
for all n>0 and some M,α>0, then also

The fast (exponential) convergence of numerical approximations is often linked to spectral approximations. In this way, the reduced basis method can be understood as a spectral method, where instead of using generic global polynomial basis functions we use problem-dependent global smooth approximation basis. The analyticity of the solutions of elliptic PDEs was exploited e.g. in a recent work [7] in the special case where  is an analytic manifold. Using complex analysis techniques and a Taylor expansion approximation of the solution u
h,p
and its parametric derivatives w
m,k
for k=1,2,…, the authors obtained a convergence rate for a reduced basis approximation as
is an analytic manifold. Using complex analysis techniques and a Taylor expansion approximation of the solution u
h,p
and its parametric derivatives w
m,k
for k=1,2,…, the authors obtained a convergence rate for a reduced basis approximation as
where 0<p<1 is the ℓ
p-summability exponent of a sequence related only to the diffusion coefficients of the problem. In particular, the convergence rate was independent of the spatial dimension d and the number of parameters P. In general, the reduced basis approximation of solutions of elliptic equations with regular coefficients has indeed been very successful. We would however like to convince the reader that analytic regularity of the solution manifold  is not necessary in order to successfully apply the reduced basis method.
is not necessary in order to successfully apply the reduced basis method.
Unfortunately, very little seems to be known about the n-width of manifolds of solutions of μ-PDEs. Very specific results concern special subspaces [10, 23]. For instance, if Y⊂X is a dense, compactly embedded, and bounded subspace with inner product (⋅,⋅) Y then the n-width of a ball B Y ⊂Y⊂X of finite radius is
where λ n are the eigenvalues of the problem
sorted in descending order (see [10], Theorem 4.5). We then obtain an algebraic decay rate for the n-width of B Y
where s≥1 similarly to (3). Provided that  we obtain also an upper bound for the n-width of
we obtain also an upper bound for the n-width of  , since then
, since then  , consequently only algebraic convergence of the reduced basis method is predicted by (23). Such results can be misleadingly pessimistic compared to practical experiences with reduced basis methods because they do not take into account the structure of the manifold
, consequently only algebraic convergence of the reduced basis method is predicted by (23). Such results can be misleadingly pessimistic compared to practical experiences with reduced basis methods because they do not take into account the structure of the manifold  nor the fact that approximation (4) inherits in some sense the structure of the manifold
nor the fact that approximation (4) inherits in some sense the structure of the manifold  .
.
4 An Extended Result of Exponential Convergence
Let us now give an example of a μ-PDE where the explicit dependence of the solution manifold on the parameters can be exhibited. Let us consider the parameter-dependent problem after discretization:
We assume that (i) the operator A 1 is invertible; (ii) the problem satisfies a global condition for the spectral radius ρ being

which we interpret as meaning that the term \(\varTheta_{1}^{a}(\mu) A_{1}\) dominates the original differential operator. Such a problem can arise for example from a discretized advection-diffusion or reaction-diffusion problem, where A 1 contains the (dominant) diffusion operator and A 2 contains all the other terms. We proceed to write explicitly the solution of this problem as
which by exploiting the global spectral condition (25) leads to the series expansion for the solution
By defining the fundamental basis vectors \(\varPsi_{k,q} := [A_{1}^{-1} A_{2}]^{k} A_{1}^{-1} F_{q}\), for k=0,1,… and q=1,…,Q f , we can write the solution as a series
Several remarks can be made about formula (26):
-
1.
In the special case A 2=0 the parametric dependence enters only through the r.h.s. and as a consequence the series (26) truncates to a finite one
$$ u = \sum_{q=1}^{Q_f} \frac{\varTheta_q^f(\mu)}{\varTheta_1^a(\mu)} \varPsi_{0,q}, $$(27)and so the greedy algorithm will always terminate after Q f steps.
-
2.
If the decay of the series coefficients in (26) is rapid, the solutions u can be well approximated by only the first few fundamental basis functions Ψ k,q , k=0,1,…,K and q=1,…,Q f . They can be computed according to an iterative procedure
$$ \varPsi_{0,q} = A_1^{-1} F_q, \qquad \varPsi_{k+1,q} = A_1^{-1} A_2 \varPsi_{k,q} \quad \mbox{for all } q=1,\ldots,Q_f $$requiring at each step one matrix multiplication and one backward substitution after obtaining once and for all the LU-decomposition of A 1.
-
3.
In general the Ψ k,q are not linear combinations of solutions of (24) so that they do not constitute a reduced basis approximation. They are, however, useful for estimating the n-width of the solution set. Provided that there exist positive sequences \(\{\gamma_{k,q}\}_{k=1}^{\infty}\) s.t. ∥Ψ k,q ∥ X ≤γ k,q for each q=1,…,Q f , we obtain an upper bound estimate for the n-width of the solution set
 of (24)
of (24)
 (28)
(28)by using the definition of the n-width, estimating upwards, and using formula (26) as

where m:=Q f ⋅n and \(X_{m}^{\varPsi} := \mbox{span} \{ \varPsi_{k,q} : k=0,\ldots,n-1, q=1,\ldots,Q_{f} \}\), i.e. the first m fundamental basis vectors. We have in fact decomposed the description of the manifold of solutions
 into two parts: the parametric regularity is carried by the coefficients Θ
1, Θ
2, \(\varTheta_{q}^{f}\), which can be taken just in
into two parts: the parametric regularity is carried by the coefficients Θ
1, Θ
2, \(\varTheta_{q}^{f}\), which can be taken just in  without affecting the n-width, and the spatial regularity, which is contained in the norm estimates γ
k,q
for the fundamental basis functions.
without affecting the n-width, and the spatial regularity, which is contained in the norm estimates γ
k,q
for the fundamental basis functions. -
4.
If the solution of (24) is approximated by the projection-based ROM in (14), i.e.
$$ \mathbb{Y}_n \bigl[\varTheta_1^a(\mu) A_1 + \varTheta_2^a(\mu) A_2 \bigr] \mathbb{X}_n^T U_n = \sum _{q=1}^{Q_f} \varTheta_q^f( \mu) \mathbb{Y}_n F_q, $$where the projectors were defined in (16), we obtain a similar formula for the reduced solution
$$ u_n(\mu) = \sum_{k=0}^{\infty} \sum _{q=1}^{Q_f} \frac{(-1)^k [\varTheta_2^a(\mu)]^k \varTheta_q^f(\mu) }{[\varTheta_1^{a}(\mu)]^{k+1}} \varPsi_{k,q}^n, $$but now with the reduced fundamental basis functions \(\varPsi_{k,q}^{n}\) defined as
$$ \varPsi_{0,q}^n = \bigl( \mathbb{Y}_n A_1 \mathbb{X}_n^T \bigr)^{-1} \mathbb{Y}_n F_q, \quad \varPsi_{k+1,q}^n = \bigl( \mathbb{Y}_n A_1 \mathbb{X}_n^T \bigr)^{-1} \mathbb{Y}_n A_2 \mathbb{X}_n^T \varPsi_{k,q}^n. $$As a result, we obtain immediately the error representation formula

Thus the quality of the ROM can directly be measured by observing how well it approximates the fundamental basis vectors, i.e. by looking at \(\| \varPsi_{k,q} - \mathbb{X}_{n}^{T} \varPsi_{k,q}^{n} \|_{X}\) for all k and q.
-
5.
Even if the global spectral condition (25) does not hold, we can try to expand the solution locally around different μ ∗ and obtain local approximation bases. This leads one to consider the hp-reduced basis method [9], where different reduced bases (analogous to p-refinement in the FEM) are constructed at different parts of the parameter domain (analogous to h-refinement in the FEM). Let
 be a nonoverlapping subdivision of the original parameter domain
be a nonoverlapping subdivision of the original parameter domain  into M subdomains. The local spectral condition requires that in each subdomain
into M subdomains. The local spectral condition requires that in each subdomain 

that is to say in each parameter subdomain
 one of the terms A
q
dominates, but the dominant part of the operator can change from subdomain to subdomain. If such a local spectral condition holds, our results extend straightforwardly to show the existence of local exponentially convergent approximation spaces.
one of the terms A
q
dominates, but the dominant part of the operator can change from subdomain to subdomain. If such a local spectral condition holds, our results extend straightforwardly to show the existence of local exponentially convergent approximation spaces.
With the n-width estimate (28) we can give an exponential convergence result extending that of [19]:
Proposition 4.1
Assume that the series (26) converges, so that

Then the
n-width of the solution set
 of (24) converges exponentially, i.e.
of (24) converges exponentially, i.e.

Proof
The n-width upper bound (28) gives for m=n⋅Q f

so that the result holds with α=−log(1−ε)/Q f and \(C = \frac{Q_{f}}{\varepsilon} \cdot \sup_{\mu, q} \{ \vert \frac{\varTheta_{q}^{f}(\mu)}{\varTheta_{1}(\mu)} \vert \| A^{-1}_{1} F_{q} \|_{X} \}\). □
Exponential convergence of the greedy reduced basis algorithm is then predicted by [3] as in (22). It should be understood that tight n-width estimates for the rate of exponential convergence cannot be obtained by such series expansions—indeed the coefficient α will tend to 0 if we let ε→0. The factor 1/Q f in the exponential is also excessively pessimistic provided that not for all q the terms converge at the same rate. In the next section we will demonstrate a problem where much faster exponential convergence of the greedy algorithm is observed, even in the parametric region when the fundamental series no longer converges rapidly.
To close this section let us briefly consider the more general case Q a >2:
If the global spectral condition
is satisfied, we can write the solution as
and applying (32) leads to
and finally
but now the fundamental basis vectors

depend explicitly on the parameter(s) μ. Let ρ (k)=(ρ 1,ρ 2,…,ρ k ) be a multi-index of dimension k and let ρ (0)=∅. We define a set of parameter-free basis functions φ k,q,ρ according to the recursion

Using the parameter-free basis we can rewrite the recursion of the fundamental basis (34) as
and so the kth level expansion for Ψ k,q will contain in general (Q a −1)k terms, and the size of the expansion blows up exponentially. Without some strong structural assumptions the series expansion method is not suitable for deriving exponentially decaying n-width estimates in the case Q a ≫1.
5 Numerical Example of a Parameter-Dependent Diffusion Problem
In this section we shall give numerical evidence of exponential convergence of n-width upper bounds and consequently of the GRBM approximation. As a test problem we consider a diffusion problem in a disk with four circular subregions Ω
1,…,Ω
4 as depicted in Fig. 2. The parametric problem can be formulated as follows: given  , find u=u(μ) s.t.
, find u=u(μ) s.t.
where the Γ k denote the four sides of the square, and \(\omega := \bigcup_{q=1}^{4} \varOmega_{q}\) is the union of the disks. The function \(\mathbb{I}_{\varOmega}\) denotes the characteristic function of the subdomain Ω. Thus the first parameter μ 1 controls the difference between the isotropic diffusion coefficient inside the disks versus the background conductivity, while the rest of the parameters μ 2,…,μ 8 enter into the boundary conditions and the source terms.
This problem exhibits the same properties as the case discussed in the previous Sect. 4 so that the solution can be written as the combination of the fundamental basis vectors thanks to the formula (26). In this case the affine expansion (5) of the problem is given by:
so that Q a =2, Q f =7, and the problem satisfies the global spectral condition (25) provided that μ 1∈[−(1−ε),1−ε] for some ε>0.
In order to compare the n-width bounds with the observed convergence rates of the weak greedy algorithm, we considered four different cases: ε=0.1, ε=0.5, ε=0.9, and ε=0.95. Note that if ε=1, the manifold of parametric solutions dimension is limited to a Q f -dimensional subspace of X as indicated by (27), and so the greedy terminates after exactly 7 iterations. In Fig. 3 we have plotted the convergence of the fundamental series terms \(\sup_{\mu} \| ( \varTheta_{2}^{a}(\mu) \varTheta_{q}^{f}(\mu) / \varTheta_{1}^{a}(\mu) ) \varPsi_{k,q} \|_{X}\) that dictate the convergence rate of the n-width upper bound (30). For the value ε=0.1 very weak convergence of the fundamental series is observed for some of the terms, namely q=2,3,4,5.
To obtain the GRBM approximation the weak greedy algorithm was driven by the residual-based a posteriori error estimator (20). In both cases the greedy was run until an absolute H 1-error below 10−3 was reached. This required n=25 basis functions for the case ε=0.1, n=21 basis functions for the case ε=0.5, n=15 basis functions for the case ε=0.9, and n=14 basis functions for the case ε=0.95. In Fig. 4 we have plotted the corresponding convergence rates of the greedy algorithm compared to the n-width upper bound predictions given by (30). In each case exponential convergence of the GRBM approximation is observed. The actual exponential decay rate depends on ε, where for ε=0.1 the n-width estimate is much too pessimistic when compared to the true rate of convergence. This is likely due to the weak convergence of some of the fundamental series terms (see Fig. 3(a)), and the result could be improved by considering more carefully the cutoff point for the different series terms for different q. However, as ε→1 the n-width estimate (30) becomes more and more indicative of the convergence rate observed during the greedy algorithm. According to Fig. 3(c–d) at the limit all the fundamental series coefficients converge at roughly the same rate, so that the bound (30) is expected to sharpen considerably.
Comparison of the n-width upper bound estimate (30) and the greedy convergence rate
6 Conclusions
We have reviewed the generalized reduced basis method for the uniform approximation of manifolds of solutions of parametric partial differential equations. These methods are typically driven by a greedy algorithm for selecting near-optimal reduced approximation subspaces. It has recently been shown that the convergence rate of the generalized reduced basis approximations is linked to the Kolmogorov n-width of the manifold of solutions. We have exhibited a model problem where the exact parameter-dependent solution can be expanded as a Neumann series, leading to a constructive proof that the n-width of the solution set in this case converges exponentially. Numerical experiments confirm that the reduced basis approximation also converges exponentially, and with a rate that is comparable to the one predicted by our n-width upper bound estimate. The predicted convergence rate is independent of the parametric regularity of the solution manifold and the number of parameters, but it does depend on the size of the affine expansion of the parametric problem. Future work involves finding more cases of parameter-dependent problems, where explicit solution formulas could be used to prove more general n-width estimates.
Notes
- 1.
The other option is to consider local or sequential approximations of the manifold, such as tracking a path on the manifold starting from a certain point and proceeding via a continuation method. In such cases we are usually not interested in the global behavior of the manifold.
- 2.
Ito and Ravindran [16] were perhaps the first ones to suggest using a Hermite ROM in a uniform approximation context, rather than in a pure continuation method. The Lagrange and Hermite ROMs were compared on a driven cavity problem, where the Hermite approach was somewhat superior. No stability problems were reported and the Hermite basis with only two basis functions was able to extrapolate solutions to much larger Reynolds numbers.
- 3.
In one of the pioneering works on RBM, Noor [24] used a Taylor ROM to build a local reduced space that was used to trace the post-buckling behavior of a nonlinear structure. The continuation idea was used also by Peterson [25] to compute Navier-Stokes solutions with increasing Reynolds number flow over a forward facing step. Again a Taylor ROM was constructed and used to extrapolate an initial guess for the Newton method at a slightly higher Reynolds number.
- 4.
In the works of Hay et al. [12, 13] sensitivity information was introduced into the proper orthogonal decomposition framework. The parametric sensitivities of the POD modes were derived and computed. The test problems were related with channel flow around a cylindrical obstacle, either by using a simple parametrization as the Reynolds number, or a more involved geometric parametrization of the obstacle. The use of a Hermite ROM considerably improved the validity of the reduced solutions away from the parametric snapshots. However, in the more involved geometrical parametrization case the Hermite ROM failed completely, as it did not converge to the exact solution even when the number of POD modes was increased.
- 5.
Carlberg and Farhat [6] proposed an approach they call “compact POD”, based on goal-oriented Petrov-Galerkin projection to minimize the approximation error subject to a chosen output criteria, and including sensitivity information with proper weighting coming from the Taylor-expansion and including “mollification” of basis functions far away from the snapshot parameter. The application was the optimization of an aeroelastic wing configuration by building local ROMs along the path to the optimal wing configuration.
References
Adomian, G.: Solving Frontier Problems of Physics: The Decomposition Method. Kluwer Academic, Norwell (1994)
Babuška, I., Szabo, B.A., Katz, I.N.: The p-version of the finite element method. SIAM J. Numer. Anal. 18(3), 515–545 (1981)
Binev, P., Cohen, A., Dahmen, W., DeVore, R., Petrova, G., Wojtaszczyk, P.: Convergence rates for greedy algorithms in reduced basis methods. SIAM J. Math. Anal. 43, 1457–1472 (2011)
Buffa, A., Maday, Y., Patera, A.T., Prud’homme, C., Turinici, G.: A priori convergence of the greedy algorithm for the parametrized reduced basis method. ESAIM Math. Model. Numer. Anal. 46(3), 595–603 (2012)
Canuto, C., Tonn, T., Urban, K.: A-posteriori error analysis of the reduced basis method for non-affine parameterized nonlinear PDEs. SIAM J. Numer. Anal. 47(3), 2001–2022 (2009)
Carlberg, K., Farhat, C.: A low-cost, goal-oriented ‘compact proper orthogonal decomposition’ basis for model reduction of static systems. Int. J. Numer. Methods Eng. 86(3), 381–402 (2011)
Cohen, A., DeVore, R., Schwab, C.: Analytic regularity and polynomial approximation of parametric and stochastic elliptic PDEs. Anal. Appl. 9(1), 11–47 (2011)
Deparis, S.: Reduced basis error bound computation of parameter-dependent Navier-Stokes equations by the natural norm approach. SIAM J. Numer. Anal. 46(4), 2039–2067 (2008)
Eftang, J.L., Knezevic, D.J., Patera, A.T.: An hp certified reduced basis method for parametrized parabolic partial differential equations. Math. Comput. Model. Dyn. Syst. 17(4), 395–422 (2011)
Evans, J.A., Bazilevs, Y., Babuška, I., Hughes, T.J.R.: N-widths, sup-infs, and optimality ratios for the k-version of the isogeometric finite element method. Comput. Methods Appl. Mech. Eng. 198(21–26), 1726–1741 (2009)
Grepl, M.A., Maday, Y., Nguyen, N.C., Patera, A.T.: Efficient reduced-basis treatment of nonaffine and nonlinear partial differential equations. ESAIM Math. Model. Numer. Anal. 41(3), 575–605 (2007)
Hay, A., Borggaard, J.T., Pelletier, D.: Local improvements to reduced-order models using sensitivity analysis of the proper orthogonal decomposition. J. Fluid Mech. 629, 41–72 (2009)
Hay, A., Borggaard, J., Akhtar, I., Pelletier, D.: Reduced-order models for parameter dependent geometries based on shape sensitivity analysis. J. Comput. Phys. 229(4), 1327–1352 (2010)
Huynh, D.B.P., Rozza, G., Sen, S., Patera, A.T.: A successive constraint linear optimization method for lower bounds of parametric coercivity and inf-sup stability constants. C. R. Acad. Sci. Paris. Sér. I Math. 345, 473–478 (2007)
Huynh, D.B.P., Knezevic, D., Chen, Y., Hesthaven, J., Patera, A.T.: A natural-norm successive constraint method for inf-sup lower bounds. Comput. Methods Appl. Mech. Eng. 199(29–32), 13 (2010)
Ito, K., Ravindran, S.S.: A reduced order method for simulation and control of fluid flows. J. Comput. Phys. 143(2), 403–425 (1998)
Lassila, T., Manzoni, A., Rozza, G.: On the approximation of stability factors for general parametrized partial differential equations with a two-level affine decomposition. ESAIM Math. Model. Numer. Anal. 46, 1555–1576 (2012)
Maday, Y.: Reduced basis method for the rapid and reliable solution of partial differential equations. In: Proceedings of the International Congress of Mathematicians, vol. III, pp. 1255–1270. Eur. Math. Soc., Zürich (2006)
Maday, Y., Patera, A.T., Turinici, G.: Global a priori convergence theory for reduced-basis approximation of single-parameter symmetric coercive elliptic partial differential equations. C. R. Acad. Sci. Paris. Sér. I Math. 335, 1–6 (2002)
Maday, Y., Patera, A.T., Turinici, G.: A priori convergence theory for reduced-basis approximations of single-parametric elliptic partial differential equations. J. Sci. Comput. 17(1–4), 437–446 (2002)
Manzoni, A.: Reduced models for optimal control, shape optimization and inverse problems in haemodynamics. PhD thesis, N. 5402, École Polytechnique Fédérale de Lausanne (2012)
Melenk, J.M.: On n-widths for elliptic problems. J. Math. Anal. Appl. 247, 272–289 (2000)
Melkman, A.A., Micchelli, C.A.: Spline spaces are optimal for L 2 n-width. Ill. J. Math. 22(4), 541–564 (1978)
Noor, A.K.: Recent advances in reduction methods for nonlinear problems. Comput. Struct. 13(1–3), 31–44 (1981)
Peterson, J.S.: The reduced basis method for incompressible viscous flow calculations. SIAM J. Sci. Stat. Comput. 10, 777–786 (1989)
Pinkus, A.: n-Widths in Approximation Theory. Ergebnisse der Mathematik und ihrer Grenzgebiete (3). Springer, Berlin (1985)
Quarteroni, A., Rozza, G., Manzoni, A.: Certified reduced basis approximation for parametrized PDEs and applications. J. Math. Ind. 1, 3 (2011). doi:10.1186/2190-5983-1-3
Rozza, G., Huynh, D.B.P., Patera, A.T.: Reduced basis approximation and a posteriori error estimation for affinely parametrized elliptic coercive partial differential equations. Arch. Comput. Methods Eng. 15, 229–275 (2008)
Tonn, T., Urban, K., Volkwein, S.: Comparison of the reduced-basis and POD a posteriori error estimators for an elliptic linear-quadratic optimal control problem. Math. Comput. Model. Dyn. Syst. 17(4), 355–369 (2011)
Veroy, K., Patera, A.T.: Certified real-time solution of the parametrized steady incompressible Navier-Stokes equations: rigorous reduced-basis a posteriori error bounds. Int. J. Numer. Methods Fluids 47(8–9), 773–788 (2005)
Acknowledgements
This contribution is published in BUMI (Bollettino Unione Matematica Italiana) as well by a special agreement between UMI (Unione Matematica Italiana) and Springer. This work celebrates the memory of Prof. Enrico Magenes (1923–2010) after the conference held in Pavia in November 2011.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Italia
About this chapter
Cite this chapter
Lassila, T., Manzoni, A., Quarteroni, A., Rozza, G. (2013). Generalized Reduced Basis Methods and n-Width Estimates for the Approximation of the Solution Manifold of Parametric PDEs. In: Brezzi, F., Colli Franzone, P., Gianazza, U., Gilardi, G. (eds) Analysis and Numerics of Partial Differential Equations. Springer INdAM Series, vol 4. Springer, Milano. https://doi.org/10.1007/978-88-470-2592-9_16
Download citation
DOI: https://doi.org/10.1007/978-88-470-2592-9_16
Publisher Name: Springer, Milano
Print ISBN: 978-88-470-2591-2
Online ISBN: 978-88-470-2592-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





 on which the field variable resides and (b) approximation of a new solution at μ
new with the “snapshots” u
h,p
(μ
m
), 1≤m≤n
on which the field variable resides and (b) approximation of a new solution at μ
new with the “snapshots” u
h,p
(μ
m
), 1≤m≤n
 , |Ξ
train|=M, in the parameter space and to use the information contained in the corresponding solutions u
h,p
(μ) for each μ∈Ξ
train (called snapshots) to find a representative subspace for the approximation of the manifold
, |Ξ
train|=M, in the parameter space and to use the information contained in the corresponding solutions u
h,p
(μ) for each μ∈Ξ
train (called snapshots) to find a representative subspace for the approximation of the manifold  . The reduced subspace X
n
of dimension n is found by solving [
. The reduced subspace X
n
of dimension n is found by solving [
 measures the distance between any subspace X
∗⊂X and the manifold
measures the distance between any subspace X
∗⊂X and the manifold  and is defined by
and is defined by

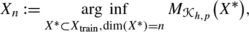
 is an approximate distance between any subspace X
∗⊂X and the manifold
is an approximate distance between any subspace X
∗⊂X and the manifold  . The choice of the function
. The choice of the function  to be used for the approximation of δ(⋅,⋅;⋅) defines which algorithm we use to choose the subspace. This is by far the most common way of constructing reduced subspaces, and we call these approaches Lagrange ROMs. In the GRBM we consider also the parametric sensitivities up to a suitable order, say K−1 (with K≥1) as part of the snapshot set
to be used for the approximation of δ(⋅,⋅;⋅) defines which algorithm we use to choose the subspace. This is by far the most common way of constructing reduced subspaces, and we call these approaches Lagrange ROMs. In the GRBM we consider also the parametric sensitivities up to a suitable order, say K−1 (with K≥1) as part of the snapshot set

 are:
are: 



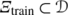 needs to be reasonably dense in the parameter space for
needs to be reasonably dense in the parameter space for  to be a good approximation of the true distance
to be a good approximation of the true distance  for all subspaces X
∗⊂X. In the POD one needs to compute the FE approximations u
h,p
(μ) for all the points in Ξ
train, which amounts to a considerable computational undertaking. In contrast, the weak greedy algorithm only needs to compute the exact solutions (and their parametric derivatives) at the n snapshots comprising the RB and only the computationally inexpensive a posteriori estimator Δ
n
(u
n
(μ)) needs to be evaluated over the entire training set. The difference in the norms used (ℓ
∞ for the greedy vs. ℓ
2 for the POD) also results in slightly different approximation behavior of the resulting bases. Typically the POD basis needed to reach a given tolerance is smaller in size but tends to be not as robust far away from the snapshots (see e.g. [
for all subspaces X
∗⊂X. In the POD one needs to compute the FE approximations u
h,p
(μ) for all the points in Ξ
train, which amounts to a considerable computational undertaking. In contrast, the weak greedy algorithm only needs to compute the exact solutions (and their parametric derivatives) at the n snapshots comprising the RB and only the computationally inexpensive a posteriori estimator Δ
n
(u
n
(μ)) needs to be evaluated over the entire training set. The difference in the norms used (ℓ
∞ for the greedy vs. ℓ
2 for the POD) also results in slightly different approximation behavior of the resulting bases. Typically the POD basis needed to reach a given tolerance is smaller in size but tends to be not as robust far away from the snapshots (see e.g. [


 of (
of (

 into two parts: the parametric regularity is carried by the coefficients Θ
1, Θ
2,
into two parts: the parametric regularity is carried by the coefficients Θ
1, Θ
2,  without affecting the n-width, and the spatial regularity, which is contained in the norm estimates γ
k,q
for the fundamental basis functions.
without affecting the n-width, and the spatial regularity, which is contained in the norm estimates γ
k,q
for the fundamental basis functions.
 be a nonoverlapping subdivision of the original parameter domain
be a nonoverlapping subdivision of the original parameter domain  into M subdomains. The local spectral condition requires that in each subdomain
into M subdomains. The local spectral condition requires that in each subdomain 

 one of the terms A
q
dominates, but the dominant part of the operator can change from subdomain to subdomain. If such a local spectral condition holds, our results extend straightforwardly to show the existence of local exponentially convergent approximation spaces.
one of the terms A
q
dominates, but the dominant part of the operator can change from subdomain to subdomain. If such a local spectral condition holds, our results extend straightforwardly to show the existence of local exponentially convergent approximation spaces.

