Keywords

1 Introduction

Recently systems of singularly perturbed differential equations are studied by many researchers all over the world. To cite a few: [1–20]. Most of the works are confined to systems with two equations and a few works are found on systems of n equations; \(n>0\) is arbitrary. Here, three types of systems of singularly perturbed differential equations are to be discussed.

2 A System of First Order Ordinary Differential Equations

Consider the system

$$\begin{aligned} E\mathbf {u}^\prime (x)+A(x)\mathbf {u}(x)=\mathbf {f}(x), \quad x \in \varOmega =(0,X] \end{aligned}$$
(1)

with \(\mathbf {u}(0)=\mathbf {\phi }\) given. E is the diagonal matrix \(E=diag(\varepsilon _i), i=1,2,\cdots ,n \) and \( A(x)=(a_{ij}(x))\) is an \(n\times n\) matrix. The functions \(a_{ij}(x)\) and \( f_i(x)\) for \(1\le i,j \le n\) are assumed to be in \(C^2(\overline{\varOmega })\) where \(\overline{\varOmega }=[0,1],\) assuming, without loss of generality, \(X=1.\) For convenience, the ordering \(\varepsilon _1< \varepsilon _2<\cdots \varepsilon _n\) is assumed. Further, the functions \(a_{ij}\) are assumed to satisfy

$$\begin{aligned} a_{ii}(x)>\sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^n |a_{ij}(x)|, i = 1,2, \cdots , n \end{aligned}$$
(2)
$$\begin{aligned} a_{ij}(x)\le 0, 1 \le i \ne j \le n \end{aligned}$$
(3)

and the singular perturbation parameters \(\varepsilon _i, i = 1,2, \cdots , n\) are assumed to satisfy

$$\begin{aligned} {\varepsilon _n} \le \dfrac{{\alpha }}{6} \end{aligned}$$
(4)

so as to accommodate all the layers well inside the domain.

With the above assumptions, the problem (1) has a solution \(\mathbf {u}\in C^{(0)}(\overline{\varOmega })\cap C^{(1)}(\varOmega )\)

As explained in [21], here also the supremum norm is used in estimates. The norms \(||\mathbf {V}|| = \max _{1\le k \le n} |V_k|\) for any \(n-\)vector \(\mathbf {V}, ||y||= \sup _{0\le x \le 1}|y(x)|\) for any scalar-valued function y and \(||\mathbf {y}|| = \max _{1 \le k \le n}||y_k||\) for any vector valued function \(\mathbf {y}\) are introduced.

The problem (1) is singularly perturbed, in the following sense. The reduced problem obtained by putting each \(\varepsilon _i = 0, \; i = 1,2, \cdots , n,\) in (1) is the linear algebraic system

$$\begin{aligned} A(x) \mathbf {u}_0(x)=\mathbf {f}(x). \end{aligned}$$
(5)

This problem (5) has a unique solution and hence arbitrary initial conditions cannot be imposed. This shows that there are initial layers at \(x=0\) for \(\mathbf {u}.\) The attracting feature of the layers is that the component \(u_n\) has an initial layer of width \(O(\varepsilon _n),\) the component \(u_{n-1}\) also has a layer of width \(O(\varepsilon _n)\) and an additional sublayer of width \(O(\varepsilon _{n-1})\) and so on. Lastly the component \(u_1\) has an initial layer of width \(O(\varepsilon _n)\) and additional sub-layers of widths \(O(\varepsilon _{n-1}), O(\varepsilon _{n-2}), \cdots , O(\varepsilon _{1}).\) The complexity of the layer pattern of the solution makes the problem more interesting. This complexity makes the derivation of bounds on the estimates of the derivatives and the error analysis more challenging.

2.1 Analytical Results

Valarmathi and Miller [19] established the maximum principle for a general system of \('n'\) linear first order singularly perturbed differential equations, with an additional result that the maximum principle satisfied by the operator

\(\mathbf {L} = ED + A(x)\) of system (1) implies that the operator \({\tilde{\mathbf {L}}}\) of any lower order system also satisfies the maximum principle.

Apart from the stability result, estimates of the derivatives of smooth and singular components derived with the help of induction will not suffice for error analysis. Novel estimates of derivatives are required. To achieve this, points of interaction of the layer functions are identified. For a system of two equations, it was Linss [9] who identified such a point. But it is Valarmathi and Miller [20] who identified a sequence of such points between the ‘n’ layer functions and came out with some interesting properties, which lead to non classical bounds for the derivatives of the singular components that are interlinked.

2.2 Shishkin Mesh

The construction of an appropriate mesh plays a vital role in solving the singular perturbation problem. As there are layer regions or inner regions and outer regions and as more information is needed inside the inner region, a piecewise uniform mesh is needed.

A piecewise uniform Shishkin mesh distributing N/2 points to the outer region and the remaining N/2 points equally to all the inner regions will serve the purpose. The Shishkin mesh suggested for problem (1) is the set of points \(\overline{\varOmega }^N = \{ x_j \}_0^N\) that divides [0, 1] into \(n+1\) mesh intervals \([0, \sigma _1] \cup ... \cup (\sigma _{n-1}, \sigma _n] \cup (\sigma _n, 1]\) where the n parameters \(\sigma _r\) separate the uniform meshes. With \(\sigma _0 = 0, \sigma _{n+1} = 1, \sigma _n\) is defined by \(\sigma _n = \min \left\{ \dfrac{\sigma _{n+1}}{2}, \dfrac{\varepsilon _n}{\alpha }\ln N\right\} \) and for \(r = n-1, n-2, ..., 2,1,\) \(\sigma _r = \min \left\{ \dfrac{r \sigma _{r+1}}{r+1}, \dfrac{\varepsilon _r}{\alpha }\ln N\right\} .\) Then on the subinterval \((\sigma _n, 1],\) a uniform mesh with N/2 mesh points is placed and on each of the intervals \((\sigma _r, \sigma _{r+1}], r = 0,1,...,n-1,\) a uniform mesh of N/2n mesh points is placed where \('n'\) is the number of perturbation parameters involved in (1).

In particular, when all the parameters \(\sigma _r, r = 1,2,...,n\) are with the left choice, the Shishkin mesh becomes a classical uniform mesh with stepsize \(N^{-1}\) through out from 0 to 1. For the other cases, the mesh is coarse in the outer region and becomes finer and finer towards the initial point. Infact \(\sigma _r, r=1,2,3,\cdots ,n\) are the points only where a change in the mesh size may occur.

2.3 Discrete Problem

To solve (1) numerically, consider the corresponding discrete initial value problem on the Shishkin mesh \(\overline{\varOmega }^N\) given by

$$\begin{aligned} E D^- \mathbf {U} + A \mathbf {U} = \mathbf {f} \; \text {on} \; \varOmega ^N, \mathbf {U} = \mathbf {u} \; \text {at the initial point}. \end{aligned}$$
(6)

Making use of the mesh geometry and the novel estimates of derivatives derived by the existence of the sequence of layer interaction points, the authors in [20] established the almost first order parameter uniform convergence.

More general case of problem (1)

In nature, many systems of multiscale dynamics, involve some components having large scale flow rates. This problem when formulated follows the form \(ED \mathbf {u} + A \mathbf {u} = \mathbf {f} \; \text {on} \; (0,1] \; \text {and} \; \mathbf {u}(0) = \mathbf {\phi }\) where \(E = \;\text {diag}(\varepsilon _i)\) with \(0< \varepsilon _1< \varepsilon _2< ... < \varepsilon _k = \varepsilon _{k+1} = ... = \varepsilon _n = 1.\) In this case, the problem is called a partially singularly perturbed initial value problem for a linear system of first order ODEs.

Establishing analytical results and error analysis demand the judicial use of certain barrier functions and the appropriate modification of the Shishkin mesh considered for problem (1). In the construction of the Shishkin mesh for solving problem (1), the number of transition parameters was fixed to be equal to the number of distinct perturbation parameters in (1). Here also, having the same strategy, the outer region gets wider as the number of transition parameters gets reduced.

2.4 Discontinuous Source Terms

In some multiscale fluid flows, it may also happen that some of the source functions \(f_i, 1 \le i \le n\) may go discontinuous at points in the domain of definition of problem (1). These discontinuities result in some interesting characteristics of the solution.

The solution, apart from its initial layers, exhibits interior layers at the points of discontinuity. Then care has to be taken in constructing the mesh because it should resolve interior layers in addition to the initial layers. Further, for a simple discontinuity at a point, the interior layers are just like the initial layers dislocated. These layer functions have a similar sequence of layer interaction points. Making use of these facts and the mesh geometry one can solve the problem with discontinuous source function.

Example 1

Consider the following system of singularly perturbed initial value problem.

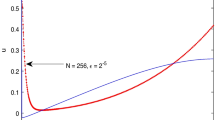
$$\begin{aligned} \left. \begin{matrix} \varepsilon _1u_1^{\prime }(t)+2(1+t)^2u_1(t)-(1+t^2)u_2(t)&{}=&{}0.5(1+t)\\ \varepsilon _2u_2^{\prime }(t)-(1+t)u_1(t)+2(1+t)u_2(t)&{}=&{}(1+\dfrac{t}{4}) \end{matrix} \right\} \end{aligned}$$

for \(\;t\;\in \;(0,1]\;\) and \(\;\mathbf {u}(0)\;=\;\mathbf {0}.\;\) The layer profile of the solution \(\mathbf {u}\) of this problem obtained by the proposed method is as in Fig. 1 for \(\varepsilon _1 = 10^{-10}, \varepsilon _2 = 10^{-7}\) and \(N=128\).

Fig. 1
figure 1

Solution profile of Example 1

Full size image
Fig. 2
figure 2

Solution profile of Example 2

Full size image
Fig. 3
figure 3

Solution profile of Example 3

Full size image

3 System of Second Order Differential Equations of Reaction—Diffusion Type

Consider the system of singularly perturbed differential equations of reaction-diffusion type with boundary values prescribed.

$$\begin{aligned} {-}E\mathbf {u}^{\prime \prime }(x)+A(x) \mathbf {u}(x)=\mathbf {f}(x), x \in \varOmega = (0,1)\nonumber \\ \mathbf {u}(0), \mathbf {u} (1) \;\;\text {given} \end{aligned}$$
(7)

E is the same as in problem (1), \(A = (a_{ij})_{n\times n},\; a_{ij}(x), \) \( f_i(x) \in C^2(\overline{\varOmega })\) and (2), (3) & (4) hold good in \(\overline{\varOmega }\). Under these assumptions the problem (7) has a solution in \(C^{(0)}(\overline{\varOmega })\cap C^{(2)}(\varOmega ).\)

For systems of this type, Paramasivam et al. [16] established maximum principle, the analytical results and a parameter uniform method of solving them on a Shishkin mesh.

The solution \(\mathbf {u}\) of the problem (7) exhibits twin boundary layers at the boundary, \(x=0\) and \(x=1.\) The component \(u_n\) exhibits twin boundary layers of width \(O(\sqrt{\varepsilon _n}),\) while \(u_{n-1}\) has twin boundary layers of width \(O(\sqrt{\varepsilon _n})\) and additional twin boundary sub layers of width \(O(\sqrt{\varepsilon _{n-1}})\) and so on. Lastly \(u_1\) has twin boundary layers of width \(O(\sqrt{\varepsilon _n})\) and additional twin boundary sub layers of widths \(O(\sqrt{\varepsilon _{n-1}}), O(\sqrt{\varepsilon _{n-2}}), \cdots , O(\sqrt{\varepsilon _1}).\)

These boundary layers also have twin layer interaction sequences which could be used with the induction method in establishing the novel estimates of the derivatives of the smooth and singular components of the solution.

The related systems of (7) which are partially singularly perturbed and which have discontinuous source vector are with higher order difficulty and are handled as in the previous case, in [22, 23].

Example 2

Consider the following singularly perturbed boundary value problem

$$\begin{aligned} \left. \begin{matrix} -\varepsilon _1u_1^{\prime \prime }(x)+5u_1(x)-u_2(x)-u_3(x)\;\;\;\;\;\;\qquad \qquad &{}=&{}x^2\\ -\varepsilon _2u_2^{\prime \prime }(x)-u_1(x)+(5+x)u_2(x)-u_3(x)\;\;\;\;\;\qquad &{}=&{}e^{-x}\\ -\varepsilon _3u_3^{\prime \prime }(x)-(1+x)u_1(x)-u_2(x)+(5+x)u_3(x)\;\;&{}=&{}1+x \end{matrix} \right\} \end{aligned}$$

for \(x\;\in \;(0,1)\) and \(\mathbf {u}(0)\;=\;\mathbf {0},\;\mathbf {u}(1)\;=\;\mathbf {0}.\) The layer profile of the solution \(\mathbf {u}\) of this problem obtained by the method suggested in [16] is presented in Fig. 2 for \(\varepsilon _1 = \dfrac{\eta }{16}, \varepsilon _2 = \dfrac{\eta }{4}, \varepsilon _3 = \eta \) where \(\eta =0.1\) and \(N=512\).

4 Systems of Singularly Perturbed Time Dependent Equations of Reaction-Diffusion Type

Consider the following parabolic initial-boundary value problem for a singularly perturbed linear system of second order differential equations

$$\begin{aligned} \frac{\partial \mathbf {u}}{\partial t} -E\frac{\partial ^2\mathbf {u}}{\partial x^2}+A\mathbf {u}=\mathbf {f},\;\mathrm {on}\; \varOmega ,\;\mathbf {u}\; \mathrm {given \; on}\; \varGamma , \end{aligned}$$
(8)

where \(\varOmega =\{(x,t): 0< x< 1, 0 < t \le T\}\), \(\overline{\varOmega }=\varOmega \cup \varGamma ,\;\; \varGamma = \varGamma _L \cup \varGamma _B \cup \varGamma _R\) with \( \mathbf {u}(0,t)=\mathbf {\phi }_L(t)\; \mathrm {on}\;\varGamma _L=\{(0,t): 0 \le t \le T\},\;\; \mathbf {u}(x,0){=}\mathbf {\phi }_B(x)\;\mathrm {on}\;\varGamma _B=\{(x, 0): 0< x < 1\},\;\; \mathbf {u}(1,t)=\mathbf {\phi }_R(t)\; \mathrm {on}\;\varGamma _R=\{(1,t): 0 \le t \le T\}.\) Here, for all \(\;(x,t) \in \overline{\varOmega },\;\mathbf {u}(x,t) = \left( u_1(x,t), u_2(x,t), \dots , u_n(x,t)\right) ^T,\) \(\mathbf {f}(x,t) = \left( f_1(x,t), f_2(x,t),\right. \) \(\left. \dots , f_n(x,t)\right) ^T,\;\)

$$E= \begin{pmatrix} &{}\varepsilon _1&{}0&{}\cdots &{}0\\ &{}0&{}\varepsilon _2&{}\cdots &{}0\\ &{}\vdots &{}\vdots &{}&{}\vdots \\ &{}0&{}0&{}\cdots &{}\varepsilon _n \end{pmatrix},\;\;\; A(x,t)= \begin{pmatrix} &{}a_{11}(x,t)&{}a_{12}(x,t)&{}\cdots &{}a_{1n}(x,t)\\ &{}a_{21}(x,t)&{}a_{22}(x,t)&{}\cdots &{}a_{2n}(x,t)\\ &{}\vdots &{}\vdots &{}&{}\vdots \\ &{}a_{n1}(x,t)&{}a_{n2}(x,t)&{}\cdots &{}a_{nn}(x,t) \end{pmatrix}.$$

The problem (8) can also be written in the operator form

$$\mathbf {L}\mathbf {u}\; = \;\mathbf {f}\;\;\mathrm {on}\;\; \varOmega ,\;\;\mathbf {u}\;\;\mathrm {given\;\; on}\;\;\varGamma ,$$

where the operator \(\;\mathbf {L}\;\) is defined by

$$\begin{aligned} \mathbf {L}\;=\;I\frac{\partial }{\partial t}-E\frac{\partial ^2}{\partial x^2} + A, \end{aligned}$$

where I is the identity matrix.

The reduced problem obtained by putting \(\varepsilon _i\;=\;0,\;i=1,2,\cdots ,n\) in (8) is defined by

$$\begin{aligned} \frac{\partial \mathbf {u}_0}{\partial t} +A\mathbf {u}_0=\mathbf {f},\;\mathrm {on}\; \varOmega ,\;\mathbf {u}_0=\mathbf {u}\;\mathrm {on}\;\varGamma _B. \end{aligned}$$
(9)

The \(\varepsilon _i\) are assumed to be distinct and, for convenience, to have the ordering \(\varepsilon _1\;<\;\cdots \;<\;\varepsilon _n.\) For all \((x,t) \in \overline{\varOmega }\), it is assumed that the components \(a_{ij}(x,t)\) of A(x, t) satisfy the inequalities

$$\begin{aligned} a_{ii}(x,t) > \displaystyle {\sum _{^{j\ne i}_{j=1}}^{n}}|a_{ij}(x,t)| \; \; \text {for}\;\; 1 \le i \le n, \;\; \text {and} \;\;a_{ij}(x,t) \le 0 \;\; \text {for} \; \; i \ne j \end{aligned}$$
(10)

and there exists a number \(\,\alpha \,\) satisfying the inequality \( 0<\alpha <\displaystyle {\min _{^{(x,t)\in \overline{\varOmega }}_{1 \le i \le n}}}(\sum _{j=1}^n a_{ij}(x,t)). \) It is also assumed, without loss of generality, that \(\sqrt{\varepsilon _n} \le \frac{\sqrt{\alpha }}{6}\) which ensures that the solution domain contains all the layers.

The norms, \(\parallel \mathbf {V}\parallel \;=\;\max _{1 \le k \le n}|V_k|\) for any n-vector \(\mathbf {V}\), \(\parallel y \parallel _D \;=\;\sup \{|y(x,t)|: (x,t)\in D\}\) for any scalar-valued function y and domain D, and \(\parallel \mathbf {y} \parallel \;=\;\max _{1 \le k \le n} \parallel y_{k} \parallel \) for any vector-valued function \(\mathbf {y}\), are introduced. When \(D=\overline{\varOmega }\) or \(\varOmega \) the subscript D is usually dropped. In a compact domain D a function is said to be Hölder continuous of degree \(\lambda ,\;0< \lambda \le 1\), if, for all \((x_1, t_1), (x_2, t_2) \in D\),

$$\begin{aligned} |u(x_1, t_1) - u(x_2, t_2)| \le C{(|x_1- x_2|^2 +|t_1-t_2|)}^{\lambda /2}. \end{aligned}$$

The set of Hölder continuous functions forms a normed linear space \(C_\lambda ^0(D)\) with the norm

$$\begin{aligned} ||u||_{\lambda ,D} = ||u||_{D} + \displaystyle \sup _{(x_1, t_1),(x_2, t_2) \in D} \frac{|u(x_1, t_1) - u(x_2, t_2)|}{{(|x_1- x_2|^2 +|t_1-t_2|)}^{\lambda /2}}, \end{aligned}$$

where \(||u||_{D} = \displaystyle \sup _{(x, t)\in D} |u(x,t)|.\) For each integer \(k \ge 1\), the subspaces \(C_\lambda ^k(D)\) of \(C_\lambda ^0(D)\), which contain functions having Hölder continuous derivatives, are defined as follows

$$\begin{aligned} C_\lambda ^k(D) = \displaystyle \{ u: \frac{\partial ^{l+m} u}{\partial x^l \partial t^m} \in C_\lambda ^0(D) \;\text {for}\; l,m \ge 0 \;\text {and}\; 0 \le l+2m \le k \displaystyle \}. \end{aligned}$$

The norm on \(C_\lambda ^0(D)\) is taken to be \(||u||_{\lambda ,k,D} = \displaystyle \max _{0\le l+2m \le k} ||\frac{\partial ^{l+m} u}{\partial x^l \partial t^m}||_{\lambda , D}\). For a vector function \(\mathbf {v} = (v_1, v_2,...,v_n)\), the norm is defined by \(||\mathbf {v}||_{\lambda , k, D} = \displaystyle \max _{1 \le i \le n} ||v_i||_{\lambda , k, D}\).

Regularity and Compatibility conditions

It is assumed that enough regularity and compatibility conditions hold for the data of the problem (8) so that the partial derivatives with respect to the space variable of the solution are continuous up to fourth order and the partial derivatives with respect to the time variable of the solution are continuous up to second order. The compatibility conditions for the problem (8) defined on a rectangular domain \(\varOmega \) is established in [3].

Sufficient conditions for the existence, uniqueness and regularity of solution of (8) are given in the following.

Assume that \( A,\; \mathbf {f} \in C_\lambda ^2(\overline{\varOmega })\), \(\mathbf {\phi }_L \in C^{1}(\varGamma _L),\;\mathbf {\phi }_B \in C^{2}(\varGamma _B)\), \(\mathbf {\phi }_R \in C^{1}(\varGamma _R)\) and that the following compatibility conditions are fulfilled at the corners (0, 0) and (1, 0) of \(\varGamma \)

$$\begin{aligned} \mathbf {\phi }_B(0) = \mathbf {\phi }_L (0)\;\;\; \text {and}\;\;\; \mathbf {\phi }_B(1) = \mathbf {\phi }_R (0),\end{aligned}$$
(11)
$$\begin{aligned} \begin{array}{lcl} \displaystyle \frac{d \mathbf {\phi }_L (0)}{dt} -E \displaystyle \frac{d^2 \mathbf {\phi }_B(0)}{dx^2}+A(0,0) \mathbf {\phi }_B(0) &{}=&{} \mathbf {f} (0,0),\\ \displaystyle \frac{d \mathbf {\phi }_R (0)}{dt} -E \displaystyle \frac{d^2 \mathbf {\phi }_B(1)}{dx^2}+A(1,0) \mathbf {\phi }_B(1) &{}=&{} \mathbf {f} (1,0) \end{array} \end{aligned}$$
(12)

and

$$\begin{aligned} \begin{array}{lcl} \dfrac{d^2}{dt^2}\mathbf {\phi }_L(0)&{}=&{}E^2\dfrac{d^4}{dx^4}\mathbf {\phi }_B(0) - 2EA(0,0)\dfrac{d^2}{dx^2}\mathbf {\phi }_B(0)- E A(0,0)\dfrac{d}{dx}\mathbf {\phi }_B(0) \\ &{}&{}- (A^2(0,0) +\dfrac{\partial A}{\partial t}(0,0) +E \dfrac{\partial ^2 A}{\partial x^2}(0,0) )\mathbf {\phi }_B(0) \\ &{}&{}-A(0,0)\mathbf {f}(0,0)+ \dfrac{\partial \mathbf {f}}{\partial t}(0,0) + E \dfrac{\partial ^2 \mathbf {f}}{\partial x^2}(0,0), \end{array} \end{aligned}$$
(13)
$$\begin{aligned} \begin{array}{lcl} \dfrac{d^2}{dt^2} \mathbf {\phi }_R(0)&{}=&{}E^2\dfrac{d^4}{dx^4}\mathbf {\phi }_B(1) - 2EA(1,0)\dfrac{d^2}{dx^2}\mathbf {\phi }_B(1)- E A(1,0)\dfrac{d}{dx}\mathbf {\phi }_B(1) \\ &{}&{}- (A^2(1,0) +\dfrac{\partial A}{\partial t}(1,0) +E \dfrac{\partial ^2 A}{\partial x^2}(1,0) )\mathbf {\phi }_B(1) \\ &{}&{}-A(1,0)\mathbf {f}(1,0)+ \dfrac{\partial \mathbf {f}}{\partial t}(1,0) + E \dfrac{\partial ^2 \mathbf {f}}{\partial x^2}(1,0). \end{array}ss \end{aligned}$$
(14)

Then there exists a unique solution \(\mathbf {u}\) of (8) satisfying \(\mathbf {u} \in C_\lambda ^4 (\overline{\varOmega })\).

As there are twin boundary parabolic layers with sub-layers, the Shishkin mesh to resolve these layers is constructed on the rectangular domain \(\overline{\varOmega }\) and a classical finite difference method is suggested and proved to be parameter-uniform first order convergent in time and almost second order convergent in space in [3].

Example 3

Consider the problem

$$\begin{aligned} \frac{\partial \mathbf {u}}{\partial t} -E\frac{\partial ^2 \mathbf {u}}{\partial x^2} + A \mathbf {u}= \;\mathbf {f}\;\;\mathrm {on}\;\; (0,1) \times (0,1],\;\;\mathbf {u}=\mathbf {0} \mathrm {\;for}\;\;x=0\;\mathrm {or}\; t=0\mathrm {\;or}\; x=1,\end{aligned}$$

where  \( E = diag(\varepsilon _1, \varepsilon _2, \varepsilon _3)\),   \(A=\) \(\begin{pmatrix} &{}6\;\;&{} -1\;\;&{} 0\\ &{}-t\;\;&{} 5(x+1)\;\;&{} -1\\ &{}-1\;\;&{} -(1+x^2)\;\; &{} 6+x\\ \end{pmatrix},\quad \mathbf {f} = \begin{pmatrix} 1+e^{x+t} \\ 1+x+t^2\\ 1+e^{t} \end{pmatrix}.\) The layer profile of the solution \(\mathbf {u}\) of this problem is displayed in Fig. 3 for \(\varepsilon _1 = 2^{-7}, \varepsilon _2 = 2^{-5}, \varepsilon _3 = 2^{-2}, M=32\) and \(N=48\).

Here for the system (8) also, its subcases of the system being partially perturbed and the source vector to have discontinuities could also be dealt with in a way similar to those in Sects. 2 and 3.