Keywords

1 Introduction

The analytical solutions of linear singularly perturbed differential equations typically contain boundary layers. To construct parameter-uniform numerical methods [1] for such problems, the location, width and strength of all layers present in the solution needs to be identified. In addition to boundary layers, interior layers can also appear in certain types of singularly perturbed problems. Interior layers can form for several reasons. For example, interior layers can appear due to the presence of turning points, non-smooth coefficients, non-smooth boundary/initial data, non-linearities or lack of compatibility at any corner points within the domain. In the case of linear problems, the strength and width of any interior layer will depend on whether the problem is of convection-diffusion or reaction-diffusion type on either side of the layer. If turning points are present (when the convective coefficient is continuous and passes through zero at some point within the domain) then the nature of any boundary or interior layer will depend on the rate at which the convective coefficient approaches its root. The level of smoothness of the problem data will also influence the creation of interior layers. In the case of singularly perturbed parabolic problems, the location of any interior layer may move with time and any layer-adaptive mesh will be required to track this movement. In the case of nonlinear problems, the location of any interior layer may not be known explicitly and detailed asymptotic information about the location of the interior layer will be required in order to construct a suitable mesh for the problem. In this paper, we review some recent results on singularly perturbed problems with interior layers.

In Sect. 2, we begin with some standard results on linear singularly perturbed problems with smooth data, where we identify sufficient regularity for the data so that no internal layer appears in the solution and the standard results on parameter-uniform numerical methods for both convection-diffusion and reaction-diffusion problems immediately apply. In Sect. 3, we introduce a discontinuity into a simple initial value problem and give the modifications in both the mesh and the analysis that are required to retain the basic result of first order parameter-uniform convergence. In Sect. 4, we discuss some results concerning interior layers appearing in linear ordinary differential equations due to discontinuities in the data. In Sect. 5 we briefly consider a particular type of singularly perturbed turning point problem with interior layers of exponential-type in the solution. In Sect. 6, we outline the issues around capturing a moving interior layer and in Sect. 7 we conclude the paper with some comments on interior layers occurring in nonlinear singularly perturbed problems.

Notation. Here and throughout the paper, C is a generic constant independent of both the singular perturbation parameter \(\varepsilon \) and N, which is the number of mesh elements used in any co-ordinate direction. Also, \(\Vert \cdot \Vert _D\) denotes the maximum pointwise norm over the set D.

2 Linear Singularly Perturbed Problems with Smooth Data

Linear second order singularly perturbed boundary value problems can be categorized into two broad problem classes: problems of reaction-diffusion or convection-diffusion type.

Consider the following class of singularly perturbed reaction-diffusion problems of the form: Find \(u \in C^{k+2}(\bar{\varOmega }),\ k \ge 0\) such that

$$\begin{aligned}&L_{\varepsilon , (1)} u:=-\varepsilon u''+b(x)u=f(x), \quad x \in \varOmega := (0,1),\ \end{aligned}$$
(1a)
$$\begin{aligned}&u(0)=u_0, u(1) =u_1; \quad b,f \in C^k(\varOmega ); \quad b(x) \ge \beta >0, \ x\in {\overline{\varOmega }}.&\end{aligned}$$
(1b)

Due to the assumption \(b(x) >0\), the differential operator is inverse-monotone. That is: For any function \(y \in C^0(\bar{\varOmega }) \cap C^2(\varOmega )\) if \(y(0) \ge 0, y(1) \ge 0\) and \( L_{\varepsilon , (1)} y(x) \ge 0, \ x \in \varOmega \) then \(y(x) \ge 0, \forall x \in \bar{\varOmega } .\) This property of the differential operator is used extensively to obtain suitable bounds on various components of the solution and in estimating the level of accuracy of any proposed approximation to the solution.

The associated reduced problem is simply \(b(x)v_0(x) =f(x)\). Note that the reduced solution \(v_0\) of any singularly perturbed problem is defined in such a way that

$$ \Vert u - v_0 \Vert _{\varOmega _0} \le C \varepsilon ^p,\quad \hbox {meas} (\varOmega \setminus \varOmega _0)= O(\varepsilon ^p \ln (1/\varepsilon )), \quad p>0 $$

and that \(v_0\) solves the associated differential equation with \(\varepsilon \) formally set to zero. In general, the reduced solution will not satisfy all the boundary conditions and, then, boundary layers form when there is a discrepancy between the boundary values of the reduced solution and the solution. To correct this discrepancy, we define the leading term of the two boundary layer functions for problem (1) to be

$$\begin{aligned} w_{L,0}(x) := (u(0)-v_0(0)) e^{-\sqrt{\frac{b(0)}{\varepsilon }}x},\quad w_{R,0}(x) := (u(1)-v_0(1)) e^{-\sqrt{\frac{b(1)}{\varepsilon }}(1-x)}. \end{aligned}$$

Then we observe that \(L_{\varepsilon , (1)} (v_0+ w_{L,0}+w_{R,0}) = O(\sqrt{\varepsilon }) \) as

$$ \Vert L_{\varepsilon , (1)} v_0 \Vert _{\bar{\varOmega }} \le C \varepsilon \quad \hbox {and} \quad \vert L_{\varepsilon , (1)} w_{L,0} (x) \vert \le C x e^{-\sqrt{\frac{b(0)}{\varepsilon }}x} \le C \sqrt{\varepsilon };$$

and \((v_0+ w_{L,0}+w_{R,0})(0){=}Ce^{-\sqrt{\frac{b(1)}{\varepsilon }}}, (v_0+ w_{L,0}+w_{R,0})(1) = Ce^{-\sqrt{\frac{b(0)}{\varepsilon }}}\). Hence, we have constructed the following asymptotic expansion

$$ u_{asy}=v_0+w_{L,0}+w_{R,0},\quad \hbox {where} \quad \Vert u-u_{asy} \Vert _{\bar{\varOmega }} \le C\sqrt{\varepsilon }.$$

From this bound, we see that f(x) / b(x) is indeed the reduced solution for the reaction-diffusion problem.

If we impose the constraint \(\varepsilon \le CN^{-2p}, p >0\), then without performing any numerical calculations the above asymptotic expansion of \(v_0+w_{L,0}+w_{R,0}\), yields an \(O(N^{-p})\)-approximate solution to the solution u with relatively low regularity assumed (i.e., let \(k=2\) in (1)). However, we wish to generate approximations without imposing a constraint of the form \(\varepsilon \le CN^{-2p}\) on the set of problems being considered. Our interest lies in designing parameter-uniform numerical methods [1] for a large set of singularly perturbed problems. Parameter-uniform numerical methods guarantee convergence of the numerical approximations, without imposing a mesh-dependent restriction on the permissible size of the singular perturbation parameter. To establish parameter-uniform asymptotic error bounds on any numerical approximations generated, we will require bounds on the derivatives of the components. The above asymptotic expansion does not yield information about the derivatives of the solution.

In place of the asymptotic expansion, we will utilize a Shishkin decomposition [2] of the solution in the analysis of appropriate numerical methods for (1). Consider the extended domain \(\varOmega ^*:=(-L,L), 1<L\) and the extended functions \(b^*,f^* \in C^k(\varOmega ^*)\) of b, f. The extended regular component: \( v^*:= v^*_0+\varepsilon v^*_1\), where the correction \(v^*_1\) to the reduced solution \(v^*_0\) satisfies

$$\begin{aligned} L^*_{\varepsilon , (1)} v^*_1 =(v^*_0)'',\quad v^*_1(-L)=v^*_1(L)=0. \end{aligned}$$

Then the regular component \(v \in C^k(\bar{\varOmega })\) satisfies the boundary value problem

$$ L_{\varepsilon , (1)} v = f,\quad v(0)=v^*(0), \ v(1) = v^*(1). $$

If \(v(0) \ne u(0)\), then a boundary layer will be present in a neighbourhood of \(x=0\). Layer components \(w_L,w_R \in C^{k+2}(\bar{\varOmega })\) at either end point, are defined as the solutions of the following homogeneous problems

$$\begin{aligned} L_{\varepsilon , (1)} w_L = 0,\ w_L(0)=u(0)-v(0), \ w_L(1) = 0;\\ L_{\varepsilon , (1)} w_R = 0,\ w_R(0)=0 , \ w_R(1) = u(1)-v(1). \end{aligned}$$

Note that \(w_L(x) \ne w_{L,0}(x)\). The Shishkin decomposition (with no remainder term) is now of the form

$$ u=v+w_L +w_R. $$

If \(b,f \in C^4(\varOmega )\) then one can establish [3, Chap. 6] the following bounds on the derivatives of the components of the solution of (1).

$$\begin{aligned} \Vert v^{(i)} \Vert _{\bar{\varOmega }}\le & {} C (1+\varepsilon ^{1-i/2}), \quad i \le 4; \\ \vert w_L^{(i)} (x) \vert\le & {} C \varepsilon ^{-i/2}e^{-\sqrt{\frac{\beta }{ \varepsilon }} x}, \quad \vert w_R^{(i)} (x) \vert \le C \varepsilon ^{-i/2}e^{-\sqrt{\frac{\beta }{ \varepsilon }} (1-x)}, \quad i \le 4. \end{aligned}$$

where \(v^{(i)}\) denotes the ith-derivative of v. Thus the solution of (1) has boundary layers of width \(O(\sqrt{\varepsilon } \log \varepsilon )\) near the end-points \(x=0\) and \(x=1\). Once the location and width of all the layers have been identified (as above) then a layer-adapted mesh can be constructed for the problem.

In the case of convection-diffusion problems of the form: Find \(u \in C^{k+2}(\bar{\varOmega }),\) \(k \ge 0\) such that

$$\begin{aligned}&L_{\varepsilon , (2)}u:= -\varepsilon u''+a(x)u' +b(x)u=f(x), \ x \in \varOmega ,&\end{aligned}$$
(2a)
$$\begin{aligned}&u(0)=u_0, u(1)=u_1; \quad a,b,f \in C^k(\varOmega ), \quad a(x) \ge \alpha >0,\ b(x) \ge 0.&\end{aligned}$$
(2b)

The reduced solution satisfies the first order problem: Find \(v_0 \in C^{k+1}(\bar{\varOmega })\) such that

$$ L_{0, (2)}v_0:= a(x)v_0' +b(x)v_0=f(x), \ x \in \varOmega , \quad v_0(0)=u(0). $$

Define the extended domain \(\varOmega ^* :=(0,L), \ L >1\) and \(a^*,b^*,f^* \in C^k(\varOmega ^*)\). The regular component is \(v^*:= v^*_0+\varepsilon v^*_1+\varepsilon ^2 v_2^*\), where

$$\begin{aligned} L^*_{0, (2)}v_0^*= & {} f^*,\quad v_0^*(0)=u(0); \quad L^*_{0, (2)}v_1^* = (v_0^*)'',\quad v_1^*(0)=0 ;\\ L^*_{\varepsilon , (2)} v_2^*= & {} (v_1^*)'',\quad v_2^*(0)=v_2^*(L)=0. \end{aligned}$$

Then \(L^*_{\varepsilon , (2)} v^* =f^*\) and \( L_{\varepsilon , (2)} v = f, v(0)=u(0) , \ v(1) = v^*(1).\) If \(a,b,f \in C^k(\varOmega )\), then \(v \in C^k(\bar{\varOmega })\). The boundary layer component satisfies the homogeneous problem

$$ L_{\varepsilon , (2)} w = 0,\quad w(0)=0, \ w(1) = u(1)-v(1). $$

Hence \(u=v+w\) and if \(a,b,f \in C^3(\varOmega )\) then [1, Chap. 3]

$$\begin{aligned} \Vert v^{(i)} \Vert _{\bar{\varOmega }} \le C (1+\varepsilon ^{2-i}); \quad \vert w^{(i)} (x) \vert \le C \varepsilon ^{-i}e^{-\alpha (1-x)/\varepsilon }, \quad i \le 3. \end{aligned}$$

Using simple stable finite difference scheme with a standard piecewise-uniform Shishkin mesh to produce a numerical approximation \(U^N\), one has for the convection-diffusion problem (2) (see, for example, [1, Chap. 3]): If \(a,b,f \in C^3(\varOmega )\) then

$$ \Vert u - \bar{U}^N \Vert _{\varOmega } \le CN^{-1} (\ln N) $$

and for the reaction-diffusion problem (1) (see, for example, [3, Chap. 6]): If \(b,f \in C^4(\varOmega )\) then

$$ \Vert u - \bar{U}^N \Vert _{\varOmega } \le CN^{-2} (\ln N)^2, $$

where \(\bar{U}^N\) is the piecewise linear interpolant of the mesh function \(U^N\). Note that, as one would expect, higher regularity is required of the data to establish higher order convergence. The regularity required of the data is dictated by the chosen construction of the solution decomposition. An alternative construction of the solution decomposition can allow one relax the constraints (imposed above) on the data [4].

If there is no modification to the standard numerical method on a layer-adapted mesh, then the above stated orders of parameter-uniform convergence can reduce for less smooth data [2, Sect. 14.2], [5]. If the data is discontinuous, then the standard numerical method will fail to be parameter-uniformly convergent [6, Table 4].

3 Singularly Perturbed Initial Value Problems with Discontinuous Data

Notation: Throughout the paper we adopt the following notation for the jump in a function at an internal point:

$$ \left[ f (d)\right] := f(d^+)-f(d^-), \ 0<d <1; $$

and we define the punctured domain by \(\varOmega _d := (0,1) \setminus \{ d\}. \)

To illustrate the effect of discontinuous data, we begin our discussion with a simple initial value problem of the form: Find \(u \in C^0(\bar{\varOmega }) \cap C^{k+1} (\varOmega _d)\) such that

$$\begin{aligned} \varepsilon u^\prime + a(x)u= f(x),\ a(x) \ge \alpha > 0, \quad x \in \varOmega _d, \end{aligned}$$
(3a)
$$\begin{aligned} u(0)=u_{0}, \quad a,f \in C^k(\varOmega _d), \quad k \ge 0. \end{aligned}$$
(3b)

Observe that the differential equation is not applied at the single interior point \(x=d\), Instead, the value of the solution at \(x=d\) is determined by requiring that the solution be continuous at this internal point. In addition, since \(a(x) \ge \alpha >0, x \in \varOmega _d\), we have the following useful monotonicity property of the first order differential operator associated with problem (3):

For any function \(g \in C^1(\varOmega _d) \cap C^0(\bar{\varOmega })\), then if \(g(0) \ge 0\) and \((\varepsilon g' +ag) (x) \ge 0\) for all \(x \in \varOmega _d\) then \(g(x) \ge 0, x \in \bar{\varOmega }\).

The solution can be decomposed into a sum \(u = v+w+z \), composed of a discontinuous regular component v, a continuous initial layer component w and a discontinuous interior layer component z. The components are defined as the solutions of the problems:

$$\begin{aligned} \varepsilon v^\prime +a(x)v= & {} f(x),\ x \in \varOmega _d,\quad a(0)v(0)= f(0),\quad a(d^+)v(d^+)= f(d^+);\\ \varepsilon w^\prime +a(x)w= & {} 0,\ x \in \varOmega _d,\quad w(0)=u(0)-v(0),\quad w(d^+)= w(d^-);\\ \varepsilon z^\prime +a(x)z= & {} 0,\ x \in \varOmega _d,\quad z(0)=0,\quad [z (d)]= -[v(d)]. \end{aligned}$$

Using the above monotonicity property of the differential operator, one can easily deduce the following bounds on these components: If \(a,f \in C^1(\varOmega _d)\) then

$$\begin{aligned} \Vert v^{(i)} \Vert _{ \varOmega _d}\le & {} C(1+ \varepsilon ^{1-i}), \qquad i=0,1,2; \end{aligned}$$
(4a)
$$\begin{aligned} \vert w (x) \vert \le C e^{-\alpha x / \varepsilon }, \quad \vert w^{(i)} (x)\vert _{ \varOmega _d}\le & {} C \varepsilon ^{-i}e^{-\alpha x/\varepsilon }, \qquad i=1,2;\end{aligned}$$
(4b)
$$\begin{aligned} z (x) \equiv 0,\quad x <d,\quad \vert z (x) \vert\le & {} Ce^{-\alpha (d-x) / \varepsilon }, \quad x \in (d,1);\end{aligned}$$
(4c)
$$\begin{aligned} \vert z^{(i)} (x)\vert _{ (d,1)}\le & {} C \varepsilon ^{-i}e^{-\alpha (d-x)/\varepsilon }, \qquad i=1,2 . \end{aligned}$$
(4d)

From these bounds we see that the solution has an initial boundary layer w in the vicinity of \(x=0\) and an interior layer to the right of \(x=d\).

Given this a priori information, an appropriate distribution of the mesh points \(\{ x_i \} _{i=0}^N\) is as follows: The end-points of the domain are included as \(x_0=0\), \(x_N=1\) and the internal point d, where the data is discontinuous, is taken to be the mesh point \(x_{N/2}\). The remaining internal mesh points \(\omega ^N = \{ x_i \} _{i=1}^{N/2-1} \cup \{ x_i \} _{i=N/2+1}^{N-1}\) are distributed so as to capture the two scales present in the solution. The domain is split into four sub-intervals \( [0,1] = [0, \sigma _1] \cup [\sigma _1,d]\cup [d, d+\sigma _2] \cup [d+\sigma _2 ,1] \), where the Shishkin transition parameters [3] are taken to be

$$\begin{aligned} \sigma _1:=\min \left\{ \frac{d}{2}, \frac{\varepsilon }{\alpha } \ln N \right\} {,}\quad \sigma _2:=\min \left\{ \frac{1-d}{2}, \frac{\varepsilon }{\alpha } \ln N \right\} {.} \end{aligned}$$

The mesh elements are distributed equally across these sub-intervals. An appropriate numerical method for this problem is: Find a mesh function U such that:

$$\begin{aligned} \varepsilon D^- U^N (x_i)+a(x^-_i) U^N (x_i)=f(x^-_i),\quad x_i \in \omega ^N \cup \{ d \},\quad U^N (0)=u (0), \end{aligned}$$

where \(D^-\) is the standard backward finite difference operator. The discrete solution U may be decomposed into the sum \(U= V +W+Z\), where the boundary layer component w is approximated by the solution W of the homogeneous problem

$$\begin{aligned} \varepsilon D^- W (x_i)+a(x^-_i) W (x_i)=0,\quad x_i \in \omega ^N \cup \{ d \}, \quad W (0)=u(0)-v (0). \end{aligned}$$

The discrete regular component V and discrete interior layer component Z are multi-valued (at \(x=d\)) functions and are defined to be

$$\begin{aligned} V:=\left\{ \begin{array}{ll} V^-, &{} x_i \in [0,d]\\ V^+, &{} x_i \in [d,1] \end{array} \right. ,\quad Z:=\left\{ \begin{array}{ll} 0, &{} x_i \in [0,d]\\ Z^+, &{} x_i \in [d,1] \end{array} \right. , \end{aligned}$$

where

$$\begin{aligned} \varepsilon D^- V^- (x_i)+a(x^-_i) V^- (x_i)=f(x^-_i),\ x_i \in (0,d],&\qquad V^-(0)=v (0);\\ \varepsilon D^- V^+ (x_i)+a(x_i) V^+ (x_i)=f(x_i),\ x_i \in (d,1],&\qquad V^+ (d)=v(d^+);\\ \varepsilon D^- Z^+ (x_i)+a(x_i) Z^+ (x_i)=0,\ x_i \in (d,1],&\qquad Z^+(d)=-[V ](d). \end{aligned}$$

Based on classical stability, truncation error analysis and the parameter-explicit bounds on the derivatives of w given in (4b), we conclude that in the initial layer region \([0,\sigma _1]\)

$$\begin{aligned} \vert W(x_i) - w(x_i) \vert _{[0,\sigma _1]} \le C N^{-1}\ln N. \end{aligned}$$

Then we note that, for \(x_i \in [\sigma _1,1]\), the error in the layer component is

$$\begin{aligned} \vert W(x_i) - w(x_i) \vert _{[\sigma _1,1]}\le & {} \vert W(x_i)\vert + \vert w(x_i) \vert \\\le & {} \vert W_\varepsilon (\sigma _1)\vert + CN^{-1}\ \le CN^{-1}, \quad \mathrm {if} \quad 2\sigma _1 < d. \end{aligned}$$

Using the bounds (4a) on the regular component we also conclude that

$$\begin{aligned} \vert V(x_i)-v(x_i) \vert \le C N^{-1}, \quad x_i \in \varOmega _d,\quad \vert V^-(d) - v(d^-) \vert \le C N^{-1}. \end{aligned}$$

Note that \(Z^+(d)=-[v(d)] +V^-(d) - v(d^-)\) and by examining the error \(\vert Z -z\vert \) on \((d,d+\sigma _2]\) and \((d+\sigma _2,1]\) separately we conclude that

$$\begin{aligned} \vert Z(x_i) - z(x_i) \vert _{[d,1]} \le CN^{-1}\ln N,\quad \mathrm {if} \quad 2\sigma _2 < 1-d. \end{aligned}$$

If \(\ 2\sigma _1 =d\) or \(\ 2\sigma _2 =1-d \) then a standard stability and consistency argument yields

$$\begin{aligned} \max _i \vert U^N(x_i) - u(x_i) \vert \le C N^{-1}\ln N. \end{aligned}$$

Hence, using linear interpolation (e.g., see [1, Theorem 3.12]), we conclude that

$$\begin{aligned} \Vert \bar{U}^N -u \Vert _{\varOmega } \le C N^{-1}\ln N, \end{aligned}$$

where \(\bar{U}^N\) is again the piecewise linear interpolant of the mesh function \(U^N\).

4 Singularly Perturbed Boundary Value Problems with Non-smooth Data

Let us now consider a reaction-diffusion two point boundary value problem with a diffusion coefficient of a constant scale \(O(\varepsilon )\) and a lack of smoothness in the data at some internal point. Find \(u \in C^1(\bar{\varOmega }) \cap C^k(\varOmega _d)\) such that

$$\begin{aligned} -\varepsilon u''+b(x)u=f(x), \ b(x) \ge \beta > 0, \ x \in \varOmega _d, \ u(0), u(1)\ \hbox {given}; \ \ b,f \in C^k(\varOmega _d). \end{aligned}$$

The associated reduced problem is \(b(x)v_0(x) = f(x), \ x \ne d\) and so if \([ (f/b)(d)] \ne 0\), then the reduced solution will be discontinuous at the internal point d. Hence, the solution will contain an internal layer function, which will exhibit layers of width \(O(\sqrt{\varepsilon }\ln \varepsilon )\) on either side of the interface point \(x=d\). Note that by requiring that \(u \in C^1(\bar{\varOmega })\) we are imposing the constraints \( \ [ u] (d) = [ u'] (d) =0 \) on the solution.

We generalize this problem to a reaction-diffusion problem with a variable diffusion coefficient having potentially different scales either side of a point of discontinuity \(x=d\) in the data. Find \( u \in C^0(\bar{\varOmega })\cap C^4 (\varOmega _d) \) such that

$$\begin{aligned} L_{\varepsilon , (3)}u:= -(\varepsilon (x) u ')' + r(x)u_\varepsilon =f,\ x \in \varOmega _d; \quad u(0), u(1) \ \hbox {given} ;\end{aligned}$$
(5a)
$$\begin{aligned} \ [ f(d) ] = Q_2,\ [ r (d)] = Q_3,\quad \ [-\varepsilon u_\varepsilon '(d)] = Q'_1\le C(\sqrt{ \varepsilon _1 }+ \sqrt{\varepsilon _2}), \end{aligned}$$
(5b)
$$\begin{aligned} \varepsilon (x) = \left\{ \begin{array}{ll}\varepsilon _1p(x), x <d \\ \varepsilon _2p(x), x>d \end{array} \right. {,}\ \varepsilon _1, \varepsilon _2>0, \ p(x) \ge \underline{p} >0,\quad x \in \varOmega _d, \end{aligned}$$
(5c)
$$\begin{aligned} p,r,f \in C^4(\varOmega _d), \qquad r(x) \ge r_0> 0,\ \frac{r(x)}{p(x)}> \beta >0, \quad x \in \varOmega _d. \end{aligned}$$
(5d)

In particular, Eqs. (5c) and (5b) above indicate that all the coefficients in (5a) may exhibit a jump at \(x = d\) and also they allow for a scaled jump in the flux \((-\varepsilon u_{\varepsilon }')\) at \(x=d\). The regular component v and singular component w of the solution are defined, respectively, as the solutions of the discontinuous problems

$$\begin{aligned} L_{\varepsilon , (3)} v = f,\quad L_{\varepsilon , (3)} w=0, \quad x \in \varOmega _d; \quad r(x) v (x)=f(x), \ x \in \{ 0,d^-,d^+,1 \} ; \\ \ [w(d)]=-[v(d)], \quad [\varepsilon w'(d)]=-[\varepsilon v'(d)]- Q'_1, \\ \quad w (0)=u(0)-v (0),\ w (1)=u (1)-v (1). \end{aligned}$$

Note that, in general, \(v, w \not \in C^0(\overline{\varOmega })\) even though their sum \(u=v+w\) is continuous. For each integer k, satisfying \(0 \le k \le 4\), these components satisfy the bounds [7].

$$ |v _\varepsilon ^{(k)}(x)|\le \left\{ \begin{array}{ll} C (1+\varepsilon _1^{1-\frac{k}{2}}), \quad &{}x<d\\ C(1+\varepsilon _2 ^{1-\frac{k}{2}}), \quad &{}x >d \end{array} \right. ,$$
$$ |w_\varepsilon ^{(k)}(x)|\le \left\{ \begin{array}{ll} C \varepsilon _1^{-\frac{k}{2}}\left( e^{-\sqrt{\frac{\beta }{ \varepsilon _1}} x}+e^{-\sqrt{\frac{\beta }{ \varepsilon _1}} (d-x)}\right) , \quad &{}x<d\\ C \varepsilon _2^{-\frac{k}{2}}\left( e^{-\sqrt{\frac{\beta }{ \varepsilon _2}} (1-x)}+e^{-\sqrt{\frac{\beta }{ \varepsilon _2}} (x-d)}\right) , \quad &{}x >d \end{array} \right. .$$

Based on these bounds, an appropriate piecewise-uniform Shishkin mesh can be constructed. However, to retain parameter-uniform second order convergence for this reaction-diffusion problem, it is necessary to employ a particular discretization of the jump conditions at the mesh point \(x_i=d\). See [7] for details.

Boundary and interior layers can be classified as either weak or strong layers. A layer is a strong layer near a point \(x=p\) if \(u'(p^-)\) or \(u'(p^+)\) is unbounded as \(\varepsilon \rightarrow 0\). A layer is a weak layer near \(x=p\), if the first derivatives \(u'(p^-)\) and \(u'(p^+)\) are bounded, but either \(u''(p^-)\) or \(u''(p^+)\) is unbounded as \(\varepsilon \rightarrow 0\). In all of the above problems, only strong interior layers appeared. When a convective term is included in the differential equation, weak interior layers can appear in the solutions. Note that, if one employs a classical finite difference operator (such as simple upwinding), then it is essential that one employs a suitable layer-adapted mesh to capture any strong internal layers present in the solution. The adverse effect of using a uniform mesh for a weak layer are minimal. Nevertheless, one still observes some improvement in the numerical results if one also uses a layer-adapted mesh in the vicinity of a weak layer. We refer to the numerical results in [8] to justify this comment.

We now look at five particular singularly perturbed problems, with a convective term present in the differential equation. These particular problems illustrate the variety of layers that can occur when the problem has discontinuous data. For all five problems, we seek to find \(u \in C^1(\bar{\varOmega }) \), with \(u(0)=u(1)=0\) and

$$\begin{aligned} -\varepsilon u''+u'=1,\ x <0.5; \quad&-\varepsilon u''-u'=-1,\ x >0.5; \end{aligned}$$
(6a)
$$\begin{aligned} -\varepsilon u''+u'=1,\ x <0.5; \quad&-\varepsilon u''+u=-1,\ x >0.5; \end{aligned}$$
(6b)
$$\begin{aligned} -\varepsilon u''+u'=1,\ x <0.5; \quad&-\varepsilon u''+2u'=-1,\ x >0.5; \end{aligned}$$
(6c)
$$\begin{aligned} -\varepsilon u''-u'=1,\ x <0.5; \quad&-\varepsilon u''+u=-1,\ x >0.5; \end{aligned}$$
(6d)
$$\begin{aligned} -\varepsilon u''-u'=1,\ x <0.5; \quad&-\varepsilon u''+u'=-1,\ x >0.5. \end{aligned}$$
(6e)

For the first four problems, we can define the following associated reduced problems

$$\begin{aligned} v_0'=1,\ x<0.5,\ v_0(0)=u(0); \quad&v_0'=1,\ x>0.5,\ v_0(1)=u(1);\\ v_0'=1,\ x<0.5,\ v_0(0)=u(0); \quad&v_0=1,\ x>0.5;\\ v_0'=1,\ x<0.5,\ v_0(0)=u(0); \quad&2v_0'=-1,\ x>0.5,\ [v_0(0.5)]=0;\\ v_0'=1,\ x <0.5,\ v_0(0)=u(0); \quad&v_0=-1,\ x >0.5,\ [v_0(0.5)]=0. \end{aligned}$$

In the case of the first two problems (6a, 6b), the reduced solution is discontinuous and a strong interior layer forms in a neighbourhood of \(x=0.5\). In the next two problem classes (6c, 6d), the reduced solution is continuous and a weak layer forms in a neighbourhood of \(x=0.5\). There is no reduced problem for the fifth problem (6e) as the solution is of order \(O(\varepsilon e^{\frac{1}{2\varepsilon }})\) throughout the domain, except in \(O(\varepsilon \ln (1/\varepsilon ))\)-neighbourhoods of the two end points.

For the first four sample problems (6a–6d), associated problem classes can be formulated and parameter-uniform numerical methods (based on standard finite difference schemes combined with appropriately fitted piecewise uniform Shishkin) were constructed in [9]. In the case of problems of the form (6e) a modification of the transmission condition from \([u'(d)]=0\) to \([(-\varepsilon u'+\gamma u)(d)]=0\) (where \(\gamma \) sufficiently large) allows one design a parameter-uniform numerical method for this modified class of problems [10].

Further effects can be built into such problem classes, such as point sources (i.e. \(\delta \)-functions) or multi-parameter problems with variable diffusion. In [11], high order parameter-uniform methods were constructed for the following two problem classes: Find \(u \in C^4 (\varOmega _d) \cap C^0(\bar{\varOmega }), \ u(0)=u_0,\ u(1) =u_1, \) such that

$$\begin{aligned} - (\varepsilon (x)u')'+a(x)u'+b(x)u=f(x), \ x \ne d, \quad \left[ - (\varepsilon u') (d)\right] =Q_1; \end{aligned}$$
(7)
$$\begin{aligned} - (\varepsilon (x)u'+a(x)u)'+b(x)u=f(x), \ x \ne d, \quad \left[ (- \varepsilon u' +au) (d)\right] =Q_2; \end{aligned}$$
(8)

and for both problem classes we assume that

$$ \varepsilon , a, b, f \in C^4(\varOmega _d); \quad b(x) \ge 0,\quad \varepsilon (x)>0, \vert a (x) \vert >0, \ x \ne d. $$

The nature of the interior layers appearing in (7) and (8) can have different character. If \(Q_1 =0\) in (7), then the strength of the interior layer depends on the sign of a(x) and on the change in the ratio of convection to diffusion at d. A strong interior layer can appear in (7) when \(a(x) > 0, x \ne d\) and

$$ \frac{\varepsilon (d^-)}{a(d^-)}<< \frac{\varepsilon (d^+)}{a(d^+)}. $$

If \(Q_2 =0\) then a strong interior layer always appears near d in (8).

Numerous different types of interior layers can appear in problem classes (5), (7) and (8), which is an indication of the rich variety of layers one can expect to occur in higher dimensional versions of these one dimensional problem classes.

5 Singularly Perturbed Turning Point Problems

Singularly perturbed differential equations with discontinuous coefficients can be viewed as approximate models for singularly perturbed nonlinear problems. For example, in the case of the quasilinear second order problem

$$\begin{aligned} -\varepsilon u'' +uu'+u=0, \quad x \in \varOmega ; \end{aligned}$$
(9a)
$$\begin{aligned} u(0)=A >1, \qquad u(1)=B <-1; \end{aligned}$$
(9b)

then an interior layer (with a profile of hyperbolic-tangent type) will appear [12, 13] in the vicinity of some internal point \(0< d_\varepsilon <1 \), where \(u(d_\varepsilon )=0\) and \(d_0:= \lim _{\varepsilon \rightarrow 0} d_\varepsilon \). The associated reduced problem to this nonlinear problem is the nonlinear first order problem

$$\begin{aligned} u_0u_0'+u_0=0, \ u_0(0)=A, \ 0< x <d_0; \quad u_0u_0'+u_0=0, \ u_0(1)=B, \ 1> x >d_0; \end{aligned}$$

which has the discontinuous solution

$$ u_0(x) =A-x, \quad 0\le x<d_0; \qquad u_0(x) =B+1-x,\quad d_0 <x \le 1. $$

For \(\varepsilon<<1\), it is natural to consider the following approximate problem for the above nonlinear problem (9). Find \(y \in C^1(\varOmega ) \) such that

$$ -\varepsilon y''+u_0y'+y=0,\quad x \in \varOmega _d, \quad y(0)=u(0),\ y(1)=u(1). $$

This linearized approximate problem is within the class of problems discussed in Sect. 3, for which parameter-uniform numerical methods have been developed in the literature [9]. However, the convective coefficient in the nonlinear problem is continuous and not discontinuous as in the above linearization of (9).

An alternative linearization of the nonlinear problem (9) would be the following class of turning point problems with a continuous convective coefficient: Find \(u \in C^3(\varOmega )\) such that

$$\begin{aligned} (-\varepsilon u''+a_\varepsilon u'+bu)(x)=f(x),\quad x\in \varOmega ;\quad u(0)>0,\ u(1)<0;\end{aligned}$$
(10a)
$$\begin{aligned} a_\varepsilon \in C^2(\varOmega ),\ a_\varepsilon (x)>0, x\in [0,d),\quad a_\varepsilon (d)=0,\quad a_\varepsilon (x)<0, x\in (d,1]. \end{aligned}$$
(10b)

Observe that the convective coefficient is continuous, but depends on the singular perturbation parameter. We also assume that the convective coefficient \(a_\varepsilon (x)\) contains it’s own interior layer. Define the limiting functions

$$ a^-_0(x):= \lim _{\varepsilon \rightarrow 0}{a_\varepsilon (x)},\ x\in [0,d) \quad \hbox {and} \quad a^+_0(x):= \lim _{\varepsilon \rightarrow 0}{a_\varepsilon (x)},\ x\in (d,1] . $$

Assume that

$$\begin{aligned}&|a_\varepsilon (x)|>|\theta \tanh {(r(d-x)/\varepsilon )} \vert ,\quad \theta>2r>0,\end{aligned}$$
(10c)
$$\begin{aligned}&\vert (a^{\pm }_{0}-a_\varepsilon )(x) \vert \le Ce^{\pm \frac{\theta }{2\varepsilon }(d-x)},\quad x\in \varOmega _d. \end{aligned}$$
(10d)

Then the solution of the above problem (10) will have an interior layer (with a profile of hyperbolic-tangent type) in an \(O(\varepsilon )\)-neighbourhood of the point d, where the convective coefficient has an interior layer. Based on this information, a parameter-uniform numerical method was constructed [14] and shown to be parameter-uniformly convergent of first order.

The nature of the interior layers appearing in problem (10) is different to the layers appearing in the solutions of singularly perturbed turning point problems of the form

$$\begin{aligned} -\varepsilon u'' +a(x) u'+b(x) u=f(x), \quad x \in \varOmega ; \\ a \in C^2(\varOmega ),\ a(d)=0,\ d \in \varOmega , b >0; \end{aligned}$$

where the convective coefficient a is independent of the singular perturbation parameter. Depending on the quantity \(b(d)/a'(d)\), there may be no interior layer or there may be layers of power-law type present at d. See [15, 16] for a discussion of these types of turning point problems.

6 Singularly Perturbed Parabolic Problems

Consider the following singularly perturbed parabolic problem: Find \(u \in C^{1+\gamma }(G), G:=(0,1) \times (0,1]\) such that

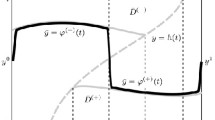
$$\begin{aligned} -\varepsilon u_{ss}+a_1u_s+b_1u+c_1u_t=f, (s,t) \in G \setminus \varGamma ,\\ \varGamma := \{ (s,t) | s=d(t), 0< d(t) <1 \} ;\\ u=g, (s,t) \in \bar{G} \setminus G;\quad b(s,t) \ge 0, \ c(s,t) \ge \gamma >0. \end{aligned}$$

As in the previous sections, interior layers can appear in the solution due to discontinuous coefficients a, b, c and/or f [17]. Nine subclasses can be identified (see [9] and [10]), which can exhibit strong or weak interior layers in the vicinity of the curve \(\varGamma \). Note that in these references, the interior layer location is known and the center of the interior layer can move with time. By using a transformation \(T:(s,t) \rightarrow (x,t)\) so that \(T:\varGamma \rightarrow \{ x=d(0) \}\) any internal layer will be located along the vertical line \(x=d\) in the computational domain (x, t) [18]. A computed solution is generated on this transformed domain so that the piecewise-uniform mesh is aligned to the curve \(\varGamma \). Shishkin [19] established that it is necessary to align the grid to the interior layer if one is seeking to construct a parameter-uniform numerical method.

Moreover, for parabolic problems interior layers can also appear when the boundary/initial conditions are not smooth [20, 21]. If there is a discontinuity in the initial condition u(s, 0) then a standard finite difference operator on a piecewise uniform mesh will not suffice to generate a parameter-uniform numerical method. A special fitted finite difference operator is required [22]. A regularization of a discontinuous initial condition is possible by replacing the initial condition with an initial condition of the form

$$ u(s,0) = A \tanh \bigl ( \frac{s-d_0}{\sqrt{\varepsilon } } \bigr ) +B. $$

In this case, assuming the convective coefficient is independent of space, the initial interior layer is transported along the curve \( \{(d(t),t): d'(t)=a(t), d(0)=d_0 \} ; \) and a parameter-uniform numerical method based on classical finite difference operator, a suitable transformation and an appropriate piecewise-uniform mesh can be constructed [23, 24].

7 Singularly Perturbed Nonlinear Problems with Interior Layers

Semilinear singularly perturbed differential equations of the form

$$\begin{aligned} {-}\varepsilon u'' +g(x,u)=0, \quad x \in \varOmega ,\quad u(0)=A,\ u(1)=B; \end{aligned}$$
(11a)

are typically constrained by a condition of the form

$$\begin{aligned} g_u(x,u) \ge \beta >0, \quad (x,u) \in \bar{\varOmega } \times [-M,M]; \end{aligned}$$
(11b)

where M is a sufficiently large number that needs to be be explicitly identified. This constraint is a restriction on the admissible type of nonlinear problem being studied. Note that requiring

$$ g_u(x,u) \ge \beta >0, \quad (x,u) \in \bar{\varOmega } \times (-\infty ,\infty ), $$

is a significantly stronger restriction to impose on the problem class. This stronger constraint guarantees a unique solution to the reduced problem and thereby regulates the problem class to a minor extension from the corresponding class of linear problems of reaction-diffusion type

$$ -\varepsilon u'' +b(x)u =f(x), \quad b(x) \ge \beta >0. $$

Interesting new phenomena can be observed when the nonlinear reduced problem \(g(x,v) =0\) has non-unique solutions. The reduced solutions are classified as stable reduced solutions if \(g_u(x,v(x)) >0,\ \forall x \in \bar{\varOmega }\) and as unstable reduced solutions if \(g_u(x,v(x)) <0,\ \forall x \in \bar{\varOmega }\).

Interior layers can appear in nonlinear problems. Typically, restrictions need to be placed on the data so that solutions to the reduced problem exist and for the solution of the singularly perturbed problem to exist and be unique. For example, in the case of the semilinear reaction-diffusion problem: Find \(u \in C^1(\bar{\varOmega }) \cap C^3(\varOmega _d)\) such that

$$\begin{aligned} -\varepsilon u'' +(1-u^2) u= f(x), x \in \varOmega _d;\qquad d =0.5;\\ u(0)=A, u(1)=B; \quad f(x)> 0, x< d, f(x) < 0, x >d; \ [ f ] (d) \ne 0; \end{aligned}$$

we impose the following limits on the input data

$$ \vert A \vert , \ \vert B \vert< \frac{1}{\sqrt{3}}, \quad \Vert f \Vert < \frac{2}{3\sqrt{3}}. $$

This problem is formulated so that a discontinuous stable reduced solution lies between two discontinuous unstable reduced solutions. Interior layers can appear in the solution of this problem and the location of the layer will be positioned around the point d, where the discontinuity in the data is located. By placing further restrictions on the data, a parameter-uniform method was constructed in [25] for this semilinear problem.

However, other semilinear problems of the form (11) can be very difficult to solve numerically. In [26] a semilinear problem of the form (11) with smooth data, where an unstable continuous reduced solution was positioned between two stable continuous reduced solutions, was examined. Using a piecewise-uniform Shishkin mesh (of an appropriate width) centered at any point in the domain \(\varOmega \), then an interior layer forms within the fine mesh, no matter where the mesh is centered [26]. Only in the exceptional case where the fine mesh is located in an \(O(\sqrt{\varepsilon })\) neighbourhood of the actual location of the interior layer will the numerical approximation be of any true value.

Parameter-uniform numerical methods (based on piecewise-uniform Shishkin meshes) have also been constructed [27] for quasilinear problems with interior layers of the form: Find \( u \in C^1(\bar{\varOmega }) \cap C^3(\varOmega _d) \) such that

$$\begin{aligned} \varepsilon u''(x) + b(x,u)u'(x) = f(x), \ x \in \varOmega _d, \qquad u (0)=A , \quad u (1)=B , \end{aligned}$$
(12a)
$$\begin{aligned} b(x,u)= \left\{ \begin{array}{ll} \displaystyle b_1(u)=-1+cu, \quad x< d \\[2ex] \displaystyle b_2(u)=1+cu, \quad x> d \end{array} \right. , \quad f(x)= \left\{ \begin{array}{ll} \displaystyle -\delta _1< 0, \quad x < d \\[2ex] \displaystyle \delta _2>0 , \quad x > d \end{array} \right. \end{aligned}$$
(12b)
$$\begin{aligned} -1< u(0)< 0, \quad 0< u(1)< 1, \quad 0 < c \le 1. \end{aligned}$$
(12c)

As in the case of the semilinear problem, additional constraints need to be imposed on the data \(\{ A,B, \Vert f \Vert , c \}\) in order for the theoretical convergence result given in [27] to apply. The numerical results in [28] suggest that the numerical approximations generated by the method described in [27] converge for a wider class of problems to that covered by the theoretical convergence analysis in [27]. Note, again, that for this problem (12) the location of the interior layer is known to be positioned at d, where both the convective coefficient b(x, u) and the forcing term f are formulated to be discontinuous.

An interesting open issue is to examine singularly perturbed problems with an interior layer, whose location is not known a priori. Many nonlinear singularly perturbed problems of interest [29–32] exhibit this phenomenon. The design of parameter-uniform numerical methods for a broad class of nonlinear singularly perturbed problems with interior layers, remains an area with significant challenges for the numerical analyst.