Keywords

1 Introduction

The thermo-MHD flow over on bluff bodies has much attention, because of its wide range of applications including those in nuclear reactors. The principle involved in MHD flow problem is that the externally imposed magnetic field will control the flow separation and modify (increase/decrease) heat transfer rate. The laminar mixed convection heat transfer from a circular subjected to different flow condition (without magnetic field) has been studied by many research through numerically, theoretically and experimentally to investigate the aspect of heat transfer rate through different methods. The thermo-MHD flow problem are interesting and very challenging because heat transfer is also controlled by magnetic field in addition to flow stabilization [1–3]. The aim of the present study is numerical solutions to the problem of laminar magnetohydrodynamic mixed convection over on isothermal horizontal circular cylinder imposed to cross flow configuration by using a fourth order compact finite difference scheme. In the formulation, we use the quasi-static approximation so that the induced magnetic field is negligible and hence the applied magnetic field can be treated as constant magnetic field.

2 Mathematical Formulation

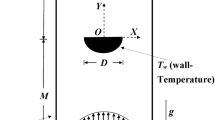
The radius of the cylinder is a (and d is diameter) and isothermal surface temperature of the cylinder is T s . It is placed horizontally in a uniform flow of an incompressible fluid with free stream velocity U ∞ and magnetic field H ∞ with its axis perpendicular to the fluid flow direction. The fluid is assumed to satisfy the Boussinesq approximation and the free stream fluid temperature is T ∞. The buoyancy force is due to variation of the fluid density with temperature in the vicinity of the cylinder. The flow considered here is from left to right and θ = 0 is taken as the downstream region and θ = π in the upstream region. The flow is assumed to be steady and polar coordinates are used with the angle are measured from upstream axis. The non dimensional parameters are defined here are Re, Pr, Gr and N where the symbols are defined in the nomenclature. The imposed external aligned uniform magnetic field H in the cylindrical polar coordinates is taken as

$$H = ({-}\cos \theta ,\sin \theta ,0)$$

and it is opposite to the incoming fluid flow. The magnetic field and the fluid flow are aligned at infinity so the electric field can be assumed to be zero. The velocity components V = (V r , V θ , 0) are expressed in terms of dimensionless stream function ψ such that the equation of continuity is satisfied automatically. In order to focus attention in the vicinity of the body (cylinder), the transformation r = exp(πξ) and θ = πη is used where r is the physical distance from the center of the cylinder and ξ represent the same on the computational plane. The transformed full Navier-Stokes, and energy equations in the streamfunction-vorticity formulation can be written as

$$\frac{{\partial^{2} \psi }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }} + \pi^{2} e^{2\pi \xi } \omega = 0$$
(1)
$$\begin{aligned} & \frac{{\partial^{2} \omega }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \omega }}{{\partial \eta^{2} }} - \frac{Re}{2}\left[ {\frac{\partial \psi }{\partial \eta }\frac{\partial \omega }{\partial \xi } - \frac{\partial \psi }{\partial \xi }\frac{\partial \omega }{\partial \eta }} \right] = \frac{RiRe}{4}\left[ {\cos (\pi \eta )\frac{\partial \phi }{\partial \xi } - \sin (\pi \eta )\frac{\partial \phi }{\partial \eta }} \right] \\ & \quad + \frac{NRe}{2}\left[ {\pi^{2} e^{2\pi \xi } \omega \mathop {\sin }\nolimits^{2} (\pi \eta ) + \sin 2(\pi \eta )\frac{{\partial^{2} \psi }}{\partial \xi \partial \eta } - \pi \,\sin 2(\pi \eta )\frac{\partial \psi }{\partial \eta } - \cos 2(\pi \eta )\frac{{\partial^{2} \psi }}{{\partial \xi^{2} }} + \pi \,\cos 2(\pi \eta )\frac{\partial \psi }{\partial \xi }} \right] \\ \end{aligned}$$
(2)
$$\frac{{\partial^{2} \phi }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \phi }}{{\partial \eta^{2} }} = \frac{RePr}{2}\left( {\frac{\partial \psi }{\partial \eta }\frac{\partial \phi }{\partial \xi } - \frac{\partial \psi }{\partial \xi }\frac{\partial \phi }{\partial \eta }} \right)$$
(3)

The problem is subjected to the following boundary conditions.

On surface of the cylinder (ξ = 0)

$$\psi = \frac{\partial \psi }{\partial \xi } = 0,\quad \omega = - e^{\pi \xi } \frac{{\partial^{2} \psi }}{{\partial \xi^{2} }},\quad \phi = 1$$

On the outer boundary of the grid (ξ → ∞)

$$\frac{\partial \psi }{\partial \xi } = e^{\pi \xi } \sin (\pi \eta ).$$

In the inflow region: ω → 0, ϕ → 0

In the outflow region: \(\frac{\partial \omega }{\partial \xi } \to 0,\quad \frac{\partial \phi }{\partial \xi } \to 0\)

The set of nonlinear coupled governing stream function, vorticity and energy Eqs. (1), (2) and (3) have been discretized by a fourth order compact finite difference method [4] that leads us to a set of algebraic equation and it is solved using multigrid method combined with Gauss-Seidel iteration procedure until a convergence criterion that the norm of dynamic residuals is below 10−5. The numerical experiments are carried out up to 512 × 512 fine grids to ensure that our results are grid independent with respect to the flow variables Re, Ri, Pr and N.

3 Results and Discussion

Numerical experiments were performed for fixed value of Reynolds number Re = 20. The behavior of flow without the magnetic field is analyzed as follows. The wake region is formed behind the cylinder for Ri = 0. The streamlines appear symmetrical about θ = 180 and θ = 0 line as seen in Fig. 1. From the same figure, it is also noted that when the magnetic field strength N is increased with Ri = 0, the suppression of the separation is observed wherein the separation length and separation angle decreases with respect to N. As the convection parameter Ri is increased the wake region behind the cylinder disappear and also noticed that the axis-symmetry is broken (see Fig. 2). The rear stagnation point moves upwards with respect to Ri. This is due to the fact that the buoyancy force which enhance the fluid flow around the cylinder. Figures 3 and 4 show the thermal fields (isotherms) for forced convection case and mixed convection case respectively. It is seen that in the absence of magnetic field (N = 0), the streamline behind the cylinder have a positive slope in comparison to the upstream streamlines because of greater influence of the buoyancy parameter in the wake region. But upon applying the magnetic field, these positive slope behind the cylinder disappear with respect to N and the reattachment point try to move toward the line of symmetry. The magnetic field modifies the plume formation and its convection. When no magnetic field is applied, high temperature gradients are seen near the front stagnation point as seen from the density of isotherm lines of Fig. 3. Coming to the rear stagnation point, the isotherms have the vertical and bent structure in the near-wake region. The application of magnetic field leads to modification of this structure so as to smoothly follow the fluid flow around the cylinder. In addition the isotherm density decreases with magnetic field strength. In the mixed convection case, if the applied magnetic field is zero then it is seen that the thermal plume with higher temperature moves upward because of the effect of thermal buoyancy induced in the flow. However, when the magnetic field is increased, the plume formation takes place towards the axis of symmetry line and hence the heat transfer is well controlled by applied magnetic field (Fig. 4). In general, the degradation of heat transfer observed in this work is in agreement with some of the experimentally reported data [5, 6].

Fig. 1
figure 1

Effect of magnetic field on the flow: Streamlines for Re = 20 with Ri = 0

Full size image
Fig. 2
figure 2

Effect of magnetic field on the mixed convective flow: Streamlines for Re = 20 with Ri = 2

Full size image
Fig. 3
figure 3

Effect of magnetic field on the heat transport. Isotherms corresponding to forced convection flow shown in Fig. 1

Full size image
Fig. 4
figure 4

Isothermal contours for the mixed convection flow for Re = 20. The flow patterns are shown in Fig. 2

Full size image