Trajectory Tracking Control of Three-Wheeled Omnidirectional Mobile Robot: Adaptive Sliding Mode Approach

Abstract

This paper proposes an adaptive and robust control for a three-wheeled omnidirectional mobile robot (TWOMR) in presence of disturbance due to friction and bounded uncertainties. Kinematic and dynamic modeling of TWOMR is done to obtain the equation of motion under the action of frictional forces. Controller is designed to track the desired path. First to make the system robust, Integral sliding mode controller (ISMC) is designed and then for estimation of design parameter and to reduce the chattering effect an adaptive integral sliding mode controller (AISMC) is built. Simulations are conducted to show the effectiveness of proposed controller for TWOMR.

1 Introduction

Omnidirectional wheel mobile robots are commonly used for applications like fork lifter, home purpose robot, omni wheel chair etc. Among various configurations like 2 wheel, 3 wheel and 4 wheel mobile robots, 3 wheel omnidirectional mobile robot is extensively used (Pin and Killough 1994). It consists of three omni wheels driven by separate motors. It has various advantages as compared to regular two or four wheel mobile robots, such as better maneuverability, ability to turn in confine spaces and ability to move in any direction. These aspects have increased the applicability of 3 wheel omnidirectional mobile robot. The kinematic and dynamic modeling of omnidirectional mobile is well presented in Tzafestas (2014) and Batlle and Barjau (2009). Earlier research work shows major use of PID controllers to control each motor. The major drawback with these types of controllers is that when the non linear effects in the dynamic environment are significant the robot is unable to track the desired trajectory. Hence, to make the system robust under such disturbances research proposed several non linear control methods like neural network techniques, fuzzy control, sliding mode control etc.

Sliding mode is extensively used for non linear control (Das and Mahanta 2014). It is a discontinuous control method to make the system robust. The desired system dynamics is maintained by defining a switching function which keeps the output states on the sliding surface. Besides having various advantages like insensitivity to disturbances and fast dynamic response, the control input and sliding function faces chattering effects due to employment of switching function. Apart from this, proper selection of switching gain is a major issue in the design process when the bounds of uncertainties are unknown. Higher selection of switching can lead to non smooth control input. Hence to eliminate the chattering effect and make the controller self tuned for unbounded uncertainties adaptive control methods are extensively used (Chen et al. 2013). Viet et al. (2012) proposed a sliding mode control law for an omnidirectional mobile manipulator but with bounded uncertainties. To track the desired trajectory in presence of unstructured uncertainties (Xu et al. 2009) employed neural network with sliding mode control approach.

The objective of this paper is to establish a robust and adaptive controller for a three wheel omnidirectional mobile robot to track the desired trajectory in presence of friction and unbounded uncertainties. The remaining content of this paper is organized in following manner. First kinematic and dynamic equations of TWOMR are derived. Next robust adaptive control law is derived and its stability is proved by Lyapunov stability criterion. The simulation results and conclusion are described in the subsequent sections.

2 Kinematic and Dynamic Modeling

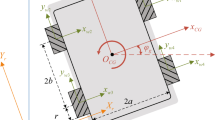
A three wheel omnidirectional mobile robot (TWOMR) is shown in Fig. 1. It consists of three omnidirectional wheels installed at 120º from each other.

Fig. 1

Schematic model of TWOMR

In Fig. 1 OXY is the fixed frame and Cxy denotes the moving frame of TWOMR. Rotation matrix

$R(\theta ) = \left[ {\begin{array}{*{20}c} {\cos (\theta )} & { - \sin (\theta )} \\ {\sin (\theta )} & {\cos (\theta )} \\ \end{array} } \right]$ and the position vector $P_{i} \in \Re^{2 \times 1} (i = 1,2,3)$ of each wheel relative to fixed frame. This position vector for each wheel is given as

$$ \begin{aligned} P_{1} = r_{O} \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right],P_{2} & = R\left( {\frac{2\pi }{3}} \right)\left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right]P_{1} = \frac{{r_{O} }}{2}\left[ {\begin{array}{*{20}c} { - 1} \\ {\sqrt 3 } \\ \end{array} } \right], \\ P_{3} & = R\left( {\frac{4\pi }{3}} \right)\left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right]P_{1} = - \frac{{r_{O} }}{2}\left[ {\begin{array}{*{20}c} { - 1} \\ {\sqrt 3 } \\ \end{array} } \right] \\ \end{aligned} $$

(1)

where $r_{O}$ is the distance between center of geometry of TWOMR and center of wheels. The drive vectors $d_{i} (i = 1,2,3,4) \in \Re^{2 \times 1}$ relative to fixed frame denotes the drive direction of each wheel which can be written as

$$ d_{1} = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right],\quad d_{2} = - \frac{1}{2}\left[ {\begin{array}{*{20}c} {\sqrt 3 } \\ 1 \\ \end{array} } \right],\quad d_{3} = \frac{1}{2}\left[ {\begin{array}{*{20}c} {\sqrt 3 } \\ { - 1} \\ \end{array} } \right] $$

(2)

$P_{o} = \left[ {\begin{array}{*{20}c} {x_{o} } & {y_{o} } \\ \end{array} } \right]^{T}$ is the position vector of geometric center relative to fixed frame. The sliding velocity of each wheel $v_{i} (i = 1,2,3)$ can be expressed in generalized form as

$$ v_{i} = \dot{P}_{o}^{T} \,R(\theta )\,d_{i} + P_{i}^{T} \,\dot{R}^{T} (\theta )\,R(\theta )\,d_{i} $$

(3)

Substituting from Eqs. (1) and (2) to Eq. (3) yields

$$ v_{i} = J\,\dot{q}_{o} $$

(4)

where, $J = \left[ {\begin{array}{*{20}c} { - \sin (\theta )} & {\cos (\theta )} & {r_{o} } \\ { - \sin \left( {\frac{\pi }{3} - \theta } \right)} & { - \cos \left( {\frac{\pi }{3} - \theta } \right)} & {r_{o} } \\ {\sin \left( {\frac{\pi }{3} + \theta } \right)} & { - \cos \left( {\frac{\pi }{3} + \theta } \right)} & {r_{o} } \\ \end{array} } \right]$ is a Jacobian matrix and $q_{o} = \left[ {\begin{array}{*{20}c} {x_{o} } & {y_{o} \quad \theta } \\ \end{array} } \right]^{T}$ is the position vector of TWOMR. From Fig. 1, linear velocity $v_{o}$ and angular velocity $w_{o}$ of TWOMR is expressed as

$$ v_{o} = \dot{x}_{o} \,\cos (\theta ) + \dot{y}_{o} \,\sin (\theta ) $$

(5)

$$ w_{o} = \dot{\theta } $$

(6)

To drive the wheels, DC motors are attached at each wheel. Force $F_{i}$ generated by ith wheel is given as

$$ F_{i} = \alpha \,u_{i} - \beta \,v_{i} $$

(7)

where $\alpha \;$ and $\beta$ are motor constants and $u_{i} (i = 1,2,3)$ is the voltage applied to each DC motor of the wheel.

The dynamic modelling of FWOMR is done using Newton’s second law of motion from which the linear and angular momentum balance equations are obtained as (Tzafestas 2014).

$$ \sum\limits_{i = 1}^{3} {(F_{i} - f_{fi} ){\mkern 1mu} R(\theta )d_{i} = m} {\mkern 1mu} \mathop P\limits^{..}_{o} $$

(8)

$$ r_{o} \sum\limits_{i = 1}^{3} {(F_{i} - f_{fi} ) = I} \,\ddot{\theta }_{o} $$

(9)

where m is the mass of TWOMR, I is the moment of inertia and $f_{fi} (i = 1,2,3)$ is the friction forces exerted at each wheel and the expression for its range of values is taken from Williams et al. (2002).

$$ f_{fi} = \frac{2}{3\pi }mg\mu_{\hbox{max} } \,\tan^{ - 1} (kv_{i} ) $$

(10)

$g$ is the acceleration due to gravity, $\mu_{\hbox{max} }$ is the maximum value of coefficient of friction and k is a constant.

Using Eqs. (4), (7) and (10), dynamic Eqs. (8) and (9) can be written as

$$ \hat{M}\,\mathop q\limits^{..}_{o} + \hat{V}\,\dot{q}_{o} = u - u_{f} $$

(11)

where $\hat{M} = \frac{1}{\alpha }(J^{ - 1} )^{T} \left[ {\begin{array}{*{20}c} m & 0 & 0 \\ 0 & m & 0 \\ 0 & 0 & I \\ \end{array} } \right],\,\hat{V} = \frac{1.5}{\alpha }(J^{ - 1} )^{T} \left[ {\begin{array}{*{20}c} \beta & 0 & 0 \\ 0 & \beta & 0 \\ 0 & 0 & {2\beta \,r_{o}^{2} } \\ \end{array} } \right],\,u = \left[ {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & {u_{3} } \\ \end{array} } \right]$ and

$$ u_{f} = \frac{1}{\alpha }(J^{ - 1} )^{T} \left[ {\begin{array}{*{20}c} { - f_{f1} \sin (\theta ) - f_{f2} \sin \left( {\frac{\pi }{3} - \theta } \right) + f_{f3} \sin \left( {\frac{\pi }{3} + \theta } \right)} \\ {f_{f1} \sin (\theta ) - f_{f2} \cos \left( {\frac{\pi }{3} - \theta } \right) - f_{f3} \cos \left( {\frac{\pi }{3} + \theta } \right)} \\ {r_{o} (f_{f1} + f_{f2} + f_{f3} )} \\ \end{array} } \right] $$

Now let $z = [\begin{array}{*{20}c} {v_{o} } & {w_{o} } \\ \end{array} ]^{T}$. Then Eq. (11) can be further simplified as

$$ \dot{z} = \hat{A}z + \hat{B}(u^{{\prime }} - u_{f}^{{\prime }} ) $$

(12)

where $\hat{A}\, = \, - [(J^{ - 1} )^{T} \,\hat{M}\,H]^{ - 1} \, \cdot \,[(J^{ - 1} )^{T} \,\hat{V}\,H]$, $\hat{B}\, = \,$$[(J^{ - 1} )^{T} \,\hat{M}\,H]^{ - 1}$, $u^{\prime}\, = \,\alpha \,u$ and $u^{\prime}_{f} \, = \,\alpha \,u_{f}$. $H = [\begin{array}{*{20}l} {\cos (\theta )} \hfill & {\sin (\theta )} \hfill & {0;} \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} ]^{ - 1}$.

In presence of bounded matched uncertainties $\xi$ Eq. (12) can be written as

$$ \dot{z} = \hat{A}z + \hat{B}(u^{{\prime }} - u_{f}^{{\prime }} + \xi ) $$

(13)

3 Controller Design

To make the system robust sliding mode control knowledge is utilized to build the controller. The main aim of the controller is to follow the desired linear velocity $v_{d}$ and desired and angular velocity $w_{d}$ of TWOMR. To design the controller velocity error is defined as

$$ e = z_{d} - z = \left[ {\begin{array}{*{20}c} {e_{1} } \\ {e_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {v_{d} - v_{o} } \\ {w_{d} - w_{o} } \\ \end{array} } \right] $$

(14)

The main challenge while using sliding mode control is the selection of sliding surface $\sigma_{i} (i = 1,2) = \left[ {\begin{array}{*{20}c} {\sigma_{1} } & {\sigma_{2} } \\ \end{array} } \right]^{T}$. For simplicity sliding surface is defined based on error which is given as

$$ \sigma = z_{d} - z + \rho \int\limits_{0}^{t} {(z_{d} - z} )d\tau $$

(15)

Differentiating Eq. (15) we get

$$ \dot{\sigma } = \dot{z}_{d} - \hat{A}z - \hat{B}(u + \xi ) + \rho (z_{d} - z) $$

(16)

To satisfy ideal sliding mode condition $\dot{\sigma } = 0$. Using Eq. (12) neglecting $u_{f}^{{\prime }}$ total control input is obtained as

$$ u_{eq} = \hat{B}^{ - 1} [\dot{z}_{d} - \hat{A}\;z + \rho \,(z_{d} - z)] $$

(17)

$u_{eq}$ brings the states on sliding surface but presence of uncertainties deviates the states and increases the error. Hence to keep the error zero a saturation function control input is added in Eq. (17). Therefore total control input is written as

$$ u_{T} = \hat{B}^{ - 1} [\dot{z}_{d} - \hat{A}\;z + \rho \,(z_{d} - z) + G\,sat(\sigma )] $$

(18)

where $\rho$ is the integral gain, G is the switching gain, and $sat\,(\sigma_{i} ) = \left\{ {\begin{array}{*{20}c} {sign\,(\sigma_{i} ),\quad \left| {\sigma_{i} } \right| > \delta > 0} \\ {\frac{{\sigma_{i} }}{\delta },\quad \left| {\sigma_{i} } \right| \le \delta } \\ \end{array} } \right.,\delta$ is a small positive constant.

The major issue in the design of controller is the estimation of design parameters. Hence to tackle the problem an adaptive law is introduced to estimate the value of G. Let $\hat{a}_{\rho }$ the estimates of G and $\lambda_{i} (i = 1,2,3)$ is a positive constant then adaptive law is defined as

$$ \begin{aligned} \dot{\hat{a}}_{\rho } & = \left[ {\begin{array}{*{20}c} {\dot{\hat{a}}_{p1} } & 0 & 0 \\ 0 & {\dot{\hat{a}}_{p2} } & 0 \\ 0 & 0 & {\dot{\hat{a}}_{p3} } \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} {\lambda_{1} \;sign\;(\sigma_{1} )} & 0 & 0 \\ 0 & {\lambda_{2} \;sign\;(\sigma_{2} )} & 0 \\ 0 & 0 & {\lambda_{3} \;sign\;(\sigma_{3} )} \\ \end{array} } \right] \\ \end{aligned} $$

(19)

Now using Eq. (19) in Eq. (18), modified adaptive integral sliding mode control law is obtained as

$$ u_{T} = \hat{B}^{ - 1} \left[ {\dot{z}_{d} - \hat{A}\;z + \rho \,(z_{d} - z)} \right] + \hat{B}^{ - 1} \;\left[ {\hat{a}_{p} \,sign\;(\sigma )} \right] $$

(20)

Theorem

The states of dynamic system given by Eq. (11) can track the desired trajectory if proposed control law is used and control parameters are selected appropriately.

Proof

Let $\tilde{a}_{\rho } = \hat{a}_{\rho } - \bar{a}_{\rho }$ is the estimated error where $\bar{a}_{\rho }$ is the nominal value of $\hat{a}_{\rho }$ and Lyapunov function is selected as

$$ V = \frac{1}{2}\,\sigma^{2} + \frac{1}{2}\,\eta_{1} \,\tilde{a}_{\rho 1}^{2} + \frac{1}{2}\,\eta_{2} \,\tilde{a}_{\rho 2}^{2} + \frac{1}{2}\,\eta_{3} \,\tilde{a}_{\rho 3}^{2} $$

(21)

Differentiating Eq. (21) and using Eq. (16) yields

$$ \dot{V} = \sigma [\dot{z}_{d} - \dot{z} + \rho (z_{d} - z)] + \eta_{1} \,\tilde{a}_{\rho 1} \,\dot{\tilde{a}}_{\rho 1} + \eta_{2} \,\tilde{a}_{\rho 2} \,\dot{\tilde{a}}_{\rho 2} + \eta_{3} \,\tilde{a}_{\rho 3} \,\dot{\tilde{a}}_{\rho 3} $$

(22)

Substituting value of from Eq. (19) Lyapunov function can be further simplified as

$$ \begin{aligned} \dot{V} & = \sigma [\dot{z}_{d} - \dot{z} + \rho (z_{d} - z)] + \sum\limits_{i = 1}^{3} {\eta_{i} \,\tilde{a}_{\rho i} \,\lambda_{i} \,sign(\sigma_{i} )} \\ & = \sigma [\dot{z}_{d} - \hat{A}\,z - \hat{B}\,\hat{B}^{ - 1} \{ \dot{z}_{d} - \hat{A}\,z + \lambda \,sign\;(\sigma ) + \rho (z_{d} - z)\} - \hat{B}\,\hat{B}^{ - 1} \xi + \rho (z_{d} - z)] \\ & \quad + \sum\limits_{i = 1}^{4} {\eta_{i} \,\tilde{a}_{\rho i} \,\lambda_{i} \,sign(\sigma_{i} )} \\ & = \sigma [ - \lambda \,sign(\sigma ) - \xi ] + \sum\limits_{i = 0}^{3} {\eta_{i} \,\tilde{a}_{\rho i} \,\lambda_{i} \,sign(\sigma_{i} )} \\ & = - \sigma [\lambda \,sign(\sigma ) + \xi ] - \sum\limits_{i = 0}^{3} {\eta_{i} \,(\bar{a}_{\rho } - \hat{a}_{\rho } )\,\lambda_{i} \,sign(\sigma_{i} )} \\ & \quad \le - \left| \sigma \right|\left( {\left| \lambda \right|\left| \sigma \right| - \left| \xi \right|} \right) - \sum\limits_{i = 1}^{3} {\left| {\eta_{i} } \right|} \left| {\lambda_{i} } \right|\left( {\left| {\bar{a}_{\rho } } \right| - \left| {\hat{a}_{\rho } } \right|} \right)\left| \sigma \right| \\ \end{aligned} $$

(23)

where $\eta < \frac{1}{\lambda }$. Therefore, it can be seen that by choosing proper value $\lambda$, derivative of Lyapunov function $\dot{V}$ can be made zero or negative. Hence error e approaches zero asymptotically. To prove the efficacy of proposed controller simulation results are presented in next section.

4 Simulation Results

For the verification of proposed control law for TWOMR, simulations are carried on MATLAB/SIMULINK 2014. Parameter values are selected as m = 9.5 kg, I = 0.17 kgm², r₀ = 0.17 m, μ_max = 0.26, and g = 9.8 m/s². To generate a U-turn trajectory desired linear velocity and angular velocity is taken as

$$ v_{d} = 0.05,\quad 0\, < \,t\, \le \,50 $$

and

$$ w_{d} = \left\{ {\begin{array}{*{20}l} {0,\quad 0\, < \,t\, < \,10\;{\text{and}}\,25\, \le \,t\, < \,35} \hfill \\ {0.2,\quad 10\, \le \,t\, < \,25\;{\text{and}}\;35\, \le \,t\, < \,50} \hfill \\ \end{array} } \right. $$

Figures 2 and 3 shows the tracking performance of linear and angular velocity of TWOMR and it can be seen that till 15 s both AISMC and ISMC provides an approximately same tracking capability in presence of friction. But between 15 and 25 s bounded uncertainty $\xi = 5\cos (t)$ is fed in, which drops the efficacy of ISMC, whereas in case of AISMC there is a sudden increase in error for a fraction of second and robustness of the robot is maintained afterwards.

Fig. 2

Linear velocity error

Fig. 3

Angular velocity error

From Figs. 4 and 5 it is evident that the sliding mode condition is satisfied for AISMC and for ISMC sliding function does not converge to zero due to lack of knowledge of G value. The smooth control input voltage fed to all three wheels with no chattering is shown in Fig. 6. In presence of friction and uncertainty it is a tedious job to select the correct value of design parameter G. Hence to tackle the problem, Fig. 7 shows the trend of $\hat{a}_{\rho }$ with time which makes the controller adaptive. The generated trajectory obtained from desired linear and angular velocity is shown in Fig. 8 and it can be seen that by AISMC the robot successfully return to its starting point whereas by ISMC it deviates from its path due to lack of adaptation law.

Fig. 4

Sliding surface 1

Fig. 5

Sliding surface 2

Fig. 6

Control voltage applied at each wheel

Fig. 7

Adaptive gain

Fig. 8

Trajectory obtained by AISMC and ISMC

5 Conclusion

In this paper an adaptive robust controller is designed for a three wheel omnidirectional mobile robot to track a U-turn trajectory in presence of friction and unbounded uncertainties. Equation of motion is derived using Newton’s second law. To make the system robust against uncertainties, chattering free and self tuned adaptive sliding mode control law is derived. The controller’s stability is verified by Lyapunov stability theorem. There are some features of the proposed algorithm. Firstly, the tracking performance of both the controller bears similar properties when there is absence of external uncertainties. Secondly, when the uncertainties are introduced AISMC converges the error to zero faster and maintains its performance for the whole simulation time compared to ISMC. Finally, the control input obtained by AISMC is smooth and chattering free.