A Brief Introduction to Quantum Phase Transitions

Abstract

In this article, we are going to present a pedagogical review of basic properties of Ising and Heisenberg models. Using these properties, we shall study basic properties of the quantum phase transition in 1D Ising model and follow it with an analogous study of the Bose-Hubbard model which is relevant to the current experimental systems involving bosons in optical lattices.

6.1 Introduction

The study of quantum phase transition has gained tremendous impetus in recent advancement in the field of ultracold atoms. The theoretical development of this subject started a long time before these experiments. In the early days, specific spin models such as the Ising and the Heisenberg models served as theoretical test beds for studying properties of these transition. In this article, we shall therefore first review, in this section, the basic properties of several spin models. This will be followed by discussions on quantum phase transition and ultracold atoms in subsequent sections.

A study of spin models is probably one of the oldest topics in condensed matter physics since they turn out to be low energy-effective models describing many strongly correlated condensed matter systems. Typically, these models are aimed at describing a set of localized spins with a given symmetry in d dimensions interacting with themselves, possibly in the presence of magnetic field. Here we shall revisit the physics of the simplest of these models, namely, models which has nearest neighbor interactions and is subjected to a magnetic field. The simplest and probably the oldest of these models is the Ising model in a transverse field whose Hamiltonian is given by

$$\begin{aligned} H_\mathrm{{Ising}}=J\sum _{\langle ij\rangle }S^{z}_{i}S^{z}_{j} -h\sum _{i}S^{x}_{i} . \end{aligned}$$

(6.1)

Here h denotes the transverse magnetic field (or $\mu _{B}$ times the magnetic field to be more accurate) and $\langle ij\rangle$ denote sum over nearest neighbors. Note that in the absence of the magnetic field, the model has a $Z_{2}$ symmetry, i.e., the Hamiltonian remains invariant under a global spin flip $S^{z}_{i}\rightarrow -S^{z}_{i}.$ This is the simplest example of the class of spin models with discrete symmetries.

The phases of the Ising model in a hypercubic lattice in d dimension is quite straightforward to obtain. In the limit of infinite transverse field, the ground state involves all the spins pointing along x. Following standard notation in the literature, we shall call this phase “paramagnet.” In the other limit, when $J\gg h,$ the nature of the phase depends on the sign of J. With our sign convention in Eq. 6.1, for $J<0,$ the system gets into a ferromagnetic phase while for $J>0,$ the ground state is antiferromagnetic. Note that each of these ground states breaks $Z_{2}$ symmetry. This point is illustrated in Fig. 6.1.

Starting from a large $x=J/h,$ if we adiabatically decrease this ratio by increasing the transverse field, the system undergoes a phase transition at some critical value of $x=x_{c}.$ For the antiferromagnetic case $(J>0),$ the transition is first order. The simplest way to see this is to note that the net magnetization $m=\sum _{i,a=x,z}S^{a}_{i}$ undergoes a discontinuous change at the transition. On the other hand, for $J<0,$ the transition is continuous. We shall discuss this case in details during our study of quantum phase transitions.

Fig. 6.1

Ground states of the Ising model for $J<0$ and $J>0$ for $|J|\gg h.$ Note that the ground state spontaneously breaks $Z_{2}$ symmetry. The two states shown in each case are degenerate and can be reached from another by a global $Z_{2}$ transformation, i.e., a simultaneous flip of all spins. Since all spins need to be flipped simultaneously, one cannot connect these states via local perturbation

Before going to discussion of other spin models, I would like to mention that the simplicity of the phases obtained for hypercubic lattices is more a property of the lattices than the model. Ising model in triangular or other non-bipartite lattices can have quite complicated phases due to a phenomenon called frustration. To see this, consider the Ising Hamiltonian (Eq. 6.1) on a 2D triangular lattice with $h=0$ and $J>0$ (antiferromagnetic interaction). Now consider a triangle in the lattice. The two vertices of the triangle can be occupied by spins pointing in opposite directions so as to minimize interaction between them as shown in Fig. 6.2. But there is no way to fill the third vertex which minimizes interaction with both the spins; the spin is therefore “frustrated.” This leads to two possible ways to fill up the third site, and consequently to two degenerate ground states. It is easy to see that this degeneracy grows exponentially with the system size N and it turns out that for the Ising model in 2D triangular lattice, the number of degenerate ground state is $\exp (0.323N^{2=3}).$ Such a huge degeneracy clearly complicates the problem of finding the true zero temperature ground state of the system. In fact, we shall see an example where this degeneracy has profound influence on phase transitions in the model.

Fig. 6.2

Frustration for antiferromagnetic Ising model in a 2D triangular lattice. It is possible to satisfy only two of the three bonds in a triangle. The satisfied bonds are shown in blue while the unsatisfied ones are shown in red. The two states shown are degenerate and such a degeneracy grows exponentially with system size

The next class of models which will be of interest to us are the XXZ models which has the Hamiltonian

$$\begin{aligned} H_\mathrm{XXZ}=J_{\perp }\sum _{\langle ij\rangle }\left( S^{x}_{i}S^{x}_{j}+S^{y}_{i}S^{y}_{j}\right) +J_{z}\sum _{\langle ij\rangle }S^{z}_{i}S^{z}_{j} . \end{aligned}$$

(6.2)

Note that here, a global rotation of the spins about the z axis leaves the system invariant, but a general rotation in 3D spin-space does not, since $J_{\perp }\ne J_{z}.$ Consequently, the model has U(1) symmetry. In contrast to Ising model discussed previously, this is an example of spin Hamiltonian with continuous symmetry. The special point $J_\mathrm{{perp}}=Jz=J$ is called the Heisenberg point of the model for which the $H_\mathrm{XXZ}$ reduces to the well-known Heisenberg model

$$\begin{aligned} H_\mathrm{{Heisenberg}}=J\sum _{\langle ij\rangle }\mathbf S _{i}\mathbf S _{j} \end{aligned}$$

(6.3)

which has SU(2) symmetry since the hamiltonian $H_\mathrm{{Heisenberg}}$ remains invariant under global rotation in spin-space. The reader is urged to verify this point.

For the rest of this section, we shall discuss the methods of obtaining the ground state and the excitation spectrum of the XXZ and the Heisenberg model. First we shall take the ferromagnetic case, for which the ground state do not break translational symmetry. Our main tool for doing this will be a mapping of these spin models to a boson model using Holstein–Primakoff (HP) transformation. The HP transformation, which is a mapping between spins and bosons can be understood as follows. We know that quantum spins must satisfy the commutation relations $\left[ S^{i}_{p},S^{j}_{q}\right] =i\hbar \varepsilon _{ijk}S^{k}_{p}\delta _{pq},$ where $\varepsilon _{ijk}$ is the antisymmetric tensor and $\delta$ denote Kronecker delta function. Now if we look at boson operators, they also satisfy commutation relations $\left[ b^{\dagger }_{i},b_{j}\right] =-i\delta _{ij}.$ From this observation, one is led to the question as to whether it is possible to express the spins in terms of bosons and vice versa. The answer is of course yes, as figured out by Holstein and Primakoff in 1940. The transformation, for spin S,  is given by

$$\begin{aligned} S^{+}_{i}=\sqrt{2S}\left( 1-\frac{b^{\dagger }_{i}b_{i}}{2S}\right) ^{1/2}b_{i},\quad S^{-}_{i}=\left( S^{+}_{i}\right) ^{\dagger },\quad S^{z}_{i}=S-b^{\dagger }_{i}b_{i} , \end{aligned}$$

(6.4)

where $S^{+}_{i}=S^{x}_{i}\pm iS^{y}_{i}$ are the spin raising and lowering operators. Note that the factors correctly $\left( 1-b^{\dagger }_{i}b_{i}/2S\right) ^{1/2}$ implements a finite Hilbert space for the spins, although that for the bosons is invite. The reader is urged to check the communication relation for the spins from Eq. 6.4.

Now let us consider the Heisenberg model on a hypercubic lattice in d dimensions with ferromagnetic interaction $(J<0).$ The ground state corresponds to all spins pointing along the z axis and hence corresponds to $S_{z}=S$ at every site of the lattice. In the boson language, this means that the ground state is a vacuum for bosons since $\langle b^{\dagger }_{i}b_{i} \rangle _\mathrm{{gnd}}=0.$ We now wish to study low-lying excitations over the FM ground state. To do this, we reexpress the Heisenberg Hamiltonian (Eq. 6.3) in terms of the bosons using Eq. 6.4. This yields

$$\begin{aligned} H_\mathrm{{excitation}}=JS\left[ \sum _{\langle ij\rangle } \left( b^{\dagger }_{i}b_{j}+\mathrm{{h.c}}\right) -2\sum _{i} b^{\dagger }_{i}b_{i}\right] +\mathrm{{O}}\left( b^{4}\right) . \end{aligned}$$

(6.5)

where we have neglected all quartic terms for the bosons. The last approximation amount to neglecting scattering among bosons. Since the ground state here corresponds to boson vacuum, for low-lying excitations, such scattering events are rare and can be neglected. The next task is to diagonalize $H_\mathrm{{excitation}}$ by going to the Fourier space which yields, in d dimensions,

$$\begin{aligned} H_\mathrm{{excitation}}=JS\sum _{k}E_{k}b^{\dagger }_{k}b_{k},\quad E_{k}=2|J|S\left( z-\gamma _{k}\right) ,\quad \gamma _{k}=\sum _\mathbf{n }e^{i\mathbf k \cdot \mathbf n } . \end{aligned}$$

(6.6)

where $z=2d$ is the coordination number for the d-dimensional hypercubic lattice and the sum over n denotes sum over nearest neighbors. $_{E}k$ here denotes energy corresponding to the low-lying excitations of the spin systems which are called spin-waves. The name originates from the fact that a finite density of the bosons at a small wave-vector k physically represents canting of spins by $\pi$ from their ground state orientation over a length scale $2\pi /k.$ At low k,  one gets $E_{k}=2JSa^{2}k^{2},$ where a is the lattice spacing. Thus the spin-waves here have quadratic dispersion which indicates vanishing group velocity at low momentum. For low $k\sim 1/L,$ the spin-wave energy vanishes and hence a very gradual canting of spins become the lowest lying excitations over the FM ground state.

Finally, we come to the case of antiferromagnets for which $J>0.$ Here the additional complication that arises is that the expected ground state corresponds to spins pointing in opposite direction at neighboring lattice sites so that $\langle S_{z}\rangle _\mathrm{{ground}}=\pm S$ on two neighboring site. This observation leads us to the fact that if we want to describe the low energy excitation over this ground state, one set of boson operators is not enough. To get around this obstacle, we divide the hypercubic lattice into two sublattices A and B such that the ground state corresponds to spins on B(A) pointing up (down). Then the HP transformation for all spins on the B sublattice is given by Eq. 6.4 whereas those for spins on A sublattice is given by

$$\begin{aligned} S^{+}_{i}=\sqrt{2S}\ a^{\dagger }_{i}\left( 1-\frac{a^{\dagger }_{i}a_{i}}{2S}\right) \quad S^{-}_{i}=\left( S^{+}_{i}\right) ,\quad S^{z}_{i}=-S+a^{\dagger }_{i}a_{i} . \end{aligned}$$

(6.7)

Comparing Eqs. 6.4 and 6.7, we find that $S^{+}_{i}$ and $S^{-}_{i}$ must switch roles to ensure a negative sign of $S_{z}.$ Next, we express the Heisenberg Hamiltonian in terms of the bosonic operators a and b. Neglecting interaction between bosons, we find

$$\begin{aligned} H^{AF}_\mathrm{{excitations}}=2JS\sum _{k}\left[ \gamma _{k}\left( a^{\dagger }_{k}b^{\dagger }_{k}+\mathrm{{h.c}}\right) +z\left( a^{\dagger }_{k}a_{k}+b^{\dagger }_{k}b_{k}\right) \right] . \end{aligned}$$

(6.8)

Note that $H^{AF}_\mathrm{{excitations}},$ though quadratic, is not quite diagonal in Fourier space due to the presence of the off-diagonal terms. To diagonalize this, we use a Bogoliubov transformation which amounts to first writing

$$\begin{aligned} \alpha _{k}=u_{k}b_{k}-v_{k}a^{\dagger }_{k},\quad \beta _{k}=u_{k}a_{k}-v_{k}b^{\dagger }_{k},\quad u^{2}_{k}-v^{2}_{k}=1 , \end{aligned}$$

(6.9)

and then finding $u_{k}$ and $v_{k}$ for which $H^{AF}_\mathrm{{excitations}}$ becomes diagonal in terms of $\alpha _{k}$ and $\beta _{k}.$ It turns out that one can write

$$\begin{aligned} H^{AF}_\mathrm{{excitations}}=\sum _{k}E_{k}\left( a^{\dagger }_{k}\alpha _{k}+\beta ^{\dagger }_{k}\beta _{k}+1\right) ,\quad E_{k}=2JzS\sqrt{\left( 1-\gamma ^{2}_{k}/z^{2}\right) } . \end{aligned}$$

(6.10)

The reader is urged to find the values of $u_{k}$ and $v_{k}$ which does the trick.

From Eq. 6.10, we note that the for low momenta the spin-waves (for hypercubic lattice) have linear dispersion: $E_{k}=2Jzsak$ which implies a finite velocity of the spin-waves at low momentum. More interestingly, we find that our starting ground state ansatz is not the correct one. To see this, let us compute ${\langle S^{B}_{z} \rangle _\mathrm{{gnd}}=NS-\langle b^{\dagger }_{k}b_{k}\rangle .}$ In terms of the $\alpha _{k}$ and $\beta _{k}$ operators, this is given by (Eq. 6.9)

$$\begin{aligned} \langle S^{B}_{z}\rangle _\mathrm{{gnd}}=NS\,-\,\Big \langle \sum _{k}u^{2}_{k}\alpha ^{\dagger }_{k}\alpha _{k}\,+\,v^{2}_{k}\beta _{k}\beta ^{\dagger }_{k}\,+\,\mathrm{{off}}\, -\,\mathrm{{diagonal \,terms}}\Big \rangle =NS-\sum _{k}v^{2}_{k}. \end{aligned}$$

(6.11)

Thus the sublattice magnetization deviates from its classical value due to quantum fluctuations, a feature that is hallmark of quantum antiferromagnets, but not of ferromagnets.

6.2 Quantum Phase Transitions

The subject of phase transition, i.e., transition between two states or phases of matter due to change of external parameters such as pressure, temperature, etc., is again an important topic in condensed matter physics. Here we shall explore only a few aspect of this important topic; for detailed study, one can refer to standard literature such as Refs. [2–4].

Standard finite temperature phase transitions occur as a result of competition of internal energy (U) and entropy (S) in the free energy of a system. Such a competition can arise in various contexts. A simple example to understand this is to consider the Ising model with $J<0$ and $h=0,$ so that at low temperature the ground state can be assumed to be ferromagnetic. Note that this is an assumption and need not be correct in all dimensions. Now let us increase the temperature so that the spins can flip. Typically, this will lead to the formation of domain walls. In $d=1,$ the domain wall corresponds to a series of flipped spins along the chain, as demonstrated in the upper panel of Fig. 6.3. It is easy to see that such a domain wall has an energy cost of 2J, whereas the entropy corresponding to such a configuration is $\simeq \ln N$ for large N. Thus the free energy of the system is $F\simeq 2J-k_{B}T\ln N<0$ for all T in the thermodynamic limit. This situation changes in higher dimensions as $d=2$ as shown in the lower panel of Fig. 6.3. Here the energy cost of forming the domain wall is 4NJ, while the entropy gain is $\ln \left( N2^{2N}\right)$ so that the free energy becomes negative above at a critical temperature $T_{c}\simeq 2J/k_{B}\ln 2.$ Thus dimensionality plays a crucial role in the phase transition.

Fig. 6.3

Domain walls for Ising model in $d=1$ and $d=2.$ Note that the energy of domain wall formation depends on system size in $d\ge 2,$ but not at $d=1$

Typically, finite temperature transitions are driven by thermal fluctuation and thus occur at a critical temperature. However, phase transitions can also occur at $T=0$ (by which we mean situations where temperature is lower than all other energy scales in the problem, and not necessarily absolute zero) where quantum fluctuations leads to a change of phase. In this case, the phase transition occurs due to competition between different terms in its Hamiltonian (such as $-J\sum _{ij}S^{z}_{i}S^{z}_{j}$ and $h\sum _{i}S^{x}_{i}$ terms in the Ising Hamiltonian defined earlier) and entropy do not play any role. One of key ingredients in understanding the behavior of a system near such a transition is the Landau–Ginzburg–Wilson paradigm. According to this paradigm, the Lagrangian density of the system in the ordered phase near the critical point for a order–disorder transition can be written in terms of the order parameter $\varDelta$ of the ordered phase as

$$\begin{aligned} f_\mathrm{{LGW}}=\varDelta ^{*}\left( \omega ^{2}-k^{2z}+r\right) \varDelta +u|\varDelta |^{4}+\cdots \end{aligned}$$

(6.12)

where ellipsis denotes all higher order terms, $r=0$ at the second-order transition point and z is called the dynamical critical exponent which determines relative scaling between space and time ($z=1$ implies relativistic invariance). Here we have assumed that the terms which are odd in $\varDelta$ are zero. This assumption, of course, need not be true in the general case. The basic point that one needs to take care of in constructing such a free energy is that it is consistent with all the basic symmetries of the microscopic Hamiltonian. Actually, in principle, such a free energy can be systematically derived from the microscopic Hamiltonian describing the system. However, except for very simple cases, this is in general impossible in practise. The key point to be emphasized here is that our failure to derive such a free energy from the microscopic Hamiltonian does not mean that we will not be able to guess its form. It only means that we will not be able to determine the precise values coefficients r,  u, etc. However, the different possibilities of the physics near the phase transition can be captured without them which makes this method very powerful. For a detailed account, see Ref. [5]. For the rest of this lecture, we are going to consider a subclass of such phase transition, namely, second-order transitions.

Next, we shall introduce the concept of universality class. As is well-known [2, 4, 5], all physically important quantities (such as equal time correlation functions of the order parameter, or energy gap) of a system exhibits power law behavior close to a second-order phase transition. This is a manifestation of the fact that phase transitions are usually accompanied by divergent length and time scales. The divergence of the time scale comes from the vanishing of the energy gap of the system $\delta E\sim \left| J-J_{c}\right| ^{z\nu }.$ The divergent length $\zeta$ comes, for example for Ising model, since the characteristics decay length of the spin–spin correlator diverges as $\zeta ^{-1}\sim \varLambda \left| J-J_{c}\right| ^{\nu },$ where $\varLambda$ is some unimportant cutoff scale. Such a power law behavior means that we can specify the behavior of the system near a phase transition by a set of exponents $\nu ,z\dots$ The physics near the transition is completely determined by these exponents; two transitions with same set of exponents will therefore have exactly same physics near the transition. The set of these exponents therefore determines the universality class of a transition. Thus the chief assertion of the universality is that the physics is independent of microscopic parameter values of the Hamiltonian which can be seen as a consequence of the presence of diverging length and time scales. In most phase transitions, the universality class of the transition can be guessed from the symmetries of the underlying Hamiltonian. However, more recent theories, have found exceptions to this rule.

We are going to see an example of such an exception in this lecture. We are now going to consider two specific examples of phase transitions. The main intention would be bringing out few key general points. First, let us consider the Ising model in $d=1$ at $T=0$ and for $J<0.$ As discussed before, there are two distinct phases of this system. The first corresponds to $h\gg |J|$ which is a quantum paramagnet with all spins pointing along x. The second is $|J|\gg h$ for which the ground state is a ferromagnet with all spins pointing wither along z or $-z.$ Now as we change h / J,  the system must go from one phase to another. The first question to ask is whether the change will occur as a transition or a smooth crossover. The answer to this question in the present model is easy to see from symmetry. We know that the system breaks $Z_{2}$ (discrete) symmetry in the ferromagnetic phase while there is no such broken symmetry in the paramagnet. This allows us to conclude that these two ground states cannot be smoothly connected—to go from one to the another one needs to have a transition.

To find out at what value of h / J this transition occurs, we consider the following. Imagine that the system is in the paramagnetic phase with the ground state corresponding to all the spins pointing along x. The basic excitation above this ground state corresponds to flipping a spin on-site i leading to an excited state $|i\rangle .$ Such a process costs an on-site energy of 2h. But now the flipped spin can move around between different sites. It is easy to see that all such states $|j\rangle$ have same energy. To compute the energy gain from such a move, consider the matrix element between states $|i\rangle$ and $|j\rangle$ are given $\langle j|H_\mathrm{{Ising}}|i\rangle =J\delta _{i,j\pm 1}.$ Thus, one is faced with a degenerate perturbation theory problem which is trivial to solve in momentum space, leading to the excitation energy E(k)

$$\begin{aligned} E(k)=2h-2J\cos (k),\quad E_{\min }=E(k=0)=2(h-J) , \end{aligned}$$

(6.13)

where $E_{\min }$ is the minimum energy of the excited state. Note that this energy touches 0 (ground state energy) for $h/J=1.$ At this point, it becomes energetically favorable to flip spins spontaneously and the ground state is destabilized. One can carry out a similar exercise staring from the ferromagnetic side and arrive at an identical answer for the critical h and E(k). It is also possible to obtain an exact result for the single particle excitations of this model for all J and h as shown in Ref. [4]:

$$\begin{aligned} E_\mathrm{{exact}}(k)=2\sqrt{J^{2}+h^{2}-2hJ\cos (ka)} \end{aligned}$$

(6.14)

which conforms to the perturbative results. All exponents of this transition can be found; the transition belongs to Ising universality class.

Finally, we shall consider the anisotropic Ising model with $J_{i,i+x},J_{i,i+y}=J>0$ and $J_{i,i+z}=J'<0$ in 3D and finite temperature but in the absence of a transverse field and in a slightly different geometry. Our aim is to show that the effect of the frustration can change the universality class of a transition. The geometry we want to consider is that of a stacked 2D triangular lattices. At high temperature, such a model must show a paramagnetic or disordered phase. At $T=0,$ the state should clearly order. This can be seen by trying to create domain wall over an ordered state. It can be easily seen that such a domain wall creation is energetically costly. Hence we expect the ordered state to hold till some finite temperature $T_{c}.$ The question is what is the nature of this ordered phase.

The answer to this question, for the considered geometry, is quite subtle. Since we are dealing with antiferromagnetic Ising model in a triangular lattice, the system is frustrated. It can be shown that the degeneracy corresponding to possible ground states grows exponentially with system size. Thus, although we are sure that there will be some ordered phase, it is not easy to guess this ordering. The aim of the rest of the section is to show that in the present case, the possible ordering comes out naturally from a proper theory of the phase transition.

To see how phase transition takes place in this model, let us rewrite the Ising model in a stacked triangular lattice in momentum space

$$\begin{aligned} H^\mathrm{{3D}}_\mathrm{{Ising}}&=\sum _{k}J(\mathbf k )S^{z}_{k}S^{z}_{-k},\nonumber \\ J(\mathbf k )&=K\left( \cos \left( k_{x}a\right) +2\cos \left( k_{x}a/2\right) \cos \left( \sqrt{3}k_{y}a/2\right) \right) -J'\cos \left( k_{z}a\right) . \end{aligned}$$

(6.15)

When $J>0,$ the minima of the dispersion occurs at $Q_{\pm }=(\pm 4\pi /3,0,0).$ Since the fluctuations about these minima are most important for destabilizing the ordered phase, we find that we need two fluctuating fields for describing this phase transition: $\psi _{\pm }=S(\mathbf Q _{\pm }+\mathbf q )=m\exp (\pm i\phi ),$ where $|\mathbf q |/|\mathbf Q _{\pm }|\ll 1.$ It can be shown that the presence of two low-energy fluctuating fields (instead of one as will be the case in absence of frustration when $J<0$) changes the universality class of the transition from Ising to XY type. The next task is to write down the effective Landau–Ginzburg free energy functional in terms of the low-energy fluctuating fields that we have identified. The thing to keep in mind while doing this is that such a functional has to be invariant under all symmetries operations of the underlying stacked triangular lattice. Following Ref. [6], one can find that such a functional can be written as

$$\begin{aligned} \mathscr {F}=\sum _{q}\left( r+\mathbf q ^{2}\right) m(q)m(-q)+u_{4}\sum _{4}m^{4}+u_{6}m^{6}+v\sum _{6}m^{6}\cos (6\phi ) \end{aligned}$$

(6.16)

where $\sum _{n}\equiv \sum _{q_{1},q_{2},\dots ,q_{n}}\delta \left( q+1+q_{2}+\cdots +q_{n}\right)$. The parameters $r,u_{4},u_{6}$, and v can be computed from microscopic theory, but their precise form will not interest us for the moment. The transition to the ordered phase takes place when $r=0.$ We note that at the transition point, v, is zero since it is irrelevant in the RG sense. Therefore, the relative phase $\phi$ between the fields $\psi _{\pm }$ is not fixed at the transition. It turns out that as we go inside the ordered phase, the magnitude of v grows and pins the relative phase to 0 (if $v<0$) or $\pi /6$ (if $v>0$). These lead to two possible ordered phases as shown in Fig. 6.4 [6]. Thus the fate of the ordered phase is determined by a variable which is (dangerously) irrelevant. The quantum counterpart of such phase transition has recently been identified in extended Bose–Hubbard models and spin systems [7, 8].

Fig. 6.4

Two possible three by three ordering for the stacked triangular lattice for $v>0$ and $v<0.$ $M_{1};M_{2};M_{3}$ represents the value of the magnetization on the three sublattices

6.3 Bose–Hubbard Model

The physics of bosons has the fascinating theoretical aspect called Bose–Einstein condensation (BEC), i.e., occupation of a single quantum state by macroscopic number of bosons at low enough temperature leading to fascinating phenomenon such as superfluidity. Moreover, there has been renewed interest in physics of these systems due to their recent experimental realizations in trapped atoms [9]. Such experiments can manipulate BECs with incredible precision. In particular, it has been possible to form an optical lattice in a system of these trapped bosons, which, when deep enough, may result in Mott localization of Bosons leading to destruction of the BEC state. Such a destruction is a result of a phase transition in the bosonic system. The physical temperatures relevant in these experiments are of the order of tens of nanokelvins (which makes these systems the coldest known place in the universe) and is at least 2–3 order of magnitudes lower than all other energy scales. Thus such a transition is an example of a quantum phase transition. In this section, we shall give a brief account of the physics associated with such a transition, by considering the simplest possible BECs, i.e., BECs formed from spin-less bosonic atoms such as $^{87}$Rb.

The optical lattice is formed by applying six counter-propagating laser beams of fixed wavelengths to the condensed Bose atoms in a trap (which can be magnetic or optical). These lasers have a electric field E and form standing waves of light in all three directions. The atoms have a polarizibility $\alpha \left( \omega ;\omega _{0}\right)$, where $\omega$ is the applied lasers frequency and $\omega _{0}$ is some characteristic frequency of the atoms. As a result, the atoms feel a potential $V=-\alpha \left( \omega ;\omega _{0}\right) |E|^{2}.$ By tuning the frequency of the applied laser, one can now make $\alpha$ positive, so that the atoms have a tendency to sit at the bottom of the potential which acts as lattice sites as shown in right panel of Fig. 6.5. Once they do that, the kinetic energy of the atoms makes them hop from one site to the next. As the lattice becomes deeper, this process is exponentially suppressed since it can be shown that the hopping amplitude $t\sim \exp \left( -\sqrt{V/E_{R}}\right)$, where $E_{R}=\hbar ^{2}/2m\lambda ^{2},$ called the recoil energy, is the basic energy scale created out of the mass (m) of the atoms and the wavelength $(\lambda )$ of the laser. The bosons which form the condensate is neutral and so the interaction between them is shortrange Van der Walls type. In the presence of a lattice, the interaction between the boson is most significant when they are on the same lattice site which we shall call U. Interaction between the atoms in the neighboring site can be neglected as a first approximation. The key point to recognize is that this interactions, unlike the hopping strength t,  do not depend exponentially on the strength of the lattice potential V.

Fig. 6.5

a Sketch of absorption imaging of bosons from a free flight. b Schematic representation of bosons in a one dimensional optical lattice. The present figure is obtained from Ref. [9]

Now consider an optical lattice with one boson per site. If the kinetic energy is large compared to the on-site interaction $(t\gg U),$ the bosons are free to hop around and therefore the ground state of the system is clearly the one in which a major number of bosons sit in the $k=0$ state. Thus the bosons form a BEC. However, if we now increase the depth of the lattice t / U becomes small, and hence a stage comes when the bosons do not find it convenient to hop around since they have to pay too much interaction energy cost to do so. In this limit all the bosons become localized. Since this localization is induced by interaction, its called a Mott insulating state.

How do we see this transition experimentally? It turns out the easiest way to look at this bosons is to switch at the lattice and the trap at the same time and let the bosons fly out. After some time of such free flight, the position distribution of these bosons can be measured by absorption imaging of the bosons in a free flight as shown in left panel of Fig. 6.5. Since the position of the bosons after a time t of such a flight depends on their starting velocity or equivalently momentum, the position distribution of these bosons actually reflect their momentum distribution inside the trap. Now if there were no lattice, all the bosons would be in the $k=0$ state (the condensate) and hence their momentum distribution will be localized around $k=0.$ On the other hand, if the bosons were in the Mott state, they are localized in real space which means their momentum can take all possible values. Thus the Mott state momentum distribution should reflect a featureless blur. As the strength of the optical lattice is increased, it is therefore expected that the momentum distribution of the bosons will crossover from a central peaked to a featureless blurred one. This is precisely what is seen in experiments as shown in Fig. 6.6. The phase transition occurs somewhere around $V_{0}\simeq 14E_{R}$ where the central bright spot disappears.

Fig. 6.6

Measurement of momentum distribution of the bosons. The lattice potential is ramped over a time period of 80 ms to its maximum value $V_{0}$ as shown in the top panel. The system is allowed to equilibrate for 20 ms and after that both the lattice and the trap potential is switched off. The position distribution of the bosons is measured after 10 ms of free flight. Note that the central peak which is the signature of superfluidity disappears at $V_{0}\simeq 14E_{R}$ signifying the onset of the Mott state. The present figure is obtained from Ref. [9]

How do we develop a theory for this transition? Well, we could try doing what we did for the Ising model. Let us first look at the Mott state when $t\ll U$ and there is an integer number of bosons per site. Neglecting the effect of hopping of bosons here, we can see that the Hamiltonian is

$$\begin{aligned} H_\mathrm{{Mott}}=U\sum _{i}\frac{1}{2}n_{i}\left( n_{i}-1\right) -\frac{\mu }{U}n_{i} . \end{aligned}$$

(6.17)

Since the Hamiltonian is on-site, one could easily find out the ground state wave function and energy. This state is given by

$$\begin{aligned} \varPsi _\mathrm{{ground}}=\prod _{i}|n_{i}=n_{0}\rangle \frac{E\left[ n_{0}\right] }{U}=\frac{1}{2}n_{0}\left( n_{0}-1\right) -\frac{\mu }{U}n_{0} , \end{aligned}$$

(6.18)

where $n_{0}\equiv (\mu /U)$ is the integer which minimizes $E\left[ n_{0}\right]$. One can easily check that

$$\begin{aligned} n_{0}&=0\ \mathrm{{for}}\ \mu \le 0\nonumber \\&=1\ \mathrm{{for}}\ 0\le \mu \le 0\nonumber \\&=2\ \mathrm{{for}}\ U\le \mu \le 2U\dots . \end{aligned}$$

(6.19)

The Mott state is the stable ground state when $t/U\ll 1.$ The next question to ask is what happens when we increase t. From the experiments, we already know the answer; the ground state becomes unstable when a critical t is reached. Now to find when the ground state is destabilized, we need to find out what are the possible excited states of the system over the ground state and when can they destabilize the ground state. Note that this line of thinking operates on the same basic principle as in study of quantum phase transition in Ising model, i.e., to find out the lowest lying excitations over the ground state of the ordered phase and check when their energy touches the ground state energy.

Fig. 6.7

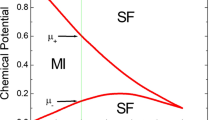
Mott-Superfluid phase boundary for $d=3$ and $n_{0}=1$. The red curve shows the mean-field phase boundary while the blue curve and the black dots denotes the phase boundary where fluctuation effects are taken into account. The Mott phase is in the shape of a lobe and has particle-hole symmetry at its tip

At finite t,  let us now consider the excited state which corresponds to addition of an extra particle/hole over the Mott ground state with $n_{0}$ particles per site. The minimum excitation energy of such states are

$$\begin{aligned} \delta E_{p}=-\mu +Un_{0}-zt\left( n_{0}+1\right) \quad \delta E_{n}=\mu -U\left( n_{0}-1\right) -ztn_{0} \end{aligned}$$

(6.20)

which destabilizes the Mott ground state at

$$\begin{aligned} t^{p}_{c}=\frac{-\mu +Un_{0}}{z\left( n_{0}+1\right) }\ t^{h}_{c}=\frac{\mu -U\left( n_{0}-1\right) }{zn_{0}} \end{aligned}$$

(6.21)

leading to a critical hopping of $t_{c}=\mathrm{{Min}}\ \left[ t^{p}_{c},t^{h}_{c}\right]$. The plot of the superfluid insulator boundary using this simple theory captures some essential features of the transition. First, we note that at the boundary between the Mott phases with $n_{0}$ and $n_{0}+(-)1$ particles, $\mu =Un_{0}(n_{0}-1)$ so that $t_{c}$ vanishes. At these points, the excited state energies $\delta E_{p}(\delta E_{h})$ vanishes for $t^{p}_{c}\left( t^{h}_{c}\right) \simeq 0$ and there is no Mott state. Second at the tip of the Mott lobe (see Fig. 6.7), where $t^{p}_{c}=t^{h}_{c}=\left( 2n_{0}+1\right) /z$ and $\mu =2m_{0}\left( n_{0}+1\right) /z\left( 2n_{0}+1\right)$, it becomes equally costly to add a particle or a hole to the system. In other words, the system possess particle-hole symmetry at this special point. This property has profound consequence on the universality class of this phase transition which we shall not dig into in details in the present article. More refined calculations such as a mean-field analysis and even those which keep track of higher order fluctuations can be done and the corresponding phase diagram is shown in Fig. 6.7. The qualitative symmetry issues that we have discussed above, however, do not change.

In conclusion, we have presented a brief pedagogical introduction to the subject of quantum phase transition in the context of spin and boson models. Such transition of course occurs in many other different systems and a detailed discussion of them is beyond the scope of the current article. However, it turns out that in many cases the insights gathered from simple models described above, provides us with powerful tools for understanding the properties of such transitions in more complicated settings. It is therefore expected that this pedagogical review is going to provide a basic introduction to the subject.