Keywords

25.1 Introduction

In this paper, the generalization to cellular neural network (CNN) model (introduced by Chua and Yang [2]) for neurons with two-way (bidirectional) time delayed connections between the neurons and itself using delay-differential equations is studied. In recent years, neural networks (especially, Hopfield type, cellular, and bidirectional associative memory, recurrent neural networks) have been applied successfully in many areas, such as signal processing, pattern recognition, associative memories [6, 8]. Processing of moving images requires the introduction of delay in the signal transmitted among the cells [7]. Brain areas are assumed to be bidirectionally (BAM) coupled forming delayed feedback loops. The malfunctioning of the neural system is often related to changes in the delay parameter causing unmanageable shifts in the phases of the neural signals [4].

We are motivated to study effectiveness of time delay as well as synaptic weights in changing the dynamics of n-dimensional BAM cellular neural network. With this motivation, we studied the global stability analysis of the system and obtained sufficient criteria with respect to synaptic weights. We investigated the system numerically without time delay showing complex dynamics including chaos but the chaotic behavior of the system is controlled as the interconnection transmission delay is introduced.

This paper is structured as follows: In Sect. 25.2 a sufficient condition for the global asymptotic stability of the equilibrium point in the delayed model is found by using Lyapunov functional method. In Sect. 25.3, numerical simulations are presented to verify the analytical results. Besides numerical results are discussed showing changes of dynamics of the system from unstable to stable (chaos control [1, 3, 5, 10]) due to time delay. Finally, some concluding remarks have been drawn on the implication of our results in the context of related work mentioned above in Sect. 25.4.

25.2 Mathematical Model with Time Delay and Global Stability

We consider, an artificial n-neuron network model of cellular neural networks time delayed connections between the neurons by the delay differential equations:

$$\begin{aligned} \frac{dx_i}{dt}=-c_ix_i(t)+a_{ii}f\left[ x_i(t)\right] + \sum _{j=1,i\ne j}^n b_{ij}f\left[ x_j(t-\tau _j)\right] ,\ c_j>0,\ i=1,2,3,\dots ,n \end{aligned}$$
(25.1)

with \(x_i(t)\) is the activation state of ith neuron at time \(t,f[x_i(t)]\) is the output state of the ith neuron at time \(t, a_{ii}\) is self-synaptic weight, \(b_{ij}\) is the strength of the jth neuron on the ith neuron at time (\(t-\tau _j\)), \(\tau _j\) is the signal transmission delay along the axon of the jth unit and is nonnegative constant and \(c_i\) (decay rate) is the rate with which the ith neuron will reset its potential to the resting state in isolation when disconnected from the network. In the following, we assume that each of the relation between the output of the cell f and the state of the cell possess following properties:

(H1) f is bounded on \(\mathscr {R}\).

(H2) There is a number \(\mu > 0\) such that \(\mid f(u)-f(v) \mid \le \mu \mid u-v\mid \) for any \(u,v\,\in \,\mathscr {R}\).

It is easy to find from (H2) that f is a continuous function on \(\mathscr {R}\). In particular, if output state of the cell is described by \(f(x_i)=\tanh (x_i),\) then it is easy to see that the function f, clearly satisfy the hypotheses (H1) and (H2). To clarify our main results, we present following two lemmas.

Lemma 25.1

For the DCNN (1), suppose that the output of the cell f satisfy the hypotheses (H1) and (H2) above. Then all solutions of the DCNN (1) remain bounded for [0,+\(\infty \)).

Lemma 25.2

Let f(t) be a nonnegative function defined on [0,+\(\infty \)) such that f(t) is integrable (that is \(\displaystyle \int ^\infty _0 f(t)\,dt < +\infty \)) and uniformly continuous on [0,+\(\infty \)). Then \(\displaystyle \lim _{t\rightarrow \infty }\) f(t) = 0.

Theorem 25.1

For the DCNN (1), suppose that the outputs of the cell [f(\(x_i\)(t)] satisfy the hypotheses (H1) and (H2) above and there exists constants \(\omega _i\,{>}\,0\), \(\omega _j\,{>}\,0\) \((i,j=1,2,\dots ,n)\) such that

$$\begin{aligned} \mu ^2\left\{ \left( 2\mid a_{ij}\mid ^2\right) + \sum _{j=1, i\ne j}^n \left( \mid b_{ij}\mid ^2 + \frac{\omega _j}{\omega _i}\mid b_{ij}\mid ^2\right) \right\} < 2c_i \; \end{aligned}$$
(25.2)

\(i=1,2,\dots ,n\), in which \(\mu \) is a constant number of the hypothesis (H2) above. Then the equilibrium \(x^*\) of the DCNN (1) is also globally asymptotically stable independent of delays.

Applying Theorem 25.1 above, we can easily establish the following corollary.

Corollary 25.1

For the DCNN (1), suppose output of the cell [f(\(x_i\)(t)] satisfy the hypotheses (H1) and (H2) above and there exists constant \(\mu \) such that

$$\begin{aligned} \mu ^2\left\{ \left( 2\mid a_{ii}\mid ^2\right) +\sum _{j=1,i\ne j}^n \left( \mid b_{ij}\mid ^2\right) \right\} <2c_i \end{aligned}$$
(25.3)

\(i=1,2,\dots ,n,\) in which \(\mu \) is a constant number of the hypothesis (H2) above. Then the equilibrium \(x^*\) of the DCNN (1) is also globally asymptotically stable independent of delays.

25.3 Numerical Results

In this section, the analytical results obtained above are verified by using numerical examples given below. We used Matlab 7.10 for simulation. Besides, in numerical portion we assume \(n=5\) and excitatory self-connections but excitatory and inhibitory interconnecting synaptic weights.

25.3.1 Example 1

 

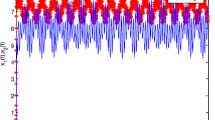
$$\begin{aligned} \dot{x}_1&=-10x_1(t)+2.1\tanh \left[ x_1(t)\right] +2.17 \tanh \left[ x_2(t-\tau )\right] \\ \dot{x}_2&=-20x_2(t)-3.5\tanh \left[ x_1(t-\tau )\right] + \tanh \left[ x_2(t)\right] +3.11\tanh \left[ x_3(t-\tau )\right] \\ \dot{x}_3&=-20x_3(t)-1.425\tanh \left[ x_2(t-\tau )\right] + 3.4\tanh \left[ x_3(t)\right] -1.1\tanh \left[ x_4(t-\tau )\right] \\ \dot{x}_4&=-30x_4(t)-1.75\tanh \left[ x_3(t-\tau )\right] +2\tanh \left[ x_4(t)\right] -1.1\tanh \left[ x_5(t-\tau )\right] \\ \dot{x}_5&=-25x_5(t)+2\tanh \left[ x_4(t-\tau )\right] +3\tanh \left[ x_5(t-\tau )\right] .\end{aligned}$$

Time series plot and phase portrait of Example 1 showing stable behavior satisfying conditions (25.3) is illustrated in Fig. 25.1.

But without any time delay and violating the restriction of weight parameters for global asymptotic stability, we consider the next example.

25.3.2 Example 2

 

$$\begin{aligned} \dot{x}_1&=-1.1x_1(t)+2.1\tanh \left[ x_1(t)\right] +2.17\tanh \left[ x_2(t)\right] \\ \dot{x}_2&=-1.5x_2(t)-2.51\tanh \left[ x_1(t)\right] +\tanh \left[ x_2(t)\right] +3.11\tanh \left[ x_3(t)\right] \\ \dot{x}_3&=-2.5x_3(t)-1.75\tanh \left[ x_2(t)\right] +3.4\tanh \left[ x_3(t)\right] -7\tanh \left[ x_4(t)\right] \\ \dot{x}_4&=-15x_4(t)-6.75\tanh \left[ x_3(t)\right] +16.9\tanh \left[ x_4(t)\right] -10.1\tanh \left[ x_5(t)\right] \\ \dot{x}_5&=-25x_5(t)+10\tanh \left[ x_4(t)\right] +30\tanh \left[ x_5(t)\right] .\end{aligned}$$
Fig. 25.1
figure 1

Solution trajectory and corresponding phase portrait in \(\left( x_1,x_2,x_3\right) \) space showing stable behavior satisfying globally asymptotically stable conditions (25.3)

Full size image

The phase portraits (Fig. 25.2) show the evidence that there exists chaotic attractors with the above set of parameter values in Example 2.

Fig. 25.2
figure 2

Solution trajectory showing chaotic behavior and corresponding phase portrait in \((x_1,x_2,x_3)\) space

Full size image
Fig. 25.3
figure 3

Control of chaos: Solution trajectory showing periodic behavior corresponding phase portrait in \(\left( x_1,x_2,x_3\right) \) space

Full size image

This chaotic nature is controlled as interconnection transmission delay is introduced (see Example 3) of the previous example with same parameter values and periodic behavior is illustrated in Fig. 25.3.

25.3.3 Example 3

 

$$\begin{aligned} \dot{x}_1&=-1.1x_1(t)+2.1\tanh \left[ x_1(t)\right] +2.17\tanh \left[ x_2(t-\tau )\right] \\ \dot{x}_2&=-1.5x_2(t)-2.51\tanh \left[ x_1(t-\tau )\right] +\tanh \left[ x_2(t)\right] +3.11\tanh \left[ x_3(t-\tau )\right] \\ \dot{x}_3&=-2.5x_3(t)-1.75\tanh \left[ x_2(t-\tau )\right] +3.4\tanh \left[ x_3(t)\right] -7\tanh \left[ x_4(t-\tau )\right] \\ \dot{x}_4&=-15x_4(t)-6.75\tanh \left[ x_3(t-\tau )\right] +16.9\tanh \left[ x_4(t)\right] -10.1\tanh \left[ x_5(t-\tau )\right] \\ \dot{x}_5&=-25x_5(t)+10\tanh \left[ x_4(t-\tau )\right] +30\tanh \left[ x_5(t)\right] .\end{aligned}$$

25.4 Discussion

A set of sufficient conditions for the global asymptotic stability of the equilibrium point in the delayed model have been shown (proofs can be established by using two lemmas, Lyapunov functional method, and combining with the techniques of inequality of DCNNs). The results obtained show some restrictions on synaptic weights and decay parameters for the global stability of the system are independent of any delay. Here, we did not assume any symmetry of the connection matrix \((b_{ij})_{n \times n}\), excitatory and inhibitory connections did not influence the sufficient criteria for global stability. Besides, we considered the output state \([f(x_i(t)]\) only satisfying hypotheses (H1) and (H2) above, not requiring them to be differentiable.

This paper also deals with chaos control by introducing time delay (see Fig. 25.3) in CNNs. Furthermore, different from the work of Yang and Huang [9] where adjustable parameter lies off the main diagonal (self-connection weights) and they have showed chaotic dynamics for particular values of weight parameter, we are able to control that type of dynamical behavior of CNNs in more generalized format. Moreover, the methods of this paper may be applicable in more complicated systems also.