Self-Organized Node Placement for Area Coverage in Pervasive Computing Networks

Abstract

In pervasive computing environments, it is often required to cover a certain service area by a given deployment of nodes or access points. In case of large inaccessible areas, often the node deployment is random. In this paper, given a random uniform node distribution over a 2-D region, we propose a simple distributed solution for self-organized node placement to satisfy coverage of the given region of interest using least number of active nodes. We assume that the nodes are identical and each of them covers a circular area. To ensure coverage we tessellate the area with regular hexagons, and attempt to place a node at each vertex and the center of each hexagon termed as target points. By the proposed distributed algorithm, unique nodes are selected to fill up the target points mutually exclusively with limited displacement. Analysis and simulation studies show that proposed algorithm with less neighborhood information and simpler computation solves the coverage problem using minimum number of active nodes, and with minimum displacement in 95 % cases. Also, the process terminates in constant number of rounds only.

1 Introduction

In many applications of pervasive computing from home and health care to environment monitoring and intelligent transport systems, it is often required to place the sensors or computing nodes or access points to offer services over a predefined area. In some cases, like mobile surveillance, vehicular networks, mobile ad hoc networks, wireless sensor networks etc., the nodes are mobile and have limited energy, limited storage and limited computation and communication capabilities. These networks are often self-organized, and can take decision based on their local information only. In wireless sensor networks (WSN), large number of sensor nodes are spatially distributed over an area to collect ground data for various purposes such as habitat and ecosystem monitoring, weather forecasting, smart health-care technologies, precision agriculture, homeland security and surveillance. For all these applications, the active nodes are required to cover the area to be monitored. Hence, for these networks, the coverage problem has emerged as an important issue to be investigated. So far, many authors have modeled the coverage problem in various ways but most of them considered static networks. For deterministic node deployment, centralized algorithms can be applied to maximize the area coverage assuming the area covered by each node to be circular or square [9, 11, 12]. Many authors solved the coverage problem by the deterministic node placement techniques to maximize the network lifetime and to minimize the application-specific total cost. In paper [3], authors investigated the node placement problem and formulated a constrained multi-variable nonlinear programming problem to determine both the locations of the nodes and data transmission pattern in order to optimize the network lifetime and the total power consumption. Authors in [10, 15] proposed random and coordinated coverage algorithms for large-scale WSNs. But unfortunately, in many potential working areas, such as remote harsh environments, disaster affected regions, toxic regions etc., sensor deployments cannot be done deterministically. For random node deployment, virtual partitioning is often used to decompose the query region into square grid blocks and the coverage problem of each block by sensor nodes is investigated [6, 13, 14].

Whether the node deployment be deterministic or random, there is little scope of improving the coverage once the nodes are spatially distributed and they are static. Hence, mobility-assisted node deployment for efficient coverage has emerged as a more challenging problem. Many approaches have been proposed so far, based on virtual force [5, 18, 20], swarm intelligence [7, 8], and computational geometry [16], or some combination of the above approaches [4, 17]. In [19], a movement-assisted node placement method is proposed based on Van Der Waal’s force where the relationship of adjacency of nodes was established by Delaunay Triangulation and force is calculated to produce acceleration for nodes to move. However, the computation involved is complex and it takes large number of iterations to converge. Authors in [1] proposed a distributed algorithm for the autonomous deployment of mobile sensors called Push and Pull, where sensors autonomously coordinate their movements in order to achieve a complete and uniform coverage. In [16], based on Voronoi diagram, authors designed and evaluated three distributed self-deployment algorithms for controlling the movement of sensors to achieve coverage. In these protocols, sensors move iteratively, eventually reaching the final destination. This procedure is also computation intensive and may take longer time to converge. Moreover each node requires the location information of its every neighbor to execute the algorithm.

In this paper, given a random node deployment over a 2-D region, a simple self-organized distributed algorithm is proposed to satisfy coverage of a given region of interest using minimum number of nodes with limited mobility. To avoid an iterative procedure, here some target points are specified deterministically by tessellating the area with regular hexagons. After deployment, each node computes the nearest target point. Next, a unique node closest to a target point is selected in a distributed fashion based on local position information only, to move towards the target point. In this way, nodes attempt to fill up the target points mutually exclusively with minimum displacement. The set of nodes selected is made active to cover the area. It is evident that compared to the works in [16, 19], the computation involved in this algorithm is significantly simple, it requires no location information of its neighbors and it converges faster in two rounds only. Analysis and simulation results show that proposed algorithm with less neighborhood information and simpler computation solves the coverage problem using minimum number of active nodes, and with minimum displacement in 95 % cases. Also, the process terminates in constant number of rounds only.

The rest of the paper is organized as follows. Section 2 defines the problem and introduces the basic scheme of area coverage. Section 3 presents the distributed algorithm for self-deployment. Section 4 evaluates the performance of the proposed protocol by simulation. Finally, Sect. 5 concludes the paper.

2 Movement Assisted Area Coverage

2.1 Problem Formulation

Let a set of $n$ nodes $\mathcal{S} = \left\{ {s_{1} ,s_{2} , \ldots ,s_{n} } \right\}$ be deployed randomly over a 2-D region $A$. It is assumed that each node is homogeneous, and covers a circular area with fixed sensing radius $r$. The goal of this paper is that given the random uniform distribution of a set of $n$ nodes over a 2-D plane, to select a subset $P\; \subseteq \;S$ and to place them at nearest target points such that the cardinality of $P$ is minimum and it covers the area. Our objective is to develop a light weight self-organized distributed algorithm for node rearrangement to reduce the amount of computation and rounds of communication, and the average distance traversed by a node, to maximize coverage utilizing minimum number of nodes. This in turn helps us to conserve energy better and hence to enhance the network lifetime.

2.2 Area Tessellation

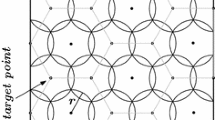
Given a rectilinear area to be covered by nodes, Fig. 1 shows a typical regular placement of nodes such that the overlapped region is minimum and the area is fully covered using minimum number of nodes. The positions of all the nodes basically defines a set of regular hexagons that tessellates the area as shown in Fig. 2. The sensor nodes are to be placed exactly on the vertices and the centers of the hexagons, termed here as the target points. In [2], it is proved that such node placement technique maximizes the area coverage using minimum number of nodes. In this case, the minimum number of nodes corresponds to the total number of target points, and can be computed easily as a function of the sensing radius $r$ as shown below.

Fig. 1

Target points for node placement

Fig. 2

Hexagons to tessellate the given area

Let $A$ be a 2-D axis-parallel rectangle $L \times W$ with $(0,0)$ as the bottom-left corner point, termed here as the origin. For any arbitrary bottom-left corner point $(x_{0} ,y_{0} )$, the co-ordinate system is to be translated appropriately. The tessellation of $A$ with regular hexagons of side $h$ is shown in Fig. 2, where $h = \sqrt 3 r$ [1]. It is to be noted that the target points lie along some rows and columns parallel to the $x$-axis and $y$-axis respectively. Rows are separated by a distance:

$$\delta w = \sqrt {h^{2} - \frac{{h^{2} }}{4}} = \frac{3}{2}r.$$

Similarly, columns are separated by a distance:

$$\delta l = \frac{h}{2} = \frac{\sqrt 3 }{2}r.$$

From Fig. 2, it is clear that, each even row-$i$ starts with a target point $(0,i.\delta w)$, whereas each odd row-$j$ starts with a target point $(\delta l,j.\delta w)$. Hence given the area $A$, the total number of rows is given by: $N_{row} = \left\lceil {\frac{W}{\delta w}} \right\rceil + 1,$. The total number of target points is,

$$N = N_{row} \cdot \left\lceil {\frac{L}{2\delta l}} \right\rceil + \left\lceil {\frac{{N_{row} }}{2}} \right\rceil .$$

Therefore, to cover the area $A$, the number of nodes to be deployed is $n \ge N$, to fill up the target points exclusively. However, in practice, with random distribution of nodes, the area to be monitored is over-deployed, and n >> N, providing sufficient redundant nodes to ensure coverage.

2.3 Nearest Target Point Computation

Let a set of $n$ nodes $\mathcal{S} = \{ s_{1} ,s_{2} , \ldots ,s_{n} \}$ be deployed randomly over a 2-D region $A$. Each node-$i$ only have the information of its physical location $(x_{i} ,y_{i} )$ and the sensing range $r$. Now to estimate the location of its nearest target point, it should have the knowledge of the origin, i.e. the bottom-left point of the area. The sink may directly broadcast it to all nodes for a static area. In case, the area of interest is dynamic, or depends on the deployment, the nodes may determine the origin as the point with minimum abscissa and ordinate of all the nodes deployed as described below. Here, during initialization, each node-$i$ broadcasts its own location $(x_{i} ,y_{i} )$, and maintains two variables initiated as $x_{{min} } = x_{i}$, and $y_{{min} } = y_{i}$ to keep the minimum abscissa and ordinate of all of the deployed nodes. It receives the messages with locations $(x_{j} ,y_{j} )$ from other nodes-$j$, and if $x_{j} \le x_{{min} }$ and/or $y_{j} \le y_{{min} }$ the values of $x_{{min} }$ ($y_{{min} }$) are changed appropriately, and if there is any update, the new message is broadcasted again, otherwise it is ignored. In this way, after sufficient time, say $T$, all the nodes will acquire the same value of $x_{{min} }$ and $y_{{min} }$ and consider it as the origin of the area under consideration. In case of an event, the affected nodes may define the event area in terms of this origin dynamically. Now, the initialization phase is completed and the next phase starts. In the worst case, each node may have to transmit $n$ messages to complete the procedure.

After initialization phase, the nearest target point is to be computed by each node. We assume that each node knows the origin $(x_{{min} } ,y_{{min} } )$ of $A$. Next, each node $i$ at location $(x_{i} ,y_{i} )$, attempts to find out its nearest target point. It computes

$$t_{x} (i) = NI\left( {\frac{{|x_{i} - x_{{min} } |}}{\delta h}} \right)$$

and

$$t_{y} (i) = NI\left( {\frac{{|y_{i} - y_{{min} } |}}{\delta w}} \right).$$

Here $NI(x)$ denotes the nearest integer value of $x$. Next, it finds the location of its nearest target point $T_{i} (x_{Ti} ,y_{Ti} )$ as:

$$\begin{aligned} y_{Ti} & = t_{y} (i) \cdot \delta w \\ x_{Ti} & = t_{x} (i) \cdot h,\quad when\,t_{x} (i)\;is\;even, \\ & = t_{x} (i) \cdot h + \frac{h}{2}\,\, otherwise. \\ \end{aligned}$$

Thus, each node finds its nearest target point and broadcasts it to its neighbors which lie within its communication range to select a unique node in a distributed fashion to be moved to a given target point exclusively. So, it is important to define the communication range of a node to define its set of neighbors.

2.4 Role of Communication Range

So far, we have mentioned the sensing range of the sensor node-$i$ that defines the circular area with radius $r$, centered at node-$i$ to be the area covered by node-$i$. When a node executes a distributed algorithm, it is very important to identify its neighborhood with which it can communicate directly. For that we should specify the communication range $r_{c}$ of a node-$i$ which indicates that when a node-$i$ transmits, a node-$j$ can receive the packet if and only if, the distance between the nodes $d(i,j) \le r_{c}$. It is important to note that for all practical purposes, $r_{c}$ is independent of $r$, since the transceiver hardware of the sensor node determines $r_{c}$ and $r$ is the property of the sensing hardware. For the proposed algorithm, it is required that each node should cooperate with its neighboring nodes which are within a distance of $2(h + r) = 2(1 + \sqrt 3 )r$. So, here we assume that $r_{c} \ge 2(1 + \sqrt 3 )r$, where $r$ is the sensing range.

3 Algorithms for Area Coverage

In wireless sensor networks, since nodes have limited computing and communication capabilities, it is always better to adopt distributed algorithms where nodes may take decisions with simple computation based on their local information only to produce a global solution.

Here initially, each node is in Active mode and knows its location and the origin ($x_{{min} } ,y_{{min} }$) of the area to be covered. In the first round, each node-$i$ assumes a virtual tessellation of the area with hexagon tiles and compute its nearest target point by Algorithm 1. It broadcasts a Target message with data $(t_{i} (x,y),d_{i} )$, where $t_{i} (x,y)$ is its nearest target point and $d_{i}$ is its distance from $t_{i} (x,y)$. Each node-$i$ waits till it receives Target messages from all of its neighbors. Then it checks if it is at minimum distance from the target $t_{i} (x,y)$. Then node-$i$ is selected to fill up the target $t_{i} (x,y)$. The case of tie may be resolved by node-id. It broadcasts Selected(i, $t_{i} (x,y)$) message and moves to $t_{i} (x,y)$ point with displacement $d_{i}$ and goes to Active state. Otherwise, it goes into the Idle state. It is clear that within the circle $C_{i}$ of radius $r$ around a target point $t_{i} (x,y)$, if there exists at least one node, it will be filled up by it. The problem arises if any circle $C_{i}$ is originally empty due to initial random node deployment. In that case, the Idle nodes will execute a second round of computation. Each idle node-$i$ finds if there is any unfilled target node around it, i.e. within the six adjacent circles overlapping with $C_{i}$. Next it finds the unfilled target points and sort them according to the distance from it. Next it follows the same procedure described above for each target unless it becomes selected or all the targets are filled up.

The distributed Algorithm 3, describes the sequence of steps of the procedure.

3.1 Complexity Analysis

It is evident that to find the target points Algorithm 1 is computed in constant time. To take decision for selecting a unique node for each target point, each node waits until it receives all the target messages from its $d$ neighbors. Each node takes $O(d)$ time to get the minimum distance from its $d$ neighbors. Therefore, Algorithm 2 computes in $O(d)$ time, where $d$ is the maximum number of neighbors of a node. Finally, each node attempts to fill up at most seven target points. Therefore, the total time complexity of the distributed algorithm (Algorithm 3) is $O(d)$. In the distributed algorithm nodes broadcast at most seven Target messages and only one Selected message. Therefore, per node at most eight messages are needed to complete the procedure. Hence, the message complexity per node is $O(1)$ only.

4 Simulation Results

In our simulation study, we assume that $n$ nodes, $250 \le n \le 300$, are distributed randomly over a $500 \times 500$ area with radius $r = 28.86$ and side of the hexagon $h = 50$. All the target points associated with the circles are computed by nodes. After executing the distributed algorithm, each node moves to its target point. The performance of the proposed algorithm is evaluated in terms of coverage, rounds of computation needed and displacement of nodes. The graphs show the average value of $20$ runs for $20$ independent random deployments of nodes.

Figure 3 shows the variation of coverage percentage with $n$, the total number of nodes deployed. If the total number of target points is $105$, for $n = 50,100,150$, the coverage percentage is found to be 47, 84.57 and 99.36 % respectively. It gives an idea that how much an area should be over deployed to achieve 100 % coverage with random node deployment.

Fig. 3

Coverage rate with number of nodes

In Fig. 4, the variation in the number of computation rounds with $n$ is presented. It is to remember that with random deployment, if there is no empty circle $C_{i}$ with center at a target $t_{i}$ and radius $r$, the procedure completes in a single round only. This fact is exactly revealed in Fig. 4. For n = 100, 150, 200, target points are filled up in two rounds whereas if $n > 200$, the proposed technique takes a single round to complete.

Fig. 4

Number of rounds for filling the target points

For a given random deployment of $n = 150$ nodes, Fig. 5 shows the distances traversed by each node to fill up target point with $r = 28.86$. It shows that in more than $95\,\%$ cases, the target is filled up by a node with minimum possible displacement. It is obvious that with greater values of $n$, this percentage can be improved further.

Fig. 5

Node displacement versus target points

5 Conclusion

In this paper, we propose a self-organized node placement algorithm to satisfy the coverage of a given region of interest in Wireless Sensor Networks. The area is logically tessellated by regular hexagonal tiles starting from an origin. To get full coverage with random deployment of $n$ nodes over a $2D$ region, we need to place unique nodes on every target point, which are essentially the vertices and the centers of the hexagons. With just the knowledge of its own location and the origin, each node executes a simple self-organized distributed algorithm $O(d)$ time complexity ($d$ is the maximum number of neighbors of a node) and constant message complexity, to fill up all the target points mutually exclusively with minimum possible displacement. In case of failure of nodes, existing free nodes may take necessary action to fill up the empty target points to make the system fault-tolerant. We evaluate the performance of our proposed model by simulation. It shows that with sufficient node density the algorithm attains full coverage using minimum number of nodes and terminates in one round only. Also, in more than $95 \,$ cases the displacement of an individual node is minimum.