Denoising of GPS Positioning Data Using Wavelet-Based Hidden Markov Tree

Abstract

Precise position and navigation with GPS is always required for both civil and military applications. The errors and biases associated with navigation will change the positional information from centimeters to several meters. To estimate and mitigate the errors in GPS positioning data, the wavelet transform is most significant technique and proven. The traditional wavelet threshold methods will work to a certain extent but are not useful to estimate the signal levels to the expected level due to their incapability for capturing the joint statistics of the wavelet coefficients. The wavelet-based hidden Markov tree (WHMT) is designed to capture such dependencies by modeling the statistical properties of the wavelet coefficients as well. In this paper, a WHMT is proposed to reduce positioning error of the GPS data. To establish proposed method, the position data are decomposed using wavelets. The obtained wavelet coefficients are subjected to Discrete Wavelet Transform (DWT) as well-proposed WHMT for noise removal. In this proposed methodology, an Expectation Maximization (EM) algorithm used for computing the model parameters. The root-mean square error (RMSE) of proposed method shows better performance comparatively classical DWT.

1 Introduction

The accuracy of positioning service for the simple stand-alone GPS system is severely affected by several types of biases and noises [1]. Those are mainly systematic and random errors. The systematic errors may be due to ionosphere, by the troposphere and clock offset. Random errors may result from satellite orbit, receiver noise, and multipath effect. The systematic errors behave like a low-frequency noise whereas the random errors are typically characterized as high-frequency noise. Filtering out these errors by applying a filter with constant length does not suit if the error behavior is not common in all the levels. If the signal is decomposed into multiscale or bands, and applying threshold gives better results than traditional filtering methods.

It is more than one decade now the wavelet transform emerged as a new tool and gained wide acceptance in the field of statistical signal and image processing. Wavelets are applied in key areas which include signal estimation, detection, classification, and filtering [2–4]. The primary properties like locality and multiresolution made wavelet transform to become an important tool to reduce the noise and its effectiveness. Donho and Johnston, in 1998, pioneered wavelet threshold methods by grouping the wavelet coefficients as significant and insignificant and are modified by certain specific rules. The optimal threshold estimation is based on the assumption that the wavelet coefficients are sparse. This assumption is invalid in the case of coarser levels leading to error in estimating the threshold. To overcome this, several researchers have proposed Bayesian approach to capture the sparseness of the wavelet coefficients .These shrinkage methods had later been improved by inter-scale and intra-scale correlation of the coefficients. Crouse et al., developed a framework for statistical signal processing based on wavelet domain Hidden Markov Tree (HMT) models [3]. This framework has enabled them to concisely model the non-Gaussian statistics of individual wavelet coefficients and statistical dependencies between coefficients. The applications of wavelets to the GPS signal processing were quite new in 1995, and Coliin and Warrant applied wavelets for GPS cycle slip correction. The authors, Fu and Rizos, widely used the method of MRA in GPS signal processing [5–9]. Authors [10–13] continued to apply wavelets for GPS signal processing for different applications and contributed significant amount of work in the field of denoising. All these methods are used for popular wavelet thresholding/Shrinkage methods.

In this paper, a new approach based on wavelet domain hidden markov tree (WHMT) model is used to mitigate the GPS position errors. To evaluate the performance of proposed method, the WHMT is compared to DWT denoising methods. Section 2 describes problem statement of denoising in GPS positioning data. The classical wavelet denoising and WHMT model are discussed in Sect. 3. Section 4 briefly explains the data collection and analysis of GPS data. Experimental results and analysis achieved in this proposed method are discussed in Sect. 5. A conclusion of the experiment is presented in Sect. 6.

2 Problem Statement

The GPS code observable for the L1 single frequency f ₁ = 1575.42 MHz is [1]

$$\rho_{i} = r_{i}^{k} + b_{i} - B^{k} + T_{i}^{k} + I_{i}^{k} + \varepsilon_{\rho{_{i}}}$$

(1)

Here ‘r’ is the true range between the ith receiver and kth satellite, where ‘b’ is the receiver clock bias, ‘B’ is the satellite clock bias, ‘T’ is the troposphere errors, ‘I’ is the ionosphere error, and ‘ɛ _ρi’ is the noise. The majority of the GPS receiver operates on single frequency and uses noisy code measurements for its simple positioning services. The GPS observables in Eq. (2) are subjected to systematic delays, i.e., ionospheric, tropospheric, and clock difference, and the random errors like receiver noise and multipath noise. The errors are more prominent in low-latitude region and solar days. During the period of disturbance, the receiver suffers from high noise level and the pseudo range noise distributed on a non-Gaussian tails. Traditional wavelet-based denoising methods cannot capture the non-Gaussian statistics nature of the wavelet coefficients.

In general, the denoising problem can be viewed as

$$\mathop y\nolimits_{i} = f(\mathop t\nolimits_{i} ) + \sigma \mathop { \in }\nolimits_{i}$$

(2)

The ‘ϵ _i ’ is standard Gaussian while noise (i.i.d). ‘σ’ is the noise level may be known or unknown. Here, the goal is to record the under laying function ‘f’ from the noisy data ‘y’ with small error.

3 Methodology

3.1 Classical Wavelet Denoising

The DWT will decompose data, and it can be represented as pair of high- and low-pass coefficients followed by down sampling by two and iterated on the low-pass output. The outputs of the low-pass filters are the scaling coefficients, and the outputs of the high-pass filter are the wavelet coefficients. The approximated coefficients are processed successively by first down sampled and split further. The detailed coefficients d _j (t) are used to estimate threshold value via median estimator to remove the high-frequency noise components. Median estimator method will estimate threshold for optimum soft threshold that minimizes the Mean Squared error (MSE). In these approaches, a prior distribution is imposed on the wavelet coefficients, which is designed to capture the sparseness of the wavelet expansions that is common to most application. The noise variance $\tilde{\sigma }_{\varepsilon }^{2}$ is estimated from the each level by the robust median estimator (MAD) [2].

$$\tilde{\sigma }_{\varepsilon }^{2} = \frac{{{\text{median}}(\left| {y_{i} } \right|)}}{ 0. 6 7 4 5}$$

(3)

The signal variance $\tilde{\sigma }_{x}$ is estimated as

$$\tilde{\sigma }_{x} = \sqrt {\hbox{max} ((\tilde{\sigma }^2_{y} - \tilde{\sigma }^{2} }) ,0)$$

(4)

Since y is modeled as zero mean, $\tilde{\sigma }_{y}$ can be found empirically as

$$\tilde{\sigma }_{y}^{2} = \frac{1}{n}\sum\limits_{i = 1}^{n} {y_{i}^{2} }$$

(5)

The classical wavelet denoising of signal can be obtained by the following steps.

• 1. Apply the DWT to the noisy data (‘y’) to obtain transformed noisy coefficients w = DWT(y) = (w _j ) _{j ∊ [1; j + 1]} where w _j  = ℜⁿ, and here $\Re$ is set of noisy coefficients at each level ‘n,’

• 2. Apply suitable thresholding function (Γ) to the transformed noisy coefficients to get ω ^∧ = Γ(w), and

• 3. Reconstruct the original signal by applying the inverse DWT to the wavelet coefficients.

The shrinkage technique may vary according to thresholding function and its applicability of wavelet coefficients.

3.2 HMT-Based Denoising

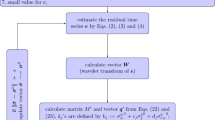
The primary properties of DWT assume that the wavelet coefficients are jointly Gaussian and statistically independent. In general, the actual signal wavelet coefficients have sparseness, and some residual dependency exists between the coefficients. To capture statistical dependencies between coefficients, a hidden markov model was introduced [3]. In this, the hidden state variables are introduced to match the wavelet coefficients, and the dependencies between the hidden state variables are well characterized. For estimating the model parameters of HMT, an EM algorithm is used. In HMT, the nested sets of coefficients are generated at every scale in wavelet decomposition process and represent as state variable across scale. This model connects the hidden states ‘S _i ’ nodes to observed wavelet coefficients W _i . Each hidden state node represents the mixture state variable (S _i ) and wavelet coefficient (‘W _i ’) as shown in Fig. 1.

Fig. 1

a Signal decomposition hierarchy of HMT model. b Flow chart for signal denoising using DWT and WHMT

(i) Modeling of Wavelet Coefficients

The wavelet coefficient of most real-world signals is sparse: a few wavelet coefficients are large, but most are small. Therefore, we associate each wavelet coefficient ‘ѡ _i ’ an unobserved hidden state variable S _i  = {S, L}. The state ‘S’ corresponds to a zero-mean, low-variance Gaussian whereas high variance, zero mean corresponds to the large state ‘L.’ Hence, the Gaussian mixture model appears to be good fit for the distribution of the wavelet coefficient data being one of the states.

Thus, the overall pdf is given by

$$f\left( {w_{i} } \right) = p\left( {S_{i} = m} \right)f\left( {w_{i} /S_{i} = m} \right)$$

(6)

where the conditional probability f(w _i /S _i  = m) of the coefficient value ‘w _i ’ given the state ‘S _i ’ corresponds to the Gaussian distribution

$$f\left( {{\raise0.7ex\hbox{${w_{i} }$} \!\mathord{\left/ {\vphantom {{w_{i} } {S_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${S_{i} }$}} = m} \right) = \frac{1}{{\sqrt {2\pi \sigma_{i,m}^{2} } }}\exp \left( { - \frac{{(w_{i} - \mu_{i,m} )^{2} }}{{2\sigma_{i,m} }}} \right)$$

(7)

(ii) Estimation of Signal

The HMT model is completely parameterized by two-component mixture of generalized Gaussian for the wavelet coefficients at each scale. The estimation of the true signal wavelet coefficients can be obtained by using of following equation:

$$w_{i}^{ \wedge } = E\left[ {w_{i} /\theta } \right] = \sum {p\left( {S_{i} = m/w_{i} ,\theta } \right)} \frac{{\sigma_{i,m}^{2} }}{{\sigma_{i,m}^{2} + \sigma_{n}^{2} }}w_{i}$$

(8)

where $p\left( {S_{i} = m/w_{i} ,\theta } \right)$ is the probability of state ‘m’ given the noisy wavelet coefficient ‘w _i ’ and the model parameters ‘Ɵ’ are computed by the EM algorithm. The variance ‘σ ² _i,m ’ common to all coefficients in given scale and the noise variance ‘σ ² _n ’ is unknown which in turn estimated through the Median Absolute Deviation (MAD) estimator.

(iii) Implementation

The flow chart for the proposed denoising method is shown in Fig. 1 and summarized as follows:

• 1. Extract the raw GPS data from single frequency GPS Receiver.

• 2. Read the RINEX observation and navigation files.

• 3. Extract ephemeris and observation data of all visible satellites

• 4. Compute the receiver position using Least Square method.

• 5. Apply the DWT to the computed position.

• 6. Reconstruct the DWT coefficients using IDWT

• 7. Train the obtained wavelet coefficients from DWT using HMT.

• 8. Apply the model-based denoise to remove the noisy coefficients.

• 9. Compute the RMSE of original and estimated coefficients.

The proposed method of GPS data processing involves two steps. The first step involves calculation of receiver position at each epoch from GPS data. The second step is to compute receiver positioning data with DWT and the proposed WHMT.

4 Data Collection and Analysis

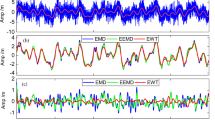
To verify the proposed method of denoising, two sets of data collected from IGS stations established at IISC Bangalore and Hyderabad as shown in Table 1, which is in RINEX format. One set of data consists of severely affected noisy data on solar eclipse day and other set consists of normal day’s data with different seasons. The collected data-sampling interval of 30 s and total 1024 epochs are taken for computation. The average receiver position of each epoch is computed and shown in Fig. 2. The original and smoothed position coordinates of WHMT method is shown in Figs. 3, 4, and 5. The error plot is shown in Fig. 6.

Table 1 Data collection

Fig. 2

The original position data signal of IISC Bangalore (15th January 2010)

Fig. 3

The original and denoised X position using WHMT

Fig. 4

The original and denoised Z position using WHMT

Fig. 5

The original and denoised Z position using WHMT

Fig. 6

The noise present in GPS positioning data

5 Results and Discussions

To evaluate the performance of the proposed method, WHMT is compared with classical DWT. In this analysis, a different seasonal data is collected and evaluated. The quality measure of this algorithm is RMSE. Different wavelet base functions considered and tested. Table 2 shows the root-mean squared error (RMSE) of the processed GPS position coordinates data using traditional denoising method DWT, as well as WHMT. As compared with the RMSE of DWT to WHMT, the WHMT shows significant improvement. The results are clearly indicating that the proposed method is best suited and promising for accurate position. In this analysis, it has been observed that the Y coordinate is noisy than other two coordinates. Among three coordinates, the coordinate Y is noisy. Further, with all wavelet basis function, the coeflet5 gives better performance.

Table 2 Position smoothing using DWT and WHMT

6 Conclusions

In this paper, the traditional DWT and proposed WHMT are used for removal of systematic and random errors of GPS positional data. The experimental result on collected data demonstrates that the proposed method can effectively remove the GPS errors and biases. This method well suited critical aviation applications like GAGAN of Indian SBAS. The median estimator (MAD) is simple and robust, and requires less computation time to estimate threshold. Therefore, here it is considered and used to denoise the position data. In future analysis, the proposed method can be tested with non-orthogonal wavelet families as well as other available threshold techniques.