Effect of Electric Field on Planar Fluid-Fluid Interfaces

Abstract

Electrohydrodynamic instabilities at fluid-fluid interfaces are being extensively explored for potential technological applications such as soft lithography. Although extensive work has been done in this field experimentally, the state of the art in the theory is the leaky dielectric model which might not be valid in certain practically relevant systems. In the present work, various scenarios where the leaky dielectric model is found lacking are identified and alternate theories have been proposed. Experimental validation is also provided to show the practical relevance of these parametric regimes, and a big picture of the interfacial instability under electric fields is obtained.

1 Introduction

Electrohydrodynamics (EHD) is the study of fluid flow under the action of an applied electric field. In the context of a planar interface between two fluids, an applied normal electric field destabilizes the interface to form columns of one fluid growing into the other [1–5]. This instability termed ‘electrohydrodynamic (EHD) instability’ carries immense technological importance. The wide applicability of this phenomenon stems from the fact that it can be modelled using the simple fundamental laws of electrostatics (Gauss’ law) and fluid dynamics (Navier-Stokes’ equations) (hence the name electrohydrodynamics) providing a robust tool for making realistic predictions about the features of the instability.

$$\displaystyle\begin{array}{rcl} \int n.\boldsymbol{E}\mathit{dS} = \frac{\rho _{f}} {\epsilon _{0}} & &{}\end{array}$$

(1)

$$\displaystyle\begin{array}{rcl} \boldsymbol{\nabla }\cdot \boldsymbol{ V } = 0& &{}\end{array}$$

(2)

$$\displaystyle\begin{array}{rcl} \rho (\partial _{t}\boldsymbol{V } +\boldsymbol{ V } \cdot \boldsymbol{\nabla }\boldsymbol{V }) = -\boldsymbol{\nabla }p +\mu \boldsymbol{ \nabla }^{2}\boldsymbol{V } +\rho _{ f}E& &{}\end{array}$$

(3)

where $\boldsymbol{E}$ is the electric field, S is the area of the interface, ρ _f is the free charge, ε ₀ is the permittivity of vacuum, $\boldsymbol{V }$ is the velocity of the fluid, p is the hydrostatic pressure and μ is the viscosity.

Electrohydrodynamics (EHD) is a term unique to the study of systems in which the effects due to current are minimal. Unlike the related field of electrokinetics, fluids that show EHD behaviour are generally dielectric materials. Pure or perfect dielectric (PD) materials have dipoles in them which align along the electric field to create a polarization field within the fluid. The Gauss’ law for such a fluid is modified to consider the contribution of the polarization to the field. The differential form of the Gauss’ law is given as

$$\displaystyle{ \nabla ^{2}\phi = \frac{\rho _{f}} {\epsilon _{0}\epsilon } }$$

(4)

where ϕ is the electric potential and ε is the dielectric constant of the fluid.

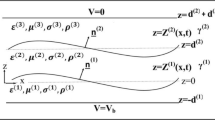
To describe the electric field in the present fluid-fluid system, a few boundary conditions across the interface are made use of. One of the condition being that the electric field vector is continuous across the interface. In the normal direction,

$$\displaystyle{ \left [\epsilon _{0}\epsilon _{i}(-\boldsymbol{\nabla }\phi _{i} \cdot \boldsymbol{\hat{ n}})\right ] = 0 }$$

(5)

where the operator $\left [X_{i}\right ]$ denotes the jump X ₁ − X ₂ across the fluid-fluid interface h(x, t). i = 1, 2 denotes the upper and the lower fluid, respectively. A balance of the tangential component of the field gives the continuity of the potentials across the interface:

$$\displaystyle{ \phi _{1} =\phi _{2} }$$

(6)

An EHD model for a real dielectric material considers both the alignment of dipoles within the fluid and the flow of a negligible yet finite free charge present in the fluid, under the action of an electric field. The term ‘leaky dielectric (LD)’ describes such a material. The assumption of an infinitesimal free charge present in an LD fluid makes this model more powerful in terms of explaining phenomena which cannot be explained by a simple PD or a perfect conductor theory. The free charge accumulates at the interface and can be estimated by a material balance where the net current across the interface is equivalent to the accumulation.

$$\displaystyle{ \partial _{t}q +\boldsymbol{ V _{1}}.\boldsymbol{\nabla }_{s}q - q\boldsymbol{\hat{n}}.(\boldsymbol{\hat{n}}.\nabla )\boldsymbol{V _{1}} = \left [\sigma _{i}\nabla \phi _{i} \cdot \boldsymbol{\hat{ n}}\right ] }$$

(7)

where q is the free charge density at the interface and $\sigma$ is the conductivity of the fluid. The last two terms on the left-hand side of the equation physically signify the surface convection of the charge and the change in the surface charge due to stretching of the interface. The right-hand side denotes the net current due to conduction. Equation (5) is modified for a leaky dielectric as (Fig. 1)

$$\displaystyle{ \left [\epsilon _{0}\epsilon _{i}(-\boldsymbol{\nabla }\phi _{i} \cdot \boldsymbol{\hat{ n}})\right ] = q }$$

(8)

Fig. 1

Schematic of a PD-PD interface with dipoles aligned under an electric field

The coupling of the electrostatics and the hydrodynamics occurs through the stress balance at the interface. The total stress which has contributions from hydrodynamic stress tensor and the Maxwell’s stress tensor is balanced by the surface tension.

$$\displaystyle{ \left [\boldsymbol{\hat{n}} \cdot \boldsymbol{\tau _{i}} \cdot \boldsymbol{\hat{ n}}\right ] =\gamma C }$$

(9)

where C is the curvature given by $C = \nabla \cdot \boldsymbol{\hat{ n}} = -\partial _{x}^{2}h/(1 + \partial _{x}h^{2})^{3/2}$. The term on the right-hand side in the above equation represents the stabilizing force due to surface tension γ. The balance of stresses in the tangential direction is given by

$$\displaystyle{ \left [\boldsymbol{\hat{t}} \cdot \boldsymbol{\tau _{i}} \cdot \boldsymbol{\hat{ n}}\right ] = 0 }$$

(10)

$\boldsymbol{\tau _{i}}$, the total stress, i.e. the sum of the hydrodynamic and the electrical stresses, for the fluid i, is given by

$$\displaystyle{ \boldsymbol{\tau _{i}} = -p_{i}I +\mu _{i}(\boldsymbol{\nabla }\boldsymbol{V _{i}} +\boldsymbol{ \nabla }\boldsymbol{V _{i}}^{T}) +\boldsymbol{\tau _{ e}} }$$

(11)

The superscript T indicates transpose, i = 1, 2 denotes the two fluid layers, and $\boldsymbol{\tau _{e}}$ is Maxwell’s stress tensor $\tau _{e} =\epsilon _{0}\epsilon \left (\boldsymbol{EE} -\frac{1} {2}E^{2}I\right )$.

Although popular for its simple and elegant mathematical formulation, the LD theory has certain limitations. With the tremendous evolution of technology, it is vital to have equivalently powerful tools for modelling and simulation. Hence, in the present chapter, the limitations of the LD theory in four scenarios which arise in contemporary technological applications of EHD are discussed and appropriate alternate theories proposed.

Early research in the field of EHD interfacial instabilities dealt with inviscid fluid interfaces [3, 4, 6], destabilizing under the combined action of gravity, surface tension and high electric fields (refer Fig. 2a, b). It is found that a critical field is required to induce an instability which consists of a typical undulation, crests of which grow to form droplet ejecting jets. The wavelength of this instability is referred to as the ‘Taylor wavelength’ and can be obtained considering the fluids to be either PD or PC materials, as water, surfactant solutions and organic solvents are the commonly used fluids in these studies.

Fig. 2

Schematic of an EHD instability at an interface when gravity is significant (a, b) and when it is negligible (c, d)

A mismatch of experimental observations with either of the PD or PC theory occurs when a dielectric fluid interface is subjected to a DC field. This is attributed to interfacial shear stresses that arise as a result of accumulation of the negligible yet finite charge, present in a real dielectric fluid, at the interface [7]. This is explained by the LD model [8–13]. Most of the fluids used practically have low conductivities which indicate a slow albeit finite charge relaxation time. This implies that true perfect dielectric behaviour can be realized, in practice, only at frequencies high enough that the rapid alteration of the field doesn’t allow the inherent free charge to migrate to the interface.

2 The Effect of AC Fields

This poses quite interesting questions as to what would happen if the frequency of the applied field is not high enough for the charges to remain fixed at their position but transits from this high value to a value which is almost constant when compared to the experimental timescale. How does the conductivity of the leaky dielectric material compete with the alternating effect of the electric field and affect the final instability? The leaky dielectric model which assumes time-invariant electric forcing cannot be used to answer the aforementioned questions, and hence, the ‘Floquet theory’ is made use of. A systematic linear stability analysis of a planar fluid interface subjected to an alternating field shows that an AC field indeed can be used to probe new regimes of system behaviour with the LD and PD behaviour being the limiting cases at a low and high frequency, respectively (refer Fig. 3). The transition from a PD behaviour to an LD behaviour occurs when the frequency equals the inverse of the charge relaxation time. It is found that this trend is same across the three orders of conductivity values studied except that the transition frequency ($\Omega _{\mathrm{trans}} =\tau _{c}$ where $\Omega$ is the scaled frequency and τ _c is the charge relaxation time) shifts to lower frequencies with decrease in the conductivity.

Fig. 3

Dependence of the maximum growth rate on frequency for a perfect dielectric-leaky dielectric system. The parameters used are ε ₁ = 1, ε ₂ = 2. 5, $\lambda = 10^{-6}$, B = 0. 01 and σ ₁ = 0

Recent electrohydrodynamic studies at planar interfaces deal more with thin films of viscous fluids as opposed to reservoirs of inviscid liquids considered in the previous studies owing to their application in producing micro-patterned devices. This thin fluid film system (parts c, d in Fig. 2), in contrast to the earlier ones, has insignificant effects of gravity due to the low length scales involved. The leaky dielectric theory for viscous systems involves the Stokes’ equation (inertial terms neglected), governing the hydrodynamics. Due to the small length scales involved in the system, the so-called thin film approximation (TFA) is found to be a useful tool in studying this instability. This approximation yields simplified evolution equations of the position of the interface (h) and the charge at the interface (q) with time.

3 The Effect of Conductivity

It is, therefore, interesting, not only to study the effect of alternating fields on the instability but also an in-depth study of how the low conductivities of these viscous fluids effect the wavelength of the instability. The key assumption in the leaky dielectric model is that the charge relaxation is instantaneous. Although quite powerful, this assumption cannot be used without a knowledge of the conductivity of the system which for deionized water itself is ∼ 10⁻⁶ S/m and can go to as low as 10⁻⁹–10⁻¹² S/m for viscous polymeric fluids. The need of the hour is a modelling tool which can predict the wavelength of the instability depending upon the conductivity.

To overcome the limitation of the LD model in the context of low conductivity fluids, non-linear analysis is used. The evolution equations of the interface position and interfacial charge, obtained after the TFA, are numerically integrated in time from an initial condition of a random disturbance of infinitesimal amplitude. The result from the simulation shows the formation of columns, the mean spacing between which has been compared to experiments carried out at the same conditions (a few representative images are given in Fig. 4). It is observed from the results of the non-linear analysis (refer Fig. 5) that the wavelength ($\lambda = 1/k_{\max }$) of the instability increases with a decrease in the conductivity of the fluid under DC fields. At very low conductivity, the wavelength predicted by the non-linear analysis is equivalent to that predicted by a perfect dielectric theory. This dependence of the instability wavelength can be explained in terms of the timescales involved in the system, namely, the charge relaxation time (τ _c ) and time for the growth (τ _s ) of the instability. The system would behave like a PD material or an LD material depending on whether τ _c  > τ _s or τ _c  < τ _s . If $\tau _{c} \approx \tau _{s}$, then it would show a transition behaviour which can be predicted by the non-linear analysis alone.

Fig. 4

Images of the instability in the form of columns rising from the pdms film and seen from the top view at different voltages. Starting from the left, the images are at 140 V & 1 mHz, 70 V & 1 mHz, 35 V & DC, 140 V & 0.3 Hz, 70 V & 10 Hz and 35 V & 1 Hz, respectively

Fig. 5

A comparison of k _max as a function of S ₂ between results obtained from experiments and non-linear analysis. The values of the parameters used in the theoretical analysis are $\epsilon _{1} = 1,\epsilon _{2} = 3,\mu _{r} = 10^{-7}$ and S ₁ = 0. The ($\cdots$) lines (a) and (b) indicate the linear LD-PD theory, and the (⋯ ) lines (c) and (d) indicate the PD-PD theory for β = 0. 65 and β = 0. 7, respectively. The (⋯ ) line curve and the ($-\cdot -\cdot$) line curve represent the results from the LD modified theory for β = 0. 65 and β = 0. 7, respectively, while the ($---$) curve and the solid line curve represent the results from the non-linear analysis for β = 0. 65 and β = 0. 7, respectively. The ∗ symbols indicate experimental results

It is interesting to study the effect of using alternating fields in the present systems. In the presence of AC fields, an additional timescale, that of the time period (τ _f ) of the AC field, becomes relevant. The interplay of all the three timescales gives a total of nine regimes which have been studied in the present work (Fig. 6). It is seen that at very low values of τ _f , in spite of the magnitude of the other two timescales (τ _c and τ _S ), the system always shows the signature of a perfect dielectric material. At very high values of τ _f , the relative values of τ _c , τ _f and the type of waveform used play an important role in deciding the wavelength of the instability. At very large τ _f (low $\Omega$), the Floquet theory always predicts a limiting value equivalent to that of an LD fluid under a DC voltage equivalent to the r.m.s voltage of the applied AC field. It is only through the non-linear analysis that one can show that this limiting case is not always an LD behaviour but depends on the conductivity of the system. To elaborate, for low conductivity fluids (i.e. $\tau _{c} >\tau _{s}$), the system behaves like a perfect dielectric material. But at such low frequencies, as the field is constant within the timescale τ _s , the system experiences the peak voltage and not the r.m.s voltage as assumed by the linear theory. It is shown that such regimes are easily realizable in experiments. A similar deviation from the linear theory is seen when $\tau _{c} <\tau _{s}$ and τ _c  ≈ τ _s at large τ _f (low $\Omega$). In the former case, the system is similar to a leaky dielectric material subjected to the equivalent of the peak voltage, while in the later case, one would obtain a limiting value as predicted by the non-linear analysis under DC fields (refer Fig. 5). At intermediate values of τ _f , a smooth transition between these limiting values is seen.

Fig. 6

A comparison of k _max as a function of $\Omega /S_{2}$ between results obtained from experiments and non-linear analysis. The values of parameters used are $\epsilon _{1} = 0,\epsilon _{2} = 3,\mu _{r} = 10^{-7},\beta = 0.6$ and S ₁ = 0. The (⋯ ) lines (a) and (b) indicate results from the linear LD-PD and PD-PD theories, respectively, under DC fields. The (⋯ ) curve indicates collapse of results from the Floquet theory for the three conductivity ranges 0.073–0.16, 1.17–2.56 and 18.73–41.08. The solid line curve, the ($-\cdot -$) line curve and the ($---$) curve indicate results from the non-linear analysis for the conductivity ranges 18.73–41.08, 1.17–2.56 and 0.073–0.16, respectively, while the corresponding experimental results are indicated by the symbols •, ■ and ∗

This study is very important as EHD instabilities in viscous thin films find direct application in the field of soft lithography. The wavelength of the instability decides the pitch of the features that can be produced on a polymeric soft film, and hence, it is vital to be able to predict this value accurately. With the previous work, it is clear that this wavelength depends critically on the conductivity of the system. It is also demonstrated that the frequency of AC fields can be used to tune the wavelength of the instability to any value between those obtained in an LD or a PD material.

4 In the ‘Small Feature Size’ Limit

With the growing popularity of nanofluidics, the demand for producing sub-micron-sized features on substrates, inexpensively, is increasing. In this regard, the EHD-based soft lithography can prove to be useful as the size of the features produced using this technique can easily be controlled by varying the system parameters such as thickness of thin film, surface tension and electric field. For a given air-polymer system, there is a practical limit to which the thickness of the thin film can be decreased to obtain smaller pattern sizes. Further decrease in the pattern sizes can be obtained by increasing the electric field applied to the system. This situation violates the TFA which has been used as a simplification tool. To overcome this limitation, the LD theory without the TFA, referred to as the ‘generalized model’ (GM) in the present work, is used. A detailed study is carried out with the GM under both DC and AC fields. A comparison of the wavelength and the growth rate of the instability as obtained from the GM and the TFA is carried out. It is seen to be dependent on the ratio of the length scales in the normal and the transverse directions, denoted by δ, with a deviation in the two theories occurring when δ ∼ O(1). A parametric plot of the exact values of the validity of the theories is provided (Fig. 7).

Fig. 7

Comparison between the model with and without the thin film approximation for the case of a PD-LD system under AC fields. The values of the parameters are $\epsilon _{1} = 1,\epsilon _{2} = 3,\mu _{r} = 0,\beta = 1,\sigma _{1} = 0$ and σ ₂ = 1. The solid line represents the TFA, ($---$) denotes B = 0. 1, ($---$) with $\bigcirc$ denotes B = 0. 3, (⋯ ) denotes B = 0. 5, ($\cdot -\cdot -\cdot$) denotes B = 2, and ($\cdot -\cdot -\cdot$) with the ∗ symbol denotes B = 15. Note that the B = 2 and B = 15 curves merge with the TFA and hence are indistinguishable

5 In the Presence of Diffuse Layers of Charge

A second outcome of working with sub-micron thick fluid layers is that of an overlap of diffuse layers (DLs) of charge formed at the electrode surface and at the fluid-fluid interface. The assumption of electroneutrality made in the LD model leads to an unrealistic picture of charge being confined to the interfacial plane alone. Although valid for perfect conductors which form equipotential surfaces under electric field, this assumption is especially violated when very thin films of fluids are used. A typical DL thickness for the commonly used polymeric liquid polydimethylsiloxane is around 10–100 nm, while the thin films used in the experiments are 100–1,000 nm thick. This estimate indicates that the thickness of the DLs of charge is comparable to the length scales in the system and in certain cases the DL from the electrode surface might overlap with that formed at the interface giving rise to a different field within the fluid. In the present work, an electrokinetic model is proposed as an alternative to the EHD LD model. In this model, the Debye-Huckel approximation is used to get a linear equation for Gauss’ law of electrostatics. That is, $\nabla ^{2}\phi =\kappa ^{2}(\phi -\phi _{b})$ where ϕ is the potential, κ is the inverse Debye length, and ϕ _b is a reference potential. The wavelength of the instability is studied as a function of the scaled inverse Debye length κ which is a ratio of the thickness of the fluid to the Debye length. The key result of this work is that as κ → 0, i.e. the Debye-layer thickness is larger than the fluid thickness, the system approaches the perfect dielectric behaviour. While in the other extreme of κ ≫ 1, the system approaches the perfect conductor behaviour. A transition from PD to PC is seen with changing κ (Fig. 8).

Fig. 8

Variation of k _max as a function of the inverse Debye length κ. The dotted line indicates results obtained from the PD-PD theory, the dashed line indicated those from the PD-PC, and the solid line indicates results from the electrokinetic theory. The values of parameters used are $\epsilon _{1} = 1,\epsilon _{2} = 3,\sigma _{1} = 0,\sigma _{2} = 10^{10},\mu _{r} = 0,\beta = 1$ and B = 1

6 Summary

To summarize, through the present work, a complete understanding of the instabilities at planar fluid interfaces under electric fields is obtained. The key outcomes are listed as follows:

• The effect of alternating fields on the instability is studied in both the cases, i.e. where gravity effects are comparable to surface tension and where they are negligible.

• Using the three different timescales inherent to the present system, a comprehensive picture of the various possible wavelengths of the instability has been studied.

• Non-linear analysis which was hitherto used for qualitative understanding of the instability has been shown to possess powerful capabilities in predicting quantitatively the wavelength of the instability, in regimes where the LD theory fails.

• A parametric study of when the thin film approximation can be used and under which conditions it is violated is carried out and the alternative generalized model is used.

• The other violation of the EHD theory which occurs when one approaches a thin film limit is that of the overlap of diffuse layers of charge. This is taken into account using an electrokinetic theory.

• To conclude, three ways of obtaining a transition behaviour with the limiting extreme cases of a PD material and an LD material have been studied:

  • By changing the frequency of the applied alternating field

  • By changing the system timescales via changing the conductivity of the fluids or the applied field

  • By changing the thickness of the fluid layers

This study furthers the understanding of the interfacial EHD phenomenon while suggesting new tools for analysis and in context to applicability to technologies like soft lithography.