Harmonic Univalent Mappings and Minimal Graphs

Abstract

We survey results and open problems in harmonic maps and minimal surface theory at a level appropriate for graduate students and others interested in contributing to the existing research. After covering some basic results, several topics are covered in more detail, including the shearing technique, inner mapping radius, convolutions, the Weierstrass Representation, determining minimal surfaces via change of variables, curvature bounds, and conjugate minimal surfaces. A variety of new and standing conjectures is included throughout. Examples are worked in detail and presented visually using ComplexTool, Mathematica, and other software packages.

2.1 Introduction

In this chapter we will discuss some topics about planar harmonic mappings. These functions can be thought of as a generalization of analytic maps, and so we will first present a brief background of analytic univalent mappings. Then we will discuss harmonic mappings with an emphasis on three topics: the shearing technique, inner mapping radius, and convolutions. Finally, we will discuss the connection between planar harmonic mappings and minimal surfaces.

2.1.1 Analytic Univalent Maps

Harmonic maps naturally generalize analytic functions by relaxing the requirement of analyticity while still retaining some important features. We begin with an overview of the relevant properties of analytic functions to make clear the analogy with harmonic maps. In both cases, we focus entirely on functions which are univalent, or one-to-one, although much interesting work has been done on multivalent functions as well.

Definition 1.1

Let $F:D \subset \mathbb{C} \rightarrow \mathbb{C}$. The function $F(x,y) = u(x,y)+iv(x,y)$ is analytic if:

• F is continuous;

• u and v are real harmonic in D; and

• u and v are harmonic conjugates (that is, $u_x=v_y$ and $u_y=-v_x$).

In this context, a function $u(x,y):\mathbb{R}^2\to\mathbb{R}$ is called real harmonic if $u_{xx}+u_{yy}=0.$

While analytic functions may map from any open, connected set in general, the following theorem allows us to restrict attention to the unit disk in many cases.

Theorem 1.2 (Riemann Mapping Theorem)

Let $G \neq \mathbb{C}$ be a simply-connected domain with $a \in G$ . Then there exists a unique univalent, onto analytic function $F: G \to \mathbb{D}$ such that $F(a) = 0$ and $F'(a)> 0.$

Thus, if D is a simply-connected, proper subset of the complex plane, we may replace the function $f:D\to \mathbb{C}$ by the function $f\circ\phi: \mathbb{D} \to\mathbb{C},$ where the existence of $\phi: \mathbb{D} \to D$ is guaranteed. Therefore, in the study of univalent (one-to-one) analytic functions, we may restrict our attention to the following class of functions.

Definition 1.3

The family of analytic, normalized, and univalent functions denoted by S is

$$ S = \{F: \mathbb{D} \to \mathbb{C}\, |\, F\;\text{is analytic, univalent with}\;F(0) = 0, F'(0) = 1\}.$$

This family of functions is also known as schlicht functions. Note that $F \in S$ implies $F(z) = z + a_2z^2 + a_3z^3 + \cdots$. The following are two essential examples that will be used throughout the chapter.

Example 1.4 (The Analytic Right Half-Plane Mapping)

$$ F_h(z)=\frac z{1 - z} = \sum_{n=1}^\infty \, z^n = z + z^2 + z^3 + \cdots \in S.$$

Example 1.5 (The Koebe Function)

$$ F_k(z) = \frac z{(1 - z)^2}= \sum_{n=1}^\infty \, nz^n = z + 2z^2 + 3z^3 + \cdots \in S.$$

Observe that F _k maps to the entire complex plane minus a slit from $-1/4$ to ∞ (Fig. 2.1).

Fig. 2.1

The image of $\mathbb{D}$ under $F_k(z)=\tfrac{z}{(1-z)^2} \in S$

Some important properties of the family S include

• The uniqueness condition in the Riemann Mapping Theorem.

• (de Branges’ Theorem) For $F \in S$, $|a_n| \le n$, for all n.

• (Koebe $\tfrac 14$-Theorem) If $F \in S$, then $F(\mathbb{D})$ contains the disk $G = \{w: |w| < \tfrac 14\}$.

See [14] for more background in univalent analytic functions.

2.1.2 Harmonic Univalent Maps

Complex-valued harmonic functions are a generalization of the analytic functions in which one of the requirements is relaxed.

Definition 1.6

Let $f:D \subset \mathbb{C} \rightarrow \mathbb{C}$. The function $f(x,y) = u(x,y)+iv(x,y)$ is a (complex-valued) harmonic function if:

• f is continuous; and

• u and v are real harmonic in D.

This definition views harmonic functions as being composed of real and imaginary parts. If D is simply-connected, we have a more useful characterization ([3]).

Theorem 1.7

If $f=u+iv$ is harmonic in a simply-connected domain G , then $f=h+\overline{g}$ , where h and g are analytic.

Note that $f=h+{~\overline{g}}$ is equivalent to $f={\mathrm{Re}} \{h+g\} + i {\mathrm{Im}} \{h-g\}$. Also, one consequence of this theorem is that a harmonic function f is represented by a power series of the form

$$ f(z)=h(z)+\overline{g(z)}={\displaystyle \sum_{{n}={0}}^{\infty}}a_nz^n+{\displaystyle \sum_{{n}={1}}^{\infty}} b_n \overline{z}^n.$$

In particular, every harmonic function with domain $\mathbb{D}$ is just the sum of analytic and coanalytic parts, represented by h and g, respectively. To see the geometric effect of including $\overline{g}$, we recall that an analytic map is called conformal if its derivative never vanishes. The conformal property means that intersecting curves in the domain are mapped to intersecting curves in the image, and the angle of intersection is preserved. A harmonic map is the sum of two maps, one which preserves angles, and another which reverses them. After some reflection, it should be clear that if $|h'(z_0)|>|g'(z_0)|,$ then the map is sense-preserving at z ₀, meaning that positive angles remain positive, and negative angles remain negative under the map f. Equivalently, we say that a function is sense-preserving if the left-hand side of a curve is mapped to the left-hand side of its image. The following theorem formalizes this intuition.

Theorem 1.8 (Lewy [22])

$f(z)=h(z)+\overline{g(z)}$ is locally univalent and sense-preserving if and only if $|\omega(z)|=|g'(z)/h'(z)| < 1$ , for all $z \in \mathbb{D}$ .

The function $\omega=g'/h'$ is known as the dilatation of $f=h+\overline{g}$.

Observe that in the harmonic case, terms involving $\overline{z}$ are permissible, but terms involving $z\overline{z}$ are not. Also, the graphics highlight the fact that the images of radial and circular lines intersect at right angles in the conformal case, but not in the harmonic case.

The boundary of $f_p(\mathbb{D})$ in Fig. 2.3 consists of concave arcs and the boundary of $f_h(\mathbb{D})$ in Fig. 2.5 gets mapped to just two points, $w=-\tfrac{1}{2}$ and $w=\infty$. These examples illustrate a difference between analytic and harmonic maps and an important fact about the boundary behavior of certain harmonic functions.

Theorem 1.9

Let $f=h+{~\overline{g}}$ be a sense-preserving harmonic map with dilatation $\omega=g'/h'$ . If $|\omega(z)|=1$ for almost all z in an arc γ of $\partial \mathbb{D}$ , then the image of γ under f is either a concave arc or a stationary point.

Example 1.10

In the following pages, graphs of functions are usually the image of the unit disk under the function in question. Also, many of these images have been created by the online applet ComplexTool [9] (Figs. 2.2–2.5).

Fig. 2.2

The image of $\mathbb{D}$ under F _p

Fig. 2.3

The image of $\mathbb{D}$ under f _p

Fig. 2.4

The image of $\mathbb{D}$ under F _h

Fig. 2.5

The image of $\mathbb{D}$ under f _h

Example 1.11

The uniqueness part of the Riemann mapping theorem fails in the harmonic case, since both maps, F _h and f _h , send the disk to the same right half-plane.

Open Problem 1

What is the analogue of the Riemann mapping theorem for harmonic mappings?

As a final point in this section, we note that, in analogy to S, we define the classes ${S_{ H}}$ and ${S_{ H}^{ O}}$ as follows.

• Analytic polynomial map: ${F_p(z)=z-\tfrac{1}{2}z^2}$

• Harmonic polynomial map: ${f_p(z)=z+\tfrac{1}{2}\overline{z}^2}$

• Analytic right half-plane map: ${F_h(z)=\frac{z}{1-z}}$

• Harmonic right half-plane map: ${f_h(z)={\rm Re} \left( \frac{z}{1-z}\right) + i{\rm Im} \left( \frac{z}{(1-z)^2} \right)}$

Definition 1.12

Let ${S_{ H}}$ be the family of complex-valued harmonic, univalent mappings that are normalized on the unit disk, that is,

$$\begin{aligned} {S}_{H} & =\{f:\mathbb{D}\rightarrow\mathbb{C}~|~f \;\mbox{is harmonic, univalent with} \\&\hspace{1.3in} f(0)=a_0=0, f_{z}(0)=a_1=1\}.\\{S}_{H}^{O} & =\{f\in {S}_{H}~|~f_{\overline{z}}(0)=b_1=0\}. \end{aligned}$$

Thus, $S \subset{S_{ H}^{ O}} \subset{S_{ H}}$. Other important classes include $K, {K_{ H}},$ and ${K_{ H}^{ O}},$ which are the subclasses of $S,{S_{ H}},$ and ${S_{ H}^{ O}}$ containing only the convex functions, which are exactly those whose image is a convex domain in $\mathbb{C}$.

We now introduce some major unsolved problems in the field that have obvious analogues in the theory of analytic functions. For years, the biggest problem in the theory of univalent analytic functions was the Bieberbach Conjecture, now known as DeBrange’s Theorem. Solving this problem allows us to know the sharp bounds on growth and distortion of harmonic maps, among other things. In the nonanalytic case, we have the following.

Conjecture 1 (Harmonic Bieberbach Conjecture)

Let

$$f(z) ={\displaystyle \sum_{{n}={0}}^{\infty}}a_nz^n+{\displaystyle \sum_{{n}={1}}^{\infty}} b_n \overline{z}^n \in{S_{ H}^{ O}}.$$

Then

• $|a_n| \leq \tfrac{1}{6}(n+1)(2n+1),$

• $|b_n| \leq \tfrac{1}{6}(n-1)(2n-1),$

• $\big| |a_n|-|b_n| \big| \leq n.$

Currently, the best bound is that for all functions $f \in{S_{ H}^{ O}}$, $|a_2| < 49$ ([15]). The conjecture is that $|a_2| \leq \tfrac{5}{2}$.

Open Problem 2

Prove a bound on $|a_2|$ that is lower than 49.

Recall that for analytic functions we have the Koebe $\tfrac 14$-Theorem, which expresses bounds on the distortion of the unit disk under normalized analytic maps. In the harmonic case, we have

Conjecture 2

If $f \in{S_{ H}^{ O}}$, then $f(\mathbb{D})$ contains the disk $G = \big\{w: |w| < \tfrac{1}{6} \big\}$.

Currently, the best result is that the range of $f \in{S_{ H}^{ O}}$ contains the disk $\big\{w: |w| < \tfrac{1}{16} \big\}$.

Open Problem 3

Prove that the radius can be increased to $K$ where $\tfrac{1}{16} < K \leq \tfrac{1}{6}$ .

2.2 Shearing

In their paper, Clunie and Sheil-Small introduced the shearing technique that provides a procedure for constructing harmonic maps $f=h+\overline{g}$ that are univalent. Before describing the shearing technique, we need the following definition.

Definition 2.1

A domain Ω is convex in the horizontal direction (CHD) if every line parallel to the real axis has a connected intersection with Ω.

We can now state the shearing theorem.

Theorem 2.2 (Clunie and Sheil-Small, [3])

Let $f=h+{~\overline{g}}$ be a harmonic function that is locally univalent in $\mathbb{D}$ (i.e., $|\omega(z)|<1$ for all $z \in \mathbb{D}$ ). The function $F=h-g$ is an analytic univalent mapping of $\mathbb{D}$ onto a CHD domain if and only if $f=h+{~\overline{g}}$ is a univalent mapping of $\mathbb{D}$ onto a CHD domain.

Summary of the Shearing Technique: To use the shearing technique we start with

• an analytic function F that is CHD, and

• an analytic function ω such that $|\omega(z)| < 1$ for all $z \in \mathbb{D}$.

Then we

• write F as $F=h-g$ and ω as $\omega=g'/h'$, and

• explicitly solve for h and g.

The resulting harmonic function $f=h+{~\overline{g}}$ is guaranteed to be univalent.

Notice that it is easy to reformulate Clunie and Sheil-Small’s shearing theorem for functions which are convex in other directions. In particular, consider the case of convex in the vertical direction (CVD) which we will use in this chapter.

Definition 2.3

A domain Ω is CVD if every line parallel to the imaginary axis has a connected intersection with Ω.

Theorem 2.4

Let $f=h+{~\overline{g}}$ be a harmonic function that is locally univalent in $\mathbb{D}$ (i.e., $|\omega(z)|<1$ for all $z \in \mathbb{D}$ ). The function $F=h+g$ is an analytic univalent mapping of $\mathbb{D}$ onto a CVD domain if and only if $f=h+{~\overline{g}}$ is a univalent mapping of $\mathbb{D}$ onto a CVD domain.

Example 2.5

Consider the analytic function

$$ F_p(z)=z-\tfrac{1}{2}z^2.$$

This is the analytic polynomial map F _p given in Example 1.10. It is CHD. Now choose a dilatation. We will choose

$$ \omega (z)= g'(z)/h'(z) =z.$$

Note that $|\omega (z)|<1 \forall z \in \mathbb{D}$. Next, set $h(z)-g(z)=F_p(z)=z-\tfrac{1}{2}z^2$. Taking the derivative of both sides, yields $h'(z)-g'(z)=1-z$. Since $g'(z)=z h'(z)$, we substitute $g'(z)$ into the previous equation to get $h'(z)=1$. Integrating this and normalizing it so that $h(0)=0$, yields $h(z)=z$. Because $g'(z)=zh'(z)$, we can solve for g to get $g(z)=\tfrac{1}{2}z^2$. Hence, by the Shearing Theorem

$$ f_p(z)=h(z)+{~\overline{g(z)}}=z+\tfrac{1}{2}{~\overline{z}}^2 \in{S_{ H}^{ O}}.$$

Thus, we have constructed a harmonic function f _p that is univalent and CHD. Note that this is the harmonic polynomial function f _p in Example 2.10.

Example 2.6

Consider

$$ F_k(z)=h(z)-g(z)=\frac{z}{(1-z)^2} \hspace{0.2in} \mbox{with} \hspace{0.2in} \omega(z)=z.$$

Using the same approach as above, we get

$$ f_k(z)=h(z)+{~\overline{g(z)}}={\mathrm{Re}} \bigg(\dfrac{z+\frac{1}{3}z^3}{(1-z)^3} \bigg)+i {\mathrm{Im}} \bigg(\dfrac{z}{(1-z)^2} \bigg) \in{S_{ H}^{ O}}.$$

The harmonic function f _k is a slit mapping which maps $\mathbb{D}$ onto $\mathbb{C}$ minus a slit on the negative real axis with the tip of the slit at $-\tfrac{1}{6}$. There is considerable evidence that f _k can fill a role in harmonic function theory similar to that of the Koebe function in analytic function theory , and for this reason, f _k is called the harmonic Koebe function.

To help explore how shearing affects the geometry between analytic and harmonic mappings, one can use the online applet ShearTool [9]. The image below demonstrates the functionality of this applet, which simultaneously plots both h-g and $h+{~\overline{g}}.$ (Fig. 2.6).

Fig. 2.6

The image of $\mathbb{D}$ under the $f=h+{~\overline{g}}$ is shown in the bottom right, where f is constructed from shearing $h(z)-g(z)=\tfrac{1}{2}\log \left(\tfrac{1+z}{1-z} \right)$ with $\omega (z)= -z^2$

Almost all examples of shearing have used dilatations that are finite Blaschke products. One important type of mappings that are not finite Blaschke products is a singular inner function. We give a brief description of this topic. For more details, see [21].

Definition 2.7

A bounded analytic function f is called an inner function if $|\lim_{r \rightarrow 1^-} f(re^{i\theta})|=1$ almost everywhere with respect to Lebesgue measure on $\partial \mathbb{D}$. If f has no zeros on $\mathbb{D}$, then f is called a singular inner function.

Every inner function can be expressed in the form

$$ f(z)=e^{i\alpha} B(z) {\rm exp}\Big(-\int\frac{e^{i\theta}+z}{e^{i\theta}-z} d\mu{\mbox{({\scriptsize $e^{i\theta}$})}} \Big),$$

where $\alpha, \theta \in R$, μ is a positive measure on $\partial \mathbb{D}$, and B(z) is a Blaschke product, i.e., $B(z)=e^{i\theta} \prod_{j=1}^{\infty} \left(\tfrac{z-a_j}{1-{~\overline{a_j}}z} \right)^{m_j}$, for some series of constants $|a_j|<1$ satisfying $\sum_{n=1}^\infty (1-|a_n|)<\infty$.

The function $f(z)=e^{\frac{z+1}{z-1}}$ is an example of a singular inner function. Weitsman [29] provided the following example.

Example 2.8

Shear

$$ h(z)-g(z)=\frac{z}{1-z}+\frac{1}{2} e^{\frac{z+1}{z-1}} \hspace{0.4in} \mbox{with} \hspace{0.4in} \omega(z)=e^{\frac{z+1}{z-1}}.$$

By a result by Pommenke [27], it can be shown that h-g is convex in the direction of the real axis. Shearing h-g with $\omega(z)=e^{\frac{z+1}{z-1}}$ and normalizing yields

$$ h(z)=\int \dfrac{1}{(1-z)^2} dz = \dfrac{z}{1-z}.$$

Solving for g we get

$$ g(z)=-\tfrac{1}{2} e^{\frac{z+1}{z-1}}.$$

The image given by the map is similar to the image given by the right half-plane map $\tfrac{z}{1-z}$ except that there are an infinite number of cusps (Fig. 2.7).

Fig. 2.7

Image of $\mathbb{D}$ under $f(z)=\tfrac{z}{1-z}-\tfrac{1}{2} e^{\frac{{~\overline{z}}+1}{{~\overline{z}}-1}}$

A technique to find harmonic mappings whose dilatations are singular inner functions involves using a theorem by Clunie and Sheil-Small [3].

Theorem 2.9

Let $f=h+{~\overline{g}}$ be locally univalent in $\mathbb{D}$ and suppose that $h+\epsilon g$ is convex for some $|\epsilon| \leq 1$ . Then f is univalent.

To develop the technique, we let $\epsilon=0$ in Theorem 2.9. This means that if h is analytic convex and if ω is analytic with $|\omega(z)|<1$, then $f=h+\overline{g}$ is a harmonic univalent mapping. To establish that a function f is convex, we will use the following theorem ([14]).

Theorem 2.10

Let f be analytic in $\mathbb{D}$ with $f(0)=0$ and $f'(0)=1$ . Then f is univalent and maps onto a convex domain if and only if

$$ {\mathrm{Re}} \bigg[1+ \dfrac{zf''(z)}{f'(z)} \bigg] \geq 0,\;\mbox{for all}\;z \in \mathbb{D}.$$

Example 2.11

Let

$$h(z) = z + 2\;\log\; (z + 1)\;\;{\rm{with}}\;\;\omega (z) = g'(z)/h'(z) = {e^{\frac{{z - 1}}{{z + 1}}}}.$$

Using Theorem 10, we can show that h is convex. Then solving for g we get $g(z)=(z+1)e^{(z-1)/(z+1)}$.

Hence,

$$ f(z)=h(z)+\overline{g(z)}=z+2\log(z+1)+(\overline{z}+1)e^{\tfrac{{~\overline{z}}-1}{{~\overline{z}}+1}}.$$

By Theorem 9, $f=h+{~\overline{g}}$ is univalent. The image of $\mathbb{D}$ under f is shown in Fig. 2.8.

Fig. 2.8

Image of $\mathbb{D}$ under $f(z)=h+{~\overline{g}}$ in Example 2.11

Open Problem 4

Construct examples of harmonic univalent functions whose dilatation is a singular inner function and determine properties of these functions.

2.3 Inner Mapping Radius

The analytic Koebe function F _k is an important function. It is extremal (or maximal) in several important senses. It is the function in S that gives equality for the coefficient bounds in deBranges’ Theorem. It is the function that maps the unit disk to a domain that contains the largest possible disk centered at the origin as described in the Koebe $\tfrac{1}{4}$-Theorem. It is the function that exhibits both the largest and smallest possible growth possible. It is the function for which the complement of its image is closest to the origin. It is conjectured that the harmonic Koebe function f _k from Example 2.6 has analogous properties in the class ${S_{ H}^{ O}}$ although these properties have not been proven (see Conjectures 1 and 2).

Recall that the tip of the slit of the harmonic Koebe function is at $-\tfrac{1}{6}$ while the tip of the slit for the analytic Koebe function is at $-\tfrac{1}{4}$. Notice that if we multiply the analytic Koebe function by $\tfrac{2}{3}$, then the images of the unit disk under $\tfrac{2}{3}F_k$ and under f _k , the harmonic Koebe function, would be the same. That is,

$$\tfrac{2}{3} F_k(\mathbb{D})=f_k(\mathbb{D}).$$

This multiplier factor of $\tfrac{2}{3}$ is known as the inner mapping radius for $f_k(\mathbb{D})$. For other functions in ${S_{ H}^{ O}}$, the inner mapping radius may be different. For example, using the analytic and harmonic versions of the right half-plane maps from Example 1.11, the inner mapping radius for $f_h(\mathbb{D})$ is 1 since $f_h(\mathbb{D})=F_h(\mathbb{D})$.

Let’s define this idea of inner mapping radius precisely.

Definition 3.1

For $f \in{S_{ H}^{ O}}$, the inner mapping radius, ${\rho_{ O}}(f)$, of the domain $f(\mathbb{D})$ is the real number $F'(0)$, where

• F is the analytic function that maps $\mathbb{D}$ onto $f(\mathbb{D})$

• $F(0)=0$

• $F'(0)>0$.

Notice that the existence of such a function F is guaranteed by the Riemann Mapping Theorem. The functions in S are normalized by requiring that $F'(0)=1$. The Riemann Mapping Theorem does not guarantee that there is a schlicht mapping to any simply-connected domain but does guarantee that we can multiply a schlicht function by some positive real number in order to map onto that domain. This positive real number is the inner mapping radius.

In the example above with the Koebe functions, $F(z)=\tfrac{2}{3}F_k(z),$ and the inner mapping radius ${\rho_{ O}}(k_0)= F'(0)=\tfrac{2}{3}$. Because of the extremal nature of the analytic Koebe function, it was conjectured that $\tfrac{2}{3} \leq{\rho_{ O}}(f) \leq 1$. This conjecture was shown not to be true in the following examples by Dorff and Suffrdge [10].

Example 3.2

This example demonstrates that the conjectured upper bound of ${\rho_{ O}}<1$ was too low. Consider the family of functions $f_{\alpha}=h+{~\overline{g}}$ constructed by shearing

$$ h(z)-g(z)=\frac{z}{1-z} \hspace{0.2in} \mbox{with} \hspace{0.2in} \omega(z) = \frac{z^2+\alpha z}{\alpha z+1},$$

where $\alpha \in \mathbb{R}$. It can be shown that if $|\alpha| \leq 1$, then $f_\alpha(z) \in{S_{ H}^{ O}}$.

Let $|\alpha| \leq 1$ and $\alpha \neq -1$, then $f_\alpha(\mathbb{D})$ is a slit domain consisting of the complex plane minus a slit along the negative real axis with the tip of the slit at $\tfrac{1}{6}\alpha -\tfrac{1}{3}$. Hence, the tip can vary from $-\tfrac{1}{6}$ to $-\tfrac{1}{2}+\epsilon$. If $\alpha = -1$, then $f_{-1}(\mathbb{D})$ is the half plane ${\mathrm{Re}} (w)> -\tfrac{1}{2}$. Thus, for this family of functions,

$$\tfrac{2}{3} \leq{\rho_{ O}}(f_\alpha) < 2.$$

Example 3.3

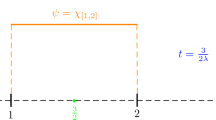
This example demonstrates that the conjectured lower bound of ${\rho_{ O}}<1$ was too high. Consider the family of functions $f_t=h+{~\overline{g}}$ constructed by shearing

$$ F_t(z)=h(z)-g(z)=\frac{z-tz^2}{(1-z)^2} \hspace{0.2in} \mbox{with} \hspace{0.2in} \omega(z) = z,$$

where $t \in [0,1]$. For $0 < t < 1$, $F_{t} (\mathbb{D})$ is the exterior of the parabola $u> - \tfrac{1 - t}{t^2} v^2 - \tfrac{t + 1}{4}$ while $f_t (\mathbb{D})$ is the exterior of the parabola $\widetilde{u}> - \tfrac{1}{t}\widetilde{v}^2 - \tfrac{1}{6} - \tfrac{t}{12}$. It can be computed that when $t=\tfrac{1}{4}$, ${\rho_{ O}}(f_t)$ is smallest, and we obtain that for $0<t<1$,

$$\tfrac{1}{2} \leq{\rho_{ O}}(f_t) \leq \tfrac{2}{3}.$$

It has been proven that

$$\tfrac{1}{4} \leq{\rho_{ O}}(f) \leq \tfrac{8 \pi \sqrt{3}}{9} < 4.837.$$

Because of the way these bounds were determined, they are probably not the tightest bounds, and it is likely they can be improved. There are no known functions in ${S_{ H}^{ O}}$ that have an inner mapping radius equal to either of these extreme values. On the other hand, from the previous two examples, we know there are specific functions that have ${\rho_{ O}}(f) =\tfrac{1}{2}$ and ${\rho_{ O}}(f) =2$. The result of ${\rho_{ O}}(f)=\tfrac{1}{2}$ in Example 3.3 was very surprising because this value did not come from a slit mapping. It is not known if there is a function in ${S_{ H}^{ O}}$ whose inner mapping radius is less than $\tfrac{1}{2}$ or larger than 2.

Open Problem 5

Prove $\tfrac{1}{2} \leq{\rho_{ O}}(f) \leq 2$ or find a harmonic map $f \in{S_{ H}^{ O}}$ such that ${\rho_{ O}}(f) < \tfrac{1}{2}$ or ${\rho_{ O}}(f)> 2$ .

The definition of the inner mapping radius can be extended to functions in ${S_{ H}}$. Let us denote the inner mapping radius of $f \in{S_{ H}}$ by $\rho(f)$. It is known that

$$0 < \rho(f) \leq 2 \pi$$

([4]). In [10] an example is constructed for which $0 < \rho(f) \leq 4$.

Open Problem 6

Prove $\rho(f) \leq 4$ or find a harmonic map $f \in{S_{ H}}$ such that $\rho(f)> 4$ .

2.4 Convolutions

The shearing technique given in Theorem 2.2 provides a way to construct harmonic functions that are univalent. This approach requires certain conditions in order to apply the technique. Convolutions is another approach to construct harmonic univalent functions. It also requires certain conditions in order to guarantee that the resulting functions are univalent. In addition, the study of convolutions is an interesting topic on its own.

The convolution of harmonic functions is a generalization of the convolution of analytic functions which is an important area in the study of schlicht functions ([28] for more information about the convolution of analytic functions). However, many of the nice theorems in the analytic case do not carry over to the harmonic case. For example, the Polya–Schoenberg conjecture which was proved by Ruscheweyh and Sheil-Small states that convexity is preserved under analytic convolution. This convexity preserving property does not hold for harmonic convolutions. But there are several open areas related to harmonic convolutions to investigate. In this section we will explore some of these. For more details about harmonic convolutions, see [6].

Let’s begin with the definition of the convolution for analytic functions.

Definition 4.1 (Analytic Convolution)

Given $F_1,F_2\in S$ represented by

$$ F_1(z)={\displaystyle \sum_{{n}={0}}^{\infty}}A_nz^n \hspace{.2in} \mbox{and} \hspace{.2in} F_2(z)={\displaystyle \sum_{{n}={0}}^{\infty}}B_nz^n,$$

their convolution is defined as

$$ F_1(z)*F_2(z)={\displaystyle \sum_{{n}={0}}^{\infty}}A_nB_nz^n.$$

As mentioned above, the analytic convolution preserves convexity since $F_1, F_2 \in K \Rightarrow F_1 * F_2 \in K$. The algebra of convolutions is also simplified by viewing certain functions as operators. For instance, $F(z)=\tfrac{z}{1-z}$ is the convolution identity because its power series is $z+z^2+z^3+\cdots$.

We define an analogous operation for harmonic functions as follows:

Definition 4.2

Given

$$\begin{aligned} f_1&=h_1+\overline{g_1}=z+{\displaystyle \sum_{{n}={2}}^{\infty}}a_nz^n+{\displaystyle \sum_{{n}={1}}^{\infty}} {~\overline{b}}_n{~\overline{z}}^n~~~\mbox{and} \\ f_2&=h_2+{~\overline{g_2}}=z+{\displaystyle \sum_{{n}={2}}^{\infty}}c_nz^n+{\displaystyle \sum_{{n}={1}}^{\infty}}{~\overline{d}}_n{~\overline{z}}^n,\end{aligned}$$

define harmonic convolution as

$$f_1*f_2=h_1*h_2 + {~\overline{g_1*g_2}}=z+{\displaystyle \sum_{{n}={2}}^{\infty}}a_nc_nz^n+{\displaystyle \sum_{{n}={1}}^{\infty}}{~\overline{b_nd_n}}{~\overline{z}}^n.$$

Harmonic convolutions involve difficulties not present in the analytic case. For instance, it is not difficult to find $f_1, f_2 \in{K_{ H}^{ O}}$ such that $f_1 * f_2 \notin{K_{ H}^{ O}}.$ In fact, $f_1 * f_2$ may even fail to be univalent. The example below illustrates this.

Example 4.3

Let $f_h=h_1+{~\overline{g}}_1 \in{K_{ H}^{ O}}$ be the harmonic right half-plane map in Example 1.11, where

$$ h_1(z) =\frac{z-\frac{1}{2}z^2}{(1-z)^2}, \hspace{.1in} g_1(z) =\frac{-\frac{1}{2}z^2}{(1-z)^2},$$

and let $f_2=h_2+{~\overline{g}}_2 \in{K_{ H}^{ O}}$ be the canonical regular 6-gon map, where

$$ h_2(z) = z+{\displaystyle \sum_{{n}={1}}^{\infty}} \tfrac{1}{6n+1}z^{6n+1}, \hspace{.1in} g_2(z) = {\displaystyle \sum_{{n}={1}}^{\infty}} \tfrac{-1}{6n-1}z^{6n-1}.$$

Then $f_h * f_2$ is not univalent, because

$$ |(g_1(z)* g_2(z))'/(h_1(z) * h_2(z))'| =|z^4(2+z^6)/(1+2z^6)|\; \nless 1, \forall z \in \mathbb{D}.$$

Open Problem 7

Let $f_1, f_2 \in{K_{ H}^{ O}}$ . Since $f_1*f_2$ is not necessarily univalent, what additional conditions can we impose upon $f_1,f_2$ so that $f_1*f_2 \in{S_{ H}^{ O}}$ ?

Several researchers have recently published results related to this question [2, 5, 12, 17, 23, 24]. Let’s look at some of these results. Theorem 4.4 ([5]) gives conditions under which local univalence of the convolution is enough to establish global univalence.

Theorem 4.4

Let $f_1=h_1+{~\overline{g}}_1, f_2=h_2+{~\overline{g}}_2 \in{S_{ H}^{ O}}$ such that $h_i(z)+g_i(z)=\tfrac{z}{1-z}$ . Let $\widetilde{\omega}$ be the dilatation of $f_1*f_2$ . If $|\widetilde{\omega} (z)|<1$ for all $z \in \mathbb{D}$ , then $f_1* f_2 \in{S_{ H}^{ O}}$ and is CHD.

Theorem 4.4 has been used to determine specific cases in which harmonic convolutions preserve univalence. In [12], the following result is proved.

Theorem 4.5

Consider the right half-plane map

$$ f_h(z)=h_1(z)+\overline{g_1(z)}=\frac{z-\frac{1}{2}z^2}{(1-z)^2}-\overline{\frac{\frac{1}{2}z^2}{(1-z)^2}},$$

and let $f=h+\overline{g} \in{K_{ H}^{ O}}$ with $h(z)+g(z)=\tfrac{z}{1-z}$ and $\omega=g'/h'=e^{i\theta}z^n (n \in{\mathbb Z}^+, \theta \in \mathbb{R})$ . If $n=1,2$ , then $f_h*f \in{S_{ H}^{ O}}$ and is CHD.

The proof of this theorem relies on properties on analytic convolutions and results about the location of zeros of symmetric polynomials. If $n>2$ in the above theorem, then $f_h*f$ fails to be univalent. In [2], we get the next theorem.

Theorem 4.6

Let $f_\theta=h_\theta+\overline{g_\theta}, f_\rho=h_\rho+\overline{g_\rho} \in{S_{ H}^{ O}}$ such that $h_\theta(z)+g_\theta(z)=h_\rho(z)+g_\rho(z)=\tfrac{z}{1-z}$ , $g' _\theta/h' _\theta = e^{i\theta}z$ , and $g' _\rho/h' _\rho=e^{i\rho}z$ ( $\theta, \rho \in \mathbb{R}$ ). Then $f_\theta * f_\rho \in{S_{ H}^{ O}}$ is CHD.

The following theorem was proved in [24]

Theorem 4.7

Let $f=h+\overline{g} \in{S_{ H}^{ O}}$ with $h(z)+g(z)=\tfrac{z}{1-z}$ and $\omega(z)=\tfrac{z+\overline{a}}{1+\overline{a}z}$ with $|a|<1$ . Then $f_h*f \in{S_{ H}^{ O}}$ and is CHD if and only if

$$\left({\mathrm{Re}} \,\text{} a \right)^2+9\left({\mathrm{Im}} \,\text{} a \right)^2\le 1.$$

There are other convolution problems that remain to be investigated. In many theorems, the canonical harmonic right half-plane function f _h is convoluted with other harmonic functions. Can similar theorems be proven if f _h is replaced with a different function? For example, consider the harmonic mapping f ₁ formed by shearing $h_1(z)+g_1(z)=\tfrac{z}{1-z}$ with other dilatations such as $\omega (z)=e^{i \theta}\tfrac{z+\overline{a}}{1+\overline{a}z}$ with $|a| < 1$ or $\omega (z)= z$.

Open Problem 8

Let $f=h+\overline{g} \in{S_{ H}^{ O}}$ with $h(z)+g(z)=\tfrac{z}{1-z}$ and $\omega=g'/h'=e^{i\theta}z^n (n \in{\mathbb Z}^+, \theta \in \mathbb{R})$ . Determine the values of $n$ for which $f_1*f$ is univalent.

Many of the harmonic convolution results, given above, require that one of the functions be a sheared half-plane. In [12] and [17], results are proven about the harmonic convolutions of strip mappings and polygons.

Open Problem 9

Determine more results about the convolutions of harmonic functions that are shears of vertical strips or polygons.

2.5 Harmonic Maps and Minimal Surfaces

Planar harmonic mappings with certain properties are related to minimal surfaces in $\mathbb{R}^3$, and it is possible to use results from one area to prove new results in the other area. Before discussing this further, we need to present some background material about minimal surfaces.

Minimal surfaces are one solution to the problem of finding the minimal surface area required to span a given curve. Minimal surfaces are guaranteed to minimize area only locally but often they provide the globally-minimal solution as well. One consequence of the area-minimizing property is that all minimal surfaces look like saddle surfaces at each point, and the bending upward in one direction is matched by the downward bending in the orthogonal direction (This equal-but-opposite bending property will be defined later as “zero mean curvature.”).

2.5.1 Background

In order to explore minimal surfaces more fully, we introduce three important concepts from differential geometry, which is the study of differentiable surfaces in space. For more details on the material from this section, [7].

A surface, $M \in \mathbb{R}^3$, can be parametrized by a smooth function $\textbf{x}:D \rightarrow \mathbb{R}^3$ if $\textbf{x}(D)=M$ and x is one-to-one. Parameterizing a surface with smooth functions allows us to do calculus with the surface and gives us a way to translate geometric concepts into rigorous analytic language. Isothermal parameterizations are essential for the study of minimal surfaces. Basically, such parametrizations map small squares to small squares. Every minimal surface in $\mathbb{R}^3$ has an isothermal parametrization.

Next, we need to discuss the idea of normal curvature. At each point p on the surface M, there is a unit normal $\textbf{n}$. The normal curvature measures how much the surface bends toward $\textbf{n}$ as you travel in the direction of the tangent vector $\textbf{w}$ at p. Specifically, given the normal vector $\textbf{n}$ at each point $p \in M$, we can find a plane ${\cal P}$ containing $\textbf{n}$ that intersects M in some curve $\textbf{c},$ which has a curvature value k. As the plane ${\cal P}$ revolves around the unit normal $\textbf{n}$ at p, we get a continuous function of curvature values $k(\theta)$. Let k ₁ and k ₂ be the maximum and minimum curvature values at p. The mean curvature of a surface M at p is $H=\tfrac{1}{2}(k_1+k_2)$.

Definition 5.1

A minimal surface is a surface M with $H=0$ at all $p \in M$.

Recall that the intuition behind vanishing mean curvature is that M is a saddle surface with positive curvature in one direction being matched by negative curvature in the orthogonal direction.

Just as the shearing theorem links analytic function theory to harmonic function theory, the Weierstrass Representation links harmonic function theory to minimal surface theory.

Theorem 5.2 (General Weierstrass Representation)

If we have analytic functions $\boldsymbol{\varphi}_k$ ( $k=1,2,3$ ) such that

• ${\phi}^2=(\varphi _1)^2+(\varphi _2)^2+(\varphi _3)^2=0$

• $|\boldsymbol{\phi}|^2 =|\varphi _1|^2+|\varphi _2|^2+|\varphi _3|^2 \neq 0$ and is finite,

then the parametrization

$$ \textbf{x} = \Big({\mathrm{Re}} \int \varphi _1(z) dz, {\mathrm{Re}} \int \varphi _2(z) dz, {\mathrm{Re}} \int \varphi _3(z) dz \Big)$$

defines a minimal surface.

We also have the following converse.

Theorem 5.3

Let M be a surface with parametrization $\textbf{x}=(x_1,x_2,x_3)$ and let $\boldsymbol{\phi} =(\varphi_1, \varphi_2, \varphi_3)$ , where $\varphi_k=\tfrac{{\partial} x_k}{{\partial} z}$.

$$ \textbf{x}\;\mbox{is isothermal} \Longleftrightarrow\boldsymbol{\phi}^2=(\varphi _1)^2+(\varphi _2)^2+(\varphi _3)^2=0.$$

If $\textbf{x}$ is isothermal, then

$$ M\;\mbox{is minimal}\;\mbox{if and only if each}\;\varphi _k\;\mbox{is analytic.}$$

We can apply the above theorems to planar harmonic mappings. First, recall $f=h+{~\overline{g}}={\mathrm{Re}} (h+g)+i{\mathrm{Im}} (h-g)$. In Theorem 5.2, choose $\varphi_1=h'+g'$ and $\varphi_2=-i(h'-g')$. Then we find $\varphi_3$ that will satisfy the requirements of the Weierstrass representation. That is,

$$\begin{aligned} 0= & (\varphi _1)^2+(\varphi _2)^2+(\varphi _3)^2 \\ = & \left(h'+g' \right)^2+\left[-i(h'-g') \right]^2 + (\phi_3)^2.\end{aligned}$$

Solving for $\varphi_3$ yields $(\varphi_3)^2= -4~h' g',$ so $\varphi_3= -2 i \sqrt{h' g'}.$

Notice that $\sqrt{h' g'}$ may not always exist as an analytic function, but whenever it does, the Weierstrass representation applies. Since $\sqrt{h' g'}=h'\sqrt{\omega},$ it is enough for the dilatation to have an analytic square root. Thus, we have the following result.

Theorem 5.4 (Weierstrass Representation - (h,g))

Let the harmonic mapping $f=h+{~\overline{g}}$ be univalent with $g'/h'$ being the square of an analytic function. Then the parametrization

$$ X=\left({\mathrm{Re}}\left(h+g\right), {\mathrm{Im}}\left(h-g\right), 2 {\mathrm{Im}}\int\sqrt{h' g'} \right)$$

defines a minimal graph whose projection is $f(\mathbb{D})$ .

MinSurfTool [9] is another applet available online that allows for quick and easy visualization of minimal surfaces (Fig. 2.9).

Fig. 2.9

The MinSurfTool applet

Example 5.5

Consider the harmonic map

$$ f(z)=h(z)+{~\overline{g(z)}}={\mathrm{Re}} \bigg[\dfrac{i}{2} \log \bigg(\dfrac{i+z}{i-z} \bigg) \bigg]+i {\mathrm{Im}} \bigg[\dfrac{1}{2} \log \bigg(\dfrac{1+z}{1-z} \bigg) \bigg].$$

It can be constructed by shearing $h(z)-g(z)=\tfrac{1}{2} \log \left(\tfrac{1+z}{1-z} \right)$ with $g'(z)/h'(z)=-z^2$ and is therefore univalent. Note that $f(\mathbb{D})$ is a square region (Fig. 2.10).

Fig. 2.10

The image of $\mathbb{D}$ under f, the harmonic square map

Since the dilatation is the square of an analytic function, we can apply Theorem 5.4. Then $x_3(z)= 2 {\mathrm{Im}} \int\sqrt{h' g'} = \tfrac{1}{2} {\mathrm{Im}} \left[i \log \left(\tfrac{1+z^2}{1-z^2} \right) \right]$.

By the Weierstrass representation, we have the parametrization of a minimal graph given by

$$\begin{aligned} \textbf{x} = & \left({\mathrm{Re}}\left(h+g\right), {\mathrm{Im}}\left(h-g\right), 2 {\mathrm{Im}}\int\sqrt{h' g'} \right) \\ =& \left({\mathrm{Re}} \bigg[\dfrac{i}{2} \log \bigg(\dfrac{i+z}{i-z} \bigg) \bigg], {\mathrm{Im}} \bigg[\dfrac{1}{2} \log \bigg(\dfrac{1+z}{1-z} \bigg) \bigg], {\mathrm{Im}} \bigg[\frac{i}{2} \log \bigg(\frac{1+z^2}{1-z^2} \bigg) \bigg] \right). \\ \end{aligned}$$

This minimal surface is Scherk’s doubly periodic surface. In Fig. 2.11 Scherk’s doubly periodic surface is shown along with the corresponding harmonic map (it is the projection of the minimal surface onto the complex plane).

Fig. 2.11

Scherk’s doubly periodic minimal surface

We might wonder if the integrals found in the Weierstrass representations are well-defined. In certain cases, they may indeed be multi-valued. But in such cases, the ill-definedness reflects the fact that surface is periodic in one or more of the coordinates, as is the case with the Scherk surfaces.

With the background we just discussed, we are ready to explore applications of harmonic maps to minimal surface theory. Our goal is to help the reader get a sense of some important techniques and to suggest some research areas.

2.5.2 Connecting Harmonic Maps to Specific Minimal Graphs

The Weierstrass Representation allows us to take an harmonic univalent function with an appropriate dilatation and lift it to a minimal graph. Several recent papers have used this technique [11, 12, 16, 18, 25, 26]. However, it is often difficult to identify the resulting minimal graphs. One approach to recognizing the minimal surface is to use a change of variable ([8]).

Example 5.6

Shearing $h(z)-g(z)=\tfrac{z}{(1-z)^2}$ with $\omega(z)=z^2$ yields the univalent harmonic slit-map

$$ f(z)=\frac{z-z^2+\frac{1}{3}z^3}{(1-z)^3}+\overline{\frac{\frac{1}{3}z^3}{(1-z)^3}}.$$

The parametrization of the corresponding minimal graph is

$$ \textbf{x}= \left({\mathrm{Re}} \left\{\frac{z-z^2+\frac{2}{3}z^3}{(1-z)^3} \right\}, {\mathrm{Im}} \left\{\frac{z}{(1-z)^2} \right\}, {\mathrm{Im}} \left\{\frac{2z^2-\frac{2}{3}z^3}{(1-z)^3} \right\} \right).$$

This is not a standard form for a known minimal surface. However, using the substitution $z \rightarrow \tfrac{\widetilde{z}+1}{\widetilde{z}-1}$ and interchanging the second and third coordinate functions, we derive the parametrization

$$\begin{aligned} \widetilde{\textbf{x}}= \left(-\tfrac{1}{4} {\mathrm{Re}} \left\{\widetilde{z}+\tfrac{1}{3} \widetilde{z}^3 \right\}, \tfrac{1}{4} {\mathrm{Im}} \left\{\widetilde{z}-\tfrac{1}{3} \widetilde{z}^3 \right\}, \tfrac{1}{4} {\mathrm{Im}} \left\{\widetilde{z}^2 \right\} \right).\end{aligned}$$

This is Ennepers surface. Thus, the original surface x is the part of Ennepers surface formed by using a right half-plane as the domain instead of the standard unit disk.

Open Problem 10

Determine the minimal graphs formed by lifting harmonic univalent mappings in any of the following papers [11, 13, 16, 25, 26].

Open Problem 11

Use the shearing technique to generate a univalent harmonic map with a dilatation that is a perfect square and use the Weierstrass representation to construct the minimal graph. Then determine what surface it is.

2.5.3 Using Harmonic Maps to Find Curvature Bounds on Minimal Graphs

Geometric function theory and Clunie and Sheil-Small’s shearing theorem allow us to find sharp bounds on growth and other important properties of harmonic maps. Using the Weierstrass representation we can translate these bounds to minimal graphs. In particular, recall that at each point p of a surface S, we let k ₁ and k ₂ be the maximum and minimum curvature values and defined the mean curvature to be $H=\tfrac{1}{2} (k_1+k_2)$. H is useful for characterizing minimal surfaces, but in other connections we use K, the Gauss curvature.

The Gaussian curvature at p is given by

$$K= k_1k_2.$$

The theorema eggregium of Gauss states that K is invariant under any deformation without stretching and is thus a good intrinsic measure of curvature. The Gaussian curvature may be put in terms of the dilatation of harmonic maps. If we denote the dilatation by $\omega(z)=g'(z)/h'(z)$, we can express the Gaussian curvature of a minimal graph with $\omega^2(z)=b(z)$ by

$$K(z)=\dfrac{-4|b'(z)|^2}{(1+|b(z)|^2)^4|h'(z)|^2}.$$

We can find a bound for K in terms of h and g. By the Schwarz–Pick lemma,

$$|b'(z)| \leq \dfrac{1-|\omega|^2}{1-|z|^2}.$$

Hence

$$|K(z)| \leq \dfrac{4}{(|g'(z)|+|h'(z)|)^2(1-|z|^2)^2}.$$

This last inequality can be used to find bounds over the origin of minimal graphs over specific planner domains. In particular,

$$|K(0)| \leq \dfrac{4}{(|h'(0)|+|g'(0)|)^2} \leq \dfrac{4}{|h'(0)|^2+|g'(0)|^2}.$$

If M is a minimal graph above the unit disk $\mathbb{D}$ and $f(0)=0$, then Hall showed that

$$|h'(0)|+|g'(0)| \geq \dfrac{27}{4\pi^2}.$$

Thus for any minimal graph above the unit disk,

$$|K(0)| \leq \dfrac{16\pi^2}{27}.$$

Several papers have considered such a situation for arbitrary points on minimal graphs over various domains. In [18], the authors considered minimal graphs over half-planes, strips, and 1-slit domains. Papers considering minimal graphs over other domains include [19, 20], and [26].

Open Problem 12

Find curvature bounds over arbitrary points for minimal graphs over domains not investigated in [18–20, 26].

2.5.4 Connecting Results About Harmonic Maps with Results About Minimal Surfaces

Since certain types of harmonic univalent functions are related to minimal graphs, it should be true that theorems and concepts from one field should relate to theorems and concepts from the other field.

One example of this concerns a harmonic convolution theorem and Krust Theorem about conjugate minimal surfaces.

Definition 5.7

Let $\textbf{x}$ and $\textbf{y}$ be isothermal parametrizations of two minimal surfaces such that their component functions are pairwise harmonic conjugates. Then, $\textbf{x}$ and $\textbf{y}$ are called conjugate minimal surfaces.

The helicoid and the catenoid are conjugate surfaces. Any two conjugate minimal surfaces can be joined through a one-parameter family of associated minimal surfaces by the equation

$$\textbf{z}=(\cos t) \textbf{x}+(\sin t) \textbf{y},$$

where $t \in \mathbb{R}$.

An important theorem in minimal surface theory is Krust Theorem.

Theorem 5.8 (Krust)

If an embedded minimal surface $X:\mathbb{D} \rightarrow \mathbb{R} ^3$ can be written as a graph over a convex domain in $\mathbb{C}$ , then all associated minimal surfaces $Z:\mathbb{D} \rightarrow \mathbb{R}^3$ are graphs.

Now consider the following less well known theorem about harmonic convolutions [3].

Theorem 5.9 (Clunie and Sheil-Small)

If $f=h+{~\overline{g}} \in{K_{ H}}$ and $\varphi \in K$ , then the functions

$$ h*\varphi +\alpha \overline{g*\varphi}$$

are univalent and close-to-convex, where $(|\alpha | \leq 1)$ and $*$ denotes harmonic convolution.

Open Problem 13

Determine theorems and properties of harmonic maps that relate to theorems and properties of minimal surfaces.

As a second example, we will prove a result about minimal surfaces using results from harmonic univalent mappings. In particular, we will consider a family of minimal surfaces known as Scherks dihedral surfaces and determine the parameter values for which these surfaces are embedded. First, some background information.

While minimal surfaces can be parametrized by the Weierstrass representation, there is no guarantee the surface will not have self-intersections. Minimal surfaces that have no self-intersections are known as embedded minimal surfaces, and they are a major interest in minimal surface theory. The family ${\cal{F}}_n(\varphi)$ of singly periodic Scherk surfaces with higher dihedral symmetry have n number of vertical planes that extend to infinity. The smallest angle, ϕ, between these symmetric planes varies (Fig. 2.12).

Fig. 2.12

Two examples from the family of Scherks dihedral surface

We can look at the projection of one piece of these surfaces onto $\mathbb{C}$ which is also the image of the unit disk under the corresponding harmonic univalent mappings (Fig. 2.13).

Fig. 2.13

The projection onto $\mathbb{C}$ of one piece from each examples in Fig. 2.13

These minimal surfaces are embedded, provided that

$$\frac{\pi}{2}-\frac{\pi}{n} < \frac{n-1}{n} \varphi < \frac{\pi}{2}.$$

We can prove this inequality using results planar harmonic mappings. We summarize the proof below.

Proof

Consider the following family of harmonic maps: $f_n(z)=h_n(z)+\overline{g_n(z)}$, $n \geq 2$, $\varphi \in [0,\tfrac{\pi}{2}]$, where

$$ h_n'(z) = \frac{1}{(z^n-e^{i\varphi})(z^n-e^{-i\varphi})}, g_n'(z) = \frac{z^{2n-2}}{(z^n-e^{i\varphi})(z^n-e^{-i\varphi})}$$

(Fig. 2.14).

Fig. 2.14

Images of the unit disk under $f=h_n+\overline{g}_n$

It is known that $f_n=h_n+\overline{g_n}$ maps $\mathbb{D}$ onto a 2n-gon, and in [25] it was shown that f _n is univalent and convex for every $\varphi \in \left(\tfrac{n}{n-1} \left(\tfrac{\pi}{2}-\tfrac{\pi}{n} \right), \tfrac{\pi}{2}\right]$. Using the Weierstrass representation, we can lift f _n to an embedded minimal surface X. Since X is over a convex domain, Krust theorem guarantees that the conjugate surfaces Y are embedded. These conjugate surfaces Y are Scherk surfaces with higher dihedral symmetry and this establishes the inequality.

Open Problem 14

Use theorems and properties about harmonic univalent mappings to prove results about minimal surfaces.

2.5.5 Using Harmonic Maps to Construct New Minimal Surfaces

In this section we show an example in which a harmonic univalent function is lifted to form a minimal graph that appears to be new. The construction is outlined below. Complete details are found in [1].

Let $f=h+{~\overline{g}}$, where

$$h\left(z\right) = \frac{1}{2} \log\left(\frac{1+z}{1-z} \right)$$

and let $\omega = \left(e^{\frac{z+1}{z-1}} \right)^2$. Since $g' = h'\omega = \tfrac{1}{1-z^2} e^{2\frac{z+1}{z-1}}$, we know that

$$g\left(z\right) = -\frac{1}{2} E_1\left(\frac{z+1}{-z+1}\right) + \frac{1}{2}E_1\left(1\right),$$

where $E_1\left(z\right)$ is the exponential integral function. By a result by Clunie and Sheil-Small, $f=h+{~\overline{g}}$ is univalent. The image of $f(\mathbb{D})$ is shown in Fig. 2.15.

Fig. 2.15

The image of $f(\mathbb{D})$ and a close up of that image

By the Weierstrass representation $f=h+{~\overline{g}}$ lifts to an embedded minimal surface (Fig. 2.16).

Fig. 2.16

Images of the minimal surface constructed from f

This surface is constructed from a harmonic univalent map that has a dilatation being a singular inner function (i.e., a function which never equals zero and which has modulus equal to one on the unit disk). One consequence of having such a dilatation is that there is no (finite) point where the function is approximately analytic. This corresponds to the idea that the minimal surface never has zero Gauss curvature. The surface also has an infinite number of cusps and a singularity with unusual behavior.

Open Problem 15

Construct other minimal surfaces from harmonic univalent maps with dilatations that are singular inner functions.

Open Problem 16

Determine the necessary and sufficient conditions for a harmonic function to have a singular inner function as its dilatation. Specifically, determine the kind of growth and boundary behavior exhibited by such harmonic functions.