Keywords

1 Introduction

With the advent of powerful digital hardware, software defined radio and radar have become an active area of research and development [1]. This in turn has given rise to many new research directions in the radar community which was previously not comprehensible. One such direction is the recently investigated multi carrier radar also called OFDM radar [2, 3].

The nature of OFDM as a communication waveform is to convey information via the phase codes applied onto the various subcarriers, which can belong to any alphabet, phase shift keying (PSK) for example [4]. After several manipulations, demodulation in the receiver eventually retrieves the transmitted phase codes and in turn, recovers the binary message. In radar, the multicarrier phase coded (MCPC) signal also assigns phase codes onto the subcarriers, however, if the constraint to convey information is not included the phase codes may be searched so that the resulting signal offers optimal radar features. Narrow main peak, low sidelobe level, low ambiguity level both in range and Doppler, are example of such features. An extensive review of the phase code strategies to optimize some of these features when a MCPC pulse is used is provided in [5, 6]. Emphasis is put on the mutual use of a train of MCPC pulses based on complementary sequences together with frequency weighting to reduce the autocorrelation sidelobe levels. These promising results also seem to impose several constraints on the number of subcarriers, symbols and pulses as the complementarity relies on cyclic shifts of one sequence in time and frequency. For applications such as netted radar, phase code strategies offering low cross-correlation properties between the pulses of the different nodes have been investigated [7]. More recently, Riché et al. investigated the possibilities offered by multicarrier signals to mitigate range ambiguities for SAR applications. Similarly, the problem consists in lowering the cross-correlation between consecutive pulses. Unlike Paichard, Riché et al. did not consider the phase codes but instead investigated the frequency content of the consecutive pulses.

Formulating other constraints such as minimizing the peak-to-envelope mean power ratio (PMEPR), minimizing the spectral leakage, etc. it is straightforward that the design of a code-based OFDM radar is a multi-objective engineering optimization problem. In this work, we use genetic algorithm (GA) to search for phase code sequences that would improve the design of MCPC pulses in terms of autocorrelation sidelobes.

There are two novelties in this paper. First of all, the use of coded MCPC pulse as a radar signal is in itself a new direction. Secondly, the use of GA to design MCPC radar pulses is also novel. We show that the GA based OFDM radar outperforms in some cases the classic Barker code based OFDM radar. The rest of the paper is organized as follows. Section 2 describes the MCPC signal considered in this work and recalls some important properties of the multicarrier signal over which the paper builds up. Section 3 discusses the phase codes generation from a GA prospect. Our objective functions are presented and the experimental setup is reviewed. In Sect. 4 our preliminary results are shown and discussed before we conclude the paper in Sect. 5.

2 Multi Carrier Phase Coded Based Radar

The use of phase codes in radar signals is not new. Likewise the well-known chirp pulse, phase coded pulses have been attractive from the early days of radar for their compression capabilities. The initial pulse length T is divided into K bits of identical duration t b  = T/K, and each bit is coded with a different phase value. Unlike communication applications that require the use of alphabets to transmit information, radar potentially support an unlimited number of K-phase code sequences. As we mentioned earlier, many criteria exist that may be used to select a specific code. In Chap. 6 [8], Levanon et al. mention the problem of finding a code that leads to a predetermined range-Doppler resolution as very complicated. For that reason, he suggests to address the problem of phase code selection with the one dimension autocorrelation function (ACF) rather than the two dimension ambiguity function (AF). Our optimization procedure described in Sect. 3 follows the same guideline.

2.1 Single Phase Coded Correlation Properties

Interestingly, when the ACF R(τ) of the single carrier phase coded pulse is considered, only few discrete samples are necessary to reconstruct the continuous function. Levanon et al. showed that in this case R(τ = it b  + η), (i is a positive integer and 0 ≤ η < t b ) given by:

$$ R(it_{b} + \eta ) = \frac{1}{{Kt_{b} }}[\eta \sum\limits_{k = 1}^{K} a_{k} a_{k - i - 1}^{*} + (t_{b} - \eta )\sum\limits_{k = 1}^{K} a_{k} a_{k - i}^{*} ] $$
(1)

is obtained by connecting, in the complex plane, the values at R(it b ) (noted R[i]) by straight lines.

$$ R(\tau ) = R(it_{b} + \eta ) = \frac{1}{{Kt_{b} }}[(t_{b} - \eta )R[i] + \eta R[i + 1]] $$
(2)

In Eq. (1) we defined the phase codes a k as zero for illegal values of k (i.e., k > K or k < 1). Note also that the pulse has been normalized by its length Kt b so that it exhibits unit energy. One consequence of this observation is that the following optimization problem of finding the phase codes that produce minimum side lobes or minimum area under R(τ) reduces to finding the phase codes that produce minimum value of either |R(it b )| ∀i or \(\sum\nolimits_{i=1}^{K-1}|R\left(it_{b}\right)|\). Chapter 6 in [8] elaborates further on the many codes that prove to offer these optimal autocorrelation properties.

2.2 Multi Carrier Phase Coded Correlation Properties

Unlike the single carrier case, the multicarrier pulse no longer offers a simple expression for the ACF R(τ). When the MCPC pulse is defined by:

$$ u(t) = \sum\limits_{n = 1}^{N} \sum\limits_{k = 1}^{K} \omega_{n} a_{n,k} r_{k} (t) \cdot exp(j2\pi n\Delta ft) $$
(3)

Levanon et al. have shown [8] in Chap. 11 that R(τ) can be expressed as:

$$\begin{aligned} |R(it_{b} + \eta )| &= | \sum\limits_{k = 1}^{N} exp(j2\pi k\frac{\eta }{{t_{b} }}) \times \sum\limits_{n = 1}^{N} \omega_{n} \omega_{k}^{*}\\ &\;\;\;\;\times [I_{1} \sum\limits_{k = 1}^{K} a_{n,k} a_{k,k - i - 1}^{*} + I_{2} \sum\limits_{k = 1}^{K} a_{n,k} a_{k,k - i}^{*} ]| \end{aligned}$$
(4)

As expressed in Eq. (3), our MCPC pulse is composed of N subcarriers equally spaced by Δf = 1/t b . Each subcarrier is weighted by ω n and is assigned the phase code a n,k where the index k denotes the symbol number ranging from 1 to K. The function r k (t) refers to the rectangular window of each of the K symbols:

$$ r_{k} (t) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad kt_{b} \le t \le (k + 1)t_{b} } \hfill \\ 0 \hfill & {\quad {\rm{elsewhere}}} \hfill \\ \end{array} } \right. $$

In Eq. (4), I 1 and I 2 are given by \( I_{1} = \eta \cdot sinc(\beta ) \cdot exp(j) \) where \( \beta = \pi (n - k)\frac{\eta }{{t_{b} }} \) and I 2 = t b δ(n − k) − I 1, [8]. When N = 1 it is easy to realize that Eq. (4) reduces to Eq. (1) except for the normalization factor, since the multicarrier pulse has not been normalized.

First null of the autocorrelation Irrespectively of the phase codes, the width of the main peak can be computed when \( \eta /t_{b} { \ll }1 \) and i = 0. Because \( I_{1} { \sim }\eta \) and \( I_{2} { \sim }t_{b} \delta (n - k) - \eta \), and assuming the weights ω n  = 1 (this assumption is of no harm for the global behaviour of the ACF), then:

$$ \begin{aligned} & |R(\eta )|\;{ \simeq }\;Mt_{b} |\sum\limits_{k = 1}^{N} exp(j2\pi k\frac{\eta }{{t_{b} }})| \\ &\; { \simeq }\;Mt_{b} |exp(j\pi (N + 1)\frac{\eta }{{t_{b} }}) \times \frac{{sin(\pi N\frac{\eta }{{t_{b} }})}}{{sin(\pi \frac{\eta }{{t_{b} }})}}| \\ \end{aligned} $$
(5)

From the second part of the expression one sees that the first null happens for η = t b /N. Of course, the larger N the better the approximation. This result will be used in Sect. 3. Note that this expression can be rearranged into δτ = 1/B where δτ is the Rayleigh resolution and B the full signal bandwidth.

Identical sequences After all efforts spent in searching for optimal phase codes in the single carrier case, early investigations with multicarrier waveforms naturally started from those existing results. One way to design the multicarrier pulse referred to identical sequence (IS) phase coding has been to apply a certain sequence repetitively onto all N subcarriers. As a result of this design strategy, the discrete ACF of the multicarrier signal becomes a scaled version of the discrete ACF of the single carrier signal when the discrete samples are taken at integer numbers of the symbol duration. Recall Eq. (4) to realize that both continuous ACFs are no more scaled version of one another. This method has the advantage that it gives a closed form expression to these discrete values but obviously ignores the behaviour of the ACF in between. However, as we mentioned previously, the multicarrier signal faces another severe constraint, namely the PEMPR. Because the IS strategy has proven to be a good solution in terms of PMEPR when the design of the pulse is complemented by a phasing technique, IS coding has been proposed in many cases [9] despite the little control on the resulting ACF.

3 GA Based Code Generation

In this section, we present our experiments to find optimal sequences for the multicarrier radar waveform, which we discussed in the previous section, when GA is the optimization process.

3.1 Objective Functions

As introduced earlier, our objective is to find an optimal coding sequence that will give us the least amount of sidelobes in the ACF. The two criteria that we use in our work are the peak sidelobe level ratio (PSLR) and the integrated sidelobe level ratio (ISLR). Both shall be set as low as possible. Accordingly, we define the following objective functions based on which we run our GA.

$$ PSLR = \frac{{\mathop { \hbox{max} }\limits_{k} |R[k]|}}{|R[0]|}\quad \quad ISLR = \frac{{\mathop {\sum }\limits_{k} |R[k]|}}{|R[0]|} $$
(6)

where we have R[0] = 1 because we normalize the ACF with respect to the main peak value before considering the ratios. R[k] refer to the values of the autocorrelation as defined in Eq. (4), taken outside the mainlobe. Note however that they are not as in Eq. (2) taken at integer number of the symbol duration but rather at consecutive samples of the oversampled ACF. For example, if the oversampling rate is N os , the time span between R[k] and R[k + 1] is t b /(N · N os ). Note that the orthogonality property of the MCPC pulse imposes a critical sampling period t s  = t b /N. Recall that the first null occurs around t b /N, hence the mainlobe of the ACF is assumed to be spanning over 2 · N os samples. Lastly, we must emphasize the fact that in this work, both objectives are investigated separately and not together. As a matter of fact, our GA optimization consists in single objective optimization.

3.2 Experimental Setup

GA procedure The execution of the genetic algorithm implemented in this work is a two-stage process. Goldberg defined this class of genetic algorithms as simple genetic algorithms (SGA) [10]. It starts with the current population, composed of L subjects. In our case, one subject is a set of N × K phase codes [a n,k ] n,k as defined in Eq. (3). In the next step, the fitness of all L subjects is assessed upon either of the two objectives given in Eq. (7). Selection is then applied. The best subject is selected twice while the weakest subject is not selected. Like this we build the intermediate population. Thereafter we randomly form pairs out of this intermediate population making sure that all pairs are composed of different elements. The next step is called recombination. Each pair produces two offsprings based on random one-point crossover. Lastly, mutation is applied in an alternate fashion. Every two generations, few elements (in our simulation we use 5) would be randomly chosen and for each element one random bit would be flipped. The condition to end the iterative optimization is based on the mean value of either fitness functions over the entire population reaching a certain threshold we would define in comparison with the results obtained with the Barker based IS MCPC pulse. Our termination condition also includes a convergence criterion on all elements of the population. Said differently, the variance of the fitness of all elements shall be small, meaning that the algorithm has reached an optimal value.

Problem encoding The first step in the implementation of any genetic algorithm is to generate an initial population. Following the canonical genetic algorithm guideline [10], this implies encoding each element of the population into a binary string. In our case, we simply encode one phase code (value between 0 and 2π) into a string of q genes and stack the N · K strings of q genes each into a larger string that we call chromosome, which is then made up of Q = N · K · q genes. This chromosome constitutes one element of the population. The larger q, the finer the resolution. In our experiments, we consider the largest value authorized by Matlab that is q = 18. The resolution is \( \Delta \theta = 2\pi /2^{q} \,{ \simeq }\,0.024 \)mrad. With the values of N and K that we consider in this paper, the size of the chromosome can be as large as 900, (N = 10 and K = 5). The search space \( {\mathcal{S}} \) “reduces” to the binary strings of length Q. Note that in case the range of authorized phase values is restrained by whatever design constrain, Q may decrease together with the search space dimension.

Population size To understand what the population size L shall be, we followed the guideline given in [11]. The starting point is to say that every point in the search space shall be reachable from the initial population by crossover only. This can happen only if there is at least one instance of every gene at each locus in the whole population. On the assumption that every gene is generated with random probability (P(1) = 1/2 and P(0) = 1/2) the probability that at least one gene is present at each locus is given by:

$$ P = (1 - (1/2)^{L - 1} )^{Q} $$
(7)

In the two cases that we investigated and report in 4 (K = 3, N = 3) and (K = 5, N = 10), we have respectively Q 1 = 162 and Q 2 = 900 for the chromosome size. From Eq. (8), we calculate the population size that would insure a probability of P = 99.9 %. We obtain respectively L 1 = 18.7 and L 2 = 21.2. For simplicity we consider L = 22 in our simulations.

4 Results and Discussions

We now present the results we obtained with our genetic algorithm and compare them with the Barker based IS MCPC pulse. The latter is chosen since Barker codes are well-known for their sidelobe reduction properties. When K = 3, the Barker based phase sequence is [π π 0] and when K = 5 case it is [π π π 0 π].Footnote 1 The IS strategy implies that this sequence is applied onto each of the N subcarriers through the a n,m terms. We could also have decided to apply on each subcarrier a cyclically time shifted version of the code, but for the sake of comparison between the different cases we stick to IS.

4.1 PSLR Based GA

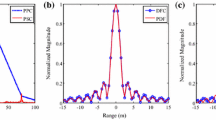
When the objective function is the PSLR, Fig. 1a, b tell that in both cases the GA converges quickly towards populations whose fitnesses are better than the Barker based IS MCPC pulse. In Figs. 1b and 2b we show the ACF of the MCPC pulse designed with phase codes resulting from our optimization. In both cases, the maximum sidelobe level outside the main lobe has been reduced by about 9 dB and 6 dB respectively. Although we did not stress this constraint in our objective function, the sidelobe level in the vicinity of the peak has been noticeably reduced. This is very valuable when high resolution is needed.

Fig. 1
figure 1

The phase codes of the MCPC pulse (N = 3, K = 3) are optimized via our PSLR based GA. a Convergence of our GA, b ACF of the MCPC pulse. In (b) the ACFs of our optimized MCPC pulse and the Barker based IS MCPC pulse are compared

Full size image
Fig. 2
figure 2

The phase codes of the MCPC pulse (N = 10, K = 5) are optimized via our PSLR based GA. a Convergence of our GA, b ACF of the MCPC pulse. In (b) the ACFs of our optimized MCPC pulse and the Barker based IS MCPC pulse are compared

Full size image

4.2 ISLR Based GA

Unlike PSLR, the ISLR of the Barker based IS MCPC pulse is rather good as it can be expected from the IS strategy. In the first case though (K = 3, N = 3), it is still possible to find optimal solutions that outperform our reference. Here, we give an example where we find an optimal solution in two steps. We start from a random initial population and converge after about 70 iterations towards an optimum (Fig. 3). We then inject four optimal elements in the initial population, complete with random elements and run again the algorithm. We observe in Fig. 4 that we converge towards optimal solutions in the vicinity of this element. This can be seen in Fig. 4b. In the other case, (K = 5, N = 10), one can guess, looking at Fig. 2b that the ISLR of the Barker based IS MCPC pulse is very low and might already be or not far from being an optimal solution. Starting from a fully random population, our algorithm slowly converged but still could not reach the Barker solution after many generations. Then, we decided to inject Barker sequences into the initial population. We started with one such sequence out of the 22 which compose the initial population. Convergence is happening but after 1800 generations we are still above the reference value. We repeated the experiment with four sequences and, as seen in Fig. 5b, our genetic algorithm quickly converged towards the Barker solution. Our findings are altogether summarized in Table 1.

Fig. 3
figure 3

The phase codes of the MCPC pulse (N = 3, K = 3) are optimized via our ISLR based GA. a Convergence of our GA, b ACF of the MCPC pulse. In (b) the ACFs of our optimized MCPC pulse and the Barker based IS MCPC pulse are compared

Full size image
Fig. 4
figure 4

The phase codes of the MCPC pulse (N = 3, K = 3) are optimized via our ISLR based GA. In the initial population we injected 4 good elements obtained in the previous search. a Convergence of our GA, b ACF of the MCPC pulse. In (b) the ACFs of our optimized MCPC pulse is compared to the MCPC pulse built from the initial good element

Full size image
Fig. 5
figure 5

a Convergence of our GA, b Convergence of our GA. In (a) one Barker based IS is injected in the initial population while in (b) four Barker based IS are injected in the initial population

Full size image
Table 1 Summary of the results
Full size table

5 Conclusion

In this paper we showed how genetic algorithms can be used to optimize the design of MCPC radar pulses. Our optimization consisted of a single objective optimization based on either of the two objective functions, the peak sidelobe level ratio or the integrated sidelobe level ratio of the autocorrelation function. We have seen that GA permitted to find better phase code sequences than the Barker based identical sequences, at least in terms of the two objectives we defined, expect in one of the cases where the latter seems to be an optimal solution. In the future, we will incorporate multiple objectives in our genetic algorithm to optimize the design of the MCPC pulse further in terms of more than one criterion, for example the peak-to-mean envelop power ratio.